Alveolar bone measurement precision for phosphor-plate images

Abstract

Objectives

To demonstrate methods for determining measurement precision and to determine the precision of alveolar-bone measurements made with a vacuum-coupled, positioning device and phosphor-plate images.

Study design

Subjects were rigidly attached to the x-ray tube by means of a vacuum coupling device and custom, cross-arch, bite plates. Original and repeat radiographs (taken within minutes of each other) were obtained of the mandibular posterior teeth of 51 subjects, and cementoenamel-junction-alveolar-crest (CEJ-AC) distances were measured on both sets of images. In addition, x-ray-transmission (radiodensity) and alveolar-crest-height differences were determined by subtracting one image from the other. Image subtractions and measurements were performed twice. Based on duplicate measurements, the root-mean-square standard deviation (precision) and least-significant change (LSC) were calculated. LSC is the magnitude of change in a measurement needed to indicate that a true biological change has occurred.

Results

The LSCs were 4% for x-ray transmission, 0.49 mm for CEJ-AC distance, and 0.06 mm for crest-height 0.06 mm.

Conclusion

The LSCs for our CEJ-AC and x-ray transmission measurements are similar to what has been reported. The LSC for alveolar-crest height (determined with image subtraction) was less than 0.1 mm. Compared with findings from previous studies, this represents a highly precise measurement of alveolar crest height. The methods demonstrated for calculating LSC can be used by investigators to determine how large changes in radiographic measurements need to be before the changes can be considered (with 95% confidence) true biological changes and not noise (that is, equipment/observer error).

In this study, measurement precision is considered to be the extent to which a numerical result can be reproduced when no biological change has taken place.¹ Measurement precision is determined by performing repeated measurements on the same subjects. The limitations of using regression analysis, correlation coefficients, and intra-class correlation coefficients for assessing repeated measurements have been described.^{2, 3} Assessing precision is critical in clinical settings when diagnostic and therapeutic decisions are made--such as, when a clinician needs to know how large the difference between baseline and follow up bone-mineral-density measurements [determined with dual-energy, x-ray absorptiometry (DXA)] needs to be before it can be considered a true (real) biological change and not just noise (equipment/observer error).⁴ The International Society for Clinical Densitometry has published position papers (http://www.iscd.org/Visitors/positions/OfficialPositionsText.cfm) and a white paper on specific methods for determining measurement precision and determining how large changes in measurements must be before they can be considered biologically real.⁵ These methods have been endorsed by national and international organizations and are routinely used clinically but have not been widely adopted in oral and maxillofacial radiology.

We vacuum coupled a previously described phosphor-plate, holding device⁶ to a x-ray tube collimator and determined for this system dental-radiographic-measurement precision based on repeated measurements of duplicate radiographs made a few minutes apart. To determine measurement precision, we used methods that are endorsed by the International Society for Clinical Densitometry. We also used Bland and Altman plots to assess differences between our original and repeat radiographic measurements, discuss limitations associated with commonly-used methods for determining measurement precision, and report our alveolar-bone measurement precision.

MATERIAL AND METHODS

Subjects, clinical sites, and image acquisition

Our Health-Insurance-Portability-and-Accountability-Act compliant study was approved by the Institutional Review Boards at Washington University School of Medicine, Southern Illinois University School of Dental Medicine, and Saint Louis University Center for Advanced Dental Education. All subjects signed informed-consent documents for participation in a clinical study. At Southern Illinois University School of Dental Medicine and Saint Louis University Center for Advanced Dental Education, we enrolled 51 subjects between 11 June 2007 and 15 February 2008. Details, such as objectives and inclusion and exclusion criteria, of the clinical study (for which our alveolar-bone, measurement-precision study was a part) are presented elsewhere.⁷

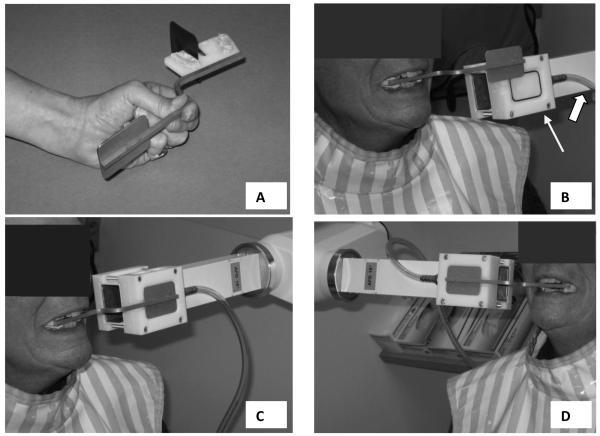
At each site, a phosphor scanner (DenOptix cephalographic phosphor systems, Dentsply International, Des Plaines, IL) was modified to produce accurate, linear responses to x-rays and moderately low noise levels.^{8, 9} Two new standard intraoral plates (BAS-SR, 30 × 40, Fuji, Tokyo, Japan) were assigned to each subject. The plates were erased for a minimum of two minutes with fluorescent light before exposure. To control the source-object-receptor alignment, a previously described device that incorporates a rigid, cross-arch bar and bite-registration material was modified for use in this study.⁶ The modification consisted of using a vacuum pump to couple the cross-arch, occlusal, registration device to the collimator on the x-ray tube head (Fig 1). The vacuum was provided with a portable vacuum pump (# S413801, Fisher Scientific, St. Louis, Missouri). The mandibular posterior teeth were radiographed because measurements from the mandibular posterior area are considered to satisfactorily represent full-mouth, bone-loss measurements.^{10, 11} Plates were exposed at 70 kVp, 7 mAs, 22 impulses at Southern Illinois University School of Dental Medicine, and 70 kVp, 7 mAs, 18 impulses at Saint Louis University Center for Advanced Dental Education. At Southern Illinois University School of Dental Medicine, 2 minutes after the right-side plate was exposed the left-side plate was exposed, and 2 minutes after the left-side plate was exposed, both plates were scanned. At Saint Louis University Center for Advanced Dental Education the time delay before scanning both plates was 4 minutes. After the plates were erased, a repeat radiograph was obtained on the left side. Because no clinically important bone change is likely to occur during the few minutes between original and repeat radiographs, differences in measurements made with original and repeat radiographs represent measurement error (that is, equipment/observer error), and this error can be used to determine measurement precision.¹ In a few instances, for which there were few teeth on the left side, the repeat radiograph was obtained on the right side. Because neither side is more difficult than the other to radiograph, no clinically or statistically significant difference in measurement precision between sides is expected.

Fig 1.

A, Plastic and stainless steel phosphor-plate, holding device with occlusal registration material on superior and inferior surfaces. B, The thin arrow points to the coupling block that is attached to the rectangular collimator. The thick arrow points to a vacuum tube. The stainless steel plate on the phosphor-plate, holding device fits into the recess on the coupling block. C and D, Phosphor-plate, holding device positioned in the subject's mouth and coupled to the coupling block for radiographing the left and right mandibular premolars and molars.

Measurements of alveolar bone

We made three types of measurements of alveolar bone: two of alveolar crest height and one of differences in x-ray transmission. For the first type of alveolar-crest-height measurement, the cemento-enamel-junction-alveolar-crest (CEJ-AC) distances were measured with ImageJ (freeware available from the National Institutes of Health, USA),¹² where possible, at the mesials and distals of the mandibular molars and premolars (Fig 2, A). High-pass filtration (<43 pixels) was used to help improve the visual definition of the crest. The CEJ-AC measurements were made on the original radiographic images and two weeks later these measurements were made on the repeated radiographic images. A two-week time interval was thought to be sufficient to prevent the observer's memory recall of landmark locations.

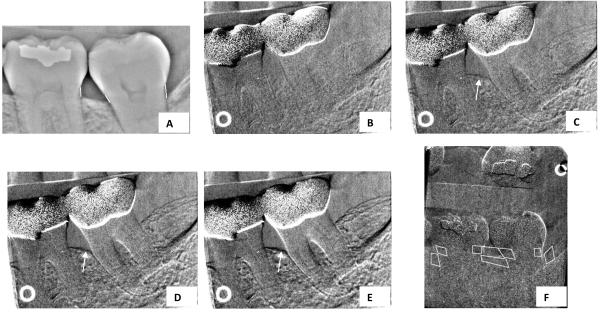
Fig 2.

A, Cemento-enamel-junction-alveolar-crest (CEJ-AC) measurements. High-pass-filtered image, features > 40 pixels removed. (High-pass image sometimes adds clarity to edge of bone.) B, Subtraction image. Simulated crest change of 0.000 mm. C, Subtraction image. Arrow points to simulated crest change of −0.042 mm. D, Subtraction image. Arrow points to simulated crest change of −0.084 mm. E, Subtraction image. Arrow points to simulated crest change of −0.127 mm. F, Regions of interest (ROIs) and reference ROIs (superimposed on tooth structure) used for transmission measurements.

For the second type of alveolar-crest-height measurement, original and repeat images were registered as previously described by minimizing trabecular noise,^{6, 13, 14} and subtraction images were measured for apparent changes in alveolar crest heights. In Fig 2, B, C, D, and E, we simulate loss of the alveolar crest. Details on how these measurements are made are presented elsewhere.⁶ One month after these measurements were made, the image registrations and measurements were repeated. This time interval was thought to be sufficient to prevent the observer's memory recall in performing subtraction and measurement procedures.

Changes in x-ray transmission (radiodensity) were measured from subtraction images, with methods previously described (Fig 2, F).⁸ A change of 0.01 unit of absorbance is equivalent to a 1% change in transmission, with the change in absorbance being proportional to change in bone mass.^{6, 8} Two months later the x-ray transmission image registrations and measurements were repeated.

Our goal was to use convenience samples (that is, samples chosen in an unstructured manner) of at least 25 subjects from the available 51 subjects to determine measurement precision for each of our 3 measurement types. No attempt was made to use the same subjects for all measurement types. For transmission measurements, the image registrations for the subtraction images were visually assessed as being good or poor. One observer (investigator, RC) made all measurements.

Statistical analyses

The statistical measures were calculated for all available data, as well as individually for different sites in the mouth. An additional subset was defined with just one measurement for each subject, for each type of measurement, with the most commonly measured sites being preferentially used.

To determine measurement precision, we calculated root-mean-square standard deviation (RMS-SD) and the 95% confidence interval for RMS-SD, as described elsewhere and in the Appendix.^{4, 15, 16} Determining the RMS-SD is preferable to determining the standard deviation of the arithmetic mean of the differences between original and repeat measurements because this latter determination underestimates the Gaussian error and results in smaller values than the RMS-SD (that is, the measurement precision appears better than it actually is, Appendix).¹⁷ The RMS-SD was used to calculate the least significant change (LSC, Appendix), which is the magnitude of change in a measurement needed to indicate that a true biological change has occurred.⁴ For our determination of LSC, we used the 95% statistical confidence level and based our calculation on one baseline measurement and one measurement made at follow-up, as would be typical in most clinical studies. We calculated RMS-SD and LSC with software available through the International Society for Clinical Densitometry (http://www.iscd.org/visitors/resources/calc.cfm).

To assess the differences between original and repeat measurements, we used Bland and Altman plots, which are the differences plotted against the averages of measurement pairs.³ For these plots, 95% of the differences should be less than ± two times the coefficient of repeatability.³ If the limits set by ± 2 (coefficient of repeatability) are clinically acceptable, the repeatability of the measurements is considered clinically acceptable. We also used the between and total sum of squares from a one-way analysis of variance table to calculate the intra-class correlation coefficient,¹⁸ regressed repeat measurements on original measurements, and calculated the product moment correlation coefficient (r) and the coefficient of determination (r²) to illustrate the limitations of these methods for assessing measurement precision. Bland and Altman plots and regression plots were created with and calculations performed with MedCalc Statistics for Biomedical Research Version 8.1.00 (MedCalc Software, Mariakerke, Belgium). We also used this software to calculate between and total sum of squares from oneway analysis of variance and used Excel (Microsoft Corporation, Redmond, WA) to calculate the intra-class correlation coefficients, RMS-SDs, LSCs, and coefficients of repeatability.

RESULTS

Precision CEJ-AC measurement

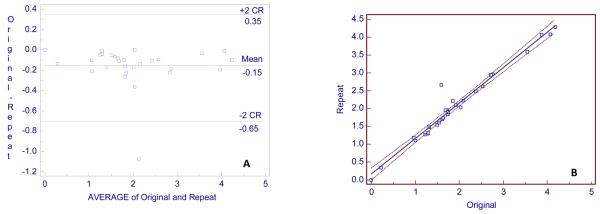
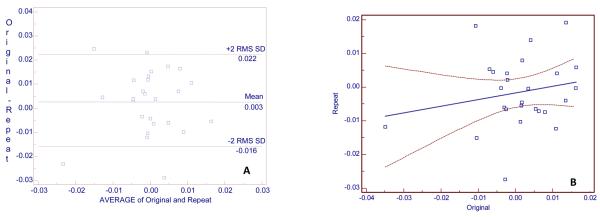
Twenty-nine subjects were used to determine CEJ-AC precision, and 13 of these subjects were also used for crest-change and transmission measurements. Seventy-eight CEJ-AC measurements were made on the original and repeat images for 29 subjects (that is, more than one CEJ-AC measurement was made for each subject). The median number of measurements per subject was 3 (1-6, range). The locations of the measurement sites are given in Table 1. The median number of measurements per site was 3. RMS-SD and LSC were calculated for all 78 measurements, for sites with ≥ 9 measurements, and for one measurement for each of the subjects. The best precision (RMS-SD = 0.11 mm) was for 9 measurements made at the mesial of tooth # 19 (mandibular left first molar) and the worst precision (RMS-SD = 0.70 mm) was for 12 measurements made at the mesial of tooth number 18 (mandibular left second molar, Table 2). The large RMS-SD in this instance is due to a single outlier point caused by an indistinctly-defined alveolar crest. For all 78 measurements for 29 subjects, the RMS-SD was 0.17 mm with a LSC of 0.48 mm, which is almost the same as the precision for the 29 measurements (one measurement per subject of the most commonly made measurements) for 29 subjects (RMS-SD = 0.18 mm with a LSC of 0.49 mm). The Bland and Altman plot for these 29 measurements is presented in Fig. 3, A. Repeat measurements were longer on average by 0.15 mm than original measurements, with repeat measurements having been made at least 2 weeks after original measurements.. The coefficient of repeatability was 0.5 mm; so 95% of the differences would lie between 0.35 and −0.65 mm. If for the 29 measurements for 29 subjects, the measurement difference >1 mm were deleted, the RMS SD would be 0.11, with a LSC of 0.29 mm, a bias of −0.12 mm, and 95% of the differences would lie between 0.10 and −0.34 mm. Fig. 3, B is the regression of repeat on original measurements, for which the correlation (r) is 0.96. The outlier in Fig. 3, A and B is the measurement at the mesial of the left second molar with > 1 mm difference between the original and repeat measurements. The intra-class correlation coefficient was 0.99.

Table 1.

Locations and numbers of sites for cementoenamel-alveolar crest (CEJAC), crest-change, and X-ray transmission measurements.

Site	CEJAC	Crest change	X-ray transmission
17 Mesial*	2
17-18		5	4
18 Distal	9
18		3	3
18 Mesial	12
18-19		24	20
19 Distal	11
19		4	3
19 Mesial	9
19-20		20	20
20 Distal	13
20		1	1
20 Mesial	12
20-21		10	6
21 Distal	3
28 Distal	1
29 Distal	2
29 Mesial	1
31 Mesial	2
32 Mesial	1
Total	78	67	57

^*Tooth numbering: teeth are numbered from #1 (maxillary right 3^rd molar) to #16 (maxillary left 3^rd molar) and from #17 (mandibular left 3^rd molar) to #32 (mandibular right 3^rd molar)

Table 2.

Measurement precision for cement-enamel junction (CEJ-AC) distance measurements.

	*n	RMS-SD (95% CI)	LSC
CEJ-AC distance
78 measurements for 29 subjects	78	0.17 (0.15–0.21)	0.48
9 measurements for 18D	9	0.12 (0.08–0.22)	0.32
12 measurements for 18M	12	0.25 (0.17–0.40)	0.70
11 measurements for 19D	11	0.19 (0.12–0.30)	0.51
9 measurements for 19M	9	0.11 (0.08–0.21)	0.31
13 measurements for area 20D	13	0.14 (0.10–0.24)	0.40
12 measurements for area 20M	12	0.17 (0.12–0.30)	0.48
29 measurements for 29 subjects	29	0.18 (0.14–0.24)	0.49

^*n = number; RMS-SD, root mean square standard deviation; LSC, least significant change

Fig. 3.

A, Bland and Altman plot for 29 CEJAC original and 29 repeat measurements (in mm) for 29 subjects. The y axis is the difference between original and repeat measurements and the x axis is the average of original and repeat measurements. B, Regression plot, with 95% confidence intervals, of repeat on original measurements. Regression equation: Repeat measurement =0.1696 +0.9921 original measurement (units = mm). R² = 0.96, r = 0.98 (95% confidence interval, 0.96 to 0.99). CR = coefficient of repeatability.

Precision crest-height measurement

Subtraction images were made from the original and repeat images for 27 subjects. Twenty-one of these subjects were also used for transmission measurements. Sixty-seven crest-height measurements were made with the subtraction images (that is, multiple, crest-heights were measured for each subject). The median number of measurements per subject was 3 (1-4, range). The locations of the measurement sites are given in Table 1 and the precision of the measurements are given in Table 3. For the various data subsets, the RMS-SD varied between 0.02 mm and 0.03 mm, and the LSC values varied between 0.06 mm and 0.09 mm. The Bland and Altman plot for these 27 measurements for 27 subjects is presented in Fig. 4, A. The measurements have a small bias: repeat measurements were longer on average by 0.01 mm than original measurements. The coefficient of repeatability was 0.04 mm; so 95% of the differences would lie between 0.03 and −0.05 mm. Fig. 4, B is the regression of repeat on original measurements, for which r = 0.62. The intra-class correlation coefficient was 0.91.

Table 3.

Measurement precision for crest-height measurements.

	*n	RMS-SD (95% CI)	LSC
Crest-height change
67 measurements for 27 subjects	67	0.03 (0.02–0.03)	0.08
24 measurements for area 18-19	24	0.03 (0.02–0.04)	0.09
20 measurements for area 19-20	20	0.02 (0.02–0.03)	0.06
27 measurements for 27 subjects	27	0.02 (0.02–0.03)	0.06

^*n = number; RMS-SD, root mean square standard deviation; LSC, least significant change

Fig. 4.

A, Bland and Altman plot of alveolar, crest-height for 27 original and 27 repeat measurements (in mm) for 27 subjects. The y axis is the difference between original and repeat measurements and the x axis is the average of original and repeat measurements. B, Regression plot, with 95% confidence intervals, of repeat on original measurements. Regression equation: Repeat measurement =0. 0.007 +0.53301 original measurement (units = mm). R² = 0.38, r = 0.62 (95% confidence interval, 0.31 to 0.81). CR = coefficient of repeatability.

Precision x-ray transmission measurement

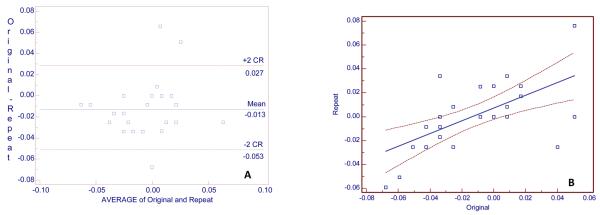
Subtraction images were made from the original and repeat images for 26 subjects. Twenty-one of these subjects were also used for alveolar, crest-height measurements. Fifty-seven measurements of x-ray transmission were made with the subtraction images (that is, multiple, transmission measurements were made for each subject). The median number of measurements per subject was 2 (1-4, range). The locations of the measurement sites are given in Table 1. The registration of images (for subtraction) was considered good for 89% (51/57) of the measurements and poor for 11% (6/57) of the measurements. RMS-SD and LSC were calculated for all 57 measurements and for the two sites with 20 measurements. We repeated these calculations for sites with good matches. The change in x-ray transmission measurements are given in Table 5. For all 57 measurements the RMS-SD was 0.012 x-ray transmission units, and the LSC was 0.034; for 26 measurements on 26 subjects the RMS-SD was 0.009 x-ray transmission units and the LSC 0.026. There was relatively little variation in precision among various sites, with the worst LSC being 0.04, which we estimate to be approximately equal to a 6% change in bone mass. The Bland and Altman plot for one measurement per subject is presented in Fig. 5, A. There is a negligible bias of 0.003 x-ray transmission units. The coefficient of repeatability was 0.019%; so 95% of the differences would lie between was 0.02 and −0.02%. Fig. 5, B is the regression of repeat on original measurements, for which r = 0.20. The intra-class correlation coefficient was 0.97.

Fig. 5.

A, Bland and Altman plot for 26 x-ray transmission original and 26 repeat measurements (absorbance units—0.01 unit = 1% transmission) for 26 subjects. The y axis is the difference between original and repeat measurements and the x axis is the average of original and repeat measurements. B, Regression of Repeat measurement on original measurement. Regression equation: Repeat measurement =0.−0.002 +0.199 original measurement (units = %). R² = 0.42, r = 0.20 (95% confidence interval, −0.20 to 0.55).

DISCUSSION

Loss in alveolar crest height is most commonly documented by measuring the radiographic distance from the cementoenamel-junction (CEJ) to the alveolar crest (AC). Although these CEJ-AC measurements provide important information on cumulative crest-height loss, there are several limitations associated with these measurements. One of these is that CEJs and ACs are often not clearly visible, especially when there are facial and lingual ACs at different levels and when the CEJs are missing or altered by caries or restorations. In addition, on radiographic images, alveolar crests are usually not anatomical, straight lines and CEJs are not anatomical points: these features represent projections of complex three-dimensional anatomy in two-dimensional images, with their radiographic positions depending strongly on subject-beam-receptor alignments. Another limitation with CEJ-AC measurements is that teeth may move over time—especially if the time periods between measurements are great, and with CEJ-AC measurements, it is difficult if not impossible to control for such movement. As a result of these limitations, in the past, the precision for CEJ-AC measurement has been relatively poor, with reported uncertainties in well-controlled studies ranging between 0.20 and 0.26 mm, with the corresponding thresholds for detecting change (least significant change, LSC) being 0.5 mm or more, and this was the case for our present study.^19-21 In our study, there was also a large systematic bias between the original and repeat CEJ-AC measurements. This bias indicates that the observer, who made the measurements, was not consistent over a period of ≥ two weeks. The bias could probably be removed by making side-by-side measurements of baseline and repeat (or recall) radiographs, as has been done by other investigators,²² but as indicated in the Bland and Altmon plot, the source of this bias needs to be addressed.

Detecting changes in alveolar crest heights with subtraction images that are registered on trabecular structures, avoids (or at least minimizes) limitations associated with CEJ-AC measurements in that trabecular architecture is reasonably stable--because of this stability, trabecular architecture is used as a forensic marker for positive identification of human remains.²³ Our data suggest that for detecting small changes in alveolar crest heights, subtraction radiography is almost an order of magnitude better than CEJ-AC measurements, with LSC values of 0.06 mm to 0.09 mm. These values are small enough that even relatively slow bone loss might be detectable in one or two years. Assuming that with subtraction radiography, a rate of loss of 0.06 mm might be detectable in one year, 10 years might be necessary before a 0.6 mm loss would be detectable with CEJ-AC measurements [that is, with our current CEJ-AC measurements, it might take about 10 years before we could be 95% confident that a true (real) loss of alveolar-crest height had occurred whereas with subtraction radiography it might take about a year before we could be 95% confident that a real loss had occurred].

The use of subtraction radiography to detect crest-height change has another advantage. At Interproximal sites (where plaque tends to accumulate), inflammatory responses to gram-negative, tooth-associated, microbial biofilms, result in the destruction of alveolar bone and the creation of interproximal craters, with cancellous bone sandwiched between ridges of facial and lingual cortical bone.²⁴ CEJ-AC measurements are typically made to the cortical-bone ridges, which do not resporb as quickly as the cancellous bone, and thus, CEJ-AC measurements usually do not measure changes in interproximal, cancellous bone. By registering images on trabecular structures below the crestal areas, small changes in interproximal, cancellous bone can be measured with image subtraction.

The LSC in x-ray transmission measurement of 4% that we determined in this study agrees with what we determined in a previous study with fewer subjects.⁶ Assuming a scatter fraction of 50% and a total mass of 1 g/cm² (as we did in our previous study), our LSC of 4% represents a 6% change in bone mass

Within dentistry, various parameters and/or definitions of measurement precision have been used to establish thresholds for changes that are considered statistically/clinically important.^25-34 As reviewed in a 1990 article and is derived in the appendix, method error (the standard deviation of the differences between original and repeat measurements divided by √2) has been used to determine thresholds of change for attachment loss and computer-aided measurements of alveolar crest height and alveolar bone mass.^{25-30, 32-36} Several measures similar to method error have been used by a group of investigators, who have worked extensively in this area.^{22, 37, 38} These investigators using 2 times the standard deviation of differences between original and repeat measurements and their impression/electronically guided alignment device (I/EGAD), determined a threshold of change of 0.52 mm for CEJ-AC measurements.²⁰ This value is similar to what these investigators had determined previously and is similar to what others (using method error and standard deviations of differences) determined for a threshold of change for CEJ-AC measurements.^{22, 34, 37-40}

In determinations of measurement precision, it has been pointed out that it is incorrect to calculate the standard deviations of the arithmetic mean of differences because this underestimates the Gaussian error (Appendix).¹⁷ This limitation is overcome by calculating the root-mean-square standard deviation (RMS-SD) and least significant change (LSC), at the 95% confidence level (Appendix).^{1, 15, 16}

The intra-class correlation coefficients that we calculated, the regression plots that we created, and the correlation analyses that we performed for our CEJ-AC and alveolar-crest measurements illustrate how misleading these procedures can be when assessing measurement precision.^{2, 3, 18, 41-43} For CEJ-AC measurements, the correlation (0.98) is much higher than is that for alveolar-crest measurements (r = 0.62), and with casual inspection, the regression line appears to have tighter confidence intervals for CEJ-AC measurements; yet the precision for CEJ-AC measurements is not as good as that for alveolar-crest measurements. The high correlation for CEJ-AC measurements compared with the correlation for alveolar-crest measurements, is largely attributable to the greater variation in CEJ-AC measurement differences compared with alveolar-crest measurement differences (that is, with alveolar-crest measurements, although the differences are small and occur over a relatively small range of values, they are large relative to one another, and thus the resulting correlation value is relatively low).¹⁸ Changing the order of the measurements used when calculating the correlation coefficient can also result in different correlations.¹⁸ This is important because ideally an indicator of measurement precision should not vary with the order of subject measurement (that is, whether or not a subject's measurements are the 1^st or 20^th measurements). The most important consideration for a clinician should be the difference between original and repeat measurements not the correlation between original and repeat measurements. The intra-class correlation coefficient (0.99) for CEJ-AC measurements is also higher than the intra-class correlation coefficient (0.91) for alveolar-crest measurements. In addition, for most people, the intra-class correlation coefficient is not easy to interpret [that is, when the number of observations is the same for each subject, the intra-class correlation coefficient equals (2 times the between sum of squares minus the total sum of squares) divided by the total sum of squares)—with the sum of squares being determined from a one-way analysis of variance].¹⁸ Problems associated with using the intra-class correlation coefficient to assess measurement precision are discussed elsewhere.²

As with alveolar-crest measurements, a number of methods have been used to determine the precision of alveolar-bone radiodensity measurements. For dual-photon absorptiometry, one investigator and her colleagues used the coefficient of variation of method error (Appendix) as a measure of precision in patients and determined a value of about 2%.^44-46 Ten years ago, this same measurement of precision was used in a comparison of manual and computer-intensive methods for radiodensity measurements.⁴⁷ The coefficients of variation for these methods were, respectively, 3.78% and 2.29%. Multiplying 2% and 2.29% by 2.77 to determine the 95% statistical confidence level for LSC, the resulting values would be 5.5% for dual-photon absorptiometry and 6.3% for the computer-intensive methods. Because these values are based on the standard deviations of arithmetic means of differences between original and repeat measurements, the Gaussian error and LSC may be underestimated.¹⁷ The coefficient of variation of 2-4% was given for ¹²⁵I absorptiometry in patients, with 5-10% given as the threshold for detecting change.⁴⁸ This would correspond to a LSC of 4-8%, but again this may be low because of the underestimation of Gaussian error. In dog maxillae, using dental radiographic images obtained at 30 kVp, repeated measures analysis of variance indicated that 7.5% decalcification could be detected.⁴⁹ In a similar study, utilizing jaw-bone samples from cadavers and phosphor plates, the threshold for detecting change in mineralization was given as 6.6%.⁵⁰ Coefficients of variation for two observers in making repeat measurements of the same images varied from 0.71 to 2.54%. These values would correspond to LSCs of 2 to 7%.

In determining precision, The International Society for Clinical Densitometry has stressed in their position papers (http://www.iscd.org/Visitors/positions/OfficialPositionsText.cfm) and a white paper that it is important that the same person make all of the measurements for a study and that each subject be serially exposed with the same equipment (that is, for a subject, serial images made with equipment from different manufacturers or different versions of the same equipment should not be used).^{5, 51} It is also important that the population and measurement site used to determine precision be representative of the population and site for which the determinations of precision will be used. Although these recommendations may be difficult to achieve in clinical studies for which sample sizes are large, they have been endorsed by various organizations (http://www.iscd.org/Visitors/positions/OfficialPositionsText.cfm). Our measurements of precision for mandibular posterior teeth would not be applicable to maxillary anterior teeth—that is, a separate measurement precision study would have to be performed for maxillary anterior teeth. It is also recommended that a sample size that results in 30 degrees of freedom be used in a precision study. This can be achieved by making original and repeat measurements on 30 subjects [that is, 2 measurements per subject − 1) × (30 subjects) = 30 degrees of freedom]. Thirty degrees of freedom assures that the upper 95% confidence limit of RMS-SD (Appendix) is not greater than 34% of the calculated value.⁵² For our study, we calculated the 95% confidence limits for RMS-SD; so we know what these limits are.

In conclusion, we used (and demonstrated) methods that have been widely indorsed for precision studies and for calculating least significant change (LSC), which is the magnitude of change in a measurement needed to indicate that a true biological change has occurred. The LSC that we determined for CEJ-AC measurements is 0.5 mm, which is the same as has been reported for CEJ-AC measurements. An important aspect of CEJ-AC measurements is that they represent cumulative past bone loss—including that caused by periodontal disease. Radiodensity measurements may also represent cumulative past alveolar bone loss, but this has not been definitively demonstrated. For our radiodensity (transmission) measurements, the LSC was 4%, which represents a change in bone mass of 6% and is similar to thresholds of change that have been reported in the past. For alveolar-crest measurements, our LSC was < 0.1 mm, which, as far as we are aware, is the smallest threshold of change for the alveolar crest that has been reported for a reasonably large sample of patients, and thus with our methods, using subtraction radiography to measure change in alveolar crest height is superior to using CEJ-AC measurements. The methods demonstrated for determining measurement precision can be used to determine how large a change needs to be in any radiographic measurement before it can be considered (with 95% confidence) a true biological change.

Table 4.

Measurement precision for X-ray transmission measurements.

	*n	RMS-SD (95% CI)	LSC
Absorbance
57 measurements for 26 subjects	57	0.01 (0.01–0.02)	0.03
51 measurements for 23 subjects with good matches	51	0.01 (0.01–0.02)	0.04
20 measurements for area 18-19	20	0.01 (0.01–0.01)	0.03
20 measurements for area 19-20	20	0.01 (0.01–0.01)	0.02
18 measurements For area 18-19 with good matches	18	0.01 (0.01–0.01)	0.03
18 measurements for area 19-20 with good matches	18	0.01 (0.01–0.01)	0.03
26 measurements for 26 subjects	26	0.01 (0.01–0.01)	0.03

^*n = number; RMS-SD, root mean square standard deviation; LSC, least significant change

APPENDIX. CALCULATIONS FOR DETERMINATIONS OF MEASUREMENT PRECISION

Calculation of root-mean-square standard deviation (RMS-SD)

RMS-SD is determined by calculating the standard deviation for each original and repeat measurement, squaring the standard deviations, summing the squared standard deviations, dividing this sum by the sample size, and taking the square root of this value, as demonstrated in the following table of arbitrarily picked values for measurements.

Case	Measurement 1 mm	Measurement 2 mm	Standard Deviation	Standard Deviation Squared
1	2	4	1.41	2.00
2	3	6	2.12	4.50
3	2	6	2.83	8.00
4	3	7	2.83	8.00
n = 4				22.50 (sum) 5.63 (sum/4) 2.37 mm (square root) = RMS-SD

Calculation of the 95% confidence interval for root-mean-square standard deviation (RMS-SD)

The asymmetric chi-square distribution is used to calculate the 95% confidence interval for RMS-SD, which is given by the following formula:¹, ²

$$\sqrt{(n-1)s^2∕{\chi }_{\alpha ∕2}^2}<\mathit{RMS}-\mathit{SD}<\sqrt{(n-1)s^2∕{\chi }_{1-\alpha ∕2}^2}$$

where s² is (RMS-SD)² and α/2 and 1−α/2 are equal to 0.025 and 0.975, which are the probabilities used for calculating the chi-square values for n − 1 degrees of freedom, where n is the number of paired measurements. These calculations were performed with Excel (Microsoft Corporation, Redmond, WA). For the above data, the sample size is 4; so the number of degrees of freedom (n − 1) is 3. The chi-square values for ${\chi }_{\alpha ∕2}^2$ and ${\chi }_{1-\alpha ∕2}^2$ for specific degrees of freedom can be determined from tables given in most statistics books of the area in the right tail of a chi-square (χ²) distribution or can be determined with a calculator at this website: http://www.fourmilab.ch/rpkp/experiments/analysis/chiCalc.html. For this example, for the lower 95% confidence interval, enter 3 degrees of freedom and the probability 0.025. For the upper 95% confidence interval, enter 3 degrees of freedom and 0.975. The resulting values are: 9.3484 and 0.2157. For the lower 95% confidence interval, the above formula becomes $\sqrt{3{(\mathit{RMS}-\mathit{SD})}^2∕9.3484}$, which reduces to $\sqrt{3{\left(2.37\right)}^2∕9.3484}=1.34\mathrm{mm}$, and for the upper 95% confidence interval, the formula is $\sqrt{3{(\mathit{RMS}-\mathit{SD})}^2∕0.2157}$, which reduces to $\sqrt{3{\left(2.37\right)}^2∕0.2157}=8.84\mathrm{mm}$; thus, the 95% confidence interval for a RMS-SD of 2.37 mm is 1.34-8.84 mm.

Calculation of standard deviation of the arithmetic mean of the differences

For this calculation, the differences between measurements are determined and the standard deviation of these differences determined. The measurement data below is the same used for the calculation of RMS-SD. Note that the standard deviation of the differences (0.96 mm) is smaller than the RMS-SD (2.37 mm) that was calculated with the same data.

Case	Measurement 1 mm	Measurement 2 mm	Difference
1	2	4	−2
2	3	6	−3
3	2	6	−4
4	3	7	−4
n = 4			0.96 (Standard deviation of differences

Calculation of the least significant change (LSC)

The following is adapted from Bone densitometry in clinical practice: application and interpretation (Bonnick SL. Totowa, N.J.: Humana Press: 2003, pp 274-275). For determining LSC for the precision value of RMS-SD, the following formula is used

$$\mathit{LSC}=z(\mathit{RMS}-\mathit{SD})\sqrt{\frac{1}{n_1}+\frac{1}{n_2},}$$

where n₁ and n₂ are the numbers of original and repeat measurements, and z is the z-score, which is the number of standard deviations from the mean of a normal distribution. The z-score can be calculated from standard normal probability distributions given in most books on statistics. There are also various websites that contain z-score calculators (http://psych-www.colorado.edu/∼mcclella/java/normal/normz.html). The z-score should be based on both tails of the normal distribution. In this example, the 95% level of statistical confidence is used; so the z-score is 1.96. In most studies, for which the goal is to detect real biological change, one measurement is made at baseline and one measurement is made at follow-up; therefore, the above equation becomes:

$$\mathit{LSC}=1.96\times (\mathit{RMS}-\mathit{SD})\sqrt{\frac{1}{1}+\frac{1}{1}},$$

which reduces to:

$$\mathit{LSC}=1.96\times (\mathit{RMS}-\mathit{SD})\sqrt{2},$$

which reduces to:

$$\mathit{LSC}=1.96\times (\mathit{RMS}-\mathit{SD})1.414,$$

which reduces to:

$$\mathit{LSC}=2.77\times (\mathit{RMS}-\mathit{SD}).$$

For our above example, the RMS-SD was 2.37 mm; therefore the LSC is 6.6 mm. If the standard deviation of the differences (0.96 mm) were used to calculate LSC, the value would be 2.8 mm.

Calculation of coefficient of repeatability and the 95% confidence interval of the arithmetic mean of the differences for Bland and Altman Plots

The coefficient of repeatability is calculated by squaring the differences between measurements 1 and 2, summing the squared differences, dividing this sum by n, and taking the square root of this value.³ The calculation is demonstrated with data from above. This calculation is specifically for measurement repeatability and is different from the calculation for the limits of agreement, which are used in comparing two methods of measurement. For our study, we used MedCalc Statistics for Biomedical Research Version 8.1.00 (MedCalc Software, Mariakerke, Belgium) to create Bland and Altman plots, but because this program calculates limits of agreement (which for this example would be −1.37 to −5.13), we used Excel (Microsoft Corporation, Redmond, WA) to calculate the coefficients of repeatability. The 95% confidence interval of the arithmetic mean of the differences is the arithmetic mean of the differences ± 2 times the coefficient of repeatability.

Case	Measurement 1 mm	Measurement 2 mm	Difference	Difference squared
1	2	4	−2	4
2	3	6	−3	9
3	2	6	−4	16
4	3	7	−4	16
n = 4			−3.25 (mean)	45 (sum)
45/4 = 11.25	$\sqrt{11.25}=-3.35$		Coefficient of Reproducibility = 2(3.35) = 6.71 mm
There is a bias in these measurements in that measurement 2 is on average 3.25 mm longer than measurement 1.
The 95% confidence interval for the mean difference between measurements 1 and 2 = −3.25 ± 6.71 = −9.96 to 3.46 mm

Calculation of method error

Method error is the standard deviation of the arithmetic mean difference between original and repeat measurements divided by √2.⁴ A derivation of method error was provided in a 1986 article on clinical measurements of periodontal disease,⁵ and the following is adapted from that article. Above it was determined that for the sample data, the standard deviation of the arithmetic mean of the differences between measurement 1 (M₁) and measurement 2 (M₂) = 0.96.

The variance of (M₁ − M₂) = variance M₁ + variance M₂ − covariance (M₁,M₂).

For repeated measurements, it is assumed that the covariance (M₁,M₂) = 0; therefore, the variance of (M₁ − M₂) = 0.96²

• = variance M₁ + variance $M_2=2M_x^2$

• = 0.92, and the error component of variance for a single measurement is $M_x^2$ (that is, 0.92/2 = 0.46 mm), and

• the standard deviation of a single measurement is $\sqrt{0.46}=0.68\mathrm{mm}$,

which is the same as method error (the standard deviation of the arithmetic mean differences between original and repeat measurements divided by √2—that is, $\frac{0.96}{\sqrt{2}}$) = 0.68 mm.

Calculation of the coefficient of variation of method error⁴

The coefficient of variation of method error is calculated in a similar fashion to the coefficient of variation in that it is 2 times method error divided by mean values for the two sets of measurements, with the resulting value multiplied by 100—as illustrated with the following data.

Case	Measurement 1 mm	Measurement 2 mm	Difference
1	2	4	−2
2	3	6	−3
3	2	6	−4
4	3	7	−4
n = 4	Mean = 2.5	mean = 5.75	standard deviation = 0.96

Method error = $\frac{0.96}{\sqrt{2}}$) = 0.68 mm, and the coefficient of variation of method error = (2(0.68))/(2.5+5.75)* 100 = 16%. This calculation is not appropriate for values such as CEJ-AC distance in that if the ability to repeat measurements remains the same, and the coefficient of variation of method error would be determined for two groups of subjects, the coefficient of variation of method error would be lower in the subjects with the greatest average CEJ-AC distance (that is, dividing method error by a larger number results in a smaller coefficient of variation of method error).