Spectroscopic and Computational Studies of (µ-Oxo)(µ-1,2-peroxo)diiron(III) Complexes of Relevance to Nonheme Diiron Oxygenase Intermediates

Abstract

With the goal of gaining insight into the structures of peroxo intermediates observed for oxygen activating nonheme diiron enzymes, a series of metastable synthetic diiron(III)-peroxo complexes with [Fe^III₂(µ-O)(µ-1,2-O₂)] cores has been characterized by X-ray absorption and resonance Raman spectroscopy. EXAFS analysis shows that this basic core structure gives rise to an Fe-Fe distance of ~3.15 Å; the distance is decreased by 0.1 Å upon introduction of an additional carboxylate bridge. In corresponding resonance Raman studies, vibrations arising from both the Fe-O-Fe and the Fe-O-O-Fe units can be observed. A change in the Fe-Fe distance affects the ν(O-O) mode, as well as the ν_sym(Fe-O-Fe) and the ν_asym(Fe-O-Fe) modes. Indeed a linear correlation can be discerned between the ν(O-O) frequency of a complex and its Fe-Fe distance among the subset of complexes with [Fe^III₂(µ-OR)(µ-1,2-O₂)] cores (R = H, alkyl, aryl, or no substituent). These experimental studies are complemented by a normal coordinate analysis and DFT calculations.

Introduction

Nonheme diiron centers have been found in the active sites of a number of metalloenzymes involved in oxygen activation.^1,2 These enzymes have diverse and essential biological functions such as the hydroxylation of methane in methane monooxygenase (MMO) and of toluene in toluene 4-monooxygenase, the generation of the catalytically essential Tyr radical in Class I ribonucleotide reductases (RNR), and the desaturation of saturated fatty acids in fatty acid desaturases. In the course of oxygen activation, O₂ binds to the diiron(II) center to form a peroxodiiron(III) intermediate, which in turn undergoes O-O bond cleavage to form high-valent intermediates, such as the diiron(IV) intermediate Q of MMO^3–5 and the diiron(III,IV) intermediate X of RNR.^6,7 Of great interest is the nature of the diiron(III)-peroxo intermediates generated by these enzymes, which to date has not been established. These intermediates have been found to exhibit a range of ν(O-O) frequencies (898 cm⁻¹ for stearoyl-acyl carrier protein Δ⁹-desaturase,⁸ 870 cm⁻¹ for RNR W48F/D84E-R2,⁹ and 851 cm⁻¹ for frog ferritin¹⁰). Developing a rationale for the different frequencies would be helpful in deducing the structures of the corresponding intermediates.

Biomimetic complexes can contribute significantly to our understanding of such transient species. Indeed there are now five reported crystal structures of (µ-peroxo)diiron(III) complexes, all with 1,2-peroxo bridges.^11–14 In these structures, the Fe-O-O-Fe units are supported by additional bridging ligands such as oxo, hydroxo, alkoxo, and/or carboxylato bridges. This study focuses on complexes with the (µ-oxo)(µ-1,2-peroxo)diiron(III) core, some of which have been reported to exhibit the lowest O-O frequencies among the diiron(III)-peroxo complexes thus far.^15–17 In this paper several complexes with the (µ-oxo)(µ-1,2-peroxo)diiron(III) core are investigated in detail by resonance Raman and X-ray absorption spectroscopies. Density-functional theory (DFT) calculations are used to aid in the interpretation of the spectroscopic data.

Experimental Section

Syntheses

Commercially available chemicals were purchased and used without further purification. The diiron(III) complexes, [Fe^III₂(O)(OH)(BQPA)₂](OTf)₃, [Fe^III₂(O)(OH)(6-Me₃-TPA)₂](OTf)₃ and [Fe^III₂(O)(AcO)₂(BPPE)](ClO₄)₂, were synthesized according to published methods^17–19 (see Scheme 1 for ligand structures). Elemental analyses were performed at Atlantic Microlab, Inc. (Norcross, GA). Caution: Perchlorate salts are potentially explosive and should be handled with care!

Scheme 1.

Ligands used in this study.

Bis(2-quinolylmethyl)-6-methylpyridyl-2-methylamine. (6-Me-BQPA)

To a solution of 2-cholromethylquinoline hydrochloride (3.5 g, 15.25 mmol) in MeCN (200 mL) at 0 °C was added Na₂CO₃ (9.6 g, 92 mmol); this mixture was then heated up to 82 °C and stirred for 30 min, 2-aminomethyl-6-methylpyridine (0.9 g, 7.62 mmol) was added and the resulting mixture was refluxed. After 3 days, the mixture was cooled to room temperature and filtered to remove solid. The filtrate was evaporated to dryness under vacuum, and the crude solid was recrystallized from hexane/ether (80/20) to obtain a pale yellow powder (85 %). ¹H NMR (CDCl₃): δ (ppm) 8.12 (d, 2H), 8.05 (d, 2H), 7.74 (m, 8H), 7.5 (m, 2H), 7.01 (d, 1H), 4.12 (s, 4H), 2.52 (s, 4H).

[Fe^III₂(O)(OH)(6-Me-BQPA)₂](OTf)₃

To a solution of bis(2-quinolylmethyl)-6-methylpyridyl-2-methylamine (0.405 g, 1 mmol) and Fe(MeCN)₂(OTf)₂ (0.436 g, 1 mmol) in dry MeCN (5 mL) at −40 °C was added tert-butyl hydroperoxide in nonane (0.22 mL, 1 mmol). After the color of the solution changed to dark red, this mixture was warmed up slowly to room temperature and 20 mL dry THF was layered above the solution. After two days, red crystals were deposited out in about 60% yield. Anal. Calcd for [Fe^III₂(O)(OH)(6-Me-BQPA)₂](OTf)₃·H₂O or C₅₇H₅₁F₉Fe₂N₈O₁₂S₃ (Found): C, 48.25 (48.00); H, 3.62 (3.75); F, 12.05 (12.09); N, 7.90 (7.72); S, 6.78 (6.58).

Preparation of Fe^III₂(O)(O₂) intermediates

For the generation of intermediates 1, 2, and 3, a MeCN solution of the Fe^III₂(µ-O)(µ-OH)(L)₂ precursor was treated with 1 equiv triethylamine at −40 °C to generate the corresponding Fe^III₂(µ-O)₂ complex. To this solution was added 10 equiv H₂O₂ to produce the Fe^III₂(µ-O)(µ-1,2-O₂)(L)₂ intermediate (1, L = 6-Me-BQPA; 2, L = BQPA; 3, L = 6-Me₃-TPA). Intermediate 4 was obtained by the reaction of its diiron(III) precursor [Fe^III₂(O)(OAc)₂(BPPE)]²⁺ with 2 equiv triethylamine and 10 equiv H₂O₂ in MeCN at −40 °C. Conversions of diiron(III) precursors to corresponding peroxo intermediates were estimated to be >90% on the basis of extinction coefficients previously reported for 2,¹⁶ 3,¹⁵ and 4.¹⁷

Physical methods

¹H NMR spectra were recorded on a Varian Unity 300 spectrometer at ambient temperature. Chemical shifts (in ppm) were referenced to the residual protonic solvent peaks. UV-vis spectra were recorded on a Hewlett-Packard 8453 diode array spectrophotometer. Resonance Raman spectra were collected on an ACTON AM-506M3 monochromator with a Princeton LN/CCD data collection system using Spectra-Physics models 2060 krypton ion and 2030-15 argon ion lasers. Low-temperature spectra of peroxo intermediates in CH₃CN were obtained at 77 K using a 135° backscattering geometry. Samples were frozen onto a gold-plated copper cold finger in thermal contact with a dewar containing liquid nitrogen. Raman frequencies were referenced to the features of indene. Slits were set for a band-pass of 4 cm⁻¹ for all spectra.

XAS data collection

XAS data were collected on beamline X9B at the National Synchrotron Light Source (NSLS) of Brookhaven National Laboratory (BNL). Fe K-edge X-ray absorption spectra were recorded on frozen solutions at around 16 K over the energy range 6.9–8.0 keV as previously described.^20–22 The storage ring condition was: 2.8 GeV, 100–300 mA. The beam vertical aperture of the pre-monochromator slits was 1 mm. Contamination of higher harmonics radiation was minimized by utilizing a harmonic rejection. The horizontal spot size of the beam on the sample was 4–6 mm. Spectra were measured with 10 eV steps below the edge, 0.3 eV steps in the edge region, and steps equivalent to 0.05 Å⁻¹ increments above the edge (region borders were 6932, 7102, and 7137 eV). An iron foil spectrum was concomitantly recorded for internal energy calibration, and the first inflection point of the K-edge energy was calibrated to 7112.0 eV. The data were recorded in fluorescence excitation mode (A_exp = (C_f/C₀)) using a solid state 13 element Ge detector.

Data analysis

Standard procedures were used to analyze the XAS data. The pre-edge background intensity was eliminated by fitting a Gaussian function to the background and a three-segment spline with fourth-order polynomial components was used to remove low-frequency background.²³ The resulting spectra were then treated with SSExafs^20,24 in order to obtain near-edge XAS (XANES) parameters. The edge was modeled as an integral of a 75% Gaussian and a 25% Lorentzian peak and the heights, positions, and widths (at half height) of the Gaussian pre-edge peaks were refined to fit the data. Pre-edge peak areas are reported as percentage of the Fe K-edge height × eV and multiplied by 100.

Analysis of the EXAFS data was performed using the program EXAFSPAK.²⁵ EXAFS refinement was carried out on k³χ(k) data, using the phase and amplitude functions obtained from FEFF.²⁶ EXAFS data fittings were performed using the back-transformation ranges provided in Table 2. For each fit, the parameters r and σ² were optimized, while n was kept fixed. n was then systematically varied in integer steps. The goodness of fit (GOF) was determined using the formula: GOF = Σ (χ_calc − χ_exp)² / N, where N is the number of data points. The threshold energy (E₀) was also varied, although it was maintained at a common value for all shells.

Table 2.

EXAFS Fitting Results for Fe^III₂(µ-O)(µ-1,2-O₂) Intermediates, 1, 2 and 4.^a

		Fe-N/O			Fe-N/O			Fe-N/O			Fe⋯C			Fe⋯Fe			GOFd
complex	fit	N	r(Å)	σ2	n	r(Å)	σ2	n	r(Å)	σ2	n	r(Å)	σ2	n	r(Å)	σ2
1	1							6	2.23	4.5							416
	2	2	1.83	4.7				4	2.24	1.8							253
	3	2	1.84	6.7				4	2.25	2.4				1	3.19	3.4	246
	4	2	1.83	5.4				4	2.25	1.4	6	3.00	2.0	1	3.16	1.5	125
	5	2	1.83	4.7				3	2.24	0.9	6	3.01	2.7	1	3.16	1.8	94
	6	2	1.83	5.0				3	2.24	1.0	4	3.00	0.3	1	3.15	2.2	90
	7	2	1.83	3.7	1	2.05	1.0b	3	2.23	0.3	4	2.99	1.1	1	3.15	3.0	43
2	1							6	2.22	6.5							270
	2	2	1.85	12.0				4	2.22	3.8							173
	2	2	1.85	11.5				4	2.23					1	3.14	5.0	123
	3	2	1.84	11.1				4	2.21	4.3	6	2.99	2.1	1	3.14	1.3	35
	4	2	1.85	11.6				4	2.21	4.4	4	2.98	0.1	1	3.12	1.6	30
	5	2	1.84	12.4				3	2.21	2.8	4	2.98	0.3	1	3.12	1.8	27
	6	2	1.81	5.0b	1	2.02	1.2	3	2.20	1.8	4	2.97	0.9	1	3.12	2.6	26
	7	2	1.81	5.0b	1	2.02	1.1	3	2.20	1.7	6	2.98	2.8	1	3.13	2.1	23
	8	2	1.82	6.7	1	2.03	3.4	3	2.21	1.7	6	2.98	2.6	1	3.13	1.9	16
4	1							6	2.18	10.0b							300
	2	2	1.88	10.4				4	2.16	6.9							164
	3	2	1.88	10.5				4	2.16	6.4				1	3.06	2.20	28
	4	2	1.87	10.1				4	2.16	6.7	6	3.08	2.1				34
	5	2	1.88	10.5				4	2.17	6.5	4	3.15	13.3	1	3.06	2.69	21
	6	1	1.86	4.7				5	2.16	11.2				1	3.06	2.64	44
	7	1	1.88	5.11				4	2.16	7.8				1	3.06	2.60	34
	8	1	1.78	3.39	1	1.92	0.4	4	2.14	6.2				1	3.05	2.44	18
	9	1	1.77	5.83	2	1.94	6.5	3	2.16	3.2				1	3.04	2.32	19
	10	2	1.88	11.98	1	1.98	4.3	3	2.16	3.2				1	3.05	2.34	20
3c		2	1.84					4	2.23		6	2.96		1	3.14

^aBack-transformation range: ~ 0.50 to 3.3 Å; Fourier-transformed range: k = 2.0 – 14.5 Å⁻¹ (1 and 2), 2.0 – 14.0 Å⁻¹ (4). Resolution = ~ 0.12 Å. σ² in units of Ų. The first two shells were fit using a scatter with oxygen parameters, whereas the third employed nitrogen parameters; however, backscatters differing by Z = 1 cannot be distinguished by EXAFS.

^bσ²-value held fixed during optimization.

^cReference ¹⁵

^dGOF = goodness of fit.

DFT Calculations

Geometry optimizations of [Fe^III₂(µ-O)(µ-1,2-O₂)(6-Me₃-TPA)₂]²⁺ were performed with the Amsterdam Density Functional (ADF) 2004.01 software package^27–29 on a cluster of 10 processors (Ace computers) using ADF basis set IV (triple-ζ with single polarization on the ligand atoms), an integration constant of 4.0, and the Vosko-Wilk-Nusair local density approximation³⁰ with the nonlocal gradient corrections of Becke³¹ and Perdew.³² Antiferromagnetic coupling between the two Fe(III) centers was incorporated into the DFT calculations with the construction of broken-symmetry (BS) wavefunctions,^33–35 in which the spin-up (α) and spin-down (β) electrons were localized on Fe1 and Fe2, respectively. Although the BS state is not a pure spin state (its wavefunction is an eigenfunction of M_s, not S²), Noodleman and coworkers have demonstrated that this approach reasonably approximates the antiferromagnetic ground state and provides accurate geometries.³⁶ The Cartesian coordinates for the DFT geometry-optimized model are available in the Supporting Information (Table S1).

Normal Coordinate Analysis (NCA)

Normal coordinate calculations used a general valence force field,³⁷ and were performed using the QCPE program 576 developed by Peterson and McIntosh, which solves the vibrational secular equation GFL = λL.³⁸ For complex 1, the large size of the molecule forced us to use a smaller model that included only the [Fe₂O₃] core. Structural parameters were derived from DFT geometry optimizations. Given the idealized C_2v symmetry of the [Fe₂O₃] unit, only one force constant was used to describe the Fe-O_oxo and Fe-O_peroxo stretching motions. Additionally, a small Fe⋯Fe force constant of +0.50 mdyn/Å was included to model the nonbonded interaction between the two Fe atoms (essentially, this mode accounts for the symmetric O-Fe-O and Fe-O-Fe bending motions). Five interaction force constants were included to account for kinematic coupling between the stretching motions of the Fe-O_oxo/Fe-O_peroxo/O-O bonds, as well as between the these motions and the Fe⋯Fe stretch. These parameters were then optimized to fit the experimentally determined frequencies, although the F(Fe⋯Fe) value was fixed. The resulting force constants are summarized in the Supporting Information (Table S3).

Results and Discussion

Four metastable Fe^III₂(µ-O)(µ-1,2-O₂) complexes were generated at low temperature from the reaction of diiron(III) precursors with H₂O₂, as depicted in Scheme 2. Intermediates 1–3 have supporting tetradentate tripodal ligands, while 4 is supported by a hexadentate dinucleating ligand that provides only three ligands in a facial array per iron (Scheme 1). Thus intermediate 4 differs from the other three in having an additional carboxylate bridge that completes the distorted octahedral coordination sphere about each iron. These complexes exhibit two intense visible absorption features with maxima near 500 and 650 nm; there is also a much weaker near IR band near 800 nm for 1–3 (Figure 1). These intermediates are further characterized by X-ray absorption and resonance Raman spectroscopies in this study, and detailed analyses are presented below.

Scheme 2.

Generation of Fe^III₂(µ-O)(µ-1,2-O₂) complexes of tetradentate ligands 6-Me-BQPA (1), BQPA (2), and 6-Me₃-TPA (3) and hexadentate ligand BPPE (4) from respective diiron(III) precursors (see Scheme 1 for ligand structures). The abbreviation “py” represents a pyridine-like ligand, while “N” corresponds to a tertiary amine nitrogen on the polydentate ligand.

Figure 1.

Visible spectra of Fe^III₂(µ-O)(µ-1,2-O₂) intermediates, 1 (—), 2 (---), 3 (⋯), and 4 (-·-) collected in MeCN at −40°C.

1. XAS studies of Fe^III₂(O)(O₂) intermediates

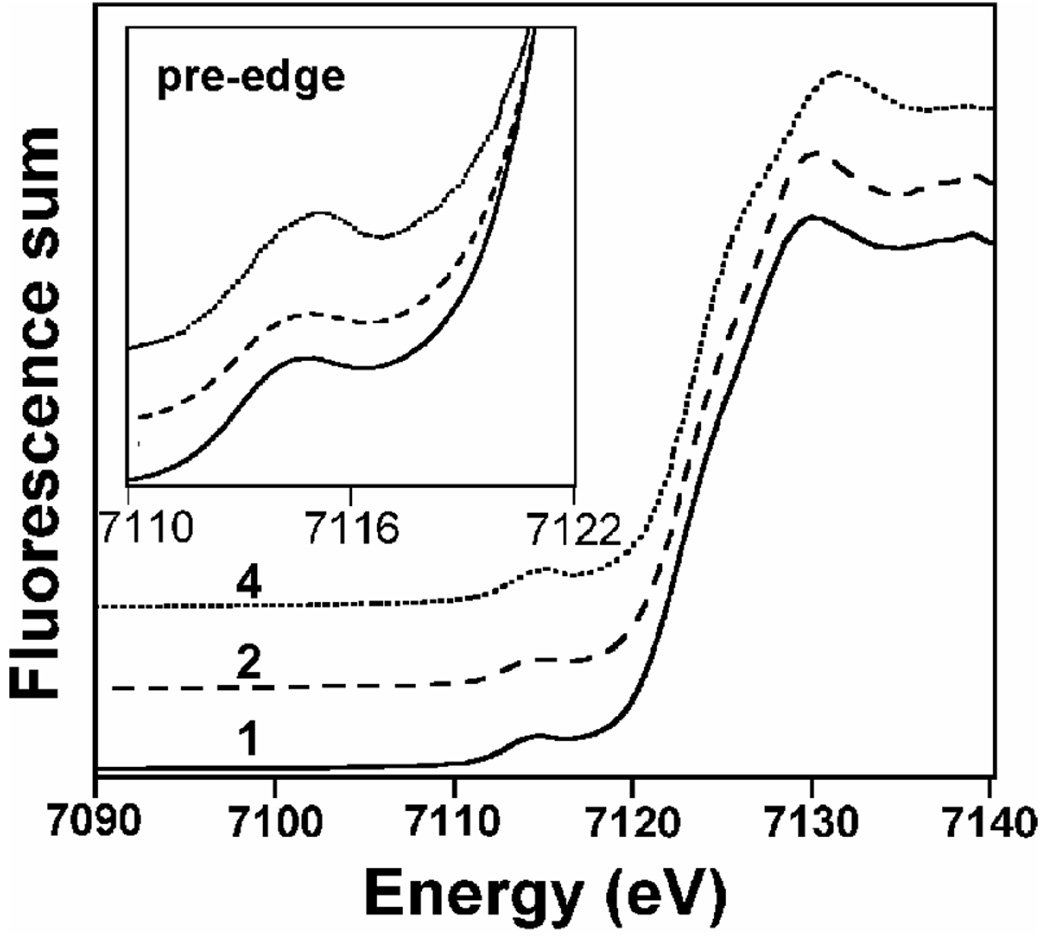
As the low thermal stability of the Fe₂(O)(O₂) intermediates made X-ray crystallography unfeasible as a method for obtaining structural information, X-ray absorption spectroscopy (XAS) was adopted as an alternative method for structural characterization of these short-lived species. X-ray absorption spectra at the Fe K-edge were measured for three Fe₂(O)(O₂) species 1, 2 and 4 (complex 3 was studied previously¹⁵) and the resulting XANES and EXAFS data are presented in Figure 2 and Figure 3, respectively. Figure 2 compares the near-edge regions of the three complexes, which provides information regarding the oxidation states and coordination environments of the metal centers. The first inflection point of the rising edge was assigned as the edge energy (E₀) associated with the transition of an electron from the Fe 1s orbital to the continuum. The values for 1, 2, and 4 are typical of iron(III) centers (Table 1). The energy of the pre-edge feature (E_preedge), at about 8–10 eV below the edge jump, corresponds to the Fe 1s→3d transitions. Interestingly, the pre-edge transition for 4 is more intense than those for 1 and 2, indicative of a larger deviation from a centrosymmetric geometry in the case of 4.

Figure 2.

Fe K-edge X-ray absorption near-edge structures (XANES, fluorescence excitation) of Fe^III₂(µ-O)(µ-1,2-O₂) intermediates, 1 (—), 2 (---), and 4 (⋯) measured at ~ 17 K.

Figure 3.

Fourier transforms of the Fe K-edge EXAFS data (k³ χ(k)) and Fourier-filtered EXAFS spectra (k³ χ(k), inset) of [Fe^III₂(O)(O₂)(6-MeBQPA)₂]²⁺ (1, top), [Fe^III₂(O)(O₂)(BQPA)₂]²⁺ (2, middle) and [Fe^III₂(O)(O₂)(OAc)(BPPE)]⁺ (4, bottom). Experimental data displayed with dashed (---) lines and fits with solid (—) lines. Back-transformation range: ~0.5 to 3.3 Å; Fourier transformed range: k = 2.0–14.5 Å⁻¹ (1 and 2) or 2.0–14.0 Å⁻¹ (4). Fit parameters for each complex are provided in Table 2 in bold and italics.

Table 1.

XAS Near-edge Features and Intensities for Complexes 1, 2 and 4.

complex	E0 (eV)	Epre-edge (eV)	Pre-edge area
1	7122.8	7114.4	20.4(9)
2	7122.7	7114.5	18.3(9)
4	7123.6	7113.6	29.1(7)

The filtered Fe K-edge EXAFS data for complexes 1, 2 and 4, along with the corresponding Fourier transforms (FT, R′ space), are shown in Figure 3 (the unfiltered data are shown in Figure S1). All three Fe₂(O)(O₂) species exhibit first-shell features between r’ = ~1.0 and 2.2 Å and one or more prominent second-shell peaks between r’ = 2.5 and 3.1 Å (where r’ is the actual metal-scatterer distance after a phase-shift correction of approximately 0.4 Å). Our EXAFS analysis of 1 revealed that the first coordination sphere consists of two O/N atoms at 1.83 Å, three N/O atoms at 2.23 Å, and an intermediate N/O scatterer at 2.05 Å (Table 2). The intense second-shell feature at r’ = ~ 2.85 Å is well fit by a single Fe scatterer at 3.15 Å, thus providing strong evidence that 1 is indeed a dinuclear complex. Proper fitting of the data also required an additional shell of 4–6 C atoms near 3.0 Å, consistent with several earlier EXAFS studies of Fe complexes with TPA-type ligands.^22,39,40

Given the similarity of their supporting ligands, it is not surprising that the bond distances obtained by EXAFS for 2 are nearly identical those found for 1 (Table 2). Importantly, the bond distances derived for 1 and 2 are quite similar to those found previously for the closely related complex, [Fe^III₂(O)(O₂)(6-Me₃-TPA)₂]²⁺ (3) (Table 2).¹⁵ Thus, despite minor differences, we can conclude that complexes 1–3 generally share the same Fe coordination environments. The two short Fe-ligand bonds at ~1.8 Å are then assigned to the bridging oxo and peroxo groups, while the four remaining first-sphere atoms between 2.02 and 2.23 Å are supplied by the N₄ supporting ligands.

These results are further supported by DFT computations performed on [Fe₂(O)(O₂)(6-Me₃-TPA)₂]²⁺. These calculations assumed antiferromagnetically coupled high-spin Fe(III) centers and a µ-1,2 binding mode for the peroxo ligand. The resulting Fe₂(O)(O₂) unit is nearly planar, with an average dihedral angle of 2.2°. As shown in Figure 4, the optimized model features Fe-O_oxo and Fe-O_peroxo bonds with nearly equal lengths of ~1.8 Å, in good agreement with the EXAFS-derived values of 1.81–1.84 Å. Moreover, the calculations point to considerable variation in the Fe-N bond distances, which is also reflected in the experimental fits. Finally, the computed Fe-Fe distance of 3.17 Å approaches the values of 3.13–3.15 Å found experimentally. Thus, our combined EXAFS/DFT approach confirms the formulation of complexes 1–3 as [Fe^III₂(µ-O)(µ-1,2-O₂)(L)₂]²⁺.

Figure 4.

Schematic showing metrical parameters computed by DFT for [Fe^III₂(O)(O₂)(6-Me₃-TPA)₂]²⁺ (3). All bond distances in Å. The Fe₂(O)(O₂) unit is essentially planar (average dihedral angle = 2.2°). For the Fe-N bond distances, the values have been averaged over the two Fe centers. Differences in coordination geometry between the two sites are minor (< 0.03 Å). See Table S1 for atomic coordinates.

Our EXAFS analysis of 4 shows that this complex deviates somewhat from the pattern established by 1–3. For instance, it is not necessary to include a carbon shell at ~3 Å, which is often required for complexes of tetradentate TPA-like ligands. Moreover, fits 8–10 in Table 2, which vary with respect to the number of scatterers in each shell of the first coordination sphere, are equally good, although we favor fit 9 because it corresponds to shells with the most reasonable set of Debye-Waller (σ²) values. The scatterer at 1.77 Å likely corresponds to the bridging oxo group, while the value of 1.94 Å represents the average of the Fe-O_peroxo and Fe-O_acetate bond distances. Importantly, the data require an Fe scatterer at 3.04 Å (Table 2). This Fe-Fe distance is approximately 0.1 Å shorter than the values found for 1–3, likely reflecting the presence of the additional carboxylate ligand bridging the Fe(III) centers.⁴¹

2. Resonance Raman studies of Fe^III₂(O)(O₂) intermediates

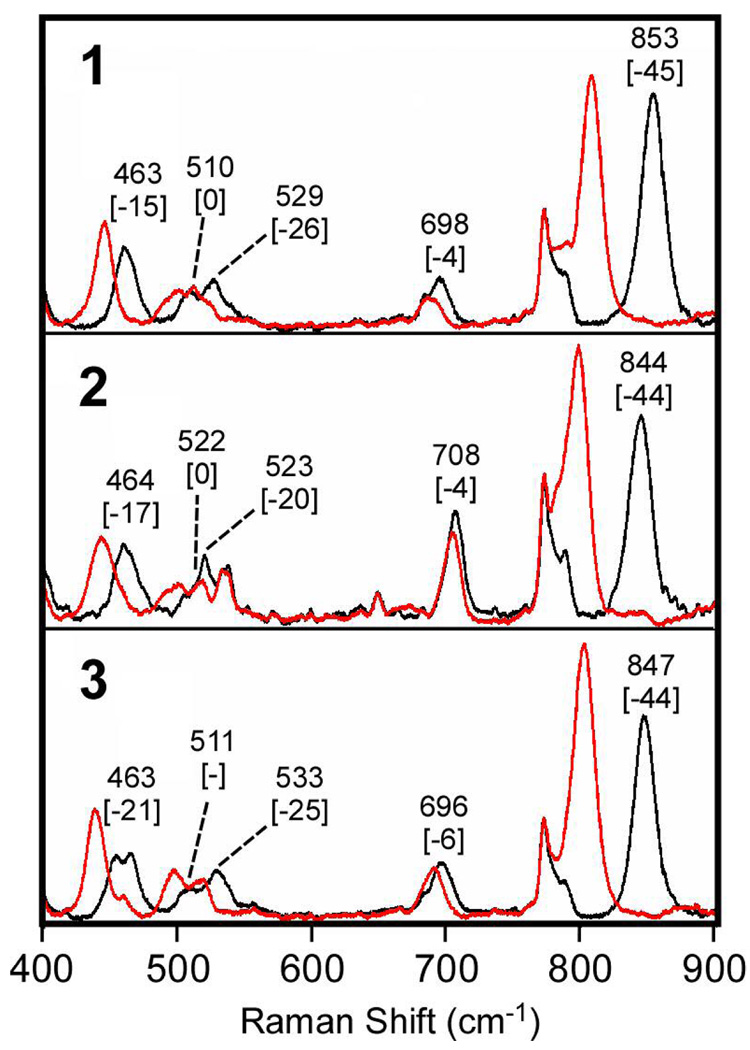
Resonance Raman spectroscopy is a very useful tool for probing the vibrations of the Fe₂(µ-O)(µ-1,2-O₂) core. In this study of 1–4, vibrations are observed that can be associated with both the Fe-O-Fe and Fe-O-O-Fe substructures. For 1–3, all five possible stretching vibrational modes of the Fe₂O₃ core have been observed and identified by isotope labeling and excitation profile experiments. The spectra are presented in Figure 5 and Figure 6, with spectra of complexes with Fe-¹⁶O-Fe cores shown in black and those with Fe-¹⁸O-Fe cores provided in red. The vibrational frequencies are tabulated in Table 3.

Figure 5.

Resonance Raman spectra obtained with 647.1-nm excitation of frozen CH₃CN solutions of (top) [Fe₂(µ-O)(µ-O₂)(6-Me-BQPA)₂]²⁺ (1) generated with 2 equiv. of Et₃N and 10 equiv. of H₂¹⁶O₂ (black) or H₂¹⁸O₂ (red); (middle) [Fe₂(µ-O)(µ-O₂)(BQPA)₂]³⁺ (2) generated with 2 equiv. of Et₃N and 10 equiv. of H₂¹⁶O₂ (black) or H₂¹⁸O₂ (red); (bottom) [Fe₂(µ-O)(µ-O₂)(6-Me₃-TPA)₂]³⁺ (3) generated with 2 equiv. of Et3N and 10 equiv. of H₂¹⁶O₂ (black) or H₂¹⁸O₂ (red). Frequencies (in cm⁻¹) are provided for [Fe₂O₃]-based modes, with the corresponding ¹⁶O₂→¹⁸O₂ shifts shown in brackets.

Figure 6.

Resonance Raman spectra of frozen CH₃CN solutions of 1 – 3 obtained with 514.5-nm excitation and for 4 obtained with 457.9-nm excitation. In all cases, the [Fe₂(µ-O)(µ-O₂)] complexes were prepared with 100 equiv. of H₂¹⁶O (black) or H₂¹⁸O (red). Frequencies (in cm⁻¹) are provided for [Fe₂O₃]-based modes, with the corresponding ¹⁶O→¹⁸O shifts shown in brackets.

Table 3.

Raman vibrational frequencies (cm⁻¹) for Fe^III₂(µ-O)(µ-1,2-O₂) intermediates 1–4 and Related Complexes A–E.

Complex	νsym (Fe-O-Fe)	νasym (Fe-O-Fe)	ν(O-O)	νsym (Fe-O2-Fe)	νasym (Fe-O2-Fe)	d (Fe-Fe)
	[Δ18O, Δ18O2]	[Δ18O, Δ18O2]	[Δ18O, Δ18O2]	[Δ18O, Δ18O2]	[Δ18O, Δ18O2]
1	510 [−16, 0]	698 [−31, −4]a	853 [0, −45]	463 [0, −15]	529 [0, −26]	3.15 Å
2	522 [−13, −]	708 [−32, −4]	844 [0, −44]	464 [0, −17]	523 [−, −20]	3.13 Å
3	511 [−12, −]	696 [−30, −6]	847 [0, −44]	463 [−, −21]	533 [−, −25]	3.14 Å
4 b	537 [−20, −]	− [−, −]	830 [0, −]	− [−, −]	− [−, −]	3.04 Å
A c			908 [−, −47]	460 [−, −13]	548 [−, 12]	3.40 Å
B d	-	695 [−, −2]	847 [−, −33]	465 [−, −19]	-	3.17 Å
C e			900 [−, −50]	471 [−, −16]		3.46 Å
D f			(884) g			3.33 Å
E h			876 [−, −48]	421 [−, −12]		4.00 Å

^aDownshift of −35 cm⁻¹ observed for the fully labeled Fe₂(¹⁸O)(¹⁸O₂) core.

^bAlthough the resonance Raman spectrum of 4 was previously published in ref 17, the reported frequency of the ν(O-O) mode (816 cm⁻¹) differs from the value of 830 cm⁻¹ listed here, which was obtained in our laboratory for direct comparisons with data for the other peroxo complexes we investigated.

^cA = [Fe₂(µ-OH)(µ-1,2-O₂)(6-Me₂BPP)]⁺ (6-Me₂BPP = N,N-bis(6-methyl-2-pyridylmethyl)-3-aminopropionate).¹⁴

^dB = [Fe₂(µ-O)(µ-1,2-O₂)(6-Me₂BPP)].¹⁴

^eC = [Fe₂(µ-1,2-O₂)(N-Et-HPTB)(OPPh₃)₂]³⁺ (N-Et-HPTB = anion of N,N,-N’,N’-tetrakis(1’-ethylbenzimidazolyl-2’-methyl)-2-hydroxy-1,3-diaminopropane). ¹²,⁴² The Raman vibrational frequencies were obtained in our laboratory (see Figure S2 in the Supporting Information).

^fD = [Fe₂(µ-1,2-O₂)(PhCOO)(Ph-bimp)]²⁺ (Ph-bimp = 2,6-bis[bis[2-(1-methyl-4,5-diphenylimidazolyl)methyl)aminomethyl]-4-methylphenolate ¹¹

^gFrequency was obtained for the related complex [Fe₂(µ-1,2-O₂)(CH₃COO)(L)]²⁺ (L = N,N’-(2-hydroxy-5-methylxylylene) bis(N-carboxymethylglycine)).⁴³

^hE = [Fe₂(µ-1,2-O₂)(PhCH₂CO₂)₂(Tp^iPr2)₂]²⁺ (Tp^iPr2 = HB(pz’)₃, where pz’ is 3,5-bis(isopropyl)-pyrazolyl.)¹³,⁴⁴

The vibrations of the Fe-O-O-Fe unit have been reported previously and consist of three modes: the O-O stretch and symmetric and asymmetric ν(Fe-O₂-Fe) deformations. Figure 5 shows the resonance Raman spectra of 1, 2, and 3 obtained with 647.1 nm excitation, in resonance with the lower energy charge transfer (CT) transition. The O-O stretch is easily identified in the 850 cm⁻¹ region, with an ¹⁶O₂→¹⁸O₂ shift of 46 cm⁻¹ that is consistent with a Hooke’s Law calculation for a diatomic O-O unit. The ν_sym(Fe-O₂-Fe) mode is readily found below 500 cm⁻¹ and exhibits an ¹⁶O₂→¹⁸O₂ shift of 15–21 cm⁻¹. On the other hand, the ν_asym(Fe-O₂-Fe) mode is found above 500 cm⁻¹ among vibrations of the Fe-O-Fe unit. In the case of 4, only the ν(O-O) mode is observed and is found at 830 cm⁻¹, which is about 20 cm⁻¹ lower in energy than those of 1 – 3.⁴⁵

In contrast to modes involving the peroxo group, vibrations arising from the Fe-O-Fe unit of Fe^III₂(µ-O)(µ-1,2-O₂) complexes have not been previously noted. However, we readily observed such modes by shifting the laser excitation to higher energies, as shown in Figure 6. The modes were definitively assigned by incorporating ¹⁸O into the oxo bridge. For 4, only one vibration at 537 cm⁻¹ is observed, which is assigned to the symmetric mode of the Fe-O-Fe unit. On the other hand, for 1 – 3, both ν_sym(Fe-O-Fe) and ν_asym(Fe-O-Fe) modes can be identified. The symmetric modes are found near 500 cm⁻¹ with ¹⁶O→¹⁸O downshifts of 12–16 cm⁻¹, while the asymmetric modes are found near 700 cm⁻¹ with ¹⁶O→¹⁸O downshifts of 30–32 cm⁻¹ (Table 3, Figure 6). The difference between 4 and the other three peroxo complexes can be ascribed to the symmetry of the Fe-O-Fe unit (Scheme 1). In 4, the two individual Fe sites are identical, while those in 1 – 3 are distinct because the oxo bridge is trans to an amine on one Fe and trans to a pyridine on the other Fe. Indeed, our DFT computations of 3 confirm the asymmetry in the Fe-O_oxo bond lengths (Figure 4). Sanders-Loehr and coworkers have previously noted that the ν_asym(Fe-O-Fe) mode becomes observable in the resonance Raman spectrum of an Fe-O-Fe complex and increases in intensity as the Fe-O-Fe unit becomes more asymmetric.^46–48 This correlation rationalizes the spectral differences observed for 1 – 4.

Previously, the ν_sym(Fe-O-Fe) and ν_asym(Fe-O-Fe) frequencies of (µ-oxo)diiron(III) complexes have been found to reflect the Fe-O-Fe angle.^18,49 When the values for 1–4 are interpreted within this framework, the Fe-O-Fe angles are deduced to be 120° for 1–3 and 110° for 4, consistent with the differences in Fe-Fe distances determined by EXAFS analysis. Moreover, the predicted Fe-O-Fe angles for 1–3 agree nicely with the value of 121° computed by DFT for 3 (Figure 4).

The excitation profiles for the symmetric Fe-O-Fe and O-O stretching modes of complex 3 (peaks at 511 and 847 cm⁻¹, respectively) are shown in Figure 7. The corresponding profiles for 1, 2 and 4 are quite similar (Figure S3). The ν(O-O) mode is strongly enhanced by excitation into the broad absorption feature at 650 nm, confirming the assignment of this band as a peroxo■ Fe(III) charge transfer transition. Conversely, the peak corresponding to the symmetric ν(Fe-O-Fe) mode is enhanced at much shorter wavelengths, indicating that the intense peaks in the near-UV region have significant contributions from oxo■ Fe(III) CT transitions. Thus, our resonance Raman data provide considerable insights into the nature of the UV-vis absorption features.

Figure 7.

Resonance Raman excitation profiles of the ν_sym(Fe-O-Fe) (–■–) and ν(O-O) (–◆–) vibrations of 3.

An unexpected feature of our resonance Raman study is the slight sensitivity of the ca. 700 cm⁻¹ mode associated with the Fe-O-Fe unit in 1–3 to ¹⁸O-labeling of the peroxo ligand (Figure 5, Table 3). The ¹⁶O₂→¹⁸O₂ downshift of 4 cm⁻¹ in the case of 1 was also observed for the fully labeled Fe₂(O)(O₂) core generated by using both H₂¹⁸O and H₂¹⁸O₂. These observations suggest coupling between modes of the Fe-O-Fe and the Fe-O-O-Fe units. To further probe the vibrational dynamics of the Fe₂(O)(O₂) core, we performed a normal coordinate analysis (NCA) using the resonance Raman data presented above. In fact, complexes 1–3 provide ideal systems for NCA due to the abundance of isotope-shift data available for all five stretching modes of the Fe₂(O)(O₂) core (Table 3). The normal coordinate analyses described herein utilized a 5-atom model of the Fe₂(O)(O₂) core derived from our DFT calculations (vide supra), in which the structural coordinates were symmetrized so as to obtain a molecule with strict C_2v symmetry (for more details see Experimental Section and Table S2). We limited our analysis to 1, since vibrational data for the fully-labeled Fe₂(¹⁸O)(¹⁸O₂) species were only available for this complex.

Table 4 compares the NCA-calculated and experimental frequencies for complex 1. It is evident that the computed force field adequately reproduces both the vibrational frequencies and ¹⁶O→¹⁸O isotope hifts, with an average deviation of 2.2 cm⁻¹. The potential energy distributions (PEDs) reveal a small but significant degree of echanical coupling between the (Fe-O-Fe) and (Fe-O₂-Fe) stretching motions, with an average of ~7 % ν(Fe-O-Fe) character in the ν(Fe-O₂-Fe) modes, and vice versa. This accounts for the fact, noted above, that the peaks near 700 cm⁻¹ associated with the Fe-O-Fe unit shift to lower frequencies upon ¹⁸O-labeling of the peroxo ligand in 1–3.

Table 4.

Comparison of Experimental and NCA-Calculated Vibrational Data for 1.

			isotope shifts
mode		frequency	Δ18O	Δ18O2	Δ(18O, 18O2)
νsym	exp	510	−16	0	−18
(Fe-O-Fe)	NCA	513	−18	−1	−20
νasym	exp	698	−31	−4	−35
(Fe-O-Fe)	NCA	697	−31	−2	−33
ν(O-O)	exp	853	0	−45	−47
	NCA	854	0	−48	−49
νsym	exp	463	0	−16	−19
(Fe-O2-Fe)	NCA	461	−1	−19	−20
νasym	exp	529	0	−26	−22
(Fe-O2-Fe)	NCA	531	−2	−22	−23

Relevant force constants derived from the NCA of 1 are shown in Table 5, along with the corresponding values obtained by Zhang et al. for [Fe₂(µ-O)(µ-1,2-O₂)(6-Me₂BPP)] (B) (where 6-Me₂-BPP is the same as 6-Me₃-TPA except that one of the pyridine rings has been replaced by a CH₂CO₂ moiety).¹⁴ Although the peroxo O-O bonds have similar strengths in the two complexes, the Fe-O force constants are ~ 15 % larger for 1 than B (Table 5), suggesting that the anionic carboxylate group weakens the Fe-O bonds relative to neutral pyridine-type donors. A similar carboxylate ligand effect has been noted for the peroxo intermediate of RNR W48F/D84E R2.⁵⁰

Table 5.

Force Constants Obtained from Normal Coordinate Analyses for 1 and B.

	Force constants (mdyn/Å)
	L = 6-MeBQPA	L = 6-Me2BPP
Internal coordinate	(1)	(B) a
r (Fe-Ooxo)	2.86	2.54
r (Fe-Operoxo)	2.17	1.84
r (O-O)	3.17	3.25

^aReference ¹⁴

Summary and Perspectives

Our studies of the diiron(III)-peroxo complexes described above have provided insight into the structural and spectroscopic properties of the [Fe^III₂(µ-O)(µ-1,2-O₂)] core. When viewed from a broader perspective (Table 3), it is clear that the nature of the bridging ligands that support the Fe-O-O-Fe unit modulate the Fe-Fe distances and, in turn, the ν(O-O) frequencies. The Fe-Fe distance can be as large as 4 Å, as in the case of [Fe₂(O₂)(Tp^iPr2)₂(O₂CCH₂Ph)₂] (E) where the (µ-1,2-peroxo)diiron(III) unit is supported by two bidentate carboxylate bridges. But the introduction of an oxo bridge dramatically decreases the Fe-Fe distance to ~3.15 Å, as found for 1 – 3. Adding a carboxylate bridge as in 4 further shortens the Fe-Fe distance by 0.1 Å, while protonating or alkylating the oxo bridge lengthens the Fe-Fe distance to an intermediate value of ~3.4 Å (e.g. complexes A, C, and D in Table 3). These differences in Fe-Fe distance give rise to ν(O-O) frequencies that span a range of ~80 cm⁻¹. Indeed, as shown in Figure 8, ν(O-O) decreases with Fe-Fe distance for the major subset of complexes that form a five-membered [Fe^III₂(µ-OR)(µ-1,2-O₂)] ring (R = H, alkyl, aryl, or no substituent). This data set validates the mechanical coupling model for the [Fe^III₂(µ-1,2-O₂)] unit conceived by Brunold and Solomon.⁴⁴ However [Fe₂(O₂)(Tp^iPr2)₂(O₂CR)₂] (E) does not belong to this subset and is a significant outlier. Unlike for those in the [Fe^III₂(µ-OR)( µ-1,2-O₂)] subset, the Fe-O-O-Fe dihedral angle for this complex is not constrained to be close to 0° and is in fact significantly larger than 0°, which may be why this complex does not fit with the correlation in Figure 8.

Figure 8.

Plot of O-O stretching frequencies as a function of Fe-Fe distance for 1–4 and related complexes (A–D) with Fe₂(µ-1,2-O₂)(µ-OR) cores (R = H (A), alkyl (C), aryl (D), or no substituent (1–4, B)). Note that since resonance Raman data are not available for D (◇), the value used here corresponds to a closely related complex (see Table 3).

As noted in the introduction, the ν(O-O) frequencies of diiron(III)-peroxo intermediates in nonheme diiron enzymes exhibit wide variations despite close similarities in active site structures. Within this class, the peroxo intermediate of ferritin exhibits the lowest ν(O-O) frequency (851 cm⁻¹).¹⁰ The presence of only one carboxylate bridge in the ferritin active site,⁵¹ compared to two in RNR and Δ⁹ desaturase,^52,53 allows space to incorporate solvent-derived monoatomic bridge(s) (like O²⁻ or HO⁻). Thus, the peroxo intermediate of ferritin likely possesses a five-membered [Fe^III₂(µ-O(H))(µ-1,2-O₂)] ring, similar to those found in the model complexes studied herein. An EXAFS study of the ferritin peroxo intermediate reported a remarkably short Fe-Fe distance of 2.53 Å, leading to the proposal that the diferric center is bridged by two monoatomic ligands in addition to peroxide.⁵⁴ However, based on Figure 8, we would predict an Fe-Fe distance in the range of 3.1 to 3.2 Å, which is more consistent with a [Fe^III₂(µ-O)(µ-1,2-O₂)(µ-1,3-O₂CR)] structure. Of course, as with [Fe₂(O₂)(Tp^iPr2)₂(O₂CCH₂Ph)₂] (E), the Fe-O-O-Fe unit in ferritin might adopt a non-planar geometry, in which case the close connection between Fe-Fe distances and ν(O-O) frequencies may break down. Regardless, our results will likely prove useful for interpreting trends in ν(O-O) frequencies among diiron(III)-peroxo intermediates of nonheme diiron enzymes.

Supplementary Material

1_si_001. Supporting Information Available.

Cartesian coordinates for the DFT geometry-optimized model of [Fe^III₂(O)(O₂)(6-Me₃-TPA)₂]²⁺ (3) (Table S1), EXAFS fitting results for the unfiltered data (Table S2 and Figure S1), force constants from our normal coordinate analysis of 1 (Table S3), resonance Raman spectra of [Fe₂(µ-1,2-O₂)(N-Et-HPTB)(OPPh₃)₂]³⁺ (C) (Figure S2), and resonance Raman excitation profiles for complexes 1, 2, and 4 (Figure S3). This material is available free of charge via the Internet at http://pubs.acs.org.