The relationship between spatial pooling and attention in saccadic and perceptual tasks

Abstract

Saccades aimed at spatially-extended targets land reliably at central locations determined by pooling information across the target shape [Melcher & Kowler, Vision Research, 1999; Vishwanath & Kowler, Vision Research, 2003]. Previous findings of saccadic errors when attempting to look at a target in the midst of distractors encouraged suggestions that pooling occurs indiscriminately, with little or no influence of a selective filter to eliminate the influence of nearby distractors. To determine the effectiveness of filtering, saccadic localization was studied for saccades made to a set of target elements (discs) interleaved with an equivalent set of distractors of a different color. With such interleaved elements, selection and spatial pooling are constrained to occur over the same spatial region. The results showed that filtering was effective and saccadic landing position was determined mainly by the target elements. Concurrent perceptual judgments made about the same stimuli (estimating the mean size of either target or distractor discs) showed better performance for the target discs than distractors, confirming that perceptual attention was allocated to the set of target elements. These results: (1) support the role of attention in setting the input to the spatial pooling process that guides saccades to spatially-extended targets, and (2) show that perceptual judgments of mean value, often thought to impose modest attentional demands, are not immune to the constraints of this pre-saccadic filter.

Introduction

The ability to encode aggregate properties of collections of elements distributed over space is fundamental to perception and to oculomotor control. For example, saccades that are directed to spatially-extended targets land reliably at a central location determined by pooling information across the target shape (He & Kowler, 1991; Melcher & Kowler, 1999; Vishwanath & Kowler, 2003, 2004; Lee, Rohrer & Sparks, 1992). Spatial pooling is important in perception as well, enabling rapid encoding of global properties of collections of elements, such as mean orientation (Cohen & Singh, 2006; Li & Westheimer, 1997), direction of motion (Watanamiuk & McKee, 1998; Williams & Sekuler, 1986), location (Vishwanath & Kowler, 2003; Denisova, Singh & Kowler, 2006; Morgan, Hole & Glennester), or size (Ariely, 2001; Chong & Treisman, 2003; 2005a,b). This paper investigates the relationship between spatial pooling and attention in saccadic and perceptual tasks.

Spatial pooling and saccades

Previous studies have offered different perspectives about how spatial pooling affects saccades. Early studies, using stimuli consisting of a small target with one or more neighboring distractors, showed that pooling can produce large saccadic errors. These studies found that saccades landed near the center of gravity (average location) of the stimulus configuration (target + distractors), rather than at the designated target (Findlay, 1982; Ottes, Van Gisbergen & Eggermont, 1985; Coëffé & O’Regan, 1987; Walker, Deubel, Schneider & Findlay, 1997; Coren & Honig, 1972). Such saccadic errors were observed when the target and distractors were contained within a spatial region covering a directional angle of about 30 degrees (at larger separations saccades usually landed on either target or distractor) (Ottes et al., 1985). These studies raised questions about the ability of selective attention to reduce or eliminate the influence of nearby distractors on saccades (He & Kowler, 1989).

Eliminating the influence of distractors on saccades is clearly important for inspecting crowded visual scenes. In natural visual scenes, saccadic targets are spatially-extended objects or configurations. Studies of saccadic localization of a variety of types of spatially-extended targets presented without surrounding non-targets have shown that saccades directed to the target as a whole land at a ‘default’ position, near the centroid of the shape, with a level of spatial precision comparable to that achieved with small target points (He & Kowler, 1991; Kowler & Blaser, 1995; McGowan, Kowler, Sharma & Chubb, 1998; Melcher & Kowler, 1999; Vishwanath & Kowler, 2003). A central default saccadic landing position that can be computed with relatively little effort by pooling information across the target shape allows the line of sight to reach consistent locations within targets without requiring the investment of cognitive resources in the planning and selection of each landing site. However, without an effective selective filter at the front end to determine the effective input to the saccadic system, saccadic errors will result due to pooling across targets and non-targets.

The question that we investigate in this study is whether spatial pooling can be limited to selected or attended information. One way to address this question is by using a stimulus consisting of spatially-interleaved target and distractor elements. With such a stimulus, both spatial pooling and selective attention must operate over the same spatial region. If pooling over targets and nearby non-targets is automatic and indiscriminate, then the saccadic landing position will be determined by the entire configuration. On the other hand, a finding that saccadic landing position is determined by the target elements would support a role for an attentional filter that limits pooling to selected elements. An interesting aspect of testing interleaved element sets is that selection cannot be made on the basis of a boundary separating targets and non-target regions. Instead, pooling and selection must operate over the same spatial region, and rely on cues other than location to segment the display into target and distractor groups (Saenz, Buracas & Boynton, 2003).

In our experiments, the targets and distractors were sets of interleaved discs of different colors. Accurate saccadic localization of the set of target discs would thus depend on the ability to pool over the selected target discs while filtering out influence of the distractors in the same spatial region.

Spatial pooling and perceptual judgments of mean size

We also studied a perceptual task with the same stimuli. The perceptual task we used, judging the mean size of the set of selected target elements, like the saccadic task, requires pooling information across the target element set (Chong & Treisman, 2003; 2005a). Mean size estimation is insensitive to the presence of interleaved distractors (Chong & Treisman, 2005a). Thus, by testing the mean size estimation task with the same stimuli used to test saccades, we would be able to verify that it is possible to differentially attend to the target element set in the presence of the set of distractors. The perceptual results thus provide a benchmark against which we can evaluate the effect of distractors on saccades.

We also included a dual-task experiment in which the mean size judgments were made about either the set of target elements or the set of non-target elements during the latency interval preceding saccades. There were two reasons for including a dual-task experiment. First, there is considerable psychophysical and physiological evidence that saccadic and perceptual mechanisms share the same attentional filter (Gersch, Kowler & Dosher, 2004; Kowler, Anderson, Dosher & Blaser, 1995; Hoffman & Subramaniam, 1995; Deubel & Schneider, 1996; Moore & Armstrong, 1993). If we find that perceptual judgments about the saccadic target elements prove to be more accurate than judgments about the interleaved nontargets, we would have additional evidence that any ability to eliminate the influence of distractors on saccades is due to selective attention. Such a result would also extend the set of results supporting a shared filter for saccades and perception to the case where attentional selection cannot be based on differences in spatial location of target and non-targets.

The second reason for including a dual-task experiment stems from recent claims that tasks such as mean size estimation place only modest demands on attention, and are performed before the level of attentional bottlenecks. Specifically, Chong & Treisman (2005a) found that while mean size judgments are sensitive to attentional selection (that is, it is not possible to make accurate judgments about unattended material), it is nevertheless possible to broaden the attentional “window” sufficiently to accurately estimate the mean size of multiple attended element sets. Similar claims have been made about the ability to make multiple judgments of numerosity (Halberda, Sires, & Feigenson, 2006). We will test this claim by running an additional condition in the dual-task experiment in which observers try to broaden their “attentional window” and improve perceptual performance on the distractors while continuing to aim saccades accurately at the targets (Kowler et al., 1995). Finding that the accuracy of the perceptual judgments made about the distractors can be improved without cost to saccadic performance, would be consistent with Chong & Treisman’s (2005a) results and show that, at least for some tasks, a broad distribution of perceptual attention can be adopted while saccades are being planned to a selected portion of the display.

Overview of experiments

Saccades and perceived mean size were tested with two interleaved sets of randomly-positioned discs of varying sizes, one set red and one green, located at an average eccentricity of 8 degrees. There were 4 experiments. Experiment 1 studied perceptual judgments of mean size of the target set during steady fixation. Experiment 2a,b studied the effect of the presence of the distractor set on saccadic localization of the target set. Given that the perceptual experiments used a mask following the critical display to control the duration of processing, a mask was also used in saccadic Experiment 2a. Masks, however, are unusual in saccadic experiments because processing time is limited naturally by the latency of the saccade itself, and because saccades landing on the mask are deprived of the normal post-saccadic visual feedback needed to maintain saccadic gain. To determine the effect of the mask, saccades were tested without the mask in Experiment 2b.

Experiment 3 was a dual-task experiment that tested perceptual judgments of mean size during the latency interval preceding saccades to one or the other element set. Perceptual judgments were made either about saccadic target set, or about the distractor set, under instructions to favor performance on either the saccadic or the perceptual task (these instructions are based on those used in previous dual-task work; see Sperling & Dosher, 1986; Kowler et al., 1995). Finding performance losses when saccades and judgments are based on different element sets supports a shared attentional filter. Experiment 4 (analogous to Experiment 3) investigated performance in the perceptual task during steady fixation under conditions designed to encourage attention to both element sets. Experiment 4 used Chong & Treisman’s (2005a) approach of testing perceptual judgments of mean size during steady fixation when the identity of the element set to be reported is not cued until the end of the trial.

Methods

Stimulus Display

Stimuli were displayed on a Dell P793 CRT monitor (13deg × 12 deg; viewing distance 115 cm, 1.46 pixels/minarc; refresh rate 75 Hz).

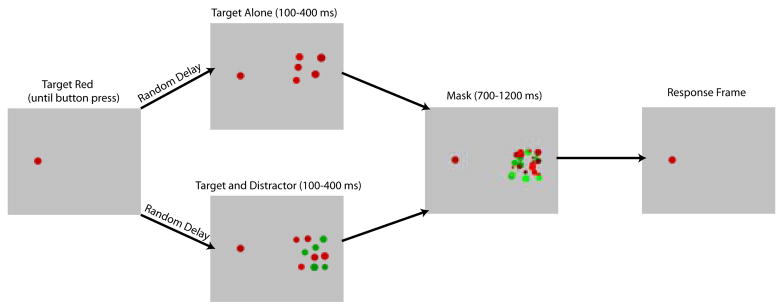
The stimulus display consisted of 4 frames, shown in Fig. 1. Frame 1 contained either a red or green fixation disc (diameter 48′) located 4 deg to the left or right of the display center. Frame 2 contained the critical discs for the trial and appeared 200–400 ms after the trial was started by a button press. Duration was 100, 200 or 400 ms. (One observer, ML, felt that 100 ms was too brief to perform any of the tasks, thus duration for this observer was increased to 150 ms.) The critical discs consisted of either: (1) 5 target discs (all red or all green), or (2) 5 target discs of one color (red or green) and 5 distractor discs of the other color. Frame 3 contained a masking stimulus of 30 partially overlapping red or green discs of varying intensity and varying size in the range of 25–100% of the fixation disc size. The mask appeared immediately after the offset of the critical frame and remained on until the end of the 1.5 second trial. Frame 4, containing only the initial fixation disc, served as a response frame in trials where a perceptual judgment was required. It remained until the response was given by a button press. No feedback as to the accuracy of responses was given.

Figure 1.

The sequence of display frames. Frame 1 contained the fixation disc whose color indicated the target set for the current trial. Following a button press and random delay (200–400 ms) the critical display containing either target elements alone (green, in the example shown) or target+distractor elements appeared, followed by a mask. The response frame remained on until the report.

The configuration of critical discs in Frame 2 was characterized by the following stimulus parameters:

Location

Discs were presented in a square bounding region (250′ × 250′) whose center was displaced either 454′, 480′, or 504′ horizontally from the center of the fixation disc. Disc locations within this region were chosen randomly with the restriction that the horizontal center of gravity (COG, average unweighted horizontal dot location) of the 5 target discs differed from the COG of the 5 distractor discs by at least 5% of the eccentricity of the square bounding region. In addition, the vertical locations of the discs were jittered by a small amount (−30′, 0′, or 30′, selected randomly on each trial) relative to display center in order to further discourage stereotypical saccadic patterns not based on actual disc locations in a given trial. Analyses were limited to the horizontal component of the saccades.

Size

The sizes of the discs were chosen to conform to the requirements of the perceptual (size estimation) task. The area of the fixation disc (which acted as the reference stimulus for the perceptual judgments) was 1811 min arc² (diam=48′). The areas of the target discs were chosen in the following way: first, the mean area of the target discs was selected randomly from one of 5 values (1584, 1698, 1811, 1924, or 2037 min arc²). Then, the areas of the individual target discs were chosen randomly from one of 4 sets. The 4 sets of areas had the same mean, but differed according to the variability and skewness of the distribution of disc sizes. Different sets were used in order to make it less likely that subjects could base judgments on the size of one or two discs (Chong & Treisman, 2003). The areas of distractor discs were determined in the same way. Mean distractor areas were either 1584, 1811, or 2037 min arc².

Color

Discs were either red (CIE chromacity coordinates x = .628, y = .338) or green (x = .278, y = .609). The luminance of the red discs was 11 cd/m² measured using a UDT colorimeter with a 400 × 400 pixel display. The luminance of the green discs (19–30 cd/m²) was determined for individual subjects by an informal method of adjustment procedure where subjects were asked to set red and green patches to have about the same brightness (we did not need and were not attempting to create strict equiluminant conditions). In the experiment, the intensity levels of each disc in the critical display was independently jittered randomly by ±20% around these values. The discs were presented against a gray background (luminance 54 cd/m²).

Procedure

Experiment 1. Perceptual judgments of mean size

Steady fixation was maintained throughout the trial as observers estimated the mean size of the set of target discs. The target disc color (red or green) was constant within a given experimental session and, in addition, was disclosed by the color of the fixation disc shown at the start of each trial. At the end of the trial the subject reported whether the mean size of the 5 target discs was greater or less than the size of the fixation disc. Two kinds of trials were tested within the same experimental session. “Target Alone” trials contained 5 discs of the same target color. “Target and Distractor” trials contained 5 target discs and 5 distractor discs. Trial type was chosen randomly and the subject did not know which it would be before the discs appeared. No feedback as to accuracy of the reports were given. Psychometric functions showing the proportion of trials in which the mean size of the target discs was judged to be larger than the standard reference disc were fit by Wiebull functions using the Psignifit algorithm (Wichman & Hill, 2001).

Experiment 2a,b. Saccades to disc clusters

Stimuli were as in Experiment 1. Instructions were the same as those used in previous studies of saccades to spatially-extended targets, namely, aim a single saccade to the set of target discs as a whole, rather than to a specific location, and give greater weight to following these instructions than to achieving a short saccadic latency (e.g., Kowler & Blaser, 1995; Vishwanath & Kowler, 2004). Secondary, corrective saccades were to be avoided because relying on corrections could induce a strategy of aiming the first saccade only part of the way to the target elements, rather than at the set of elements themselves. In Experiment 2a the critical display was followed by the mask (as in Experiment 1). In Experiment 2b the critical display remained on until the end of the 1.5 sec trial and no mask was presented.

Experiment 3. Dual task: Saccadic localization and concurrent perceptual judgments of mean size

In dual task sessions, subjects made both saccades and size judgments in the same trial. In some sessions perceptual judgments were made about the same set of discs that were the saccadic targets. In the other sessions the saccades and perceptual judgments were based on different sets of discs. When saccades and perceptual judgments were made with different disc sets, two different instructions were used, tested in separate sessions. The “emphasize saccade” instruction stressed the importance of aiming saccades to the target disc set, sacrificing the accuracy of the perceptual judgments about the distractor discs if necessary. The “emphasize percept” instruction was the opposite, and asked observers to try to improve their perceptual judgments, sacrificing saccadic performance if needed. These two types of instructions were used by Kowler et al. (1995) to study saccades and attention using a letter recognition task. Control sessions were also run in which only one of the tasks (saccadic or perceptual) was performed.

Experiment 4. Perceptual judgments while attending to both disc clusters

Stimuli and procedures were the same as in Experiment 1 (Perceptual judgments of mean size) except that the color of the fixation disc was gray so that the observer did not know which set of discs to evaluate until the end of the trial. The disc set was disclosed by changing the fixation disc to either red or green (randomly intermixed) after the mask was removed. The presentation time of the critical discs was 200 ms.

Subjects

Four subjects were tested (ML, SDK, ES and GT). Three (ML, SDK, and ES) were tested in Experiments 1, 2 and 4. ML, GT, and ES were tested in Experiment 3. All were paid volunteers, naïve as to the purpose of the experiments, and had normal (uncorrected) vision.

Eye movement recording and analyses

Two-dimensional movements of the right eye were recorded by a Generation IV SRI Double Purkinje Image Tracker (Crane & Steele, 1978). The subject’s left eye was covered and the head was stabilized on a dental biteboard.

The voltage output of the Tracker was fed on-line through a low pass 100 Hz filter to a 12-bit analog to digital converter (ADC). The ADC, controlled by a PC, sampled eye position every 2 ms. The digitized voltages were stored for later analysis. Voltage from a photocell that recorded stimulus onset and offset directly from the display monitor was fed into a channel of the ADC and recorded along with the eye position samples to ensure accurate temporal synchronization between stimulus display and eye movement recording.

Tracker noise level was measured with an artificial eye after the tracker had been adjusted so as to have the same first and fourth image reflections as the average subject’s eye. Filtering and sampling rate were the same as those used in the experiment. Noise level, expressed as a standard deviation of position samples, was 0.4′ for horizontal and 0.7′ for vertical position.

Recordings were made with the tracker’s automatically movable optical stage (auto-stage) and focus-servo disabled. These procedures are necessary with Generation IV Trackers because motion of either the auto-stage or the focus-servo introduces larger artifactual deviations of Tracker output. The focus-servo was used, as needed, only during inter-trial intervals to maintain subject alignment. This can be done without introducing artifacts into the recordings or changing the eye position/voltage analog calibration. The auto-stage was permanently disabled because its operation, even during inter-trial intervals, changed the eye position/voltage analog calibration.

The beginning and end positions of saccades were detected off-line by means of a computer algorithm employing an acceleration criterion (Gersch et al., 2004). The value of the criterion was determined empirically for individual observers by examining a large sample of analog records of eye position. Saccades as small as the microsaccades that may be observed during maintained fixation (Steinman, Haddad, Skavenski & Wyman, 1973) could be reliably detected by the algorithm. Trials were eliminated if tracker lock was lost during the trial or if saccadic latency was < 100 ms, too brief for the saccade to have been planned on the basis of the stimulus. This led to elimination of 5% of trials for ML, 3% for SDK, 12% for ES and 6% for GT.

Results

Experiment 1. Perceptual judgment of mean size

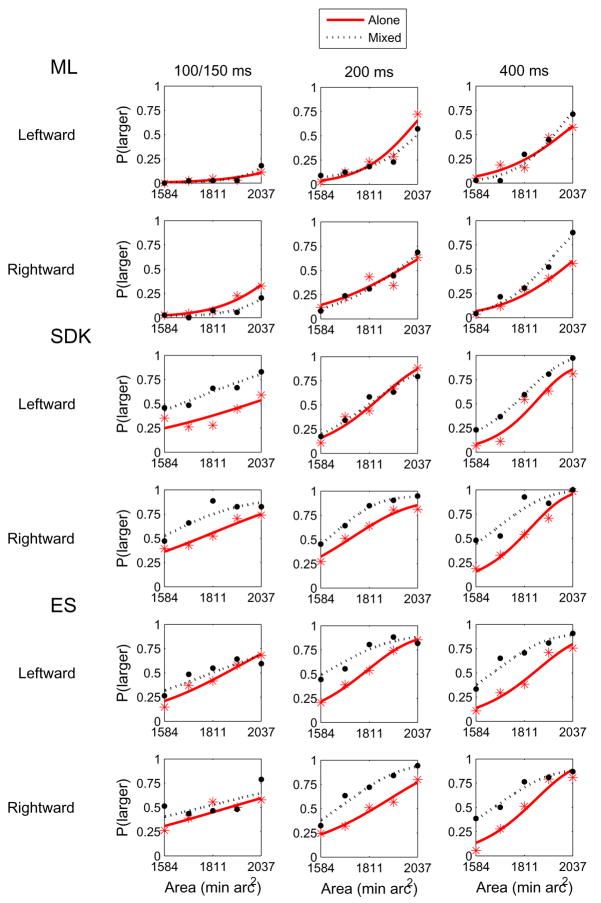
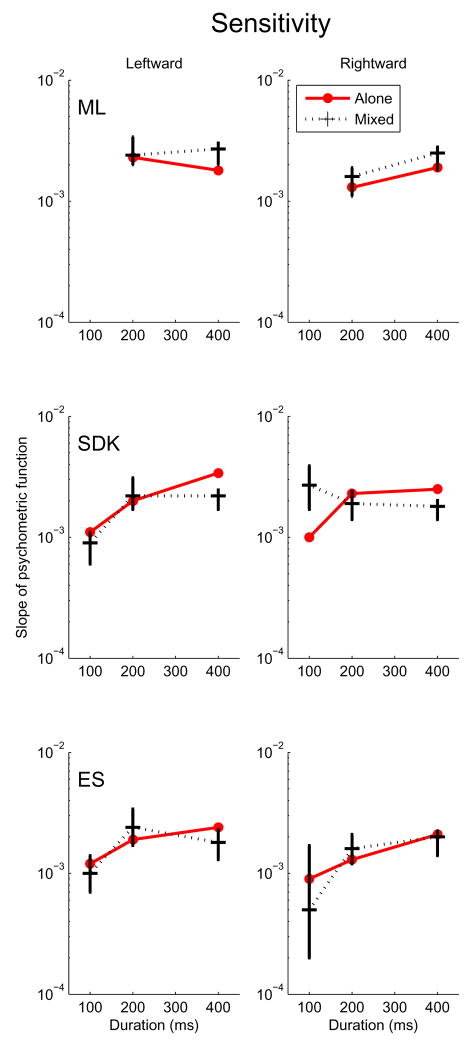
Perceptual discrimination of the mean size of the set of target discs is shown by the psychometric functions in Fig. 2, with separate graphs for each of the 3 observers and 3 critical frame durations. Performance for stimuli containing target discs alone, and targets along with distractors, are plotted on the same graph. The presence of the distractors did not impair discrimination of mean size. The only case where sensitivity was impaired by the distractors was for observer SDK at the longest duration, as can be seen from the plots of slopes of the psychometric functions in Fig. 3. Comparison of the psychometric functions in Fig. 2 shows that the presence of distractors led to a small bias (<10%) in two observers (SDK and ES) to overestimate mean size. These results confirm the ability to perceptually segregate targets and distractor sets, and show that pooling across target elements is only modestly affected by the interleaved nontargets.

Figure 2.

Psychometric functions showing proportion of trials in which the target discs were judged as having a larger mean size than the reference (fixation) disc as a function of the mean area of the target disc set. Data were fit by Weibull functions obtained using the Psignifit algorithm (Wichman & Hill, 2001). Target elements were to the left or right of fixation. Each datum point in the psychometric functions is based on approximately 40 observations.

Figure 3.

Sensitivity (slope at the 50% point of the fitted psychometric function) as a function of critical frame duration. Target elements were to the left or right of fixation.

Experiment 2a. Saccades to disc clusters followed by masks

This section will describe the results obtained when the duration of the critical display was varied and the critical display was followed by a mask. Experiment 2b tests performance when no mask was present.

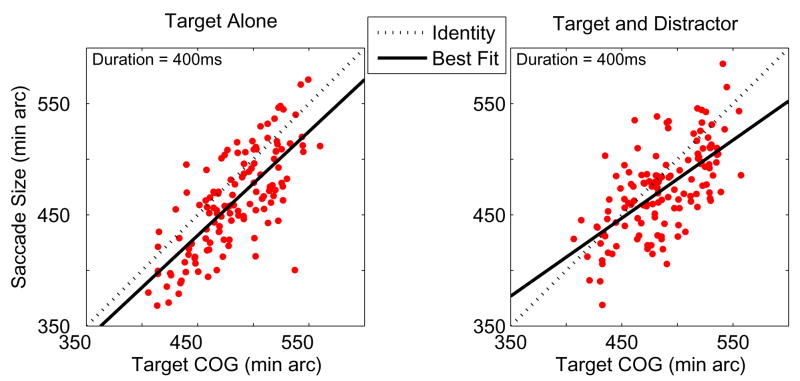
To evaluate the effect of the distractors on saccades, we first consider saccades made to the target discs presented alone. An example of a scatterplot showing saccadic landing positions as a function of the target COG, along with the best fitting straight line, is shown in Figure 4 (left panel) for observer SDK’s leftward saccades made with the longest (400 ms) critical display duration. Scatterplots were analyzed for all observers, directions, and display durations. Table 1 shows key parameters of the scatterplots, namely, slopes of the best fitting line, standard deviation of landing positions around the best fitting line, and coefficients of correlation between the landing position and target COG. Slopes were close to 1 for the longest critical frame duration for all 3 observers and both saccadic directions. Standard deviations around the best fit line were 6–9% of the saccade size, a level of variability that is characteristic of saccades to small, single targets, where pooling across elements is not involved (Kowler & Blaser, 1995). The parameters of the scatterplots with the longest stimulus duration are about the same as those reported in the past for saccades to random dot fields (McGowan et al., 1998; Melcher & Kowler, 1999).

Figure 4.

Scatterplots showing horizontal saccadic landing position as a function of horizontal center-of-gravity (COG) of the target discs for observer SDK with the 400 ms critical frame duration, with target elements alone (left) or target+distractors (right). Target elements were to the left of fixation. The bold line shows the best fitting straight line. Each scatterplot is based on about 130 observations.

Table 1.

Parameters of linear fits: Saccades to target discs alone (Experiment 2a).

Leftward							Rightward
Duration	Slope	Intercept	SD	R2	Latency (ms)	N	Duration	Slope	Intercept	SD	R2	Latency (ms)	N
ML							ML
400 ms	1.16 [±0.19]	96 [±94]	35	0.52	314 (73)	129	400 ms	1.31 [±0.18]	−153 [±86]	33	0.63	261 (73)	122
200 ms	0.98 [±0.16]	11 [±78]	32	0.50	224 (48)	145	200 ms	1.03 [±0.17]	−32 [±81]	34	0.51	201 (37)	137
150 ms	1.02 [±0.18]	29 [±86]	37	0.47	205 (47)	144	150 ms	1.07 [±0.15]	−51 [±73]	30	0.59	191 (46)	134
SDK							SDK
400 ms	0.93 [±0.15]	−11 [±71]	30	0.55	330 (158)	131	400 ms	0.99 [±0.14]	−4 [±65]	28	0.58	333 (171)	146
200 ms	0.68 [±0.16]	−129 [±77]	30	0.34	220 (65)	141	200 ms	0.85 [±0.15]	52 [±73]	28	0.49	230 (67)	133
100 ms	0.51 [±0.16]	−216 [±76]	34	0.22	235 (66)	148	100 ms	0.52 [±0.17]	220 [±80]	36	0.21	245 (65)	144
ES							ES
400 ms	0.83 [±0.19]	−55 [±93]	36	0.37	462 (214)	127	400 ms	0.93 [±0.27]	9 [±129]	41	0.33	465 (196)	100
200 ms	0.76 [±0.19]	−95 [±90]	37	0.32	339 (126)	138	200 ms	0.82 [±0.21]	64 [±100]	38	0.32	320 (117)	133
100 ms	0.47 [±0.19]	−212 [±90]	34	0.17	327 (72)	126	100 ms	0.69 [±0.19]	125 [±90]	38	0.27	328 (62)	144

Parameters (slope, intercept) of the best fit straight lines for scatterplots of saccadic landing position vs. the center of gravity of the target discs for 3 critical frame durations, when target discs were presented alone. Numbers in parentheses denote 95% confidence intervals.

SD is the root mean square error (RMSE) about the best fit line.

Table 1 also shows that for two observers (SDK and ES) slopes decreased and variability increased for the shorter critical durations (<=200 ms), indicating that for the shorter durations the target COG became a poorer predictor of landing position, even without distractors. (The role of the mask in accounting for performance of these observers at the shorter durations will be considered in Experiment 2b.)

The same analysis of saccadic landing positions as a function of target COG, described above for stimuli with target discs alone, was carried out for the stimuli with targets and distractors. A representative scatterplot is shown in Fig. 4, and parameters of all scatterplots in Table 2. ML and ES were not affected much by distractors (slopes were about the same as found with the target elements alone in Table 1), whereas SDK showed significantly shallower slopes, particularly for the shorter durations. Standard deviations around the best fitting line (also in Table 2) were slightly larger in the presence of distractors. This suggests some influence of the distractors on saccades.

Table 2.

Parameters of linear fits: Saccades to target and distractor discs (Experiment 2a).

Leftward							Rightward
Duration	Slope	Intercept	SD	R2	Latency (ms)	N	Duration	Slope	Intercept	SD	R2	Latency (ms)	N
ML							ML
400 ms	1.15 [±0.19]	99 [±90]	37	0.54	300 (71)	131	400 ms	1.01 [±0.17]	−16 [±84]	36	0.48	249 (50)	149
200 ms	0.97 [±0.17]	19 [±80]	34	0.50	220 (38)	137	200 ms	0.95 [±0.16]	−7 [±78]	32	0.47	199 (38)	154
150 ms	0.85 [±0.19]	−43 [±91]	38	0.39	210 (54)	127	150 ms	1.02 [±0.17]	−40 [±79]	33	0.52	189 (32)	141
SDK							SDK
400 ms	0.70 [±0.15]	−131 [±72]	30	0.40	296 (169)	134	400 ms	0.69 [±0.17]	141 [±83]	33	0.31	307 (158)	144
200 ms	0.64 [±0.17]	−148 [±80]	34	0.30	217 (57)	135	200 ms	0.46 [±0.14]	244 [±69]	30	0.20	230 (81)	168
100 ms	0.37 [±0.17]	−285 [±82]	34	0.11	228 (68)	143	100 ms	0.30 [±0.19]	325 [±89]	37	0.08	230 (62)	126
ES							ES
400 ms	0.76 [±0.25]	−90 [±118]	43	0.25	475 (214)	113	400 ms	0.85 [±0.17]	46 [±81]	35	0.40	439 (208)	152
200 ms	0.60 [±0.23]	−168 [±109]	42	0.19	344 (138)	119	200 ms	0.86 [±0.21]	48 [±99]	41	0.35	346 (115)	130
100 ms	0.66 [±0.16]	−135 [±77]	34	0.33	338 (89)	134	100 ms	0.96 [±0.22]	1 [±104]	39	0.38	319 (75)	128

Parameters (slope, intercept) of the best fit straight lines for scatterplots of saccadic landing position vs. the center of gravity of the target discs for 3 critical frame durations, when target discs were presented along with distractor discs. Numbers in parentheses denote 95% confidence intervals.

SD is the root mean square error (RMSE).

To better assess how distractors affected saccades, we fit a model to the data in which saccadic landing position on each trial was determined by a weighted COG. In the model (described in more detail in the Appendix), saccadic landing position on a given trial, P_t, was assumed to be a linear function (slope m, intercept b) of the weighted center-of-gravity of the disc locations (plus Gaussian noise), where the weight assigned to the target disc locations (T_t) was α, and the weight assigned to the distractors (D_t) was 1- α. Thus,

$${\text{P}}_{\text{t}}=\text{m}({\text{T}}_{\text{t}}\alpha +{\text{D}}_{\text{t}}[1-\alpha ])+\text{b}$$ (1)

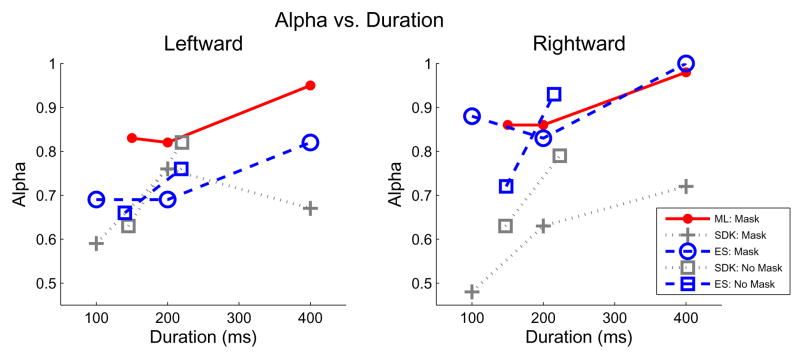
Values of α near 1 would indicate little or no influence of distractors; values near .5 would indicate equal weighting of target and distractors (i.e., indiscriminate averaging). We determined the value of α that best predicted the set of obtained landing positions by means of the maximum likelihood method described in the Appendix (McGowan et al., 1998). The estimated values of the weighting parameter α, shown in Fig. 5, ranged between about .6 and .9, with α increasing with stimulus duration and observer ML showing the highest values, i.e., most effective screening of distractors. Significance tests (described in the Appendix and summarized in Table A1) showed that the estimated values of α provided a signficantly better fit to the set of landing positions (p<.05) than setting α=.5 (targets and distractors weighted equally) in all cases except SDK’s shortest duration. This allows us to reject the hypothesis of indiscriminate averaging. Tests also showed that except for ML’s and ES’s longest durations, most values of α were significantly less than 1. Thus, the test of the weighted COG model shows that saccades were not determined by indiscriminate pooling across target and distractors, nor was selection perfect.

Figure 5.

Value of the weighting parameter, α, determined by fitting the weighted COG model (see eq. 1 and Appendix) for all 3 observers as a function of either critical frame duration for the masked condition (Experiment 2a) or the average saccadic latency for the no-mask condition (Experiment 2b). Higher values of α indicate that results were better accounted for by assigning a greater weight to target discs. Target elements were to the left or right of fixation.

Table A1.

Results of fitting the weighted CoG model to the data from the mask condition (experiment 2a).

Leftward									Rightward
Duration	Model	α	Slope	Int	SD	R2	L	p	Duration	Model	α	Slope	Int	SD	R2	L	p
ML									ML
400 ms	W	0.95	1.23	137	36	0.54	656.8		400 ms	W	0.98	1.03	−27	36	0.48	744.4
	F	1.00	1.15	99	36	0.54	657.0	0.52		F	1.00	1.01	−16	36	0.48	744.5	1.00
	F	0.50	1.22	131	47	0.23	690.5	<.001*		F	0.50	0.96	11	46	0.14	781.1	<.001*
200 ms	W	0.82	1.29	171	33	0.53	673.0		200 ms	W	0.86	1.16	−107	32	0.48	750.3
	F	1.00	0.97	19	34	0.50	676.6	<.01*		F	1.00	0.95	−7	32	0.47	752.3	<.05*
	F	0.50	1.30	172	40	0.29	700.7	<.001*		F	0.50	1.09	−73	39	0.23	780.9	<.001*
100 ms	W	0.83	1.12	88	37	0.41	639.6		100 ms	W	0.86	1.26	−155	32	0.53	689.6
	F	1.00	0.85	−43	38	0.39	641.2	0.07		F	1.00	1.02	−40	33	0.52	692.0	<.05*
	F	0.50	1.18	117	43	0.21	657.5	<.001*		F	0.50	1.13	−93	41	0.23	724.8	<.001*
SDK									SDK
400 ms	W	0.67	1.20	108	27	0.50	633.0		400 ms	W	0.72	1.15	−77	31	0.38	699.7
	F	1.00	0.70	−131	30	0.40	645.6	<.0001*		F	1.00	0.69	141	33	0.31	707.4	<.0001*
	F	0.50	1.25	129	29	0.43	642.1	<.001*		F	0.50	1.08	−44	34	0.26	711.9	<.001*
200 ms	W	0.76	0.95	−2	34	0.34	665.7		200 ms	W	0.63	0.89	38	28	0.31	798.9
	F	1.00	0.64	−148	34	0.30	669.0	<.01*		F	1.00	0.46	244	30	0.20	811.6	<.0001*
	F	0.50	0.95	2	36	0.22	676.5	<.001*		F	0.50	0.86	54	29	0.28	803.2	<.025*
100 ms	W	0.59	0.85	−53	32	0.23	696.9		100 ms	W	0.48	0.89	42	33	0.26	618.5
	F	1.00	0.37	−285	34	0.11	706.9	<.0001*		F	1.00	0.30	325	37	0.08	632.3	<.0001*
	F	0.50	0.83	−65	32	0.22	698.2	0.26		F	0.50	0.89	41	33	0.26	618.5	0.90
ES									ES
400 ms	W	0.82	1.00	22	42	0.27	583.3		400 ms	W	1.00	0.85	46	35	0.40	757.3
	F	1.00	0.76	−90	43	0.25	584.7	0.10		F	1.00	0.85	46	35	0.40	757.3	1.00
	F	0.50	0.89	−24	46	0.15	591.8	<.001*		F	0.50	0.87	38	42	0.14	784.7	<.001*
200 ms	W	0.69	1.03	34	41	0.24	610.7		200 ms	W	0.83	1.10	−66	41	0.36	666.2
	F	1.00	0.61	−168	42	0.19	614.3	<.01*		F	1.00	0.86	48	41	0.35	667.6	0.09
	F	0.50	1.04	38	42	0.19	614.5	<.05*		F	0.50	1.17	−98	45	0.22	679.2	<.001*
100 ms	W	0.69	1.07	62	33	0.39	657.1		100 ms	W	0.88	1.14	−84	38	0.39	648.3
	F	1.00	0.66	−135	34	0.33	662.8	<.001*		F	1.00	0.96	1	39	0.38	649.2	0.17
	F	0.50	1.16	107	34	0.32	664.6	<.001*		F	0.50	1.02	−24	44	0.18	667.3	<.001*

Model W is the model where α was free to vary.

Model F is a model where the value of α was fixed at either .5 or 1.0.

Slope and Int are the values of the slope and intercept of the given model (m and b in eq. A1).

SD is the root mean square error (RMSE) about the best fit line given by the model.

L the negative log of the maximum likelihood of the given model (eq. A2).

p values were obtained from testing the fit of Model W relative to the fits of two different versions of model F where α was fixed to be either .5 or 1.0 (df=1, see equation A4).

^*indicates Model W is a significantly better fit than Model F.

Experiment 2b. Saccades to disc clusters without masks

The data described above were collected using a mask because we wanted the stimulus to be the same as that used in the perceptual experiments, where a mask was needed to limit processing time. Masks, however, produce problems for saccades because whenever saccades land after a mask appears (a frequent occurrence with the shorter display durations; see mean latencies in Tables 1 and 2) the saccadic system is deprived of the post-saccadic feedback needed to maintain appropriate gain (the ratio between target eccentricity and saccade size) (McLaughlin, 1967; Wallman & Fuchs, 1998; Bahcall & Kowler, 1999, 2000). This raises the question of whether the mask also may have impaired the ability to filter out the distractors.

Two observers, SDK and ES, were tested in the same experiment as above (Experiment 2a), but without masks. The critical display remained visible until the end of the 1.5 second trial. Given that concern about the role of the mask was greatest for the shorter display durations (100 ms and 200 ms), subjects were instructed to try to keep saccadic latencies short. After data were collected, trials were divided into two sets. The latencies in the first set ranged between 100 and 180 ms (mean=143 ms, SD=21, N=562 for ES; mean=146 ms, SD=19, N=1052 for SDK). Latencies in the second set ranged between 180 and 280 ms (mean=216 ms, SD= 25, N=378 for ES; mean=222 ms, SD=28, N=1054 for SDK). Trials with latencies > 280 ms (7% for ES and 12% for SDK were not analyzed.

Removing the mask led to better performance when the target discs were presented alone. Slopes of the straight lines fit to the scatterplots relating landing position to target COG were not significantly different from 1, and standard deviations of landing positions around the best fit line decreased to about 4–6% of eccentricity (Table 3). Thus, allowing normal post-saccadic feedback improved the accuracy and precision of saccades relative to the target COG when the target discs were presented alone, even when processing time (which was limited by saccadic latency) was <= ~ 220 ms, equivalent to that available in Experiment 2a when the critical display was followed by masks.

Table 3.

Parameters of linear fits: No mask condition (Experiment 2b).

No Mask: Target Alone
Leftward							Rightward
	Slope	Intercept	SD	R2	Latency (ms)	N		Slope	Intercept	SD	R2	Latency (ms)	N
SDK							SDK
Short	0.94 [±0.07]	−31 [±36]	20	0.71	147 (19)	248	Short	0.99 [±0.09]	3 [±41]	25	0.66	148 (20)	269
Long	1.01 [±0.08]	1 [±37]	21	0.74	224 (27)	241	Long	1.03 [±0.08]	−19 [±37]	23	0.70	221 (29)	299
ES							ES
Short	0.85 [±0.13]	−36 [±61]	25	0.54	140 (21)	148	Short	0.90 [±0.15]	32 [±72]	28	0.53	146 (21)	129
Long	1.03 [±0.17]	27 [±82]	26	0.64	213 (22)	79	Long	1.07 [±0.15]	−35 [±71]	27	0.64	217 (28)	115
No Mask: Target and Distractor
Leftward							Rightward
	Slope	Intercept	SD	R2	Latency	N		Slope	Intercept	SD	R2	Latency	N
SDK							SDK
Short	0.48 [±0.07]	−259 [±36]	22	0.36	145 (19)	298	Short	0.55 [±0.09]	217 [±43]	25	0.38	147 (20)	237
Long	0.84 [±0.08]	−79 [±40]	23	0.64	220 (27)	228	Long	0.79 [±0.08]	100 [±36]	24	0.60	223 (29)	286
ES							ES
Short	0.54 [±0.13]	−186 [±64]	27	0.31	140 (21)	151	Short	0.56 [±0.16]	203 [±75]	29	0.28	148 (22)	134
Long	0.98 [±0.22]	5 [±107]	32	0.48	219 (26)	83	Long	0.84 [±0.20]	72 [±95]	31	0.41	215 (25)	101

Parameters (slope, intercept) of the best fit straight lines for scatterplots of saccadic landing position vs. the center of gravity of the target discs, when target discs were presented alone and with interleaved distractor discs. Numbers in parentheses denote 95% confidence intervals. Stimuli were not masked. Trials were divided according to saccadic latency; ‘Short’: latency < 180 ms and ‘Long’: latency > 180ms.

SD is the root mean square error (RMSE).

Removing the mask, however, did not improve the ability to screen out the distractors. Applying the weighted COG model described above to the data obtained in the unmasked condition produced values of the weighting parameter α that were almost the same as those found for the masked condition with equivalent processing times (Fig. 5). The obtained values of α without masks were, once again, significantly different from 1 and significantly different from .5 (Table A2).

Table A2.

Results of fitting the weighted CoG model to the data for the no-mask condition (experiment 2b).

Leftward									Rightward
	Model	α	Slope	Int.	SD	R2	L	p		Model	α	Slope	Int	SD	R2	L	p
SDK									SDK
Short	W	0.63	0.90	−58	20	0.50	1310.5		Short	W	0.63	1.02	−12	22	0.52	1069.7
	F	1.00	0.48	−259	22	0.36	1347.7	<.0001*		F	1.00	0.55	217	25	0.38	1100.1	<.0001*
	F	0.5	0.923	−48.5	21	0.45	1323.507	<.0001*		F	0.5	1.056	−29	23	0.47	1082.064	<.0001*
Long	W	0.82	1.09	40	22	0.66	1024.6		Long	W	0.79	1.09	−46	23	0.64	1296.7
	F	1.00	0.85	−79	23	0.64	1033.7	<.0001*		F	1.00	0.79	100	24	0.60	1311.6	<.0001*
	F	0.5	1	76.6	28.5	0.42	1087.537	<.0001*		F	0.5	1	−83	28.8	0.41	1366.403	<.0001*
ES									ES
Short	W	0.66	0.96	15	24	0.44	696.5		Short	W	0.72	0.90	36	28	0.34	634.8
	F	1.00	0.54	−186	27	0.31	711.6	<.0001*		F	1.00	0.56	203	29	0.28	640.6	<.001*
	F	0.5	0.921	−7.38	26	0.36	705.816	<.0001*		F	0.5	0.846	60.1	30	0.24	644.079	<.0001*
Long	W	0.76	1.41	208	30	0.54	400.9		Long	W	0.93	0.92	32	31	0.42	490.3
	F	1.00	0.98	5	32	0.48	406.2	<.005*		F	1.00	0.84	72	31	0.41	490.5	0.5
	F	0.5	1.328	172	35.8	0.36	414.823	<.0001*		F	0.5	0.817	81	37.4	0.15	509.043	<.0001*

Model W is the model where α was free to vary.

Model F is a model where the value of α was fixed at either .5 or 1.0.

Slope and Int are the values of the slope and intercept of the given model (m and b in eq. A1).

SD is the root mean square error (RMSE) about the best fit line given by the model.

L the negative log of the maximum likelihood of the given model (eq. A2).

p values were obtained from testing the fit of Model W relative to the fits of two different versions of model F where α was fixed to be either .5 or 1.0 (df=1, see equation A4).

^*indicates Model W is a significantly better fit than Model F.

While eliminating the mask did not affect the value of α, it did result in less overall saccadic variability, shown by the smaller standard deviations of landing position around the weighted COG (SD’s in no-mask condition were 4–6% of eccentricity, Table A2. SD’s in the masked condition were 6–9% of eccentricity, Table A1). The reduction in overall variability, similar to that observed when target elements were present alone, without comparable changes in weighting parameter α, suggests that the mask in Experiment 2a was detrimental to saccades in ways unrelated to the selection of target elements.

These results show that selection of interleaved target elements among distractors is effective, but not perfect, even with brief processing times and no mask following the critical display.

Experiment 3. Dual task: Saccadic localization and concurrent perceptual judgments of mean size

This dual-task experiment uses the same stimuli as Experiment 2a (400 ms critical frame duration). Observers made a saccade to the set of designated target discs while trying to estimate the mean size of either the target set, or, in separate experimental sessions, the distractor set. The purposes of this dual-task experiment were to: (1) find out whether the attentional filtering needed to eliminate the effects of distractors on saccades also affected perceptual performance, and (2) determine whether a mean size estimation task allows greater perceptibility of non-target elements than the perceptual tasks used in prior studies of saccades and perceptual attention.

There were 3 dual-task conditions tested in separate sessions: (1) saccades and judgments made using the same set of discs; (2) saccades and judgments made using different sets of discs, where priority was given to the saccadic task (“emphasize saccade”), and (3) saccades and judgments made using different sets of discs, where priority was given to the perceptual task (“emphasize percept”).

Figure 6 shows the dual-task results in the form of Attentional-Operating Characteristics (AOC’s), in which saccadic performance is plotted along the abscissa and perceptual performance along the ordinate. Saccadic performance is represented by the weighting parameter α (see Eq. 1) representing the relative weight assigned to target discs. (Table A3 summarizes the results of fitting the weighted COG model to the data.) Perceptual performance is represented by the slope of the psychometric functions at the 50% point. Performance when each task, saccadic or perceptual, was performed alone is shown by the data points plotted along each axis line. The intersection of the single task results (the dashed lines) represents the independence point, i.e., the performance expected if both tasks can be done as well concurrently as when they were done alone (Sperling & Melchner, 1975).

Figure 6.

Attentional Operating Characteristics. Saccadic performance (represented by the value of weighting parameter α, Eq. 1) vs. Perceptual performance (represented by slope of the psychometric functions at the 50% point). Performance plotted along each axis comes from single-task (saccadic or perceptual) results. Intersection of single-task results (dashed line) is the independence point. Remaining data points show dual-task results (saccadic and perceptual task concurrently) when saccades and perceptual judgments were based on the same set of elements (triangle), or saccades and perceptual judgments were based on different sets of elements under instructions to give higher priority to the saccadic task (diamonds) or to the perceptual task (squares). Each datum point is based on approximately 100 observations.

Table A3.

Results of fitting the weighted CoG model to the data obtained in the dual-task conditions (Experiment 3).

Leftward								Rightward
Conditio n	α	Slope	Int	SD	R2	L	p	α	Slope	Int	SD	R2	L	p
M L								M L
Saccadic Task A lone	0.87	0.95	−3	31	0.42	686.9		0.81	1.27	−129	34	0.52	688.8
Dual Tasks:
Same Target Set	0.78	1.06	48	30	0.46	1342.7	<.05*	0.81	1.23	−112	33	0.51	1520.1	0.96
Different Target Sets: ES	0.66	1.21	123	30	0.45	1378.2	<.001*	0.79	1.07	−35	31	0.43	1442.0	0.56
Different Target Sets: EP	0.49	0.98	24	29	0.32	946.3	<.001*	0.60	0.84	66	30	0.25	928.6	<.001*
GT								GT
Saccadic Task A lone	1.00	0.87	−51	36	0.40	1723.3		0.95	1.04	−28	36	0.46	1604.8
Dual Tasks:
Same Target Set	0.78	1.07	43	33	0.42	2382.4	<.001*	0.79	1.13	−69	36	0.40	2352.4	<.001*
Different Target Sets: ES	0.81	1.04	26	36	0.35	2423.8	<.001*	0.76	1.11	−63	36	0.38	2350.5	<.001*
Different Target Sets: EP	0.86	1.05	27	38	0.37	2402.6	<.01*	0.91	0.98	12	35	0.42	2232.8	0.43
SDK								SDK
Saccadic Task A lone	0.67	1.20	108	27	0.50	633.0		0.72	1.15	−77	31	0.38	699.7
Dual Tasks:
Same Target Set	0.74	0.99	8	20	0.61	1710.5	<.001*	0.77	1.04	−31	23	0.57	1829.5	<.05*
Different Target Sets: ES	0.62	1.10	64	23	0.51	1851.6	<.05*	0.70	0.96	5	25	0.42	1769.9	0.57
Different Target Sets: EP	0.53	0.99	17	22	0.47	1773.5	<.001*	0.61	1.02	−28	24	0.44	1715.8	<.001*

ES: Emphasize Saccade

EP: Emphasize Percept

Slope and Int are the values of the slope and intercept of the given model (m and b in eq. A1).

SD is the root mean square error (RMSE) about the best fit line given by the model.

L the negative log of the maximum likelihood of the given model (eq. A2).

p values were obtained fro m testing the fit of the weighted COG Model W relative to a model F where ^α was set to the value obtained when the saccadic task was done alone (df=1, see equation A4).

^*indicates Model W is a significantly better fit than Model F.

The inverted triangles in the AOC’s show saccadic and perceptual performance when both were based on the same set of discs. For GT’s saccadic performance and ML’s leftward saccades values of α were significantly smaller when concurrent perceptual judgments were made about the target elements (see Fig. 6 and Table A3). SDK’s α values were larger when the perceptual task was added. None of the observers showed decreased levels of perceptual performance when doing both saccadic and perceptual tasks on the same set of target elements (see Appendix and Table A3 for the statistical analyses).

There were large losses in the perceptual performance in all observers when saccades and perceptual judgments were based on different sets of elements. Under the “emphasize saccade” instruction (diamond shaped symbols), where priority was given to the saccadic task, perceptual performance suffered greatly, with slopes of the psychometric functions smaller by about a factor of 10 from what was observed when saccades and judgments concerned the same set of discs. With these values, perceptual performance was near chance levels. Saccadic performance suffered as well in some cases, with significant decreases in α for ML (leftward saccades) and GT (both directions) relative to saccadic performance in the single task case.

The attempts to shift some attention away from the saccadic targets (even at a potential cost to saccades) in the “emphasize percept” condition was expected to improve perceptual performance. We found, however, no improvement (see the square symbols in Fig. 6). Some attention may have shifted away from the target elements, as shown by decreased values of weighting parameter α for ML and SDK. But this sacrifice of saccadic performance did not result in improved perceptual judgments. This means that none of our observers could find a strategy that would allow them to efficiently distribute attention between the two fields of elements. The saccadic and perceptual tasks were completely incompatible when performed on different sets of elements.

Experiment 4: Perceptual judgments while attending to both disc sets

The inability to direct a saccade to one set of discs while concurrently making judgments about the mean size of the other set raised the question of whether this incompatibility was limited to concurrent saccadic and perceptual tasks. We, therefore, conducted a new experiment similar to that of Chong and Treisman (2005a) in which observers did not know in advance of each trial which set of discs they would have to judge, and thus were encouraged to encode and remember the mean sizes of both sets of dics. This task was performed during steady fixation (no saccades to either set of discs).

The experimental stimuli and procedures were the same as those for the single task perceptual experiment (Experiment 1), except that the initial fixation disc was gray, and the color of the discs whose mean size had to be reported was disclosed by a change in the color of the fixation disc to either red or green after the mask was removed. Presentation duration was 200 ms.

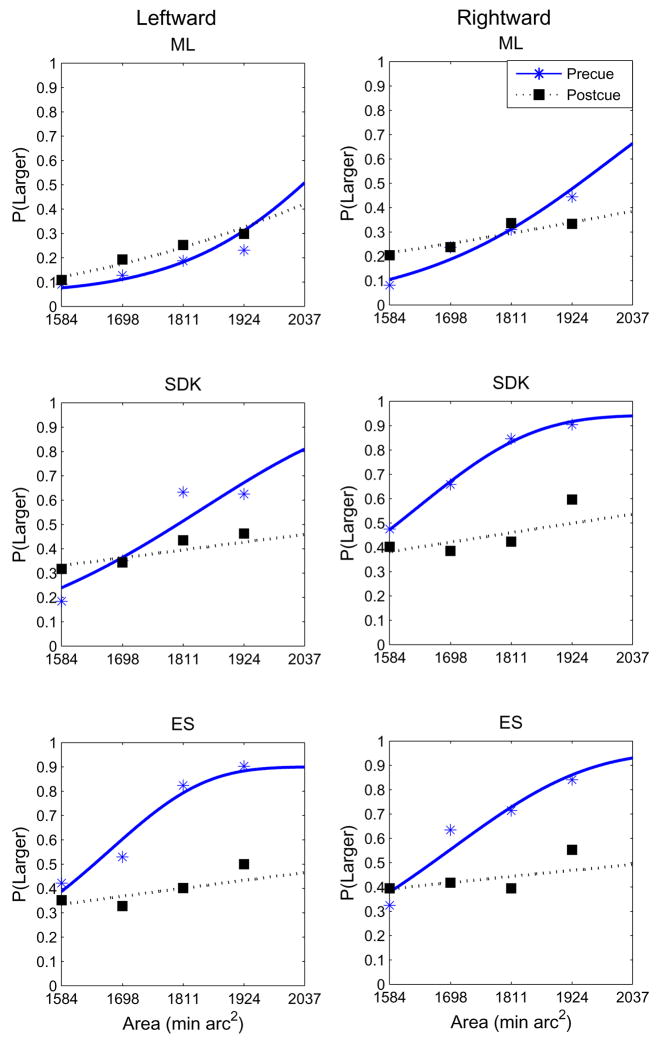
Figure 7 shows that the ability to discriminate the size of the discs was much poorer when it was not known in advance which set would have to be reported. Thus, it was not possible during the limited presentation time to perceive and remember the mean sizes of both sets of discs. These results are not in agreement with those of Chong & Treisman (2005a), but are compatible with the difficulties observers had in attending to both element sets in Experiment 3, although the processes responsible for the performance losses in Experiments 3 and 4 are not necessarily the same.

Figure 7.

Psychometric functions when a pre-cue indicated which element set was to be reported and when there was no pre-cue. Each function shows the proportion of trials in which the target discs were judged as having a larger mean size than the reference (fixation) disc as a function of the mean area of the target disc set. Data were fit by Weibull functions obtained using the Psignifit algorithm (Wichman & Hill, 2001). Target elements were to the left or right of fixation. Each datum point in the psychometric functions is based on approximately 40 observations.

Discussion

Making accurate saccades to selected objects or to configurations of elements in a crowded visual field requires a selective filter to determine the effective target of the saccade, and a spatial pooling process to compute the saccadic landing position by averaging across the selected target. Previous findings of saccadic errors when attempting to look at a target in the midst of distractors raised questions about the contribution of the proposed selective filter, and suggested that spatial pooling could occur indiscriminately. The present results show that filtering is compatible with spatial pooling. We tested a stimulus consisting of interleaved target and distractor elements. Thus, there was no boundary separating the two sets of elements, and selection rested solely on the perceptual property (a color difference, in this case) that distinguished target and nontarget elements. We found that, despite the absence of the boundary, it was possible to reduce or eliminate the influence of distractors on the saccades.

The ability to reduce the effects of the interleaved distractors on saccades argues against automatic or indiscriminate pooling of signals across a given spatial region. The present results show that effective filtering is possible even in the absence of location cues that distinguish the saccadic target from the distractors. Analogous results have been obtained for smooth pursuit, where superimposed targets and distractors were overlapping fields of moving random dots, distinguishable solely by differences in their patterns of motion, rather than by spatial location (Kowler, Van der Steen, Collewijn & Tamminga, 1984; Niemann, Ilg, & Hoffman, 1994).

Filtering was not perfect

Filtering, however, was not perfect. The distractors interfered with saccadic performance to some degree, with their effects varying across observer and processing time. The effect of the distractors on saccades was captured by a weighted COG model in which a maximum likelihood method (Appendix) was used to find the relative weights of target and distractor elements that best predicted the set of obtained saccadic landing positions. The obtained weights approached 1 (no influence of distractors) for the longest processing time (400 ms), and were typically about .7 for shorter processing times.

Imperfect filtering, however, was not unique to saccades. Perceptual performance in the mean size estimation task during steady fixation (Experiment 1) showed that distractors produced either a small reduction in discriminability (for observer SDK) or a small bias to report that the sizes of the discs were larger than the reference size (for both SDK and ES). ML showed no effect of distractors on perceptual performance, and a very small effect of the distractors on saccades. The fact that distractors had some influence on the perceptual judgments suggested a limit on the ability to segregate and attend to the set of target elements. We cannot, however, rule out “leakage” of unattended distractor elements into the computation of the saccadic endpoint.

The effect of attending to the saccadic target on perception

Results of the dual-task experiment (Experiment 3) showed that it was not possible to plan a saccade to one set of elements while making accurate perceptual judgments about the other set. Perceptual judgments about the set of non-targets fell to near chance levels as saccades to the targets were being planned. Attempts to shift some attention away from the saccadic targets resulted in poorer saccadic performance (decreased weight assigned to target elements), but no consequent improvement in perceptual performance. The presence of nontargets by themselves was not responsible for the perceptual loss, as shown by the superior performance in the single-task conditions. Thus, the performance losses in the perceptual task during the dual-task condition represented the effects of attention.

Comparable perceptual losses during saccadic preparation have been found for other perceptual tasks, such as character recognition (Kowler et al., 1995; Hoffman & Subramaniam, 1995; Deubel & Schneider, 1996) or orientation discrimination (Gersch et al., 2004), when saccadic and perceptual targets were in different spatial locations. In these previous studies, however, partial shifts of attention from the saccadic to the perceptual targets produced a drop in saccadic performance levels and significant perceptual improvements (Kowler et al., 1995). In fact, even relatively modest changes in saccadic performance led to substantial perceptual gains (see also Khurana & Kowler, 1986). But here we find a different pattern in that there were no perceptual improvements even in the face of large losses in saccadic performance. The lack of any perceptual benefit was surprising. It may reflect strong attentional demands of the mean size task, or it may reflect difficulties in dividing attention between spatially-interleaved (as opposed to spatially adjacent) elements (see also below).

Interference among perceptual tasks

The strong interference between perceptual judgments and saccades when each was based on a different set of elements was echoed in Experiment 4, which required encoding and remembering the mean size of each set during steady fixation. Perceptual performance was near chance levels when the color of the target element set to be judged was not disclosed until the end of the trial. These perceptual results show that difficulty in attending to both element sets was not limited to the pairing of the perceptual judgments with the saccadic task in Experiment 3.

The poor performance in Experiment 4 does not support Chong & Treisman’s (2005a) conclusion that mean size estimates can be performed concurrently on multiple sets of interleaved elements independent of the constraints of an ‘attentional bottleneck’. Among the possible factors contributing to the differences between our results and Chong & Treisman’s is that we used a mask to limit processing duration, thus performance was limited by the number of elements that could be successfully encoded and remembered prior to the appearance of the mask (Liss & Reeves, 1983). Another difference in procedure was that our stimuli were presented within 4 deg regions at an average eccentricity of 8 degrees, whereas Chong & Treisman’s stimuli were larger and centered about the fovea. Further work will be needed to evaluate the stimulus parameters responsible for the differences in the results. Whatever the answer proves to be, the fact that stimulus parameters have become an issue shows that there are limits to the ability to concurrently evaluate mean stimulus properties during periods of time comparable to typical fixation pauses of the eye, and that the encoding of mean values does not always occur prior to an attentional bottleneck, but instead is subject to attentional constraints.

A shared attentional filter

The ability to reduce or eliminate the influence of the interleaved distractor elements on saccades does not support indiscriminate spatial pooling over targets and distractors. Our results demonstrate attentional control over saccades when targets and distractors are distributed across the same spatial region. The attentional filter, combined with spatial pooling, makes it possible to aim saccades accurately to chosen targets in crowded visual environments.

Concurrent perceptual judgments of mean value also depended upon attention, either during steady fixation or during pre-saccadic intervals. Estimation of mean value appeared to be a task that could have escaped the attentional limits connected to the planning of saccades, but it did not. The issue of whether any significant perceptual judgment is independent of pre-saccadic attention shifts when we inspect the visual environment remains to be resolved.

Appendix

In the weighted center-of-gravity model (Model W) saccadic landing position on a given trial, P_t, is a linear function (slope m, intercept b) of the weighted center-of-gravity of the disc locations, where the weight assigned to the target disc locations (T_t) is α and the weight assigned to the distractors (D_t) is 1-α.

$$P_t(\alpha ,m,b)=m(\alpha T_t+[1-\alpha ]D_t)-b$$ (A1)

Parameter values were determined by maximizing the likelihood expression (L_w) where

$$L_w\left(\alpha ,m,b\mid {\left\{S_t\right\}}_{t=1}^N\right)={\prod }_{t=1}^n\frac{1}{\sqrt{2\pi \sigma }}exp\frac{-{[P_t(\alpha ,m,b)-S_t]}^2}{2{\sigma }^2}$$ (A2)

and

$$\sigma =\sqrt{\frac{{\displaystyle \sum _{t=1}^n}{(P_t(\alpha ,m,b)-S_t)}^2}{N-1}},$$ (A3)

S_t is the landing position of the saccade for a given trial t, P_t is the predicted landing position (eq. 1) on trial t, and N is the number of trials. The values of α, m and b that maximized the value L_w were determined by a constrained multidimensional nonlinear minimization function (fmincon) implemented in Matlab. Parameter values are shown in Table A1 for the masked condition (Experiment 2a), Table A2 for the no-mask condition (Experiment 2b) and Table A3 for both the single and the dual task conditions of Experiment 3.

Maximum likelihood values were also computed for a second two-parameter model (Model F) using an identical procedure, except that the likelihood (L_F) was computed with α set a fixed value. The value of α was set to 1 (no effect of distractors) or to .5 (equal weighting of target and distractors) for Experiments 2a and 2b. For Model F in Experiment 3, a maximum likelihood value was computed for the dual-task conditions while α was set to the value obtained in the single-task (saccades only) condition.

To determine whether allowing the parameter α to vary in Model W provided a significantly better fit to the data than fixing α in Model F, the following statistic was computed:

$$\mathrm{\Psi }(\text{W},\text{F})=-2ln\left[\frac{\mathrm{\Lambda }(F)}{\mathrm{\Lambda }(W)}\right]$$ (A4)

where Λ(F) is the maximized likelihood value calculated for Model F and Λ(W) the maximized likelihood value calculated for Model W. Ψ(W,F) is asymptotically distributed as chi-square (degrees of freedom equal to 1, the difference in the number of free parameters of the two models) under the null hypothesis that the more restrictive model F is correct (See McGowan et al., 1998; Hoel, Port and Stone, 1971, for further details). Thus, values of Ψ(W,F) too large to have plausibly come from a chi-square distribution with 1 degree of freedom provide evidence against the null hypothesis, and thus indicate that allowing the target weight α to take on values determined by maximizing the likelihood expression (eq. A2) significantly improved the fit of the model. The significance levels obtained for the 3 different experiments (Experiments 2a, 2b and 3) are shown in Tables A1, A2, and A3, respectively.