Invited Review Article: Imaging techniques for harmonic and multiphoton absorption fluorescence microscopy

Abstract

We review the current state of multiphoton microscopy. In particular, the requirements and limitations associated with high-speed multiphoton imaging are considered. A description of the different scanning technologies such as line scan, multifoci approaches, multidepth microscopy, and novel detection techniques is given. The main nonlinear optical contrast mechanisms employed in microscopy are reviewed, namely, multiphoton excitation fluorescence, second harmonic generation, and third harmonic generation. Techniques for optimizing these nonlinear mechanisms through a careful measurement of the spatial and temporal characteristics of the focal volume are discussed, and a brief summary of photobleaching effects is provided. Finally, we consider three new applications of multiphoton microscopy: nonlinear imaging in microfluidics as applied to chemical analysis and the use of two-photon absorption and self-phase modulation as contrast mechanisms applied to imaging problems in the medical sciences.

INTRODUCTION

Second and third harmonic generations (SHG and THG, respectively) and two-photon excitation fluorescence (TPEF) are currently the most widely used contrast mechanisms in nonlinear optical microscopy. The nonlinear contrast is based on second and third-order nonlinear light-matter interactions that are induced at the focus of a high numerical aperture (NA) microscope objective. Since these nonlinear optical effects are proportional to the second or third power of the fundamental light intensity, essentially only the light at the focal plane of the optic efficiently drives the nonlinearity. This effectively eliminates out-of-focus contributions and results in the optical sectioning inherent to nonlinear imaging techniques. Therefore, it is a straightforward task to generate a sharp, two-dimensional (2D) image when nonlinear optical signals are utilized. The excitation beam is simply raster scanned across the focal plane, and the signal intensity (from the desired optical nonlinearity or nonlinearities) is measured as a function of this beam position. Extrapolation to three-dimensional (3D) images requires only one further step recording a series of these images as a function of depth by either scanning the specimen through the focal plane (stepping axially) or vice versa.

These nonlinear light-matter interactions can be described by a polarization P, induced by an intense optical electric field E,¹

$$\mathit{P}={\chi }^{\left(1\right)}\mathit{E}+{\chi }^{\left(2\right)}\mathit{E}\mathit{E}+{\chi }^{\left(3\right)}\mathit{E}\mathit{E}\mathit{E}+\cdots ,$$ (1)

where χ⁽¹⁾ is the linear susceptibility tensor representing effects such as linear absorption and refraction, χ⁽²⁾ is the second-order nonlinear optical susceptibility, and χ⁽³⁾ is the third-order nonlinear susceptibility. SHG is a second-order process, whereas, TPEF and THG are both third-order processes. Notably, Eq. 1 shows that the same excitation source can induce several nonlinear effects simultaneously.

In the microscope, nonlinear signals are induced in a femtoliter focal volume. This reduces the sampled molecular ensemble as compared to macroscopic measurements, where the nonlinear responses are observed over a large volume. Microscopy measurements can reveal unique molecular features of microscopic objects that are otherwise obscured by the ensemble-averaged measurements. For example, SHG is symmetry forbidden in homogeneous suspensions even for noncentrosymmetric structures;¹ however, if the laser focal volume is smaller than the investigated object, spatially confined excitation at an interface between two media provides centrosymmetry breaking that reveals the second-order nonlinearity of the molecules.^{2, 3} Therefore, molecular aggregates and cellular structures that form interfaces can be readily investigated with SHG microscopy.

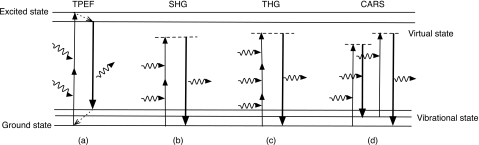
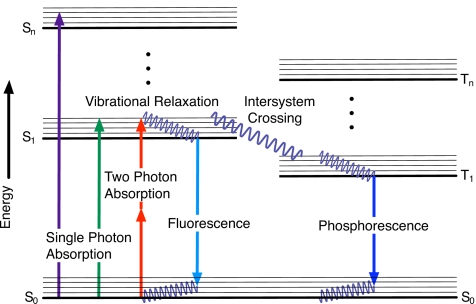
Nonlinear optical effects are characterized by new components of the radiated E-field generated from the acceleration of charges in the media as the nonlinear polarization [second, third, and higher terms in Eq. 1] is driven by the incident electric field. The generation of harmonics is a parametric process described by a real susceptibility. It differs significantly from nonparametric processes, such as multiphoton absorption, which have a complex susceptibility associated with them.¹ For parametric processes, the initial and final quantum-mechanical states are the same, as illustrated in Fig. 1 panels (b)–(d). In the time between these states, the population can momentarily reside in a “virtual” level (represented by dashed horizontal lines in Fig. 1), which is a superposition of one or more photon radiation fields and an eigenstate of the molecule. Since parametric processes conserve photon energy, no energy is deposited into the system. In nonparametric processes, the initial and final states are different as represented in Fig. 1a, so there is a net population transfer from one real level to another. Nonparametric interactions lead to photon absorption that may induce effects such as bleaching and thermal damage; however, near resonant parametric processes are resonantly enhanced and at these wavelengths the absorption of the laser radiation also increases. A tradeoff between the laser intensity and the choice of radiation wavelength is needed in order to obtain the strongest nonlinear signals while minimizing bleaching and∕or photodamage.

Figure 1.

Schematic representation of nonlinear processes: (a) TPEF, (b) SHG, (c) THG, and (d) CARS. Wiggly lines represent incoming and radiated photons, dashed lines represent virtual states, and dashed arrows nonradiative relaxation processes.

It is important to know the nonlinear absorption spectrum of the sample in order to make a good choice of optimal wavelength for excitation. For biological samples with absorption in the visible spectral range, the excitation wavelength has to be tuned away from the linear absorption bands of the sample. Usually, infrared (IR) excitation wavelengths are employed for this purpose but they also provide deeper penetration of the light into biological tissue, reaching up to a few hundred microns in highly scattering specimens.⁴ The noninvasiveness of nonlinear microscopy has been demonstrated by imaging fruit fly embryos during development using harmonic generation⁵ and by imaging periodically contracting cardiomyocytes⁶ and myocytes from fruit fly larva.⁷

Although TPEF is the most frequently used contrast mechanism in nonlinear microscopy, the first nonlinear microscope constructed was based on SHG.^{8, 9} The applications of nonlinear microscopy multiplied after the initial demonstration of a TPEF microscope and its application for biological imaging by Denk et al.¹⁰ The introduction of stable solid state titanium:sapphire (Ti:sapphire) femtosecond lasers further facilitated the development of nonlinear microscopy. THG microscopy was introduced by Barad et al.¹¹ in 1997. Since then, the use of several other nonlinear contrast mechanisms such as sum frequency generation,¹² the optical Kerr effect,¹³ and coherent anti-Stokes Raman scattering (CARS)^{14, 15, 16} has been implemented [see Fig. 1d]. Also, different nonlinear contrast mechanisms have been combined into a single multicontrast instrument. For example, simultaneous detection of TPEF, SHG, and THG signals has been realized for chloroplasts^{4, 17} and cardiomyocytes.¹⁸ These simultaneously obtained images can be correlated and compared, giving rich information about the structural architecture and molecular distribution within the sample.^{19, 20}

Nonlinear microscopy is a rapidly growing area of research. With the exception of TPEF, which is firmly established as a valuable approach for biomedical imaging, other nonlinear contrast mechanisms are going through the stage of major technical development. Harmonic generation microscopy applications are partly limited by the lack of commercial instrumentation offered by the major microscope manufacturers. Most of the work on nonlinear microscopy has been published in engineering literature; however, biological investigations are starting to emerge, especially with SHG detected in the excitation (epi) direction, which can be readily detected with modifications to commercially available TPEF microscopes.

In Sec. 2 we introduce and discuss various aspects of the instrumentation involved in nonlinear microscopy. First, we introduce the general layout for a multicontrast microscope. Then, we discuss the measurement of ultrashort laser pulses at the focus of a high NA optic, an essential tool for characterizing and optimizing the instrument performance. The section concludes with a review of the different scanning mechanisms and techniques in use for high-speed imaging. The second major section of this work presents introductions to, and discussions about, the applications of TPEF, SHG, THG, as well as multicontrast microscopy. Finally, some recent applications of TPEF for chemical analysis and developments involving new nonlinear contrast mechanisms in microscopy are discussed.

INSTRUMENTATION

Nonlinear microscopes share many common features with confocal laser scanning microscopes. In fact, many research groups have implemented multiphoton excitation fluorescence by coupling femtosecond or picosecond lasers into a confocal scanning microscope^{21, 22} and using a nondescanned port for efficient detection of the nonlinear signal (see discussion by Zipfel et al.²³). The functionality of multiphoton microscopes can be enhanced by implementing detection schemes to allow multicontrast detection in the transmission and∕or excitation direction. The first part of this section describes a typical layout for such instrument, followed by an introduction to techniques that allow the characterization of the excitation laser pulses at the focal plane of a high NA objective. Such characterization is critical not only for optimal nonlinear imaging but also, as explained later, for reducing the effects of photobleaching in TPEF. Finally, this section concludes with a discussion of factors that limit high-speed imaging and, in particular, we offer a review of scanning techniques.

Multicontrast microscope architecture

Traditionally, three parallel detection channels have been used in confocal and TPEF microscopes, where the emission signal is divided into different spectral ranges by dichroic mirrors and optical filters or by separating the signal with a dispersive optical element. Similarly, spectral separation can be applied for detecting second and third harmonic signals along with fluorescence. Backward scattered and backward coherently generated harmonics are usually much weaker than the forward generated signals; therefore, forward detection of harmonics can be accomplished with lower excitation intensities. On the other hand, detection in transmission requires a more extensive modification of the scanning microscope setup. The easiest way of building a transmission mode harmonic generation microscope is by using a high NA condenser, available on some commercial microscope models, followed by the detector.^{21, 24} Three-channel simultaneous backward and forward detection of harmonics requires extensive modifications of commercial microscopes²⁵ or construction of a whole setup from scratch.¹⁹ The instrumentation of nonlinear microscopes has been extensively reviewed by different authors.^{17, 25, 26}

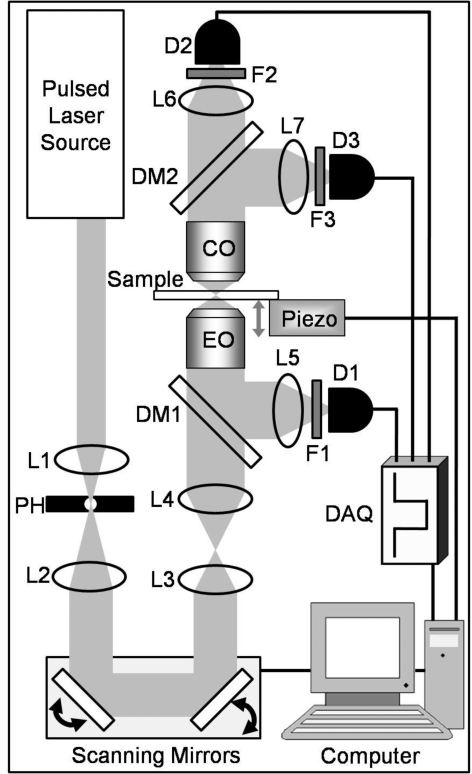
Figure 2 presents the optical outline of a multicontrast nonlinear microscope capable of TPEF, SHG, and THG detection. The laser is coupled to the microscope via two mirrors (not shown). Inside the microscope, the beam is expanded with a telescope (lenses L1 and L2) to fill the clearance aperture of the scanning mirrors. The same telescope also spatially filters the beam with an appropriate pinhole located at the focus between the two lenses. The expanded beam is coupled to two galvanometric scanning mirrors that can raster scan the beam in lateral directions. A second telescope, consisting of an achromatic lens (L3) and a tube lens (L4), is used to expand the beam to match the entrance aperture of the excitation objective (EO). The tube lens is designed to correct for aberrations of the objective, thus it is important to match lens and objective from the same manufacturer. After the second telescope, the collimated beam is transmitted through the dichroic mirror (DM1) and is coupled into the EO. Almost all nonlinear microscopes are constructed using commercially available refractive objectives; however, since most objectives are designed for the visible spectral range, care must be taken to choose objectives that have been designed to work in the infrared region.²⁷ For achieving optimal resolution with an objective, a high uniformity of the excitation beam intensity across the entrance aperture of the optic is required. Overfilling the entrance aperture often helps to achieve good uniformity and meet the specified NA of the objective. It is recommended to test the alignment of the microscope on a regular basis by recording the lateral and axial point spread functions (PSFs).²⁸

Figure 2.

Schematic of a multicontrast microscope (not to scale). L: lenses; PH: pinholes; DM: dichroic mirrors; EO: excitation objective; F: optical filter; D: detector; CO: collection objective; DAQ: data acquisition card.

The generated nonlinear signals can be collected with the same microscope objective EO, separated by the dichroic mirror (DM1), which is specifically chosen for the given fundamental and fluorescence or harmonic emission wavelengths and focused with a lens (L5) through the filter (F1) onto the detector (D1) (see Fig. 2). Interference or band pass filters are used in front of the detector for filtering scattered fundamental light and spurious signals outside the desired bandwidth. The detectors might consist of single element devices, such as photomultiplier tubes (PMT) or avalanche photodiodes, or charge-coupled device (CCD) cameras—in this last case, L5 is placed so that it forms the image of interest onto the CCD. When single element detectors are used, pixel and line clock signals must be used to synchronize the data acquisition with the scanner system; for CCD cameras, it is only necessary to synchronize the shutter with the start and end of frame.

It is also possible to detect the signals in the forward direction using a high NA collection objective (CO). The CO has to have a NA similar or higher than the EO in order to achieve optimal collection of the signals. Attention must be given to the transmission curve of CO, especially for THG detection when lasers with excitation wavelengths less than 1000 nm are used. After CO, the collimated beam is passed to the detectors. Either one detector with appropriate filters or several detectors recording different signals separated by dichroic mirrors can be used. Alternatively, the nonlinear optical response can be coupled to a spectrometer, and a whole spectrum can be recorded at each pixel.²⁹ In this case, the harmonic and fluorescence images are constructed by obtaining the pixel intensities from a selected spectral range. In Fig. 2, after CO, the collimated beam is passed through a dichroic mirror (DM2) for separation of SHG and THG signals. The second harmonic is focused onto the detector (D2) by lens (L6) and filtered by the interference filter (F2). Similarly, THG is reflected from dichroic mirror (DM2) and focused onto detector (D3) with lens (L7), after filtration with interference filter (F3).

For single element detection, signal integration, lock-in, or photon counting methods can be employed for recording the nonlinear signal. Most microscope manufacturers use a signal integration approach; however, nonlinear responses that originate from biological samples typically have very low intensities. In most cases less than one photon per excitation pulse is detected. In this situation, photon counting detection becomes the method of choice; however, photon counting can be saturated with high excitation intensities. This has to be taken with caution, but usually does not present a big problem because the excitation power can be reduced or higher scanning rates can be implemented.

For the microscope presented in Fig. 2, a three-channel counter card is used to record the signal from all three detectors simultaneously. The three recorded images can be directly compared and a statistical analysis can be performed on a pixel by pixel basis.¹⁹ A simultaneous detection scheme eliminates the problem of artifacts from signal bleaching or movement of the sample during imaging.

To obtain 3D images, optical sectioning can be performed by translating the sample, moving the EO, or changing the divergence of the collimated beam at the entrance of the EO–which results in focusing at different depths.³⁰ If transmission detection is implemented, the focal volumes of the excitation and COs have to overlap; therefore, axial scanning by translating the sample along the optical axis with a piezoelectric stage (see Fig. 2, piezo) usually gives the best results.

The laser source for a nonlinear microscope has to be carefully chosen for suitability with the particular sample and microscope setup. Parameters such as power output, repetition rate, energy per pulse, and emission wavelength have a direct impact on imaging. An average power of around 10 mW at the sample is typically required for harmonic imaging; however, more power is needed for weak harmonic generation sources as well as for bleaching measurements. The typical transmission of a laser scanning microscope is usually between 15% and 40%. The repetition rate of the laser is another important factor to consider. For constant average powers, the increase in repetition rate must be balanced against the loss in per pulse energy. More importantly, in TPEF measurements, fast repetition rates may not allow relaxation of long lasting molecular excited states which can build up leading to annihilation and may result in reduced fluorescence lifetimes³¹ or in increased intersystem crossing which can lead to photobleaching. Furthermore, if time correlated single photon counting (TCSPC) measurements are used, the repetition period should be several times longer than the measured lifetime. Extended cavity oscillators can be used to increase the signal yield while addressing all these problems.³²

Since many endogenous fluorophores (autofluorophores) absorb light in the visible region and tissue penetration is greater for longer wavelengths, IR lasers are a good choice for nonlinear microscopy. Some examples of autofluorophores are nicotine adenine dinucleiotide (NADH) in muscle cells¹⁹ and chlorophyll in plants.²⁹ For THG excited by laser emission wavelengths under 1000 nm, the microscope coverslips, the CO, as well as the detector focusing lens and interference filters must transmit the UV light. Also, the water absorption lines must be avoided; hence lasers in the 800–1300 nm spectral window are desired. The most commonly used femtosecond lasers are Ti:sapphire, typically they offer pulse durations of around 100 fs and 76–100 MHz repetition rates. Several publications have focused on the benefits of femtosecond Yb:KGd(WO₄)₂ and Cr:forsterite lasers emitting at 1030 and 1250 nm, respectively.^{4, 33} Both lasers provide good penetration into tissue and decreased sample damage for certain biological samples. Due to the high laser stability, pulsed Yb doped fiber lasers emitting around 1030 nm are becoming very attractive and might become the most popular laser sources for nonlinear microscopy in the future.

Characterization of pulses at the focus of a high NA optic

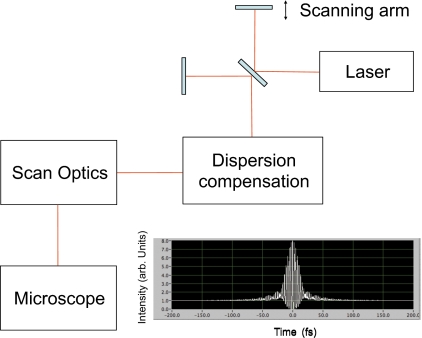
It is critical to efficient nonlinear imaging, especially in the presence of photobleaching (see section about photobleaching in two-photon fluorescence), to create a focus that is transform limited in space and time. However, the pulse needs to be transform limited at the plane of the sample and not at the input to the microscope; thus, it is important to characterize the spatiotemporal focal volume at the full NA of the excitation optic. In general, this means that collinear methods must be used to interrogate the focal volume. A basic system for measuring the pulsewidth at focus is shown in Fig. 3. Essentially, the excitation laser is first tuned to the wavelength and pulsewidth that will be used for imaging. The laser output is directed through a Michelson interferometer. This creates two beams that are fully collinear. One arm of the interferometer needs to be equipped with a rapid scanning stage—this allows the pulses from the two arms to be rapidly sheared against one another as a function of time. The output of the interferometer then goes through any dispersion compensation optics, through the scan optics, and into the microscope. This configuration makes it possible to characterize the focus exactly as it will be used for imaging and to optimize the pulsewidth in real time.³⁴ Lateral shearing interferometers have also been used to characterize the pulsewidth at focus.^{35, 36} This is a compact interferometer design that can be inserted into the beam path much as you would a filter.³⁵

Figure 3.

System schematic for pulse measurement at the focus of high NA optic. By adding a simple Michelson interferometer at the input of the beam path to the microscope system, interferometric autocorrleation traces of the pulse can be made at the focus of the objective in the microscope. A second-order intensity autocorrelation trace is shown, prior to being optimized—the wings of the trace show uncompensated dispersion as a result of the scan optics, and microscope optics.

Independent of the interferometer design, an optical nonlinearity must be introduced at the focal plane of the microscope—this acts as the “gate” and enables collinear, nonlinear intensity correlation measurements. The nonlinear medium can be something as simple as a solution of the fluorophore that will be used to tag the specimen. In this case the signal is produced by TPEF and an interferometric second-order intensity autocorrelation measurement results (see Fig. 3). The fluorophore can be prepared in a simple cell mounted between coverslips—particularly important when using objectives that are designed to image through a standard coverslip glass type and thickness—in this way important aberrations, such as spherical aberration, are properly compensated and the measurement is performed in a manner commensurate with the actual imaging conditions.

Amat-Roldán et al.³⁷ pointed out a particularly useful specimen for performing pulse characterization measurements in microscopes—corn starch. The specimen is entirely innocuous and readily available from your local grocer! Starch granules mounted in water between coverslips produce a strong SHG signal with excitation wavelengths ranging from 700 to 1300 nm—essentially covering the entire tuning range of Ti:sapphire as well as Yb-based and Cr:Fosterite ultrafast lasers. Normally SHG signals are detected in transmission; however, it has been our experience that there is sufficient signal from the starch granules that the measurements can, in fact, be made in the epi direction. By using a SHG signal as opposed to TPEF, more sophisticated pulse characterization is possible. For example, Amat-Roldán et al.³⁷ demonstrated that by spectrally resolving the autocorrelation signal, the phase of the excitation pulse can be extracted. This can be extremely useful in those instances where pulse shape impacts the imaging. TPEF autocorrelation measurements are useful for “tweeking” up the system—but they do not provide an unambiguous determination of the pulse shape, and all phase information is lost.

Another approach that works over an extensive wavelength range and is straightforward to implement is the use of GaAsP (Refs. ^{38, 39}) or ZnSe (Ref. ⁴⁰) photodiodes. When properly mounted in the specimen plane of the EO, they can be used to characterize the pulsewidth through a photocurrent produced by two-photon absorption (TPA) within the photodiode. The pulsewidth can be measured through an autocorrelation measurement, and the spatial focal quality can be determined by scanning the photodiode along the excitation axis. Notably, LaFratta et al.³⁸ have used GaAsP diodes to perform noninterferometric cross-correlation measurements between two lasers—important for any multibeam imaging applications.

THG from a glass coverslip can also be an effective method for pulse characterization resulting in third-order interferometric autocorrelation traces.^{41, 42, 43} Fringe-free, background-free autocorrelation measurements can be made by using two beams that are circularly polarized, but in opposite directions—left and right. The background-free methods enable spatial characterization of the beam not only along the excitation direction but also along the lateral direction as well by performing spatial autocorrelation measurements of the beam—in this case shearing the two beams across one another in space as opposed to time. In background-free mode, if the temporal autocorrelation trace is spectrally resolved, the phase information of the pulse can also be retrieved.⁴⁴

Finally, it should be noted that entirely linear, interferometric methods can be used to characterize the focus.^{40, 45, 46} Jasapara et al. used spectrally resolved interferometry to characterize how 10 fs pulses were distorted when focused by a 205 and a 1005 0.85 NA. objectives. Amir et al. demonstrated how this method can be used in a single-shot configuration to extract the spatial and temporal characteristics of an ultrashort pulse at the focus of a high NA objective.

High-speed multiphoton imaging

The ultimate goal in microscopy is an instrument capable of acquiring 3D images in real time with submicron spatial resolution. Typically real time is understood as at least 30 frames∕s (video rate); nonetheless, for many dynamical processes this speed is insufficient. Therefore, the meaning of “real time” depends on the rate of the particular process that one is ultimately interested in studying. Independent of our definition of real time, the imaging speed is ultimately limited by the excitation and emission cross sections of the sample for the particular nonlinear process involved. In principle one could increase the excitation power to increase the photon yield; however, damage to the sample imposes a hard limit on this approach.

While the signal production rate depends on the nature of the sample, the choice of excitation source will also have an impact in the emitted signal level and ultimately the frame rate that can be achieved as illustrated here. Assuming a typical Ti:sapphire oscillator with a pulse duration of 100 fs, repetition rate of 76 MHz, and an average power of 1 W, for a focal area of 5 μm in diameter, these numbers translate to a peak intensity of 670 GW∕cm²—well above the damage threshold of most specimens. For the sake of argument, we clearly have sufficient per pulse intensity even with modest focus conditions to efficiently excite an optical nonlinearity. As a reference point, if we assume no signal limitations from the sample or collection system and are using our typical laser source, the maximum limit for image production would be 76×10⁶ pixels∕s (corresponding to one excitation pulse per pixel and one photon per excitation pulse). However, if we require an image contrast of 8 bits, at least 255 pulses per pixel are therefore needed. Thus, for a 256 by 256 pixel image the maximum image rate would be approximately 4.6 images∕s. Clearly, methods exist for achieving high frame rates—these numbers simply provide an initial guide as to the potential scaling limitations that are encountered when designing a high-speed imaging system.

In order to estimate a reasonable frame rate, we assumed that only a single photon is produced per excitation pulse. In practice we have found this to be an entirely reasonable assumption, and, in fact, find that this number is even high for many samples! To further illustrate this point consider the following. The number of absorbed photon pairs per excitation pulse can be estimated by the expression¹⁰

$$n\approx \frac{P^2\alpha }{\tau f^2}{\pi }^2\frac{{\text{NA}}^4}{{\left(hc\lambda \right)}^2},$$ (2)

where P is the average laser power, α is the molecular TPA cross section, τ is the pulse duration, f is the laser repetition rate, NA the NA of the objective, and λ is the excitation wavelength. The reported TPA cross sections for a wide array of intracellular absorbers are between 10⁻⁴⁸ and 10⁻⁵⁰ GM (GM, Goppert–Mayer, is the unit for the TPA cross section, 1 GM=10⁻⁵⁰ cm⁴ s photon⁻¹).^{47, 48, 49, 50} Assuming α=10⁻⁴⁹ GM, 5 mW of light at a central wavelength of 800 nm at the sample, a pulse duration of 100 fs, a repetition rate of 76 MHz, focused down with a 1.2 N.A. objective, we would then expect approximately 2.6×10⁶ photon pairs absorbed per second per absorber. This means that only one pair of photons is absorbed per fluorophore for every 29 laser pulses!

In addition to the photons produced per excitation pulse, two other practical factors limit the speed of image acquisition: the scan speed and the detection system. Many systems use a low noise CCD camera for detection because this eliminates the need for synchronization with the scanning device. On the other hand, the use of imaging devices, such as CCD cameras is ineffective at imaging deep into scattering specimens—the scattered light creates an undesirable background. Ultimately the frame rate of the CCD can be a limiting factor. Alternatively, the use of fast detectors, such as PMTs, enables fast acquisition rates even when used with scattering media, at the cost of a more complex synchronization scheme. We now proceed to discuss different scanning and detection mechanisms and their tradeoffs with respect to high-speed imaging.

Scanning systems

In this subsection we review the different scanning strategies that have been implemented in nonlinear microscopy, including multifocal approaches. We also present some scanning mechanisms that might become attractive in the future, as their technologies mature. In a typical microscope, a telescope (L3 and L4 in Fig. 2) is used to image the deflected beam coming out of the scanning device to the back aperture pupil of the EO. This ensures that the angular displacement of the scanners gets translated into a tilt of the beam in the back aperture without any beam displacement at this location. In turn, this means that the focal volume will raster a 2D area as the scanners move. The choice of scanner will have an impact not only on the image acquisition speed but also in the field of view, beam quality, aberrations, dispersion characteristics, and total power throughput of the instrument.

Acousto-optic scanning

The working principle of these devices is acousto-optic (AO) diffraction based on the elasto-optical effect.^{51, 52} When an acoustic wave travels in an optical medium, it induces a periodic modulation in the index of refraction of the material, thus effectively creating a diffraction grating responsible for the deflection. The relative amplitude of the beam diffracted into different orders is given by the Raman–Nath equations.^{53, 54} This set of equations describes different regimes for the diffraction process determined by the ratio of the interaction length L within the crystal, to the characteristic length L₀=Λ²∕λ, where Λ is the wavelength of the acoustic wave and λ is the optical wavelength inside the material. The cases L⪡L₀ and L>L₀ accept analytic solutions. The first limit is called the Raman–Nath regime, and in this case the AO diffraction results in a large number of diffracted orders. The maximum intensity diffracted into the first order is limited to 34% of the total incident laser power. The second limiting case is called the Bragg regime. In this case the diffraction appears predominantly in the first order with a theoretical maximum diffraction efficiency of 100%. For this reason, most AO devices are designed to work in the Bragg regime. In general, the total deflection angle ΔΘ with respect to the direction of propagation of the zero-order optical beam, in the small angle approximation, is linearly proportional to the applied acoustic frequency bandwidth Δf, namely,

$$\Delta \Theta =\frac{\lambda \Delta f}{V},$$ (3)

where V is the velocity of sound in the medium.

There are two types of AO devices used for beam deflection: AO deflectors (AODs) and AO modulators (AOMs). Both devices are very similar and based on the same working principle. An AOD relies mainly on the variation of the acoustic frequency in order to change the angle of deflection and thus steer the optical beam. AOMs are used, as their name implies, to modulate the amplitude or frequency of the diffracted beam. In order to satisfy momentum conservation in the operation of AO devices over their entire bandwidth, the acoustic beam needs to be narrow. In addition, for AOMs the optical beam must have a divergence approximately equal to that of the acoustic beam, in order to achieve the desired intensity modulation.

For practical applications of AODs there are two important parameters to consider: speed and resolution. The resolution (N) is defined as the total angular deflection ΔΘ divided by the angular divergence of the diffracted beam (δθ). If the divergence of the optical beam is much smaller than the divergence of the sonic beam, then the divergence of the diffracted beam is equal to that of the incident beam. This translates into δθ being inversely proportional to the diameter D of the incident optical beam. Thus it follows that

$$N=\frac{\Delta \Theta }{\delta \theta }=\frac{\lambda \Delta f∕V}{\lambda ∕D}=\tau \Delta f,$$ (4)

here τ=D∕V is the transit time of the acoustic wave across the optical beam and is therefore a measure of the random-access time of the device. This relationship clearly shows that there is a tradeoff between resolution and speed, and that for design purposes it is desirable to maximize the frequency bandwidth applied to the AOD.

Under the right conditions, AOMs can also be used as beam scanners.⁵⁵ Their main advantage over AODs is that they feature shorter access times as a result of the requirement that the optical beam be focused—the value of D is decreased. On the other hand, they also have decreased resolution compared to AODs due to the fact that the achievable scan range is smaller. Bullen et al.⁵⁶ have reported on a microscope that uses both AOMs (Isomet 1205C) and AODs (Isomet LS55V) interchangeably. For their system, they report the following operational parameters: (a) for the AOMs: a 7 μm spot size at the sample (using a 100×, Fluar, 1.3 NA, Zeiss objective), 15 resolvable spots (as given by the Rayleigh criteria), a scan angle of 56 mrad, a diffraction efficiency of 40%–80% (depending on scan angle), and maximum scan rate of 200 000 points∕s; (b) for the AODs: a 2 μm spot size at the sample (using a 100×, Fluar, 1.3 NA, Zeiss objective), 65 resolvable spots (as given by the Rayleigh criteria), a scan angle of 80 mrad, a diffraction efficiency of 60% (independent of scan angle), and maximum scan rate of 100 000 points∕s. These numbers nicely illustrate the tradeoffs involved in choosing devices.

One of the main attractions for choosing AO scanners (over mechanical scanners) is the possibility of direct random access to different points within the sample. If specific points of interest are identified within the sample, it is possible to use AO devices to address them individually and sequentially at high speeds as reported by Rózsa et al.⁵⁷ In this reference, the authors report that their system is, in principle, capable of acquiring data from as many as 100 different 3D points within the sample at kilohertz repetition rates. They demonstrated the system for only ten data points and measured throughputs of 80% with access times of 1–3 μs per data point.

A major challenge to the use of AO devices is that they are made of highly dispersive materials. Propagation of ultrashort pulses through such media radically alters the pulse duration, and thus is detrimental to the efficiency of the generated signal. Several authors have shown that it is possible to compensate these spatiotemporal distortions and have achieved a large field of view by using a pair of large aperture (13 mm) AOD in combination with an AOM.^{58, 59, 60, 61}

Galvanometric and resonant scanning

This is probably the most widespread scanning technology used in microscopy. This is due to its flexibility, throughput, and price. On the other hand this approach is significantly slower than AO solutions; but for acquisition speeds of a few frames per second or slower, it is sufficient. Galvanometric scanners consist of a mirror attached to a shaft that can rotate through a given angular range. Since the technology uses a mirror to redirect the beam, there are no problems due to dispersion and losses are minimal. Obviously in order to scan larger beams, bigger, and thus bulkier, mirrors are needed; this has a direct impact on the achievable scanning speed due to inertial effects. A galvanometric scanner can operate over a broad frequency range: from zero to a top frequency, that is, limited to slightly less than the scanners’ mechanical resonant frequency. It is also possible to use a galvanometric scanner to position the beam anywhere within the allowed linear scan region.

The principle of operation of a galvanometer is similar to that of a motor.⁵¹ The magnetic field produced by an arrangement of permanent magnets is augmented or diminished by the field from a variable current electromagnet. The change in the field forces a magnet or an iron to move angularly. As noted above, a given scanner is bandwidth limited; therefore, it is not possible to exactly track an arbitrarily applied waveform. Typically a sawtooth is used as the driving waveform, but the scanner is incapable of reaching the “instantaneous” fly-back time required by such a waveform. It is important to keep these bandwidth limitations in mind when scanning and confine the angular range for data acquisition to the region where the scan response is linear with respect to the applied current. If this limitation is not observed, the dwell time for a pixel in the middle of the angular range will not be the same as that of a pixel on the edge, possibly resulting in image artifacts.⁶²

A second form of scan technology, very close to galvanometers, is resonant scanning.^{63, 64} The main difference, as compared with galvanometers, is that the only moving part in the resonant scanner is a single-turn coil, which dramatically lowers the damping in the scanning system and allows it to be able to vibrate at very high frequencies, close to its mechanical resonance. Since these scanners are designed to work close to resonant frequency, their angular displacement can be quite large. For example, there are 10 kHz resonant scanners capable of 60° scan angles. These scanners do not offer random access of points within their scanning range. They produce a sinusoidal scanning pattern at frequencies as high as 24 kHz.⁶⁵ In order to take advantage of the full sinusoidal scan, data must be acquired in both, the forward and backward directions. Also, due to the variation in data rate acquisition when using a sinusoidal oscillation, in practical implementations, one typically acquires data only during the “linear” part of the sine wave.⁶⁶ In principle one can compensate for the different data rates at different parts of the sinusoidal wave by adjusting the pixel acquisition time. It is possible to follow the position of the scanner and use this information to generate a lookup table of pixel dwell times versus position; however, this requires stringent temporal synchronization that complicates the data acquisition.

Polygonal mirror scanning

Polygonal mirrors have been used to obtain very high frame rates with two-photon and CARS microscopy.^{67, 68} In this scheme, the geometrical center of a multifaceted (polygonal) mirror is attached to the shaft of a fast rotating (thousands of revolutions per minute) motor. As the motor rotates the facets of the mirror will deviate an incoming beam, thus creating a scanned linear pattern. The required data rate is the main factor to consider in deciding the rotation speed needed for a particular application. Several factors play a role in the decision of the number of facets needed as well as the polygon size. These factors include incoming beam diameter (D), its angle of incidence (α), desired duty cycle (η, ratio of active scan time to total time), number of points per scan (N), and angular deviation needed (Θ, in degrees). The last three factors are usually determined by the particular application. Any irregularities in the mirror facets or between them will result in errors in the scanning pattern. Also, it is important to realize that the transition between facets lead to dead times between scans since the beam is clipped and scattered at these regions.

As an example, we provide expressions that relate the parameters enumerated above to the characteristics of the polygonal mirror, for details, the reader is referred to the literature.^{51, 69} As defined above the duty cycle is the ratio between the active scan time to the total time. An equivalent definition relating beam diameter to facet width (W) is η=1−D_m∕W, where D_m=Dt∕cos α is the effective beam diameter projected onto the facet and t is a factor that provides a safety range to avoid clipping the beam with the edge of each facet as the mirror is rotated. Notice that small values of α lead to a smaller footprint of the beam and thus to a smaller mirror facet, which reduces the cost of the system. In general, the larger the required duty cycle (40%–80% duty cycles are common), the more expensive the device; this is due to the fact that large values of η require wider mirrors (reflected in larger values of W). The required number of facets (n) can be found by the expression n=720η∕Θ. Once the width of each mirror facet and their number are known, one can calculate the outer polygon diameter using

$$D_{outer}=\frac{W}{\left(1-\eta \right)\text{sin}\left(\pi ∕n\right)}.$$ (5)

These expressions make clear the tradeoffs involved in selecting a mirror. The cost will increase with increasing mirror size and with speed. For low velocity polygonal mirrors, ball bearings are used in order to keep the price reasonable. However, at high rotation speeds or large payloads some problems might arise with precision bearings, such as lubrication, vibration control, particle generation, and even shipment methods. Fast rotating mirrors (>4000 rpm) require aerodynamic air bearings, which are very expensive. If, on top of this, the required mirror diameter is large, then several sets of bearings might be needed in order to correctly balance the mirror.

Multifocal approaches

While it is possible to employ faster scanning devices to achieve higher image acquisition rates in multiphoton microscopy, this approach has fundamental technological limitations. A possible alternative is to parallelize the image acquisition process using more than one focal volume at a time,⁷⁰ thus reducing the acquisition time significantly for existing scanning technologies. Typical maximum peak intensities to avoid undesirable effects such as continuum generation, self-focusing, or damage to biological samples are roughly of the order of 200 GW∕cm².^{71, 72} For the typical Ti:sapphire system, as specified earlier, this peak intensity is achieved with only 12 mW of power when focused down to a diameter of 1 μm. Assuming a microscope with a total throughput of 40% means that only approximately 3% of the available average power can be used without damaging the sample. This is an enormous waste of expensive laser photons!

One possible approach that takes advantage of the available laser power is to use widefield illumination. This technique was implemented for TPEF microscopy by underfilling the back aperture of the objective with the excitation beam. This reduces the effective NA of the system and therefore creates a plane of illumination instead of just a point.^{73, 74} The detection is done with the same EO but at full NA, thus recovering diffraction limited resolution. In this modality, the signal must be imaged onto a camera. A frame rate of 30 Hz was reported using this method. However, by reducing the effective NA of the excitation beam, the sectioning capability is sacrificed which results in increased signal to noise and decreased contrast. Nonetheless, this technique is very easy to implement and requires no scanning. The image acquisition speed in this instance is essentially limited by the signal production rate of the sample and∕or the frame rate of the CCD camera.

One of the first schemes proposed to use the excitation laser more effectively in multiphoton microscopy involved using a line focus instead of point excitation. The line focus is created with cylindrical optics and is scanned in a perpendicular direction (relative to the line) with a galvanometric scanner in order to form a 2D image. Since only one scanner is involved in this approach, extremely high frame rates are in principle possible. This scheme was first demonstrated for TPEF by Brakenhoff et al.⁷⁵ in 1996 and has more recently been applied to THG by Oron et al.⁷⁶

Notably, when a line focus is used, the sectioning capability of the nonlinear signal is strongly degraded due to the fact that the beam is focused in only one dimension. For example, Brakenhoff reported that using a 1.3 NA objective, a point focus would have an axial sectioning of ∼1 μm, but using the line excitation with the same objective increases the axial resolution to ∼5 μm.^{75, 77} Oron et al.⁷⁸ recently proposed and demonstrated a novel scheme to overcome this limitation. Their technique relies on angular dispersion of the input beam, which is more effective at eliminating out-of-focus contributions along the long axis of the excitation beam.⁷⁹ Using this method for TPEF line-focus microscopy, an axial resolution of 1.5 μm has been reported.⁸⁰ The frame rate for this report was10 Hz but is easily scalable using faster detectors.

A different approach to parallelize the image acquisition in nonlinear microscopy is to use the excess laser power to generate an array of focal points. This idea was first proposed and demonstrated in 1998.^{77, 81} In the first reference, the authors used a rotating 5×5 microlens array to produce frame rates as high as 225 frames∕s, essentially limited by the readout time of their camera. Authors of the second report proposed to use a static microlens array and a pair of galvanometric scanners driven in a Lissajous pattern to avoid edge effects. They also studied the relation between axial sectioning capability and foci separation at the sample; they found that in order to avoid degrading the sectioning ability, a foci separation of approximately 7.3 μm (using a 1.3 NA objective) at the sample is required. The degradation is due to interference of the different focal points when they are too close together, and can be avoided by introducing a delay of a few picoseconds between foci. For example, Egner et al.⁸² produced delays by introducing a thin glass slide of variable thicknesses placed next to the lenslet array. They also concluded that for an aberration-free imaging system, interfoci distances smaller than approximately seven wavelengths lead to sectioning degradation. Several other groups have developed the microlens technique refining different aspects and extending it beyond TPEF.^{71, 83, 84, 85} Properly implemented, multifocal multiphoton microscopy (MMM) makes a much more efficient use of laser power and can reduce the image acquisition time from ∼1 s to 10–50 ms.⁷¹

An elegant method of creating multiple foci while simultaneously delaying consecutive beams is to employ beamsplitters.^{73, 86, 87} Indeed, this implementation has found its way into commercial systems (TriM scope, LaVision BioTec, Goettingen, Germany).⁸⁸ A temporal delay of a few picoseconds is introduced between adjacent foci by the different optical path lengths that the beams have to travel within the beamsplitter system. A nice advantage of the beamsplitter approach is that the relative spacing between focal points can be smoothly varied. If the spacing between the foci in a 2D array is small (or they are made to overlap), it is, in fact, possible to use the array to produce an image without scanning. For example, Fricke et al.⁸⁶ reported producing an 8×8 array of foci, with a 10 ps time delay between foci, and an interfoci separation of 0.5 μm, to generate an image on a CCD camera without scanning.

More recently Sacconi and co-workers reported using a high efficiency diffractive optical element (DOE) to create multiple foci.^{89, 90, 91} Used in combination with two galvanometric scanners, they obtained TPEF images with a field of view of 100×100 μm and a resolution of 512×512 pixels in approximately 100 ms.⁹² Their DOE generates a 4×4 foci array with 25 μm separation between foci (using a 60×, 1.4 NA objective) with 75% diffraction efficiency. The use of a DOE permits a very uniform (∼1%) intensity distribution at the focal plane, this is in sharp contrast with microlens arrays that might have intensity fluctuations as high as 50% from their central part to their edges. Jureller et al.⁹³ used a DOE to produce a 10×10 hexagonal array of foci which was scanned using two galvanometric mirrors driven by white noise. This stochastic scanning strategy is designed to efficiently fill the image space and the authors estimate that they can achieve image rates of ∼100 frames∕s.

All the schemes presented so far for MMM operate in an imaging modality, and thus they are not well suited for imaging deep into scattering samples. Recently some solutions to this limitation have been explored. Two of these solutions are based on a compromise between a detector with larger individual pixels and the number of foci that can be excited. For example, Kim et al.⁹⁴ proposed using a novel type of detector, namely, a multianode PMT (MAPMT). It is based on the same operating principle as a PMT except that it has 64 independent active areas arranged in a 8×8 matrix. This detection can be coupled into a MMM with an 8×8 array of foci. The main modification to a traditional MMM imaging setup is that, in order to have a one-to-one correspondence between foci and active areas on the MAPMT, it is necessary to descan the signal. The authors report 320×320 pixel images taken at 19 frames∕s. The second proposed solution involves the use of a new readout design for a CCD camera. It is called a segmented CCD and consists of a CCD chip that has been divided in 16 segments for readout purposes.⁷² In MMM the main frame rate limitation comes from the readout time of the CCD. In this new design, each segment of the CCD is read by an independent amplifier; thus increasing the overall frame rate. The maximum frame rate achievable with this hardware is 1448 Hz, a single segment CCD chip of comparable size would be limited to 160 Hz. In their paper, the authors demonstrate the principle using an array of 36 foci scanned onto the sample by two resonant scanners. They report a frame rate of 640 Hz, this constitutes the highest frame rate for MMM achieved yet.

By extending the time delay between foci from picoseconds to nanoseconds, MMM becomes possible using single element detectors such as PMTs, in a nonimaging modality. This has the advantage that multifocal techniques can be extended for use with highly scattering specimens. In addition, this approach has the unique capability of simultaneously imaging two or more separate focal planes within the sample.^{30, 95} In this case, the signal from the detector must be electronically demultiplexed in order to assign a spatial position to each signal photon and render an image. Using this technique, Sheetz et al.⁹⁶ have been able to image up to six different focal planes simultaneously.

Other approaches

In this subsection we briefly touch on other alternative scanning technologies. These techniques are either still under development or have not been applied to scanning microscopy. It is uncertain if they will provide robust alternatives to the better established methods. These scanning techniques include liquid crystal modulators, microelectromechanical systems (MEMSs), piezoelectric actuators, and electro-optic modulators. A liquid crystal modulator consists of a thin layer of liquid crystals sandwiched between two transparent electrodes and placed between crossed polarizers. Applying a bias to the electrodes changes the orientation of the molecules, this allows the modulation of the transmitted light. It is possible to achieve phase-only or amplitude-only modulation using elliptical polarization states.⁹⁷ Using this technology it is possible to steer a laser beam to achieve scanning patterns.^{98, 99} Some advantages of this approach are that it provides access to custom scanning patterns, and that it can also be used to implement axial scanning by modulating the phase of the optical beam. This last capability has been demonstrated;⁹⁸ the authors report a 200 μm axial range with 3.5 μm resolution using a 20× objective and a 30 μm range with 1 μm resolution for a 100× objective.

A second technology that holds potential for high-speed scanning is MEMS. In general, MEMS devices consist on the integration of mechanical elements, sensors, electronics, and actuators at very small dimensions. In particular, the elements relevant for scanning are micromirror arrays. They consist of a small mirror suspended by torsional bars and that are driven by a magnetic field produced by a coil around it.^{100, 101} These devices are essentially a very small-scale version of galvanometric mirrors. A commercial microscope by Olympus has incorporated this technology with a single element MEMS measuring 4.2×3 mm and is used to perform horizontal scans. The resonant frequency of this device ranges from 3.9 to 4.1 kHz and is capable of angular deviations from 2.1° to 16°.¹⁰² A 2D MEMS scanner has been incorporated into a confocal hand-held microscope capable of 4 images∕s with a field of view of 400×260 μm by Ra et al.¹⁰³

Another alternative to galvanometric scanners is piezoelectric driven actuators. Several companies offer mirrors with resonant frequencies of several kilohertz.^{104, 105} These actuators could be implemented into current scanning systems, although their small deviation angles (few milliradians) are a limitation for broader use. Finally, electro-optic modulators can also be employed for beam steering.⁵¹ This technology is based on inducing a gradient in the index of refraction across a crystal by inducing a standing wave. This gradient produces increasing retardation transversely to the beam profile, thus deviating it. Although this is similar to AOM, these technologies have fundamental differences in that an electro-optic modulator (EOM) is terminated reflectively to induce the standing wave and the sound wavelength used is longer than the beam diameter. Light is deflected by θ=cLV∕w², where L and w are the crystal length and diameter, V is the applied voltage, and c is a constant that depends on the material properties. Although their displacement power is small, EOM offers the advantage of deviating the full beam and not only one diffraction order. Also, they provide better pointing stability than an AOM. EOM can achieve rates of 100 kHz. Although they have not been applied to scanning microscopy, they have found application in laser tweezers due to their increased throughput.¹⁰⁶

CONTRAST MECHANISMS

In this second part, we present a brief introduction to each of the three main contrast mechanisms used in nonlinear microscopy. Each section includes a review of the applications that have been demonstrated, especially in biological systems. The paper concludes with a review of a novel application of TPEF for chemical analysis in microfluidics and two new contrast mechanisms that hold promise for biological and medical sciences: TPA and self-phase-modulation.

TPEF

Since its first demonstration nearly two decades ago,¹⁰ TPEF microscopy has revolutionized the field of scanning laser microscopy and provided a tremendous tool for biological imaging. The basic principle of TPEF is shown schematically in Fig. 1a. Two photons from the laser source are absorbed near simultaneously by the fluorophore molecule. After some nonradiative decay, a fluorescent photon is emitted and can be collected to generate an image. As all contrast mechanisms based in fluorescence, TPEF suffers from photobleaching, this phenomenon is discussed in more detail later. Additionally, the use of very high intensities for excitation can lead to higher-order (>2) photon interactions in the focal volume, excitation saturation,²³ increased photobleaching,¹⁰⁷ and photodamage.^{108, 109}

Equation 2 shows that the number of TPEF signal photons depends linearly on the TPA cross section (α), which is a quantitative measure of the probability that a particular molecule will absorb two photons simultaneously. The more commonly reported quantity is actually the two-photon action cross section which is the product of α with the fluorescence quantum yield.^{49, 50, 110, 111} Two-photon action cross sections at peak absorption wavelengths range from 10⁻⁴ GM for NADH^{49, 112} to about 50 000 GM for cadmium selenide-zinc sulfide quantum dots.¹¹¹ NADH exhibits very weak autofluorescence,^{113, 114, 115, 116} yet it is often present in high enough concentrations as to provide an important window into cellular metabolism.¹¹⁷ Comparing relative amounts of reduced NADH in vivo has been used to noninvasively monitor changes in metabolism and provide a potential indicator of carcinogenesis.¹¹⁸

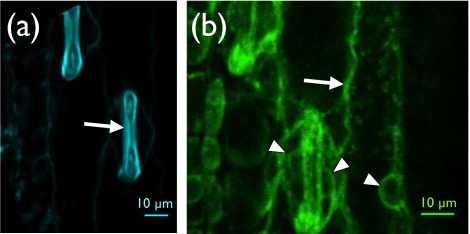
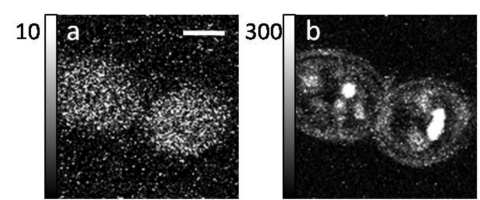
For those cases where endogenous fluorescence is absent, one can use fluorophores that are engineered to have two important application-specific properties: they have electron transitions that absorb at commonly available laser source wavelengths and they have an affinity for particular molecules and will attach to the molecules of interest within the sample. Cell labeling can be done in vivo by injecting synthetic dyes directly into the vasculature or by introducing fluorescent proteins such as green fluorescent proteins and its spectral variants via molecular genetics. As an example, Fig. 4 shows two TPEF images obtained from a maize leaf that is labeled with yellow fluorescent protein (YFP) and taken at two different excitation wavelengths: 800 and 1040 nm. In panel (a) essentially only the Guard cells (arrow) in the epidermis of the maize leaf are visible—they exhibit a strong endogenous autofluorescence for the excitation wavelength of 800 nm. Panel (b) is the same image area but an excitation wavelength of 1040 nm is used. The 1040 nm light effectively excites the protein tagged with the YFP (RAB2A::YFP). The image clearly shows protein localization in the cell cytoplasm (arrow) and around the nuclei in cells (arrowheads). (The localization of RAB2A::YFP shown in B is expected for the protein, which is involved in vesicle trafficking in maize cells.^{119, 120}) Additionally, “caged” compounds such as Ca²⁺, which are activated upon irradiation, provide useful probes for calcium-sensitive cellular processes and are predominant reporters of neuronal activity.^{121, 122, 123} A very promising advancement in exogenous labeling is the development of quantum dots. These semiconductor nanocrystals have very high TPA cross sections and provide access to intracellular processes and long-term in vivo observations of cell trafficking.^{111, 124} It is worth noting that endogenous fluorophores can be used in conjunction with the various labeling options to provide multicolor labeling of various tissue elements and subcellular domains within a single biological sample.¹²⁵

Figure 4.

Autofluorescence and expression of YFP-labeled protein in maize leaves. Panel (a), Guard cells (arrow) in the epidermis of a maize leaf show cell wall autofluorescence at excitation wavelength of 800 nm. Panel (b) A plant expressing a protein tagged with YFP (RAB2A::YFP) shows protein localization in the cell cytoplasm (arrow) and around the nuclei in cells (arrowheads) at excitation wavelength of 1040 nm. The localization of RAB2A::YFP shown in (b) is expected for the protein, which is involved in vesicle trafficking in maize cells.

Creative engineering of bright fluorescent labels that span a wide range of excitation wavelengths¹²⁶ continues to advance TPEF microscopy as an in vivo and in vitro biological imaging tool. Combined with advances in ultrafast lasers, fluorescence imaging now enables examination of live organ tissue at depths of up to 1 mm.^{125, 127} Studies have been done to investigate cerebral blood flow,^{128, 129} neuronal activity,^{130, 131} and spine morphology,^{132, 133, 134} yielding key insights into the functionality and possible presence of disorders in the brain. Long-term, high-resolution TPEF imaging of the neocortex in living animals has enabled researchers to study the growth and progression of implanted tumors^{135, 136} and other pathological conditions such as Alzheimer disease.^{137, 138, 139} Visualizing the blood flow response in three dimensions to induced aneurisms enables a deeper understanding of how the brain functions during a stroke.¹²⁹ Similar works have been done to study the mammalian kidney,^{140, 141} heart,¹¹⁷ and skin.¹¹⁵

TPEF imaging technologies have evolved from optics laboratory research platforms to compact, mechanically flexible microscopes for in vivo imaging in a clinical setting. High throughput fiber optic imaging configurations combined with miniature gradient-index (GRIN) lens has led to the design of miniaturized two-photon microscopes^{122, 142} and microendoscopes.^{143, 144, 145} These portable, lightweight microscopes show tremendous promise for biomedical research and noninvasive imaging—potentially eliminating the need for multiple biopsies when identifying and tracking cancerous cells.

The development of commercially available, turnkey, tunable femtosecond lasers that can span the 800–1300 nm wavelength range has elevated TPEF microscopy to a powerful tool for examining cellular and subcellular functions within living tissue. Advancements in the engineering of high action cross section fluorophores will likely further improve the ability to image deeply into scattering tissue while minimizing photobleaching and photodamage. In the next subsection we describe how the lifetime of the fluorescence can be use as an important image contrast mechanism. This is followed by a discussion of the basic mechanisms of photobleaching and some strategies to reduce its effects in TPEF imaging and fluorescent lifetime imaging.

Fluorescence lifetime Imaging

Images recorded by TPEF show a fluorescence intensity distribution map of the sample where the fluorescence intensity is proportional to the concentration of the fluorophores; however, the intensity also depends on the fluorescence lifetime. Fluorescence lifetime can be used as another contrast mechanism for imaging, this is achieved in fluorescence lifetime imaging microscopy (FLIM).¹⁴⁶ This technique can be implemented in time or frequency domain detection. For the frequency domain detection, continuous-wave (cw) lasers modulated at a high frequency are employed; while for time domain, FLIM is based on pulsed ultrafast lasers. Since nonlinear excitation inherently requires using a femtosecond or picosecond laser, time-domain FLIM is easily implemented. FLIM can be accomplished in wide field or in a scanning configuration. In wide-field microscopy a gated CCD camera is synchronized with the laser pulses.^{147, 148} High frequency camera gating is usually accomplished by coupling an image intensifier to a CCD camera. In time-domain measurements, a sequence of time-gated images is recorded at different delays with respect to the excitation pulse. The lifetime at each pixel is obtained by fitting exponentials to the reconstructed fluorescence decays.¹⁴⁸ Recently, spatially resolved FLIM measurements in a wide-field microscope were performed using TCSPC detection with a multichannel plate photomultiplier combined with a quadrant detector.^{149, 150} This method can give higher time resolution and low background noise taking advantage of TCSPC detection. A wide-field FLIM has parallel detection over many thousands of pixels, which enables fast measurements of spatially resolved fluorescence decays at a high temporal resolution. However, it is applicable only to fluorescence mapping from surfaces such as intact leaves,¹⁵¹ or investigations of thin low scattering samples such as a single layer of cells,^{152, 153} because out-of-focus fluorescence largely contributes to the image. Axial resolution in the fluorescence as well as regular bright field microscopy is limited—especially with thicker specimens. The axial resolution can be dramatically improved with tightly focused femtosecond pulses in a nonlinear excitation laser scanning microscope where a single channel detector is used as compared to a 2D array detector in wide-field microscopy. Fluorescence lifetimes can be recorded for each pixel with TCSPC.¹⁵⁴ TCSPC has inherent background signal rejection, and therefore is highly suited for low excitation intensity applications. In TCSPC detection, the arrival time at the detector for each signal photon is obtained, and a histogram of the arrival times is constructed, representing the fluorescence decay. The fluorescence decay is fitted with a multiexponential decay function to obtain the fluorescence lifetimes. A fluorescence lifetime image can be constructed from the lifetime values obtained at each pixel. Fluorescence lifetimes can then be used as a contrast mechanism for imaging, revealing differences in fluorescence quenching, or distribution of several fluorophores within the image.¹⁵⁴

Fluorescence lifetime imaging can be combined with spectral resolution, recording the fluorescence decay information at several wavelengths. This multidimensional detection technique can be implemented in spectrally resolved fluorescence lifetime microscopy (SLIM). In SLIM, a monochromator is placed after a confocal pinhole and fluorescence is dispersed onto a linear detector array. For each detected photon, the linear detector array records the arrival time, and also the channel number. Therefore, temporal and spectral information are recorded for each pixel.¹⁵⁴ The spectrotemporal information provides better differentiation of fluorophores in mixtures. FLIM and SLIM are very promising techniques that have recently emerged.¹⁵⁴

Photobleaching of fluorescent markers in two-photon excitation microscopy

Photobleaching of fluorescent molecules is a well known, although not fully understood phenomena in fluorescence microscopy. Also known simply as bleaching or fading, the process of photobleaching reduces the ability of a fluorophore to re-emit absorbed energy in the form of a fluorescent photon. While this property can be useful for some experimental measurements,^{155, 156} photobleaching is, in general, an undesirable effect in fluorescence microscopy. The most obvious adverse affect of photobleaching is a decrease in viewing time of fluorescent samples owing to a reduction in the flux of signal photons as a function of time. For example, biological time scales are often much longer than the time scale for appreciable bleaching to occur, limiting the window in which a biological process can be viewed. Furthermore, the spatial resolution of an image is closely related to the signal-to-noise ratio;²⁸ this is due to the Poisson-statistical nature of photons, the upshot of which being that the measurement of more photons results in a more accurate determination of position within the sample. Clearly then, while photobleaching can be advantageous in certain experiments, it is undesirable in fluorescence microscopy.

Two photon excitation microscopy (TPEM) eliminates some of the problems associated with bleaching in confocal microscopy simply by the nature of TPA.¹⁰ Since TPA only occurs efficiently in the focus of the laser, bleaching is limited to that same volume. This is in contrast to confocal microscopy, in which the sample fluoresces over the entire path of the focused laser due to the much larger linear absorption cross section, leading to bleaching in regions of the sample that are not imaged to the detector. Thus TPEM avoids out-of-focus photobleaching and allows for the sample to be optically sectioned without bleaching occurring prior to image collection. Nonetheless, it has been demonstrated that photobleaching in TPEM occurs more quickly than in confocal microscopy,¹⁰⁷ again serving to limit the viewing time and leading to degradation of image quality over successive images.

There has been considerable interest in studying the underlying mechanism of photobleaching in the hopes of reducing, and ideally eliminating, its presence in TPEM. While a solution for eliminating photobleaching entirely has thus far gone undiscovered, much has been learned about the processes that contribute to bleaching, thereby allowing for numerous advances to be made in reducing rates of bleaching and increasing fluorescence yield in typical TPEM setups. The majority of these advances have been made by manipulation of the femtosecond laser pulse trains used to activate TPA. In order to understand how these various techniques work to minimize bleaching, it is useful to first examine the photokinetics of fluorescent molecules from a theoretical standpoint.

A fluorescent molecule can be represented schematically by a Jablonski diagram, as shown in Fig. 5, which shows the electronic (bold lines) and vibrational (light lines) energy levels of the fluorophore. Here S and T denote singlet and triplet states, respectively, while the subscript integers refer to the level of the excited state. The Jablonski diagram shows the pathways that an excited molecule may take for relaxation. Some of those pathways, such as fluorescence and phosphorescence, are radiative and result in the emission of a photon. Other processes such as vibrational relaxation are nonradiative. Using a simplified version of the Jablonski diagram (in which the vibrational energy levels are ignored), it is a straightforward exercise to develop a set of differential equations that describe the population dynamics of each level of the molecule based on rates of competing population transfer mechanisms.^{157, 158, 159, 160} If it is assumed that no photobleaching occurs, the population densities within the molecule soon reach the steady state. By including a loss of population from excited energy levels within the molecule, each occurring with some rate constant, it is possible to account for photobleaching in this model.¹⁵⁷

Figure 5.

Schematic representation of the electronic (bold lines) and vibrational (light lines) energy levels within a fluorescent molecule. Nonradiative transitions such as vibrational relaxation are shown with wavy lines, while radiative transitions such as TPA and fluorescence are represented with straight arrows. There can also be a nonradiaive internal transition (not shown) of excited molecules down to the ground state.

Photobleaching has been found to result from several different energy transfer pathways inside fluorescent molecules. For example, it is well known from various studies that the first excited singlet state of a fluorescent molecule has a lifetime on the order of a few nanoseconds, while the lifetime of the first triplet state typically extends from a few microseconds to milliseconds. This difference in decay rates means that shortly after excitation begins, excited molecules will begin to accumulate in the triplet state. Because it is the radiative relaxation from the S₁ state to the ground state S₀ that is responsible for the fluorescence signal, a decrease in the population of S₁ clearly leads to a decrease in fluorescence yield. One solution to this problem is reported by Donnert et al.,¹⁶¹ in which they reduced the repetition rate of the excitation source to allow the excited triplet state to decay between successive pulses. Dubbed T-Rex (triplet-state relaxation) or D-Rex (dark-state relaxation), this scheme allows those molecules that exist in excited states other than S₁ to relax back to the ground state before the next excitation pulse. By permitting these molecules to relax between successive excitations, the accumulation of molecules in undesirable excited states, especially T₁, is significantly reduced, and the bleaching rates as well as fluorescence yield are dramatically improved. In another study by Ji et al.,¹⁶² the repetition rate of the excitation source was increased by splitting each pulse in the excitation train into 128 pulses of equal energy. Similar gains in fluorescence signal and reductions in bleaching rates were found with this method.

There are, however, multiple processes that govern the photobleaching rates of fluorescent molecules. For example, it has also been shown that bleaching rates are closely related to chemical reactions between the dye and its environment, as well as the dye with itself.^{159, 160} In this case, it is typically the result of oxidation of the fluorophore, due to reactions with a triplet excited state of the molecule, that chemically alters the molecules such that they can no longer fluoresce. This has been known for some time, and several techniques to reduce the interaction of excited states with oxygen have been introduced, all with some measure of success in reducing photobleaching.^{159, 160, 163} These techniques have not, however, succeeded in turning off photobleaching altogether.

Other studies have been aimed at examining what effect the shape of the temporal intensity envelope has on photobleaching in TPEM. It has long been known that it is necessary to compensate the dispersion induced by the microscope elements in order to maintain the highest possible two-photon efficiency.¹⁶⁴ In recent years, several studies have been reported in which high-order phase correction has been employed to study not only the improvement in image contrast but also rates of photobleaching as well.¹⁴¹ In another study, an adaptive learning algorithm was used in an attempt to find the optimal pulse shape for minimizing photobleaching rates.¹⁶⁵ While it was reported that the rate of photobleaching was indeed decreased by a factor of 4, the two-photon fluorescence signal was significantly decreased as compared to imaging with nearly transform limited pulses. Conversely, it has been shown that the optimal pulse for imaging under photobleaching conditions is indeed transform limited.¹⁴¹ Despite increased bleaching rates found with these pulses, the total number of fluorescence photons emitted is dramatically improved for typical imaging time scales.

Although photobleaching in TPEM is an obstacle to many biological assays, especially in vivo, many schemes have been developed to slow bleaching rates and increase total fluorescence photon flux as a function of time. With the rapid increase in techniques to slow bleaching in the past several years, it is apparent that bleaching is becoming a limiting factor to many applications of fluorescent microscopy. While many schemes exist to minimize the affects of photobleaching in TPEM, in some cases it is possible to eliminate the need for fluorescence detection, and therefore photobleaching, by imaging with harmonic generation or absorption.

SHG microscopy

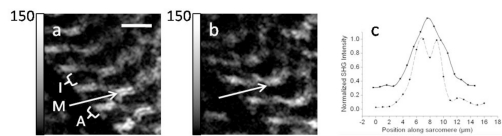
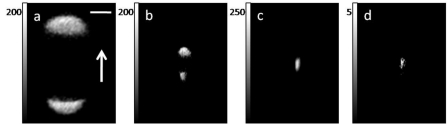
SHG microscopy has been gaining popularity due to being label-free, biologically compatible, and noninvasive. This imaging modality can probe molecular organization on the micro- as well as the nanoscale. Figure 1b represents the process schematically. Since the second-order polarizability depends on the square of the electric field, reversing the electric field does not reverse the polarizability direction, hence, the tensor vanishes in centrally symmetric media.¹ This SHG cancellation occurs whenever emitters are aligned in opposing directions within the focal volume of the laser. Such situation occurs in isotropic media and media with cubic symmetry. Nonlinear emission dipoles aligned in an antiparallel arrangement produce SHG exactly out of phase, and hence the signals cancel due to destructive interference. For example, noncentrally symmetric glucose molecules arranged in a noncentrosymmetric crystalline structure produce intense SHG; however, when dissolved in water, the glucose becomes randomly dispersed, and no SHG is produced. Selective SHG cancellation due to central symmetry has recently been observed in several biologically relevant systems including lipid vesicles infused with styryl dye,¹⁶⁶ anisotropic bands in muscle cells,⁷ and plant starch granules.¹⁷ In biological materials where SHG emitters are well organized in noncentrosymmetric microcrystalline structures, the SHG from different emitters adds coherently resulting in very intense SHG. Some examples of such structures include the aforementioned starch granules and other polysaccharides,^{4, 167} collagen,^{168, 169} striated muscle,^{19, 168} and chloroplasts.⁴ As previously mentioned, SHG from some biological samples, for example, starch granules, is strong enough to allow pulse characterization measurements not only in the forward³⁷ but also in the backward direction.¹⁷⁰

Backward propagated SHG comes from backscattered forward propagated SHG and from direct emission, possible from surfaces³ as well as scatterers smaller than the wavelength of light.¹⁷¹ SHG radiation has been detected in the epidirection in live human muscle tissue,¹⁷² small cellulose fibrils,¹⁷³ the outer rim of starch granules,¹⁷⁴ enamel,¹⁷⁵ and live animal muscle imaging.¹⁷² Backward propagated SHG promises to be an indispensable contrast mechanism for microendoscope investigations in the near future.

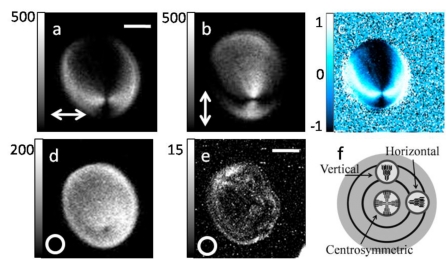
Intense second harmonic can be generated at an interface or boundary between two optically different materials since the central symmetry is broken.¹⁷⁶ Microscopic SHG imaging can be achieved from a monolayer of molecules at an interface or molecules asymmetrically arranged in lipid membranes.¹⁶⁶ This provides a sensitive tool for studying molecules adsorbed on a surface.³ Even in centrally symmetric media, an interface can generate intense SHG due to the high electric field gradient.¹⁷⁷ This effect recently has been shown to occur in semiconductor nanowires.¹⁷⁸ In practice, the surface SHG might be difficult to distinguish from the bulk SHG.¹⁷⁹ For reviews on the surface SHG techniques, the reader is referred to the literature.^{180, 181} The importance of crystalline order and centrosymmetric organization of molecules for SHG is demonstrated in the following two examples: starch granule and anisotropic bands of striated muscle cells.

Starch granule imaging

A starch granule is a centrosymmetric biocrystalline structure that extends radially outward from a hilum, the nucleus of the grain. Figure 6 shows an image of a starch granule from potato recorded with SHG microscopy using a Ti:sapphire laser. Images were obtained using linearly polarized light oriented horizontally in (a) and vertically in (b), as well as using circularly polarized light in panels (d) and (e). Panel (c) shows a polarization anisotropy A image calculated pixel by pixel from images (a) and (b) by the formula A=(I_⊥−I_p)∕(I_⊥+I_p), where I_⊥ and I_p are the pixel intensities for linearly polarized lights oriented horizontally and vertically, respectively. Circularly polarized light highlights the entire starch granule except for the central part, where the centrosymmetric structure of the hilum is located, as shown schematically in Fig. 6f. The hilum also remains dark in the SHG images recorded with linearly polarized light [Figs. 6a, 6b]. Linearly polarized excitation reveals two lobes with SHG generated parallel to the polarization of the laser beam. The highlighted SHG structure can be understood by noting that the focal volume of the microscope objective is much smaller than the granule. The volume is raster scanned in the focal plane to construct the image pixel by pixel. Therefore, the SHG intensity in each pixel depends on the net orientation of the nonlinear dipoles and the polarization of the laser beam. The images constructed from individual pixels reveal that the SHG intensity follows a cos² θ dependency, where θ is the angle between the linear polarization of the laser and net orientation of nonlinear dipoles. The lobelike structure reveals the radial arrangement within the granule, with a centrosymmetrically arranged hilum in the center of the grain [see Fig. 6f]. The polarization anisotropy image, Fig. 2c, is very similar to the so-called maltese cross image of the starch granule observed in a linear polarization microscope.¹⁸² The anisotropy value along the vertical and horizontal axes in this image is nearly 1, indicating a good radial alignment of the nanocrystallites in the starch granule. The anisotropy image shows that the nanocrystallites bend away from the radial orientation throughout the granule, and that the periphery of the granule is particularly well aligned.

Figure 6.

SHG imaging of potato starch granule. Different polarizations of the fundamental laser radiation were used as indicated in the bottom left corner of the panels, including linearly polarized light oriented horizontally (a) and vertically (b), as well as circularly polarized light (d) and (e). The polarization anisotropy image shown in (c) was calculated from images (a) and (b). Image (e) presents a pre-treated starch granule in 68 °C water for 20 s and shows a reduction in SHG intensity due to the heat treatment. The scale bar in (a) is 3 μm and 20 μm for (e). A schematic model of a starch granule is shown in (f).

Muscle imaging

Similarly to the starch granule, the biocrystalline structure of the anisotropic bands (A-band) of sarcomeres in muscle cells generates strong SHG. The characteristic striated structure of the myocytes from Drosophila melanogaster larva muscle can be seen in Fig. 7a. Myofilaments in each anisotropic band are arranged in a hexagonal crystalline structure.¹⁸³ Each myofilament consists of myosin molecules arranged antiparallel in the center of the filament (M-line) and protrudes over several microns in two opposite directions along the myofibril. The M-line manifests itself in a dark band, resulting in a double-banded appearance of the anisotropic band in Fig. 7a. When myocytes are stretched, the period of the striated structure increases mainly due to the elongation of the dark regions, the so-called isotropic bands (I-band) [Fig. 7b]. Unexpectedly, the double bands evolve into single bands and the M-line disappears in most of the sarcomeres. This is clearly seen from the anisotropic band profiles of the stretched and unstretched myocyte in Fig. 7c. The centrosymmetric arrangement that leads to the cancellation of the SHG radiation gets distorted during stretching. Some dipoles separate from each other and lose their counterpart, or separation of the dipoles changes the emitted SHG phase differences, leading to constructive interference and to an increase in the SHG intensity. This feature can be used to correlate the change in sarcomere size with SHG intensity during myocyte contraction.⁷

Figure 7.

A comparison between SHG imaged structures of unstretched (a) and stretched (b) muscle cells from Drosophila melanogaster larva. The arrows point to the same sarcomere which appears in its double-banded form in the nonstretched myocyte (a), and in its single banded structure for the stretched myocyte (b). A line profile of the indicated (arrow) sarcomeres is plotted in (c) showing that unstretched sarcomeres have a double peak and stretched sarcomeres have a single peaked A-band. The anisotropic muscle regions, indicated by A, produce SHG; while the isotropic muscle regions, indicated by I, show no SHG. The position of the M-line is indicated by M. The scale bar is 8 μm.

In both examples given above, the starch hilum and the M-lines of the myocytes appear as dark regions inside the bright SHG areas of the semicrystalline biological structure. Similar SHG cancellation effects can be observed in noncentrosymmetric membranes doped with SHG emitters and adhered to one another¹⁸⁴ or in chloroplasts due to the antiparallel stacking of photosynthetic thylakoid membranes in the grana.¹⁷

THG microscopy

THG is dipole allowed in inhomogeneous as well as homogeneous media.¹ Although THG is induced in bulk media, certain restrictions on the generation are imposed when focusing a laser beam with a high NA microscope objective.¹⁸⁵ Already in 1969, during the early stage of nonlinear optics investigations on harmonic generation, Ward and New¹⁸⁶ showed that THG vanishes under tight focusing in gases. These results can be understood in terms of the phase anomaly or Gouy phase—a π phase shift experienced when going through a focus in normally dispersive materials. This sign reversal results in the destructive interference of THG signals originating from opposite sides of the focal point, thus canceling any signal in the far field.¹⁸⁶ The solution of the paraxial wave equation for the amplitude of third harmonic (A_3ω) can be written as follows:¹

$$A_{3\omega }\left(z\right)=\frac{i6\pi \omega }{nc}{\chi }^{\left(3\right)}{A}_{\omega }^3{J}_{3\omega },\text{where}{J}_{3\omega }\left(\Delta k,z_0,z\right)={\int }_{z_0}^z\frac{e^{i\Delta k{z}^{\prime }}}{{\left(1+\frac{2i{z}^{\prime }}{b}\right)}^2}d{z}^{\prime }.$$ (6)

This equation shows that the third harmonic depends on the third power of the amplitude of the fundamental electric field A_ω, χ⁽³⁾, and the phase-matching integral J_3ω. This integral can be calculated numerically for any arbitrary structural configuration with z₀ being the z value at the entrance to the nonlinear medium. In Eq. 6, b represents the confocal parameter and Δk is the phase matching expressed as Δk=3k_ω−k_3ω. For focused Gaussian beams inside a homogeneous nonlinear medium, the phase-matching integral J_3ω can be expressed analytically as

$$J_{3\omega }\left(\Delta k,z_0,z\right)=\{\begin{array}{cc}0,& \Delta k\le 0\\ \frac{1}{2}\pi b^2\Delta k{e}^{-b\Delta k∕2},& \Delta k>0.\end{array}\phantom{\}}$$ (7)

This equation shows that the integral equals zero for normally dispersive materials, even for perfect phase matching (Δk=0). Thus no THG is observed in the far field when a beam is focused into a material with normal dispersion.

However, THG can be observed if the focal symmetry is broken, for example, by the presence of an interface between two materials with different refractive indexes or third-order susceptibilities. Although THG appears at interfaces,¹⁸⁷ it is a volume effect since THG is radiated from the bulk of the media on both sides of the interface.¹⁸⁸ There has been some recent reviews of THG microscopy in the literature that the reader is encouraged to consult.^{17, 25, 26} We now proceed to examine two examples of THG imaging: polystyrene beads and yeast. The first example is relevant in order to illustrate some of the features and artifacts that are present in nonlinear imaging.

Polystyrene bead imaging

The sensitivity of THG to heterogeneities present in media forms the basis for THG microscopy.¹¹ In order to demonstrate that THG depends on the size of the object and orientation of the interfaces with respect to the laser beam propagation, several different sized polystyrene beads were imaged in 3D. The image stacks were rendered in 3D and are presented in the axial view in Fig. 8, where the laser enters from the bottom, and the signal is collected above the bead. This is in contrast with all other images in this paper, which are presented in the lateral view, where the laser propagates into the page. The axial PSF of a 1030 nm laser focused by a 1.3 NA oil immersion objective is about 1 μm. Therefore, the two beads shown in panels (a) and (b) of Fig. 8, with diameters of 10 and 3 μm, respectively, are larger than the PSF, while beads equal or smaller than the PSF are shown in panels (c) and (d) for 1 and 0.1 μm beads, respectively.

Figure 8.

Axial views of polystyrene beads of different sizes imaged with THG. The bead sizes are 10, 3, 1, and 0.1 μm, for panels (a) through (d), respectively. The laser propagation direction is indicated by the arrow. The scale bar is 5 μm.

It is important to understand typical images produced with THG and relate them to the actual structure of the imaged object. Figure 8 shows that beads larger than the PSF, panels (a) and (b), emit THG only from the top and bottom interfaces, where the laser focal volume experiences a change in index of refraction between the surrounding matrix and the polystyrene material. The bottom interface, at the input side of the laser, appears to be more compact than the top; this is due to the distortion of the beam induced by the propagation through the structure that results in a larger PSF. It is important to note that no signal originates from the middle of the large beads, where the laser focal volume experiences a homogenous polystyrene media. Also, there is no THG radiated from the sides of the bead, this is because the interface is parallel to the laser propagation direction; therefore, breaking of the transverse beam symmetry of the focal volume is almost negligible. These characteristics of the radiated THG for objects larger than the PSF could lead to misinterpretations of acquired images, producing the impression that the image consists of two disjoint objects, while in reality it is just one object.

In the case of the polystyrene beads smaller or comparable to the axial PSF, panels (c) and (d) of Fig. 8, the THG reveals a continuous volume comparable in size to the PSF. Interestingly, even for the 1 μm bead [Fig. 8c], the bottom side appears to be narrower with better defined border than the top of the bead, thus indicating some beam distortion even over such short propagation distance. For the 0.1 μm bead, Fig. 8d, a very weak signal is observed, it is at least one order of magnitude weaker than the larger beads. Since THG is generated in the bulk, the reduced volume of the bead explains this effect. It is also noteworthy that the image of the 0.1 μm bead, panel (d), does not appear to be significantly smaller than the image of the 1 μm bead, panel (c). Of course this is just due to the inability of the instrument to resolve objects below the diffraction limited resolution.

THG imaging selection rules are the same regardless of particle size. Thus, subwavelength spatial heterogeneities could serve to enhance the THG in certain systems, i.e., a multilayer structure.^{187, 189} THG intensity also depends on the difference of the refractive indexes of the structure and the surrounding media, as well as on the hyperpolarizabilities of the molecules and their ordering in the structure. THG from different structural arrangements has been modeled by numerical integration of the phase-matching integral, Eq. 6.^{190, 191}

Yeast imaging

An example of THG imaging of a biological sample is presented for baker’s yeast, Saccharomyces cerevisiae. Figure 9b shows the intense THG image produced by this sample, while Fig. 9a shows the same sample imaged with TPEF. Using an excitation wavelength of 1030 nm, there is almost no fluorescence produced by the yeast cells. This points to very low linear and multiphoton absorption at this wavelength, thus allowing the use of high laser powers to generate strong harmonic signals. Imaging yeast with a 800 nm wavelength from a Ti:sapphire laser produces photodamage at low intensities due to strong TPA. The THG image reveals the typical morphology of the cell, the cell wall emits strong THG most probably due to the microfibril structure of glucan and chitin.¹⁹² The inner part of the cell contains several organelles, of size comparable to the PSF, that are very strongly highlighted by the THG. Similarly to the small bead examples in Figs. 8c, 8d, subdiffraction sized cellular organelles show up as ∼1 μm solid bodies within the cell. The isolation of the organelles and staining with a mitochondria staining dye, tetramethylrhodamine methyl ester (TMRM), revealed that the observed organelles are predominantly mitochondria, while lipid bodies might give a strong THG signal as well.^{193, 194} Mitochondria are multilamellar membranous bodies reaching up to 500 nm in length for baker’s yeast.¹⁹⁵ The multilamellar arrangement of the organelle renders enhancement of the third harmonic. The image in Fig. 9b also reveals other characteristic subcellular structures of yeast: the nucleus and vacuole can be seen as the two larger dark areas of 2–3 μm in diameter with a weak intensity rim. The absence of signal inside one of the bodies, compared to the weak background signal in the rest of the inner cell volume occupied by the cytoplasm, indicates a higher homogeneity of the medium inside the body.

Figure 9.

Baker’s yeast imaged with TPEF (a) and THG (b). The THG image clearly shows the cell wall and some internal organelles, predominately mitochondria. The scale bar is 3 μm.

Besides baker’s yeast imaging, THG has been used for visualization of biological membranes,¹⁸⁵ cell walls,¹⁸⁵ and multilayered structures such as grana of chloroplasts,^{4, 17, 185} aggregates of LHCII,¹⁷ and cristae in mitochondria.¹⁹ THG was also observed in rhizoids from green algae,¹⁹⁶ erythrocytes,¹⁹⁷ cultured neurons and yeast cells,¹⁹⁸ human glial cells,¹⁹⁹ muscle cells,^{19, 183} Drosophila embryos,²⁰⁰ sea urchin larval spicules,²⁰¹ hamster oral muscosa,²⁰² lipid bodies,¹⁹³ and tooth enamel.¹⁷⁵

Multicontrast nonlinear microscopy

Since laser excitation can simultaneously generate several nonlinear optical responses, different contrast mechanisms can be used to record parallel images of the same structure with the instrumentation previously discussed.^{4, 19, 203, 204} Multicontrast microscopy appears to be very beneficial when different nonlinear responses reveal different functional structures of the same biological object. For example, a multicontrast SHG and TPEF microscope was used to image labeled lipid vesicles,¹⁶⁶ labeled neuroblastoma cells,²⁰⁵ muscle and tubulin structures,¹⁶⁸ and labeled neurons.²⁰⁶ Simultaneous THG and TPEF detection was used for imaging human glial cells,¹⁹⁹ while THG and SHG microscopies were used to monitor mitosis in a live zebrafish embryo.⁵ All three contrast mechanisms were implemented to image mitochondria in cardiomyocytes,¹⁹ chloroplasts^{4, 203, 204} and photosynthetic pigment-protein complexes.²⁰³

Parallel images can be directly compared on a pixel by pixel basis. Although SHG, THG, and TPEF images originate from the same structure, their image contrast mechanisms are fundamentally different. The comparison of images obtained with coherent and noncoherent contrast mechanisms can be very challenging because homogeneous structures cannot be visualized in SHG or THG, but might be visible in fluorescence. Additionally, differences appear for signal generation at structural interfaces, where optical properties change between two media. For THG and surface SHG, the signal maximum appears at the central position of the interface, whereas for the interface between bulk-fluorescing and nonfluorescing structures, only half of the onset intensity will be reached at the interface position. The maximum TPEF signal intensity is observed when the full focal volume is immersed in the media. Therefore, image comparisons will always have to be taken with caution.

It is always beneficial to deconvolve microscopy images with the PSF of the particular contrast mechanism. PSFs are different for each nonlinear response and unique to the optical setup, so a different PSF should be recorded for each contrast mechanism and for each microscope objective. Nondeconvolved images appear to be blurred due to the finite size of the focal volume. If deconvolution is not performed, comparison may lead to artifacts; for example, two neighboring structures may be revealed by different contrast mechanisms and may appear to overlap because of the effect of blurring.

Structural cross-correlation image analysis

Images obtained with different nonlinear contrast mechanisms can be directly compared using the method of structural cross-correlation image analysis (SCIA), initially developed for multicontrast imaging of myocytes.¹⁹ The method relies on a pixel by pixel comparison of simultaneously acquired images. The algorithm can also be applied for comparison of images recorded sequentially, as long as the scan conditions for all the images are identical. The SCIA procedure starts with a standardization of the images by applying lower and upper pixel intensity thresholds to remove (set to zero) low signal noise as well as artificially occurring high signal spikes or “gliches” in the image. Next, the images, A(x,y) and B(x,y), are normalized to the maximum intensity and compared to each other pixel by pixel. The coordinates of the pixel in the image are denoted by x and y. The cross-correlated image, I(x,y), can be calculated as follows:

$$I\left(x,y\right)=\sqrt{A\left(x,y\right)\cdot B\left(x,y\right)}.$$ (8)

In addition to the correlated image, the algorithm produces two uncorrelated images, A∩¬B, and B∩¬A, where ∩ is the logical intersection and ¬ is the logical not. The uncorrelated images are constructed as follows:

$$\left(A\cap \neg B\right)\left(x,y\right)=\{\begin{array}{cc}A\left(x,y\right),& I\left(x,y\right)=0\\ 0,& I\left(x,y\right)\ne 0,\end{array}\phantom{\}}$$ (9)

$$\left(B\cap \neg A\right)\left(x,y\right)=\{\begin{array}{cc}B\left(x,y\right),& I\left(x,y\right)=0\\ 0,& I\left(x,y\right)\ne 0.\end{array}\phantom{\}}$$

The three images are mutually exclusive and can be represented by three distinct colors within a single image. The algorithm can be naturally extended to simultaneously correlate three images, this would result in seven mutually exclusive images. One triple correlation image A∩B∩C, three partial double correlations; A∩B∩¬C, A∩C∩¬B, and B∩C∩¬A, as well as the uncorrelated images; A∩¬B∩¬C, B∩¬A∩¬C, and C∩¬A∩¬B. The seven image correlations resulting from three-channel SCIA are mutually exclusive, so for each pixel, only one of the seven channels will have intensity greater than zero. This allows us to color each of the seven images in different colors, and then to combine them into one image. The colors will not overlap and the combined colocalized image will reveal multicontrast information from all three channels in one single image.

SCIA is advantageous over a standard overlay, even in the simpler two-channel case. In overlays, when two pixel intensities are nonzero, the resulting color is not unique and depends on the colors and intensities of the two pixels, very often resulting in a confusing picture. The SCIA algorithm avoids this problem because each of the seven resulting correlation images is assigned a unique color. For three-channel correlations, overlay is typically not attempted due to the confusion of colors. The 2D correlated structures can be assembled into 3D structures if the same settings of the SCIA algorithm are used for each 2D slice. The three-channel SCIA has been implemented for multicontrast microscopy of chloroplasts.¹⁷ What follows are two examples of SCIA images: two channel SCIA of mitochondria in cardiomyocytes and three channel SCIA in chloroplasts.

Imaging of mitochondria in cardiomyocytes

Figure 10 shows an example of multicontrast imaging which was used to provide evidence that THG is effectively generated from mitochondria in muscle cells.¹⁹ Only a small portion of the cardiomyocyte is shown in the image. Muscle cells were stained with TMRM, a mitochondria-specific dye,²⁰⁷ and imaged with TPEF and THG as shown in Figs. 10a, 10b, respectively. TMRM is a cationic dye permeable to lipid membranes and accumulates in compartments with a high negative potential according to the Nernst equilibrium. The TPEF image, Fig. 10a, shows spherical structures organized in rows protruding from the upper right corner to the lower left corner of the image. The structural pattern is very characteristic for the spatial arrangement of mitochondria, which are situated in rows along the myofibrils in a cardiomyocyte.²⁰⁸ The THG image, Fig. 10b, resembles a very similar pattern to the TPEF image. The correlated image, Fig. 10c, shows that most of the THG overlaps with TPEF, confirming that the THG signal originates mostly from the mitochondria. The THG generated by the mitochondria is rather intense; this is due, probably, to the multilamellar structure of mitochondria containing cristae, which is the densely folded inner membrane and outer membrane. As mentioned before, it has been shown that multilayer structures can enhance the THG signal if the third harmonic generated from each interface interferes constructively with the other ones.¹⁸⁷

Figure 10.

2D projections of 3D rendered multicontrast microscopy images of TMRM labeled mitochondria in myocytes. TPEF from TMRM is shown in (a), THG in (b), two-channel correlation in (c), uncorrelated MPF in (d), and uncorrelated THG in (e). The scale bar is 5 μm.

The two uncorrelated images, pure TPEF and THG signals, are presented in Figs. 10d, 10e, respectively. Only a small part of the structure appears in uncorrelated images. The uncorrelated TPEF signal might be due to the presence of autofluorescence and accumulation of TMRM not only in mitochondria but also in the sarcoplasmic reticulum, which is not highlighted with THG. In addition, TPEF has a larger PSF than THG resulting in the appearance of hollow shell-like structures in the uncorrelated TPEF image, Fig. 10d. The uncorrelated THG, Fig. 10e, is mostly located at the periphery of the myocyte structure; it originates from membranous cellular structures other than labeled mitochondria. Since the strongest THG signal is generated when an interface is positioned perpendicular to the propagation of the beam, it is not surprising that there are additional structures highlighted by the THG that are not labeled by TMRM.

Imaging of chloroplasts

Multicontrast imaging of individual chloroplasts and photosynthetic subcellular organelles from plant cells can be performed in situ and in vivo.^{4, 17, 185} Chloroplasts contain grana, which are photosynthetic membranes organized in a multilamellar fashion, somewhat similar to the crista of mitochondria discussed above. Since harmonics are mostly propagated in the forward direction, usually thin slices of a leaf or isolated chloroplasts are chosen for multicontrast microscopy. Upon illumination with Yb:KGW laser radiating at 1030 nm, carotenoid molecules undergo two-photon excitation.²⁰⁹ Carotenoids are located at close proximity with chlorophylls in photosynthetic pigment-protein complexes; therefore, efficient excitation energy transfer from carotenoids to chlorophylls takes place. Subsequently, chlorophyll fluoresces in the 650–720 nm spectral range. Figures 11a, 11b, 11c show isolated chloroplasts immobilized in polyacrylamide gel and imaged simultaneously with TPEF emitted from chlorophylls, SHG, and THG, respectively. The SCIA correlation image is presented in Fig. 11d. The chlorophyll fluorescence from the TPEF channel can be used to identify grana and stroma regions, where pigment-protein complexes reside inside the chloroplast. Although the fluorescence can be easily observed at low excitation powers, higher illumination powers are required to simultaneously generate harmonics but they induce fluorescence quenching in the photosynthetic membranes.²¹⁰ The fluorescence intensity distribution is more homogeneous than the other signals, but varies from one chloroplast to another due to fluorescence quenching as illustrated by Fig. 11a.

Figure 11.

Multicontrast microscopy of freshly isolated face aligned chloroplasts from pea leaves Pisum savitum. Chlorophyll fluorescence in the range of 650–720 nm is shown in (a), SHG in (b), THG in (c), and the combined correlated image in (d). Uncorrelated SHG is green, uncorrelated THG is blue, uncorrelated TPEF is red and correlated TPEF and THG is cyan. The scale bar is 3 μm.

The SHG image, Fig. 11b, shows a two-lobed structure in the middle of one of the chloroplasts. The signal originates from a starch granule. The lower chloroplast does not contain starch and shows very little SHG. Strong SHG has previously been observed from isolated pigment-protein complexes (LHCII), the most abundant pigment-protein complexes in chloroplasts.^{178, 203} Each LHCII is embedded at the same orientation in the grana and stroma membranes of the chloroplast; however, the double stroma membranes and stacked thylakoid membranes in the grana are staggered, where every second membrane is flipped. This organization creates a centrosymmetric arrangement of pigment-protein complexes resulting in great reduction of SHG.

Intense THG can be generated from chloroplasts in plant cells due to the high hyperpolarizability of chlorophyll and especially carotenoid molecules. The photosynthetic membranes span across the chloroplast generating THG in the whole volume. In addition, the concentration of pigment-protein complexes is higher in the grana region, and the multilayer structure of the grana enhances THG as compared to the corresponding monolayer interfaces. The grana structures are on the order of a few hundred nanometers in diameter; therefore, THG reveals the grana regions as structures comparable to the size of the PSF inside the chloroplast. The grana arranged in a ringlike fashion at the periphery of the chloroplasts can be seen in Fig. 11c. The THG intensity of the grana changes depending on whether the thylakoid membranes are oriented perpendicular or parallel to the beam propagation axis, as well as on the number of membrane layers within the focal volume.¹⁷

The correlation image, Fig. 11d, reveals the starch granule as uncorrelated SHG in green. As was shown in the previous section, starch granules do not produce bulk THG or TPEF at this wavelength. The correlation image also reveals regions related to the grana, which are colored predominantly purple in the lower chloroplast and blue in the upper chloroplast. The fluorescence of the upper chloroplast is highly quenched; therefore, correlation lights up the grana in blue as a noncorrelated THG region. The purple color represents the grana, which has relatively high fluorescence and THG signals. The red regions in the middle of the chloroplasts show that uncorrelated TPEF originates mostly from the stroma membrane. Imaging with multicontrast microscopy at different depths and different orientations of polarization can reveal many details of the 3D organization of individual chloroplasts.

New applications

In this section we offer examples of two new applications in the field of nonlinear microscopy. The first example addresses the use of TPEF, in combination with microfluidic devices, to perform chemical analysis, while the second actually refers to new contrast mechanisms (TPA and self phase modulation) in the medical sciences.

Multiphoton imaging in microfluidics

An emerging application for multiphoton microscopy is for the measurement of dynamic molecular and cellular properties in miniaturized analysis systems, often called microfluidics. Molecular kinetics studies in microfluidics have revealed properties such as the activation energy,²¹¹ the presence of rate-limiting steps,²¹² and the structures of transitional states.²¹³ On the cellular level microfluidics have been used to classify and to sort cells by size and fluorescence.^{214, 215} Microfluidic channel dimensions are typically tens to hundreds of micrometers. In microfluidics there is no turbulence and mixing is diffusion limited. The driving force and mixing geometry can select the local fluid velocity and species concentration so as to isolate the effect of a given stimulus on a substrate. Detection in microfluidics requires focused, sensitive optical probes such as is possible with multiphoton microscopy. In addition tightly focused excitation reduces the intensity of scattered light from the narrow channel walls and increases the accuracy with which the effect of the local velocity and concentration can be identified.

In situ quantitative imaging of product formation inside a microfluidic was demonstrated using CARS microscopy by Schafer et al.²¹⁶ Spectra collected during the proton transfer reaction between acetic acid and pyrrolidine were decomposed into contributions from reactants and product with submicron spatial resolution, with ∼mM sensitivity and on a millisecond time scale. Label-free detection of the size distribution of mouse adipocyte cells was demonstrated by Wang et al. also using CARS microscopy.²¹⁷ Detection was provided by a laser line scan oriented perpendicular to the flow. The length of each cell was calculated given the scan rate of the laser and the local fluid velocity.

Zugel et al. employed TPEF to detect the natural fluorescence of proteins and aromatic compounds in the deep UV in a common non-UV transparent microfluidic.²¹⁸ They determined the migration rates of constituents in the reaction of the substrate L-leucine beta-naphthylamine with the enzyme leucine aminopeptidase by microfluidic electrophoresis. The sensitivity of their system in a continuous flow arrangement was 30 nM for the enzyme solution. Excitation was provided by a cavity-dumped dye laser producing 10 ps pulses at 580 nm with 120 mW average power. In another microfluidic electrophoresis experiment Schulze et al. detected the separation of a mixture of aromatic compounds by TPEF in a borofloat glass microfluidic.²¹⁹ They used a Ti:sapphire laser producing 320 mW of average power and ∼100 fs pulses and reached a detection sensitivity of 10–50 μg ml⁻¹ at 420 nm.

The fluid velocity and mixing behavior within the microfluidic—important factors in understanding molecular events that exhibit shear, time, or concentration dependence—can also be quantified by multiphoton microscopy. Dittrich et al. determined the local fluid velocity by two-photon spectroscopy.²²⁰ Two foci were displaced laterally within the channel and by fluorescence cross correlation the magnitude of the fluid velocity parallel to the vector between the foci was calculated. Mixing behavior can also be evaluated by TPEF as demonstrated by Schafer and co-workers.²²¹ A quenching reaction was resolved at a mixing junction, and the local concentration of the quenching species, potassium iodide, was calculated using the Stern–Volmer model.

These experiments demonstrate the utility of multiphoton microscopy both for dynamic molecular and cellular analyses and for tracking the local concentration and fluid velocity. The multiphoton probe is well suited for the sensitive, confined detection required in microfluidics, and there is much potential for real-time analysis in this carefully controlled environment.

TPA and self-phase modulation

Although TPEF, SHG, and THG provide important and powerful tools for the study of biological systems, new contrast mechanisms continue to be explored. In particular, two nonlinear interactions have recently found applicability in microscopy, namely, self-phase modulation (SPM). In contrast with TPEF, that is restricted to molecules that exhibit fluorescent transitions from the excited state, TPA can be observed in all molecules. SPM results from variations of the index of refraction of a medium with the incident light intensity, this, in turn, leads to a modulation of the light phase. This modulation can depend on factors such as environment and the presence of localized structures. Both of these effects occur at the excitation wavelength and are very weak compared to linear processes such as scattering or absorption. These make it very hard to detect any signatures produced by them. One current implementation uses pulse shaping to force these processes to produce a signal at a wavelength other than the exciting beam.^{222, 223} This is accomplished by shaping the input pulse spectra—a hole is placed in the middle of the pulse spectra. Both TPA and SPM tend to refill this spectral hole, and since there are no other signals in this particular spectral region, they can be detected in the spectral domain free of background contributions. Using the SPM technique Yurtsever et al. have been able to identify the oxygenation level of hemoglobin,²²⁴ while Fischer et al.²²⁵ have applied the SPM technique to study neuronal activity.

PERSPECTIVES

Multiphoton microscopy provides a flexible and powerful tool for the study of biological systems both in situ and in vitro. TPEF has been widely used and is now considered a well established imaging tool. Harmonic imaging microscopy is a relatively new imaging technique that allows visualization of biological structures without staining; although still in its development stage, it has encountered many applications as exemplified above. The demonstration of epidetected harmonic signals opens new possibilities to apply harmonic signals for endoscopic imaging in biomedical research and diagnostics. The simultaneous combination of second and third harmonics yields structural details, which are otherwise unattainable; such as, sensitivity for multilayered structures, or, changes in nonlinear properties of the materials. These different contrast mechanisms can be implemented in a single instrument; thus, providing rich information about the structure of the object of interest. In particular, the nonlinear signals can yield interesting orientation dependent information about the organization of structures below the diffraction limit. Multimodal imaging and guided endoscopic microsurgery are examples of future directions, within the biomedical sciences, where harmonic microscopy will certainly play an important role.

It is certain that in the future we will see more biological applications of harmonic generation microscopy especially in live cellular imaging. Also, new applications of existing contrast mechanisms will continue to be explored not only in microfluidics but also in other fields. The field of nonlinear microscopy will continue to grow via development of new imaging contrast mechanisms, such as TPA and SPM, as well as their implementation into multicontrast microscopes. Development of novel laser sources, new fluorophores and better understanding of photobleaching will also impact the field. Nonlinear microscopy also has the perspective of being combined with other imaging modalities such as ultrasound or magnetic resonance imaging; therefore providing complementary information for biological or medical studies. The future of the field, and especially the expansion of its applicability, seem to have much to offer to the advancement of science.