Abstract
A quantum mechanical∕molecular mechanical minimum free energy path (QM∕MM-MFEP) method was developed to calculate the redox free energies of large systems in solution with greatly enhanced efficiency for conformation sampling. The QM∕MM-MFEP method describes the thermodynamics of a system on the potential of mean force surface of the solute degrees of freedom. The molecular dynamics (MD) sampling is only carried out with the QM subsystem fixed. It thus avoids “on-the-fly” QM calculations and thus overcomes the high computational cost in the direct QM∕MM MD sampling. In the applications to two metal complexes in aqueous solution, the new QM∕MM-MFEP method yielded redox free energies in good agreement with those calculated from the direct QM∕MM MD method. Two larger biologically important redox molecules, lumichrome and riboflavin, were further investigated to demonstrate the efficiency of the method. The enhanced efficiency and uncompromised accuracy are especially significant for biochemical systems. The QM∕MM-MFEP method thus provides an efficient approach to free energy simulation of complex electron transfer reactions.
INTRODUCTION
Calculating accurate free energies for many enzyme-catalyzed electron transfer (ET) processes is challenging because biological ET reactions often involve complicated interactions between enzyme, substrate, and cofactors.1 The conformational dynamics makes calculating the redox potentials much more difficult than calculating the ionization potential in gas phase. Thus, many methods have been developed to compute the redox free energies. The continuum solvent model is one of the most popular approaches to describe the role of solvent in ET processes because of its simplicity.2, 3, 4, 5, 6, 7, 8, 9, 10 Although the continuum solvent model can reveal essential physics of redox processes in solution, the dependence on parameters of the solute radii and the lack of the details of the structures or the thermodynamics motivated the employment of explicit solvent models in molecular dynamics (MD) simulation of redox reactions.11, 12, 13 The pioneering works by Bader and co-workers14, 15 and Warshel and co-workers16, 17, 18, 19, 20 used MD simulation to sample the explicit solvent phase space and provided insights of the free energy profiles for several solution ET processes. To reveal the structural and energetic changes of the redox molecules at the electronic level, Sprik and colleagues employed the Car–Parrinello MD method21 to describe both the solute and the solvent and obtained accurate reorganization energies and geometrical information for solution ET reactions.22, 23, 24, 25, 26, 27, 28, 29 However, the high computational cost and finite system size limit the application of the ab initio MD method.24, 30
With well balanced computational cost and accuracy, the combined quantum mechanical and molecular mechanical (QM∕MM) method31 becomes a very promising approach to simulate the biological ET processes, in which one treats the redox centers quantum mechanically and the rest of the system molecular mechanically.32 In previous work, we have shown that the “on-the-fly” ab initio QM∕MM calculation with direct MD sampling can be used to calculate the free energies for redox reactions in solution with satisfactory agreement with experimental data.33 However, the cost of ab initio QM∕MM calculation is still high, as such direct QM∕MM MD simulations are only affordable with very limited timescales for small systems.33, 34, 35 For large biomolecular systems, the computational cost for the QM calculation of the active site and phase space sampling of the protein severely limit the application of the direct QM∕MM MD simulations. Although the semiempirical QM methods, including the empirical valence bond model36 and the self-consistent-charge density functional tight-binding method,37 can largely reduce the computational cost in the QM evaluations,38, 39, 40, 41 the reliability and transferability of the semiempirical QM methods still limited their applications.
The dual need for both accurate QM evaluations and broad phase space sampling is crucial for not only the ET reactions but also general reaction processes in solution and in enzymes. Therefore, several ab initio QM∕MM simulation methods, including QM-FE,42 frozen density functional theory (DFT),43, 44 and QM∕MM-FE have been developed.45 The QM∕MM-FE method, developed in our laboratory, has shown advantages in many studies of enzymatic reactions.35, 46, 47, 48, 49, 50, 51, 52, 53 However, the strong dependence of the QM geometry on the MM conformations limited its application to reactions in solution.54, 55 To eliminate this limitation, we recently developed the QM∕MM minimum free energy path (QM∕MM-MFEP) method,55, 56 which has been successfully applied to simulations of chemical reactions in solution and enzymes.57, 58 Through geometry optimizations of the QM subsystem on the potential of mean force (PMF) surface, the QM∕MM-MFEP method generates a series of intermediate states with the minimum free energies along the reaction coordinate, thus avoids the expensive on-the-fly QM evaluations in the direct QM∕MM MD sampling. It also provides a robust approach to obtaining well-defined reaction path in solution and in enzymes.
For redox processes, since we focus here on the thermodynamic free energy changes instead of the free energy barriers in chemical reactions, obtaining the entire MFEP is unnecessary, as the redox free energy is a state function and independent on the reaction path. Therefore, only the geometries of the reduced and the oxidized states need to be optimized on their corresponding PMF surfaces, then an arbitrary path can in principle be chosen to connect the end points for free energy calculation. With the optimized geometries of the end points, we can use the fractional number of electrons (FNE) to serve the reaction order parameter of the electronic states, which has been verified to be an effective approach to describe redox processes.33 The linear interpolation of the geometries of the end points can be performed for the fractional electronic states to build a smooth alchemical reaction path for the free energy simulation of redox processes. In this manner, we even avoid the geometry optimization for the intermediate states and further reduce the computational cost of the free energy simulation.
In this article, we present the redox free energy simulation using the new QM∕MM-MFEP method combined with the fractional electron approach to calculate the free energies for redox reactions in solution. This paper is organized as follows. We first briefly introduce the basic theory in the QM∕MM-MFEP method. Then we show the practical procedures of the new method and the computational details of the simulation in Sec. 3. In Sec. 4 we compare the simulation results with our previous work and experiments, and also demonstrate the significantly enhanced efficiency in the QM∕MM-MFEP method. Finally we conclude with Sec. 5.
THEORY
Geometry optimization on the potential of mean force surface
To avoid performing the on-the-fly QM evaluations in the direct sampling of the phase space, we describe the thermodynamics of the solute with the PMF of the QM subsystem and only sample the phase space of the solvent with molecular mechanics.55, 56
In the QM∕MM representation, the PMF and the gradient of PMF with respect to the solute degrees of freedom can be written as
| (1) |
| (2) |
where A(rQM) is the PMF, rQM is the solute geometry, rMM is the solvent conformation, E(rQM,rMM) is the total potential energy of the molecular system, 1∕β is the Boltzmann constant times temperature, and the symbol ⟨⋯⟩ denotes the ensemble average.
Equations 1, 2 build the foundation for geometry optimization on the PMF surface. Since the solute geometry and the solvent ensemble are mutually dependent, we can solve the self-consistent problem with iterative procedure. However, the straightforward implementation of the optimization method requires sampling of the solvent ensemble after every movement of QM geometry. To improve the computational efficiency, the optimization is instead performed in a fixed ensemble.55, 56 The first snapshot of the QM geometry is set as a reference, and the free energy is defined to be relative to the reference
| (3) |
where Eref is the potential energy of the reference geometry, i.e., , Aref is the free energy of the reference, and {rMM} is the ensemble sampled with the reference QM geometry. According to Eq. 3, the PMF gradient in this method is then55
| (4) |
The PMF gradient in Eq. 4 gives the steepest direction to the minimum. When the distribution of e−β[E(rQM)−Eref] is converged, one can use various optimization methods to minimize the free energy. The optimized QM geometry is then used to generate a new ensemble of MM conformations in next cycle. This procedure can be iterated until convergence is reached.
Utilization of a finite reference ensemble, i.e., Eqs. 3, 4, requires special technical considerations in practice. Since the free energy is computed by the free energy perturbation (FEP) method [Eq. 3], the accuracy of ΔA depends on the overlapping of the phase space of two states. If the phase spaces of two states differ significantly, the computed ΔA cannot be trusted. Similar problems have been in fact discussed in the case of Jarzynski fast-growth simulation method.59, 60, 61 Because of this problem, in FEP simulations with classical force fields, an empirical rule is often implemented such that ΔA of a single FEP simulation cannot be larger than 2kT;60 however, changes in electronic state without much change of geometry can easily cause energy fluctuations more than a few kT. According to cumulant expansion, the free energy can be expanded to the second order as
| (5) |
| (6) |
where σ2=⟨E2⟩−⟨E⟩2 is the fluctuation of potential energies. When we minimize the free energy ΔA, the average potential ⟨E⟩ is minimized while the fluctuation σ2 is maximized. For systems with flat potential surfaces, the QM geometries will be lead to conformations with maximum statistic errors. We here applied another approach to resolve this problem. In all geometry optimization algorithms currently employed in our study and implemented in popular packages such as GAUSSIAN03, the goal is to identify the local minimum within a single state. In such a case, one can make a valid assumption that the entropy of any point in this state is constant. Therefore, one may minimizes ΔH, instead of ΔA, in our QM∕MM-MFEP optimizations. Under this assumption, the objection function for geometry minimization is ⟨E(rQM,rMM)⟩ with the gradient
| (7) |
In this manner, the higher order terms are excluded in the minimization and the statistic errors are thus reduced.
Redox free energy calculation using fractional electron approach
Calculating accurate free energy difference between two distinct states usually requires some techniques such as FEP or thermodynamic integration (TI) methods. To characterize the electronic states, most redox free energy simulations introduced the mixing coefficient of the energy functions of the two states,20, 22, 39, 40, 62 or the FNE as the reaction order parameter.33, 63, 64, 65 Because the free energy is a state function, in principle, the choice of the order parameter will not change the free energy difference. However, different choices of the order parameter will affect the convergence of the simulations and accuracy of the final results.66
Our previous work has implemented the FNE as a novel order parameter for the QM∕MM TI calculation of redox free energies. In this work, we also use the FNE to connect the reduced and the oxidized states of the solute and use the FEP method to calculate accurate redox free energy. Specifically, we here choose the order parameter as a combination of the FNE and the geometrical difference between the two final states. That is, after the structural optimization for the two end states with the QM∕MM-MFEP method, the intermediate structures were generated by linear interpolation between the structures of the two end states; each intermediate state was also assigned a FNE linearly interpolated from the changes of electron number in the redox processes. Although one could use only the FNE to define the intermediate states and correspondingly optimize the structures for each state before the FEP simulation. Our approach will be computationally more efficient because of the smooth structural change between different intermediate states and the elimination of the geometry optimization on the QM PMF for the intermediate states.
In the FEP method, we then divide the whole ET process into several intervals and perform sampling on a series of the intermediate states {λi}i=0,…,n, characterized by different values of the FNE and the corresponding geometries obtained from the linear interpolation. The overall free energy difference can be obtained by summing up the free energy change in each sampling interval,
| (8) |
| (9) |
where λ is the reaction order parameter, i denotes the ith intermediate state, n is the total number of states sampled, and the symbol ⟨⋯⟩λi designates the ith ensemble. i=0 denotes the reactant state, and i=n denotes the product state. ΔE(λi→λi+1) is the potential energy difference between two electronic states, which can be computed with the QM∕MM-FE approach developed in previous work.45, 55, 56 By turning λ0 to λn, we drive the system from the reduced electronic state to the oxidized state. Although the ΔA obtained in Eq. 9 does not include the zero-point energy and the vibrational contribution to the redox free energy, those terms can be estimated using frequency analysis within the harmonic approximation.
COMPUTATIONAL DETAILS
To validate the QM∕MM-MFEP method for the calculation of redox free energies, we first applied the method to simulate the aqueous iron and ruthenium complexes, which have been studied using the more substantiated direct QM∕MM MD method in our previous work.33 For further demonstration of the efficiency and accuracy of the QM∕MM-MFEP method, we performed two additional simulations for flavin derivatives: lumichrome (LC) and riboflavin (RF). The entire LC and RF molecules are treated quantum mechanically and their chemical structures are shown in Fig. 1.
Figure 1.
Molecular diagrams of flavin derivatives: (a) LC and (b) RF. The LC and RF molecules are treated quantum mechanically in the simulation.
The geometries of the solute were optimized for both the reduced and the oxidized states on their corresponding PMF surfaces. The iterative sequential sampling and optimization followed the procedures in our previous paper.55 In the iterative geometry optimizations, each MD sampling was performed for 64 ps after a 16 ps equilibration.
After the solute geometries were optimized for both reduced and oxidized states, the redox process was divided into 11 sampling intervals for the FEP calculation, i.e., n=11 in Eq. 8, and the linear interpolation of the solute geometries was performed to generate a series of geometries of the QM subsystem with fractional electrons to smoothly connect the end points. To calculate the free energy, a new MD sampling was performed for each intermediate state rQM,λi with the solute in the corresponding FNE state. In the FEP calculation, the MD sampling was increased to 128 ps after a 32 ps equilibration for better statistic convergence. Finally, the free energy contributions from zero-point energy and thermodynamic vibration were estimated by frequency analysis using the GAUSSIAN03 program.67
The MD simulations were carried out with the program SIGMA,68, 69 while the QM calculations were performed with GAUSSIAN03.67 The electrostatic potential fit charges of QM subsystem were obtained with our recently developed method,70 which improves the numerical stability of the charges on the atoms in the QM region. Since the Ewald summation for charged systems with a local basis set has not been implemented, we here use a QM-MM interaction distance cutoff. Following the protocol in the previous work,55 the dual cutoffs were used in the simulations, with the short cutoff to be 14 Å and the long cutoff to be 28 and 20 Å for the metal ions and organic molecules, respectively. The long cutoff was chosen as such to ensure the convergence of QM∕MM electrostatic interactions and the final redox free energies.33, 71, 72 The cutoff for the organic systems were chosen as 20 Å because the net charge of the system is between 0 and −1, which is smaller than that of the metal systems. Additional FEP calculation with 25 Å cutoff for the LC molecule was performed to demonstrate the convergence of the long distance interactions (see Sec. 4).
The metal complexes were modeled with the same configuration in the previous work:33 The ions and six coordinating water molecules were treated quantum mechanically and were solvated in cubic boxes with the dimensions 64×64×64 Å3, which contained 8.6×103 TIP3P water molecules as the solvent.12 For the flavin derivatives, the LC and RF molecules are treated quantum mechanically and solvated in cubic boxes with the dimensions: 64×64×64 Å3 for LC and 54×62×62 Å3 for RF, respectively. The dimensions of the boxes were chosen such that the solutes were surrounded by solvent layers with thickness at least greater than the corresponding long cutoff. All systems were simulated under NVT conditions with temperature T=300 K.
RESULTS AND DISCUSSIONS
Geometry optimization on the PMF
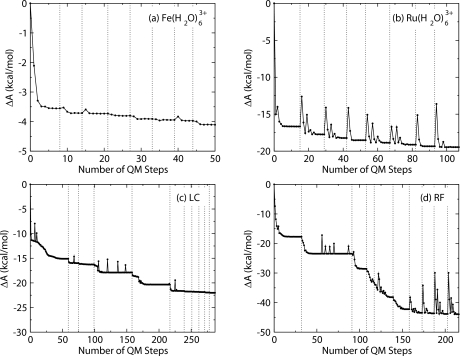
In the QM∕MM-MFEP method, each geometry optimization was performed on the PMF surface in a fixed MM ensemble. The MM ensemble was then updated with the optimized solute geometry. The converged MM ensemble and the corresponding fully optimized QM geometry is critical to the accuracy and reliability of the method. Figure 2 shows the convergence of the four systems in the oxidized states in terms of the free energy variation. The horizontal axis is the number of QM evaluations in the geometry optimization. Each dashed line denotes the termination of one QM optimization cycle, where a new MM ensemble was sampled. The free energies of the systems converged to plateaus after 8–10 cycles of iterative sequential sampling and geometry optimization for both the aqueous metal complexes and the flavin derivatives. The spikes in the free energy variations were generated by the optimization algorithm employed in the GAUSSIAN03 program, which are frequently observed in various systems.55
Figure 2.
Convergence of the relative free energies during the geometry optimization for (a) , (b) , (c) LC, and (d) RF in QM∕MM-MFEP method. The reduced states of the systems converge similarly as the oxidized states shown here. The vertical dash lines separate different MM ensembles obtained by sequential sampling. Within the region between two dash lines, the dotted lines are the relative free energies of the systems during the QM optimizations on their PMF surfaces in the corresponding MM ensembles. The systems converge after 8–10 cycles of MM sampling and QM optimizations.
Redox free energies
With the QM subsystems optimized on the PMF surfaces in fully converged MM ensembles, the FEP simulation was then performed to evaluate the redox free energies for the systems. The oxidation free energies of and obtained from Eq. 9 are 5.70 and 5.01 eV, respectively. These values do not include the contributions from vibrational entropy and zero-point energies.
With the harmonic approximation, frequency calculations can be performed in the QM∕MM-MFEP method to estimate the free energy contribution from the solute vibrational entropy ΔGvib. In the direct QM∕MM MD method, the vibrational dynamics of QM subsystem is represented by the classical motions of solute from MD sampling. Thus, the vibrational contribution is already included. In the QM∕MM-MFEP method, we estimated the vibrational contributions of the solutes through the frequency calculations on the enthalpy surfaces. The vibrational frequencies of the QM subsystems were calculated in the mean field of the solvent that is represented by MM point charges. The ΔGvib for and are estimated to be 0.042 and 0.027 eV, respectively. After the correction, the oxidation free energies are 5.74 eV for and 5.04 eV for . As shown in Table 1, these values are comparable to the results obtained in a previous study using the direct QM∕MM MD method, where the oxidation free energies were calculated to be 5.82 eV for and 5.14 eV for . The discrepancy between the two methods is 0.07–0.10 eV or 1.6–2.3 kcal∕mol, which is within the statistic deviations.
Table 1.
Oxidation free energies of metal complexes calculated with direct QM∕MM MD and QM∕MM-MFEP methods. Units are in eV.
| ΔG | ΔGvib | ΔG+ΔGvib | ΔGZPE | ΔGabs | |||
|---|---|---|---|---|---|---|---|
| Direct | ⋯ | ⋯ | 5.82a | ⋯ | ⋯ | 5.0∕5.6d | |
| MFEP | 5.70 | 0.04 | 5.74b | 0.10 | 5.84c | ||
| Direct | ⋯ | ⋯ | 5.14a | ⋯ | ⋯ | 4.4∕5.1d | |
| MFEP | 5.01 | 0.03 | 5.04b | 0.06 | 5.10c |
Values reported in Ref. 33, which already included the free energy contributions from vibrational dynamics.
In order to compare with the results using the direct QM∕MM MD method, the vibrational contributions ΔGvib are estimated and added to the results for QM∕MM-MFEP method.
ΔGabs are the absolute redox free energies, included the corrections from both vibrational dynamics ΔGvib and zero-point energies ΔGZPE. The results using direct QM∕MM MD method did not include ΔGZPE.
Besides the vibrational entropy, another missing term is the difference in the zero-point energy between the two redox states. Since the zero-point energy calculation in the direct QM∕MM MD method is expensive but not dominant, this term was omitted. However, in the QM∕MM-MFEP method, the zero-point energy of different redox states can be easily estimated through frequency calculations on the optimized geometries. The free energy corrections from zero-point energy ΔGZPE are about 0.10 eV and 0.06 eV for and , respectively. Including the correction from both vibrational entropy and zero-point energy, the absolute oxidation free energies ΔGabs obtained from the QM∕MM-MFEP method for and are 5.84 and 5.10 eV, respectively.
The experimental values are measured relative to the standard hydrogen electrode (SHE), which is artificially set to be zero. Therefore, the absolute value of the oxidation free energies for SHE should be added in the experimental data when we compare the theoretical values to experiments. However, the measurements of are not very accurate and disputable, with a range from 4.2±0.4 to 4.84 eV.73, 74, 75, 76, 77 In Tables 1, 2, the experimental values of the absolute oxidation free energies are listed as two sets of data with the minimum and maximum values of .
Table 2.
Comparison of oxidation free energies of LC and RF calculated with QM∕MM-MFEP methods to experiments. Units are in eV.
| MFEPa | Experimental datab | ΔΔGc | |||||
|---|---|---|---|---|---|---|---|
| ΔG | ΔGvib+ZPE | ΔGabs | ΔG0 | MFEP | Expt. | ||
| LC∕LC⋅− | 3.16 | 0.07 | 3.23 | −0.502 | 3.7∕4.3 | ⋯ | ⋯ |
| RF∕RF⋅− | 3.41 | 0.07 | 3.48 | −0.292 | 3.9∕4.5 | 0.25 | 0.21 |
ΔG are the values before any correction. ΔGvib+ZPE are the corrections considering the vibrational contributions and zero-point energies. ΔGabs are values of absolute oxidation free energies including the corrections from both vibrational contributions and zero-point energies.
Experimental data are based on the standard redox free energies ΔG0 from Ref. 82, which are relative to the SHE. , the values of the absolute oxidation free energy for SHE, were measured to be from 4.2 to 4.84 eV (Refs. 73, 74, 75, 76, 77). The experimental absolute free energies are therefore obtained as .
Relative oxidation free energy difference between the LC and RF molecules.
Because the computational cost in the simulation of LC and RF molecules using the direct QM∕MM MD method is very expensive, the two bio-organic systems were only simulated using the QM∕MM-MFEP method. As shown in Table 2, the oxidation free energies of the redox couples LC∕LC⋅− and RF∕RF⋅− are evaluated to be 3.16 and 3.41 eV, respectively. Since we here used a shorter cutoff (20 Å) than that of metal systems (28 Å), we performed FEP calculations with 25 Å cutoff for LC∕LC⋅−. The oxidation free energy is 3.12 eV with 25 Å cutoff and 3.16 eV with 20 Å cutoff, respectively. The 0.04 eV difference between the FEP calculations suggests that the long range electrostatic potential converged at the distance of 20–25 Å. The correction from ΔGvib and ΔGZPE is coincidentally to be about 0.07 eV for both LC and RF systems, which leads to 3.23 and 3.48 eV as the absolute oxidation free energies for LC and RF, respectively.
The experimental oxidation potentials of the LC∕LC⋅− and RF∕RF⋅− couples are −0.502 and −0.292 V. Taking the Nernst equation (ΔG=−nFΔE), the relative oxidation free energy difference ΔΔG between the two couples is 0.21 eV. The result obtained from QM∕MM-MFEP method is 0.25 eV, which is in excellent accordance with the experimental value.
Computational efficiency
The agreement between the oxidation free energies calculated using the two methods indicates that the QM∕MM-MFEP method is at least as accurate as the direct QM∕MM MD method. In the Table 3, we compared the efficiency between the direct QM∕MM MD and the QM∕MM-MFEP methods when performing similar simulations to calculate redox free energies. Using LanL2DZ basis set,78 the aqueous metal complexes contain 100 basis functions. The direct QM∕MM MD simulation spent about 40 days on dual Intel Xeon 3.60 GHz CPUs to complete 20 ps MD sampling with 20 000 times of the on-the-fly QM evaluations. The QM∕MM-MFEP simulations on the same systems performed about 8 cycles of QM optimization and sequential MD sampling in 20 days, with each cycle consisting of 80 ps sampling. If we want to perform the direct QM∕MM MD simulations for 20 ps on LC or RF molecule, the estimated computational time would exceed 400 days. In contrast, the QM∕MM-MFEP simulation of the LC and RF molecules were completed in 25 and 45 days, respectively. As the system becomes larger, the advantage of the QM∕MM-MFEP method is more significant. The computational efficiency is promoted about 15–30 folds for the two bio-organic systems because the on-the-fly QM evaluations are avoided and the thermodynamics is described by the PMF of the QM subsystem. For the systems in this paper, the linear interpolation was performed to build the path for free energy simulation. However, we need to point out that a smooth connection between the redox states through the FNE cannot be guaranteed in all cases. Caution may be needed in the simulation of special systems with FNE to reduce possible artifacts caused by DFT method.30, 79, 80, 81 Also, if the interpolated reaction path is bumpy, e.g., for reactions with significant geometrical changes between the redox states, the optimization for a smooth path is desired to reach the convergence. Even if the optimization of a reaction path rather than an interpolated path is necessary, the computational cost in terms of time may not significantly increase since the optimization of the intermediate states can be performed parallelly.
Table 3.
Efficiency comparison between direct QM∕MM MD and QM∕MM-MFEP methods.
| Systemsa | LC∕LC⋅− | RF∕RF⋅− | ||||
|---|---|---|---|---|---|---|
| Total atoms | 19 | 28 | 47 | |||
| Basis set | LanL2DZ | 6-31+G∗∗ | 6-31+G∗∗ | |||
| Number of basis | 100 | 392 | 613 | |||
| QM evaluation timeb | 3 min | 30 min | 100 min | |||
| Method | Direct | MFEP | Directc | MFEP | Directc | MFEP |
| Sampling length | 20 ps | 80 ps | 20 ps | 80 ps | 20 ps | 80 ps |
| QM evaluation number | 20 000×6 | 100×2 d | 20 000×6 e | 300×2 d | 20 000×6 e | 300×2 d |
| Total real timef | 40 days | 20 days | 400 days | 25 days | 1400 days | 45 days |
M=Fe,Ru.
These are the approximate time costs for a single QM evaluation. The time costs here are based on running GAUSSIAN03 program on dual Intel Xeon 3.60 GHz CPUs.
The direct QM∕MM MD simulations are not performed for LC and RF. The corresponding parameters and time costs are estimations only.
The geometry optimizations are only necessary for the reduced and the oxidized state of solute.
Assume using the same setup of simulations as in Ref. 33, where TI method with six sampling intervals is used.
These are the approximate time costs for performing the entire simulations.
CONCLUSION
In this work, we have implemented the QM∕MM-MFEP method to calculate redox free energies, with significantly enhanced efficiency and uncompromised accuracy. We have verified the validity and accuracy of the QM∕MM-MFEP method by repeating the calculation of redox free energies for and aqueous complexes. The results from the QM∕MM-MFEP method agree well with those from the direct QM∕MM MD method, with about 0.1 eV difference in the oxidation free energy. To demonstrate the efficiency of the QM∕MM-MFEP method, two larger biochemical molecules, LC and RF, are further investigated. The oxidation free energies of the redox couples LC∕LC⋅− and RF∕RF⋅− were evaluated to be 3.23 and 3.48 eV, respectively. The relative free energy difference ΔΔG is 0.25 eV, which is very close to the experimental value of 0.21 eV. The computational time for the two bio-organic systems is shortened by about 15–30 folds compared to the direct QM∕MM MD. The high accuracy and the enhanced MD sampling of the QM∕MM-MFEP method shows promise for applications of the studies on redox reactions in biochemistry.
ACKNOWLEDGMENTS
Support from the National Institutes of Health, Project No. 5R01GM061870-08, is gratefully appreciated.
References
- Bixon M. and Jortner J., Adv. Chem. Phys. 106, 1 (1999). [Google Scholar]
- Marcus R. A., J. Chem. Phys. 24, 966 (1956). 10.1063/1.1742723 [DOI] [Google Scholar]
- Marcus R. A., J. Chem. Phys. 24, 979 (1956). 10.1063/1.1742724 [DOI] [Google Scholar]
- Born M. Z., Physik 10.1007/BF01881023 1, 45 (1920). [DOI] [Google Scholar]
- Onsager L., J. Am. Chem. Soc. 58, 1486 (1936). 10.1021/ja01299a050 [DOI] [Google Scholar]
- Kirkwood J. G., J. Chem. Phys. 7, 911 (1939). 10.1063/1.1750343 [DOI] [Google Scholar]
- Rosso K. and Rustad J., J. Phys. Chem. A 104, 6718 (2000). 10.1021/jp994164h [DOI] [Google Scholar]
- Uudsemaa M. and Tamm T., J. Phys. Chem. 107, 9997 (2003). [Google Scholar]
- Jaque P., Marenich A., Cramer C., and Truhlar D., J. Phys. Chem. C 111, 5783 (2007). 10.1021/jp066765w [DOI] [Google Scholar]
- Warshel A., Papazyan A., and Muegge I., JBIC, J. Biol. Inorg. Chem. 2, 143 (1997). 10.1007/s007750050119 [DOI] [Google Scholar]
- Berendsen H. J. C., Postma J. P. M., van Gunsteren W. F., and Hermans J., Intermolecular Forces (Reidel, Dordrecht, Holland, 1981). [Google Scholar]
- Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. 79, 926 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- Berendsen H. J. C., Grigera J. R., and Straatsma T. P., J. Phys. Chem. 91, 6269 (1987). 10.1021/j100308a038 [DOI] [Google Scholar]
- Kuharski R. A., Bader J. S., Chandler D., Sprik M., Klein M. L., and Impey R. W., J. Chem. Phys. 89, 3248 (1988). 10.1063/1.454929 [DOI] [Google Scholar]
- Bader J. S. and Chandler D., J. Phys. Chem. 96, 6423 (1992). 10.1021/j100194a059 [DOI] [Google Scholar]
- Warshel A., J. Phys. Chem. 86, 2218 (1982). 10.1021/j100209a016 [DOI] [Google Scholar]
- Warshel A. and Hwang J. -K., J. Chem. Phys. 84, 4938 (1986). 10.1063/1.449981 [DOI] [Google Scholar]
- Hwang J. -K. and Warshel A., J. Am. Chem. Soc. 109, 715 (1987). 10.1021/ja00237a013 [DOI] [Google Scholar]
- Hwang J. K., King G., Greighton S., and Warshel A., J. Am. Chem. Soc. 110, 5297 (1988). 10.1021/ja00224a011 [DOI] [Google Scholar]
- King G. and Warshel A., J. Chem. Phys. 93, 8682 (1990). 10.1063/1.459255 [DOI] [Google Scholar]
- Car R. and Parrinello M., Phys. Rev. Lett. 55, 2471 (1985). 10.1103/PhysRevLett.55.2471 [DOI] [PubMed] [Google Scholar]
- Blumberger J. and Sprik M., J. Phys. Chem. B 108, 6529 (2004). 10.1021/jp036610d [DOI] [Google Scholar]
- Blumberger J., Bernasconi L., Tavernelli I., Vuilleumier R., and Sprik M., J. Am. Chem. Soc. 126, 3928 (2004). 10.1021/ja0390754 [DOI] [PubMed] [Google Scholar]
- Blumberger J. and Sprik M., J. Phys. Chem. B 109, 6793 (2005). 10.1021/jp0455879 [DOI] [PubMed] [Google Scholar]
- Tateyama Y., Blumberger J., Sprik M., and Tavernelli I., J. Chem. Phys. 122, 234505 (2005). 10.1063/1.1938192 [DOI] [PubMed] [Google Scholar]
- Blumberger J., Tavernelli I., Klein M. L., and Sprik M., J. Chem. Phys. 124, 064507 (2006). 10.1063/1.2162881 [DOI] [PubMed] [Google Scholar]
- Sulpizi M., Raugei S., VandeVondele J., Carloni P., and Sprik M., J. Phys. Chem. B 111, 3969 (2007). 10.1021/jp067387y [DOI] [PubMed] [Google Scholar]
- Costanzo F., Sulpizi M., Guido Della Valle R., and Sprik M., J. Chem. Theory Comput. 4, 1049 (2008). 10.1021/ct8000415 [DOI] [PubMed] [Google Scholar]
- Blumberger J., J. Am. Chem. Soc. 130, 16065 (2008). [DOI] [PubMed] [Google Scholar]
- Ayala R. and Sprik M., J. Phys. Chem. B 112, 257 (2008). 10.1021/jp0748516 [DOI] [PubMed] [Google Scholar]
- Warshel A. and Levitt M., J. Mol. Biol. 103, 227 (1976). 10.1016/0022-2836(76)90311-9 [DOI] [PubMed] [Google Scholar]
- Blumberger J., Phys. Chem. Chem. Phys. 10, 5651 (2008). 10.1039/b807444e [DOI] [PubMed] [Google Scholar]
- Zeng X., Hu H., Hu X., Cohen A. J., and Yang W., J. Chem. Phys. 128, 124510 (2008). 10.1063/1.2832946 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cascella M., Magistrato A., Tavernelli I., Carloni P., and Rothlisberger U., Proc. Natl. Acad. Sci. U.S.A. 103, 19641 (2006). 10.1073/pnas.0607890103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S., Hu P., and Zhang Y., J. Phys. Chem. B 111, 3758 (2007). 10.1021/jp067147i [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warshel A. and Weiss R. M., J. Am. Chem. Soc. 102, 6218 (1980). 10.1021/ja00540a008 [DOI] [Google Scholar]
- Elstner M., Porezag D., Jungnickel G., Elsner J., Haugk M., Frauenheim T., Suhai S., and Seifert G., Phys. Rev. B 58, 7260 (1998). 10.1103/PhysRevB.58.7260 [DOI] [Google Scholar]
- Olsson M. H., Sharma P. K., and Warshel A., FEBS Lett. 579, 2026 (2005). 10.1016/j.febslet.2005.02.051 [DOI] [PubMed] [Google Scholar]
- Formaneck M. S., Li G., Zhang X., and Cui Q., J. Theor. Comput. Chem. 1, 53 (2002). 10.1142/S0219633602000075 [DOI] [Google Scholar]
- Li G., Zhang X., and Cui Q., J. Phys. Chem. B 107, 8643 (2003). 10.1021/jp034286g [DOI] [Google Scholar]
- Bhattacharyya S., Stankovich M., Truhlar D., and Gao J., J. Phys. Chem. A 111, 5729 (2007). 10.1021/jp071526+ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandrasekhar J., Smith S. F., and Jorgensen W. L., J. Am. Chem. Soc. 107, 154 (1985). 10.1021/ja00287a028 [DOI] [Google Scholar]
- Wesolowski T. A. and Warshel A., J. Phys. Chem. 97, 8050 (1993). 10.1021/j100132a040 [DOI] [Google Scholar]
- Olsson M., Hong G., and Warshel A., J. Am. Chem. Soc. 125, 5025 (2003). 10.1021/ja0212157 [DOI] [PubMed] [Google Scholar]
- Zhang Y., Liu H., and Yang W., J. Chem. Phys. 112, 3483 (2000). 10.1063/1.480503 [DOI] [Google Scholar]
- Cisneros G., Liu H., Zhang Y., and Yang W., J. Am. Chem. Soc. 125, 10384 (2003). 10.1021/ja029672a [DOI] [PubMed] [Google Scholar]
- Hu P. and Zhang Y., J. Am. Chem. Soc. 128, 1272 (2006). 10.1021/ja056153+ [DOI] [PubMed] [Google Scholar]
- Wang L., Yu X., Hu P., Broyde S., and Zhang Y., J. Am. Chem. Soc. 129, 4731 (2007). 10.1021/ja068821c [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang M., Lu Z., and Yang W., J. Chem. Phys. 121, 101 (2004). 10.1063/1.1757437 [DOI] [PubMed] [Google Scholar]
- Cisneros G., Wang M., Silinski P., Fitzgerald M., and Yang W., Biochemistry 43, 6885 (2004). 10.1021/bi049943p [DOI] [PubMed] [Google Scholar]
- Wang M., Lu Z., and Yang W., J. Chem. Phys. 124, 124516 (2006). 10.1063/1.2181145 [DOI] [PubMed] [Google Scholar]
- Corminboeuf C., Hu P., Tuckerman M., and Zhang Y., J. Am. Chem. Soc. 128, 4530 (2006). 10.1021/ja0600882 [DOI] [PubMed] [Google Scholar]
- Kastner J., Senn H., Thiel S., Otte N., and Thiel W., J. Chem. Theory Comput. 2, 452 (2006). 10.1021/ct050252w [DOI] [PubMed] [Google Scholar]
- Klahn M., Braun-Sand S., Rosta E., and Warshel A., J. Phys. Chem. B 109, 15645 (2005). 10.1021/jp0521757 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H., Lu Z., Parks J. M., Burger S. K., and Yang W., J. Chem. Phys. 128, 034105 (2008). 10.1063/1.2816557 [DOI] [PubMed] [Google Scholar]
- Hu H., Lu Z., and Yang W., J. Chem. Theory Comput. 3, 390 (2007). 10.1021/ct600240y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H., Boone A., and Yang W., J. Am. Chem. Soc. 130, 14493 (2008). 10.1021/ja801202j [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parks J. M., Hu H., Rudolph J., and Yang W., J. Phys. Chem. B (submitted).
- Hummer G. and Szabo A., Proc. Natl. Acad. Sci. U.S.A. 98, 3658 (2001). 10.1073/pnas.071034098 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H., Yun R. -H., and Hermans J., Mol. Simul. 28, 67 (2002). 10.1080/08927020211971 [DOI] [Google Scholar]
- Park S. and Schulten K., J. Chem. Phys. 120, 5946 (2004). 10.1063/1.1651473 [DOI] [PubMed] [Google Scholar]
- Kirkwood J. G., J. Chem. Phys. 3, 300 (1935). 10.1063/1.1749657 [DOI] [Google Scholar]
- Vuilleumier R., Sprik M., and Alavi A., J. Mol. Struct. 506, 343 (2000). [Google Scholar]
- Tavernelli I., Vuilleumier R., and Sprik M., Phys. Rev. Lett. 88, 213002 (2002). 10.1103/PhysRevLett.88.213002 [DOI] [PubMed] [Google Scholar]
- Sit P. H.-L., Cococcioni M., and Marzari N., Phys. Rev. Lett. 97, 028303 (2006). 10.1103/PhysRevLett.97.028303 [DOI] [PubMed] [Google Scholar]
- Dellago C., Bolhuis P. G., and Chandler D., J. Chem. Phys. 108, 9236 (1998). 10.1063/1.476378 [DOI] [Google Scholar]
- Frisch M. J., Trucks G. W., Schlegel H. B.et al. , GAUSSIAN 03, Revision D.02, Gaussian, Inc., Wallingford, CT, 2004.
- Hu H., Elstner M., and Hermans J., Proteins 50, 451 (2003). 10.1002/prot.10279 [DOI] [PubMed] [Google Scholar]
- Mann G., Yun R. H., Nyland L., Prins J., Board J., and Hermans J., Proceedings of the 3rd International Workshop on Algorithms for Macromolecular Modelling (Springer-Verlag, Berlin, 2002).
- Hu H., Lu Z., and Yang W., J. Chem. Theory Comput. 3, 1004 (2007). 10.1021/ct600295n [DOI] [PubMed] [Google Scholar]
- Hummer G., Pratt L. R., and Garcia A. E., J. Phys. Chem. A 102, 7885 (1998). 10.1021/jp982195r [DOI] [Google Scholar]
- See EPAPS Document No. E-JCPSA6-130-004917 for the phase potential effect of the cutoff treatment. For more information on EPAPS, see http://www.aip.org/pubservs/epaps.html.
- Donald W., Leib R., O’Brien J., Bush M., and Williams E., J. Am. Chem. Soc. 130, 3371 (2008). 10.1021/ja073946i [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly C., Cramer C., and Truhlar D., J. Phys. Chem. B 110, 16066 (2006). 10.1021/jp063552y [DOI] [PubMed] [Google Scholar]
- Reiss H., J. Phys. Chem. 89, 4207 (1985). 10.1021/j100266a013 [DOI] [Google Scholar]
- Gomer R., J. Chem. Phys. 66, 4413 (1977). 10.1063/1.433746 [DOI] [Google Scholar]
- Marcus Y., J. Chem. Soc., Faraday Trans. 87, 2995 (1991). 10.1039/ft9918702995 [DOI] [Google Scholar]
- Hay P. J. and Wadt W. R., J. Chem. Phys. 82, 270 (1985). 10.1063/1.448799 [DOI] [Google Scholar]
- VandeVondele J. and Sprik M., Phys. Chem. Chem. Phys. 7, 1363 (2005). 10.1039/b501603g [DOI] [PubMed] [Google Scholar]
- Mori-Sanchez P., Cohen A. J., and Yang W., Phys. Rev. Lett. 100, 146401 (2008). 10.1103/PhysRevLett.100.146401 [DOI] [PubMed] [Google Scholar]
- Cohen A. J., Mori-Sanchez P., and Yang W., Science 321, 792 (2008). 10.1126/science.1158722 [DOI] [PubMed] [Google Scholar]
- Wardman P., J. Phys. Chem. Ref. Data 18, 1637 (1989). [Google Scholar]