A polarizable force-field model for quantum-mechanical-molecular-mechanical Hamiltonian using expansion of point charges into orbitals

Abstract

We present an ab initio polarizable representation of classical molecular mechanics (MM) atoms by employing an angular momentum-based expansion scheme of the point charges into partial wave orbitals. The charge density represented by these orbitals can be fully polarized, and for hybrid quantum-mechanical-molecular-mechanical (QM∕MM) calculations, mutual polarization within the QM∕MM Hamiltonian can be obtained. We present the mathematical formulation and the analytical expressions for the energy and forces pertaining to the method. We further develop a variational scheme to appropriately determine the expansion coefficients and then validate the method by considering polarizations of ions by the QM system employing the hybrid GROMACS-CPMD QM∕MM program. Finally, we present a simpler prescription for adding isotropic polarizability to MM atoms in a QM∕MM simulation. Employing this simpler scheme, we present QM∕MM energy minimization results for the classic case of a water dimer and a hydrogen sulfide dimer. Also, we present single-point QM∕MM results with and without the polarization to study the change in the ionization potential of tetrahydrobiopterin (BH₄) in water and the change in the interaction energy of solvated BH₄ (described by MM) with the P₄₅₀ heme described by QM. The model can be employed for the development of an extensive classical polarizable force-field.

INTRODUCTION

Atomistic simulation of macromolecular chemical and biological systems is an essential and integral part of computational chemistry and computational biology research. The force-field based atomistic classical molecular-mechanical (MM) simulation and the hybrid multiscale quantum-mechanical-molecular-mechanical (QM∕MM) simulation are central to such studies. Whether it is a purely MM or a hybrid QM∕MM calculation, the simplified point-charge prescription of the classical MM atoms hinders our ability to correctly polarize the MM system. This in turn forbids us to have a correctly polarized QM charge density in a multiscale QM∕MM calculation. The latter is quite important for studying the change in the electronic structure of the protein active site (described by QM) by the influence of MM molecules or molecular fragments and is crucial for studying the protein reaction mechanism and their inhibition. Another fallout of the pointlike MM-atom charges, for multiscale QM∕MM calculations, is the divergence of the QM∕MM electrostatic interaction at short ranges arising from the Coulomb singularity of a point charge. The divergence produces an unphysical perturbation of the electronic structure of the QM region. Here we address both these issues simultaneously by employing an ab initio partial wave expansion of the MM-atom point charges into atomic type orbitals. First, the interaction of these orbitals with the QM electronic structure provides a renormalization of the Coulomb interaction and removes the divergence at short ranges. Second, with the orbital representation, we can polarize the MM-atom charge and can have mutual polarization with the QM system.

Here we provide a brief account of the polarizable force-field (FF) development. Polarizable FF developments are mostly concentrated on the modeling of water that has a permanent dipole and, besides, its apparently simple structure provides quite a complex system to model with a classical description. The complexity may be understood from the fact that until this date, there is no particular model that satisfies both the bulk and the few-body structural properties (hydrogen-bonding features) of water, though there are models that satisfy a wide range of water characteristics.¹ The existing polarizable water models treat the water molecule with a rigid geometry (fixed O–H bond lengths and H–O–H angle) and the polarizability is mainly simulated either by (1) a fluctuating charge approximation^{2, 3} or (2) by additional point-dipole, polarizable dipole, or Drude oscillator working in the limit of point dipole placed at or around the center of mass of the water molecule.^{4, 5, 6, 7} The majority of the polarizable water models developed over the past decades demonstrate that a smearing of atomic point charges needs to be employed in order to appropriately balance the electrostatic interactions at short ranges.^{6, 7} In particular, this balance of short-range electrostatic interaction is crucial for reproducing the hydrogen-bonding geometry of water and significantly contributes to the density variation of water over temperature.

The above mentioned studies are consistent with the development of the hybrid QM∕MM method, which demonstrates that a correction for the short-range electrostatic interaction between QM and MM fragments is quite crucial. Without such a correction, either with a smearing of point charges^{8, 9, 10} or with an empirical potential,¹¹ it is expected that there will be an unphysical perturbation or “spilling” of QM charge densities around point-charge MM atoms sitting near a QM system. Consequently, it may be emphasized here that to develop a polarizable QM∕MM Hamiltonian, it will be counterproductive to employ a point-dipole or a polarizable dipole water model developed for classical simulations as the point dipole will create more pronounced spilling of QM charges. This is because the QM-charge-classical-dipole interaction will diverge faster (1∕r²) than the QM-charge-classical-charge interaction (1∕r) at short ranges. So, for QM∕MM, we propose to expand the classical atom point charges with s, p, etc., orbitals to incorporate the polarizability effect of the classical molecule. This is to emphasize that the expansion of MM charges with s-type Gaussian and Slater orbital is widely practiced in both classical and QM∕MM methods. Here, we introduce a normalized bound expansion scheme and we show that allowing for higher order orbitals one can incorporate the polarizability of the atoms in a consistent way. This scheme is free from any divergence of the short-range electrostatic interaction arising from a point or polarizable dipole as the expansion naturally leads to a renormalization of the Coulomb potential. Thus, it is expected to provide a clear advantage over a point or polarizable dipole scheme as the expansion of classical atom point charges into s-type, p-type, etc., orbitals will be able to include the effect of higher order polarization (quadrupole, octupole, etc.) of the atoms in a comprehensive manner and will be devoid of short-range divergence.

In our previous communication, we presented¹⁰ an angular momentum-based expansion scheme using the Slater orbital and performed a first order calculation, that is, with zero angular momentum or s-wave expansion only. The major difficulties in employing a higher order angular momentum in the expansion scheme were (1) in the derivation of exact analytical expressions for the energy and forces (which are crucial from the point of view of managing the computational time requirement) and (2) obtaining optimum values for the expansion coefficients and exponents of the Slater functions so that the employed orbitals appropriately mimic the polarization at short distances and satisfy the Coulomb potential of the MM atom at intermediate and large distances. In generating the electrostatic potential (ESP) charges for the atoms in a molecule, the Coulomb potential generated by the assigned point charges on each atom is fitted to the ESP obtained from a QM calculation. The fitting is done beyond a critical radius, which is of the order of 1.4 times the van der Waals radius of an atom.¹² Thus, one of the crucial aspects in our partial wave orbital expansion is that our expansion coefficients and exponents must be such that, at and above that critical radius, they produce the Coulomb potential of the point charges. To obtain the expansion coefficients, we employ a variational scheme for the QM energy, while to obtain the exponents, we use the criteria of ESP charge fitting. After presenting the methodology, we shall employ the GROMACS-CPMD QM∕MM code developed by interfacing¹³ the MM program GROMACS (Groningen machine for chemical simulations)¹⁴ with the density functional theory-based QM program CPMD (Car–Parrinello molecular dynamics).¹⁵

POLARIZABLE DESCRIPTION OF MM ATOMS: THE PARTIAL WAVE EXPANSION MODEL

The Mulliken population analysis¹⁶ provides the basics of a point-charge prescription of an atom as the following:

$$q_j=Z_j-\sum _{\mu ∊j}{\left(\mathbf{P}\mathbf{S}\right)}_{\mu \mu },$$ (1)

where Z_j is the nuclear charge of the atom j and the summation is over the basis functions centered on j. For a closed shell system, (PS)_μμ is given by

$$\sum _{\mu }{\left(\mathbf{P}\mathbf{S}\right)}_{\mu \mu }=2\sum _{\alpha }^{N∕2}\int d^{3}r{\mid {\psi }_{\alpha }\left(\mathbf{r}\right)\mid }^2,$$ (2)

with

$${\psi }_{\alpha }=\sum _{\mu =1}^K{C}_{\mu \alpha }{\varphi }_{\mu },$$ (3)

where N is the number of electrons with ϕ_μ being the basis set. (PS)_μμ is interpreted as the number of electrons associated with ϕ_μ.

As we obtain q_j from the right-hand side (RHS) of Eq. 1, all the polarization information and anisotropic charge distribution of the atom are lost. Here, given a point charge q_j, we want to find a form similar to the RHS of Eq. 1 as closely as possible. Further, we want the expression to be devoid of point charges (such as Z_j) so that the developed QM∕MM Hamiltonian does not encounter any Coulomb divergence. Thus, we seek a minimal representation of q_j as^{9, 10}

$$q_j=q_j\int d^3{r}^{\prime }{\mid \psi \left({\mathbf{r}}^{\prime }\right)\mid }^2,$$ (4)

where the order parameter ψ(r^′) is expanded into partial wave orbitals as

$$\psi \left({\mathbf{r}}^{\prime }\right)=\sum _{n,\ell ,m}{\varphi }_{n\ell m}=\sum _{n,\ell ,m}{C}_{n\ell m}{\mathcal{R}}_{n\ell }\left(r^{\prime }\right)Y_{\ell m}\left(\widehat{r^{\prime }}\right),$$ (5)

where r^′ is an arbitrary point in space, ϕ_nℓm are the orthonormal basis set, R_nℓ(r^′) are the Laguerre polynomials, $Y_{\ell m}\left(\widehat{r^{\prime }}\right)$ are the spherical harmonics, n is the shell number (principal quantum number), ℓ is the angular momentum quantum number associated with an orbital, and m is the magnetic quantum number. ℓ=0,1,2,…n−1; m=−∣ℓ∣ to +∣ℓ∣. C_nℓm are the expansion coefficients to be determined so as to obtain appropriate polarization. The charge density at any point r^′ is proportional to

$${\mid \psi \left({\mathbf{r}}^{\prime }\right)\mid }^2=\sum _{n^{\prime },{\ell }^{\prime },m^{\prime }}\sum _{n,\ell ,m}{C}_{n^{\prime }{\ell }^{\prime }{m}^{\prime }}^{\ast }{C}_{n\ell m}{\mathcal{R}}_{n^{\prime }{\ell }^{\prime }}^{\ast }\left(r^{\prime }\right){\mathcal{R}}_{n\ell }\left(r^{\prime }\right)Y_{{\ell }^{\prime }{m}^{\prime }}^{\ast }\left(\widehat{r^{\prime }}\right)Y_{\ell m}\left(\widehat{r^{\prime }}\right).$$ (6)

This is to emphasize that to obtain the effect of mutual polarization the expansion coefficients need to be adjusted during each self-consistent-field (SCF) cycle (using the developed variational scheme). For this, it is important to reduce the size of the expansion coefficient matrix. We now start working for an optimal scheme: we choose to keep one orbital for each partial wave type (s, p, d, etc.), and thus we recast the expansion in Eq. 5 as

$$\psi \left({\mathbf{r}}^{\prime }\right)=\sum _{\ell ,m}{C}_{\ell m}{\mathcal{R}}_{\ell +1,\ell }\left(r^{\prime }\right)Y_{\ell ,m}\left(\widehat{r^{\prime }}\right).$$ (7)

For ℓ_max=1, that is for an expansion up to p-wave, which will be explicitly considered in this work, it takes the following explicit forms:

$$\psi \left({\mathbf{r}}^{\prime }\right)=C_{00}{\mathcal{R}}_{1,0}\left(r^{\prime }\right)Y_{00}\left(\widehat{r^{\prime }}\right)+C_{1-1}{\mathcal{R}}_{2,1}\left(r^{\prime }\right)Y_{1-1}\left(\widehat{r^{\prime }}\right)+C_{10}{\mathcal{R}}_{2,1}\left(r^{\prime }\right)Y_{10}\left(\widehat{r^{\prime }}\right)+C_{11}{\mathcal{R}}_{2,1}\left(r^{\prime }\right)Y_{11}\left(\widehat{r^{\prime }}\right),$$ (8)

$$=C_{00}{\psi }_{00}\left({\mathbf{r}}^{\prime }\right)+C_{1-1}{\psi }_{1-1}\left({\mathbf{r}}^{\prime }\right)+C_{10}{\psi }_{10}\left({\mathbf{r}}^{\prime }\right)+C_{11}{\psi }_{11}\left({\mathbf{r}}^{\prime }\right),$$ (9)

$$=\sum _{\ell ,m}{C}_{\ell m}{\psi }_{\ell m}\left({\mathbf{r}}^{\prime }\right).$$ (10)

With the above expansion for ψ(r^′), the charge density ρ(r^′) due to a point charge q can be represented as

$$\rho \left({\mathbf{r}}^{\prime }\right)=q{\mid \psi \left({\mathbf{r}}^{\prime }\right)\mid }^{\mathbf{2}}=\sum _{{\ell }^{\prime },m^{\prime }}\sum _{\ell ,m}{\rho }_{{\ell }^{\prime }{m}^{\prime };\ell m}\left({\mathbf{r}}^{\prime }\right).$$ (11)

To reveal all the components of ρ explicitly, we represent them in the following matrix form:

$$\rho \left({\mathbf{r}}^{\prime }\right)\equiv \left(\begin{array}{cccc}{\rho }_{00;00}\left({\mathbf{r}}^{\prime }\right)& {\rho }_{00;1-1}\left({\mathbf{r}}^{\prime }\right)& {\rho }_{00;10}\left({\mathbf{r}}^{\prime }\right)& {\rho }_{00;11}\left({\mathbf{r}}^{\prime }\right)\\ {\rho }_{1-1;00}\left({\mathbf{r}}^{\prime }\right)& {\rho }_{1-1;1-1}\left({\mathbf{r}}^{\prime }\right)& {\rho }_{1-1;10}\left({\mathbf{r}}^{\prime }\right)& {\rho }_{1-1;11}\left({\mathbf{r}}^{\prime }\right)\\ {\rho }_{10;00}\left({\mathbf{r}}^{\prime }\right)& {\rho }_{10;1-1}\left({\mathbf{r}}^{\prime }\right)& {\rho }_{10;10}\left({\mathbf{r}}^{\prime }\right)& {\rho }_{10;11}\left({\mathbf{r}}^{\prime }\right)\\ {\rho }_{11;00}\left({\mathbf{r}}^{\prime }\right)& {\rho }_{11;1-1}\left({\mathbf{r}}^{\prime }\right)& {\rho }_{11;10}\left({\mathbf{r}}^{\prime }\right)& {\rho }_{11;11}\left({\mathbf{r}}^{\prime }\right)\end{array}\right).$$ (12)

The coefficients C_ℓm, which are needed to evaluate ρ, are being determined during the energy minimization of the QM-MM interaction presented in Sec. 5. Without the influence of QM and other MM atoms, ρ_00;00(r^′) should be the sole contributor to the QM-MM energy. Thus, the terms like ρ_00;10(r^′) can be thought of representing the induced polarization, induced by QM and other MM atoms. As the QM charge density is also being influenced during the QM-SCF calculation, the final QM-MM interaction is expected to lead to dispersion interaction, among others, and to interfere with the atom-atom van der Walls interaction presented by the 1∕r⁶ term of the Lennard–Jones (LJ) potential. In developing the present QM∕MM interaction Hamiltonian, our intention was not to interfere with any classical FF parameter used in the calculation though it is understood that for the development of a fully polarizable FF, the classical FF parameters need to be readjusted. Thus, first, we present the calculation for the energy and forces arising out of the above expansion in full and validate our result through numerical simulation. Then we explore suitable simplification for the QM∕MM Hamiltonian that can be used for calculations with reasonable computational demand.

EXPRESSION FOR THE ENERGY AND FORCES

The resulting ESP of a MM charge q_j at any point r is given by

$$V\left(\mathbf{r}\right)=q_j\int d^3{r}^{\prime }\frac{{\mid \psi \left({\mathbf{r}}^{\prime }\right)\mid }^2}{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }=q_j\sum _{{\ell }^{\prime }=0}^{{\ell }_{\text{max}}^{\prime }}\sum _{m^{\prime }=-\mid {\ell }^{\prime }\mid }^{+\mid {\ell }^{\prime }\mid }\sum _{\ell =0}^{{\ell }_{\text{max}}}\sum _{m=-\mid \ell \mid }^{+\mid \ell \mid }{V}_{{\ell }^{\prime }{m}^{\prime };\ell m}\left(\mathbf{r}\right),$$ (13)

where

$$V_{{\ell }^{\prime }{m}^{\prime };\ell m}\left(\mathbf{r}\right)=C_{{\ell }^{\prime }{m}^{\prime }}^{\ast }{C}_{\ell m}\int d^3{r}^{\prime }\frac{{\mathcal{R}}_{{\ell }^{\prime }+1,{\ell }^{\prime }}^{\ast }\left(r^{\prime }\right){\mathcal{R}}_{\ell +1,\ell }\left(r^{\prime }\right)Y_{{\ell }^{\prime },m^{\prime }}^{\ast }\left(\widehat{r^{\prime }}\right)Y_{\ell ,m}\left(\widehat{r^{\prime }}\right)}{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid },$$ (14)

$$=\sum _{L=0}^{\ell +{\ell }^{\prime }}\Gamma \left({\ell }^{\prime }{m}^{\prime },\ell m;L\right){\mathcal{R}}_{{\ell }^{\prime }\ell }^L\left(r\right)Y_{L,m-m^{\prime }}\left(\widehat{r}\right).$$ (15)

The simplification to Eq. 15 from Eq. 14 and the explicit forms of the constants Γ(ℓ^′m^′,ℓm;L) and the full analytical form of the radial distribution function ${\mathcal{R}}_{{\ell }^{\prime }\ell }^L\left(r\right)$ are given in detail in Appendix A. $Y_{L,m-m^{\prime }}\left(\widehat{r}\right)$ is the usual spherical harmonics determining the angular distribution of the charge density. It is to be noted that for the maximum value of ℓ^′,ℓ taken here as 1, one would get L=0,1,2. This means that V(r) would lead to potentials for charge (L=0), dipole (L=1), and quadrupole (L=2) interactions. It is interesting to note that the potential V(r) as given by Eqs. 13, 15 turns out to be purely real since the complex part of $Y_{L,m-m^{\prime }}\left(\widehat{r}\right)$ cancels out once the summation over ℓ^′,m^′,ℓ,m is performed. This exhibits the usefulness of the expansion scheme.

The “orbital” representation of a point charge and the derivation of analytical expressions for the ESP and forces due to such a polarizable charge distribution are the principal contributions of this paper. For future reference, we also write down the expression for the forces that are also fully analytical in form. The force components F_xk (x₁≡x, x₂≡y, and x₃≡z) on a locally integrated charge density ρ_μ present at the position r are given by

$$F_{x_k}\left(\mathbf{r}\right)=q_j{\rho }_{\mu }\sum _{{\ell }^{\prime }=0}^{{\ell }_{\text{max}}^{\prime }}\sum _{m^{\prime }=-\mid {\ell }^{\prime }\mid }^{+\mid {\ell }^{\prime }\mid }\sum _{\ell =0}^{{\ell }_{\text{max}}}\sum _{m=-\mid \ell \mid }^{+\mid \ell \mid }-\frac{\partial }{\partial x_k}{V}_{{\ell }^{\prime }{m}^{\prime };\ell m}\left(\mathbf{r}\right),$$ (16)

where

$$\frac{\partial }{\partial x_k}{V}_{{\ell }^{\prime }{m}^{\prime };\ell m}\left(\mathbf{r}\right)=C_{{\ell }^{\prime }{m}^{\prime }}^{\ast }{C}_{\ell m}\sum _{L=0}^{\ell +{\ell }^{\prime }}\Gamma \left({\ell }^{\prime }{m}^{\prime },\ell m;L\right)\left[Y_{L,m^{\prime }-m}\left(\widehat{r}\right){\mathcal{R}}_{{\ell }^{\prime }\ell }^{\left(1\right)L}\left(r\right)\times \frac{\partial r}{\partial x_k}+Y_{L,m^{\prime }-m}^{\left(\theta \right)}\left(\widehat{r}\right){\mathcal{R}}_{{\ell }^{\prime }\ell }^L\left(r\right)\times \frac{\partial \theta }{\partial x_k}+Y_{L,m^{\prime }-m}^{\left(\varphi \right)}\left(\widehat{r}\right){\mathcal{R}}_{{\ell }^{\prime }\ell }^L\left(r\right)\times \frac{\partial \varphi }{\partial x_k}\right].$$ (17)

The derivatives ${\mathcal{R}}_{{\ell }^{\prime }\ell }^{\left(1\right)L}\left(r\right)$, $Y_{L,M}^{\left(\theta \right)}\left(\widehat{r}\right)$, and $Y_{L,M}^{\left(\varphi \right)}\left(\widehat{r}\right)$ are defined in the Appendix A. In Appendix B, we provide the expression for the potential corresponding to the diagonal terms of the MM-atom density matrix.

THE QM∕MM INTERACTION HAMILTONIAN FOR POLARIZABLE-ORBITAL MM ATOMS

In a QM∕MM hybrid calculation, the total Hamiltonian of the system is partitioned in the following way:^{17, 18, 19}

$$H=H_{\text{QM}}+H_{\text{MM}}+H_{\text{QM}∕\text{MM}},$$ (18)

where H_QM∕MM accounts for the interaction between the QM subsystem and the MM atoms. In general, H_QM∕MM contains Coulomb (long-range) and short-range interactions (dispersion and short-range repulsion) and is taken as the following (in a.u.):^{17, 18, 19}

$$H_{\text{QM}∕\text{MM}}=-\sum _{\begin{array}{c}i∊\text{QM}\\ j∊\text{MM}\end{array}}\frac{e_i{q}_j}{\mid {\mathbf{r}}_i-{\mathbf{R}}_j\mid }+\sum _{\begin{array}{c}\nu ∊\text{QM}\\ j∊\text{MM}\end{array}}\frac{Z_{\nu }{q}_j}{\mid {\mathbf{R}}_{\nu }-{\mathbf{R}}_j\mid }+\sum _{\begin{array}{c}\nu ∊\text{QM}\\ j∊\text{MM}\end{array}}4{ϵ}_{\nu j}\left\{{\left(\frac{{\sigma }_{\nu j}}{\mid {\mathbf{R}}_{\nu }-{\mathbf{R}}_j\mid }\right)}^{12}-{\left(\frac{{\sigma }_{\nu j}}{\mid {\mathbf{R}}_{\nu }-{\mathbf{R}}_j\mid }\right)}^6\right\},$$ (19)

where r_i, R_ν, and R_j represent the position vector for the ith electron, νth nucleus of the QM subsystem, and jth MM atom, respectively; Z_ν is the nuclear charge of the νth nucleus. The short-range repulsion and attractive mutual average polarization (dispersion) between the QM and MM atoms have been modeled using the LJ potential;²⁰σ and ϵ are the parameters defining the LJ potential.

With the above partial wave expansion for the ESP charge, one can describe the Coulomb interaction energy between the jth MM atom and the QM subsystem as

$$E_{\text{QM}∕\text{MM}}^{\text{Coul}}=E_{\rho q_j}+E_{Z_{\nu }{q}_j},$$ (20)

where

$$E_{\rho q_j}=q_j\int d^{3}r\rho \left(\mathbf{r}\right)\int d^3{r}^{\prime }\frac{{\mid \psi \left({\mathbf{r}}^{\prime }-{\mathbf{R}}_j\right)\mid }^2}{\mid {\mathbf{r}}^{\prime }-\mathbf{r}\mid }=q_j\int d^{3}r\rho \left(\mathbf{r}\right)V\left(\mathbf{r}-{\mathbf{R}}_j\right),$$ (21)

$$E_{Z_{\nu }{q}_j}=\sum _{\nu ∊\text{QM}}{Z}_{\nu }\left({\mathbf{R}}_{\nu }\right)\int d^3{r}^{\prime }\frac{{\mid \psi \left({\mathbf{r}}^{\prime }-{\mathbf{R}}_j\right)\mid }^2}{\mid {\mathbf{r}}^{\prime }-{\mathbf{R}}_{\nu }\mid }=\sum _{\nu ∊\text{QM}}{Z}_{\nu }\left({\mathbf{R}}_{\nu }\right)V\left({\mathbf{R}}_{\nu }-{\mathbf{R}}_j\right),$$ (22)

where Z_ν is the charge of the ionic core of the νth QM atom (i.e., sum of the nuclear and inner electron charges). V is given by Eq. 13 in terms of its partial wave components. The QM∕MM electrostatic force components F_x,F_y,F_z on the jth MM atom are simply the sum of the derivatives of the energy (forces on QM atoms are evaluated numerically inside the CPMD code):

$$F_{x_k}\left(j\right)=-\frac{\partial }{\partial x_k}\left\{E_{\rho q_j}+E_{Z_{\nu }{q}_j}\right\}=q_j\int d^{3}r\rho \left(\mathbf{r}\right)\left\{-\frac{\partial }{\partial x_k}V\left(\mathbf{r}-{\mathbf{R}}_j\right)\right\}+\sum _{\nu ∊QM}{Z}_{\nu }\left({\mathbf{R}}_{\nu }\right)\left\{-\frac{\partial }{\partial x_k}V\left({\mathbf{R}}_{\nu }-{\mathbf{R}}_j\right)\right\},$$ (23)

where we again have k=1,2,3 and x₁≡x, x₂≡y, and x₃≡z.

DETERMINATION OF THE COEFFICIENTS C_ℓm USING THE VARIATIONAL PRINCIPLE

As described above, the partial wave orbital model is capable of introducing dipole, quadrupole, and higher order multipole interactions with appropriate anisotropy in the charge distributions of the atoms. For isotropic polarization (variation of potential as 1∕rⁿ; n=2,3,4,…), the coefficients of the partial wave expansion $C_{\ell m}^j$ can easily be chosen from the simulation data. However, to introduce angular anisotropy, the coefficients need to be chosen in a consistent way. Here we present a variational scheme to determine the optimum value of the partial wave expansion coefficients $C_{\ell m}^j\equiv C_{\tau }^j$, for the jth MM atom interacting with QM and other MM atoms. This is to mention that a consistent determination of the coefficients $C_{\ell m}^j$ for all the atoms j requires the diagonalization of a 4N_MM×4N_MM eigenvalue matrix (four coefficients for each of N_MM number of MM atoms) and the computation time increases with the square of N_MM. Here instead of minimizing the whole QM∕MM energy, we follow a simpler scheme whose computational demand increases linearly with N_MM, i.e., we maximize the interaction energy of each MM charge with its QM∕MM surrounding, which is the equivalent to the diagonalization of N_MM number of 4×4 matrices and determine the coefficients of each MM atom considering its interaction with the rest of MM atoms and the QM system.

Thus, the overall Coulomb interaction energy $E_{\text{Coul}}^j$ of the jth MM atom with the QM system and other MM atoms is given by

$$E_{\text{Coul}}^j=\sum _{\mu }{E}_{{\rho }_{\mu }{q}_j}+\sum _{\nu }{E}_{Z_{\nu }{q}_j}+\sum _{i\ne j}{E}_{q_i{q}_j}.$$ (24)

We now employ a variational principle

$$\frac{\partial }{\partial C_{\tau }^j}{E}_{\text{Coul}}^j=0,$$ (25)

where τ≡{ℓ,m}; ρ_μ represents the locally integrated electronic charge density on the three-dimensional grid points with which the CPMD calculations are facilitated. We represent $E_{\mathrm{Coul}}^j$ as

$$E_{\text{Coul}}^j=\sum _{\mu }{\rho }_{\mu }{q}_j\int d^3{r}^{\prime }\frac{{\mid \psi \left({\mathbf{r}}^{\prime }-{\mathbf{R}}_j\right)\mid }^2}{\mid {\mathbf{r}}^{\prime }-{\mathbf{r}}_{\mu }\mid }+\sum _{\nu }{Z}_{\nu }{q}_j\int d^3{r}^{\prime }\frac{{\mid \psi \left({\mathbf{r}}^{\prime }-{\mathbf{R}}_j\right)\mid }^2}{\mid {\mathbf{r}}^{\prime }-{\mathbf{R}}_{\nu }\mid }+\sum _{i\ne j}{q}_i{q}_j\int d^3{r}^{\prime }\frac{{\mid \psi \left({\mathbf{r}}^{\prime }-{\mathbf{R}}_j\right)\mid }^2}{\mid {\mathbf{r}}^{\prime }-{\mathbf{R}}_i\mid }=q_j\sum _{\tau ,{\tau }^{\prime }}{C}_{{\tau }^{\prime }}^j{C}_{\tau }^j\left[\sum _{\mu }{\rho }_{\mu }⟨{\varphi }_{{\tau }^{\prime }}\mid \frac{1}{\mid {\mathbf{r}}^{\prime }-{\mathbf{r}}_{\mu }\mid }\mid {\varphi }_{\tau }⟩+\sum _{\nu }{Z}_{\nu }⟨{\varphi }_{{\tau }^{\prime }}\mid \frac{1}{\mid {\mathbf{r}}^{\prime }-{\mathbf{R}}_{\nu }\mid }\mid {\varphi }_{\tau }⟩+\sum _{i\ne j}{q}_i⟨{\varphi }_{{\tau }^{\prime }}\mid \frac{1}{\mid {\mathbf{r}}^{\prime }-{\mathbf{R}}_i\mid }\mid {\varphi }_{\tau }⟩\right]=q_j\sum _{\tau ,{\tau }^{\prime }}{C}_{{\tau }^{\prime }}^j{C}_{\tau }^j\left[V_{{\tau }^{\prime }\tau }^{\mu }+V_{{\tau }^{\prime }\tau }^{\nu }+V_{{\tau }^{\prime }\tau }^i\right]=q_j\sum _{\tau ,{\tau }^{\prime }}{C}_{{\tau }^{\prime }}^j{C}_{\tau }^j{V}_{{\tau }^{\prime }\tau }^{\text{total}}.$$ (26)

Now we construct a Lagrangian

$$\mathcal{L}\left(C_{\tau },C_{{\tau }^{\prime }};E\right)=q_j\sum _{\tau ,{\tau }^{\prime }}{C}_{{\tau }^{\prime }}^j{C}_{\tau }^j{V}_{{\tau }^{\prime }\tau }^{\text{total}}-E\left(\sum _{\tau }{C}_{\tau }^2-1\right)$$ (27)

and seek

$$\frac{\partial }{\partial C_{\tau }^j}\mathcal{L}\left(C_{\tau },C_{{\tau }^{\prime }};E\right)=0.$$ (28)

Equations 27, 28 provide

$$\sum _{{\tau }^{\prime }}{C}_{\tau }^{\prime }{V}_{{\tau }^{\prime }\tau }^{\text{total}}-E{C}_{\tau }=0,$$ (29)

where E is the Lagrange multiplier, τ=ℓ(ℓ+1)+m+1={1,2,3,4} for {ℓ,m}={0,0},{1,−1},{1,0},{1,1}. We solve the eigenvalue equation using the LAPACK library functions²¹ and obtain values C_τ for each MM-atom j.

RESULTS AND DISCUSSIONS

To discuss our results, first we demonstrate the validity of the theoretical formalism and the numerical code considering a full interplay of angular anisotropy. Thereafter we discuss the suitability of further simplification and provide results considering an isotropic polarization scheme.

To understand the merit of the polarizable orbital model, we consider the polarization of a unit MM charge placed in the field of a QM hydrogen molecule. We place a unit negative point charge (a) along the molecular axis of H₂ treated quantum mechanically and (b) perpendicular to the molecular axis. The molecular axis of H₂ is taken along z-axis. Thus, for aligned setting, we place the negative MM point charge on z-axis while for perpendicular setting, we place the MM charge along the x-axis. For the aligned setting, the MM charge will see an axial distribution of charge pertaining to H₂. Thus, the p₀ configuration that provides a dumbbell shape along the z-axis would be the most favorable for the configuration of minimum energy. For aligned setting, we obtained the largest value for the coefficient C₁₀ of the expansion (Table 1), which validates the predicted physical scenario. When the unit negative charge is placed perpendicular to the molecular axis, it is expected to experience stronger repulsion where the QM electron density is maximum, that is, near the nuclear centers. Thus, in this configuration, the two torus shaped p-wave configurations provided by p_±1 should have the highest contribution toward minimum energy. From Table 1, we see that C₁₋₁ and C₁₁ have the highest values among the four coefficients.

Table 1.

Normalized coefficients C_ℓm as obtained from variational approach.

	C00	C1−1	C10	C11
Case a	0.262	0.025	−0.964	−0.025
Case b	0.134	−0.670	−0.288	0.670

To demonstrate the resulting shapes of the MM charge for the two different scenarios as described by the expansion coefficients shown in Table 1, we generated the MM charge distribution in the form of Gaussian cube files and plotted them in Figs. 12 using the VMD molecular visualization program.²² The coefficients and the shape of the perturbed MM charge distribution (displayed in Figs. 12) are in conformity with the expected shapes thus confirming the validity of the methodology and the developed numerical code.

Figure 1.

The shape of a unit negative MM-atom charge after expansion using s3p partial wave orbitals and polarization by the QM system of a H₂ molecule when the charge is placed aligned (slightly off, to offset singularity in the potential) with the H₂ nuclear axis.

Figure 2.

The shape of a unit negative MM-atom charge after expansion using s3p partial wave orbitals and polarization by the QM system of a H₂ molecule when the charge is placed along a perpendicular bisector to the H₂ nuclear axis.

A MM charge polarizes according to the influence provided by the QM system and other MM charges and the polarization effect of MM on QM can be taken into account through the QM∕MM interaction Hamiltonian, H_QM∕MM. However, we face some challenges. First challenge comes from the fact that the QM∕MM van der Waals interaction and the Pauli repulsion between the QM and MM atoms are still governed by the classical FF and we cannot interfere²³ with these interactions unless we want to readjust the classical FF parameters. The second challenge comes from the fact that the anisotropy of the polarization effect requires that the polarization state of the MM atoms, and hence the coefficients, be evaluated self consistently at each SCF cycle. With the present state of computational ability, this latter exercise is not a practical option, except for small test cases. So, we now focus on introducing some simplification to the above scheme and present a simpler isotropic polarizable model for the expensive QM∕MM simulation.

To reach the goal of an isotropic form of the polarization interaction, we see that retaining only the diagonal terms of the density matrix represented by Eq. 12 will render the ϕ-dependence of the charge density but there will still be a θ-dependence. In accordance with the final expressions provided in Appendix B, we see that the choice C₁₁=C₁₀=C₁₋₁=to be determined, meaning the same contribution from all the three p-wave amplitudes renders θ-dependence, too. These two simplifications reduce the computational time up to a great extent while introducing the polarization of the MM atoms in an isotropic way as has been done in the case of polarization through point dipoles.⁴ However, compared to the case of a point dipole, the present scheme has an appropriate renormalization of interaction at short distances, arising from the smearing of charges into orbitals. Without this renormalization, as in the case of any point-dipole employed polarizable model, the QM∕MM interaction diverges strongly at short distances leading to occasional collapse of the simulation as found in the CHARMM-QCHEM QM∕MM model with Drude oscillator based polarization considered in the CHARMM part.²⁴ In addition, our development provides full polarization of MM charges if the restriction on the expansion coefficients is relaxed, and this can be easily achieved in further code development with the advent of more powerful computational facilities.

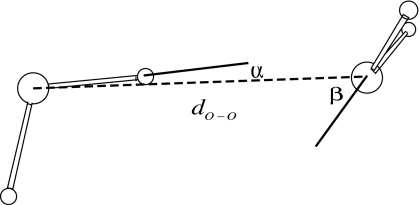
We consider the application of the present polarizable scheme first to the classic case of a water dimer with the H-bond donor water molecule treated with MM and the H-bond acceptor water molecule with QM. This conformation exposes the lone-pair electrons of the QM-oxygen to the H-bond and provides the opportunity for a crucial test of the QM∕MM Hamiltonian as the polarization of the MM-atom point charges is expected to affect the mutual orientation of the water molecules (Fig. 3). In particular, the angle β is modulated by the interaction of the MM charges with the localized charge density lobes (known as lone-pair electrons) of the oxygen atom from the QM subsystem. In water, the measured values of the angles α and β are reported to be in the range of 6°±20° and 57°±10°, respectively.²⁵ Using elaborate fully QM calculational schemes [GAUSSIAN98 (Ref. ²⁶) and CPMD (Ref. ¹⁵)] we find that the angles α and β are also quite sensitive to the calculational scheme used.¹⁰ In a QM∕MM calculation, the sensitivity rests upon the QM∕MM Hamiltonian as it describes the electrostatic interaction between the two water molecules. Employing only the s-wave expansion of the point charges,¹⁰ we did not obtain accurate results for the angles α and β as compared to the experimental data²⁵ and sophisticated QM calculations. In a pure MM force field, these angles are obtained by a suitable choice of parameters that define the Coulomb and van der Waals interactions. In a previous QM∕MM calculation,⁸ employing the EGO-CPMD interface, the partial charges on the hydrogen and oxygen atoms were adjusted for an isolated dimer, which basically produced α and β angles closer to those obtained by elaborate calculations or experiment. We argue that the angles α and β should be a consequence of the interaction between the polarized atoms in the MM subsystem and the charge densities in the QM subsystem. Thus, any suitable expansion of the MM-atom point charges into s- and p-orbitals should appropriately represent the angles α and β.

Figure 3.

Angular correlations of a water dimer.

In Table 2, we demonstrate the consequences of a variation of s- and p-wave contributions. The results demonstrate that when only 1s-wave expansion is used both angles α and β are not in full accordance with extensive QM results. As we add isotropic polarizability (p-wave contribution) to each MM atom, the values of the angles α and β start improving. We show the effect of adding increased amount of isotropic polarizability by taking increasing values for C_1m (m=−1,0,1) (The weight of the s-wave contribution decreases through the normalization of the constants: ${\sum }_{\ell ,m}{C}_{\ell m}^2=1.0$.) With the inclusion of p-wave and renewed normalization of the electrostatic potential, we find that the hydrogen bond distance d_H–O and oxygen-oxygen distance d_O–O increases with increasing value of C_1m. This indicates an overall increase in the O–O repulsion and an overall decrease in the H⋯O attractive interaction with increasing isotropic polarization. In our previous study,¹⁰ to obtain a better hydrogen-bonding geometry, we had to increase the LJ parameter σ of the oxygen atoms from 3.150 61 to σ=3.250 61 Å to introduce the required repulsion. However, the use of the s3p polarization scheme for point charges leads to an increase in the oxygen-oxygen repulsion and thus there is no need to adjust the LJ parameters and we revert σ back to its TIP3P value of 3.150 61 Å. We choose the constant to fit the hydrogen bond length to experimental value of 1.98 Å. Accordingly, we choose the values of C_1m=0.1, which provides a hydrogen bond length of 1.99 Å.

Table 2.

Demonstrating the effect of p-wave contribution: QM∕MM results for the geometry of a water dimer using QM∕MM[MT-BLYP] [s3p]. [Coefficients C₀₀ and C_1m are given in their unnormalized form (inputs); the code normalizes them.]

Model	C00	C1m	dH-bond (Å)	dOO (Å)	∠α	∠β
Expt.a	⋯	⋯	⋯	2.98	6±20°	57±10°
s	1.0	0.0	1.98	2.96	0.3°	69.7°
s3p	1.0	0.05	1.94	2.92	2.5°	65.2°
s3p	1.0	0.1	1.99	2.96	6.8°	58.8°
s3p	1.0	0.15	2.03	2.99	7.9°	56.0°
s3p	1.0	0.2	2.05	3.01	8.0°	56.7°
s3p	1.0	0.3	2.09	3.05	8.5°	55.2°

^aReference ²⁵.

In Table 3, we present the results for the QM∕MM calculation on water-dimer performed by using the parameters selected above. We compare the experimental data²⁵ for the geometry of water dimer with the results obtained from different ab initio calculations using GAUSSIAN98,²⁶CPMD,¹⁵ and QM∕MM calculations with CPMD-GROMACs hybrid program. The QM∕MM results are obtained by employing plane wave expansions with (1) s-wave only and (2) s- and p-orbitals (represented as s3p result), respectively. For the QM subsystem, we used a QM simulation box size of 18×18×18 a.u.³ and a plane wave cutoff of 120 Ry for SG-LDA and 110 Ry for MT-BLYP functionals. The ESP charges on the MM atoms are set by performing ab initio QM calculations¹⁰ on a single water molecule and are taken as −0.786 a.u. for oxygen and 0.393 a.u. for hydrogen. For full QM calculations with both the GAUSSIAN98 and CPMD programs, there is a consistent improvement of the dimer structure when more sophisticated approximations of ab initio or density functional theory are employed. On the other hand, QM∕MM calculations with only s-wave expansion for MM point charges exhibit a contradictory picture for ∠β. When more sophisticated exchange functionals are used (BLYP) bond distances improve substantially and the ∠β increases by about 4% for Slater orbital delocalization¹⁰ and by about 5% for Gaussian orbital delocalization.⁸ For a pure QM calculation, on the other hand, ∠β decreases when the BLYP functional is used instead of LDA (∠β assumes a value close to the experimental median value of 57°). When the polarized MM atoms are used (by expanding the point charges into s- and p-orbitals), the QM∕MM results fall in line with the pure QM calculations—∠β decreases when BLYP functional is used (∠β assumes a value close to the experimental median of 57°). These results are obtained with the following set of parameters: $C_{00}^2=1.0$, $C_{11}^2=0.1$, $C_{10}^2=0.1$, $C_{1-1}^2=0.1$, and ξ=λ_s∕r_c, ζ=λ_p∕(σ)^1∕3, where λ_s and λ_p are the parameters for s- and p-wave exponentials and r_c is the covalent radius of the atom and σ is the atomic polarizability. The values of the parameters λ_s and λ_p are taken as 1.3 and 1.3884, respectively. These values set the contribution of the p-wave to be around 25% and that of the s-wave be around 75%. It is worth mentioning that the parameter ζ of the p-wave exponent, which is related to the atomic polarizability σ, is quite sensitive to geometry optimization.

Table 3.

QM, MM, and QM∕MM results for the structure and binding energy of the water dimer.

Model	Basis set	dH-bond (Å)	dOO (Å)	∠α	∠β
Experimenta	⋯	⋯	2.976	6±20°	57±10°
Fully QM results
GAUSSIAN[MP4]	6-311+G(d,p)	1.981	2.942	0.6°	58.1°
GAUSSIAN[B3LYP]	6-311+G(d,p)	1.933	2.900	3.5°	54.1°
GAUSSIAN[BLYP]	6-311+G(d,p)	1.950	2.927	3.8°	57.0°
GAUSSIAN[LDA]	6-311+G(d,p)	1.727	2.707	5.6°	61.7°
CPMD[BLYP]b	Plane wave	1.982	2.961	0.9°	54.1°
CPMD[LDA]c	Plane wave	1.752	2.742	0.6°	57.0°
Hybrid QM∕MM results
CPMD[BLYP]∕GROMACSd	pw∕[s3p]	1.989	2.962	6.8°	58.8°
CPMD[BLYP]∕GROMACSe	pw∕[s]	1.982	2.963	0.3°	69.7°
CPMD[LDA]∕GROMACSf	pw∕[s3p]	1.986	2.952	5.5°	60.7°
CPMD[LDA]∕GROMACSg	pw∕[s]	1.971	2.950	2.3°	67.4°

^aReference ²⁵.

^bCPMD results using Martin–Truhler pseudopotential with BLYP functional.

^cCPMD results using Godecker pseudopotential with LDA functional.

^dQM∕MM results using Martin–Truhler pseudopotential with BLYP functional for CPMD and partial wave expansion ℓ_max=1;(s,p₁,p₀,p₋₁) for MM atoms.

^eQM∕MM results using Martin–Truhler pseudopotential with BLYP functional for CPMD and partial wave expansion ℓ_max=0;(s) for MM atoms.

^fSame as in Footnote d but using Godecker pseudopotential with LDA functional.

^gSame as in Footnote e but using Godecker pseudopotential with LDA functional.

To further demonstrate the effect of MM-atom polarization on the molecular geometry, we consider another system: hydrogen sulfide (H₂S) dimer that contains the highly polarizable sulfur atom. The polarizability of sulfur (2.9 ų) is about four times to that of oxygen (0.79 ų), and we expect that the calculations on the H₂S dimer will provide a sensitive test for the plane wave expansion approach. Table 4 shows the results for the H₂S dimer. Due to lack of experimental data on the structure of H₂S dimer, we compare the QM∕MM results only with QM calculations obtained with the GAUSSIAN98 and CPMD programs. Using GAUSSIAN98, with 6-311+G(d,p) basis set, we find that the use of a better exchange correlation functional (from LDA to BLYP) results in a decrease in the value of both angles. Ab initio calculations, like MP2 and MP4, show a drastic reduction in the value of the angle β, while the angle α is found to increase slightly (see Table 4). For QM∕MM, when we employ only delocalization (with s-wave expansion) for the MM-atom point charges, we find ∠α=4.0° and ∠β=87.1°. As we add the polarization effect through the inclusion of p-wave expansion, we find that both angles reduce to ∠α=0.8° and ∠β=82.3°, and agree more closely with the GAUSSIAN98 results obtained with the BLYP functional. This demonstrates that the polarized MM-atom charges influence the geometry in the right direction as was conjectured.

Table 4.

Results for the structural data of the hydrogen sulfide dimer.

Results	dH-bond (Å)	dSS (Å)	∠α	∠β
QM: Gaussian
G98[MP4]a	2.91	4.25	1.3°	64.6°
G98[BLYP]b	2.86	4.22	0.0°	79.0°
G98[LDA]c	2.39	3.77	1.0°	81.2°
QM: CPMD
CPMD[MT-BLYP]d	2.93	4.30	0.6°	78.5°
QM∕MM: CPMD-GROMACS
QM∕MM[MT-BLYP] [s3p]e	2.92	4.27	0.8°	82.3°
QM∕MM[MT-BLYP] [s]f	2.37	3.72	4.0°	87.1°

^aGAUSSIAN98 [MP4∕6-311+G(d,p)].

^bGAUSSIAN98 [BLYP∕6-311+G(d,p)].

^cGAUSSIAN98 [LDA∕6-311+G(d,p)].

^dCPMD [MT-BLYP].

^eQM∕MM with s- and p-wave (m_ℓ=0,±1) expansions with OPLS parameters (Ref. ³⁶).

^fQM∕MM with s-wave expansions with OPLS parameters.

So far, we have demonstrated the effect of polarization on the molecular geometry of dimers of small molecules as water and hydrogen sulfide. Next we will show the effect of introducing a polarized description of MM-atom point charges on the electronic properties of a molecular system. We present calculations for two different systems: first, we study the change in the ionization potential (IP) and electron affinity (EA) of (6R)-5,6,7,8-tetrahydrobiopterin (BH₄) solvated in water. BH₄ is an important cofactor responsible for the electron transfer to the iron ion (Fe²⁺) of the P₄₅₀ heme group of the enzyme nitric oxide synthase²⁷ (NOS) that catalyzes the production of nitric oxide in cells. We consider the system of a BH₄ molecule in solution [602 TIP4P (Ref. ²⁸) water molecules] and perform single-point QM∕MM calculations with BH₄ in its neutral, anion, and cation forms in the QM part, and the water in the MM part. In all three cases, the MM charges are described by s- and p-orbitals. In Table 5, we provide the results for the IP and EA of BH₄. The results are obtained with soft Vanderbilt (VDB) pseudopotentials²⁹ for the QM part, with a wave function cutoff of 30 Ry and density cutoff of 180 Ry.

Table 5.

The EA and IP of BH₄ cofactor calculated with various partial wave expansions for the MM point charge.

ℓmax	Neutral (a.u.)	Cation (a.u.)	Anion (a.u.)	IP (kcal∕mol)	EA (kcal∕mol)
Gas phase	−157.851 756	−157.599 563	−157.876 687	158.20	15.68
In solution	QM∕MM
Point charge	−158.029 414	−157.760 226	−158.061 139	168.81	19.83
ℓmax=0	−158.032 468	−157.762 401	−158.074 108	169.50	26.06
ℓmax=1	−158.011 596	−157.743 046	−158.050 377	168.35	24.21

Table 5 shows that the inclusion of p-wave expansion for the MM atoms influences the electronic structure of BH₄ resulting in a change in the EA and IP. The use of p-wave in the expansion leads to a decrease in EA with 1.85 kcal∕mol and with 1.15 kcal∕mol in the IP. The results in Table 5 emphasize that only delocalization of MM charges (s-wave expansion) is not enough for an accurate description of the electrostatic structure of the QM fragment (in this case BH₄), and the inclusion of polarization of MM atoms using p-wave expansion could provide a substantial improvement in the electronic properties of the QM subsystem.

Finally, we describe the effect of including p-wave expansion on the interaction energy of BH₄ with the heme group of inducible nitric oxide synthase (iNOSoxy). The QM∕MM system (containing 32 758 atoms) is made of one iNOSoxy enzyme monomer (pdb id: 1NSI, containing the BH₄ cofactor) solvated in TIP4P water.²⁸ The derivation of OPLS parameters for BH₄ has been described in Ref. 30. The heme group of the iNOSoxy monomer [containing the iron ion (Fe²⁺, singlet state) and the PPIX porphyrin ring], the H₂O ligand (ligated to Fe²⁺), and part of the cysteine residue (Cys₂₀₀) ligated to Fe²⁺ are defined as the QM subsystem (80 QM atoms excluding one link atom). The rest of the protein, the BH₄ cofactor, and water form the MM subsystem. In the crystal structure of 1NSI,³¹ BH₄ makes two hydrogen bonds with one propionate group of heme. First we have performed a QM∕MM energy minimization of the QM∕MM system for 300 steps. Because the use of a p-wave polarization is computationally expensive, we first performed geometry optimization using s-wave delocalization only. This optimization reduces the maximum force on atoms to about 350 kJ∕mol nm and retains the two hydrogen bonds of BH₄ with propionate group of heme. The lengths of the two hydrogen bonds following the optimization are 1.93 and 1.88 Å. The heme-BH₄ interaction energy is 39.99 kcal∕mol when s-wave delocalization of MM charges is used. Next, we performed a single-point QM∕MM calculation by adding the p-wave polarization. The results reveal that the inclusion of p-wave polarization alter the electronic structure of the QM fragment significantly providing a change in electronic energy of 0.64 a.u. (402.3 kcal∕mol, Table 6). The QM∕MM interaction energy between BH₄ and heme increases by about 50% (62.08 kcal∕mol, Table 6) underscoring the need to include the polarization effect. The significant increase in the heme-BH₄ interaction energy indicates that any simulation with the p-wave expansion included in the QM∕MM Hamiltonian is expected to lead to a stronger hydrogen bond between the BH₄ cofactor and the heme group. Also, the change in the QM energy due to the inclusion of p-wave expansion is significant indicating substantial change in the electronic structure of the heme residue. This change in electronic structure is quite important to study the resting and reactive states of heme and its inhibition by potential drug candidates.

Table 6.

QM∕MM interaction energy of BH₄ (MM) and the P₄₅₀ heme (QM), evaluated with partial wave expansion for MM-atom charges up to s- and p-orbitals.

ℓmax	QM energy (a.u.)	QM-MM energy (a.u.)	BH4-QM interaction energy (kcal∕mol)
ℓmax=0	−477.898 433	−1.474 816	39.99
ℓmax=1	−478.539 494	−2.137 498	62.08

SUMMARY

We have developed a partial wave expansion scheme using angular momentum algebra that can be used to replace point charges by delocalized and polarized distributions of charge densities. We provide analytical expressions for the ESP and forces for such an extended and polarized charge distribution considering partial wave expansions up to p-orbitals. Performing QM∕MM calculations on several molecular systems, we demonstrate the degree of influence the polarized MM charges can have on the QM subsystem. The results show that the polarization of MM charges (introduced through p-wave expansion) significantly improves the angular correlations in the geometry of water and hydrogen sulfide dimers, produces a net influence on electronic properties such as the IP and EA of tetrahydrobiopterin cofactor in solution, and significantly alters the electronic structure of the P₄₅₀ heme group of NOS. The energy of the P₄₅₀ heme changes by 402.3 kcal∕mol and the interaction energy of BH₄ with the heme group increases by 50%. These results indicate that polarization effects due to the MM atoms could significantly influence the electronic properties of a QM subsystem in a QM∕MM calculation and can produce more accurate potential energy surfaces and interaction∕binding energies.

APPENDIX A: EVALUATION OF ELECTROSTATIC POTENTIAL FOR AN ARBITRARILY POLARIZED CHARGE DISTRIBUTION

From Eq. 14, we have

$$V_{{\ell }^{\prime }{m}^{\prime };\ell m}\left(\mathbf{r}\right)=C_{{\ell }^{\prime }{m}^{\prime }}^{\ast }{C}_{\ell m}\int d^3{r}^{\prime }\frac{{\mathcal{R}}_{{\ell }^{\prime }+1,{\ell }^{\prime }}^{\ast }\left(r^{\prime }\right){\mathcal{R}}_{\ell +1,\ell }\left(r^{\prime }\right)Y_{{\ell }^{\prime },m^{\prime }}^{\ast }\left(\widehat{r^{\prime }}\right)Y_{\ell ,m}\left(\widehat{r^{\prime }}\right)}{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }.$$ (A1)

Taking the partial wave expansion for 1∕∣r−r^′∣ given by³²

$$\frac{1}{\mid \mathbf{r}-{\mathbf{r}}^{\prime }\mid }=4\pi \sum _L\sum _M\frac{1}{2L+1}\frac{r_{<}^L}{r_{>}^{L+1}}{Y}_{L,M}^{\ast }\left(\widehat{r^{\prime }}\right)Y_{L,M}\left(\widehat{r}\right),$$ (A2)

we express Eq. A2 as

$$V_{{\ell }^{\prime }{m}^{\prime };\ell m}\left(\mathbf{r}\right)\left(\mathbf{r}\right)=4\pi C_{{\ell }^{\prime }{m}^{\prime }}^{\ast }{C}_{\ell m}\sum _L\sum _M{Y}_{L,M}\left(\widehat{r}\right)\int d{r}^{\prime }{r}^{\prime 2}\frac{r_{<}^L}{r_{>}^{L+1}}{\mathcal{R}}_{{\ell }^{\prime }+1,{\ell }^{\prime }}^{\ast }\left(r^{\prime }\right){\mathcal{R}}_{\ell +1,\ell }\left(r^{\prime }\right)\times \int d\widehat{r^{\prime }}{Y}_{{\ell }^{\prime },m^{\prime }}^{\ast }\left(\widehat{r^{\prime }}\right)Y_{\ell ,m}\left(\widehat{r^{\prime }}\right)Y_{L,M}^{\ast }\left(\widehat{r^{\prime }}\right).$$ (A3)

The integral for the angular part containing three angular momenta can be found in a standard textbook dealing with angular momentum and the result can be written as³³

$$\int d\widehat{r^{\prime }}{Y}_{{\ell }^{\prime },m^{\prime }}^{\ast }\left(\widehat{r^{\prime }}\right)Y_{\ell ,m}\left(\widehat{r^{\prime }}\right)Y_{L,M}^{\ast }\left(\widehat{r^{\prime }}\right)={\left(-1\right)}^{m^{\prime }}{\left[\frac{\left(2{\ell }^{\prime }+1\right)\left(2\ell +1\right)}{4\pi \left(2L+1\right)}\right]}^{1∕2}\left(\begin{array}{ccc}{\ell }^{\prime }& \ell & L\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}{\ell }^{\prime }& \ell & L\\ -m^{\prime }& m& M\end{array}\right).$$ (A4)

But the integral vanishes unless M=−m^′+m. So, the summation over M can be taken out. Here $\left(\genfrac{}{}{0ex}{}{{\ell }^{\prime }\ell L}{m^{\prime }mM}\right)$ also expressed as C(ℓ^′ℓL;m^′mM) are the Clebsch–Gordan coefficients or C-coefficients.³⁴ With this result for the angular integration A4, we get

$$V_{{\ell }^{\prime }{m}^{\prime };\ell m}\left(\mathbf{r}\right)=4\pi C_{{\ell }^{\prime }{m}^{\prime }}^{\ast }{C}_{\ell m}{\left(-1\right)}^{m^{\prime }}\sum _L{\left[\frac{\left(2{\ell }^{\prime }+1\right)\left(2\ell +1\right)}{4\pi \left(2L+1\right)}\right]}^{1∕2}\left(\begin{array}{ccc}{\ell }^{\prime }& \ell & L\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}{\ell }^{\prime }& \ell & L\\ -m^{\prime }& m& M\end{array}\right)Y_{L,M}\left(\widehat{r}\right)\times \int d{r}^{\prime }{r}^{\prime 2}\frac{r_{<}^L}{r_{>}^{L+1}}{\mathcal{R}}_{{\ell }^{\prime }+1,{\ell }^{\prime }}^{\ast }\left(r^{\prime }\right){\mathcal{R}}_{\ell +1,\ell }\left(r^{\prime }\right)=4\pi C_{{\ell }^{\prime }{m}^{\prime }}^{\ast }{C}_{\ell m}{\left(-1\right)}^{m^{\prime }}\sum _L{\left[\frac{\left(2{\ell }^{\prime }+1\right)\left(2\ell +1\right)}{4\pi \left(2L+1\right)}\right]}^{1∕2}\left(\begin{array}{ccc}{\ell }^{\prime }& \ell & L\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}{\ell }^{\prime }& \ell & L\\ -m^{\prime }& m& M\end{array}\right)Y_{L,M}\left(\widehat{r}\right)\times \left[\frac{1}{r^{L+1}}{\int }_0^{r}d{r}^{\prime }{r}^{\prime L+2}{\mathcal{R}}_{{\ell }^{\prime }+1,{\ell }^{\prime }}^{\ast }\left(r^{\prime }\right){\mathcal{R}}_{\ell +1,\ell }\left(r^{\prime }\right)+r^L{\int }_r^{\infty }d{r}^{\prime }{r}^{\prime 1-L}{\mathcal{R}}_{{\ell }^{\prime }+1,{\ell }^{\prime }}^{\ast }\left(r^{\prime }\right){\mathcal{R}}_{\ell +1,\ell }\left(r^{\prime }\right)\right].$$ (A5)

This is a general expression for partial wave expansion of any order (ℓ,ℓ^′=0,1,2,3,…).

Here we consider expansions up to p-wave: ${\ell }_{\max },{\ell }_{\max }^{\prime }=1$. This will enable one to include charge-charge (L=0), charge-dipole (L=1), and charge-quadrupole (L=2) interactions through the summation over L in Eq. A5. For ${\ell }_{\max },{\ell }_{\max }^{\prime }=1$, the radial functions that will appear in Eq. A5 are R₁₀(r^′) and R₂₁(r^′). According to the one-electron hydrogen atom type wave function, they are given by³⁵

$$R_{10}\left(r^{\prime }\right)=2a^{-3∕2}{e}^{-r^{\prime }∕a}=2{\alpha }_0^{3∕2}{e}^{-{\alpha }_0{r}^{\prime }},$$ (A6)

$$R_{21}\left(r^{\prime }\right)=\frac{1}{\sqrt{24}}{a}^{-3∕2}\frac{r^{\prime }}{a}{e}^{-r^{\prime }∕2a}=\frac{2}{\sqrt{3}}{\alpha }_1^{5∕2}{r}^{\prime }{e}^{-{\alpha }_1{r}^{\prime }},$$ (A7)

where α₀=1∕a and α₁=1∕2a; a=0.5 a.u. is the Bohr radius. We can generalize them as

$$R_{\ell +1,\ell }\left(r^{\prime }\right)=\frac{2}{\sqrt{2\ell +1}}{\alpha }_{\ell }^{\left(2\ell +3\right)∕2}{r}^{\prime \ell }{e}^{-{\alpha }_{\ell }{r}^{\prime }}.$$ (A8)

Accordingly, we rewrite Eq. A5 as

$$V_{{\ell }^{\prime }{m}^{\prime };\ell m}\left(\mathbf{r}\right)={\left(-1\right)}^{m^{\prime }}4C_{{\ell }^{\prime }{m}^{\prime }}^{\ast }{C}_{\ell m}\sum _L{\left[\frac{\left({\alpha }_{{\ell }^{\prime }}^{2{\ell }^{\prime }+3}\right)\left({\alpha }_{\ell }^{2\ell +3}\right)}{\left(2L+1\right)}\right]}^{1∕2}\left(\begin{array}{ccc}{\ell }^{\prime }& \ell & L\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}{\ell }^{\prime }& \ell & L\\ -m^{\prime }& m& m-m^{\prime }\end{array}\right)\sqrt{4\pi }{Y}_{L,m-m^{\prime }}\left(\widehat{r}\right)\left\{\frac{1}{r^{L+1}}{\int }_0^{r}d{r}^{\prime }{r}^{\prime L+2+\ell +{\ell }^{\prime }}{e}^{-\left({\alpha }_{{\ell }^{\prime }}+{\alpha }_{\ell }\right)r^{\prime }}+r^L{\int }_r^{\infty }d{r}^{\prime }{r}^{\prime 1-L+\ell +{\ell }^{\prime }}{e}^{-\left({\alpha }_{{\ell }^{\prime }}+{\alpha }_{\ell }\right)r^{\prime }}\right\}={\left(-1\right)}^{m^{\prime }}4C_{{\ell }^{\prime }{m}^{\prime }}^{\ast }{C}_{\ell m}\sum _L{\left[\frac{4\pi \left({\alpha }_{{\ell }^{\prime }}^{2{\ell }^{\prime }+3}\right)\left({\alpha }_{\ell }^{2\ell +3}\right)}{\left(2L+1\right)}\right]}^{1∕2}\left(\begin{array}{ccc}{\ell }^{\prime }& \ell & L\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}{\ell }^{\prime }& \ell & L\\ -m^{\prime }& m& m-m^{\prime }\end{array}\right)Y_{L,m-m^{\prime }}\left(\widehat{r}\right)\left\{\frac{1}{r^{L+1}}{\left[-\sum _{k=0}^{L_a}\frac{e^{-{\lambda }_{{\ell }^{\prime }\ell }{r}^{\prime }}\left(L_a\right)!r^{\prime L_a-k}}{\left(L_a-k\right)!{\lambda }_{{\ell }^{\prime }\ell }^{k+1}}\right]}_0^r+r^L{\left[-\sum _{k=0}^{L_b}\frac{e^{-{\lambda }_{{\ell }^{\prime }\ell }{r}^{\prime }}\left(L_b\right)!r^{\prime L_b-k}}{\left(L_b-k\right)!{\lambda }_{{\ell }^{\prime }\ell }^{k+1}}\right]}_r^{\infty }\right\},$$ (A9)

where L_a=L+2+ℓ+ℓ^′, L_b=1−L+ℓ+ℓ^′, and λ_ℓ^′ℓ=_αℓ^′+α_ℓ. Finally, we represent V_{ℓ^′m^′;ℓm}(r) as

$$V_{{\ell }^{\prime }{m}^{\prime };\ell m}\left(\mathbf{r}\right)=\sum _{L=0}^{\ell +{\ell }^{\prime }}\Gamma \left({\ell }^{\prime }{m}^{\prime },\ell m;L\right){\mathcal{R}}_{{\ell }^{\prime }\ell }^L\left(r\right)Y_{L,m-m^{\prime }}\left(\widehat{r}\right),$$ (A10)

where Γ is a constant and R is the radial distribution function and they are given by

$$\Gamma \left({\ell }^{\prime }{m}^{\prime },\ell m;L\right)={\left(-1\right)}^{m^{\prime }}4C_{{\ell }^{\prime }{m}^{\prime }}^{\ast }{C}_{\ell m}{\left[\frac{4\pi \left({\alpha }_{{\ell }^{\prime }}^{2{\ell }^{\prime }+3}\right)\left({\alpha }_{\ell }^{2\ell +3}\right)}{\left(2L+1\right)}\right]}^{1∕2}\left(\begin{array}{ccc}{\ell }^{\prime }& \ell & L\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}{\ell }^{\prime }& \ell & L\\ -m^{\prime }& m& m-m^{\prime }\end{array}\right),$$ (A11)

$${\mathcal{R}}_{{\ell }^{\prime }\ell }^L\left(r\right)=\left\{-\frac{\left(L_a\right)!}{r^{L+1}}\left[\sum _{k=0}^{L_a}\frac{e^{-{\lambda }_{{\ell }^{\prime }\ell }r}{r}^{L_a-k}}{\left(L_a-k\right)!{\lambda }_{{\ell }^{\prime }\ell }^{k+1}}-\frac{1}{{\lambda }_{{\ell }^{\prime }\ell }^{L_a+1}}\right]+r^L\left(L_b\right)!\sum _{k=0}^{L_b}\frac{e^{-{\lambda }_{{\ell }^{\prime }\ell }r}{r}^{L_b-k}}{\left(L_b-k\right)!{\lambda }_{{\ell }^{\prime }\ell }^{k+1}}\right\}=-\left[\frac{{\left(-1\right)}^{L_a+1}\left(L_a\right)!}{{\lambda }_{{\ell }^{\prime }\ell }^{L_a+1}{r}^{L+1}}+e^{-{\lambda }_{{\ell }^{\prime }\ell }r}\left\{\sum _{k=0}^{L_a}\frac{\left(L_a\right)!r^{\ell +{\ell }^{\prime }+1-k}}{\left(L_a-k\right)!{\lambda }_{{\ell }^{\prime }\ell }^{k+1}}-\sum _{k=0}^{L_b}\frac{\left(L_b\right)!r^{\ell +{\ell }^{\prime }+1-k}}{\left(L_b-k\right)!{\lambda }_{{\ell }^{\prime }\ell }^{k+1}}\right\}\right].$$ (A12)

The first derivative of ${\mathcal{R}}_{{\ell }^{\prime }\ell }^L\left(r\right)$ with respect to r, needed to evaluate the force, is given by

$$\frac{\partial }{\partial r}{\mathcal{R}}_{{\ell }^{\prime }\ell }^L\left(r\right)=-\left[e^{-{\lambda }_{{\ell }^{\prime }\ell }r}\left\{-\sum _{k=0}^{L_a}\frac{\left(L_a\right)!r^{\ell +{\ell }^{\prime }+1-k}}{\left(L_a-k\right)!{\lambda }_{{\ell }^{\prime }\ell }^k}+\sum _{k=0}^{L_b}\frac{\left(L_b\right)!r^{\ell +{\ell }^{\prime }+1-k}}{\left(L_b-k\right)!{\lambda }_{{\ell }^{\prime }\ell }^k}+\sum _{k=0}^{L_a}\frac{\left(L_a\right)!\left(\ell +{\ell }^{\prime }+1-k\right)r^{\ell +{\ell }^{\prime }-k}}{\left(L_a-k\right)!{\lambda }_{{\ell }^{\prime }\ell }^{k+1}}-\sum _{k=0}^{L_b}\frac{\left(L_b\right)!\left(\ell +{\ell }^{\prime }+1-k\right)r^{\ell +{\ell }^{\prime }-k}}{\left(L_b-k\right)!{\lambda }_{{\ell }^{\prime }\ell }^{k+1}}\right\}+\frac{{\left(-1\right)}^{L_a}\left(L+1\right)\left(L_a\right)!}{{\lambda }_{{\ell }^{\prime }\ell }^{L_a+1}{r}^{L+2}}\right].$$ (A13)

APPENDIX B: ELECTROSTATIC POTENTIAL FOR DIAGONAL TERMS (ℓ^′=ℓ;m^′=m)

From Appendix A, we see that the potential arising from the diagonal terms of the density matrix representation 12 correspond to ℓ^′=ℓ and m^′=m (which leads to M=−m+m^′=0) and are given by

$$V_{\ell m;\ell m}\left(\mathbf{r}\right)=\sum _{L=0}^{2\ell }\Gamma \left(\ell m,\ell m;L\right){\mathcal{R}}_{\ell \ell }^L\left(r\right)Y_{L,0}\left(\widehat{r}\right)=\sum _{L=0}^{2\ell }{\Gamma }^{\prime }\left(\ell m,\ell m;L\right){\mathcal{R}}_{\ell \ell }^L\left(r\right)P_L\left(\text{cos}\theta \right),$$ (B1)

where P_L(cos θ) is the Legendre polynomial and

$${\Gamma }^{\prime }\left(\ell m,\ell m;L\right)=\sqrt{\frac{2L+1}{4\pi }}\Gamma \left(\ell m,\ell m;L\right)={\left(-1\right)}^{m}4C_{\ell m}^2{\alpha }_{\ell }^{2\ell +3}\left(\begin{array}{ccc}\ell & \ell & L\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}\ell & \ell & L\\ -m& m& 0\end{array}\right),$$ (B2)

$${\mathcal{R}}_{\ell \ell }^L\left(r\right)=-\left[\frac{{\left(-1\right)}^{L+2\ell +3}\left(L+2\ell +2\right)!}{{\lambda }_{\ell \ell }^{L+2\ell +3}{r}^{L+1}}+e^{-{\lambda }_{\ell \ell }r}\left\{\sum _{k=0}^{L+2\ell +2}\frac{\left(L+2\ell +2\right)!r^{2\ell +1-k}}{\left(L+2\ell +2-k\right)!{\lambda }_{\ell \ell }^{k+1}}-\sum _{k=0}^{1-L+2\ell }\frac{\left(1-L+2\ell \right)!r^{2\ell +1-k}}{\left(1-L+2\ell -k\right)!{\lambda }_{\ell \ell }^{k+1}}\right\}\right],$$ (B3)

where λ=2α_ℓ. For ℓ=0, that is, for the special case of a spherically symmetric expansion of the charge in s-wave, the potential reduces to

$$V_{00;00}\left(\mathbf{r}\right)={\Gamma }^{\prime }\left(00,00;0\right){\mathcal{R}}_{00}^0\left(r\right)P_0\left(\text{cos}\theta \right)=4C_{00}^2{\alpha }_0^3\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\end{array}\right){\mathcal{R}}_{00}^0\left(r\right)=4C_{00}^2{\alpha }_0^3{\mathcal{R}}_{00}^0\left(r\right)=4C_{00}^2{\alpha }_0^3\times \frac{1}{4{\alpha }_0^3}\left[\frac{1}{r}-\frac{e^{-{\lambda }_{00}r}}{r}-{\alpha }_0{e}^{-{\lambda }_{00}r}\right]=C_{00}^2\left[\frac{1}{r}-\frac{e^{-{\lambda }_{00}r}}{r}-{\alpha }_0{e}^{-{\lambda }_{00}r}\right],$$ (B4)

which is the same as derived in our previous work¹⁰ with the normalization $C_{00}^2=1$. For ℓ=1, we have three different components: V_10;10, V_11;11, and V_1−1;1−1.

$$V_{10;10}\left(\mathbf{r}\right)=\sum _{L=0,2}{\Gamma }^{\prime }\left(10,10;L\right){\mathcal{R}}_{11}^L\left(r\right)P_L\left(\text{cos}\theta \right)=\sum _{L=0,2}4C_{10}^2{\alpha }_1^5\left(\begin{array}{ccc}1& 1& L\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}1& 1& L\\ 0& 0& 0\end{array}\right){\mathcal{R}}_{11}^L\left(r\right)P_L\left(\text{cos}\theta \right),$$ (B5)

$$V_{11;11}\left(\mathbf{r}\right)=\sum _{L=0,2}{\Gamma }^{\prime }\left(11,11;L\right){\mathcal{R}}_{11}^L\left(r\right)P_L\left(\text{cos}\theta \right)=-\sum _{L=0,2}4C_{11}^2{\alpha }_1^5\left(\begin{array}{ccc}1& 1& L\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}1& 1& L\\ -1& 1& 0\end{array}\right){\mathcal{R}}_{11}^L\left(r\right)P_L\left(\text{cos}\theta \right),$$

$$V_{1-1;1-1}\left(\mathbf{r}\right)=\sum _{L=0,2}{\Gamma }^{\prime }\left(1-1,1-1;L\right){\mathcal{R}}_{11}^L\left(r\right)P_L\left(\text{cos}\theta \right)=-\sum _{L=0,2}4C_{1-1}^2{\alpha }_1^5\left(\begin{array}{ccc}1& 1& L\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}1& 1& L\\ 1& -1& 0\end{array}\right){\mathcal{R}}_{11}^L\left(r\right)P_L\left(\text{cos}\theta \right),$$

where θ is the angle associated with the vector r and the sum restricts to L=0 and 2 since the Clebsch–Gordan coefficients vanish for ℓ^′+ℓ+L=odd. Thus, ${\mathcal{R}}_{11}^L\left(r\right)$, which is common to all three terms above, has two surviving components corresponding to L=0 and 2 and are given by

$${\mathcal{R}}_{11}^0\left(r\right)=\left[\frac{4!}{{\lambda }_{11}^{5}r}+e^{-{\lambda }_{11}r}\left\{\sum _{k=0}^4\frac{4!r^{3-k}}{\left(4-k\right)!{\lambda }_{11}^{k+1}}-\sum _{k=0}^3\frac{3!r^{3-k}}{\left(3-k\right)!{\lambda }_{11}^{k+1}}\right\}\right],$$ (B6)

$${\mathcal{R}}_{11}^2\left(r\right)=\left[\frac{6!}{{\lambda }_{11}^7{r}^3}+e^{-{\lambda }_{11}r}\left\{\sum _{k=0}^6\frac{6!r^{3-k}}{\left(6-k\right)!{\lambda }_{11}^{k+1}}-\sum _{k=0}^1\frac{r^{3-k}}{\left(1-k\right)!{\lambda }_{11}^{k+1}}\right\}\right],$$

Referring to the radial functions ${\mathcal{R}}_{11}^0\left(r\right)$ and ${\mathcal{R}}_{11}^2\left(r\right)$ above, we see that the potentials arising from the diagonal terms [Eq. B5] lead to 1∕r and 1∕r³ dependences (but no 1∕r² dependence). This is because, in general, the asymptotic form of the potential is 1∕r^L+1 [as can be seen from Eq. A12] and the diagonal terms, for which ℓ^′=ℓ, leads to L=0,2, since the nonvanishing of Clebsch–Gordan coefficients are constrained by ℓ^′+ℓ+L=even. From Eq. B5, we also see that apart from the 1∕r dependence, all higher order dependences are associated with an angle given by P_L(cos θ) for the diagonal terms and by Y_LM(θ,ϕ), in general. For off-diagonal terms with ℓ^′=0;ℓ=1, or vice versa, the condition ℓ^′+ℓ+L=even requires L=odd, thus leading to potentials of the form 1∕r².

In the present application of the model, we focus on the elimination of any angular dependence as otherwise the simulation will require the determination of the coefficients at every SCF cycle. To eliminate the θ dependence, and to arrive at an isotropic polarization scheme, we consider C₁₀=C₁₁=C₁₋₁≡C_1m. Using the properties of the Clebsch–Gordan coefficients that C(1,1,L;−1,1,0)=(−)^2−LC(1,1,L;1,−1,0),³⁴ the sum of the three potentials given in Eq. B5 can then be written as

$$V_{\ell =1{\ell }^{\prime }=1}\left(\mathbf{r}\right)=\sum _{L=0,2}4C_{1m}^2{\alpha }_1^5\left(\begin{array}{ccc}1& 1& L\\ 0& 0& 0\end{array}\right)\times \left[\left(\begin{array}{ccc}1& 1& L\\ 0& 0& 0\end{array}\right)-2\left(\begin{array}{ccc}1& 1& L\\ -1& 1& 0\end{array}\right)\right]\times {\mathcal{R}}_{11}^L\left(r\right)P_L\left(\text{cos}\theta \right).$$ (B7)

Here, for L=2, the term within the third bracket vanishes $\left[\sqrt{2∕3}-2\sqrt{1∕6}\right]$ (see p. 225 of Ref. 34). Thus, the above equation reduces to

$$V_{\ell =1{\ell }^{\prime }=1}\left(\mathbf{r}\right)=4C_{1m}^2{\alpha }_1^5\left(\begin{array}{ccc}1& 1& 0\\ 0& 0& 0\end{array}\right){\mathcal{R}}_{11}^0\left(r\right)=-\frac{4}{\sqrt{3}}{C}_{1m}^2{\alpha }_1^5{\mathcal{R}}_{11}^0\left(r\right)$$ (B8)

leading to isotropic polarization.