Abstract
Isotropic periodic sum (IPS) is a method for the calculation of long-range interactions in molecular simulation based on the homogeneity of simulation systems. Three IPS models, 3D IPS, 2D IPS, and 1D IPS have been developed for three common types of homogeneous systems. Based on the fact that 3D IPS can well describe the long-range interactions of a heterogeneous system if a local region larger than the homogeneity scale is used, this work presents a method based on 3D IPS to calculate long-range interactions for all kinds of simulation systems, including homogeneous, heterogeneous, and finite systems. Unlike the original 3D IPS method that uses a local region defined by the cutoff distance, this method uses a local region larger than that defined by the cutoff distance to reach the homogeneity scale. To efficiently calculate interactions within such a large local region, this method split long-range interactions into two parts, a cutoff part and a long-range part. The cutoff part is calculated by summing over atom pairs within a cutoff range (about 10 Å), and the long-range part is calculated using the discrete fast Fourier transform (DFFT) technique. This method is applied to electrostatic and van der Waals interactions for both periodic and non-periodic systems. Example simulations demonstrate that this method can accurately and efficiently calculate long-range interactions for molecular simulation.
INTRODUCTION
Isotropic periodic sum (IPS) is a method for the calculation of long-range interactions in molecular systems.1 The concept of the IPS method is using isotropic distributed images of a local region around each particle to represent remote environment for the calculation of long-range interactions beyond the local region. The difference between the IPS method and lattice sum methods such as Ewald summation2 lies in the shape and distribution of remote images for long-range interaction calculation. The images used in lattice sum calculation are identical to those generated from periodic boundary conditions and are discretely positioned at lattice points in space. The images for IPS calculation are imaginary, which means they do not explicitly exist in a simulation system, and are distributed in an isotropic and periodic way around each particle. For fully homogenous systems, the IPS images are distributed equally in all three dimensions and the method is called 3D IPS. Analytic solutions for 3D IPS are available for many potential types1 and the calculation of long-range interactions is very efficient.
The underlying assumption of the IPS method is that the simulation system is homogenous and isotropic over the size of the local region (defined by the local region radius, Rc), and for convenience the local region for 3D IPS calculation is defined to be the same as the region within a cutoff distance rc. However, in many cases a simulation system is not homogenous in such a length scale (∼10 Å). To accurately describe the long-range interaction of heterogeneous systems, 3D IPS has to use a local region large enough to cover the heterogeneous range, up to the size of the simulation system or the periodic boundary boxes. Obviously, it is highly time consuming to do direct pairwise calculation with such a large cutoff distance.
In this work, we present an efficient way to perform 3D IPS calculation with a local region larger than the cutoff distance, Rc>rc, so that it can be applied to heterogeneous simulation systems. To avoid confusion, we call this new method 3D IPS∕DFFT because it uses DFFT to achieve efficient calculation with a large local region. We identify previous methods developed for systems of specific homogeneities as 3D IPS, two-dimensional (2D) IPS, and one-dimensional (1D) IPS methods. The difference between the 3D IPS∕DFFT method and the 3D IPS method is the size of the local region. The 3D IPS method uses a local region defined by the cutoff distance, while the 3D IPS∕DFFT method uses a much larger local region than the cutoff region. In the following sections, we present the algorithm of the 3D IPS∕DFFT method, and through several sample calculations we demonstrate the accuracy and efficiency of this method.
METHOD AND ALGORITHM
3D IPS potentials
In molecular simulation, a particle often has long-range interactions with its surrounding particles. The number of surrounding particles can be huge if the system is not a finite one. A convenient way to handle macroscopic systems is using periodic boundary conditions (PBCs) to replicate a limited system throughout the space and using these PBC images to represent remote structures in long-range interaction calculation.
Summation of long-range interactions over these PBC images is a computation intensive task, and many lattice sum methods have been developed to address this problem. Instead of using the PBC images, the IPS method uses so called isotropic periodic images for long-range interaction calculation. It should be noted that using IPS to calculate long-range interactions will not change the way a simulation is performed, and a simulation system can have any type of PBC or no PBC at all. The isotropic periodic images are purely imaginary and are used only to derive the IPS potentials.
In a molecular system, the energy of a particle is the sum of interactions with all other particles. For a particle i, it is convenient to define a spherical region of radius Rc centered at this particle as its local region, so that the interactions with particle i can be divided into local interactions within the local region, and long-range interactions outside the local region.
| (1) |
where rij is the distance between particle i and particle j, and εij is their interaction energy.
If we assume the structure beyond the local region can be represented by the isotropic periodic images of the local region, the summation over all particles beyond the local region becomes a function of the local region structure,
| (2) |
Here, the summation ∑rij⩽Rc runs over all particles, including any PBC image particles, that are within the range of Rc from particle i. ϕij(rij,Rc) represents the long-range contribution as a function of rij and Rc. is called the 3D IPS potential, which is the sum of the pair interactions within the local region and the image interactions,
| (3) |
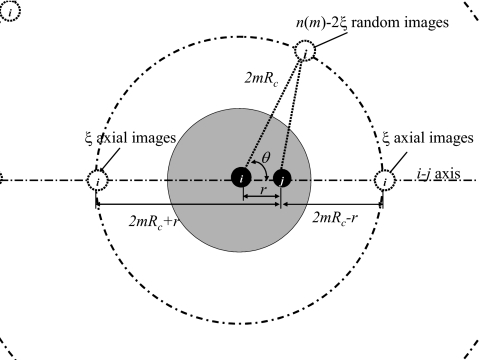
The isotropic periodic images of a particle are distributed on spherical shells with radii of 2mRc, where m is the shell index ranging from 1 to infinity, as shown in Fig. 1. Two types of images, random images and axial images, are defined to represent the distribution of images on each shell. The random images are evenly distributed on the shells, and the interaction of particle j with each shell image can be calculated by the following integral:
| (4) |
Here, r is the distance between particles i and j, and θ is the angle between the line linking particles i and j and the line between particle j and the image of particle i. We drop subscript “ij” here for convenience.
Figure 1.
The distribution of isotropic periodic images of particle i on its image shells. The mth image shell has a radius of 2mRc and hasn(m)=24m2+2 images. The images consist of 2ξ axial images andn(m)−2ξ random images. ξ is solved from Eq. 8. For electrostatic potential, ξele=1. For Lennard-Jones dispersive and repulsive potentials, ξdisp≈0.187 672 and ξrep≈0.532 459.1 Particle j interacts with all images of particle i. The image shells of particle j are not shown here, which would be centered at particle j.
The axial images are positioned at the points where the line linking the two particles crosses the shells. The interactions between particle j and the axial images of particle i on the mth shell is
| (5) |
The number of images on each shell is proportional to the volume of the shell,
| (6) |
If we assume there are 2ξ axial images on each shell, there are n(m)−2ξ random images on the mth shell. The total interaction of particle j with the images of particle i is
| (7) |
The combination of the random images and the axial images produces a periodic effect, i.e., the forces from particle i and its images to particle j cancel when particle j is at the boundary of the local region of particle i.
| (8) |
By solving ξ from Eq. 8, we can calculate the total interactions between particle j and the images of particle i from Eq. 7 and therefore the 3D IPS potential from Eq. 3.
The 3D IPS potential has analytic form for many commonly used potentials.1 For electrostatic interaction,
| (9) |
where q1 and q2 are the charges of the two interacting particles, its 3D IPS image interaction is
| (10) |
where γ is the Euler’s constant, , and ψ(z) is the digamma function ψ(z)=Γ′(z)∕Γ(z), and . As explained in the previous work,1 the isotropic periodic sum in the form of Eq. 7 does not converge for electrostatic potential. Instead, Eq. 10 is the sum calculated against a reference state wherer=0.
The IPS analytic solutions are often very complicated and are time consuming to compute directly. Instead, we use numerical functions that fit these analytic solutions for an efficient calculation in simulations. By expanding Eq. 10 into a power series, we have
| (11) |
where ψ(n)(z) is the nth derivative of the digamma function: ψ(2)(1)=−2.404 113 8, ψ(4)(1)=−24.886 266, ψ(6)(1)=−726.011 48, ψ(8)(1)=−40 400.978, ψ(10)(1)=−3.630 593 3×106, ψ(12)(1)=−4.790 603 8×108.
However, even when expanded to r12, the error is still significant. Instead, we adopt the polynomial function form of Eq. 11 and fit it into the analytic solution, Eq. 10, to obtain the coefficients,
| (12) |
The average deviation of this function from the analytic solution, Eq. 10, is 2×10−8q1q2∕Rc.
Lernnard-Jones potential can be separated into repulsion and dispersion terms,
| (13) |
where ε0 and r* are the energy minimum and the minimum distance. A=ε0r*12 and C=2ε0r*6 are the constants for repulsion and dispersion interactions, respectively. We get the following polynomials by fitting into the dispersion and repulsion analytic solutions:1
| (14) |
| (15) |
The average deviations from analytic solutions are and for dispersion and repulsion interactions, respectively.
Isotropic periodic model for heterogeneous systems
Heterogeneous systems are often the objects of simulation studies. Heterogeneity of a system is defined by the size of nonrepeating structures. For example, in liquid water, molecule distances are 2.8 Å or larger. It is highly heterogeneous in any region within a 2.8 Å radius where number and type of atoms are very different from one place to another. A region must include at least two to three shells of molecules to be considered homogenous. While for a gas phase system, a region must be large enough to include at least a few, say, 10, particles on average. We refer to the size to make a local region representative of a system as the homogeneity scale. A system is a homogenous system in a length scale larger than the homogeneity scale, or a heterogeneous one in a length scale smaller than the homogeneity scale. To apply 3D IPS to heterogeneous systems, the local region radius must be larger than the homogeneity scale to make the homogenous approximation valid.
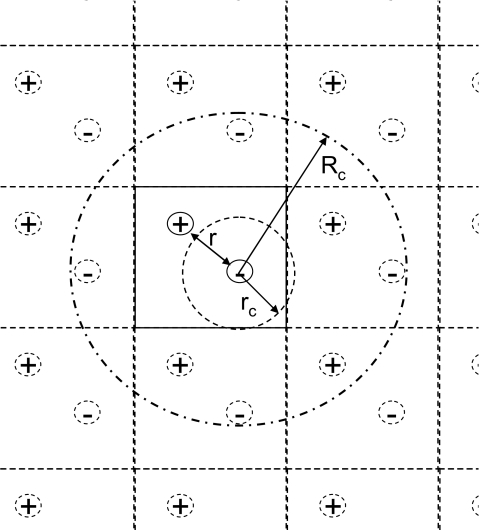
A simple case of a heterogeneous system is a two-ion periodic system as shown in Fig. 2. With a small cutoff distance of rc, one ion often falls out of the sight of the other, therefore, such a region is hard to be representative of the system. If we look at the system with the images created by the PBC, we can see that the PBC forces the system to be repeated throughout the space. With a local region radius Rc larger than the PBC size, a local region has a reasonable number of particles and can be a good representative of the system. With such a large local region radius, 3D IPS energies can well approximate the long-range interactions. Therefore, to use 3D IPS to describe this heterogeneous system, it is desirable to use a local region (defined by Rc) larger than the cutoff regions (defined by rc).
Figure 2.
A two-ion periodic system with a square periodic boundary condition. A region within a small radius of rc as compared to the PBC size is highly heterogeneous. However, a region within a large radius of Rc would be much closer to a homogeneous system due to the PBC.
When Rc is larger than the PBC size, the lattice symmetry from the PBC will be imposed into long-range interactions. Obviously, the IPS energies will approach that of the lattice sum when Rc becomes infinitely large. There are cases where symmetric interactions from PBC images must be avoided. For example, in protein folding simulations, the conformational distribution could be altered by image interactions. In this case, the IPS method can be used with a local region smaller than the PBC box size to avoid image interactions. In addition, the IPS method can be easily applied to many potential types, which makes it a convenient choice for molecular simulation.
The original 3D IPS method sets the local region radius, Rc, the same as the cutoff distance, rc, and sums over all atom pairs within the cutoff distance to calculate long-range interactions. For heterogeneous systems, a much larger Rc should be used and a pairwise calculation with such a large rc would be very time consuming. Instead of using a large rc, the method presented here uses a regular rc for pairwise calculation and treats the remaining portion with the discrete fast Fourier transform (DFFT) technique to achieve an efficient calculation of 3D IPS potentials with large Rc.
We define a smoothing function ϑ(r,rc) to split the IPS potential into two smooth parts, the cutoff (C) part, εC(r,rc), and the long-range (LR) part, εLR(r,rc,Rc).
| (16a) |
The cutoff part goes to zero at the cutoff distance rc.
| (16b) |
The long-range part is the difference between the IPS energy, Eq. 3, and the cutoff part, Eq. 16b.
| (16c) |
As mentioned in the previous work,1 IPS potentials have a nonzero boundary energy. To avoid energy discontinuities when particles move across the boundary, boundary energies are subtracted from the IPS potentials and calculated separately. Therefore, the actual long-range part used in the calculation is
| (16d) |
And the boundary energy is defined as
| (16e) |
The boundary energies are summed separately in a simulation,
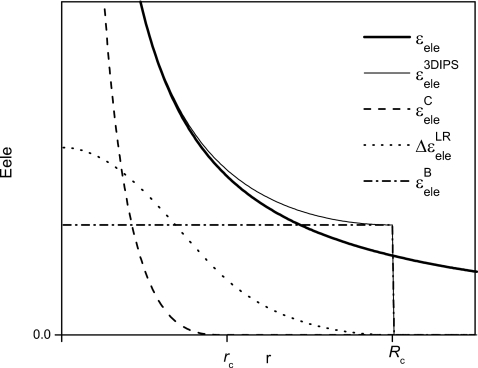
Here, N is the number of particles and M is the number of PBC image particles. V is the volume of the simulation system. Figure 3 illustrates the electrostatic energy and its IPS potential, as well as its cutoff part, long-range part, and the boundary energy.
Figure 3.
The electrostatic potential and its 3D IPS with a local region of radius Rc. The 3D IPS electrostatic potential is split into a cutoff part, , and a long-range part, , which is shown as , and the IPS boundary energy, .
The total IPS energy is a sum over all particle pairs within Rc,
| (17) |
The cutoff sum Ec can be calculated in a pair wise way just like the cutoff methods, and the long-range sum ΔELR can be calculated using the DFFT technique. The details of the calculation are explained in the following subsections.
Cutoff sums
A smoothing function, ϑ(r,rc), is used to make the cutoff part, Eq. 16b, and its corresponding forces smooth within the cutoff distance rc. It is required to satisfy the following boundary conditions:
| (18a) |
| (18b) |
| (18c) |
In this work, we use a polynomial smoothing function,
| (19) |
For electrostatic potential, Eq. 9, we can derive the following smoothing function from Eq. 18:
| (20) |
For Lernnard-Jones potential, the repulsion part is short ranged and its 3D IPS is calculated only within the cutoff distance rc, using Eq. 15 with Rc=rc. For the dispersion part,
| (21) |
We can derive the smoothing function from Eq. 18,
| (22) |
Long-range sums
The long-range sum collects the IPS contribution leftover by the cutoff sum. To efficiently calculate the long-range sum, we use the DFFT technique the same way as the particle-mesh-Ewald method.3 For Lennard-Jones potential, only the long-range sum of the dispersion term is calculated. The repulsion term is often too small beyond the short-range cutoff distance as compared to the dispersion term. Because the dispersion term is atom type dependent, to simplify the calculation, we transform the atom pair dependent dispersion parameters Cij, to a transferable quantity di, which is defined as the dispersion momentum to measure the contribution of each atom to long-range dispersion interactions. For an atom i, its interaction with a remote system can be written as
| (23) |
Here, is an average distance to the remote system. The approximation is valid when the distance is very large as compared to the system size. The total interaction of a system with a remote system is
| (24) |
From Eq. 24, we have . Combined with Eq. 23, we have
| (25) |
In any simulation box, atomic charges and dispersion momentums can be distributed over a set of predefined grid points (k1,k2,k3), where k1=1,2,…,K1, k2=1,2,…,K2, and k3=1,2,…,K3. Assume the charges and dispersion momentums of a simulation system of N particles areq={q1,q2,…,qN} and d={d1,d1,…,dN}. After spreading q and d on the grid points, we have grid distributions Q and D. We find that Cardinal b spline is a very convenient way to do the spreading.3 If Mn(u) represents the b-spline function of the nth order, we have
| (26) |
| (27) |
Here, the inner summations are taken over all integers n1,n2,n3.
With the discrete charges and dispersion momentums, discrete Fourier transform can be used to calculate interaction summations. Here, we use F(A) to represent the discrete Fourier transform of array A(k1,k2,k3),
| (28) |
and F−1(A) to represent the inverse discrete Fourier transform,
| (29) |
The convolution between two arrays can be done in Fourier space,
| (30) |
Therefore, the electrostatic long-range sum can be calculated in the following way:
| (31) |
Here, ΔεLR(k1,k2,k3) is the energy array,
| (32) |
The energy-type subscript is dropped here to indicate that Eq. 32 applies to all energy types. The Fourier transform of q can be approximated by
| (33) |
where
| (34) |
We have
| (35) |
and
| (36) |
The long-range sum of electrostatic interaction, Eq. 31, can be rewritten to
| (37) |
Similarly, the dispersion long-range sum is
| (38) |
Pressure tensors are important quantities in molecular simulation. The contributions from these long-range sums are calculated directly as a summation in the Fourier space,
| (39) |
Here, α and β stand for either x, y, or z, and.
The forces acting on each particle can be derived from the long-range energies, Eqs. 37, 38.
| (40) |
∂Q∕∂α and ∂D∕∂α are calculated based on Eqs. 26, 27 from the property of the b-spline functions,
| (41) |
IPS for finite systems
So far, we described heterogeneous systems with periodic boundaries. This approach can be extended to finite systems such as proteins in vacuum, with some modifications.
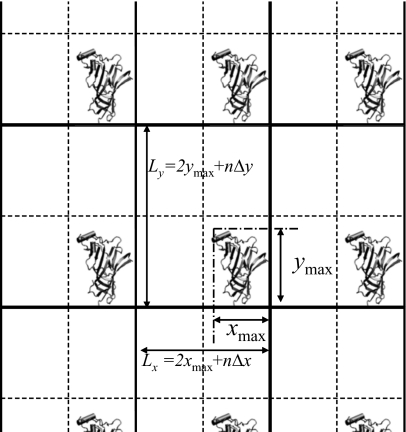
The first modification is to create a virtual periodic boundary for DFFT. The size of the boundary box is twice the maximum dimensions of the actual system plus b-spline widths,
| (42) |
Here, n is the order of b spline and Δx, Δy, and Δz are the grid sizes in the x, y, and z directions, respectively. The charges and dispersion momentums are spread over the grid points in the PBC box according to Eqs. 26, 27. The second modification is that the local region radius will be infinity, Rc=∞. The 3D IPS interaction with an infinity local region radius becomes purely the original pair potential: ε3DIPS(r,Rc→∞)=ε(r). To avoid interaction with images created by the virtual PBC, the long-range sum must be limited to a half of the box size in each dimension,
| (43) |
Here, xij, yij, and zij are the differences of coordinates in the x, y, and z directions, respectively. Figure 4 illustrates the virtual PBC box defined for a protein in vacuum. With these modifications, we can get rid of the artificial image interactions due to the virtual periodic boundary condition while taking advantage of DFFT, and a finite system can be treated in the same way as a periodic boundary system described above.
Figure 4.
The virtual periodic boundary for a finite system as defined by Eq. 42.
Algorithm of the IPS method for heterogeneous systems
The 3D IPS∕DFFT method has two steps. The first step is the calculation of the cutoff sum using Eq. 16b for each of the particle pairs within the cutoff distance rc, which is done the same way as many cutoff methods4 and we do not repeat those here. The second step is the calculation of the long-range sum, which is described below:
-
(1)
define grids over the periodic boundary box. The suggested grid size is 2–3 Å. For finite systems, a rectangular virtual periodic boundary box is defined based on the system size. To minimize the virtual periodic boundary box, it is recommended to orient the periodic boundary box along the principle axis of the system. Calculate b-spline modes along each dimension: ∣b1(m1)∣2, ∣b2(m2)∣2, and ∣b3(m3)∣2;
-
(2)
calculate the long-range energy arrays, ΔεLR(k1,k2,k3), and the long-range pressure tensor arrays, , according to Eq. 32. Fourier transform these discrete functions to obtain , , , and . This step need not be repeated if the simulation box size and grid definition do not change;
-
(3)
spread charges and dispersion momentums onto grid points to obtain Q and D according to Eqs. 26, 27; Fourier transform Q and D to obtain F(Q) and F(D);
-
(4)
loop through the grid points to sum the long-range energies and pressure tensors according to Eqs. 37, 38, 39 and calculate and for force calculation;
-
(5)
inverse Fourier transform to get and , and calculate forces on each atom according to Eq. 40.
At each molecular dynamics step, steps (2)–(5) are repeated to obtain energies, forces, and pressure tensors. The parameters that users can choose are the cutoff distance rc, the local region radius Rc, and grid sizes Δx, Δy, and Δz, as well as the order of b spline. For efficiency, rc∼10 Å would be recommended. Rc should be chosen according to the heterogeneity of a simulation system. For homogenous systems such as small molecule solutions, Rc=20 Å would be enough to accurately calculate energies and forces. For typical heterogeneous systems, a Rc of twice the longest PBC box side would be enough to produce accurate energies, forces, as well as pressure tensors.
SIMULATION DETAILS
This method has been implemented into CHARMM5and is available in CHARMM version c35. CHARMM force field6 version 27 is used in all simulations reported here. The cutoff distance rc is set to 10 Å by default, and the local region radius Rc, is set to be twice the longest side of the PBC box if not otherwise stated. The grid sizes are set to be rc∕4, except otherwise stated. The order of b spline is set to 6. All simulations were performed in parallel with four processors on a quad-core 2.2 GHz operon computer. SHAKE algorithm7 is used to fix bond lengths, and a time step of 2 fs is used.
In some comparison cases, the particle-mesh-Ewald (PME) method3, 8 is used for electrostatic energy calculation. All PME calculations uses the sixth order b-spline interpolation. The grid sizes are around 1 Å and the width of the Gaussian distribution, κ, is set to be 0.34.8 The force-switch method4 is used for Lennard-Jones energy calculation for the purpose of comparison.
RESULTS AND DISCUSSION
Accuracy and efficiency in long-range energy calculations are major concerns in molecular simulation studies. Here, we use five example systems to demonstrate the accuracy and efficiency of the 3D IPS∕DFFT method. For Lennard-Jones potentials, the results with a large cutoff can be used as the “correct” answer for comparison purposes; for electrostatic energies, the PME results are used as standard for periodic boundary systems; and noncutoff calculation results are the standard for finite systems.
A two-ion periodic system
A system of two ions represents an extreme case of heterogeneous systems (Fig. 2). In this system, a sodium ion and a chloride ion are enclosed in a 40×40×40 Å3 cubic periodic box. They have one positive and one negative unit charge, respectively. Their Lennard-Jones parameters are , r*Na+=2.7275 Å,, and r*Cl−=4.54 Å. The following combination rules are adopted:
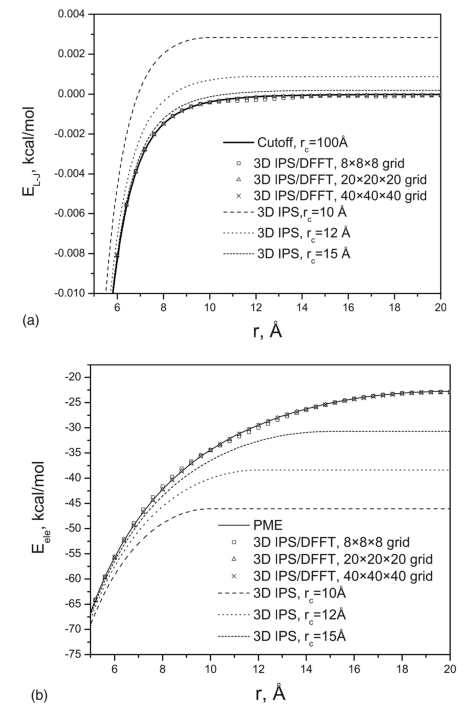
The sodium ion is kept at the origin, and the chloride ion is placed at different positions along the z axis. We calculated the electrostatic and Lennard-Jones (L-J) energies of the system as a function of the distance between the two ions. Figure 5a compares the L-J energies from different methods. The results from the cutoff method with a large cutoff distance, rc=100 Å, are used as the standard. As can be seen, the 3D IPS method with rc=10, 12, and 15 Å produces large deviations from the large cutoff results. The deviation becomes smaller with larger rc. The results from the 3D IPS∕DFFT method at three different grids, 8×8×8, 20×20×20, and 40×40×40, are very close to the large cutoff results. Figure 5b compares the electrostatic energies from different methods. Here, PME results are used as the standard. Clearly, 3D IPS, which assumes a fully isotropic system with a relatively small local region, underestimates the two particle interactions but approaches the “correct” results (PME) when rc increases. To make 3D IPS reproduce the PME electrostatic energies, a large cutoff would be needed. These 3D IPS results support the approximation that with large cutoff distances, 3D IPS can describe heterogeneous systems. Obviously, the 3D IPS∕DFFT method can well reproduce the “correct” results. Even with a very coarse grid, 8×8×8, corresponding to a grid size of 5×5×5 Å3, we still have a fairly good agreement. Because usually the long-range sum costs less than the cutoff sum with a normal cutoff of 10 Å if the grid size is larger than 1 Å, we suggest using a grid size between 2–3 Å to save computing time without sacrificing too much in accuracy. Further increase in grid size produces little to gain in computing cost.
Figure 5.
(a) Lennard-Jones energies of a two-ion system calculated with different methods. The 3D IPS energies approach the large cutoff (rc=100 Å) energies as rc increases. The 3D IPS∕DFFT energies are very close to the large cutoff energies, even with a coarse grid, 8×8×8. (b) Electrostatic energies of a two-ion system calculated with different methods. The 3D IPS energies approach PME energies as rc increases. The 3D IPS∕DFFT energies are very close to PME energies, even with a coarse grid, 8×8×8.
Bulk water
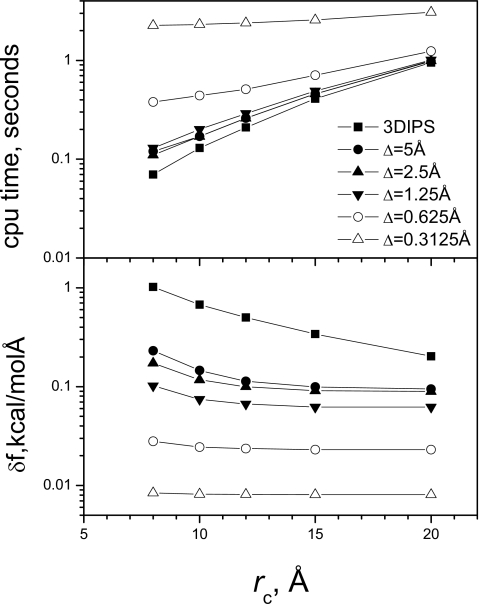
We use 2180 TIP3P9 water molecules with a 40×40×40 Å3 cubic periodic boundary condition to represent a bulk water system. This system is a homogeneous system and provides an example to show how much improvement this 3D IPS∕DFFT method has over the original 3D IPS method. We performed energy calculations with this system to examine the effect of cutoff distances and grid sizes on the accuracy of forces and computing cost. Figure 6 shows force deviation and cpu times of the 3D IPS method and this 3D IPS∕DFFT method as a function of the cutoff distance. The force deviation is calculated against the 3D IPS result with rc=Rc=25 Å, which is also the local region radius for the 3D IPS∕DFFT calculation. We examined different grid sizes, from 0.3125 to 5 Å. It is clear to see that with the same cutoff distance the 3D IPS∕DFFT has much improved accuracy even with a very coarse grid, Δ=5 Å. Obviously, a finer grid results in a more accurate result. Also, a larger cutoff distance corresponds to a more accurate result. The top panel of Fig. 6 shows the CPU time for the energy calculation. Reducing grid size from 5 to 1.25 Å does not significantly increase the CPU time. Increasing the cutoff distance always increases cpu time. Therefore, this data suggests that a grid size around 2 Å and a cutoff distance around 10 Å is a reasonable combination in terms of accuracy and computing cost for this system.
Figure 6.
Force deviations (lower panel) and CPU times (upper panel) of 3D IPS and 3DIPS∕DFFT (Rc=25 Å) at different cutoff distances. The calculation is for a bulk water system with 2108 TIP3P water molecules in a 40×40×40 Å3 cubic box. The deviations are against the 3D IPS result with rc=Rc=25 Å.
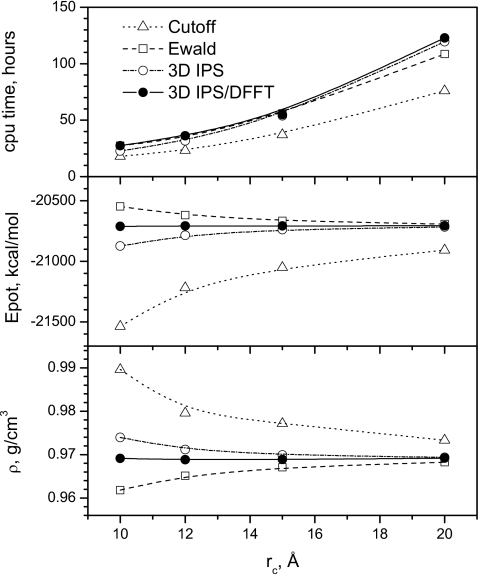
This bulk water system is simulated for 2 ns at a temperature of 300 K and a pressure of 1 atm. The NPT simulations started with a 40×40×40 Å3 cubic periodic boundary condition. Figure 7 shows the average densities, potential energies, and CPU times from simulations with a force-switch cutoff method,4 PME, 3D IPS, and the 3D IPS∕DFFT methods. Slight cutoff dependence in average properties is observed for PME and 3D IPS, while much stronger dependence is observed for the cutoff results. It should be noted that the dependence in the PME results is mainly due to the Lennard-Jones interaction, which is calculated with the force-switch cutoff method.4 The 3D IPS∕DFFT produces almost cutoff-independent results. It is clear to see that at large cutoff distances, all simulations approach the same result. The top panel of Fig. 7 shows the CPU time of these simulations. The CPU times are relatively similar for all simulations because the short range pairwise interaction dominates the total cost. The cutoff method takes the least time. With small cutoff distances, 3D IPS is faster than the 3D IPS∕DFFT and the PME methods, while at large cutoff distances, PME is faster than 3D IPS and the 3D IPS∕DFFT methods. Overall, PME, 3D IPS, and the 3D IPS∕DFFT are very close in computing cost. However, the 3D IPS∕DFFT results at a 10 Å cutoff distance are more accurate than other methods with cutoff distances as large as 20 Å. Therefore, even for homogenous systems, the 3D IPS∕DFFT is a better choice in terms of accuracy and computing cost.
Figure 7.
The densities (lower panel), potential energies (middle panel) and CPU times (upper panel) of the bulk water NPT simulations.
Water interfaces
A water interface system is created by enlarging the PBC box length of the above system along the z axis, so that a gas phase is produced above and below the water liquid. There are 2180 TIP3P water molecules in the 40×40×80 Å3 orthorhombic periodic boundary box. Figure 8 shows a snapshot of this system. This is a typical heterogeneous system involving phase equilibrium. In this system, 2 ns MD simulations at constant temperature (300 K), constant volume (40×40×80 Å3) are performed with PME, 3D IPS, 2D IPS, and the 3D IPS∕DFFT method. Here, 2D IPS is a method designed specifically for two dimensional partial homogenous systems.1, 10
Figure 8.
A water interface system with 2108 TIP3P water molecules in a 40×40×80 Å3 orthorhombic boundary box.
An important property of interface systems is the surface tension. Because the surface tension is very sensitive to long-range interactions, an accurate calculation of surface tension is often time consuming. The surface tension is evaluated from
| (44) |
where Lz is the size of the simulation box normal to the interface, Pzz is the normal component of the internal pressure tensor and Pxx and Pyy are the tangential components. Since the MD simulations here contain two interfaces (see Fig. 8), the prefactor 0.5 is required to obtain γ on a per interface basis.
Pressure tensors are sensitive to long-range structures. Periodic boundary conditions impose such long-range symmetries into simulation systems. For pressure tensor related simulations, the ideal setup is to have the local region radius Rc in the 3D IPS∕DFFT method less than a half of the shortest box side to avoid the symmetry effect due to periodic boundary conditions. In the case that the box size is small as compared to the homogeneity scale, i.e., the thickness of the water layer in this case, it is recommended to set the Rc to twice that of the longest box side or larger to equally consider all images in every direction.
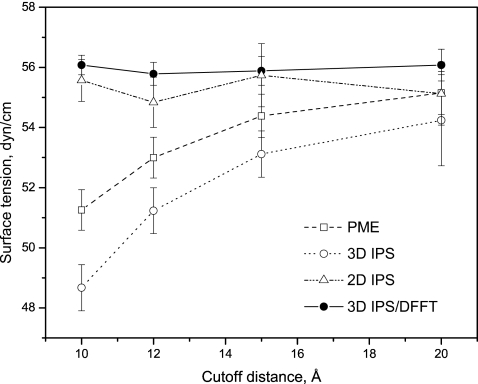
Figure 9 shows the surface tension results from different methods. As can be seen, the results from PME and 3D IPS strongly depend on the cutoff distance, while 2D IPS and the 3D IPS∕DFFT method produce results showing little dependence on the cutoff distance. Obviously, as the cutoff distance increases, the results from PME and 3D IPS approach that from 2D IPS and the 3D IPS∕DFFT methods. We can see that to calculate surface tension, the 3D IPS∕DFFT method with a normal cutoff distance, rc=10 Å, is more efficient in the interface system simulation.
Figure 9.
The surface tension of the water interface calculated from simulations with different methods.
Another property that is sensitive to the long-range interaction is the electrostatic potential profile across the layer, which is calculated by a double integration of the Poisson’s equation,
| (45) |
where ρc(z) and ψ(z) are the charge density and electrostatic potential along the z direction, respectively.
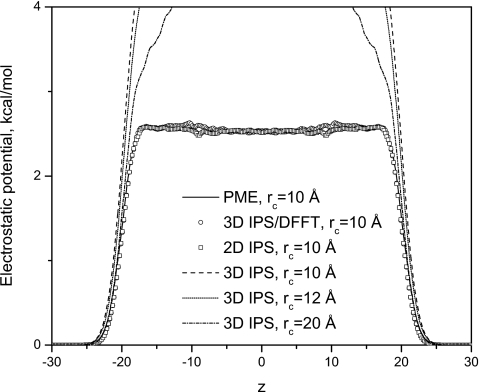
Figure 10 shows the electrostatic potential profiles calculated from simulations using the PME, 3D IPS, 2D IPS, and the 3D IPS∕DFFT methods. Clearly, 3D IPS cannot produce correct electrostatic potential profiles with small cutoff distances. However, as the cutoff distance increases, the result from 3D IPS becomes closer to the PME result. The 2D IPS, the 3D IPS∕DFFT, as well as the PME method, produce almost identical results.
Figure 10.
The electrostatic potential profile cross the water interface system from simulations with different methods.
These results indicate that both the 3D IPS∕DFFT method and the 2D IPS method can accurately describe the long-range interactions of this interface system. The 3D IPS∕DFFT method is much faster than the 2D IPS because its short-range cutoff contains much fewer atom pairs than the cylinder cutoff in the 2D IPS method.1
A sodium aqueous system
Solvation of an ion involves interactions far beyond the simulation box. The small number of ions in a simulation box makes the system highly heterogeneous. The solvation energy of an ionic solution can reflect the enthalpy effect as well as the entropy effect of charged ions onto the solvent, which provides a good case to examine the 3D IPS∕DFFT method.
We performed MD simulations of a sodium aqueous solution in both charged and neutral states to examine the energy difference, defined as the electrostatic solvation energy,
| (46) |
Here, Eaq and Evac represent the average potential energies of the system with and without water in the same periodic boundary box, and q=1 and q=0 represent the charged and neutral states of the solvated ion, respectively. The system contains one sodium ion and 265 TIP3P water molecules. Simulations of 20 ns are performed at 300 K and in a 20×20×20 Å3 cubic periodic boundary box for both the charged and neutral states with PME, 3D IPS, and the 3D IPS∕DFFT method. A cutoff distance of 10 Å is used for all simulations.
Table 1 lists the electrostatic solvation energies from different simulations. As can be seen, 3D IPS underestimates the solvation energy by approximately 3 kcal∕mol as compared to the PME result. This difference indicates that the homogenous approximation with a cutoff of 10 Å causes significant error for the salvation energy calculation. By contrast, the 3D IPS∕DFFT method produces results very close to the PME results, supporting the idea that with a cutoff larger than the homogeneity scale, 3D IPS can well approximate a heterogeneous system. Table 1 also lists the result of the 3D IPS∕DFFT method with different grid sizes. Clearly, the results are almost independent of grid sizes. The CPU times of the 3D IPS∕DFFT method are comparable to those of the PME method.
Table 1.
Electrostatic solvation energies of a sodium ion calculated with different methods. K1, K2, and K3 are the grid numbers along the three sides of the 20×20×20 Å3 cubic box.
| Methods | K1 | K2 | K3 | Esolv, kcal∕mol | Time, hours |
|---|---|---|---|---|---|
| PME | 20 | 20 | 20 | −67.17±0.19 | 28.86 |
| 3D IPS | ⋯ | ⋯ | ⋯ | −64.75±0.50 | 23.80 |
| IPS | 6 | 6 | 6 | −67.38±0.19 | 28.57 |
| IPS | 8 | 8 | 8 | −67.42±0.19 | 27.98 |
| IPS | 12 | 12 | 12 | −67.32±0.19 | 28.08 |
| IPS | 20 | 20 | 20 | −67.75±0.19 | 29.74 |
| IPS | 6 | 12 | 20 | −67.67±0.19 | 27.85 |
Proteins in vacuum
Systems without periodic boundary conditions are clearly heterogeneous by nature. By imposing a virtual periodic boundary and avoiding interactions with images, the 3D IPS∕DFFT method can be applied to such finite systems.
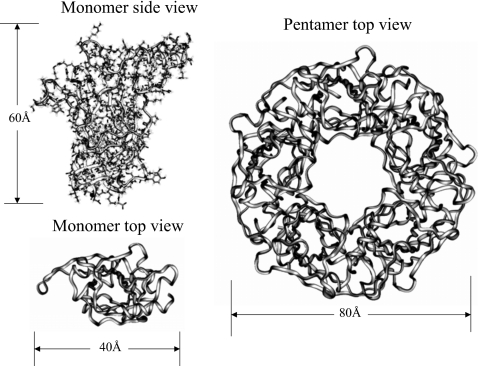
We chose the x-ray structure of acetylcholine binding protein (ACHBP) (Ref. 11) (PDB code: i9b) to examine the energy calculation for nonperiodic systems. We use its monomer and pentamer as examples of systems of small and large sizes. Figure 11 shows the image of this protein in its monomer and pentamer form.
Figure 11.
acetylcholine binding protein (ACHBP) (PDB code: i9b) in its monomer and pentamer forms. The backbones are shown as ribbons. For clarity, atoms are not shown in the top views.
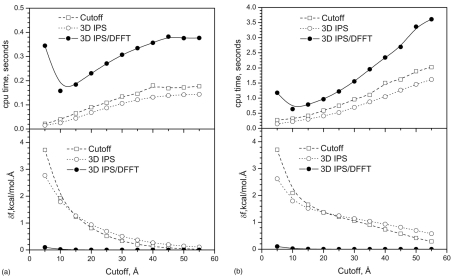
Figures 12a, 12b show the force root-mean-square deviations and CPU times at different cutoff distances for the monomer and pentamer. Even though 3D IPS shows better results than the cutoff method at small cutoff distances, they both show significant force deviations with the cutoff distances up to 50 Å. By contrast, the 3D IPS∕DFFT result is better than these two methods by an order of magnitude.
Figure 12.
The root-mean-square deviations (rmsd) of the forces and cpu times from the cutoff method, 3D IPS, and the 3D IPS∕DFFT method with different cutoff distances. The rmsd is calculated against the forces calculated with no cutoff. (a) the ACHBP monomer, i9b; (b) the ACHBP pentamer, (i9b)5.
For the monomer, the 3D IPS∕DFFT costs more CPU time than the cutoff method at a given cutoff distance. However, at 10 Å, the 3D IPS∕DFFT method has a force deviation, δf, of 0.019 kcal∕mol Å, while for the cutoff (force-switch) method, δf=1.92 kcal∕mol Å. Even with a cutoff distance of 50 Å, the cutoff method has δf=0.022 kcal∕mol Å. Therefore, the 3D IPS∕DFFT method can reach a better accuracy with a 10 Å cutoff than the force-switch method with a cutoff distance of 50 Å. In other words, to reach the same accuracy, the 3D IPS∕DFFT method needs less CPU time. This is obvious for large systems. For the pentamer, at a 10 Å cutoff, the 3D IPS∕DFFT method can reach δf=0.022 kcal∕mol Å with 0.158 s of CPU time. The force-switch method with a cutoff distance of 55 Å can only reach an accuracy of δf=0.289 kcal∕mol Å, but uses 2.03 s of CPU time. Clearly, for small systems, accurate forces can be calculated by summing directly over all atom pairs, while for large systems, the 3D IPS∕DFFT method is a superior way to efficiently get accurate forces.
CONCLUSIONS
The 3D IPS∕DFFT method is an efficient way to calculate 3D IPS potentials with a local region larger than that defined by the cutoff distance. A large local region is the key to account for the heterogeneity of a simulation system. With periodic boundary conditions, any simulation system looks like a pseudohomogeneous system with a local region large than the periodic boundary. With an infinity large local region, the IPS potential would be the same as the lattice sum.
The 3D IPS∕DFFT method has the advantage over the lattice sum methods when the periodic boundary symmetry is to be avoided in long-range interaction. A system can be simulated with a periodic boundary larger than its homogeneity scale so that the 3D IPS∕DFFT method can avoid periodic boundary symmetry by using a local region larger than the homogeneity scale but smaller than the periodic boundary box. In addition, the 3D IPS∕DFFT method can be easily extended to other potential types.
Through several example systems, we demonstrate that the 3D IPS∕DFFT method is accurate and efficient. For homogenous systems, the 3D IPS∕DFFT method produces better results than the original 3D IPS method. For a 2D homogenous system, this method produces very similar results to the 2D IPS method but is much more efficient. For nonperiodic systems, this method produces very good approximation to noncutoff methods and is much more efficient for large systems. In summary, this method provides a convenient approach to do long-range energy calculation for molecular simulation of all kinds of systems.
ACKNOWLEDGMENTS
We thank Richard Pastor for many fruitful discussions and comments. Richard Venable and Linda Chen have done extensive testing on the method. X.W. would like to thank Michael Crowley for his help in the implementation of DFFT.
References
- Wu X. and Brooks B. R., J. Chem. Phys. 10.1063/1.1836733 122, 044107 (2005). [DOI] [Google Scholar]
- Ewald P. P., Ann. Phys. 10.1002/andp.19213690304 64, 253 (1921). [DOI] [Google Scholar]
- Essmann U., Perera L., Berkowitz M. L., Darden T., Lee H., and Pedersen L. G., J. Chem. Phys. 10.1063/1.470117 103, 8577 (1995). [DOI] [Google Scholar]
- Steinbach P. J. and Brooks B. R., J. Comput. Chem. 10.1002/jcc.540150702 15, 667 (1994). [DOI] [Google Scholar]
- Brooks B. R., Bruccoleri R. E., Olafson B. D., States D. J., Swaminathan S., Jaun B., and Karplus M., J. Comput. Chem. 10.1002/jcc.540040211 4, 187 (1983). [DOI] [Google Scholar]
- A. D.MacKerell, Jr., Bashford D., Bellott M., R. L.Dunbrack, Jr., Evanseck J. D., Field M. J., Fischer S., Gao J., Guo H., Ha S., Joseph-McCarthy D., Kuchnir L., Kuczera K., Lau F. T. K., Mattos C., Michnick S., Ngo T., Nguyen D. T., Prodhom B., W. E.ReiherIII, Roux B., Schlenkrich M., Smith J. C., Stote R., Straub J., Watanabe M., Wiorkiewicz-Kuczera J., Yin D., and Karplus M., J. Phys. Chem. B 10.1021/jp973084f 102, 3586 (1998). [DOI] [PubMed] [Google Scholar]
- Ryckaert J. P., Ciccotti G., and Berendsen H. J. C., J. Comput. Phys. 10.1016/0021-9991(77)90098-5 23, 327 (1977). [DOI] [Google Scholar]
- Feller S. E., Pastor R. W., Rojnuckarin A., Bogusz S., and Brooks B. R., J. Phys. Chem. 10.1021/jp9614658 100, 17011 (1996). [DOI] [Google Scholar]
- Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. 10.1063/1.445869 79, 926 (1983). [DOI] [Google Scholar]
- Klauda J. B., Wu X., Pastor R. W., and Brooks B. R., J. Phys. Chem. B 10.1021/jp068767m 111, 4393 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brejc K., van Dijk W. J., Klaassen R. V., Schuurmans M., van Der O. J., Smit A. B., and Sixma T. K., Nature (London) 10.1038/35077011 411, 269 (2001). [DOI] [PubMed] [Google Scholar]