Quantitative evaluation of simultaneous reconstruction with model-based crosstalk compensation for ^99mTc∕¹²³I dual-isotope simultaneous acquisition brain SPECT

Abstract

A model-based method has been previously developed to estimate and compensate for the crosstalk and downscatter contamination in simultaneous ¹²³I∕^99mTc dual-isotope SPECT imaging. In this method, photon scatter in the object is modeled using the effective source scatter estimate technique. Photon interactions with the collimator-detector are estimated using precalculated Monte Carlo simulated point response functions. Two different approaches, simultaneous and alternating model-based compensations, have been proposed for iterative reconstruction-based crosstalk and downscatter contamination compensation. In this work, both model-based approaches were evaluated in the context of quantitative accuracy when imaging the dopaminergic system using both Monte Carlo simulated and experimentally acquired data. Results indicate that model-based estimates of the crosstalk and downscatter contamination in both energy windows were in good agreement with the truth for the simulated data. The effects of the contamination reduced image contrast and overestimated absolute activity in all structures by up to 66%. Compensation using both model-based approaches improved image contrast. Errors in absolute activity quantitation were also reduced to less than ±5% for most brain structures. The accuracy of striatal specific binding potentials, calculated as the ratio of activity in various striatal structures to the background, was also greatly improved after model-based compensation. In conclusion, model-based compensation of simultaneously acquired images of ^99mTc and ¹²³I labeled brain imaging agents provided image quality and quantitative accuracy that were comparable to the image without crosstalk. Both proposed compensation approaches can potentially be applied clinically, but when reconstruction time is a limiting factor, the alternating model-based compensation may be preferable.

INTRODUCTION

SPECT systems have the ability to simultaneously acquire images in several energy windows. This provides the ability to simultaneously image two or more tracers, each labeled with an isotope emitting photons of different energies. This simultaneous imaging capability has several potential advantages, including improved efficiency, reduced patient discomfort and cost, and perhaps most important, production of images that are perfectly registered in space and time. In recent years, several pharmaceuticals labeled with technetium-99m (^99mTc) or iodine-123 (¹²³I) have been developed for SPECT imaging of the dopamine transporter (DAT) or the dopamine D2-like receptors (D2R) in the dopaminergic system.^{1, 2, 3, 4} As a result, simultaneous imaging of both presynaptic and postsynaptic activities using a ^99mTc labeled DAT ligand, such as ^99mTc-TRODAT, and an ¹²³I labeled D2R agent, such as ¹²³I IBZM or ¹²³I-IBF, has been proven to be feasible and clinically attractive.^{5, 6, 7, 8} Quantitative assessment of these images has the potential to provide a reliable method for differentiating Parkinson syndromes and monitoring disease progression or the effects of therapy.^{9, 10, 11, 12, 13, 14, 15} However, due to the close proximity of the imaging photopeaks of ^99mTc and ¹²³I (140 keV for ^99mTc and 159 keV for ¹²³I), there is significant crosstalk contamination in the images from both isotopes.^{16, 17} Crosstalk contamination can severely degrade image quality and quantitative accuracy and makes simultaneous imaging less clinically useful.

We have previously developed a model-based crosstalk estimation method that can provide accurate estimation of the crosstalk in simultaneously acquired ^99mTc∕¹²³I dual-isotope images. The method includes detailed modeling of photon interactions in both the object and the collimator-detector system.¹⁸ The contamination from downscatter of high-energy photons emitted from ¹²³I was found to be a significant source of contamination and is thus explicitly modeled. This crosstalk contamination model can be used as the basis for iterative reconstruction-based crosstalk compensation. In previous work, alternating reconstruction and crosstalk estimation steps were used to separately compensate for the crosstalk in ^99mTc and ¹²³I images [alternating model-based crosstalk compensation (altMBCC)], where the estimated crosstalk was added to the forward projection steps during the reconstruction.¹⁸ We have also investigated the use of a simultaneous iterative reconstruction method [simultaneous model-based crosstalk compensation (simMBCC)] for crosstalk compensation.¹⁹ The simMBCC method was previously proposed and investigated in the context of ^99mTc∕²⁰¹Tl simultaneous dual-isotope cardiac imaging.²⁰ In simMBCC, both the ¹²³I and ^99mTc activity distribution estimates are reconstructed simultaneously from projection images acquired in the ¹²³I and ^99mTc energy photopeak windows. The projection and backprojection operations include all the possible image-to-projection interactions including attenuation, scatter, and collimator-detector response of the photopeak photons, as well as modeling of the crosstalk contamination between the two isotopes. The use of joint iterative reconstruction for dual-isotope images has also been investigated by Ouyang et al.²¹ However, in their work, the scatter and crosstalk from scatter photons was estimated independently using Monte Carlo simulation and kept constant during the joint iterative reconstruction.

In this work, a detailed evaluation and comparison of both approaches (altMBCC and simMBCC) of the model-based method was performed in terms of quantitative accuracy and precision in simultaneous ¹²³I∕^99mTc dual-isotope brain SPECT studies of the dopaminergic system using Monte Carlo simulated and experimentally acquired phantom data. The images from data with crosstalk contamination reconstructed without and with crosstalk compensation using the altMBCC and simMBCC methods were evaluated and compared to images reconstructed from data without crosstalk.

MATERIALS AND METHODS

Model-based crosstalk estimation

The following is a brief introduction to the model-based crosstalk estimation. For details, please refer to Ref. 18. In simultaneous ¹²³I∕^99mTc dual-isotope imaging, due to the finite energy resolution of the detector system and interactions of photons with the object and collimator-detector system, photons emitted by one isotope can be detected in another isotope’s energy window. The contamination caused by these photons degrades the image quality and is referred to as crosstalk contamination. The crosstalk contamination in the ^99mTc projections includes photons from a variety of processes. In addition to the 159 keV photons used for imaging, ¹²³I decay also emits high-energy photons with energies ranging from 182 to 783 keV and a total abundance of ∼3%. Downscatter of those photons into both the ^99mTc and ¹²³I energy windows can contaminate the images for both isotopes.

Let the ¹²³I and the ^99mTc activity distributions be f_I and f_Tc, respectively, and the ¹²³I and ^99mTc projections be p_I and p_Tc, respectively. Then the projection operation can be written as

$$p_{\text{I}}=F_{\text{I}}^{\text{I}}{f}_{\text{I}}+F_{\text{I}}^{\text{Tc}}{f}_{\text{Tc}},$$ (1)

$$p_{\text{Tc}}=F_{\text{Tc}}^{\text{Tc}}{f}_{\text{Tc}}+F_{\text{Tc}}^{\text{I}}{f}_{\text{I}},$$

where $F_{\mathrm{I}}^{\mathrm{I}}$ and $F_{\mathrm{Tc}}^{\mathrm{Tc}}$ are the projection operators for each isotope into its own photopeak-energy window and $F_{\mathrm{I}}^{\mathrm{Tc}}$ and $F_{\mathrm{Tc}}^{\mathrm{I}}$ are the operators describing crosstalk contamination from Tc into I and I into Tc, respectively. Note that in this notation, the superscript represents the source isotope and the subscript represents the target energy window. The ¹²³I operators can be further decomposed into $F_x^{{\mathrm{I}}_{159}}$ and $F_x^{{\mathrm{I}}_{\mathrm{HE}}}$, representing the contribution from its 159 keV and high-energy photons, respectively, into energy window x.

In the model-based method, the crosstalk and downscatter contamination are estimated using models for the $F_{\mathrm{Tc}}^{{\mathrm{I}}_{159}}$, $F_{\mathrm{Tc}}^{{\mathrm{I}}_{\mathrm{HE}}}$, and $F_{\mathrm{I}}^{\mathrm{Tc}}$ that include the photon interactions inside both the object and the collimator-detector system. Photon scatter inside the object is modeled using the effective source scatter estimation (ESSE) technique, where an effective scatter source is estimated for each projection view based on object-independent scatter kernels obtained using Monte Carlo (MC) simulations.²² Photon interactions with the collimator-detector system are modeled using collimator-detector response functions (CDRFs). The CDRFs are computed using MC simulations where photons with known energies are propagated through the collimator-detector system and detected in the energy window of interest. For photons that are not scattered in the object, the CDRFs are computed using sources emitting photons with the same energies and abundances as for the isotope. Because scattered photons have a broad energy distribution, CDRFs for scattered photons are computed using sources that emit a continuous distribution of photon energies. A different CDRF was used for each effective scatter source energy and computed using a source emitting photons with uniformly distributed energies spanning the effective source’s energy range. The energy ranges for the effective sources were chosen to roughly correspond to regions with a flat energy spectrum of scattered photons as described previously.¹⁸ The CDRFs for these photons with intermediate energies are then used to model photons that scatter both in the object and collimator detector and produce a net energy from these interactions that falls within the photopeak-energy windows. The CDRFs include the effects of interactions in the collimator-detector system and the detector’s finite energy resolution. The details of this model-based method are given in Ref. 18.

Reconstruction-based crosstalk compensation

Crosstalk compensation can be performed by subtracting the crosstalk estimate from the projection data, but this is usually accompanied by a large increase in image noise and the need to handle negative pixel values. For better results, crosstalk can be compensated for by adding the estimate to the projections during each iteration or model it during the iterative reconstruction process. Similar to iterative reconstruction-based scatter compensation, reconstruction-based crosstalk compensation can provide images with both less bias and reduced noise.^{20, 23} In this work two approaches that combined the iterative reconstruction and the model-based methods to compensate for the effects of crosstalk and downscatter contamination were evaluated. For both approaches, the iterative ordered subsets expectation maximization (OS-EM) reconstruction algorithm was used. A fast implementation of the ESSE techniques was also used to speed up the scatter and crosstalk estimation processes.²⁴

The model-based method requires an estimate of the activity distribution, $f_{\mathrm{I}}^n$ and $f_{\mathrm{Tc}}^n$, in order to estimate the crosstalk. The two model-based approaches use different methods to obtain these estimates. In the first approach, $f_{\mathrm{I}}^0$ and $f_{\mathrm{Tc}}^0$ are reconstructed separately without crosstalk compensation. Here “0” indicates that the images are from reconstructions without crosstalk compensation. The crosstalk and downscatter contamination in both energy windows can then be estimated by projecting these reconstructed images, i.e., $F_{\mathrm{Tc}}^{\mathrm{I}}{f}_{\mathrm{I}}^0$ and $F_{\mathrm{I}}^{{\mathrm{I}}_{\mathrm{HE}}}{f}_{\mathrm{I}}^0+F_{\mathrm{I}}^{\mathrm{Tc}}{f}_{\mathrm{Tc}}^0$. Next, a new set of images, $f_{\mathrm{I}}^1$ and $f_{\mathrm{Tc}}^1$, is reconstructed with the compensation for the crosstalk and downscatter contaminations performed by adding the estimated contamination to the forward projection step in the OS-EM algorithm. Note that the initial reconstructions $f_{\mathrm{I}}^0$ and $f_{\mathrm{Tc}}^0$ are contaminated, so the crosstalk and downscatter contamination estimate based on them will be larger than the true crosstalk. It is necessary to repeat this process of reconstruction and crosstalk estimation iteratively. Because in this approach image reconstruction and crosstalk estimation are alternated and performed independently, it was therefore referred to as altMBCC. In the above reconstruction steps, it is important to compensate for the attenuation, scatter, and CDRF of the photopeak photons. Otherwise, the bias caused by those degrading factors will reduce the accuracy of the crosstalk and downscatter estimation.

The second approach used a variation of the OS-EM algorithm where the images of both isotopes are reconstructed simultaneously from two projection windows, and the effects of crosstalk and downscatter contamination are modeled during the reconstruction process based on the image estimates for each subset. The modified OS-EM algorithm can be written as

$$x_i^{\text{new}}=\frac{x_i^{\text{old}}}{{\sum }_{j∊\left(S_{m,\text{I}}\cup S_{m,\text{Tc}}\right)}{f}_{ji}}\left[\sum _{j∊\left(S_{m,\text{I}}\cup S_{m,\text{Tc}}\right)}{f}_{ji}\frac{p_j}{{\sum }_k{f}_{jk}{x}_k^{\text{old}}}\right].$$ (2)

where j∊(S_m,I∪S_m,Tc) means the backprojection is done for the projection bins p_j from the subset m of both p_I and p_Tc. The image estimate x_i∊[f_I,f_Tc] means that the images of two isotopes are reconstructed simultaneously. The f_ji is the element of projection matrix F, which is

$$F=\left[\begin{array}{l}{F}_{\text{I}}^{\text{I}},F_{\text{I}}^{\text{Tc}}\\ F_{\text{Tc}}^{\text{I}},F_{\text{Tc}}^{\text{Tc}}\end{array}\right].$$ (3)

Since F models all the physics of the projection processes including crosstalk and downscatter contamination, the crosstalk compensation is performed during the reconstruction. This approach has the potential to offer more accurate crosstalk compensation with less noise. Note here that the attenuation, scatter, and CDRF of the photopeak photons are also modeled in the matrix F and thus compensated for during the reconstruction.

Because the images are reconstructed simultaneously in this approach, it is referred to as simMBCC method. The differences between simultaneous reconstruction (OS-EM-simMBCC) and the standard OS-EM reconstruction algorithm for a single image set of projections are that, for each subset, the reconstructed image voxels include those from the images of both isotopes, the projection data come from two energy windows, and, most important, the projection and backprojection operations contain all the possible image-to-projection interactions including crosstalk and downscatter contamination. To increase reconstruction speed, further optimization of the algorithm can be conducted by using an unmatched projector and backprojector pair. For example, the projection matrix still includes all the possible physical processes discussed above, while in the backprojection matrix the scatter and crosstalk are not modeled.²⁰ This last approach was used in this work.

Image generation

To evaluate both altMBCC and simMBCC, MC simulation and physical phantom experiments were performed. In a simulation study one knows the true activities and the exact location of brain regions. In addition, the simulated phantom can be more anatomically realistic in representing the brain structures compared to a physical phantom. So, in this work, the investigation was focused on simulated results. However, experimental studies provide important validation and additional information about factors seen in clinical studies. Using such data can provide information about the sensitivity of the model-based crosstalk compensation method to mismatch between parameters of the imaging system model assumed in the simulations on which the crosstalk model is based and the physical parameters of a real acquisition system. Detailed descriptions of the studies are presented below.

Monte Carlo simulation study

MC simulated projections of the digitized Zubal brain phantom were used to evaluate the model-based crosstalk compensation method.²⁵ The phantom was contained in a 256×256×124 matrix with a voxel size of 1.1×1.1×1.4 mm³. A previously validated MC simulation code was used for the simulation.²⁶ In this simulation, the interaction of photons with the collimator-detector system was modeled using an accelerated and previously validated method based on precomputed angular response functions. A parallel-hole LEHR collimator and a 9.5 mm (3∕8 in.) thick crystal was simulated, giving a spatial resolution of 9.2 mm FWHM at 15 cm from the face of the collimator. For the ¹²³I simulation, the 15 most abundant ¹²³I photon emissions were included. Projection images were generated in 128×128 bins at 128 views over 360° with a 0.24 cm bin size. A 15 cm radius of rotation was used. The energy windows were 130–150 keV for the ^99mTc projections and 150–171 keV for the ¹²³I projections. The upper and lower thresholds of the ^99mTc and ¹²³I windows, respectively, were modified from the traditional 15% energy windows to avoid overlap.

Projection data for five different organ structures corresponding to the left and right putamens, left and right caudate nuclei, and the background, which included both gray matter and white matter, were simulated separately. Scaling and summing the projections of these structures allowed us to model different uptake ratios between the regions. The ¹²³I and ^99mTc projections were also simulated separately. A total of 4×10⁹ decays were simulated in the MC simulation for each isotope. This number of decays provided projections whose profiles showed very little evidence of noise fluctuations. For each isotope, projections in both isotopes’ energy windows were simulated. This provided the single isotope projection image and the true crosstalk projection for the other isotope. The crosstalk and single isotope projections were then scaled and summed to produce simultaneous images with different ^99mTc to ¹²³I activity concentration ratios.

Using the data obtained from simulations described above, projections modeling five different activity distributions of the ^99mTc and ¹²³I were generated (Table 1). Those distributions included the modeling of the normal striatal uptake of ¹²³I labeled D2R agents (distributions I–III) or the ^99mTc labeled DAT agents (distribution IV) with a specific binding potential (SBP) [defined as (striatal−background)∕background] of 4.0. Reduced SBPs (ranging from 0 to 2) of ¹²³I D2R agents (distributions IV and V) or ^99mTc DAT agents (distributions I–III and V) in caudates or putamens were also modeled. These distributions were chosen based on the dopamine transporter or receptor agent uptake that might be seen in normal patients and patients with Parkinsonism.^{12, 27, 28, 29, 30, 31} Since the injected ^99mTc activity relative to that for ¹²³I may also vary, this effect was also studied.

Table 1.

Activity distributions used in the study. Note that all the activity concentrations were normalized to that of ¹²³I background.

Distribution		Relative activity concentration
		Left caudate	Left putamen	Right caudate	Right putamen	Background
I	I	5	5	5	5	1
	Tc	5	3	5	3	1
II	I	5	5	5	5	1
	Tc	2.5	0.5	2.5	0.5	0.5
III	I	5	5	5	5	1
	Tc	1.5	1.5	2.5	2.5	0.5
IV	I	3	3	3	3	1
	Tc	10	10	10	10	2
V	I	3	5	3	5	1
	Tc	10	6	10	6	2

Projections of a 159 keV point source in air at 15 cm from the face of collimator were also simulated. The collimator-detector sensitivity for ¹²³I imaging was then calculated by dividing the number of geometrically collimated photons by the number of total simulated photons. Similar procedures were also used to estimate the detector sensitivity for ^99mTc imaging. The sensitivity was later used to transfer reconstructed image counts to the number of decays used in the simulation.

Image reconstruction

Using low noise MC simulated projections, 50 noise realizations were generated for each distribution. The mean total counts in the projections without crosstalk contamination were ∼25 000 counts per view and varied for the different distributions. These count levels were selected based on the clinical patient data with an injected activity of 740 MBq ^99mTc-TRODAT or 185 MBq ¹²³I-IBZM. These projections were then reconstructed using the OS-EM reconstruction algorithm.³² A rotation-based projector and backprojector were used in the OS-EM implementation. The OS-EM code included the ability to reconstruct multiple images from multiple projection energy windows as described above. To evaluate model-based crosstalk compensation, the simultaneous images were reconstructed without crosstalk compensation (OSEM-None), with alternating model-based crosstalk compensation (OSEM-altMBCC), and with simultaneous model-based crosstalk compensation (OSEM-simMBCC). To serve as a standard for compensation, projections of separate acquisitions of each isotope with no crosstalk and downscatter contamination were also reconstructed (OSEM-Single), i.e., the 159 and 140 keV photon images which are also referred to as contamination-free images.

For all the reconstructions, including both simulated and experimental data, up to 30 iterations with 32 subsets per iteration were used. Compensation for attenuation, scatter, and CDRF of the imaging photopeak photons was applied in all reconstructions. The attenuation maps contained the attenuation coefficients appropriate for the photopeak energy of each isotope. Scatter of the imaging photopeak photons was modeled in the reconstruction using the ESSE method.²² The CDRF for the imaging-photopeak photons to their own energy window, including collimator penetration and scatter, was estimated using MC simulation of a point source emitting photopeak-energy photons in air at various distances from the face of collimator.

The root mean square error (RMSE), calculated as described in Sec. 2F, from different numbers of iterations were then compared to find the optimal number of iterations, i.e., the one giving the best trade-off between quantitative accuracy and noise.

Quantification and PVE compensation

To perform the quantitative study, unity filled region of interest (ROI) mask images having voxel values of 1 inside the ROI and zero outside were generated from the phantom. The numbers of voxels in the ROI maps were 90 470 for the background, 283 and 272 for the left and right caudates, and 309 and 262 for the left and right putamens, respectively.

The mean pixel values in each of the five ROIs were then measured using the corresponding ROI mask images. Post-reconstruction partial volume compensation (PVC) was performed using a perturbation-based geometric transfer matrix (pGTM) method.³³ This method is based on the geometric transfer matrix method, where each region is assumed to have uniform activity uptake.³⁴ If a brain has n distinct ROIs with true activities T_i (i=1,…,n) then the measured activity t_i in the ith ROI_i from SPECT imaging can be expressed as a linear transformation of the true activities:

$$\stackrel{⃑}{t}=W\cdot \stackrel{⃑}{T},$$ (4)

where $\stackrel{⃑}{T}$ is the vector of true activities with elements T_i and $\stackrel{⃑}{t}$ is the vector of measured activities with elements t_i. The matrix W is called the geometric transfer matrix (GTM). Elements, w_ji, of the pGTM represent the transfer coefficient of activity in region i into region j. When the GTM is known, the true activity $\stackrel{⃑}{T}$ can be solved by inverting Eq. 2. In the pGTM method, elements of the transfer matrix, i.e., the pGTM matrix, which include the spill out of activity from the region and spill in of activity from neighboring regions, are estimated by projecting an image obtained by adding each ROI as a perturbation to the reconstructed image. The perturbed images are then reconstructed and the reconstructions of the projections of unperturbed images are then subtracted. The total counts in the resulting images in each ROI are then used to obtain the elements of the transfer matrix.

After PVC, absolute quantitation was obtained by dividing the measured ROI values by the detector sensitivity. Finally, the mean and standard deviation of the absolute activity estimates and the SBP values from 50 noise realizations were computed and the percentage biases from the true values were calculated using

$$\text{bias}\%=\frac{\text{estimate}-\text{true}}{\text{true}}\times 100\%.$$ (5)

In Eq. 5, truth is with reference to the actual MC simulated activity. RMSEs of the estimates from the true values were also calculated and used as a figure of merit to select the optimal number of iterations. The formula used to calculate the RMSE for n noise realizations is given by

$$\text{RMSE}=\sqrt{\frac{{\sum }_{i=1}^n{\left({\text{estimate}}_i-\text{true}\right)}^2}{n}}.$$ (6)

Experimental phantom study

Experimental projections of a striatal brain phantom (Radiological Support Devices, Inc., Long Beach, CA) were acquired using a Siemens E.CAM SPECT system. A parallel-hole low-energy high-resolution collimator was used, providing a spatial resolution of 0.75 cm FWHM at 10 cm from the collimator face. Projections were acquired using a 128×128 projection matrix at 128 views over 360° with a projection bin size of 0.24 cm and an acquisition time of 40 s per view. The same energy windows and radius of rotation used in the MC simulation study were used. Separate acquisitions were performed with the phantom filled with ¹²³I and ^99mTc. The bed and phantom were carefully marked so the phantom could be returned to the same position for both acquisitions. During both acquisitions, projections were acquired into both energy windows. This allowed summing projections to form simultaneous dual-isotope projections.

For the ¹²³I acquisition, the activity concentrations in the different compartments were 110 kBq∕ml for the background, 212 and 1770 kBq∕ml for the left and right caudates, and 154 and 222 kBq∕ml for the left and right putamens, respectively. The activity concentrations used for ^99mTc acquisition were 130 kBq∕ml for the background, 654 and 305 kBq∕ml for the left and right caudates, and 775 and 334 kBq∕ml for the left and right putamens, respectively.

The volumes of the compartments were estimated by subtracting the weight of the dry empty compartment from the compartment filled with water. The various solutions introduced into the compartments were prepared by diluting a solution containing a known amount of activity (measured in a dose calibrator) to a known volume of water.

After the SPECT acquisition, a CT scan of the phantom was performed using a GE Millennium VH SPECT∕CT system. The CT scan provided an attenuation map in a 128×128×128 matrix with a voxel size of 0.221 cm. The attenuation coefficients in the map were automatically translated by the GE software to represent attenuation coefficients for the ^99mTc. The attenuation map was then bilinear interpolated to the same pixel size as the projection image and manually registered with a SPECT image reconstructed using filtered backprojection. This attenuation map was used in the OSEM-based reconstructions and model-based crosstalk estimation. Because this is a rigid phantom, the error introduced by registration was expected to be small.

A single projection of a 10 MBq point source in air was also measured for each isotope. The geometric collimator-detector sensitivity was then calculated by dividing the measured counts by the point source activity and the acquisition time and scaled by the ratio between the number of geometrically collimated photopeak photons and the total detected photons calculated based on MC simulation. The value thus determined was 0.077 counts∕kBq∕s (170 cpm∕uCi) for ¹²³I and 0.09 counts∕kBq∕s (200cpm∕uCi) for ^99mTc. The sensitivity was later used to transfer the counts from reconstructed images to an absolute activity concentration value with a unit of kBq∕ml or uCi∕ml.

In order to generate the ROI map of each compartment in the phantom, an MRI scan of the phantom was also performed, producing a digitized image of the phantom in a 256×256×124 matrix. The transaxial pixel size in the MRI image was 1.05×1.05 mm² with a 1.4 mm slice thickness. During the scan the striatal compartments were filled with a contrast agent (gadopentetate dimeglumine) to give a striatum to background ratio of 100 to 1. The MRI image was then segmented into five ROIs of the left and right putamens, left and right caudates, and the background. Each ROI mask image at the resolution of the MRI image was converted to one at the resolution of the SPECT image by interpolation and thresholding. Finally the ROI mask images were manually registered with the SPECT images to an accuracy of better than 1 voxel. The numbers of voxels in the ROIs were 146 for both the left and right caudates, 208 and 235 for the left and right putamens, and 84 781 for the background.

The projection images were reconstructed with OSEM-NC, OSEM-single, OSEM-altMBCC, and OSEM-simMBCC. For ¹²³I imaging the 159 keV only projections could not be directly measured, i.e., they contained downscatter contamination from the high-energy ¹²³I photons. Thus the model-based downscatter compensation (OSEM-altMBDC) (Ref. ³⁵) was used to compensate for downscatter contamination to generate single isotope data without contamination. Mean pixel values in each ROI in the reconstructed image were computed and divided by the detector sensitivity and acquisition time to give the total activity estimates in each ROI. The pGTM method was applied to these activity estimates to provide partial volume effect compensated estimates. The biases in the estimated activities were computed with respect to the actual activities placed in the corresponding compartments in the phantom. These actual activities were measured using a dose calibrator.

RESULTS

Monte Carlo simulation results

Model-based crosstalk estimation

To demonstrate the importance of various sources of contamination, the fractions of crosstalk and downscatter photons detected in each energy window were computed. In the projection of activity distribution I, crosstalk from ¹²³I represented about 50% of the total counts in the ^99mTc window. For other activity distributions, the amount of ¹²³I crosstalk in the ^99mTc window ranged from 31% (distributions IV and V) to 66% (distributions II and III) depending on the ^99mTc to ¹²³I activity concentration ratio. Crosstalk from the ^99mTc into the ¹²³I image, however, only contributed 1%–3% of the total counts, while the downscatter from high-energy photons contributed up to 39% of the total counts in the ¹²³I window. In addition, scatter of imaging photopeak photons also contributed 11% in their own windows.

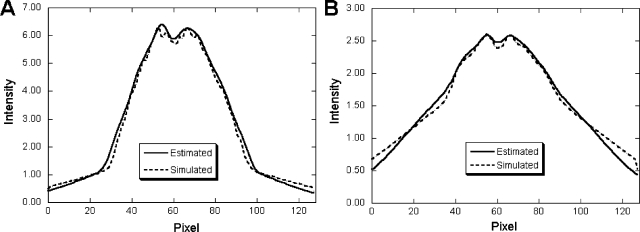
Figure 1 shows horizontal profiles through the posterior projection view through the striatal region. These profiles compare the model-based crosstalk and downscatter contamination estimates in the ^99mTc and ¹²³I energy windows with the MC simulated results for distribution I. For both energy windows, the estimated results were in good agreement with the MC simulations. There was some discrepancy in the tails of the estimated downscatter and crosstalk in the ¹²³I window. Because in the projection algorithms used in the crosstalk model the attenuation is estimated based on the path perpendicular to the face of collimator, there are some errors when modeling high-energy photons that penetrate the collimator at large incident angles. However, the disagreement between the model and MC simulation is small, and, as will be demonstrated below, these disagreements did not produce noticeable artifacts or degradations in quantitative accuracy.

Figure 1.

Comparison of model-based and MC simulated contamination estimates from distribution I. The graphs show (a) ¹²³I crosstalk contamination into ^99mTc window projection and (b) sum of high-energy photon downscatter contamination and ^99mTc crosstalk contamination in ¹²³I window projection. The figures are the horizontal profiles through the posterior projection view through the striatal region.

Convergence of crosstalk compensation

From Fig. 1 it can be seen that the crosstalk and, especially, the downscatter contamination contain mainly low frequency information. Thus, during this study, it was found that model-based estimates using images reconstructed with different numbers of iterations varied little except for the first several iterations. In addition, it only took a few alternations for estimated crosstalk and downscatter contamination to converge to the truth for the altMBCC method. So, for OSEM-altMBCC, a total of four alternations were used with four iterations used for the reconstructions in each alternation steps. We found this was enough iterations and alternations to estimate the crosstalk and downscatter contamination quite accurately. For the final reconstruction, a larger number of iterations (up to 30 iterations) was used in order to improve the spatial resolution of the fine structures such as the putamen and caudate.

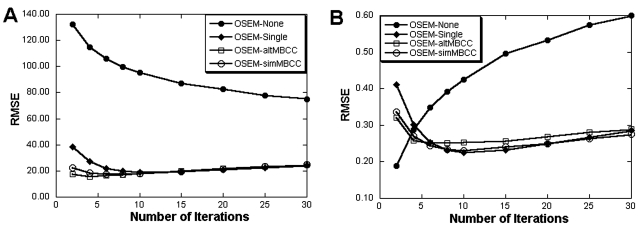
Figure 2 plots the RMSE of the ^99mTc activity estimates and SBP values from distribution I as a function of the number of iterations for the different crosstalk compensation methods. In Fig. 2, the number of iterations for OSEM-altMBCC is that for the final reconstructions (after four alternations). Results from OSEM-Single, OSEM-altMBCC, and OSEM-simMBCC behaved similarly, with the RMSE converging in about ten iterations. For more iterations, the increasing image noise degraded the precision of the measurements and caused the RMSE to increase. For images without the crosstalk compensation, accuracy of activity estimates continued to improve out to at least 30 iterations (the highest number of iterations investigated). However, the RMSE was much larger than for images with crosstalk compensation, and the RMSE for the SBP values increased monotonically after the first iteration. Based on these RMSE results, ten iterations of OS-EM were used for all methods in the studies described below.

Figure 2.

The RMSE versus number of iterations for the left caudate from distribution I. The graphs show the RMSE for (a) the absolute activity estimate and (b) the SBP.

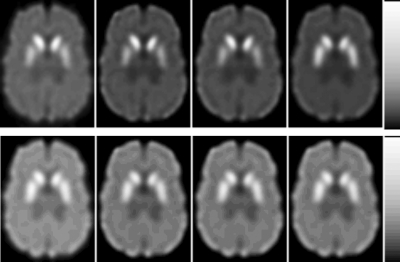
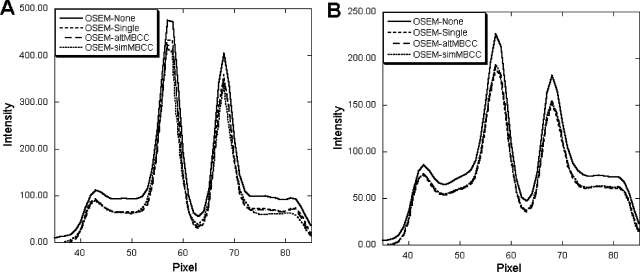
Figure 3 shows one slice of the reconstructed images obtained with the different methods after ten iterations. Horizontal profiles through the images shown in Fig. 3 are plotted in Fig. 4. The effects of crosstalk and downscatter contamination are obvious in both the ¹²³I images and ^99mTc images, where the image contrast was reduced by contamination and the area outside the brain has nonzero activity. The profiles indicate that activities in the reconstructed image were artifactually increased without crosstalk and downscatter contamination compensation. After model-based compensation, the image contrast was improved and the profiles were in good agreement with those from contamination-free images, indicating the effectiveness of the compensation methods.

Figure 3.

Reconstructed images from different crosstalk∕downscatter compensation methods after ten iterations. From left to right, the images were reconstructed using OSEM-None, OSEM-Single, OSEM-altMBCC, and OSEM-simMBCC, respectively. Top row shows ^99mTc images from distribution I and the bottom row shows ¹²³I images from distribution IV. These distributions were chosen because they represent the worst case for the two isotopes.

Figure 4.

Horizontal profiles through images shown in Fig. 3 across the caudate. The graphs are from (a) ^99mTc images from distribution I and (b) ¹²³I images from distribution IV.

Quantitation

Percentage biases and standard deviations of the mean absolute activity estimates from the 50 noise realizations are listed in Table 2 for distributions I, III, and V. Note that the standard deviations are shown as a percentage of the mean activity value. The results from distribution II are similar to those from distribution III, and distribution IV’s results are similar to V (they have the same background ^99mTc to ¹²³I ratio); thus those data are not included in the table. The biases and standard deviations in Table 2 represent the quantitative accuracy and precision of each method over multiple noise realizations. As expected, without compensation crosstalk and downscatter contamination increased the activity estimates and resulted in overestimation of both the ¹²³I activities and ^99mTc activities for all the structures. The degree of the overestimation depended on the activity concentration ratios between the two isotopes in the ROI and surrounding regions. For example, the bias of ^99mTc activity estimates in the left putamen ranged from 12.97%±4.44% for distribution V (^99mTc:¹²³I=6:5) to 52.91%±9.08% for distribution III (^99mTc:¹²³I=3:10). After model-based compensation, biases of activity estimates were greatly reduced and less than ±5% for both ¹²³I and ^99mTc in all the distributions. The results were close to those for images reconstructed from contamination-free projections (OSEM-Single). The relative standard deviations of the activity estimates for each distribution were not affected by the compensation and were similar for all the reconstruction methods (Table 2), indicating that the model-based compensation does not increase imprecision in activity estimates.

Table 2.

Percentage biases of activity estimates from MC simulation experiments. The data are presented as bias±standard deviation.

Distribution	Isotope	Method	Left caudate	Left putamen	Right caudate	Right putamen	Background
I	123I	None	9.26±4.29	3.52±3.52	9.45±4.13	5.11±3.61	14.42±0.33
		Single	2.65±3.88	−0.29±3.00	2.15±3.74	1.01±3.97	−1.20±0.31
		altMBCC	1.74±4.18	−1.05±3.42	1.45±4.14	−0.01±3.53	−2.22±0.27
		simMBCC	2.20±4.16	−0.94±2.87	1.59±4.14	0.32±3.03	−1.74±0.27
	99mTc	None	20.28±5.05	26.68±5.75	22.02±4.89	27.87±6.67	32.28±0.44
		Single	3.50±3.43	−0.02±4.98	3.19±4.24	−0.17±6.12	0.40±0.35
		altMBCC	0.49±3.53	−2.19±5.22	0.18±4.29	−2.14±5.78	−1.98±0.35
		simMBCC	0.77±4.29	−1.31±5.12	0.47±4.29	−1.25±5.54	−1.16±0.33
III	123I	None	6.49±4.09	2.91±3.44	8.09±3.94	5.39±4.35	12.46±0.39
		Single	2.65±3.88	−0.29±3.00	2.15±3.74	1.01±3.97	−1.20±0.31
		altMBCC	1.14±3.99	−1.33±3.37	0.86±3.68	0.21±4.22	−2.72±0.32
		simMBCC	1.27±3.99	0.12±8.46	0.99±3.66	0.36±4.21	−2.24±0.35
	99mTc	None	60.98±10.76	52.91±9.08	39.95±5.98	33.28±7.77	66.29±0.70
		Single	4.47±7.66	−0.56±7.70	3.86±7.06	0.71±5.28	0.35±0.54
		altMBCC	−1.55±8.41	−3.97±6.93	−1.54±5.33	−3.04±7.06	−4.31±0.53
		simMBCC	0.12±8.46	−2.55±7.03	−0.80±5.30	−2.47±7.00	−2.80±0.53
V	123I	None	19.95±5.22	7.04±3.60	19.84±6.05	8.44±3.92	17.65±0.32
		Single	0.16±5.26	0.55±2.88	−0.59±5.21	1.87±3.37	−1.30±0.32
		altMBCC	2.00±4.93	0.28±3.52	1.25±5.75	1.59±3.73	−1.49±0.26
		simMBCC	2.53±5.01	0.49±3.53	1.72±5.78	1.76±3.67	−0.85±0.27
	99mTc	None	10.12±2.48	12.97±4.44	10.12±2.66	13.06±4.35	16.57±0.27
		Single	2.66±2.74	0.53±3.75	3.33±2.05	−0.05±4.64	0.53±0.26
		altMBCC	1.41±2.43	−1.36±4.16	1.35±2.57	−0.99±4.12	−0.54±0.26
		simMBCC	1.87±2.41	−0.89±4.22	1.51±2.59	−1.11±4.15	−0.10±0.22

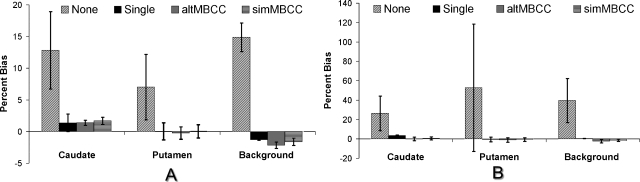
Figure 5 shows the average and standard deviation of caudate, putamen, and background activity estimate percentage biases over all five distributions. These values are measures of a method’s robustness with respect to patient variations. Ideally, a method would have a low bias for all the patients (implying low standard deviation of the bias) in order to provide reliable diagnostic information. From the figure one can see that, after model-based compensation, the variations of bias over different activity distributions were much smaller than those without compensation and were similar to the single isotope images. This indicates that the model-based method removed the patient dependence of the quantitative accuracy in dual-isotope imaging.

Figure 5.

Average and standard deviation of activity estimate percentage biases over all five distributions: (a) ¹²³I activities; (b) ^99mTc activities.

The percentage biases and standard deviations of the striatal SBP estimates over 50 noise realizations are listed in Table 3 for distributions I, III, and V. Figure 6 shows the average and standard deviations of SBP estimate percentage biases over all five distributions. Without crosstalk compensation and because of the overestimation of background activities, the SBPs for all the striatal compartments in the ^99mTc images were underestimated, with the biases ranging from −4.6% to −25%. After model-based compensation, biases in the SBPs for the ^99mTc images were less than ±4%. The biases in ¹²³I SBP estimates ranged from 4% to −12% without compensation. Overestimation of the SBP was obtained in the distributions where the ^99mTc to ¹²³I ratio was high (e.g., in both caudate and putamen in distribution IV and caudate in distribution V). Unlike crosstalk contamination from ¹²³I into ^99mTc, crosstalk from ^99mTc into the ¹²³I image is caused by the limited energy resolution of the detector system and results largely from unscattered photons and resembled the distribution of ^99mTc. So, its effects on quantitation were regional instead of affecting the entire brain. Thus, for distributions IV and V, the striatum, where the ^99mTc to ¹²³I ratio (10:3) was much higher than in the background (2:1), had more crosstalk contamination than the background, and the SBP was thus overestimated. On the other hand, for distributions I–III, the activity ratios for the two isotopes were similar in both the striatum and the background. For these cases, the effects of crosstalk were similar and the SBPs were mostly underestimated. Compensation using the model-based method corrected the underestimation of the ¹²³I SBP in most situations, with errors in the range ±5%. Again, Fig. 6 shows that, after compensation, the variation of biases among different distributions was much smaller than those from data without compensation.

Table 3.

Percentage biases of SBP calculated from MC simulation. The data are presented as mean±standard deviation.

Distribution	Isotope	Method	Left caudate	Left putamen	Right caudate	Right putamen
I	123I	None	−5.25±4.95	−11.90±3.98	−5.43±4.66	−10.17±4.18
		Single	4.88±4.95	1.16±3.79	4.24±4.76	2.79±5.15
		altMBCC	5.07±5.44	1.49±4.34	4.68±5.09	2.83±4.61
		simMBCC	5.02±5.39	1.03±3.65	4.25±5.24	2.63±4.03
	99mTc	None	−11.33±4.87	−6.36±6.57	−9.70±4.66	−5.00±7.67
		Single	3.85±4.18	−0.64±7.45	3.46±5.41	−0.87±9.23
		altMBCC	2.90±6.07	−0.31±8.07	2.76±5.55	−0.24±9.00
		simMBCC	2.45±6.31	−0.31±7.78	2.06±5.39	−0.13±8.62
III	123I	None	−6.63±4.75	−10.63±4.08	−4.86±4.61	−7.86±4.96
		Single	4.88±4.95	1.16±3.79	4.24±4.76	2.79±5.15
		altMBCC	4.95±5.20	1.79±4.49	4.59±4.82	3.76±5.40
		simMBCC	4.48±5.18	1.29±4.48	4.12±4.79	3.72±5.37
	99mTc	None	−7.07±9.76	−12.07±8.16	−19.80±4.82	−24.82±5.91
		Single	4.17±11.58	−1.35±11.86	4.38±8.96	0.45±6.66
		altMBCC	4.33±13.29	0.53±11.02	3.62±7.07	1.66±9.31
		simMBCC	4.51±13.10	0.39±10.80	2.56±6.91	6.42±9.16
V	123I	None	2.93±6.94	−11.28±4.07	2.79±8.03	−9.82±4.40
		Single	2.22±8.09	2.35±3.70	1.08±8.11	4.02±4.24
		altMBCC	4.31±7.52	2.25±4.57	4.17±8.81	3.90±4.80
		simMBCC	5.12±7.60	1.70±4.57	3.89±8.78	3.30±4.71
	99mTc	None	−6.92±2.69	−4.63±5.69	−6.91±2.86	−4.52±5.58
		Single	2.66±3.41	0.01±5.71	3.48±2.61	−0.86±6.69
		altMBCC	2.45±3.07	−1.23±6.26	2.38±3.25	−0.67±6.23
		simMBCC	2.46±3.06	−1.19±6.31	2.01±3.27	−1.52±6.26

Figure 6.

Average and standard deviation of SBP estimate percentage biases over all five distributions: (a) ¹²³I SBP; (b) ^99mTc SBP.

Experimental result

For the experimental data, crosstalk contamination from ^99mTc contributed 2% of the total counts in the ¹²³I window, while the ¹²³I crosstalk represented 52% of the total counts into ^99mTc window. The percentage biases of the activity estimates in each ROI are listed in Table 4. In agreement with the MC simulation study, without MBCC, crosstalk and downscatter contamination caused overestimation in all the structures. The most affected region for the ¹²³I images was the left putamen, where the ^99mTc to ¹²³I ratio was 5.0 and a 25% overestimation of ¹²³I activity was observed. The ^99mTc to ¹²³I ratio was 0.17 in the right caudate, which had the largest error in its ^99mTc activity estimate. The downscatter of high-energy photons emitted from ¹²³I in the right caudate also contaminated neighboring regions and resulted in large biases, such as 157%, 38%, and 50% for the region itself, the right putamen, and the background, respectively. The quantitative accuracy was greatly improved by crosstalk compensation, resulting in a bias smaller than 5% in most regions for both isotopes, and was in good agreement with single isotope images.

Table 4.

Percentage biases of activity estimates from experimental data.

Isotope	Method	Left caudate	Left putamen	Right caudate	Right putamen	Background
123I	None	17.42	25.24	8.70	8.17	12.16
	Singlea	0.21	−4.41	6.97	0.30	−1.56
	altMBCC	0.09	2.50	6.58	0.50	−1.11
	simMBCC	0.11	2.43	6.51	0.47	−1.13
99mTc	None	21.61	19.40	157.04	37.89	50.49
	Single	−0.12	−0.15	−0.14	−0.69	−0.15
	altMBCC	0.81	2.38	5.94	1.03	0.55
	simMBCC	0.79	2.29	5.91	0.89	0.32

^aThe single isotope image of ¹²³I was reconstructed with compensation for downscatter contamination.

Measurement of activity using the dose calibrator and of the compartment volumes can contribute to errors in the experimental results. In these experiments, the camera sensitivity was measured on the same day as the experiment using a point source whose activity was measured on the same dose calibrator used to measure activities placed in the various phantom compartments. As a result, errors in the activity measurements would cancel out and not affect the errors reported here. The effect of errors in the measured volumes is harder to assess. These could certainly have contributed to the errors in the activity concentrations. However, as the volumes of the compartments were measured using electronic scales with high accuracy and precision, and were thus accurate to better than a few parts per 1000, it is unlikely that the contribution of these volume errors to the overall error was very large.

DISCUSSION

In simultaneous ^99mTc∕¹²³I dual-isotope imaging, the amount of crosstalk depends on the activity concentration ratios between the two isotopes in both the regions of interest and the surrounding area. In our simulation of dopaminergic system imaging, the ^99mTc to ¹²³I background activity concentration ratios varied from 0.5 to 2.0, resulting in a significant amount of crosstalk from the ¹²³I into the ^99mTc images but less crosstalk from ^99mTc into ¹²³I images. In some other studies, such as simultaneous imaging of brain perfusion using ^99mTc-HMPAO and neurotransmission with ¹²³I-IBZM, where the concentration of ^99mTc can be much higher than the ¹²³I in the brain, crosstalk from ^99mTc into ¹²³I can be as high as 10%. In the ¹²³I images, about 40% of the total counts could be attributed to the downscatter contamination, which contained mainly low frequency information caused by the collimator penetration and scatter of the high-energy photons. Crosstalk from ¹²³I into ^99mTc arises from both 159 keV and high-energy photons. Due to the close proximity of the two photopeaks, crosstalk caused by photopeak photons was mostly from unscattered or low-scatter-order photons. Images of this crosstalk resembled those from the original images, and this crosstalk greatly affected the accuracy of regional quantification. Meanwhile, the crosstalk and downscatter contamination from high-energy photons was low frequency and affected a large area. The effects of this contamination were to reduce the image contrast and produce overestimates for all the regional activity estimates. Furthermore, the amount of error depends strongly on the activity concentration ratio of the two isotopes and varies significantly among different patients.

Compensation using the model-based method reduced the effects of the crosstalk and downscatter contamination. The two approaches to model-based compensation behaved similarly, with both methods providing accurate quantitation without significantly altering the precision. Among the two approaches, altMBCC is easier to implement and faster than the simMBCC method. In our study, it took ∼24 h to perform 4 alternations of altMBCC and 30 iterations in the final reconstructions on a workstation with a 2.2 GHz AMD Althon CPU. By contrast, simMBCC required more than 90 h to finish 30 iterations. The simMBCC method also required seven to ten times more memory than the single isotope image reconstruction to store the various images and the crosstalk estimates. The simMBCC code used in this study was not optimized for computation speed. Its speed could be improved by optimization of the algorithms, especially by implementing it on a multiple-core CPU. Carefully comparing results in Tables 2, 3, one can see that the simMBCC offers slightly less bias and better precision than the altMBCC method because the crosstalk is modeled and updated during the reconstruction. However, this difference was small and might not be worth the increase in computation time. One minor advantage of simMBCC is that it requires fewer parameters such as the number of iterations between an update of the crosstalk estimate than altMBCC. However, this seems a relatively minor advantage as it is likely that the final results are not very sensitive to these parameters and that a fixed set of these parameters could be determined for a given application. One potentially more significant advantage of simMBCC is that it can be more readily applied to multiple-isotope (n>2) studies. For altMBCC, application to more than two isotopes would introduce additional complexity in terms of the order of alternation of the isotopes.

The accuracy of activity estimates from the two approaches also converged similarly as a function of number of iterations. Using a large number of iterations in the OS-EM reconstruction improved the spatial resolution, providing accurate activity estimates for small structures. However, noise and image artifacts increased with number of iterations, resulting in reduced precision in the activity estimates. In contrast, because the background covers a large area and has a large number of total counts, its activity estimates had high precision (Table 2) and converged quickly with number of iterations. Because the pGTM-based PVC helps recover the loss in accuracy of activity estimates caused by the resolution blur, it improved convergence of the activity estimates and improved the accuracy of both activity and SBP estimates. Nonetheless, the standard deviation of the estimates increased after PVC, degrading the precision. This loss of precision after PVC has been reported previously.^{34, 36} The net effects of improved accuracy and degraded precision are summarized in the RMSE of the activity estimates. As shown in Fig. 2, the trade-off between accuracy and precision caused the RMSE first to decrease at early iterations and then start to increase after the tenth iteration.

Model-based methods have a number of advantages over energy-spectrum-based crosstalk compensation methods: they only require acquisition of both isotopes’ image in a slightly modified traditional energy windows; they do not require the ability to acquire images in many additional energy windows; the detailed physics models provide accurate crosstalk contamination estimates; and reconstruction-based compensation does not increase noise as much as other methods. Nonetheless, there are also limitations and approximations in the model-based methods. For instance, the model-based method cannot model contributions from activity outside the field of view. The complexity of the models used also demands large amounts of computational power. In future work, both approaches to the model-based method could be refined and optimized to further reduce reconstruction time.

CONCLUSION

In conclusion, crosstalk contamination in simultaneous ^99mTc∕¹²³I dual-isotope imaging is complicated by the close proximity of the two imaging photopeaks and the high-energy photons emitted by ¹²³I decay. It also depends on the activity concentration ratio of the two isotopes in the regions of interest. The model-based method takes into account the photon interactions inside both the object and the collimator-detector system, including the contributions from both the two photopeak photons and the high-energy photons. The estimated crosstalk and downscatter were in good agreement with the MC simulated results. Two different approaches to iterative reconstruction-based compensation for crosstalk and downscatter contamination were proposed. Both approaches behaved similarly and provided images approaching the quality of contamination-free images. Quantitative accuracy was also greatly improved without affecting the precision, especially when post-reconstruction partial volume compensation was applied. Of importance, after MBCC, the accuracy did not depend on the patient’s activity distribution. Among the two methods, simMBCC is more computationally demanding than altMBCC while offering slightly better performance. When reconstruction speed is the primary concern, the altMBCC method may be preferable.

DISCLOSURE

Some of the reconstruction codes used in this work have been licensed to GE Healthcare for inclusion in a commercial product. Under separate licensing agreements between the General Electric Co. and the Johns Hopkins University and the University of North Carolina at Chapel Hill and GE Healthcare, Dr. Frey is entitled to a share of royalty received by the universities on sales of products described in this article. The terms of this arrangement are being managed by the Johns Hopkins University in accordance with its conflict of interest policies.