Abstract
Matrix inversion tomosynthesis (MITS) uses known imaging geometry and linear systems theory to deterministically separate in-plane detail from residual tomographic blur in a set of conventional tomosynthesis (“shift-and-add”) planes. A previous investigation explored the effect of scan angle (ANG), number of projections (N), and number of reconstructed planes (NP) on the MITS impulse response and modulation transfer function characteristics, and concluded that ANG=20°, N=71, and NP=69 is the optimal MITS imaging technique for chest imaging on our prototype tomosynthesis system. This article examines the effect of ANG, N, and NP on the MITS exposure-normalized noise power spectra (ENNPS) and seeks to confirm that the imaging parameters selected previously by an analysis of the MITS impulse response also yield reasonable stochastic properties in MITS reconstructed planes. ENNPS curves were generated for experimentally acquired mean-subtracted projection images, conventional tomosynthesis planes, and MITS planes with varying combinations of the parameters ANG, N, and NP. Image data were collected using a prototype tomosynthesis system, with 11.4 cm acrylic placed near the image receptor to produce lung-equivalent beam hardening and scattered radiation. Ten identically acquired tomosynthesis data sets (realizations) were collected for each selected technique and used to generate ensemble mean images that were subtracted from individual image realizations prior to noise power spectra (NPS) estimation. NPS curves were normalized to account for differences in entrance exposure (as measured with an ion chamber), yielding estimates of the ENNPS for each technique. Results suggest that mid- and high-frequency noise in MITS planes is fairly equivalent in magnitude to noise in conventional tomosynthesis planes, but low-frequency noise is amplified in the most anterior and posterior reconstruction planes. Selecting the largest available number of projections (N=71) does not incur any appreciable additive electronic noise penalty compared to using fewer projections for roughly equivalent cumulative exposure. Stochastic noise is minimized by maximizing N and NP but increases with increasing ANG. The noise trend results for NP and ANG are contrary to what would be predicted by simply considering the MITS matrix conditioning and likely result from the interplay between noise correlation and the polarity of the MITS filters. From this study, the authors conclude that the previously determined optimal MITS imaging strategy based on impulse response considerations produces somewhat suboptimal stochastic noise characteristics, but is probably still the best technique for MITS imaging of the chest.
Keywords: tomosynthesis, three-dimensional imaging, NPS, chest, radiography, pulmonary nodule
INTRODUCTION
The limited angle nature of tomosynthesis makes it an especially flexible technique capable of producing 3D data with very short scan times, low cumulative exposure, and in situations where the acquisition geometry is restricted.1 The resolution in tomosynthesis reconstructions is nearly equivalent to that of the image receptor in two of the image dimensions but is limited by the narrow scan angle in the third dimension (plane-to-plane, or z).
Conventional backprojection (“shift-and-add”) tomosynthesis reconstructions2 are degraded by the presence of substantial tomographic blur which obscures in-plane detail.3 Matrix inversion tomosynthesis (MITS) is a reconstruction method which deterministically distinguishes between in-plane detail and residual tomographic blur using knowledge on the imaging geometry and linear systems theory.1, 4, 5, 6, 7, 8, 9, 10, 11 As such, MITS is powerful for its ability to fully render in-plane anatomy, while reducing the visibility of structures located outside the reconstructed slice.
MITS is especially effective in imaging of the chest,10, 11 where the visibility of anatomy in radiographic projection images is obscured by very complex overlapping structure. By rendering distinct slice images, MITS makes both normal and abnormal in-plane anatomy more conspicuous than traditional radiographic or conventional tomosynthesis imaging techniques and is likely to improve measures of detectability.10
In a previous study, we examined the effects of varying the MITS scan angle (ANG), number of projections (N), and number of reconstructed planes (NP) or plane separation (PSEP) on the linear system characteristics of MITS planes,11 and concluded that the optimal imaging strategy for MITS chest imaging entailed setting ANG=20°, N=71, and NP=69. This linear system optimization considered constraints imposed by our prototype tomosynthesis system as well as clinical considerations for chest tomosynthesis implementation. In particular, we are constrained by a maximum scan angle of 25°, a maximum frame rate of 6.4 frames∕s, data truncation due to a stationary detector, and the desire to complete the tomosynthesis scan during a single breath-hold to eliminate respiratory motion during the procedure.
Although the previous study sufficiently characterized the impact of scan parameters on structured noise (i.e., anatomy and artifacts), it did not evaluate their impact on stochastic noise in MITS images. This is particularly relevant, given the fact that the pure MITS solution is known to enhance low-frequency stochastic noise.1 We believe that it is important to characterize the MITS stochastic noise for several reasons. First, the impact of acquisition parameters on the noise frequencies most relevant to the pulmonary detection task is currently unknown, and we may be able to further optimize the MITS technique based upon its stochastic noise properties, without substantially degrading its rendering of anatomy. In addition, a thorough evaluation of MITS stochastic noise properties will aid in determining the optimum dose needed for pulmonary nodule detection because it provides a basis for understanding the signal-to-noise ratio (SNR) at the frequencies important for pulmonary nodule detection. Finally, the characterization of stochastic noise in MITS images is a starting point from which we may compare the SNR performance (and hence the detection performance) of MITS relative to other competing reconstruction algorithms. Neither dose optimization nor an algorithm comparison is included in the current study, but they are the source of future work.
To characterize the MITS stochastic noise properties, the current study evaluates the impact of tomosynthesis scan angle (ANG), number of projection images (N), and number of reconstructed planes (NP) [and∕or plane separation (PSEP)] on the stochastic exposure-normalized noise power spectrum (ENNPS) in MITS reconstructed planes, as well as in precursor projection data and conventional tomosynthesis images.
BACKGROUND
MITS overview
Detailed descriptions of the MITS algorithm have been presented in previous publications.1, 9 MITS functions as a means for distinguishing between true in-plane detail and residual tomographic blur from overlying anatomy in a set of reconstructed conventional tomosynthesis planes. Knowledge of the imaging geometry is incorporated with linear systems theory to model the process of conventional tomosynthesis reconstruction. This leads to a set of linear equations, each of which contains information about the makeup of one conventional tomosynthesis plane in terms of true in-plane detail and the blurring kernels that describe how detail from other planes in the set is rendered in the reconstructed plane. Finally, the set of equations is solved deterministically in the Fourier domain to separate in-plane detail from degrading tomographic blur. This step is implemented using a simple (NP×NP) matrix inversion operation for each spatial frequency in the reconstructed images, followed by matrix multiplication. The resulting MITS planes exhibit increased visibility of in-plane structure due to the deterministic removal of tomosynthesis blur which originates from other planes in the reconstruction set.
MITS noise
One complication of direct matrix inverse solutions is their tendency to enhance stochastic noise when matrices are poorly conditioned for the inversion operation. Poorly conditioned frequency-domain blur matrices arise in the lowest frequencies of MITS from the fact that the low-frequency components of the blurring functions are very similar across all conventional tomosynthesis planes.
Similarity in matrix components presents a problem, as the denominator in all terms of the inverse solution contains the determinant of the blur matrix. When the blur elements themselves are very similar, the determinant approaches zero, and the elements of the resultant inverse solution are very large. (In fact, the zero-frequency component is the same for all of the blurring functions, and so the inverse operation is entirely indeterminate for that frequency.) In this event, the pure MITS solution multiplies the conventional tomosynthesis spectra by very large numbers in order to solve exactly for the true in-plane structure. Any low-frequency stochastic noise in the conventional tomosynthesis planes is thereby amplified by the large multiplicative factors in the MITS solution.
Figure 1 displays a plot of the logarithm of the condition number of the blur matrix as a function of vertical spatial frequency for the previously determined optimal MITS imaging technique. A large condition number (the ratio of the largest singular value to the smallest singular value in the matrix) indicates that enhancement of stochastic noise will occur in the inverse solution. The plot confirms that the pure MITS solution is prone to stochastic noise amplification at the lowest vertical spatial frequencies. Smaller spikes in the matrix condition numbers can also be seen at selected mid and high frequencies and likely occur when the sinc-shaped blurring functions11 happen to coincide such that they share similar values, leading to a very small determinant.
Figure 1.
Plot of the logarithm of the condition number of the blur matrix, as a function of vertical spatial frequency, for ANG=20°, N=71, NP=69, and PSEP=4.4 mm.
To suppress low-frequency noise, a frequency blending scheme is employed, whereby MITS content is suppressed at the lowest frequencies and reinforced with corresponding low-frequency information from the conventional tomosynthesis solution. The frequency blending strategy is implemented as
| (1) |
where MITSfb is the frequency-blended reconstruction, MITS is the original matrix inversion solution, CONV is the conventional tomosynthesis solution, f represents spatial frequency, FW is a constant weighting factor, and σ controls the width of the Gaussian blending function. FW is typically assigned a value of 0. 025 to render planes with lung shading similar to that in projection radiographic images, and selecting σ=0.1 cycle∕mm reasonably suppresses low-frequency MITS noise. Feedback from clinical radiologists at our institution has led to the selection of σ=0.1 in order to suppress low-frequency noise while also giving a radiograph-like appearance to the MITS images. It should be noted that this setting is somewhat specific to chest imaging, which is rather unique in its large dynamic range and complexity of structures, from air-filled lungs to dense mediastinum.
Figures 23 show a human thoracic MITS plane with σ=0.01 cycle∕mm and σ=0.1 cycle∕mm, respectively (ANG=20°, N=61, NP=59, and PSEP=5 mm). When the frequency blending kernel is too small, as in this example, vertical low-frequency noise substantially degrades the quality of the reconstruction. Selecting σ=0.1 cycle∕mm adequately suppresses low-frequency MITS noise, improving MITS image quality.
Figure 2.
Human thoracic MITS plane reconstructed with σ=0.01 cycle∕mm (ANG=20°, N=61, NP=59, and PSEP=5 mm) exhibits substantial low-frequency noise.
Figure 3.
Human thoracic MITS plane reconstructed with σ=0.1 cycle∕mm (ANG=20°, N=61, NP=59, and PSEP=5 mm) demonstrates effective low-frequency noise suppression and excellent rendition of anatomy.
METHODS FOR CHARACTERIZING NOISE IN MITS PLANES
MITS implementation
MITS projection data were acquired with a prototype chest tomosynthesis imaging system9 which contains a commercial indirect flat-panel detector (41×41 cm2; 0.2 mm pitch; Revolution™; GE Medical Systems, Milwaukee, WI), furnished with rapid-readout electronics that allow a maximum read-out rate of 6.4 frames∕s. Our laboratory constructed custom-built computer-controlled motion hardware which moves and rotates a ceiling-mounted x-ray tube along a vertical path, parallel to the stationary detector, and yields a maximum scan angle of 25°.
Raw projection images were preprocessed to correct for nonuniformities in detector gain and offset, and downsampled from 2048×2048 to 1024×1024 to improve computational efficiency. Prior to tomosynthesis reconstruction, a logarithmic operation was performed to transform raw projection grayscale data from transmitted intensity into integrated attenuation thickness values.1
Measuring the NPS
Although several methods exist for quantifying image noise, noise power spectrum (NPS) analysis is commonly used due to its ability to characterize image variance as a function of spatial frequency.12, 13 For the linear vertical motion used in our prototype chest imaging system, MITS filtration is only applied along the columns of conventional tomosynthesis data. Thus, image noise is not symmetric with respect to the horizontal and vertical image dimensions, and predicting its effect on human observer performance is nontrivial. We are most concerned with noise manifest in the vertical spatial frequencies (v) of MITS reconstructions due to the noise amplification characteristics of the inverse solution, as described in Sec. 2B. This paper will examine only vertical stochastic noise characteristics in MITS planes, as vertical noise (in the v frequencies) is generally larger in magnitude than horizontal noise (in the u frequencies) in MITS reconstructions.
To examine the noise characteristics in each step of the MITS image formation process, we computed the NPS in experimentally acquired raw projection images, log-transformed projection images, conventional tomosynthesis reconstructions, and MITS reconstructions (with frequency blending applied as described in Sec. 2B) for various combinations of MITS imaging parameters: ANG=5°, 10°, 15°, 20°, 25°; N=21, 31, 41, 51, 61, 71; and NP=19, 29, 39, 49, 59, 69 (NP<N and total reconstructed thickness of 30 cm). Image data were collected with the prototype system described in Sec. 3A, in the same manner that MITS human subject data are collected, including the use of continuous tube motion with no detector scrub frames, 120 kVp, 0.2 mm added Cu filtration, and an antiscatter grid (13:1, 78 line pairs∕cm) with vertically oriented septa. An 11.4 cm acrylic slab was placed immediately in front of the detector∕grid∕faceplate assembly to simulate beam hardening and scatter from tissue in the lung region.
For each acquisition technique, ten projection data sets (realizations) were acquired in identical fashion. Exposure settings were chosen from preset system mA s stations, so that the cumulative scan tube output was as close to 61.0 mA s (the technique setting for a typical 30 cm subject, as measured at the nipple line) as allowable. Cumulative tube output (single-image mA s setting multiplied by N) ranged from 57 to 67 mA s. Acquisition frame rates were selected in such a manner that the total acquisition time was roughly 11 s for all techniques.
All NPS measurements were performed on mean-subtracted image data in order to remove structured nonstochastic image components, including grid artifacts and image shading. Ensemble average images were created by computing the mean value of each pixel over the ten realizations of a particular image. Averaging was performed after full processing of the image data (i.e., mean tomosynthesis reconstruction planes were generated by averaging over the ensemble of ten tomosynthesis slices, each fully processed from a unique set of projection data). Finally, an ensemble average image was subtracted from each realized image to yield mean-subtracted image data.
The NPS were calculated in a manner similar to that described in the literature.14 Regions of interest (ROIs) with size of 128×128 pixels were extracted from the central region of mean-subtracted images. A 4×7 arrangement of ROIs (512×896 pixels) in each original 1024×1024 image was used for noise analysis. Image edges were excluded to avoid potential nonuniformities near the detector boundaries, and the top and bottom 256 pixels were discarded to avoid regions of tomosynthesis planes containing truncated image data.
Two-dimensional (2D) NPS were obtained by averaging the absolute magnitude squared of the 2D FFTs from each ROI after normalization to account for ROI and pixel size,
| (2) |
where ⟨∣FT(u,v)∣2⟩ represents the ensemble average across all ROIs of the squared Fourier magnitudes, NPIXx and NPIXy are the dimensions of the discrete 2D Fourier transform (equivalent to the ROI dimensions), and Δx and Δy are the horizontal and vertical pixel pitch of the down-sampled images. COR is the mean-subtraction correction factor, which accounts for the fact that image variance in a mean-subtracted image is artificially reduced because the mean image contains a fraction of the stochastic information from each individual image realization,
| (3) |
where NREAL refers to the number of data sets (realizations) used to compute mean images for the mean-subtraction step. For our analysis, NREAL=10, COR=10∕9, NPIXx=NPIXy=128, and Δx=Δy=0.4 mm.
Four columns on either side of the vertical spatial frequency axis (v axis) of NPS(u,v) were averaged to generate a one-dimensional estimate of NPS(v).14 Finally, individual NPS(v) estimates were averaged over the ensemble of ten realizations to yield the NPS for raw and log-transformed projection images, conventional tomosynthesis slices, and MITS planes for each imaging technique.
Normalizing the NPS for exposure to yield the ENNPS
Stochastic image variance is dependent upon the amount of radiation detected. This makes difficult a direct comparison of NPS from planes reconstructed with various tomosynthesis techniques, as in our case each N setting delivered a slightly different cumulative exposure (due to the discrete mA s stations on our prototype system). Furthermore, a comparison of the NPS in individual projection images acquired with varying tomosynthesis parameters is hindered by the fact that the exposure per projection is inversely proportional to N (for fixed cumulative scan exposure).
A reasonable solution is to normalize the NPS in a manner that accounts for entrance exposure differences. Assume two tomosynthesis techniques, with
| (4) |
| (5) |
where λ is the mean entrance exposure in a projection image, N is the number of projection images acquired during the tomosynthesis scan, and K and J are proportionality constants. Then, the cumulative entrance exposure delivered during the two tomosynthesis scans can be stated as
| (6) |
| (7) |
Assuming that noise arises primarily from independent Poisson count statistics, the ideal variance in raw individual projection images from the two data sets is thus equivalent to mean exposure,
| (8) |
| (9) |
As part of tomosynthesis reconstruction, a log transform is performed on the raw projection data.1 We apply a function of the form
| (10) |
where a is the original pixel value, amax is the maximum possible pixel value, C is a constant which defines the desired output latitude, and b is the new pixel value after transformation.
It can be shown by way of propagation of error that variance in log-transformed projection images from our two hypothetical tomosynthesis techniques is related as
| (11) |
Thus, variance is reduced in log-transformed images as exposure is increased.
Under the uncorrelated Poisson noise assumption, variance in conventional tomosynthesis planes, which are created by summing shifted (log-transformed) projection images, has the relation
| (12) |
and is inversely proportional to the cumulative exposure used in the creation of the images.
For an accurate accounting of the entrance exposure delivered during the tomosynthesis acquisitions, we placed an exposure meter at the center of the raw beam near the plane of the detector and measured the cumulative exposure delivered during repetitive scans with each imaging technique. Table 1 lists the measured exposure and the cumulative tube output (mA s) for each tomosynthesis acquisition technique.
Table 1.
Measured exposure (mR) and cumulative tube output (mA s) for each tomosynthesis acquisition technique.
| Technique | Cumulative exposure (mR) | Cumulative tube output (mA s) |
|---|---|---|
| ANG=5°, N=71 | 85.4±0.0 | 56.8 |
| ANG=10°, N=71 | 85.2±0.0 | 56.8 |
| ANG=15°, N=71 | 84.8±0.1 | 56.8 |
| ANG=20°, N=71 | 84.5±0.1 | 56.8 |
| ANG=25°, N=71 | 83.8±0.1 | 56.8 |
| ANG=20°, N=61 | 95.4±0.1 | 61.0 |
| ANG=20°, N=51 | 101.3±0.1 | 63.8 |
| ANG=20°, N=41 | 103.3±0.1 | 65.6 |
| ANG=20°, N=31 | 97.9±0.2 | 62.0 |
| ANG=20°, N=21 | 108.6±0.1 | 67.2 |
Employing the Poisson variance relationships derived in Eqs. 9, 11, 12, the measured exposure was used to normalize the NPS to give the ENNPS, which is independent of exposure, for images at each step in the MITS reconstruction process (raw projection images, log-transformed projection images, conventional tomosynthesis planes, and MITS planes). In accordance with Eq. 9, which shows that the Poisson variance in raw projection images is proportional to exposure, the ENNPS for raw projection images were obtained by dividing NPS curves by the average mR per projection. For log-transformed projection images, the ENNPS were instead computed by multiplying the NPS by the average mR per projection, as Eq. 11 shows that variance in log-transformed images is inversely proportional to exposure. Likewise, all tomosynthesis ENNPS estimates were made by multiplying the NPS by the appropriate cumulative mR values listed in Table 1 to account for the tomosynthesis variance relationship described in Eq. 12. It should be noted that ENNPS estimates in log-transformed projection data and tomosynthesis planes cannot be compared directly to ENNPS estimates in raw projection images, as no attempt was made to account for the constants in the log transformation [Eq. 10].
Resulting ENNPS curves for raw projection data have units of du2 mm2 mR−1, where “du” refers to digital units. The log transform in Eq. 10 cancels the du term, and the ENNPS curves for log-transformed projection and tomosynthesis data thus have units of mm2 mR.
ENNPS RESULTS FROM MEAN-SUBTRACTED IMAGE DATA
A summary of ENNPS behavior as tomosynthesis scan parameters are varied is shown in Table 2. Figure 4 displays ENNPS curves generated from raw projection data acquired at all projection locations during motion of the x-ray tube, with ANG=20° and (a) N=71 and (b) N=21. Noise amplitude in raw projection data is shown to be independent of N, even at high spatial frequencies, where one might expect to see a difference due to the relative magnitude of additive electronic noise in the low- and high-exposure data. (For the same cumulative exposure, increasing N reduces the exposure per projection.)
Table 2.
ENNPS correlation with tomosynthesis scan parameters. The symbol “+” or “−” indicates an increase or decrease in the ENNPS as the scan parameter is increased (i.e., positive or negative correlation, respectively). An “X” is used to indicate a table entry that does not apply to a given imaging technique.
| N | ANG | NP | Plane location (distance from detector) | |
|---|---|---|---|---|
| Raw projections | None | − | X | X |
| Conventional tomosynthesis | + at low frequencies, − at mid and high frequencies | − at low frequencies, + at mid and high frequencies | X | Increased low-frequency noise in anterior planes, and mid- and high-frequency noise spikes in central and posterior planes |
| MITS | − at low and mid frequencies | + at low and mid frequencies | − at low and mid frequencies | Increased low- and mid-frequency noises in both anterior and posterior planes |
Figure 4.
ENNPS curves from unlogged (raw) projection data at all tube locations acquired with ANG=20° and (a) N=71 (1.19 mR∕image), (b) N=21 (5.17 mR∕image).
Figures 5a, 5b show the ENNPS of raw projection data acquired at two different orientations (the center and top of the tomosynthesis scan) for ANG=20° and all N (N=21, 31, 41, 51, 61, and 71). Noise in raw center projections is observed to be consistent across all techniques (N=21, 31, 41, 51, 61, and 71) but slightly higher than the noise in projections acquired at the top of the angular motion.
Figure 5.
Raw data ENNPS curves for all N (N=21, 31, 41, 51, 61, and 71; ANG=20°) from the (a) center projection location and (b) top projection location.
ENNPS for log-transformed projection images acquired at the center projection location for all N (N=21, 31, 41, 51, 61, and 71; ANG=20°) are shown in Fig. 6. Like raw projection ENNPS, properly normalized ENNPS for log-transformed projection images acquired at the same tube location are observed to be independent of exposure and therefore N.
Figure 6.
Log-transformed data ENNPS curves for all N (N=21, 31, 41, 51, 61, and 71; ANG=20°) at the center projection location.
Figure 7 shows that varying the number of projections, however, has some effect on noise in the anterior region of conventional tomosynthesis reconstructions. ENNPS curves are shown for anterior, central, and posterior conventional tomosynthesis planes, with ANG=20° and varying N (N=21, 31, 41, 51, 61, and 71). In the anterior conventional tomosynthesis plane, a low-frequency noise spike is evident, whose amplitude increases with N. Central and posterior planes do not exhibit elevated low-frequency noise but instead contain small noise peaks throughout the mid and high frequencies. Low-frequency ENNPS values in central and posterior planes are roughly equivalent to those of the logged projection data shown previously. However, at high frequencies, the ENNPS of conventional tomosynthesis planes is substantially lower than the high-frequency ENNPS of the logged projection data.
Figure 7.
ENNPS for (a) the anterior plane, (b) the center plane, and (c) the most posterior plane in conventional tomosynthesis reconstructions, with varying N (N=21, 31, 41, 51, 61, and 71; ANG=20°).
Figure 8 illustrates the effect of scan angle on noise at different conventional tomosynthesis reconstruction depths. ENNPS curves are shown for the most anterior, central, and posterior planes, as well as the average across all planes, from conventional tomosynthesis reconstructions with N=71, and varying ANG (5°, 10°, 15°, 20°, and 25°). Low-frequency noise spikes in anterior planes are more pronounced with narrow scan angles, while wide scan angles appear to be more prone to small mid- and high-frequency noise peaks.
Figure 8.
ENNPS curves for the (a) most anterior plane, (b) center plane, (c) most posterior plane, and (d) average of all planes in conventional tomosynthesis reconstructions with N=71 and varying ANG (ANG=5°, 10°, 15°, 20°, and 25°).
Figure 9 shows the effect of varying the number of projections on noise in MITS reconstructions. Averaged ENNPS curves (over all planes in each reconstruction set) are displayed for MITS reconstructions with coarse plane spacing (ANG=20°, NP=19, and PSEP=16.7 mm) for N=21, 31, 41, 51, 61, and 71. The ENNPS appear to be essentially independent of N, except in the frequency range 0.15–0.60 cycle∕mm. In this frequency range, noise is reduced as N is increased, although little improvement is noted above N=51. In all cases, noise in the frequency-blended MITS planes appears to be largely suppressed at frequencies below ∼0.15 cycle∕mm.
Figure 9.
ENNPS curves for MITS reconstructions with ANG=20°, NP=19, PSEP=16.7 mm, and varying N (N=21, 31, 41, 51, 61, and 71).
Figure 10 shows how MITS noise amplification is not uniform across all planes in a reconstruction set. The scatterplot displays ENNPS curves for all planes in a single MITS reconstruction with fine plane spacing (ANG=20°, N=71, NP=69, and PSEP=4.4 mm). Low-frequency noise (<0.5 cycle∕mm) is significantly elevated in the 5 most anterior and posterior planes of the reconstruction, but is fairly uniform throughout the remaining 59 centrally located planes.
Figure 10.
ENNPS curves for all planes in the MITS reconstruction with ANG=20°, N=71, NP=69, and PSEP=4.4 mm.
Figure 11 illustrates the effect of varying the number of reconstructed planes (and therefore plane separation) on the MITS noise power. Averaged ENNPS curves (over all planes in each reconstruction set) are shown for MITS reconstructions with ANG=20°, N=71, and varying NP (NP=19, 29, 39, 49, 59, and 69). Low-frequency noise in the region below 0.5 cycle∕mm worsens slightly as NP is increased from 19 to 39, but then decreases steadily as NP is increased. Mid- and high-frequency noises are not affected by variations in the number of reconstructed MITS planes.
Figure 11.
Average ENNPS curves (across all planes in a single reconstruction set) for MITS reconstructions with ANG=20°, N=71, and varying NP (NP=19, PSEP=16.7 mm; NP=29, PSEP=10.7 mm; NP=39, PSEP=7.9 mm; NP=49, PSEP=6.25 mm; NP=59, PSEP=5.2 mm; and NP=69, PSEP=4.4 mm).
Figure 12 shows how the MITS noise power varies with scan angle. Averaged ENNPS curves (over all planes in each reconstruction set) are shown for MITS reconstructions with N=71, NP=69, PSEP=4.4 mm, and varying ANG (ANG=5°, 10°, 15°, 20°, and 25°). MITS noise appears to worsen with increasing scan angles, particularly in the region spanning 0.15–0.5 cycle∕mm.
Figure 12.
Average ENNPS curves (across all planes in a single reconstruction set) for MITS reconstructions with N=71, NP=69, PSEP=4.4 mm, and ANG=5°, 10°, 15°, 20°, and 25°.
DISCUSSION
In a previous paper,11 we presented an analysis of the MITS impulse response, which concluded that the optimal techniques for MITS chest imaging on our prototype system are ANG=20°, N=71, and NP=69. This conclusion was based solely upon the deterministic resolution properties of the MITS algorithm and did not account for stochastic noise differences between the various possible scan parameter settings. The current study was designed to examine the effect of MITS scan parameters on the stochastic noise in MITS planes.
It should be noted that a linear systems approach can be used to predict stochastic noise characteristics in MITS planes, assuming uncorrelated noise in the projection data and precursor conventional tomosynthesis planes. Using this approach, according to Eq. 2, we would expect noise power in conventional tomosynthesis and then the MITS planes to be amplified by the square of the magnitude of the filters applied to the logged projection data, as noise power is proportional to the square of the Fourier spectra. The reconstruction of conventional tomosynthesis planes can be carried out in the frequency domain by simply summing phase-shifted spectra from the original projection data. Thus, the filter magnitudes all have a value of unity for conventional tomosynthesis reconstruction, and we would not expect a change in the shape of the noise power spectra due to conventional tomosynthesis reconstruction, when noise is uncorrelated across the set of projections.
The MITS solution further multiplies the spectra in each conventional tomosynthesis plane by values which can be quite large at the lowest spatial frequencies, and then sums the results across the entire set of conventional tomosynthesis planes in order to generate a single MITS plane. We would therefore expect noise power in MITS planes to simply be enhanced by the sum of the square of the MITS matrices (filter magnitudes), where the set of precursor conventional tomosynthesis planes have uncorrelated noise. Unfortunately, we must always expect plane-to-plane noise correlation to arise across a stack of conventional tomosynthesis planes, as they are each reconstructed by applying slightly different shifts to the same initial set of projection data. Furthermore, MITS noise amplification is also affected by the fact that the MITS filters are made up of both positive and negative constituents. Thus, the spectra from some conventional tomosynthesis planes are added, while others are subtracted to generate the final MITS solution. The impact of the noise correlation across a stack of conventional tomosynthesis planes, coupled with varying polarity in the MITS filters, makes the prediction of noise in MITS images less than trivial.
The results of the current study suggest the following actual correlations between exposure-normalized noise power spectra and tomosynthesis scan parameters using real projection data with correlated stochastic noise.
ENNPS in projection data and conventional tomosynthesis planes
The fact that the ENNPS in raw projection images does not vary with N (Fig. 4) implies that even for the low exposures associated with large N, the level of baseline electronic noise in the detector is insignificant compared to x-ray quantum noise. Thus, selecting N=71 (the optimal setting from our previous system response analysis) appears to incur no noticeable noise penalty in projection data acquired with the detector used in this study.
It is worth noting that the ENNPS in raw projection images acquired at the top of the scan motion is slightly (∼5%) lower than that in images acquired at the center location (Fig. 5), which indicates that the detected radiation is reduced with source angulation. This is easily explained by the longer attenuation path through the tissue-simulating plastic, as well as a slightly larger source-to-imaging distance at wide-angle projection locations.
Somewhat surprisingly, the simple shifting and adding of projection data to form conventional tomosynthesis planes appears to have a noticeable effect on the shape of the ENNPS curves. A comparison of conventional tomosynthesis ENNPS curves in Figs. 78 with the ENNPS of log-transformed projection data in Fig. 6 confirms that all conventional tomosynthesis planes show substantially reduced noise magnitude at the mid and high spatial frequencies (above ∼0.15 cycle∕mm) compared to log-transformed projection images. However, anterior conventional tomosynthesis planes, as well as planes generated with large N or small ANG, generally exhibit substantially increased noise at the lowest spatial frequencies (below ∼0.15 cycle∕mm). Furthermore, central and posterior conventional tomosynthesis planes often display small noise spikes (still of lower magnitude than the ENNPS trend line for log-transformed projection data) at the mid and high frequencies, and this noise is enhanced by the use of small N or large ANG.
The likeliest explanation for the observed ENNPS trends in Figs. 78 is that low-frequency noise peaks in conventional tomosynthesis data are indicative of spatially correlated noise across multiple projection images, while the general suppression of mid- and high-frequency noise results from averaging that is performed during non-integer image shifts. The size of the relative shift of projection images when creating conventional tomosynthesis (shift-and-add) planes is proportional to ANG and the plane-to-detector distance and inversely proportional to N. Thus, from the ENNPS curves in Figs. 78, we conclude that small relative shifts of projection data generate a buildup in noise at the lowest spatial frequencies (below ∼0.15 cycle∕mm), while large relative shifts lead to small magnitude noise spikes in mid and high spatial frequencies in conventional tomosynthesis planes. The number of reconstructed planes has no impact on the ENNPS in conventional tomosynthesis planes, as each plane is reconstructed independent of NP.
ENNPS in MITS: General noise characteristics in MITS planes
Figure 9 shows that noise in MITS reconstructions is generally of the same magnitude as noise in conventional tomosynthesis planes (Figs. 78) for spatial frequencies above ∼0.5 cycle∕mm. It is also evident that the frequency blending performed for low-frequency noise suppression [Eq. 1] may be more aggressive than necessary at the very lowest spatial frequencies, as there is substantially less noise evident below 0.15 cycle∕mm in frequency-blended MITS planes than in conventional tomosynthesis images.
Furthermore, in Fig. 10 it is apparent that only 7 out of 69 MITS planes reconstructed with the previously defined optimal setting (ANG=20°, N=71, and NP=69) exhibit any substantial noise amplification relative to conventional tomosynthesis reconstructions, and these were only the most anterior and posterior planes in the reconstruction set. Conventional tomosynthesis planes were also shown to exhibit low-frequency noise enhancement in the most anterior planes (Fig. 8), and this may be the cause of the noise enhancement in the anterior MITS planes. However, it is not understood why MITS would also enhance noise in the posterior planes, as this is not predicted by the magnitude of the MITS filters for those planes. We can only surmise that some combination of the noise correlation across the stack of conventional tomosynthesis planes along with the varying polarity of the MITS filters is likely to be the cause of this observation. To avoid this noise, it may be possible to either expand the reconstruction volume such that the noisy planes fall outside our region of interest, or to perform adaptive frequency blending, such that the central planes are left with more of the original MITS low frequencies. Both possibilities are being investigated as a solution to this problem.
ENNPS in MITS: Effect of number of projections (N)
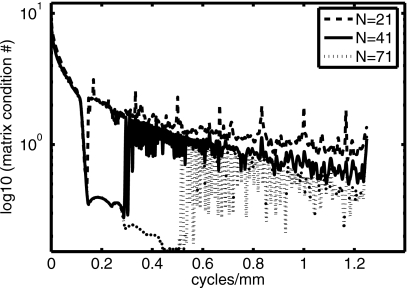
Figure 9 shows that when N is small, there is notable amplification of MITS noise for spatial frequencies between 0.15 and 0.5 cycle∕mm. This likely results from the fact that the MITS matrix conditioning gets worse as N decreases (large matrix condition numbers equate to large MITS filter values and thus more noise enhancement), as shown in the plot below.
The matrix conditioning trends in Fig. 13 suggest that MITS noise at frequencies above 0.15 cycle∕mm is expected to decrease with increasing N, and the effect is particularly pronounced for frequencies of 0.15–0.5 cycle∕mm, matching the experimental results seen in the ENNPS plots in Fig. 9.
Figure 13.
Plot of the logarithm of the MITS matrix condition number, as a function of vertical spatial frequency, for ANG=20°, NP=19, PSEP=16.7 mm, and varying N (N=21, 41, and 71).
ENNPS in MITS: Effect of scan angle (ANG)
Figure 12 suggests that increasing ANG actually results in a moderate enhancement of noise in MITS planes for spatial frequencies between 0.2 and 0.8 cycle∕mm. The mechanism for this enhancement is unclear, as it runs counter to what we would expect from a linear systems analysis of MITS. To illustrate the point, a plot of the sum of the square of the magnitude of the MITS filters as a function of spatial frequency is shown in Fig. 14 for varying ANG.
Figure 14.
Plot of the sum of the square of the MITS filter magnitudes, as a function of vertical spatial frequency, for N=71, NP=69, PSEP=4.4 mm, and varying ANG (ANG=10°, 15°, and 20°).
It can be seen that linear systems theory predicts that MITS noise at frequencies below 0.8 cycle∕mm should decrease with increasing ANG for uncorrelated noise input. The fact that the MITS ENNPS in this region actually increases with increasing ANG suggests that noise correlation in the conventional tomosynthesis data plays a substantial role in determining the MITS noise characteristics.
ENNPS in MITS: Effect of number of reconstructed planes (NP)
The effect of NP on noise in MITS reconstructions is also difficult to decipher. For N=71 (our previously selected optimum), we see in Fig. 11 that low-frequency noise worsen a bit as NP is raised from 19 to 39, but actually improves as NP is raised from 39 to 69. This result runs counter to the notion that MITS noise should increase as NP increases due to degraded matrix conditioning. A plot of the sum of the square of the MITS filters is displayed Fig. 15, suggesting that MITS noise should worsen with increasing NP when noise in the conventional tomosynthesis planes is uncorrelated.
Figure 15.
Plot of the sum of the square of the MITS filter magnitudes, as a function of vertical spatial frequency, for ANG=20°, N=71, and varying NP (NP=19, PSEP=16.7 mm; NP=29, PSEP=10.7 mm; NP=39, PSEP=7.9 mm; NP=49, PSEP=6.25 mm; NP=59, PSEP=5.2 mm; and NP=69, PSEP=4.4 mm).
The fact that the measured trends conflict with the trends predicted by a linear systems analysis suggests that noise correlation also plays a substantial role in governing MITS noise power as a function of NP.
CONCLUSIONS
We believe that the differences between predicted MITS noise trends based upon matrix conditioning alone and our actual experimental observations are most likely due to interactions between the MITS inverse filters and the correlation of noise from plane-to-plane within the initial conventional tomosynthesis reconstructions. Plane-to-plane noise correlation in conventional tomosynthesis images results from the fact that all of the reconstructed planes are formed from the same set of projection images, differing only in the shifts applied during the shift-and-add process. The small scan angles used in tomosynthesis result in only small shifts during the shift-and-add reconstruction, and thus noise in the image tends to be correlated across any set of conventional tomosynthesis planes. This is potentially further enhanced by noise correlation across the set of initial projection images. If the noise in each conventional tomosynthesis plane was instead uncorrelated with that in other planes, then matrix conditioning would suggest that noise would decrease in MITS images as NP decreased and ANG increased. The fact that we noted the opposite effects suggests an interplay between the MITS filter functions and the correlation of noise from plane to plane as these parameters are changed.
We concluded in our previous study11 that the optimal MITS imaging technique for chest imaging uses the parameter settings ANG=20°, N=71, and NP=69. However, these results were determined from a purely deterministic impulse response analysis and did not consider the impact of the scan parameters on stochastic noise in MITS planes. The results of the current study suggest that while selecting N=71 and NP=69 (the maximum values determined by clinical constraints) conveniently does minimize the stochastic noise in MITS images, the selection of a 20° scan angle appears to incur slightly more stochastic noise in the range of 0.2–0.8 cycle∕mm than narrower scan angles. Thus, the optimum technique according to deterministic figures of merit is close to the optimum determined according to stochastic measures, differing only in the selection of the scan angle. From Fig. 12, it can be seen that ANG=20° leads to roughly a 50% increase in the peak ENNPS compared to selecting ANG=5°. Unfortunately, ANG is also the parameter that most substantially impacts the MITS depth-resolution characteristics (i.e., slice thickness), and the full width at half maximum of the MITS impulse response function in the plane-to-plane dimension was shown in our previous work11 to increase from ∼4 to ∼11 mm when ANG was decreased from 20° to 5°. As we are especially interested in improving the detection of subtle nodules of the order of 5 mm in diameter that are often unseen in 2D chest radiographs, the volume averaging created by using a narrow scan angle is likely too great a price to pay for slightly improved stochastic noise characteristics.
This reasoning is further supported by a study showing that structured noise is a much greater impediment than stochastic noise for many detection tasks, including the detection of subtle pulmonary nodules.15 Thus, maintaining a large scan angle is likely necessary for the task of detecting subtle pulmonary nodules in MITS images, and we believe that the noise penalty incurred by selecting ANG=20° is not likely substantial enough to argue against the improvement in slice thickness that a 20° scan provides for MITS imaging of the chest. This conclusion is supported by our preliminary clinical experience as well: 20° clinical MITS chest data acquired at our institution during a 21 subject MITS pilot study generally appeared to exhibit acceptable stochastic noise characteristics when the MITS scan exposure was held equivalent to that of a lateral film-screen radiograph.10
Although we have chosen to not to change our standard MITS chest imaging technique based upon the results of this study, we do believe that the MITS stochastic noise trends reported in this paper will be of use for a variety of MITS imaging tasks, such as orthopedic imaging,16 and will also provide helpful guidance for select cases of MITS chest imaging where the detection task appears to be stochastic noise limited (e.g., for large patients or for the detection of nodules in the mediastinum). The results presented here are especially valuable, given that the MITS noise trends often contradict those predicted by a simple linear system theory analysis, and the effort required for a true noise power analysis, such as this one, is substantial. Furthermore, certain noise characteristics observed in the projections (e.g., low exposure images do not exhibit enhanced noise) and conventional tomosynthesis planes (e.g., low-frequency noise is enhanced when shifts of projection data are small) are likely to be applicable to anyone investigating noise in tomosynthesis images, regardless of the reconstruction algorithm they use.
Finally, we expect the results of this study to be useful as we seek to determine the optimum dose needed for pulmonary nodule detection in MITS images, as well as for future comparisons of different tomosynthesis reconstruction algorithms.
ACKNOWLEDGMENTS
This work was supported in part by grants from the National Institutes of Health (Grant No. RO1 CA80490) and G. E. Medical Systems. Duke University and GE Healthcare jointly own a patent on the tube movement strategies in tomosynthesis.
References
- J. T.DobbinsIII and Godfrey D. J., “Digital x-ray tomosynthesis: Current state of the art and clinical potential,” Phys. Med. Biol. 10.1088/0031-9155/48/19/R01 48, R65–R106 (2003). [DOI] [PubMed] [Google Scholar]
- Ziedses des Plantes B. G., “Eine neue methode zur differenzierung in der roentgenographie (planigraphie),” Acta Radiol. (1921–1962) 13, 182–192 (1932). 10.3109/00016923209135135 [DOI] [Google Scholar]
- Grant D. G., ““Tomosynthesis: A three-dimensional radiographic imaging technique,” IEEE Trans Biomed. Eng. 19, 20–28 (1972). 10.1109/TBME.1972.324154 [DOI] [PubMed] [Google Scholar]
- J. T.DobbinsIII, Powell A. O., and Weaver Y. K., “Matrix inversion tomosynthesis: Initial image reconstruction,” RSNA 73rd Scientific Assembly, Chicago, Illinois, 1987. (unpublished).
- J. T.DobbinsIII, US Patent No. 4,903,204 (February 20, 1990).
- Warp R. J., Godfrey D. J., and J. T.DobbinsIII, “Applications of matrix inverse tomosynthesis,” Proc. SPIE 10.1117/12.384512 3977, 376–383 (2000). [DOI] [Google Scholar]
- Godfrey D. J., Warp R. J., and J. T.DobbinsIII, “Optimization of matrix inverse tomosynthesis,” Proc. SPIE 10.1117/12.430908 4320, 696–704 (2001). [DOI] [Google Scholar]
- J. T.DobbinsIII, Godfrey D. J., and McAdams H. P., in Advances in Digital Radiography: RSNA Categorical Course in Digital Radiography, edited by Samei E. and Flynn M. J. (Radiological Society of North America, Oak Brook, 2003). [Google Scholar]
- Godfrey D. J., Rader A., and J. T.DobbinsIII, “Practical strategies for the clinical implementation of matrix inversion tomosynthesis (MITS),” Proc. SPIE 10.1117/12.480352 5030, 379–390 (2003). [DOI] [Google Scholar]
- J. T.DobbinsIII, McAdams H. P., Song J. W., Li C. M., Godfrey D. J., DeLong D. M., Paik S. H., and Martinez-Jimenez S., “Digital tomosynthesis of the chest for lung nodule detection: Interim sensitivity results from an ongoing NIH-sponsored trial,” Med. Phys. 10.1118/1.2937277 35, 2554 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Godfrey D., McAdams H. P., and J. T.DobbinsIII, “Optimization of the matrix inversion tomosynthesis (MITS) impulse response and modulation transfer function characteristics for chest imaging,” Med. Phys. 10.1118/1.2170398 33, 655–667 (2006). [DOI] [PubMed] [Google Scholar]
- J. T.DobbinsIII, “Image quality metrics for digital systems,” in Handbook of Medical Imaging, Physics and Psychophysics Vol. 1, edited by Beutel J., Kundel H. L., and Van Metter R. L. (SPIE, Bellingham, 2000), Chap. 3. [Google Scholar]
- Siewerdsen J. H., Cunningham I. A., and Jaffray D. A., “A framework for noise-power spectrum analysis of multidimensional images,” Med. Phys. 10.1118/1.1513158 29, 2655–2671 (2002). [DOI] [PubMed] [Google Scholar]
- J. T.DobbinsIII, Ergun D. L., Rutz L., Hinshaw D. A., Blume H., and Clark D. C., “DQE(f) of four generations of computed radiography acquisition devices,” Med. Phys. 10.1118/1.597627 22, 1581–1593 (1995). [DOI] [PubMed] [Google Scholar]
- Samei E., Flynn M. J., and Eyler W. R., “Detection of subtle lung nodules: Relative influence of quantumand anatomic noise on chest radiographs,” Radiology 213, 727–734 (1999). [DOI] [PubMed] [Google Scholar]
- Duryea J., J. T.DobbinsIII, and Lynch J. A., “Digital tomosynthesis of hand joints for arthritis assessment,” Med. Phys. 10.1118/1.1543573 30, 325–333 (2003). [DOI] [PubMed] [Google Scholar]