Abstract
Segmentation is one of the first steps in most computer-aided diagnosis systems for characterization of masses as malignant or benign. In this study, the authors designed an automated method for segmentation of breast masses on ultrasound (US) images. The method automatically estimated an initial contour based on a manually identified point approximately at the mass center. A two-stage active contour method iteratively refined the initial contour and performed self-examination and correction on the segmentation result. To evaluate the method, the authors compared it with manual segmentation by two experienced radiologists (R1 and R2) on a data set of 488 US images from 250 biopsy-proven masses (100 malignant and 150 benign). Two area overlap ratios (AOR1 and AOR2) and an area error measure were used as performance measures to evaluate the segmentation accuracy. Values for AOR1, defined as the ratio of the intersection of the computer and the reference segmented areas to the reference segmented area, were 0.82±0.16 and 0.84±0.18, respectively, when manually segmented mass regions by R1 and R2 were used as the reference. Although this indicated a high agreement between the computer and manual segmentations, the two radiologists’ manual segmentation results were significantly (p<0.03) more consistent, with AOR1=0.84±0.16 and 0.91±0.12, respectively, when the segmented regions by R1 and R2 were used as the reference. To evaluate the segmentation method in terms of lesion classification accuracy, feature spaces were formed by extracting texture, width-to-height, and posterior shadowing features based on either automated computer segmentation or the radiologists’ manual segmentation. A linear discriminant analysis classifier was designed using stepwise feature selection and two-fold cross validation to characterize the mass as malignant or benign. For features extracted from computer segmentation, the case-based test Az values ranged from 0.88±0.03 to 0.92±0.02, indicating a comparable performance to those extracted from manual segmentation by radiologists (Az value range: 0.87±0.03 to 0.90±0.03).
Keywords: computer-aided diagnosis, mass segmentation, mass characterization, active contour, ultrasonography, breast mass
INTRODUCTION
Ultrasonography (US) has been shown to be an effective modality for characterizing breast masses as malignant or benign.1, 2, 3 Stavros et al.1 achieved a sensitivity of 98.4% and a specificity of 67.8% by use of sonography to distinguish 750 benign and malignant lesions. Taylor et al.4 demonstrated that the combination of US with mammography increased the specificity from 51.4% to 63.8%, the positive predictive value from 48% to 55.3%, and the sensitivity from 97.1% to 97.9% in characterizing 761 breast masses.
Studies have shown that computer-aided diagnosis (CAD) can assist radiologists in making correct decisions by providing an objective and reproducible second opinion.5, 6, 7, 8 Accordingly, CAD systems have been developed to characterize breast masses on US images as malignant or benign. Chenet al.9 used the autocorrelation feature extracted from regions of interest (ROIs) containing the mass in an artificial neural network (ANN) to classify 140 pathologically proven solid nodules on US images. The area Az under the receiver operating characteristic (ROC) curve was 0.96. Horsch et al.10 evaluated their CAD system on a database of 400 cases. The average Az value of 11 independent experiments was of 0.87. Sahiner et al.11 investigated the computerized characterization of breast masses on 3D US volumetric images. By analyzing 102 biopsy-proven masses, they achieved an Az value of 0.92. Joo et al.12 segmented the masses in a preselected ROI using an automated algorithm. An experienced radiologist reviewed and corrected the segmentation result, from which five morphological US features were extracted. An ANN classifier was used to characterize the masses. Their classifier was developed based on 584 histologically confirmed cases and was tested on an independent data set of 266 cases. The test Az value was 0.98.
In most CAD systems, lesion segmentation is one of the first steps. In US images of breast masses, speckles, posterior acoustic shadowing, heterogeneous image intensity inside the mass, indistinct mass boundary, and line structures caused by reverberation pose difficulties to segmentation. Several research groups have proposed automated or semiautomated methods for segmenting masses on US images and compared the computer segmentation with manual segmentation. Chow and Huang13 used watershed transform and active contour (AC) model to automatically segment mass boundaries. An area overlap ratio (AOR1) was defined as the ratio of the intersection area of the computer and manual segmentations to the area of the manual segmentation. On an ultrasonic data set containing 7 benign and 13 malignant breast masses, their method achieved an average AOR1 of 0.81. In the method developed by Horsch et al.,14 after preprocessing, potential lesion margins were determined through gray-value thresholding, and the lesion boundaries were determined by maximizing a utility function on the potential lesion margins. An area overlap ratio (AOR2) was defined as the ratio of the intersection area of the computer and manual segmentations to the area of the union of the two. Their automated algorithm correctly segmented 94% of the lesions in 757 images, where correct segmentation was defined as an AOR2 of 0.4 or higher. Madabhushi and Metaxas15 developed an automated method to segment ultrasonic breast lesions, which combined intensity and texture with empirical domain specific knowledge along with directional gradient and a deformable shape-based model. In a data set of 42 US images, their method achieved an average true-positive fraction of 75.1% and a false-positive fraction of 20.9% when compared to manual segmentation. A semiautomated mass segmentation method based on region growing was proposed by Sehgal et al.16 On a data set of 40 malignant and 40 benign masses, the mean AOR2 was 0.69±0.39 by using manual segmentation as gold standard.
Sahiner et al.11 developed an AC method to segment breast masses on 3D US volumetric images, in which a 3D ellipsoid drawn by a radiologist was used as an initialization for the AC model. Our previous studies11 indicated that a properly initialized AC model was able to adequately delineate the mass boundary. However, the performance of the AC segmentation depended on the proper estimation of an initial contour. In the current study, we propose a new method to segment breast masses on 2D US images. This method automatically estimates an initial contour for the AC model based on a manually identified point approximately at the mass center, referred to as initialization point below. A two-stage AC method iteratively refined the initial contour and performed self-examination and correction on the segmentation result, which reduced the dependence of the performance of the AC model on initialization. In this new method, we specifically addressed how to overcome the difficulties in segmentation of breast masses on US images such as shadowing, heterogeneous image intensity inside the mass, and line structures caused by reverberation. To evaluate the accuracy of the method, we compared the computer segmentation to two radiologists’ manual delineation. We also examined the sensitivity of the method to the variation of the initialization point by evaluating the segmentation performance when the initialization point was moved to the vicinity of the radiologists’ initialization point. The goal of our CAD system is to characterize the mass as malignant or benign. To evaluate the effect of the automated segmentation on our mass CAD system, the classification accuracy based on feature spaces extracted from computer segmentation and manual segmentation and the classification accuracy of radiologists’ visual assessment for likelihood of malignancy (LM) were compared.
MATERIALS AND METHODS
Figure 1 illustrates the flowchart of the segmentation method. Based on the initialization point, an ROI which contained the mass approximately at the center was automatically extracted. The ROI image was then multiplied with an inverse Gaussian function to suppress the heterogeneous image intensity inside the mass. Next, a preliminary mass region was separated from the background by k-means clustering. If the preliminary mass region extended to the ROI border, background correction was performed on the ROI image to improve the separation between the mass region and the background. The above steps were then repeated again on the background-corrected image to separate an improved preliminary mass region. The preliminary mass region was used as the initial contour for the AC model. To reduce the dependence of the performance of the AC model on initialization, a two-stage AC segmentation was implemented. If the outcome of the first-stage AC met a predefined criterion, it was used as the final result. Otherwise, it was automatically adjusted, and the second-stage AC was performed using the adjusted contour as initialization. Depending on an automated evaluation criterion, the final segmentation result was selected as the resulting contour of either the first-stage or the second-stage AC.
Figure 1.
Flowchart of the new segmentation method.
Data set
A data set was collected with institutional review board (IRB) approval from the files of patients who had undergone breast US imaging in the Department of Radiology at the University of Michigan. All US images were acquired using a GE Logiq 700 scanner with an M12 linear array transducer. For this study, 100 malignant and 150 benign masses from 250 patients were obtained from our malignant and benign databases, respectively, which were consecutively collected. The pathology of all masses was biopsy proven. The average patient age was 52 years (range: 14–95 years). A total of 488 US images depicting these masses were selected as described below. The average mass size, measured as the largest diameter, was 9.2 mm (range: 1.8–37.0 mm). The average pixel size was 103 μm (range: 75–183 μm).
We randomly partitioned the patient cases into two subsets T1 and T2, which included 129 and 121 masses, respectively. For the set T1, after reading the pathology and radiology reports, an experienced radiologist (R1) selected images corresponding to the biopsy-proven mass. The radiologist was asked to select two orthogonal US views for each mass. However, for some masses two orthogonal views were not available, and only one view was selected. In each image, the radiologist identified the approximate center of the mass, measured the mass size in two orthogonal directions, manually outlined the mass using a graphical user interface, and provided an LM rating, as described in more detail below. A second radiologist (R2) followed the same procedure to select and read images in the set T2. T1 included 258 images from 56 malignant and 73 benign masses, and T2 included 231 images from 44 malignant and 77 benign masses.
After finishing the assigned set, each radiologist read the images (identified mass center, measured mass size, manually segmented the mass, and provided LM rating) selected by the other radiologist without accessing the pathology and radiology reports. That is, R1 read images selected by R2 from T2 and R2 read images selected by R1 from T1. In this manner, both radiologists read all of the selected images. One image from set T2 contained two masses, and the two radiologists read different masses. This image was excluded and our final data set T2 included 230 images. The approximate mass center identified by the two radiologists were used for computer segmentation, which was the only manual input required for the segmentation method.
The LM rating scale covered the range of 0%–100% likelihood of malignancy. Because the LM estimate has large variations and the 1% increment far exceeds the reproducibility of the reader ratings,17 we divided the scale into 12 discrete levels. An LM rating of 1 (0%) was reserved for a definitely benign mass. Ratings of 2 and 3 represented masses with <2% likelihood of malignancy and between 2% and 14% likelihood of malignancy, respectively. LM ratings of between 4 and 11 represented likelihood of malignancy between 15% and 94%, with increments of 10% at each step. An LM rating of 12 was reserved for masses with a likelihood of malignancy >94%. The finer divisions at the low and high ends of the scale were selected because of the significance of the probably benign (2% threshold) and the highly suggestive (>94%) assessments according to BI-RADS. The distribution of the LM ratings provided by the two radiologists for all masses in each image are plotted in Figs. 2a, 2b, respectively. Some malignant masses were given low LM ratings while some benign masses were rated as highly likely to be malignant, indicating that many of the masses may not have the typical characteristics of malignant or benign masses. A bubble scatter plot of R1’s and R2’s LM ratings is shown in Fig. 3. The figure indicates that R1’s and R2’s LM ratings have high correlation.
Figure 2.
Distribution of LM ratings provided by (a) R1 and (b) R2.
Figure 3.
The correlation between LM ratings of R1 and R2.
Automated ROI extraction
In order to extract from the original US image an ROI image which contained the mass approximately at the center, we estimated the initial boundary points of the mass by searching for the largest gradient points surrounding the mass center. The original image was first smoothed by convolving with a Gaussian filter (σ=1.5 pixels) to remove noise. Let (cx,cy) denote the coordinate of the initialization point in the original image. Starting from (cx,cy), L radial lines at equal angular increments were generated, as shown in Fig. 4. Let p=(xr,l,yr,l) denote a point on the lth radial line where r is the distance between the point and (cx,cy). The gradient g(xr,l,yr,l) was calculated as the difference of the average image intensity in two approximately 11×11 pixel square regions S1 and S2, one on each side of (xr,l,yr,l), and with an orientation determined by the lth radial line as shown in Fig. 4,
| (1) |
where and represent the average image intensities in the square regions S1 and S2 of the smoothed image, respectively. The distance of S1 to the initialization point is larger than that of S2. The gradient is expected to be large and positive when (xr,l,yr,l) is on the mass boundary.
Figure 4.
Radial lines (l=1,2,…,L) and rings generated to estimate the initial mass boundary points. The ring Γk is shaded in gray. The gradient at point p=(xr.l,yr,l) is approximated by the difference of the gray levels in two squares S1 and S2.
In US images, some breast structures or line structures caused by reverberation may have strong edges. If we simply take the maximum gradient point along each radial line as the initial mass boundary point, those points with high gradient but not on the mass boundary may be detected. In order to reduce the chance of choosing spurious high gradient points as initial mass boundary points, we designed a method, described below, to search for the highest total gradient strength among annular regions of various sizes and shapes surrounding the mass. A region with the highest total gradient strength would most likely contain the largest number of mass boundary points, thus mitigating the effect of individual high gradient nonboundary points.
A sequence of concentric rings Γk centered at the initialization point was defined to constrain the region for searching the largest gradient points along the radial lines (Fig. 4). In a given ring Γk, the maximum gradient gmax(k,l) along each radial line l was found by moving p along l within Γk. The gradient strength Gk in the ring Γk was defined as the sum of gmax(k,l) over L radial lines:
| (2) |
The ROI containing the mass was defined based on the ring Γk that had the highest gradient strength Gk, as described below in more detail.
The search region constrained by the ring Γk on the lth radial line was represented by the start radius rstart(k,l) and the end radius rend(k,l) which are the distances from the mass center to the inner rim and outer rim of the ring on the lth radial line, respectively. The relationship between rstart(k,l) and rend(k,l) was defined as
| (3) |
where Rrange=30 pixels in our implementation. To define different rings covering different mass shapes, the start radius was initialized using an ellipse with long axis a and short axis b,
| (4) |
and then was varied iteratively by
| (5) |
The corresponding end radius for the (k+1)th ring was calculated using Eq. 3. The iteration continues until one of the end radii rend(k,l), l=1,2,…,L, reached the border of the image. The value of Δr was chosen as 6 pixels after experimenting with a range of pixels. Two consecutive rings therefore overlapped by 24 pixels radially.
We used different initializations for the start radius by varying the long axis a and short axis b. First, a was fixed at r0 and b was varied as r0,2r0,3r0… until the end radius reached the border of the image. Then, b was fixed at r0 and a was varied as r0,2r0,3r0… until the end radius reached the border of the image. The value of r0 was set to 6 pixels. Different pairs of a and b defined different ellipse shapes for the initialization of the start radius. When a=b=r0, the shape of the ring is circular.
After the ring that had the highest gradient strength was obtained by comparing the gradient strength Gk over all rings for a given pair of a and b and over all pairs of a and b, the maximum gradient points along the radial lines in that ring were regarded as the estimated initial mass boundary points. Based on these estimated boundary points, an ROI image R(i,j) (i∊[1,w] and j∊[1,h]) was extracted from the original image. The dimensions of the ROI, width w and height h, were estimated as the smallest rectangle containing all initial mass boundary points with slight expansion in all directions in order to include the mass margins within the ROI image. The amount of the expansion was chosen to be 30% of the size of the rectangle. Figures 56 show two examples, in which (a), (b), and (c) show the original image, estimated initial mass boundary points, and defined ROI region, respectively. In these two examples, R1’s initialization point was used for computer segmentation.
Figure 5.
Segmentation example of an irregular malignant mass: (a) original image; (b) estimated initial mass boundary points (marked by •) using R1’s initialization point (marked by x); (c) estimated ROI region; (d) extracted ROI after being multiplied by an inverse Gaussian function; (e) preliminary mass region resulting from clustering and object selection; (f) ROI image after background correction; (g) refined preliminary mass region contour which was used as initialization of AC segmentation; (h) first-stage AC segmentation; (i) adjusted contour; (j) second-stage AC segmentation which was chosen as final computer segmentation; (k) R1’s manual segmentation; (l) R2’s manual segmentation.
Figure 6.
Segmentation example of a spiculated malignant mass: (a) original image; (b) estimated initial mass boundary points (marked by •) using R1’s initialization point (marked by x); (c) estimated ROI region; (d) extracted ROI after being multiplied by an inverse Gaussian function; (e) preliminary mass region resulting from clustering and object selection; (f) ROI image after background correction; (g) refined preliminary mass region contour which was used as initialization of AC segmentation; (h) first-stage AC segmentation; (i) adjusted contour; (j) second-stage AC segmentation which was chosen as final computer segmentation; (k) R1’s manual segmentation; (l) R2’s manual segmentation.
Separation of preliminary mass region
The heterogeneous image intensity inside the mass makes it difficult to separate a preliminary mass region from the background directly by clustering. To suppress the heterogeneous intensity inside the mass, we multiplied the ROI image with an inverse Gaussian function:
| (6) |
where
and is the radiologist’s initialization point in the ROI image. The width of the Gaussian function in the horizontal and vertical directions depended on σx and σy, which were determined by the width and height of the ROI image,
| (7) |
Next, k-means clustering18 was applied to RG(i,j) which resulted in one or several disjoint objects. Morphological filtering19 and object selection were then operated on the binary image as follows: Closing (circular structuring element with a radius of 3 pixels) was first implemented to connect white pixels and smooth object boundary. Hole filling was then applied to fill holes in objects, and erosion (circular structuring element with a radius of 5 pixels) was employed to cut off additional structures from the main objects. Object selection was performed by removing small objects and objects with a centroid-to-ROI center distance larger than one-quarter of the ROI width or height and then finding the largest remaining object. Dilation operation (circular structuring element with a radius of 5 pixels) was performed on the selected object, the result of which was the preliminary mass region. Figures 5d, 6d show examples of the inverse-Gaussian-filtered image RG(i,j), and Figs. 5e, 6e show the objects selected as the preliminary mass region.
The preliminary mass region obtained above was expected to be contained within the ROI. However, in some cases, the preliminary mass region extended to the ROI border, as shown in the examples in Figs. 5e, 6e. One possible reason for this was extensive posterior or side shadowing. Using the preliminary mass region containing shadowing as initialization for AC segmentation might result in an inaccurate segmentation. Therefore, the preliminary mass region was automatically checked. If it extended to the ROI border, background correction was performed by utilizing an exponential mask to increase the image intensity near the border of the original ROI image and thus to improve the separation between the mass region and the background. The exponential mask was defined as
| (8) |
in which C0 and λ(i,j) depended on which border of the ROI the preliminary mass region extended to. For example, if the preliminary mass region extended to the bottom of the ROI, C0 was the average image intensity in a rectangular region at the bottom of the ROI and λ(i,j)=(h−j)∕(h∕d0). We chose d0=20 through empirical study. The mask was designed to increase the brightness at the bottom of the ROI, and the amount of added brightness decreased exponentially toward the top of the ROI. Background correction with an exponential mask was intended to improve the separation between the preliminary mass region and the background not only in case of shadowing but whenever the initial clustering resulted in an oversegmented boundary that extended to any of the four borders of the ROI. The expressions of C0 and λ(i,j) were computed similarly for the conditions in which the preliminary mass region extended to the top, left, or right borders of the ROI by replacing (h−j) in the numerator with the distance from the respective border. Figures 5f, 6f show examples of the background-corrected images. After background correction, the above steps (multiplication with inverse Gaussian, clustering, closing, hole filling, erosion, object selection, and dilation) were repeated on the background-corrected ROI image to extract a refined preliminary mass region. Examples of the contour of the refined preliminary mass region are shown in Figs. 5g, 6g.
Two-stage active contour segmentation
The AC model is a high-level segmentation method that locates the object boundary by minimizing an energy function.20 To accurately segment the object, the energy terms include external energy terms, which are usually defined in terms of the image gray levels and the image gradient magnitude, and internal energy terms relating to features such as the continuity and the smoothness of the object contour. The internal energy terms can compensate for noise or apparent gaps in the image gradient, which may mislead segmentation methods that do not include such terms. The minimization of the energy function is usually an iterative process. It starts from an initial contour and iteratively updates the contour by minimizing the energy function. In our implementation, the object contour was represented by a set of vertices. The energy of the contour was the sum of the energy of each vertex. The energy function was a linear combination of four terms: gradient magnitude, continuity, curvature, and balloon energy. At a given iteration, a neighborhood of each vertex was examined and the vertex moved to the point that minimized the energy function. Details of the AC segmentation method and our implementations can be found in the literature.11, 20, 21, 22
Our previous studies indicated that the performance of the AC segmentation depends on the initialization of the model. If the initialization is far away from the mass boundary, the AC segmentation may not be able to completely locate the mass boundary. Two examples are shown in Figs. 56. In Fig. 5, the initialization of the AC model [Fig. 5g] is far away from the mass boundary and the AC segmentation fails to locate the mass boundary, as shown in Fig. 5h. Figure 6 shows that, with a proper initialization [Fig. 6g], the AC model was able to move the initial contour close to the true mass boundary [Fig. 6h].
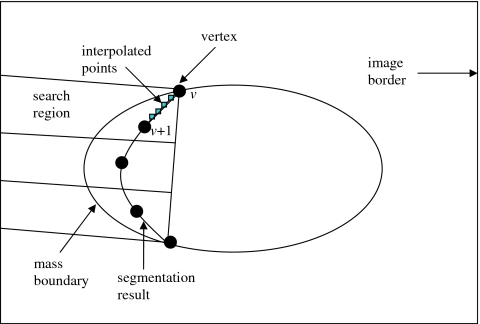
To reduce the dependence of the performance of the AC segmentation on initialization, a two-stage AC segmentation was proposed. The first-stage AC used the contour of the preliminary mass region as an initialization for the object contour. The result of the AC segmentation was examined according to a criterion, which was defined on the basis of the image intensity gradient magnitude along the resulting contour. Let (iv,jv) denote vertices of the first-stage AC result, where v=1,2,…,V and V is the total number of vertices. At each vertex v, the average image gradient magnitude of v and four interpolated points between the v and v+1 were computed and denoted as uv. The gradient magnitude was calculated using the method developed in our previous work.11 The mean and the standard deviation of uv (v=1,2,…,V), and σgrad, were calculated. If vertices v and v+1 were close to the mass boundary, the value of uv was expected to be high. If the resulting contour located most part of the mass boundary but missed several small portions, the values of uv for vertices on these small portions would be lower than that of vertices near the mass boundary. Hence, we examined uv for each vertex and locally adjusted those neighboring vertices whose uv were less than a threshold. In our implementation, at each vertex v, uv was compared to. If three or more neighboring vertices were found to have a uv less than , the vertices corresponding to these points were moved to minimize a simplified energy function, which contained only two terms, the gradient magnitude energy and the curvature energy, while other vertices were fixed. The definitions of these energy terms were the same as those in our previous implementation.11 If there were less than three neighboring vertices with uv less than or the vertices did not neighbor to each other, these vertices were not moved. For each vertex requiring adjustment, we defined a search region in which we searched for the point that minimized the energy function and moved the vertex to that point. As shown in Fig. 7, the search region for each vertex was a rectangular region normal to the line segment between the two ends of the string of vertices that needed adjustment and constrained by the image border. After these local adjustments, a second-stage AC segmentation was performed using the adjusted contour as initialization. The image intensity gradient magnitude along the first- and the second-stage AC boundaries were compared. The one with higher average gradient magnitude along the contour was chosen as the final result.
Figure 7.
The adjustment of the first-stage AC segmentation result.
Figures 5i, 6i show examples of the adjusted contour after the first-stage AC segmentation. In Fig. 5i, the contour was adjusted because some segments were away from the mass boundary and exhibited low gradient magnitude. It can be observed that the adjustment moved the vertices with low gradient magnitude close to the mass boundary that had a higher gradient magnitude. In Fig. 6i, the lower right corner of the contour was adjusted because it had low gradient magnitude due to shadowing. Figures 5j, 6j show the result of the second-stage AC segmentation. In both cases, the second-stage AC segmentation was chosen as the final segmentation result. For comparison, Figs. 5k, 6k show R1’s manual segmentation, and Figs. 5l, 6l show R2’s manual segmentation.
Feature extraction and classification
It is difficult to have ground truth for lesion segmentation because it is cost prohibitive to correlate boundaries seen on pathological slides with those seen on images. Radiologists’ manual segmentation provides a reference standard but it involves subjective judgment and intra- and interobserver variations. Alternatively, since the main purpose of segmentation in CAD is to extract features for lesion characterization, the classification accuracy and consistency can be used as criteria to determine if the segmentation is adequate. To investigate the performance of mass characterization, we extracted texture, width-to-height, and posterior shadowing features based on the computer segmentation and manual segmentation by radiologists. The extraction methods for these features have been described in detail previously.11 A linear discriminant analysis (LDA) (Ref. 23) classifier with stepwise feature selection was designed to classify the masses as malignant or benign using a two-fold cross validation method. The two data subsets T1 and T2 described in Sec. 2A served once as the training and once as the test partition in the two cycles of two-fold cross validation. The stepwise feature selection process uses three threshold values, Fin, Fout, and tolerance, based on the F statistics, for feature entry, feature elimination, and tolerance of correlation for feature selection, respectively. Since the appropriate values of these thresholds were not known a priori, they were estimated from the training set using a leave-one-case-out resampling method and simplex optimization. This procedure has been described in more detail previously.24 The chosen Fin, Fout, and tolerance values were then used to select a set of features from the training subset, and the weights for the LDA classifier were also estimated from the training subset. The test subset was thus independent of the classifier training in each cross validation cycle. In the test set, the LDA scores of the same mass seen on different images were averaged and were analyzed using the ROC methodology.25 The classification performance was measured in terms of the area Az under the ROC curve. Computer segmentation was initialized two times: First with R1’s initialization point and second with R2’s initialization point. Two-fold cross validation was performed for both initializations.
Radiologists’ classification
Figures 2a, 2b show the distribution of LM ratings provided by two radiologists for all masses in each image. To compare the performance of the classifiers to radiologists’ visual assessment of the masses, the LM ratings of a radiologist for different views of the same mass were averaged, and an Az value was estimated based on these average ratings.
Performance measures of segmentation
To quantify the performance of the computer segmentation, we used two area overlap measures and one area error measure.22, 26 Let A represent the area of the evaluated segmentation and Aref represent the area of the reference segmentation. AOR1 is defined as the ratio of the intersection area of the two segmentations relative to the area of the reference segmentation:
| (9) |
AOR2 is defined as the ratio of the intersection area to the union area of the two segmentations:
| (10) |
where ∣⋅∣ denotes cardinality. The area error measure (AEM) is defined as the percentage of area error for the evaluated segmentation area:
| (11) |
Sensitivity to initialization
Our algorithm is initialized using a manually identified point approximately at the mass center. Since there will be variation in identifying the mass center by the user of the segmentation method, we investigated the sensitivity of our algorithm to the variation of the mass center identified by the two radiologists. An offset of ΔR, 0, or −ΔR was added to the abscissa and ordinate of each radiologist’s initialization point. Thus, a total of nine locations were investigated (including the identified mass center). The offset was determined by the size of the mass. Based on the area of radiologist’s segmentation, A′, the equivalent radius of a mass, R′, was estimated by
| (12) |
The offset was determined as
| (13) |
The value of δ was computed using two sets of mass centers identified by the two radiologists. One radiologist’s segmentation result was used as reference, from which the radius of the mass, R′, was obtained. The value of ΔR was calculated as the distance between the mass centers identified by the two radiologists. From Eq. 13, δ was computed in each image. Over the set of masses, the value of δ was found to be 0.21±0.22 and 0.22±0.22 (mean±sd) for using R1’s and R2’s segmentations as reference to estimate R′, respectively. To investigate the sensitivity of the segmentation method to the variation of initialization, δ was chosen as 0.2.
RESULTS
Evaluation of final segmentation
Since the two radiologists provided mass outlines, both R1’s and R2’s manual segmentations could be used as the reference. In the first comparison, both the computer segmentation and R2’s segmentation were evaluated with R1’s manual segmentation serving as the reference. The AORs (or AEM) of the computer and R2 were compared for each mass. In the second comparison, the roles of R1 and R2 were reversed, so that both the computer segmentation and R1’s segmentation were evaluated with R2’s manual segmentation serving as the reference. When R1’s segmentation was used as the reference, the mass center identified by R1 was used as the initialization point, and likewise for R2’s segmentation. The results of the first and second comparisons are shown in Tables 1, 2, respectively.
Table 1.
Comparison of the computer-vs-R1 segmentation and R2-vs-R1 segmentation.
| AOR1 | AOR2 | AEM (%) | |
|---|---|---|---|
| Computer vs R1 | 0.82±0.16 | 0.74±0.14 | −6±29 |
| R2 vs R1 | 0.84±0.16 | 0.76±0.15 | −2±29 |
| p value | <0.03 | <0.01 | 0.45 |
Table 2.
Comparison of the computer-vs-R2 segmentation and R1-vs-R2 segmentation.
| AOR1 | AOR2 | AEM (%) | |
|---|---|---|---|
| Computer vs R2 | 0.84±0.18 | 0.71±0.16 | 5±38 |
| R1 vs R2 | 0.91±0.12 | 0.76±0.15 | 17±36 |
| p value | <0.01 | <0.01 | <0.01 |
The computer segmentation exhibited a high overlap with radiologists’ segmentation, as shown in Tables 1, 2. When R1 was used as the reference, computer segmentation had AOR1 and AOR2 values of 0.82±0.16 and 0.74±0.14, respectively. When R2 was used as the reference, the corresponding values were 0.84±0.18 and 0.71±0.16. However, the agreement between the radiologists’ segmentations were higher, with AOR1 and AOR2 values of 0.84±0.16 and 0.76±0.15 when R1 was used as the reference and 0.91±0.12 and 0.76±0.15 when R2 was used as the reference. The overlap between computer-vs-radiologist segmentation was compared to that between radiologist-vs-radiologist segmentation using a paired test. For example, if R1 was used as the reference and AOR1 was used as the overlap criterion, then AOR1 between the computer and R1 for a mass would constitute the first sample of the pair, and AOR1 between R2 and R1 for the same mass would constitute the second sample. Since the normal probability plot of the paired differences did not form a straight line, which indicated that the paired differences were not normally distributed, we used the Wilcoxon signed rank test, which is a nonparametric equivalent of the paired t-test for the statistical comparison. Our results indicate that the overlaps (AOR1 and AOR2) between the two radiologists were significantly larger than that between the computer and a radiologist (p<0.03, Tables 1, 2).
In terms of mass size, R1 segmented a larger mass area than R2. AEMs between the two radiologists were −2%±29% and 17%±36%, when R1 and R2 served as the reference, respectively. AEM between the computer and R1 was −6%±29%, and that between the computer and R2 was 5%±38%. The computer-segmented mass area was therefore, on average, smaller than that of R1 but larger than that of R2. When R1 was used as the reference, the difference in AEM between the computer and R2 did not reach statistical significance. When R2 was used as the reference, the computer had significantly lower AEM than R1 (p<0.01, Wilcoxon signed rank test).
The distribution of the three measures of computer segmentation are shown in Fig. 8 for R1 and R2 serving as the reference. To evaluate the fraction of successful segmentation, a threshold of 0.5 for AOR2 was chosen such that the segmentation was regarded as “successful” if AOR2 exceeded the threshold. The AOR2 measure was chosen based on the study by Horsch et al.14 but a more strict threshold (0.5 instead of 0.4) was used to rate the segmentation as successful. The computer segmentation successfully segmented masses in 94% (459∕488) and 89% (434∕488) of the images when R1 and R2 served as the reference, respectively.
Figure 8.
Distribution of three measures of computer segmentation.
Effect of second-stage AC
To evaluate whether the second-stage AC segmentation is useful, we computed the AORs (AOR1 and AOR2) of the first-stage AC and final stage AC using the same radiologist’s segmentation as reference and compared the AOR values of the two stages. When R1 was used as the reference, the first-stage AC segmentation had AOR1 and AOR2 values of 0.81±0.16 and 0.73±0.14, respectively. The first-stage AORs were significantly lower than the corresponding AORs of the final AC segmentation, the AOR1 and AOR2 values of which were 0.82±0.16 and 0.74±0.14, respectively (p<0.02). When R2 was used as the reference, the first-stage AORs were 0.83±0.18 and 0.71±0.16, respectively. AOR1 was significantly lower (p=0.03) but AOR2 showed no significant difference (p=0.23) when compared with the corresponding AORs of the final AC segmentation, the AOR1 and AOR2 values of which were 0.84±0.18 and 0.71±0.16, respectively. For masses for which the final segmentation made a substantial difference in the AORs compared to those of the first-stage AC segmentation, the effect of the final segmentation was largely beneficial. When R1 was used as the reference, there were 24 images for which AOR1 of the first-stage segmentation differed from that of the final segmentation by more than ±0.1. In 19 of these images, the final segmentation had a higher AOR1, while in the remaining 5 images, the first-stage segmentation had higher AOR1. Corresponding comparisons for other pairings of radiologists and AOR measures are summarized in Table 3.
Table 3.
Number of images for which the area overlap between the first-stage AC segmentation and the reference radiologist differed by more than ±0.1 compared to that between the final segmentation and the reference radiologist.
| Reference radiologist | AOR1(Afinal,Aref)>AOR1(Afirst,Aref)+0.1 | AOR1(Afirst,Aref)>AOR1(Afinal,Aref)+0.1 | AOR2(Afinal,Aref)>AOR2(Afirst,Aref)+0.1 | AOR2(Afirst,Aref)>AOR2(Afinal,Aref)+0.1 |
|---|---|---|---|---|
| R1 | 19 | 5 | 11 | 5 |
| R2 | 22 | 3 | 17 | 8 |
Classification evaluation
Figure 9 compares the test ROC curves for classifiers based on feature spaces extracted from R1’s manual segmentation and computer segmentation with R1’s initialization point. Figure 9a shows the test results for the first cycle of cross validation (train on T1, test on T2), for which the test Az values were 0.90±0.03 and 0.89±0.03 for R1’s manual segmentation and computer segmentation, respectively. Figure 9b shows the test results for the second cycle of cross validation (train on T2, test on T1), for which the corresponding Az values were 0.87±0.03 and 0.92±0.02, respectively. Also shown in Fig. 9a is the ROC curve derived from the LM ratings of R1 for the test set (T2), which had an Az value of 0.90±0.03. Since R1 was not blinded to the pathology reports before she provided LM ratings for T1, the corresponding ROC curve was not plotted for Fig. 9b. Figure 10 is the counterpart of Fig. 9 by switching the roles of R1 and R2. The Az values are summarized in Table 4. The difference between the Az values of the ROC curves in each of Figs. 9a, 9b, 10a, 10b did not reach statistical significance (p>0.05) as estimated by the CLABROC program.
Figure 9.
Mass-based ROC curves for classifiers designed using manual segmentation by R1 and computer segmentation initialized by R1 for the two cycles of cross validation: (a) Train in set T1 and test in set T2 and (b) train in set T2 and test in set T1. Also shown in (a) is the ROC curve derived from the LM ratings of R1. The difference in the Az values between pairs of ROC curves for each test set did not achieve statistical significance (p>0.05).
Figure 10.
Mass-based ROC curves for classifiers designed based on manual segmentation by R2 and computer segmentation initialized by R2 for the two cycles of cross validation: (a) Train in set T1 and test in set T2 and (b) train in set T2 and test in set T1. Also shown in (b) is the ROC curve derived from the LM ratings of R2. The difference in the Az values between pairs of ROC curves for each test set did not achieve statistical significance (p>0.05).
Table 4.
Two-fold cross validation test Az values for the feature spaces extracted from the reference radiologist’s manual segmentation and computer segmentation initialized with the reference radiologist’s initialization point. Since R1 was blinded to the pathology report when she provided LM ratings for T2 and R2 was blinded to the pathology report when she provided LM ratings for T1, the Az values derived from these ratings are also shown. The statistical significance (p value) in the difference between the Az values based on manual segmentation and computer segmentation and that between the Az values based on LM ratings and computer segmentation are also shown.
| Reference radiologist | Az (test set: T2) | Az (test set: T1) | ||||
|---|---|---|---|---|---|---|
| Manual segmentation | Computer segmentation | LM rating | Manual segmentation | Computer segmentation | LM rating | |
| R1 | 0.90±0.03 (p=0.40) | 0.89±0.03 | 0.90±0.03 (p=0.84) | 0.87±0.03 (p=0.37) | 0.92±0.02 | |
| R2 | 0.89±0.03 (p=0.53) | 0.88±0.03 | 0.88±0.03 (p=0.37) | 0.90±0.03 | 0.91±0.02 (p=0.57) | |
Sensitivity to initialization
To investigate the sensitivity of the segmentation method to the initialization point, we implemented the segmentation method based on nine seed points in the vicinity of the radiologist’s initialization point, computed the average of these nine segmentation results, and compared it with the segmentation result based on radiologist’s initialization point. Table 5 summarizes the comparison result, in which two sets of comparisons were performed based on R1’s and R2’s initialization point. When compared with the segmentation based on radiologist’s initialization point, the average of the nine segmentations showed a slightly lower performance. The decrease in AORs (AOR1 and AOR2) ranged from 0.03 to 0.04. The AEM was the same for R1’s initialization point but increased from 5% to 8% for R2’s initialization point. The success segmentation ratio (AOR2>0.5) averaged over the nine seed points decreased from 94% to 88% for R1 serving as reference and from 89% to 85% for R2 serving as reference.
Table 5.
Sensitivity of the computer segmentation to variation of initialization point. Computer segmentation result based on radiologists’ initialization point and the average of nine computer segmentation results based on nine variations of radiologists’ initialization point were compared.
| Initialization point | AOR1 | AOR2 | AEM (%) | Success ratio (AOR2>0.5) (%) |
|---|---|---|---|---|
| R1’s initialization point | 0.82±0.16 | 0.74±0.14 | −6±29 | 0.94 |
| Average of computer segmentations based on nine variations of R1’s initialization point | 0.78±0.19 | 0.70±0.17 | −6±34 | 0.88 |
| R2’s initialization point | 0.84±0.18 | 0.71±0.16 | 5±38 | 0.89 |
| Average of computer segmentations based on nine variations of R2’s initialization point | 0.81±0.19 | 0.68±0.17 | 8±42 | 0.85 |
DISCUSSION
In this study, we developed an automated method to segment breast masses on US images, which only requires a manually identified point approximately at the mass center as input. Initial mass boundary points were automatically estimated by searching for the maximum gradient points in a sequence of concentric rings of various shapes and sizes centered at this initialization point. This search method used the total gradient strength in a given ring to identify the most likely mass boundary region rather than the individual maximum gradient along an entire radial line, thus reducing the chance of choosing spurious high gradient points as initial mass boundary points. This is one of the most important steps that we designed to improve the robustness of segmentation in the noisy US image background. Although the initial mass boundary points detected by the maximum gradient search method were not used to initialize the AC, they played a vital role in the automated extraction of the proper ROI to contain the mass. The ROI affected all subsequent steps, including the selection of the variance of the inverse Gaussian function, the region for clustering that determined the AC initialization, and the region for finding the final mass boundary by AC segmentation. Therefore, the detected initial mass boundary points had a direct impact on the final segmentation result.
Our results indicate that the computer segmentation had a large overlap with radiologists’ manual segmentation and had a relatively small percentage area error (Tables 1, 2). The relationship between the three measures (AOR1, AOR2, and AEM) evaluated in this paper has been explored previously, and it is known that any two of these measures are sufficient to determine the third and a few other performance measures.22, 26 Since there is no consensus as to whether AOR1 or AOR2 might be more informative as a measure of the performance of a segmentation method relative to a reference, both overlap measures were evaluated.
In many applications in medical image interpretation, including segmentation, there is no absolute gold standard. Therefore, using a single radiologist’s manual outline as the gold standard may provide an incomplete assessment of the accuracy of the computer segmentation. In this study, we attempted to address this problem by obtaining manual outlines from two radiologists and comparing the agreement between the computer and a radiologist to that between two radiologists. Our results indicated that when AOR1 or AOR2 was used to evaluate the segmentation, the agreement between the radiologists was significantly higher than that between the computer and either one of the radiologists. The differences in the mean AORs between computer-vs-radiologist and the corresponding radiologist-vs-radiologist shown in Tables 1, 2 ranged from 0.02 to 0.07, which was smaller than the standard deviations shown in the same tables. This indicates that there was a small but consistent difference between computer-vs-radiologist overlaps and radiologist-vs-radiologist overlaps for each mass. When AEM was used to evaluate the segmentation and R1 served as the reference, the difference between the computer and R2 did not reach statistical significance, and when the roles of R1 and R2 were reversed, the computer had significantly lower area error compared to R1. The AEM measure indicates that the mass area automatically segmented by the computer was within the inter-radiologist variation in this study.
To reduce the dependence of the performance of AC segmentation on initialization, we proposed a two-stage AC segmentation. Our results indicate that the second-stage segmentation was useful. In terms of the overlaps with R1, the final segmentation had significantly higher AOR1 and AOR2 than the first-stage AC segmentation. When R2 was used as reference, one overlap measure (AOR1) for the final segmentation was significantly higher than that for the first-stage AC segmentation but the other overlap measure (AOR2) did not show a significant difference. Our results also indicate that, in those images where there was a substantial difference (a difference in absolute overlap of 0.1 or larger) between the AORs of the final segmentation and the first-stage AC segmentation, the final segmentation was largely superior (Table 3). The percentage of images where there existed a substantial difference was less than 6%, which indicates that the AORs obtained from the first-stage and final AC segmentation were similar in most images.
We use an AOR2 threshold of 0.5 to evaluate the fraction of successful segmentation. The computer segmentation was successful in 94% and 89% of the images when R1 and R2 served as the reference, respectively. The reasons for segmentation failures included indistinctive mass boundary, strong edge of the surrounding tissue, and complicated structures inside the mass.
Table 4 summarizes the case-based test Az values of classifiers designed based on feature spaces formed from computer segmentation and radiologists’ manual segmentation and that derived from radiologists’ LM ratings. The Az values of the classifiers based on computer segmentation did not show a significant difference from the corresponding classifiers based on manual segmentation and those derived from radiologist’s blinded visual assessment. This indicates that our current classification method, which uses texture, posterior shadowing, and width-to-height features as input, may be robust to small variations in segmentation. Future work includes the investigation of the dependence of classification accuracy on segmentation when morphological features that describe the shape of the segmented mass are included in the feature space. To derive a mass-based ROC curve, the LM ratings by radiologist or the LDA scores by the computer classifier for two different views of the same mass were averaged. In a clinical examination, more than two views are often examined, and the integration of the information by radiologists is usually more complex than averaging the level of suspicion from different views. As a result, the Az values obtained from the radiologists’ visual assessment in this study may not represent the true performance of the radiologists.
The computer segmentation was initialized by a manually identified point approximately at the mass center. Some of our processing steps, e.g., the determination of the approximate ROI containing the mass and multiplication by an inverse Gaussian function, depended on this initialization point. Different initialization points would therefore result in different computer segmentation. Since the initialization point is subject to inter- and intra-observer variations, it is important to examine the sensitivity of the automated segmentation to this variation. We simulated intra-observer variation by initializing the computer segmentation with nine seed points in the vicinity of the radiologists’ initialization point and compared the average AORs, AEM, and success segmentation ratio from these nine seeds to the corresponding values obtained from the original initialization point. The variation range of the initialization point was chosen as 0.2 of the mass size, which was estimated from the variation between two radiologists’ initialization points. The average measures showed slightly worse performance, indicating that the variation of initialization point had an effect on the segmentation result, although this effect was small within a reasonable variation range of the initialization point.
Our study had a number of limitations. First, the US images in our data set were acquired using the same US machine. In our future work, we will investigate whether our new automated segmentation method would perform similarly for images acquired using different US machines. Second, in a breast US examination, many images of the mass are often acquired to more completely characterize the mass. In our study, only two orthogonal views that best depict the lesion were selected by the radiologists. The performance of our computer system on other views is a topic for future study. Third, all masses in our data set were biopsy proven, which means that masses that were not suspicious enough to be recommended for biopsy, e.g., those that were determined to be simple cysts by US, were not included. Although we expect that the performance of our system on cystic masses would be at least comparable to that on our current data set because most cysts have high contrast and sharp boundaries, this would have to be verified with an independent data set that includes all types of masses.
CONCLUSION
We designed and evaluated an automated method to segment breast masses on ultrasound images, which automatically estimates an initial boundary for AC segmentation based on a manually identified seed point approximately at the mass center. A two-stage AC method iteratively refined the initial contour and performed self-examination and correction on the segmentation result. We evaluated the performance of the automated method by comparing the computer segmentation to the manual segmentation by two radiologists. Although the computer segmentation exhibited high agreement with radiologists’ segmentation, the results between the two radiologists were more consistent. The newly designed two-stage segmentation method significantly improved the agreement with radiologists’ segmentation compared to the single-stage AC segmentation. Feature spaces were formed based on computer segmentation and radiologists’ manual segmentation, and classifiers were designed to characterize masses as malignant or benign based on each feature space. The difference between the classifier performances based on the two feature spaces did not reach statistical significance, indicating that our CAD system performs similarly whether it uses experienced radiologist’s segmentation or our newly developed computer segmentation.
ACKNOWLEDGMENT
This work is supported by USPHS Grant Nos. CA 118305 and CA 091713.
References
- Stavros A. T., Thickman D., Rapp C. L., Dennis M. A., Parker S. H., and Sisney G. A., “Solid breast nodules: Use of sonography to distinguish between malignant and benign lesions,” Radiology 196, 123–134 (1995). [DOI] [PubMed] [Google Scholar]
- Rahbar G., Sie A. C., Hansen G. C., Prince J. S., Melany M. L., Reynolds H. E., Jackson V. P., Sayre J. W., and Bassett L. W., “Benign versus malignant solid breast masses: US differentiation,” Radiology 213, 889–894 (1999). [DOI] [PubMed] [Google Scholar]
- Hong A. S., Rosen E. L., Soo M. S., and Baker J. A., “BI-RADS for sonography: Positive and negative predictive values of sonographic features,” AJR Am. J. Roentgenol. 184, 1260–1265 (2005). [DOI] [PubMed] [Google Scholar]
- Taylor K. J. W. et al. , “Ultrasound as a complement to mammography and breast examination to characterize breast masses,” Ultrasound Med. Biol. 10.1016/S0301-5629(01)00491-4 28, 19–26 (2002). [DOI] [PubMed] [Google Scholar]
- Chan H. P., Sahiner B., Helvie M. A., Petrick N., Roubidoux M. A., Wilson T. E., Adler D. D., Paramagul C., Newman J. S., and Gopal S. S., “Improvement of radiologists’ characterization of mammographic masses by computer-aided diagnosis: An ROC study,” Radiology 212, 817–827 (1999). [DOI] [PubMed] [Google Scholar]
- Huo Z. M., Giger M. L., Vyborny C. J., and Metz C. E., “Breast cancer: Effectiveness of computer-aided diagnosis-observer study with independent database of mammograms,” Radiology 10.1148/radiol.2242010703 224, 560–568 (2002). [DOI] [PubMed] [Google Scholar]
- Hadjiiski L. M. et al. , “improvement of radiologists’ characterization of malignant and benign breast masses in serial mammograms by computer-aided diagnosis: An ROC study,” Radiology 10.1148/radiol.2331030432 233, 255–265 (2004). [DOI] [PubMed] [Google Scholar]
- Sahiner B., Chan H. P., Roubidoux M. A., Hadjiiski L. M., Helvie M. A., Paramagul C., Bailey J., Nees A., and Blane C., “Computer-aided diagnosis of malignant and benign breast masses in 3D ultrasound volumes: Effect on radiologists’ accuracy,” Radiology 10.1148/radiol.2423051464 242, 716–724 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen D. R., Chang R. F., and Huang Y. L., “Computer-aided diagnosis applied to US of solid breast nodules by using neural networks,” Radiology 213, 407–412 (1999). [DOI] [PubMed] [Google Scholar]
- Horsch K., Giger M. L., Venta L. A., and Vyborny C. J., “Computerized diagnosis of breast lesions on ultrasound,” Med. Phys. 10.1118/1.1429239 29, 157–164 (2002). [DOI] [PubMed] [Google Scholar]
- Sahiner B., Chan H. P., Roubidoux M. A., Helvie M. A., Hadjiiski L. M., Ramachandran A., LeCarpentier G. L., Nees A., Paramagul C., and Blane C. E., “Computerized characterization of breast masses on 3-D ultrasound volumes,” Med. Phys. 10.1118/1.1649531 31, 744–754 (2004). [DOI] [PubMed] [Google Scholar]
- Joo S., Yang Y. S., Moon W. K., and Kim H. C., “Computer-aided diagnosis of solid breast nodules: Use of an artificial neural network based on multiple sonographic features,” IEEE Trans. Med. Imaging 10.1109/TMI.2004.834617 23, 1292–1300 (2004). [DOI] [PubMed] [Google Scholar]
- Chow T. W. S. and Huang D., “Estimating optimal feature subsets using efficient estimation of high-dimensional mutual information,” IEEE Trans. Neural Netw. 16, 213–224 (2005). 10.1109/TNN.2004.841414 [DOI] [PubMed] [Google Scholar]
- Horsch K., Giger M. L., Venta L. A., and Vyborny C. J., “Automatic segmentation of breast lesions on ultrasound,” Med. Phys. 10.1118/1.1386426 28, 1652–1659 (2001). [DOI] [PubMed] [Google Scholar]
- Madabhushi A. and Metaxas D. N., “Combining low, high-level and empirical domain knowledge for automated segmentation of ultrasonic breast lesions,” IEEE Trans. Med. Imaging 10.1109/TMI.2002.808364 22, 155–169 (2003). [DOI] [PubMed] [Google Scholar]
- Sehgal C. M., Cary T. W., Kangas S. A., Weinstein S. P., Schultz S. M., Arger P. H., and Conant E. F., “Computer-based margin analysis of breast sonography for differentiating malignant and benign masses,” J. Ultrasound Med. 23, 1201–1209 (2004). [DOI] [PubMed] [Google Scholar]
- Hadjiiski L., Chan H. P., Sahiner B., Helvie M. A., and Roubidoux M. A., “Quasi-continuous and discrete confidence rating scales for observer performance studies: Effects on ROC analysis,” Acad. Radiol. 14, 38–48 (2007). 10.1016/j.acra.2006.09.048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sahiner B., Chan H. P., Petrick N., Wei D., Helvie M. A., Adler D. D., and Goodsitt M. M., “Image feature selection by a genetic algorithm: Application to classification of mass and normal breast tissue on mammograms,” Med. Phys. 10.1118/1.597829 23, 1671–1684 (1996). [DOI] [PubMed] [Google Scholar]
- Russ J. C., The Image Processing Handbook (CRC, Boca Raton, 1992). [Google Scholar]
- Kass M., Witkin A., and Terzopoulos D., “Snakes: Active contour models,” Int. J. Comput. Vis. 10.1007/BF00133570 1, 321–331 (1988). [DOI] [Google Scholar]
- Williams D. J. and Shah M., “A fast algorithm for active contours and curvature estimation,” CVGIP: Image Understand. 10.1016/1049-9660(92)90003-L 55, 14–26 (1992). [DOI] [Google Scholar]
- Sahiner B., Petrick N., Chan H. P., Hadjiiski L. M., Paramagul C., Helvie M. A., and Gurcan M. N., “Computer-aided characterization of mammographic masses: Accuracy of mass segmentation and its effects on characterization,” IEEE Trans. Med. Imaging 10.1109/42.974922 20, 1275–1284 (2001). [DOI] [PubMed] [Google Scholar]
- Lachenbruch P. A., Discriminant Analysis (Hafner, New York, 1975). [Google Scholar]
- Wei J., Chan H. -P., Sahiner B., Hadjiiski L. M., Helvie M. A., Roubidoux M. A., Zhou C., and Ge J., “Dual system approach to computer-aided detection of breast masses on mammograms,” Med. Phys. 10.1118/1.2357838 33, 4157–4168 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metz C. E., Herman B. A., and Shen J. H., “Maximum-likelihood estimation of receiver operating characteristic (ROC) curves from continuously-distributed data,” Stat. Med. 17, 1033–1053 (1998). [DOI] [PubMed] [Google Scholar]
- Way T. W., Hadjiiski L. M., Sahiner B., Chan H. -P., Cascade P. N., Kazerooni E. A., Bogot N., and Zhou C., “Computer-aided diagnosis of pulmonary nodules on CT scans: Segmentation and classification using 3D active contours,” Med. Phys. 10.1118/1.2207129 33, 2323–2337 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]