Harmonic segregation through mistuning can improve fundamental frequency discrimination

Abstract

This study investigated the relationship between harmonic frequency resolution and fundamental frequency (f₀) discrimination. Consistent with earlier studies, f₀ discrimination of a diotic bandpass-filtered harmonic complex deteriorated sharply as the f₀ decreased to the point where only harmonics above the tenth were presented. However, when the odd harmonics were mistuned by 3%, performance improved dramatically, such that performance nearly equaled that found with only even harmonics present. Mistuning also improved performance when alternating harmonics were presented to opposite ears (dichotic condition). In a task involving frequency discrimination of individual harmonics within the complexes, mistuning the odd harmonics yielded no significant improvement in the resolution of individual harmonics. Pitch matches to the mistuned complexes suggested that the even harmonics dominated the pitch for f₀’s at which a benefit of mistuning was observed. The results suggest that f₀ discrimination performance can benefit from perceptual segregation based on inharmonicity, and that poor performance when only high-numbered harmonics are present is not due to limited peripheral harmonic resolvability. Taken together with earlier results, the findings suggest that f₀ discrimination may depend on auditory filter bandwidths, but that spectral resolution of individual harmonics is neither necessary nor sufficient for accurate f₀ discrimination.

INTRODUCTION

The ability of human listeners to discriminate small differences in pitch, as estimated by the f₀ difference limen (f₀ DL), is typically best when at least some low-numbered harmonics are present (Houtsma and Smurzynski, 1990; Shackleton and Carlyon, 1994). Studies that have measured f₀ DLs as a function of the lowest harmonic present have usually found an abrupt transition between good and poor performance as the lowest harmonic number is increased from around 9 to 12 (Houtsma and Smurzynski, 1990; Bernstein and Oxenham, 2003), at least for f₀’s in the adult speech range, between about 100 and 200 Hz. The reasons underlying the dependence of f₀ discrimination on harmonic number are not fully understood, although most emphasis has been placed on differences in peripheral resolvability between low- and high-numbered harmonics (Houtsma and Smurzynski, 1990; Shackleton and Carlyon, 1994; Bernstein and Oxenham 2006a, b).

There is some evidence suggesting a link between peripherally resolved harmonics and good pitch perception. First, the relatively abrupt increase in f₀ DL with increasing lowest harmonic number typically matches the point at which effects of component phases are first observed (Houtsma and Smurzynski, 1990; Shackleton and Carlyon, 1994; Bernstein and Oxenham, 2006a, b). Phase effects indicate interactions between neighboring components, suggesting that the harmonics are at least partially unresolved at the point where f₀ DLs increase. Second, recent studies have demonstrated a relationship between the minimum harmonic spacing required for relatively accurate f₀ discrimination performance and auditory filter bandwidth in hearing-impaired listeners (Bernstein and Oxenham, 2006b), as well as in normal-hearing listeners at different sound intensities (Bernstein and Oxenham, 2006a). Because auditory filter bandwidth, relative to harmonic spacing, is thought to determine the degree to which harmonics are resolved, the link between filter bandwidth and f₀ DLs could be viewed as evidence that resolved harmonics are necessary for good pitch perception.

On the other hand, there are some grounds to question the relationship between harmonic resolvability and f₀ DLs. For instance, it has been found that increasing the number of peripherally resolved harmonics by presenting successive harmonics to alternating ears (i.e., the odd harmonics to one ear and the even harmonics to the other) does not improve f₀ DLs or pitch identification performance for stimuli consisting of either two (Houtsma and Goldstein, 1972; Arehart and Burns, 1999) or many (Bernstein and Oxenham, 2003) harmonics. Thus, a reasonable summary of the results so far might be that resolved harmonics seem to be necessary (Houtsma and Smurzynski, 1990; Shackleton and Carlyon, 1994; Bernstein and Oxenham 2006a, b) but not sufficient (Houtsma and Goldstein, 1972; Bernstein and Oxenham, 2003) for good pitch perception.

An alternative interpretation is that f₀ DLs are not related to harmonic resolvability at all, but only to auditory filter bandwidth. De Cheveigné and Pressnitzer (2006) illustrated this point in their recent model, which assumes that the coding of f₀ within a given auditory filter depends on the relationship between the stimulus period (1∕f₀) and the duration of the impulse response of the auditory filter. Specifically, if the impulse response of the filter is shorter than the period of the waveform, the f₀ will not be well represented. Because the impulse response is inversely related to filter bandwidth, which in the case of the auditory system is roughly proportional to center frequency, it follows that the accuracy of f₀ coding will decrease with increasing harmonic number (de Cheveigné and Pressnitzer, 2006). This type of approach can in principle account for why f₀ DLs are affected by changes in filter bandwidth, without being dependent on harmonic resolvability per se. In other words, according to de Cheveigné and Pressnitzer’s (2006) formulation, peripherally resolved harmonics are neither necessary nor sufficient for good pitch perception.

The aim of the present study was to provide an empirical test of the link between harmonic resolvability and pitch perception, with the aim of dissociating peripheral resolvability from harmonic number and filter bandwidth. Our starting point was the finding by Bernstein and Oxenham (2003) that presenting successive harmonics to alternating ears improved the peripheral resolvability of individual harmonics, but did not affect f₀ DLs. This result is puzzling because, in principle, listeners could have attended just to the ear with the even harmonics, and extracted a pitch corresponding to twice the nominal f₀, with half the harmonic number (e.g., the 12th harmonic of 100 Hz could have been interpreted as the 6th harmonic of 200 Hz). The fact that listeners were not able to utilize this strategy could be interpreted in at least two ways. First, pitch may be extracted from a representation in which the input from each ear is automatically fused, forming an unresolved “central spectrum” (Zurek, 1979); in this case harmonics would need to be resolved in both the monaural and binaural sense. Second, the harmonics may be resolved within the central representation, but the odd harmonics may inhibit activation of a harmonic template at twice the f₀. According to this interpretation, the pitch of a complex sound is extracted by selecting the centrally stored harmonic template that best matches the set of individual component frequencies present in the input stimulus (Goldstein, 1973). Presumably both a 100- and 200-Hz template would be activated by a diotic 100-Hz tone complex. However, spurious octave confusions might be avoided if the activation of the 200-Hz template were reduced by inhibitory inputs at intermediate component frequencies associated with the odd harmonics of the 100-Hz tone complex. In the case of a dichotic 100-Hz complex, the odd components in one ear might still inhibit the 200-Hz template that would otherwise be activated by the even components in the other ear.

It is likely that this putative inhibition mechanism is susceptible to auditory grouping and segregation constraints, in order to avoid interference between simultaneous complex tones with different f₀’s. Just as the perceptual removal of a frequency component via mistuning or onset disparity reduces that component’s contribution to the pitch of a tone complex (e.g., Moore et al., 1985; Darwin and Ciocca, 1992; Darwin et al., 1995), such manipulations might be predicted to reduce its role in inhibiting the activation of a particular harmonic template. Auditory grouping by harmonicity may explain the contrast between the results of Bernstein and Oxenham (2003) and those of Beerends and Houtsma (1986), who showed that listeners were able to independently identify the f₀ of two two-tone complexes presented to opposite ears. The fact that the harmonics presented to opposite ears in the Bernstein and Oxenham (2003) study shared the same fundamental frequency may have encouraged their perceptual fusion.

In this study, we introduced constant but small mistunings of all the odd harmonics to encourage their perceptual segregation from the even harmonics, as has been done for individual harmonics in the past (e.g., Moore et al., 1985; Darwin and Ciocca, 1992; Darwin et al., 1995). We tested both diotic (all harmonics to both ears) and dichotic (odd and even harmonics to opposite ears) conditions. The predictions were as follows: (1) if f₀ DLs depend on harmonic resolvability within a “central spectrum” (Zurek, 1979), then a slight mistuning of the odd harmonics should have little or no effect on resolvability, and so should not affect f₀ DLs at all; (2) if f₀ DLs depend on monaural (peripheral) harmonic resolvability, but mistuning is sufficient to perceptually segregate components presented to opposite ears, then the mistuning should improve f₀ discrimination in the dichotic condition but not in the diotic condition, where performance is limited by peripheral resolvability of the harmonics; (3) if f₀ DLs do not depend on harmonic resolvability at all, but rather on the harmonic number associated with the perceived f₀ (or filter bandwidths), then mistuning the odd harmonics should improve performance in both diotic and dichotic conditions by facilitating the perceptual segregation of the odd and even harmonics.

EXPERIMENT 1: FUNDAMENTAL FREQUENCY DISCRIMINATION

Methods

Stimuli

This experiment measured f₀ discrimination performance as a function of f₀ for diotic and dichotic harmonic complexes and complexes in which the f₀ of the odd harmonics was shifted relative to that of the even harmonics. All complexes were bandpass filtered into a fixed spectral region (Shackleton and Carlyon, 1994; Bernstein and Oxenham, 2005; 2006a, b). This paradigm was employed instead of fixing the f₀ and varying the harmonic number (e.g., Houtsma and Smurzynski, 1990; Bernstein and Oxenham, 2003) for two reasons. First, in a fixed-f₀ paradigm, an alternative cue to f₀ discrimination exists based on the spectral region occupied by the components presented. While the usefulness of this cue can be diminished by applying a random rove to the lowest harmonic presented from interval to interval (Houtsma and Smurzynski, 1990; Bernstein and Oxenham, 2003; Moore et al., 2006), such a cue can still influence the f₀ DL estimate in the case of large f₀ DLs associated with high-order harmonics (Bernstein and Oxenham, 2003; Moore et al., 2006). Second, the fixed bandpass-filter paradigm allows an estimate of the f₀ needed to achieve a fixed level of f₀ discrimination performance via an adaptive tracking technique (e.g., Krumbholz et al., 2000). Because this technique was used in experiment 2 to determine the size of the mistuning required to induce a change in f₀ discrimination accuracy, experiment 1 also used a bandpass filter paradigm, to maintain similar stimulus parameters across the two experiments. Experiment 1A measured f₀ discrimination performance for diotic and dichotic, harmonic and f₀-shifted complexes. Experiment 1B provided a control that compared f₀ discrimination performance for complexes consisting of both even and odd harmonics with performance for complexes consisting of only odd harmonics.

The stimuli and methods in this experiment were similar to those employed by Bernstein and Oxenham (2006a, b). The stimuli consisted of 300-ms (including 30-ms raised cosine rise and fall ramps) bandpass-filtered random-phase tone complexes. A new set of phases was selected independently from a uniform distribution for each 300-ms tone complex. The bandpass filter was held constant throughout the experiment, with 1.5- and 3.5-kHz corner frequencies and 50 dB∕octave low- and high-frequency slopes. The filtering operation was implemented in the spectral domain by first adjusting the amplitude of each sinusoidal component, then summing all the components together.

Tone complexes were constructed by selecting even and odd harmonics from the same f₀ (harmonic conditions) or from two different f₀’s (f₀-shifted conditions), whereby the f₀ for the odd components (f_0,odd) was 3% higher than the f₀ for the even component frequencies (f_0,even). In the remainder of the paper the f₀ reported is the f_0,even. Even and odd harmonics were presented either diotically (all components to both ears) or dichotically (even and odd components to opposite ears), for a total of four conditions. For all conditions, filtered complexes consisting of only even or only odd components were synthesized separately. In the diotic conditions, the even and odd complexes were summed together and presented to both ears simultaneously. In the dichotic conditions, odd and even components were randomly assigned to the right and left ears on a trial-by-trial basis. Fundamental frequency discrimination was tested for seven average values of f₀ (50, 75, 100, 125, 150, 175, and 200 Hz).

To reduce the effectiveness of loudness as an alternative discrimination cue, the root-mean-squared amplitude of the combined even components was first equalized across the three intervals and then a random level perturbation was added to each interval, chosen from a uniform distribution of ±2.5 dB. The odd components were scaled to maintain the same level per component as the even components in each interval. In addition, f_0,base was roved from trial to trial within a run, chosen from a uniform distribution between ±5% of the average f₀. This was intended to encourage listeners to compare the pitches of the stimuli in each of the intervals of one trial, rather than comparing the pitch of each interval with some internally stored representation of the f_0,base, although the f₀ roving may not have been effective for low f₀’s where measured f₀ DLs were relatively large.

All stimuli were presented in a threshold equalizing noise (TEN; Moore et al., 2000), lowpass filtered at 10 kHz and set at a level of 40 dB sound pressure level (SPL) per equivalent rectangular bandwidth (ERB_N; Glasberg and Moore, 1990), which reduced the possibility of the use of combination tones and off-frequency listening. The noise was presented diotically to reduce the possibility of a binaural signal-detection advantage in the diotic stimulus conditions. The 0-dB sensation level (SL) reference for each individual listener was defined as the average detection threshold for 1.5-, 2.5- and 3.5-kHz probe tones presented monaurally to the left ear in monaural TEN (range: 35.4–37.1 dB SPL across the seven listeners who participated in experiments 1 through 4). Each equal-amplitude component (before filtering, where applicable) was presented at an average 12.5 dB SL (adjusted for each listener). With the 50 dB∕octave filter slopes, only tones falling within about 1∕4 octave above and below the upper and lower filter cutoff frequencies, respectively, (1261–4162 Hz) were audible.

Procedure

Fundamental frequency DLs were estimated in a three-interval three-alternative forced-choice (3I-3AFC) adaptive procedure, using a two-down, one-up algorithm to track the 70.7% correct point on the psychometric function (Levitt, 1971). The three intervals were separated by gaps of 300 ms. The background noise (TEN) was gated on 200 ms before the first interval and gated off 100 ms after the third interval, producing a total noise duration of 1800 ms in each trial.

Two intervals contained a stimulus with a base f₀ (f_0,base) and the other interval contained a complex with a higher f₀. The listener’s task was to identify the interval containing the complex with the higher pitch. Feedback (correct∕incorrect) was provided following each response. The f₀ difference (Δf₀), which was initially set to 15.8% of the f₀, changed by factors of 1.59 and 1.26 until the second and fourth reversals, respectively, and then changed by a factor of 1.12 for six more reversals. The f₀ DL was estimated as the geometric mean of the Δf₀’s at the last six reversal points. Measurements were repeated four times for each f₀ and condition, for a total of 112 runs per listener. Each listener received at least 2 h of practice before data collection began.

Listeners

A list of the seven listeners that participated in the study (four of whom participated in experiment 1A) is shown in Table 1, which includes information about age, gender, musical background, and the experiments in which each listener participated. All listeners had normal hearing (15 dB hearing level or less re ANSI-1996 at octave frequencies between 0.25 and 8 kHz). The five musicians each had at least four years of formal training.

Table 1.

Details of the normal-hearing listeners who participated in the study.

Listener	Age	Gender	Musician	Experiment
				1A	1B	2	3	4A	4B
1	20	M	No	X		X	X
2	31	F	Yes	X	X	X	X	X	X
3	28	F	No	X		X	X	X
4	51	F	Yes	X		X	X	X
5	36	F	Yes		X				X
6	22	M	Yes		X			X	X
7	24	M	Yes		X				X

Control experiment

A control experiment (1B) provided a baseline measure for the performance that would be expected if f₀ discrimination was based on the even or odd harmonics alone. Fundamental frequency DLs were measured in four listeners (Table 1) as a function of f₀ for diotic harmonic complexes containing all harmonics or odd harmonics only, bandpass filtered as described above. Performance for complexes containing only even harmonics were inferred from the all-harmonics conditions with 2f₀ (e.g., the 200-Hz all-harmonics condition was equivalent to a 100-Hz even-harmonics-only condition). Measurements were performed for the same seven f₀’s (50–200 Hz) as experiment 1A, plus three additional f₀’s (37.5, 250, and 300 Hz) that allowed additional comparisons between the all- and odd-harmonics conditions and the inferred even-harmonics situation. Each listener received at least 2 h of practice before data collection began.

Results

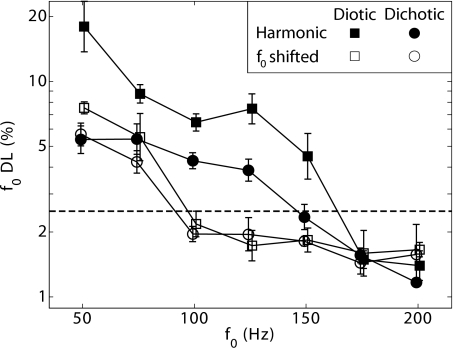
The mean results from experiment 1A are shown in Fig. 1. Geometric-mean f₀ DLs across the four listeners are plotted as a function of f₀ for the four experimental conditions, with error bars indicating the standard error. Results for each individual listener were generally consistent with the mean results and are not shown. These results are discussed along with the results of a repeated-measures analysis of variance (RMANOVA) with three within-listener factors: f₀, f₀ shift of the odd harmonics (0 or 3%) and mode of presentation (diotic or dichotic). The reported degrees of freedom throughout this study reflect a Huynh-Feldt (1976) correction that was applied wherever necessary.

Figure 1.

Mean results of experiment 1A across four listeners. Estimated f₀ DLs are plotted function of f₀ for bandpass filtered tone complexes. Error bars indicate ± one standard error across the four listeners. The dashed line indicates an f₀ DL of 2.5%, the fixed f₀ difference used in experiment 2. An f₀ discrimination benefit was obtained by shifting the f₀ of the odd harmonics for both diotic and dichotic stimuli. A smaller f₀ discrimination benefit was also obtained for harmonic stimuli under dichotic presentation.

Three key findings are apparent in the data. First, f₀ DLs tended to decrease (improve) with increasing f₀, consistent with previous findings (e.g., Bernstein and Oxenham, 2005), as confirmed by a significant main effect of f₀ [F(6,18)=25.7, p<0.0005]. Second, the f₀ at which the transition from relatively large (4% or more) to relatively small f₀ DLs (less than 2.5%, horizontal dashed line) occurred was approximately an octave higher in the harmonic conditions than in the f₀-shifted conditions, consistent with a significant main effect of f₀ shift [F(1,3)=83.8, p<0.005]. Third, in the harmonic conditions, dichotic presentation yielded smaller f₀ DLs for those f₀’s that yielded relatively poor performance (f₀ DLs>4%) under diotic presentation, as suggested by a significant main effect of diotic versus dichotic presentation [F(1,3)=36.2, p<0.01]. Because the interaction between f₀ shift and mode of presentation was not significant [F(1,3)=1.27, p=0.34], an effect of dichotic presentation in the f₀-shifted conditions cannot be ruled out, although it was only visually apparent in harmonic conditions. A significant three-way interaction between f₀, f₀ shift, and mode of presentation [F(2.1,6.3)=5.7, p<0.05] is consistent with the observation that the benefit of dichotic presentation was mainly observed in harmonic, low-f₀ conditions, although there was also a small effect at the lowest f₀’s for the f₀-shifted conditions.

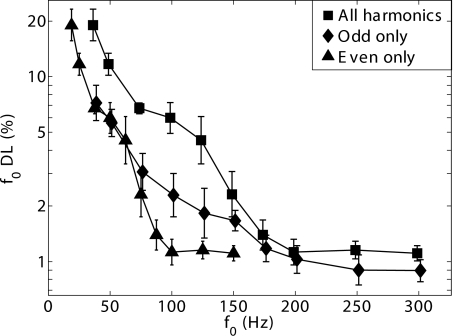
The results of control experiment 1B are shown in Fig. 2. Geometric-mean f₀ DLs across the four listeners are plotted as a function of f₀ for the all-harmonics (squares) and odd-harmonics only conditions (diamonds). The all-harmonics data are replotted (triangles) at half the f₀ to represent the even-harmonics only condition. The odd-harmonics data were compared to the all-harmonics and even-harmonics conditions in two separate RMANOVAs, each with two factors: f₀ and condition (odd versus all or odd vs. even harmonics). While all ten f₀’s were included in the odd- versus all-harmonic RMANOVA, only the six f₀’s that were represented in both conditions were included in the odd-versus even-harmonics comparison (37.5, 50, 75, 100, 125, and 150 Hz).

Figure 2.

Mean results of experiment 1B across four listeners. Estimated f₀ DLs are plotted as a function of f₀ for bandpass filtered tone complexes containing all harmonics or odd harmonics only. The all-harmonics data are replotted as an even-harmonics only condition by dividing the f₀ by two. Error bars indicate ± one standard error across the four listeners.

Both analyses showed a main effect of f₀ [odd versus all: F(4.7,14.1)=83.8, <0.0005; odd versus even: F(5,15)=34.8, p<0.0005], reflecting the improvement in f₀ DLs observed with increasing f₀. In contrast to previous studies, no clear plateau in performance is reached at very low f₀’s. This is probably due to our use of very low f₀’s, extending down to values that are close to the lower absolute limits of pitch perception (Krumbholz et al., 2000; Pressnitzer et al., 2001).

Presenting only the odd harmonics yielded a clear benefit to f₀ discrimination performance: There was a significant main effect of condition in the odd versus all comparison [F(1,3)=43.6, p<0.01]. Nevertheless, the improvement yielded by presenting the odd harmonics alone was not as great as the improvement yielded by presenting the even harmonics alone: There was also a significant main effect of condition in the odd versus even comparison [F(1,3)=20.6, p<0.05]. There was a significant interaction between f₀ and condition in the all versus odd comparison [F(9,27)=5.1, p<0.0005], reflecting the observation that the improvement yielded by presenting the odd harmonics only occurred for low and not high f₀’s. Although the difference between the odd and even conditions was visually apparent only for higher f₀’s, the interaction between f₀ and condition did not reach significance [F(4.0,12.1)=2.78, p=0.08]. This may be due in part to the reduced number of f₀’s available for this comparison and the relatively low statistical power afforded by four subjects.

Discussion

The main finding of this experiment is that shifting the f₀ of the odd harmonics with respect to the even harmonics improved f₀ discrimination at low f₀’s. For the diotic condition (Fig. 1; squares), the results with the shifted components (open squares) closely matched those with the purely harmonic components (filled squares), when the f₀’s of the former were doubled. In other words, performance in the shifted condition was as good as if the odd harmonics were completely absent. In terms of the three hypotheses laid out in the introduction, this basic result seems to rule out the first, “central spectrum” hypothesis (Zurek, 1979). This is because the 3% shift in the frequencies of the odd harmonics is unlikely to increase the peripheral resolvability of the harmonics: Although the shift increased the frequency spacing between each even and the higher adjacent odd harmonic, it also decreased the spacing between the even harmonic and its lower adjacent odd harmonic, resulting in no predicted gain in resolvability. This prediction is tested empirically in experiment 3.

The second finding is that the improvement in f₀ discrimination produced by f₀-shifted odd harmonics was found for both the diotic and dichotic conditions. This finding seems to rule out the second hypothesis presented in the introduction, that peripherally resolved harmonics are necessary for good pitch discrimination: As discussed above (and addressed in experiment 3) shifting the f₀ of the odd harmonics is unlikely to have increased the peripheral resolvability of the harmonics, but still led to an improvement in f₀ discrimination.

The results of experiment 1B (Fig. 2) provide further evidence in support of the idea that f₀ discrimination performance is not governed by peripheral resolvability. Improving resolvability by removing the even harmonics did not yield the small (<2%) f₀ DLs generally associated with low order harmonics that was observed for the f₀-shifted conditions of experiment 1A, or for the even-harmonics-only condition in experiment 1B. The odd-harmonics-only condition did nevertheless yield some improvement in f₀ discrimination performance, relative to the diotic condition with all harmonics present. One possible explanation for this improvement is that listeners were able to track the frequencies of the individual harmonics, which would become more prominent with the doubling of the frequency spacing between components in any one ear, without necessarily extracting the f₀.

A similar explanation, in terms of listening to individual harmonics, may also explain the difference in f₀ DLs between the dichotic and diotic conditions observed in experiment 1A (Fig. 1). This finding contrasts with those of Bernstein and Oxenham (2003), who found, if anything, a small increase in f₀ DLs when going from diotic to dichotic conditions. This may be because the Bernstein and Oxenham (2003) randomly assigned even and odd harmonics to left and right ears on an interval-by-interval basis,1 whereas in the current study the assignment was made on a trial-by-trial basis, with the same assignment holding for all three intervals of the trial. This may have increased listeners’ ability to perform the task in the current study by tracking individual harmonics, listening selectively to one ear, rather than extracting a pitch based on the f₀. Such a strategy is most likely to have been used in the dichotic conditions with f₀’s in the range of 100–175 Hz, where the effect of diotic versus dichotic presentation was observed, and where pitch discrimination was relatively poor, but peripherally resolved harmonics would have become available under dichotic presentation. In any case, dichotic presentation in the current study yielded only a modest improvement in f₀ DLs relative to the improvement yielded by shifting the frequencies of the odd harmonics. Thus, any benefit to f₀ discrimination through increased peripheral resolvability via dichotic presentation was overshadowed by the effect of shifting the frequencies of the odd harmonics.

EXPERIMENT 2: MAGNITUDE OF THE ODD-HARMONIC F₀ SHIFT

Rationale

Experiment 1 used a 3% shift in the f₀ of the odd harmonics to perceptually segregate them from the even harmonics. This is consistent in some ways with earlier work showing that a shift of as little as 1% is sufficient for a single harmonic to be heard as a separate object against the background of the remaining complex (Moore et al., 1986). On the other hand, it has also been shown that single mistuned harmonics can continue to contribute to the pitch of the overall complex at much greater mistunings (Darwin and Ciocca, 1992; Darwin et al., 1995). The fact that our mistuning of 3% improved f₀ discrimination performance in a manner consistent with the perceptual segregation of the even and odd components suggests that the “harmonic sieve,” outside which components fail to be combined within a single pitch estimate (Duifhuis et al., 1982), is narrower than 3% for the current conditions. Experiment 2 sought to determine more accurately the bandwidth of this putative sieve by estimating the minimum odd-harmonic mistuning necessary to improve f₀ discrimination performance.

Methods

This experiment directly estimated the f₀ associated with the transition point between low and high f₀ DLs, rather than measuring f₀ discrimination for a range of f₀ values as was done in experiment 1. A 3I-3AFC procedure adaptively varied the f₀ while fixing the f₀ difference between the f_0,base in the two reference intervals and the higher f₀ in the target interval. The f₀ difference was fixed at 2.5% (dashed line in Fig. 1), which was selected because it fell between the small f₀ DLs (∼1–2%) associated with relatively high f₀’s and the large f₀ DLs (4% or greater) associated with relatively low f₀’s for each listener and condition in experiment 1. The f_0,base was initially set to 250 Hz and was changed by a factor of 1.26 for the first two reversals points, 1.12 for the next two reversal points, and 1.047 for the last six reversal points. The f₀ DL transition point was estimated as the geometric mean of the f₀’s at the last six reversal points.

Stimuli were presented both diotically and dichotically as in experiment 1. Six different values of Δf₀ (f_0,odd−f_0,even) were tested: 0, 1, 2, 3, 4%, and −4%. The 0 and 3% percent conditions correspond to the harmonic and f₀-shifted conditions of experiment 1. The −4% condition tested whether the effect was symmetric for both negative and positive mistunings of the odd harmonics. The same four listeners from experiment 1A participated in this experiment (Table 1). Measurements were repeated four times for each listener and condition, for a total of 48 runs per listener. Each listener received at least 2 h practice before data collection began.

Results and discussion

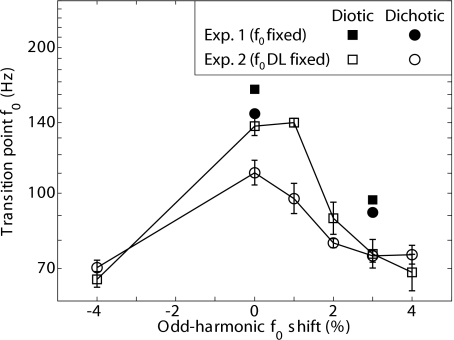
Estimates of the f₀ DL transition point—the f₀ required to achieve an f₀ DL of 2.5%—are plotted as a function of Δf₀ for both diotic (open squares) and dichotic conditions (open circles) in Fig. 3. Three important findings are apparent in the results. First, the paradigm employed in experiment 2 yielded an estimate of the variation in the f₀ DL transition point across conditions similar to that observed in experiment 1. Estimates of the f₀ DL transition points (the f₀ required to achieve a 2.5% f₀ DL) in experiment 1 were derived by linearly interpolating between the data points in Fig. 1, and are plotted as filled squares (diotic) and circles (dichotic) in Fig. 3. Although the transition point estimates were overall 20–35% higher in experiment 1 than in experiment 2, both experiments show a shift of about a factor of 2 in the f₀ DL transition point for a 3% odd-harmonic f₀ shift in the diotic conditions, and about a 10 (experiment 1) or 20% reduction (experiment 2) in the transition point under dichotic as compared to diotic presentation in the harmonic conditions.

Figure 3.

Mean results of experiment 2 across four listeners. The minimum f₀ needed to yield an f₀ DL of 2.5% is plotted as a function of the magnitude of the odd-harmonic f₀ shift. Error bars indicate ± one standard error across the four listeners.

The second important finding is that a shift of about 2% in the f₀ associated with odd harmonics was needed to produce a shift in the f₀ transition point, although some additional benefit was observed as the size of the shift increased beyond 2%. The variation in the transition point as a function of the degree of f₀ shift was confirmed by a significant main effect of f₀ shift [F(5.0,14.9)=42.3, p<0.0005]. As in experiment 1, dichotic presentation led to improved f₀ discrimination for the harmonic (0%) condition and for small f₀ shifts (1% and perhaps 2%). This observation was supported by a significant main effect of mode of presentation [F(1,3)=32.5, p<0.05] and a significant interaction between mode of presentation and f₀ shift [F(2.7,8.0)=5.1, p<0.05]. Separate RMANOVAs confirmed that an effect of f₀ shift on the transition point was observed under both diotic and dichotic presentation [diotic: F(4.2,12.7)=28.1, p<0.0005; dichotic: F(5,15)=16.5, p<0.0005], although the shift in the transition point was larger under diotic presentation as a result of the smaller benefit provided by dichotic presentation in the f₀-shifted conditions. The 2% odd-harmonic frequency shift required to yield the f₀ discrimination benefit is somewhat less than the 3% point at which the contribution that a mistuned harmonic makes to the overall pitch of a tone complex begins to diminish (Darwin and Ciocca, 1992; Darwin et al., 1995). It may be that the simultaneous mistuning of all of the odd harmonics further encouraged their reduced contribution to the pitch percept associated with the even harmonics, such that a smaller frequency shift was needed to yield the f₀ discrimination benefit. The extent to which the f₀ discrimination benefit depends on the harmonic relationship between the frequency-shifted odd components remains an open question that could be addressed by randomizing the degree and direction of the mistuning of individual components.

Finally, the benefit to f₀ discrimination of mistuning the odd harmonics was also observed in the Δf₀=−4% condition where, on average, frequency components were spaced more closely together than in the 0% conditions. This suggests that the benefit obtained from frequency shifting the odd components is not due to improved harmonic resolvability because, if anything, average peripheral resolvability would decrease when the odd components are shifted lower in frequency by 4%. Experiment 3 examines more closely the effect of frequency shifting the odd components on the ability to hear out individual harmonics.

EXPERIMENT 3: HEARING OUT HARMONICS

Rationale

Experiment 1 showed that the improvement in f₀ discrimination obtained by shifting the f₀ of the odd components was observed whether the even and odd harmonics were presented diotically or dichotically. This suggests that the observed improvement in f₀ discrimination was not related to peripheral harmonic resolvability. Nevertheless, this result does not rule out the possibility that peripheral resolvability may play a role in determining f₀ discrimination performance, as shifting the frequencies of the odd harmonics could have affected peripheral resolvability. This experiment tested this possibility directly by measuring the ability of listeners to “hear out” the frequencies of individual harmonics. An improvement in the ability to hear out harmonics as a result of odd-harmonic frequency shifting would leave open the possibility that increased peripheral resolvability may have contributed, at least in part, to the improved f₀ discrimination performance observed in experiment 1A. On the other hand, if the frequency shift does not systematically improve the ability to hear out harmonics, a role of peripheral resolvability could be ruled out as the basis for the f₀ discrimination benefit observed for f₀-shifted stimuli.

Methods

The method used was similar to that of Bernstein and Oxenham (2003; 2006a), whereby listeners discriminated the frequency of a pure tone presented in isolation from that of a component embedded in a tone complex. Each trial consisted of two intervals, each with a 500-ms duration, separated by 300 ms. The second interval contained a bandpass-filtered tone complex, identical to that of experiment 1, except that one harmonic (the target tone) was gated on and off in time, with three bursts of a 150 ms sinusoid, including 30 ms raised-cosine onset and offset ramps between bursts, separated by 25 ms silent gaps. The onset of the first burst and the offset of the last burst of the target tone were synchronous with the onset and offset of the remaining components in the complex, respectively. The first interval contained a single stimulus frequency (the comparison tone) gated on and off in the same manner as the target tone.

The frequency of the comparison tone (f_comp) was selected from a uniform distribution ranging from 1575 to 1675 Hz (near the low-frequency cutoff of the bandpass filter used to define the harmonic complexes). This eliminated the possibility that listeners could base their responses on the absolute frequency of the comparison tone alone, which would be a confounding factor if the f_comp were set to be higher or lower than a particular value or range of f_targ. For a particular trial, the f_targ was set to be either 4% higher or lower than the selected f_comp (each with probability 0.5), and the f₀ of the tone complex was set relative to the f_targ based on the target harmonic number. The listener was required to discriminate whether the target was higher or lower in frequency than the comparison tone. Feedback was provided following each response.

The same four stimulus conditions from experiment 1 were presented (diotic and dichotic, harmonic and f₀ shifted). Also like experiment 1, in the f₀-shifted conditions, f_0,odd was shifted 3% higher than the f_0,even. In the dichotic conditions, the even harmonics in interval 2 and the comparison tone in interval 1 (which was always to be compared to an even target harmonic in interval 1) were presented to the right ear, while the odd harmonics were presented to the left ear. This was done, rather than randomly assigning even and odd harmonics to right and left ears as in experiment 1, so that listeners would not have to shift their attention on a trial-by-trial basis to hear out the comparison and target tones. Each run consisted of four trials for each of nine target harmonic numbers (N=4, 6, 8, 10, 12, 16, 20, 24, and 32), presented in random order, for one of the four conditions. These values of N correspond to an f₀ range of approximately 50–400 Hz for the mean f_comp of 1625 Hz. Twelve runs were presented for each condition, for a total of 48 runs per listener.

All stimuli were presented in the same wideband TEN background as experiment 1, which was turned on 200 ms before the start of the first interval and turned off 100 ms following the end of the second interval. Each component (before filtering, where applicable) was presented at 12.5 dB SL (adjusted for each listener). Level randomization was not used in this experiment, because overall loudness variations would not have provided a usable cue. The same four listeners (Table 1) from experiments 1A and 2 participated in this experiment. Each listener received at least 2 h of practice before data collection began.

Results

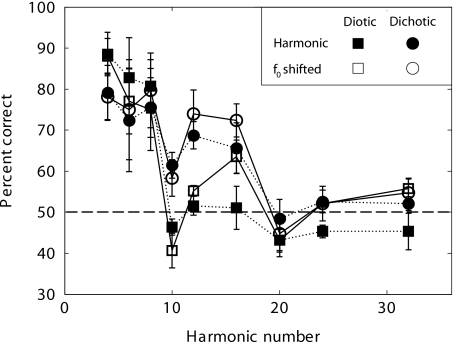
The mean percent correct scores in discriminating the frequencies of the target and comparison tones are plotted as a function of harmonic number in Fig. 4. Error bars indicate the standard error across the four listeners. The horizontal dashed line indicates chance performance. A RMANOVA with three within-listener factors (N, mode of presentation, f₀ shift) was performed to test the significance of trends observed in the data. Performance generally deteriorated from near perfect (100%) to near chance (50%) across the tested range of N in all conditions, consistent with a significant main effect of N [F(2.5,7.4)=11.9, p<0.005], as expected given previous results (Bernstein and Oxenham, 2003; 2006a). Most importantly, the results indicate that the relationship between performance and harmonic number was mainly dependent on mode of presentation (diotic or dichotic) and not the f₀ shift. Although there was no significant main effect of mode of presentation [F(1,3)=3.1, p=0.18], there was a significant interaction between mode of presentation and N [F(8,24)=4.4, p<0.005], reflecting the observation that mode of presentation affected performance mainly near the center of the range of N’s presented, but not at high or low N’s where ceiling and floor effects likely influenced the results. Under diotic presentation, performance dropped from about 75% or more to near chance as N increased from eight to ten. In the dichotic conditions, there was a dip in performance for N=10, but performance then improved again before dropping to near chance for N=20. This factor-of-two increase in the N at which performance dropped to chance, also observed by Bernstein and Oxenham (2003), is consistent with the idea that the ability to hear out individual harmonics is a function of peripheral resolvability, since the peripheral frequency spacing between harmonics is doubled under dichotic presentation. In contrast to the effect of mode of presentation, there was neither a significant main effect of f₀ shift [F(1,3)=2.7, p=0.20] nor any significant two- or three-way interactions between f₀ shift and the other variables (f₀ shift×N: p=0.29; f₀ shift×mode of presentation: p=0.93; f₀ shift×N and mode of presentation: p=0.51). These results suggest that shifting the f₀ of the odd harmonics did not affect listeners’ ability to hear out the individual components. It is possible that the relatively low statistical power of the ANOVA for detecting higher-order interaction effects may have rejected as nonsignificant some differences that are visually apparent in the data (e.g., the diotic N=16 condition). To increase the possibility of detecting the effects of, and interactions with, the f₀ shift, an additional ANOVA was performed on only those data in the diotic conditions where an f₀ shift in the odd components benefited f₀ discrimination performance in experiment 1 (N=10, 12 or 16). Within this subset, the main effect of N remained significant [F(2,6)=8.2, p<0.05] and the main effect of f₀ shift remained nonsignificant (p=0.31). The f₀ shift × N interaction just failed to reach significance (p=0.058), raising the possibility that listeners might have benefited from the f₀ shift in the instance of the diotic N=16 condition. Nevertheless, the value of N below which performance was consistently above chance was not affected by the f₀ shift.

Figure 4.

Mean results of experiment 3 across four listeners. Percent correct in discriminating between a reference tone and a target frequency component of a tone complex is plotted as a function of the harmonic number of the target tone. Error bars indicate ± one standard error across the four listeners. In contrast to the f₀ DL data (Fig. 1), little or no benefit to hearing out harmonic frequencies was observed as a result of the odd-harmonic f₀ shift, while a large benefit was obtained under dichotic presentation.

Discussion

The results show that the ability to hear out the frequencies of individual harmonics depended on the harmonic number and mode of presentation (diotic or dichotic), whereas the 3% upward shift in the frequencies of the odd components did not result in a consistent or statistically significant improvement. Most importantly, performance fell to chance at the same harmonic number whether or not the odd harmonics were shifted (diotic: 10th harmonic; dichotic 20th harmonic). This finding contrasts with the f₀ discrimination results of experiments 1 and 2, where the f₀ shift greatly benefited performance, shifting by an octave the f₀ transition point between relatively poor and good f₀ discrimination performance, while dichotic presentation yielded only a limited improvement from very poor (f₀ DL ∼10%) to less poor (f₀ DL ∼5%) performance generally associated with unresolved harmonics. The possibility that the f₀ shift improved the ability to hear out harmonics under limited circumstances (e.g., for N=16) cannot be completely ruled out. Nevertheless, there was no clear evidence of a systematic improvement in the ability to hear out the frequencies of individual harmonics as a result the harmonic f₀ shift. Therefore, it is unlikely that the substantial improvement in f₀ discrimination across a range of f₀’s that was observed in experiment 1 could be explained in terms of an improved ability to hear out individual harmonics. Instead, these results generally support the conclusions of experiment 1 that f₀ discrimination can be improved by perceptual segregation mechanisms (i.e., mistuning the odd harmonics), but not by the increased peripheral resolvability of harmonics (i.e., dichotic presentation).

Nonmonotonicities were observed in all four conditions of this experiment, whereby the performance functions each showed a local minima at N=10. Bernstein and Oxenham (2003; 2006a) observed similar nonmonotonicities near N=10. This result could reflect the phenomenon of “unmasking” (Hartmann and Goupell, 2006), whereby the frequency component just above the target harmonic becomes “separately audible” during the silent intervals of the gated harmonic. Discrimination judgments based on the frequency of this salient “unmasked” harmonic rather than that of the gated target harmonic would yield diminished performance. However, it is not clear why the unmasking phenomenon would only have this effect for N=10 and not other harmonics. Further experiments involving pitch matching to the gated harmonic (e.g., Hartmann and Goupell, 2006), and not simply pitch discrimination, may shed light on this result.

EXPERIMENT 4: PITCH MATCHES

Rationale

The main finding from experiments 1 and 2 was that shifting the f₀ of the odd harmonics, with respect to that of the even harmonics, resulted in improved f₀ discrimination performance. The pattern of results can be explained by assuming (1) that shifting the frequencies of the odd components decreased their contribution to the perceived pitch associated with the even components, and (2) that the resulting octave pitch shift yielded improved f₀ discrimination performance because performance is based on the perceived harmonic number—that is, the ratio between the absolute frequency and the f₀ associated with the perceived pitch of a stimulus. This experiment tested whether the f₀ shift of the odd harmonics did indeed produce an octave pitch shift in those conditions that yielded improved f₀ discrimination performance. A pitch-matching paradigm was used to determine the pitch perceived under the various conditions of experiment 1. Experiment 4A examined pitch matches to the diotic and dichotic f₀-shifted and the dichotic harmonic stimuli of experiment 1A. Experiment 4B examined pitch matches for the stimuli consisting of only odd harmonics from experiment 1B.

Methods

In experiment 4A, four listeners (Table 1) performed pitch matches by comparing the pitch of a diotic harmonic tone complex (assumed to yield a pitch at the f₀, regardless of harmonic number) with the pitch of a tone complex from one of the other three altered-stimulus conditions that were presented in experiment 1 (diotic f₀ shifted, dichotic harmonic, or dichotic f₀ shifted). The purpose of this experiment was to determine the perceived pitch associated with each altered stimulus. To address this question, the f₀ of a particular altered stimulus was held fixed as the reference (the altered-reference condition, AREF) while the listener adjusted the f₀ of the diotic harmonic complex to match the pitch. To test whether the pitch matches would depend on which of the two stimulus f₀’s was controlled by the listener, a control condition was also included, whereby the f₀ of the diotic tone complex was held fixed while the listener adjusted the f₀ of the altered stimulus (the altered-comparison condition, ACOMP).

In each pitch-matching run, two tone complexes were presented, each with a 300-ms duration, separated by 500 ms. The tone complexes were constructed in an identical manner to those described in experiment 1, including the background TEN, except that level and f₀ roving were not applied. The tone complex for which the listener had control over the f₀ was presented first (comparison stimulus), followed by the tone complex that was held constant throughout the run (reference stimulus). For the reference stimulus, the starting phase of each component was randomly selected from a uniform distribution, and then held fixed throughout the run. For the comparison stimulus, the starting phases were randomly selected each time the comparison f₀ (f_0,comp) was adjusted. Following each presentation of the two sequential complexes, the listener had eight choices, selected by virtual buttons displayed on a computer monitor, and selected via mouse click: (1–6) increase or decrease the f_0,comp by a large, medium, or small amount, (7) hear the same two stimuli again without manipulating the f_0,comp, or (8) indicate that the match was satisfactory. The step sizes for the large, medium, or small f₀ adjustments were 4, 1, and 1∕4 semitones, respectively. The smallest step size in the pitch matching procedure (corresponding to about 1.5%) would not be expected to be sensitive enough to detect small shifts in the perceived pitch on the order of 1–3% that have been observed in other studies of the effect of frequency shifting individual components on the perceived pitch (e.g., Moore et al., 1985; Darwin and Ciocca, 1992). However, this experiment was mainly concerned with testing the hypotheses that the shift in the f₀ DL transition point by a factor of about 2, observed in experiment 1, is related to an octave shift in the perceived pitch.

In pilot runs, it was found that listeners almost always matched an altered tone complex (i.e., f₀ shifted and∕or dichotic) with a diotic harmonic tone complex that was near either the f₀ or twice the f₀(2f₀) of the altered complex. Therefore, the range of starting f₀’s was specified to be symmetrical (on a log scale) around this zero- to one-octave range of matches. For AREF runs, the starting f_0,comp was randomly selected from a range of −0.25 to +1.25 octaves relative to the reference f₀ (f_0,ref). The range of possible f_0,comp values was limited to the range of −1 to +2 octaves relative to the f_0,ref. If a listener attempted to increase or decrease the f_0,comp outside of this range, the f_0,comp would simply stay at its previous value for the next stimulus presentation. For ACOMP runs, the starting f_0,comp was randomly selected from a range of −1.25 to +0.25 octaves and the range of f_0,comp was limited to −2 to +1 octaves relative to the f_0,ref. An analysis of the results (not shown) indicated that there was no systematic relationship between the starting value of f_0,comp and the pitch match.

For each of the three altered tone complex conditions (diotic shifted, dichotic shifted, and dichotic harmonic), each listener completed ten AREF pitch matches with the f₀ of the altered complex held fixed at each of the seven f₀’s that were tested in experiment 1. Each listener also completed ten ACOMP pitch matches each with the f₀ of the diotic harmonic complex held fixed at 100, 125, 150, 175, and 200 Hz, for a total of 360 pitch matches. The 50- and 75-Hz f₀’s were not included in the latter pitch matches because listeners were generally unable to provide a reliable match of altered tone complex to these low-pitched diotic harmonic stimuli. For conditions involving dichotic complexes, even and odd components were assigned to the left and right ear, respectively, for five of the ten pitch-match runs, and vice versa for the remaining five runs. Before the testing phase, each listener completed one practice pitch match for each condition (for a total of 36 practice runs). An additional experiment (4B) determined the perceived pitch associated with the odd harmonics only. Four listeners (Table 1) completed the pitch matching task by comparing the pitch associated with a complex containing only odd harmonics to a complex containing all harmonics for the same ten f₀’s that were tested in experiment 1B. Each listener received at least 20 min practice before data collection began.

Results

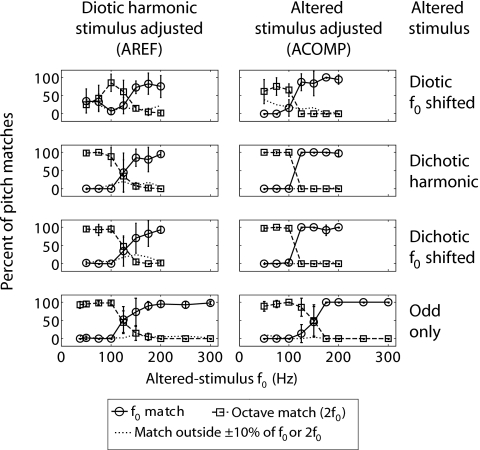
The AREF data (left column of Fig. 5) indicate the perceived pitch of each altered stimulus. Across all listeners and conditions, the overwhelming majority of pitch matches were close to the f₀ of the reference stimulus or its octaves. In the AREF conditions, the diotic harmonic stimulus was matched to within 10% of either the f_0,ref or 2f_0,ref on 94% of the trials across listeners. In the ACOMP conditions, the altered stimulus was matched to within 10% of either 0.5 f_0,ref or f_0,ref on 91% of the trials. The left column of Fig. 5 plots the percentage of trials for which each of these outcomes occurred as a function of the f_0,ref (the ACOMP data shown in the right column are discussed below). Each row represents one of the four altered-stimulus conditions: Diotic f₀-shifted, dichotic harmonic, dichotic f₀-shifted, and odd only. Circles and squares show the proportion of responses for which the perceived pitch of the altered stimulus was within 10% of the f₀ or within 10% of twice the f₀, respectively. The dashed lines indicate the proportion of pitch matches that did not fall within ±10% of the f₀ or 2f₀.

Figure 5.

Mean results of experiment 4 across four listeners. Left column: Summary of pitch matches for the AREF conditions, where the f₀ of the altered tone complex (dichotic, f₀-shifted or odd-only) is held constant and the listener adjusts the f₀ of the diotic harmonic complex. The proportion of pitch matches that were within ±10% of the f_0,ref (circles) or twice the f_0,ref (squares) are plotted as a function of the f_0,ref. Right column: Summary of pitch matches for the ACOMP condition, where the f₀ of the diotic harmonic complex is held fixed and the listeners adjust the f₀ of the altered stimulus to match. The proportion of pitches that were within ±10% of the f_0,ref (circles) or half the f_0,ref (squares) are plotted as a function of the f_0,ref. For both columns, the dotted line indicates the proportion of matches that did not fall within ±10% of the f_0,ref or within ±10% an octave above (left panel) or below (right panel) the f_0,ref. Error bars indicate ± one standard error across the four listeners.

Pitch matches at each f₀ can be grouped into four categories. The first two categories are a clear match at the f₀ or its octave, indicated by circles or squares near 100%, respectively, suggesting a clear and unambiguous pitch percept. The third category is a bimodal distribution of pitch matches, where matches were equally apportioned between the f₀ and its octave, indicated by circles and squares both near 50% (i.e., the 125-Hz f₀ in all four panels), suggesting either a bistable percept, where sometimes one pitch was heard, sometimes another, or an ambiguous pitch that could not be clearly assigned to either octave. The large error bars in these cases indicate that some subjects consistently matched to the f₀, while others matched to the octave. The fourth and final category is a broad distribution of matches, with a roughly equal number of matches near the f₀, its octave, or outside of the ±10% ranges surrounding these values (i.e., the 50- and 75-Hz diotic f₀-shifted conditions), suggesting an ambiguous and unstable pitch percept.

Overall, these plots indicate that each stimulus alteration (dichotic presentation, f₀ shift and odd-harmonics only) had a similar effect on the perceived pitch. The pitch was roughly equal to the f₀ for altered-stimulus f₀’s above 125 Hz, and equal to 2f₀ for altered-stimulus f₀’s below 125 Hz, with a bistable pitch at 125 Hz (and 150 Hz in the odd-only condition). The only exceptions to this trend were for low f₀’s of 50 or 75 Hz in the diotic f₀-shifted condition, where the pitch was ambiguous, often producing matches outside of the ±10% range surrounding the f₀ and 2f₀. The ambiguous pitch in these diotic f₀-shifted conditions may reflect the complex beat patterns that result from peripheral interactions between the even and frequency-shifted odd components.

The ACOMP data are plotted in the right column of Fig. 5. For direct comparison with the AREF data, these data are also plotted as a function of the f₀ of the altered stimulus, which in this case was the dependent variable over which the listener had control. For each altered-stimulus type, the matched f₀’s were grouped into 25-Hz-wide bins with midpoints ranging from 50 to 200 Hz (or 50 to 300 Hz in the odd-only conditions). The percent of trials (averaged across listeners) for which the matched altered-stimulus f₀’s that fell in each bin were within ±10% of the fixed diotic harmonic reference or its octave are plotted as circles and squares, respectively. For some combinations of f₀ and condition (especially f₀’s⩾100 Hz), at least one of the listeners had no pitch matches that fell within a particular bin. In such cases, the proportion of f₀ or octave matched trials were averaged across the remaining listeners.

Overall, the ACOMP conditions yielded very similar results to the AREF conditions, with only two small differences. First, the crossover from a match at the f₀ to a match at the octave occurred at a slightly different f₀ DL in the ACOMP conditions (higher than the AREF crossover in the odd-only conditions, lower in the other conditions). Second, the matches at the lowest f₀’s in the diotic f₀-shifted conditions were less ambiguous in the ACOMP than in the AREF case. One possible explanation for these slight differences is that listeners had control over the altered-stimulus f₀ in the ACOMP conditions, and therefore could have steered away from more ambiguous pitches associated with these stimuli.

Discussion

In experiment 1A, the stimuli that showed the most benefit from the f₀ shift were those with a 100- or 125-Hz f₀, and to some extent a 150-Hz f₀ (Fig. 1). The upper left panel of Fig. 5 shows that for the 100- and 125-Hz f₀’s, the diotic f₀-shifted stimuli yielded an octave shift in the perceived pitch. The octave shift in the perceived pitch is consistent with a pitch based on the even components alone, and suggests that for these stimuli, f₀ discrimination performance is determined by the harmonic number of the perceived pitch of the stimulus.

For the dichotic stimuli, the pitch matches were the same in the harmonic and f₀-shifted conditions (second and third rows of Fig. 5). For the dichotic harmonic stimuli, the doubling of the f₀ match relative to the diotic harmonic condition was not associated with an improvement in a shift in the f₀ DL transition point. In this case, poor pitch discrimination performance might be expected if the pitch were extracted from the envelope repetition rate, which would be shifted by an octave relative to the diotic case as result of the doubling of the peripheral spacing between adjacent components in each ear. Although the octave shift in the 100 and 125 Hz dichotic f₀-shifted conditions (Fig. 5, third row), where an f₀ discrimination improvement was observed in experiment 1A, might also reflect a doubling in the envelope repetition rate, it would be surprising for a pitch based on the envelope repetition rate to be as discriminable as the pitch associated with resolved harmonics, as was observed for the 100–150 Hz f₀-shifted dichotic conditions in experiment 1A. This argues in favor of the idea that the octave shift reflects a pitch percept associated with the even components alone.

Taken together, the results of the pitch matching and f₀ discrimination data argue that f₀ discrimination performance is determined by the harmonic number of the perceived pitch of the stimulus, except in cases where the pitch is extracted from the envelope repetition rate, in which case discrimination is always poor.

GENERAL DISCUSSION

The role of the auditory periphery

The main goal of this study was to determine the extent to which peripheral and∕or central harmonic resolvability governs performance in f₀ discrimination tasks. In terms of the three hypotheses laid out in the introduction: (1) harmonic resolvability, as defined by a “central spectrum” combining the spectra from the two ears, does not appear to limit performance; (2) peripheral (monaural) resolvability also seems not to limit performance; and (3) good f₀ discrimination seems not to depend directly on harmonic resolvability at all, but instead on the harmonic number associated with the perceived f₀. These results therefore appear to provide strong evidence against models of pitch perception that depend solely on spectrally resolved harmonics for good performance (e.g., Goldstein, 1973; Wightman, 1973; Terhardt, 1974).

Taken in isolation, these results might suggest little or no relationship between peripheral auditory filtering and f₀ discrimination. This conclusion would, however, contradict our earlier findings of a strong relationship between auditory filter bandwidths and f₀ discrimination, both as a function of overall level in normal-hearing listeners (Bernstein and Oxenham, 2006a), and as a function of degree of hearing loss (and filter widening) in hearing-impaired listeners (Bernstein and Oxenham, 2006b). Instead, a parsimonious interpretation of the available results is that f₀ discrimination depends on auditory filter bandwidth, but not on harmonic resolvability per se. Of course, in most everyday situations the two measures co-vary, as wider auditory filters imply poorer harmonic resolvability. It is only through the technique of mistuning harmonics to induce perceptual segregation (present study), and of presenting harmonics to opposite ears (Bernstein and Oxenham, 2003), that we were able to dissociate them.

We are aware of only one model that explicitly dissociates auditory filter bandwidth from harmonic resolvability, as our data suggest should be the case. As mentioned in the introduction, the model of de Cheveigné and Pressnitzer (2006) is explicitly based on filter bandwidths, but does not depend on harmonic resolution and is based instead on a variant of the temporal autocorrelation function (Licklider, 1951; Meddis and O’Mard, 1997). However, that model, in its current form, is not sufficiently developed to provide quantitative predictions for our data. The following section uses another variant of the autocorrelation function to test whether such an approach can, in principle, account for the perceptual effects of mistuning odd and even harmonics from each other.

Autocorrelation model

Autocorrelation (AC) models of pitch perception (Licklider, 1951; Meddis and Hewitt, 1991a, b; Meddis and O’Mard, 1997) account for the human ability to extract the missing f₀ based on periodic temporal information in auditory nerve fiber (ANF) responses. The AC model proposed by Bernstein and Oxenham (2005) is a modification of that of Meddis and O’Mard (1997), in which individual AC functions are first calculated in a population of simulated ANFs with characteristic frequencies (CFs) distributed across the tonotopic range of the cochlear partition, and then summed to produce a single f₀ estimate. Like the AC model of de Cheveigné and Pressnitzer (2006), that of Bernstein and Oxenham (2005) contains a CF-dependent limitation on the range of lags for which the AC can be computed—an essential ingredient in accounting for the deterioration in f₀ discrimination performance with increasing harmonic number, independent of absolute frequency. These models differ in that this lag-range limitation is directly related to the characteristics of peripheral auditory filters in the case of de Cheveigné and Pressnitzer (2006), but is applied in an ad hoc manner by Bernstein and Oxenham (2005), such that the latter model is unlikely to account for the effects of broadened auditory filters on f₀ discrimination observed by Bernstein and Oxenham (2006a, b). This difference should be largely inconsequential for the current experiments, where stimuli were presented at a fixed level in normal-hearing listeners, such that auditory filter characteristics were unlikely to vary across conditions.

Meddis and O’Mard (1997) showed that an AC model of pitch perception was able to account for the decreased influence of a mistuned harmonic on the overall pitch percept associated with a harmonic complex as the degree of mistuning increases (Darwin et al., 1994). Given this result, we hypothesized that the modified AC model of Bernstein and Oxenham (2005) might account for the improved f₀ discrimination resulting from the 3% odd-harmonic mistuning in the current study, as follows. As the odd harmonics become mistuned, their contribution to the pitch associated with the even harmonics will be reduced. Since the predicted f₀ discrimination performance of the model depends on the harmonic number associated with the perceived f₀ (i.e., the ratio between the first peak in the autocorrelation function and the absolute frequency region of the stimulus), a doubling of the perceived pitch might yield improved predicted performance. To test this hypothesis, the diotic harmonic and f₀-shifted stimuli of experiment 1A were presented to the modified AC model of Bernstein and Oxenham (2005).

The modified AC model consists of an outer∕middle ear bandpass filter, a gammatone filterbank (Patterson et al., 1992) consisting of 40 channels with characteristic frequencies (CFs) logarithmically spaced between 1.5 and 5 kHz to simulate basilar-membrane filtering, followed by a model of inner hair cell and auditory nerve processing (Sumner et al., 2002). An autocorrelation function in each channel was calculated for the binary stochastic spike train generated in response to each stimulus. The periodicity-range limitation was then applied by weighting the calculated autocorrelation in each channel relative to the channel’s CF using the parameter values given by Bernstein and Oxenham (2005) that best fit the psychoacoustic f₀ discrimination data described in that study.2 A summary autocorrelation function (SACF) was produced by adding the weighted autocorrelation functions across channels. This was repeated 100 times for each stimulus. An optimal-detector d^′ metric (Van Tress, 2001) was then generated for pairs of stimuli differing in f₀ for 30 log-spaced values of Δf₀ ranging from 0.5% to 30% of the f₀. The f₀ DL estimate was defined as the minimum Δf₀ to yield a value of d^′ greater than some fixed threshold value. The only deviations from the modeling procedure described in Bernstein and Oxenham (2005) were (1) the threshold d^′ was manipulated to allow a better fit to the data, and (2) d^′ was defined as exceeding threshold if it remained above threshold for three consecutive values of Δf₀ (instead of the requirement that d^′ exceed threshold for all larger values of Δf₀ tested).

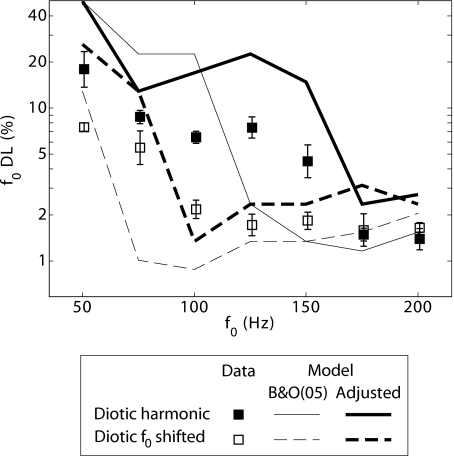
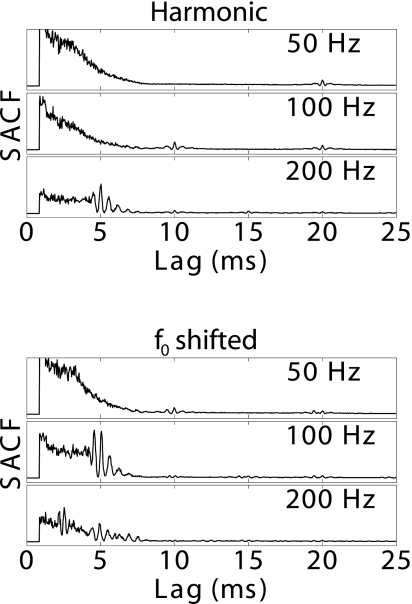
Figure 6 replots the data from the diotic conditions of experiment 1 (symbols) and the results of the model simulations (lines). The thin solid and dashed lines show model predictions for the harmonic and f₀-shifted conditions, respectively, based on the set of model parameters defined by Bernstein and Oxenham (2005), except that the threshold d^′ was changed to 6×10⁴ (instead of 7.91×10⁴). These very large values of d^′ emerge because of the large number of simulated ANFs and autocorrelation lag points providing information about the stimulus f₀, and because no attempt was made to add further “internal noise” to limit performance. The model successfully accounted for the decrease in f₀ DLs with increasing f₀ seen in the psychoacoustic data of experiment 1A. This correct behavior of the model as a function of f₀ was expected given the modeling results of Bernstein and Oxenham (2005), and is a result of the CF-dependent lag window modification applied to the individual channel autocorrelation calculations. More importantly for the current study, the model also accounted for the improvement in f₀ discrimination performance in the f₀-shifted condition, with the f₀ DL transition shifting toward lower f₀’s by approximately a factor of 2. The reason for the successful prediction of the f₀-shift benefit can be found in the SACFs that underlie the model’s f₀ DL estimates. Mean SACFs across 100 stimulus presentation are shown in Fig. 7 for harmonic and f₀-shifted stimuli at three different f₀’s (50, 100, and 200 Hz). For each f₀, the odd-harmonic f₀ shift introduces an additional SACF peak at half the lag (double the periodicity) of the first peak of the harmonic SACF. In the harmonic condition, peaks at this lag in the individual channel AC functions associated with the even components tend to destructively interfere with the AC functions associated with the odd components. With the f₀ of the odd components shifted, the destructive interference is removed and the additional peak appears. This additional peak yields an SACF function similar to that observed for the harmonic stimulus at 2f₀ (compare the 50- and 100-Hz f₀-shifted conditions to the 100- and 200-Hz harmonic conditions, respectively). The additional SACF peak falls at a more favorable lag relative to the autocorrelation lag weighting function, yielding the f₀ discrimination benefit.

Figure 6.

Predictions of the Bernstein and Oxenham (2005) autocorrelation model of f₀ discrimination performance for the diotic harmonic (solid lines) and f₀-shifted (dashed lines) tone complexes presented in experiment 1A. Thin lines show model predictions with model parameters as specified by Bernstein and Oxenham (2005). Thick lines show model predictions with lag-range limitation parameters adjusted to better account for the locus of the transition from large to small f₀ DLs. Diotic data from experiment 1 (Fig. 1) are replotted as closed (harmonic) and open (f₀-shifted) squares.

Figure 7.

Mean SACFs across 100 stimulus presentations produced by the Bernstein and Oxenham (2005) autocorrelation model in response to diotic tone complexes that were presented to listeners in experiment 1. The effect of the odd-harmonic f₀ shift (lower panel) was to produce an additional SACF peak at half the lag of the first peak for the corresponding harmonic condition (upper panel). This additional peak occurs at a more favorable lag relative to the CF-dependent lag-range limitation, yielding the f₀ discrimination benefit observed in Fig. 6.

The model was not entirely successful at accounting for the diotic f₀ discrimination data. First, the model predicted a larger difference between the f₀ DLs for low and high f₀’s than was observed experimentally, a failing that was also noted by Bernstein and Oxenham (2005). Second, the locus of the transition point from large to small f₀ DLs occurs at a lower range of f₀’s in the model results (100–125 Hz and 50–75 Hz for the harmonic and f₀-shifted conditions, respectively) than in the experimental data (125–175 Hz and 75–100 Hz, respectively). The locus of this transition in the model more closely matched that of the data when the lower cutoff of the lag-range limitation was adjusted to a harmonic number of 8.0 (instead of 10.8) and of the d^′ threshold was set to 4.2×10⁴ (thick solid and dashed lines in Fig. 6). However, this change in parameters would also be likely to shift the f₀ DL transition toward a lower harmonic number in the modeling results of Bernstein and Oxenham (2005), thereby yielding a poorer fit to the data in that study. Some further adjustment of the lag-window parameters may be required to fit a broader range of f₀ discrimination data than those presented in the current study and that of Bernstein and Oxenham (2005).

The place-dependent autocorrelation models of Bernstein and Oxenham (2005) and de Cheveigné and Pressnitzer (2006) are in principle consistent with the relative lack of benefit to f₀ discrimination performance provided by dichotic presentation of even and odd harmonics observed in experiment 1A and by Bernstein and Oxenham (2003), because they do not depend on peripheral resolvability to account for harmonic-number dependence of f₀ DLs. An initial attempt was made to test the Bernstein and Oxenham (2005) model for the dichotic stimuli presented in experiment 1A. Discrimination predictions were generated using the same procedure described above, except that SACFs were calculated by summing the SACFs from the two ears. This simulation did not produce satisfactory results, predicting a large deficit in performance under dichotic presentation (results not shown). Further work is needed to determine whether this is a basic failing of the model. It may be that a different method of combining binaural information in the model would yield more satisfactory results.

Concurrent source segregation

Although the predictions of the modified AC model are generally consistent with the diotic f₀ discrimination data, they do not generally agree with the pitch matching data of experiment 4 (Fig. 5). The model predicts a doubling of the perceived pitch with the introduction of the f₀ shift across all f₀’s, as evidenced by the appearance of the additional SACF peak at half the lag. In contrast, an octave shift in the perceived pitch was only observed experimentally at 100 and 125 Hz (Fig. 5, upper left panel). This discrepancy may be reconciled if for higher f₀’s listeners were segregating the even and odd harmonics into separate objects, each with its own pitch, rather than extracting a single pitch from the stimulus as a whole. While segregation is more likely to have occurred in the dichotic conditions where f₀ and ear of presentation were both available as segregation cues, listeners may have been able to segregate even and odd harmonics in at least some of the diotic f₀-shifted conditions, especially for f₀’s of 175 Hz and above where resolved harmonics were most likely available. This raises an interesting paradox at 150 Hz (lowest harmonic=10) where resolved harmonics were not available (Fig. 4), but perceptual segregation of two distinct percepts is needed to reconcile the data and model results. Indeed, the results of Micheyl et al. (2006) suggest that listeners may be able to hear out the pitch of a complex tone with low-order harmonics in the presence of a second complex tone for a large f₀ differences (seven-semitones or about a 50%), even when the two complexes would not yield any resolved harmonics when combined. Perhaps the perceptual segregation of the mistuned odd harmonics from the even harmonics is facilitated by the fact that many odd harmonics are mistuned simultaneously. In conditions close to the limits of resolvability (i.e. the lowest harmonic number=10), this effect may be sufficient to yield two distinct pitch percepts.

Temporal fine structure

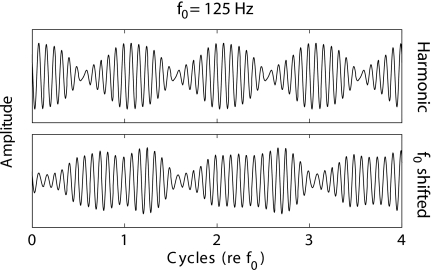
Moore et al. (2006) have argued that the deterioration in f₀ discrimination performance with increasing harmonic number may reflect a reduction in the usefulness of temporal fine structure information, rather than just a progressive reduction in peripheral harmonic resolvability. While the lack of a limiting role of peripheral resolvability observed in the current study is generally consistent with the view, the question remains as to whether the odd-harmonic f₀ shift improved the availability of pitch cues in the temporal fine structure. Moore (1982) suggested that for stimuli where harmonics are unresolved and therefore interact within individual auditory filters, the pitch could be extracted from the fine-structure peak located near the envelope peak. According to this argument, the presence of multiple fine-structure peaks of similar amplitude occurring near the envelope peak would yield a less precise estimate of the pitch than a waveform with only one high-amplitude fine-structure peak per period. Figure 8 shows a snapshot of the output of a single fourth-order gammatone filter (Patterson et al., 1992), centered at 1500 Hz, in response to 125-Hz random-phase harmonic (upper panel) and f₀-shifted (lower panel) tone complexes. The filter at 1500 Hz was chosen because it represents the low-frequency edge of the stimulus bandpass filter, where the lowest-order harmonics (that generally yield the best discrimination performance) are present. While the odd-harmonic f₀ shift greatly benefited performance for the 125 Hz condition in experiment 1A, if anything, a greater number of prominent fine-structure peaks appear near the peaks in the envelope for f₀-shifted than for the harmonic stimulus in Fig. 8, which according to Moore (1982) should lead to a less discriminable pitch percept. Therefore, although an explanation for the f₀-shift benefit in terms of the temporal fine structure argument of Moore et al. (2006) cannot be ruled out, these plots do not appear to be consistent with such an explanation.

Figure 8.

Output of a single gammatone filter with CF=1500 Hz in response to a 125 Hz diotic harmonic tone complex (upper panel) and an f₀-shifted tone complex (lower panel).

SUMMARY AND CONCLUSIONS

Fundamental frequency discrimination was measured for bandpass-filtered harmonic complexes as a function of f₀. In line with earlier studies, f₀ DLs increased (worsened) substantially when harmonics below about the 10th were no longer present. However, when the odd harmonics were mistuned by a constant percentage, performance improved to the extent that the results were the same as when only even harmonics were present. Similar patterns of results were observed whether the odd and even harmonics were presented to the same or different ears (experiment 1). The amount of mistuning necessary to eliminate the perceptual interference from the odd harmonics was about 3%, although 2% was sufficient to observe some release (experiment 2). Although mistuning the odd harmonics dramatically improved f₀ DLs, it had no reliable effect on the ability of listeners to hear out individual harmonics, suggesting that the mistuning did not systematically improve the resolvability of the harmonics (experiment 3). In the f₀ region over which harmonic mistuning improved performance, the mistuning typically led to a doubling in the perceived f₀, in line with expectations from a pitch based on the even harmonics only (experiment 4). Taken together with previous studies, these results indicate that peripherally resolved harmonics are in themselves neither necessary nor sufficient to support accurate pitch perception.