Quantification of breast density with dual energy mammography: A simulation study

Abstract

Breast density, the percentage of glandular breast tissue, has been identified as an important yet underutilized risk factor in the development of breast cancer. A quantitative method to measure breast density with dual energy imaging was investigated using a computer simulation model. Two configurations to measure breast density were evaluated: the usage of monoenergetic beams and an ideal detector, and the usage of polyenergetic beams with spectra from a tungsten anode x-ray tube with a detector modeled after a digital mammography system. The simulation model calculated the mean glandular dose necessary to quantify the variability of breast density to within 1∕3%. The breast was modeled as a semicircle 10 cm in radius with equal homogenous thicknesses of adipose and glandular tissues. Breast thicknesses were considered in the range of 2–10 cm and energies in the range of 10–150 keV for the two monoenergetic beams, and 20–150 kVp for spectra with a tungsten anode x-ray tube. For a 4.2 cm breast thickness, the required mean glandular doses were 0.183 μGy for two monoenergetic beams at 19 and 71 keV, and 9.85 μGy for two polyenergetic spectra from a tungsten anode at 32 and 96 kVp with beam filtrations of 50 μm Rh and 300 μm Cu for the low and high energy beams, respectively. The results suggest that for either configuration, breast density can be precisely measured with dual energy imaging requiring only a small amount of additional dose to the breast. The possibility of using a standard screening mammogram as the low energy image is also discussed.

INTRODUCTION

According to the WHO, as of 2005, breast cancer is the fifth most common cause of cancer death, responsible for over half a million deaths per year worldwide and the leading cause of all cancer deaths in women.¹ Breast density, the percentage of glandular breast tissue, has been shown to be a strong indicator of breast cancer risk.^{2, 3, 4, 5, 6, 7, 8, 9, 10} The positive association between breast density and subsequent breast cancer risk originally reported by Wolfe used a qualitative classification scheme where images of the breast were visually assessed and assigned to one of four empirically derived categories: N1–primarily fat, P1≤25% prominent ducts, P2≥25% prominent ducts, and DY dense fibroglandular tissue. He reported a progressive stepwise increase in future breast cancer risk: N1–lowest risk, P1–low risk, P2–high risk, and DY–highest risk.^{2, 3}

Since the Wolfe report, a variety of approaches for measuring breast density, both areal and volumetric, have subsequently been described. Areal-based techniques have included qualitative and quantitative classification schemes,^{2, 11, 12} and also quantitative numerical estimations derived from manual and automatic segmentation of a digital image histogram and pixel values.^{11, 13, 14, 15, 16, 17, 18, 19} Although most of these quantitative measures provide a continuous measure of breast density, a notable limitation is the binary classification of a pixel into either 100% fibroglandular or 100% adipose tissue. Additionally, an areal measurement ignores the physical 3D character of a real breast. Breasts of different thicknesses can potentially all yield the same measurement of areal breast density yet correspond to widely varying volumetric breast density values. Volume-based techniques are able to overcome these limitations. These techniques have included attempts to standardize^{20, 21} and calibrate^{22, 23, 24} mammographic image data. However, these techniques require certain assumptions to be made in order to measure two independent quantities (e.g., breast density, and thickness) from a single image. A common limitation of such techniques is the assumption of uniform breast thickness.

Dual energy imaging can also be used to quantify breast density and has the advantage of measuring thicknesses of adipose and glandular tissues separately. While the female breast is composed largely of glandular and adipose tissue, dual energy imaging in mammography^{25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41} has primarily focused on the imaging of a third material such as calcium,^{25, 26, 28, 32, 33, 34, 37, 40, 41} iodine,^{29, 30, 35, 42} or neoplastic breast tissue.^{27, 38, 39, 43} In the above cases, information about the two primary tissues is often ignored, either by eliminating their contrast,^{26, 27, 38, 39, 43} considering them as a single tissue,³³ or shifting focus to a third material.^{25, 31, 44} There are a small number of reports on the use of dual energy imaging to measure breast density. Early simulation work by Breitenstein and Shaw³⁶ predicted dual energy SNR tissue composition values at a fixed level of exposure for selected dual kVp and single kVp techniques with spectra from a molybdenum target x-ray tube. Dual energy x-ray absorptiometry (DXA) has previously been applied to the measurement of breast density.⁶ However, the clinical application of this technique was hampered by the beam spectra of the DXA system, which are not optimal for measuring breast density. Dual energy mammography is not currently being used for breast density measurement.

The purpose of this simulation study is to investigate the use of dual energy imaging for the quantification of breast density. Two cases were evaluated. The first case considered the use of monoenergetic beams and an ideal photon counting detector, designed to predict the peak performance possible when using dual energy imaging to quantify breast density. The second modeled x-ray spectra from an investigational mammography system with an energy integrating detector, a tungsten target, and rhodium and copper beam filters for the low and high energy images. The two techniques were studied and the effects of varying beam energies, dose ratios, and prepatient filtration on breast density are presented for a range of breast thicknesses.

THEORY

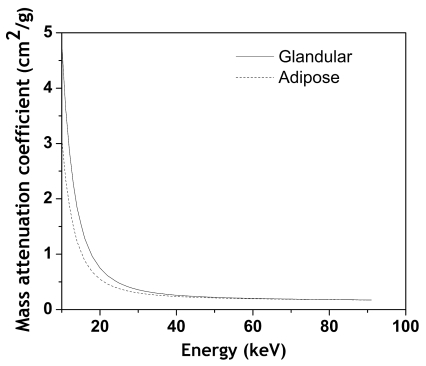
The basis for dual energy imaging is the differential attenuation of glandular and adipose tissues as a function of energy. Mass attenuation curves for the two tissues are shown in Fig. 1. The figure shows that in order to maximize the differential attenuation, the mean energy of the low energy beam needs to be as low as possible and the mean energy of the high energy beam needs to be as high as possible. An analytical computer simulation model modeling x-ray photon transport was developed to investigate the technique feasibility over the range of expected breast densities and thicknesses encountered in clinical mammography.

Figure 1.

Plot showing the energy dependence of x-ray attenuation for glandular and adipose tissue.

Calculation of breast density

The low and high energy detector signals are functions of glandular and adipose tissue thicknesses:

$$S_i=S_i(t_g,t_a),i=l,h.$$ (1)

The tissue thicknesses can be determined by inverting the system of equations:

$$t_j=t_j(S_l,S_h),j=g,a.$$ (2)

Each pixel provides a measurement of each tissue thickness. The breast density d for a pixel can be expressed

$$d=\frac{t_g}{t_g+t_a}.$$ (3)

The total breast density, D, is then defined as the average over all pixel measurements within the breast shadow (N):

$$D=\frac{{\sum }_{i=1}^{N}d}{N}.$$ (4)

Breast density measurement uncertainty

The measurement uncertainty in breast density for the whole breast (D) can be written using propagation of error:

$${\sigma }_D^2={\left(\frac{\partial D}{\partial t_g}\right)}^2{\sigma }_{t_g}^2+{\left(\frac{\partial D}{\partial t_a}\right)}^2{\sigma }_{t_a}^2+2\left(\frac{\partial D}{\partial t_g}\right)\left(\frac{\partial D}{\partial t_a}\right){\sigma }_{t_g{t}_a}.$$ (5)

After substituting in expressions for the partial derivatives, the uncertainty can be written as

$${\sigma }_D^2={\left(\frac{t_a}{{(t_g+t_a)}^2}\right)}^2{\sigma }_{t_g}^2+{\left(\frac{-t_g}{{(t_g+t_a)}^2}\right)}^2{\sigma }_{t_a}^2+2\left(\frac{t_a}{{(t_g+t_a)}^2}\right)\left(\frac{-t_g}{{(t_g+t_a)}^2}\right){\sigma }_{t_g{t}_a}.$$ (6)

Expressions for ${\sigma }_{t_g}^2$, ${\sigma }_{t_a}^2$, and σ_tgta are functions of the detector signals S_l and S_h. Their derivation follows from a similar analysis, presented in the Appendix, and can be written as

$${\sigma }_{t_g}^2=\frac{\frac{{\left(\overline{{\mu }_a\left(E_h\right)}\right)}^2}{{\mathrm{SNR}}_{S_l}^2}+\frac{{\left(\overline{{\mu }_a\left(E_l\right)}\right)}^2}{{\mathrm{SNR}}_{S_h}^2}}{{(\overline{{\mu }_a\left(E_l\right)}\overline{{\mu }_g\left(E_h\right)}-\overline{{\mu }_g\left(E_l\right)}\overline{{\mu }_a\left(E_h\right)})}^2},$$ (7)

$${\sigma }_{t_a}^2=\frac{\frac{\overline{{\mu }_g^2\left(E_h\right)}}{{\mathrm{SNR}}_{S_l}^2}+\frac{\overline{{\mu }_g^2\left(E_l\right)}}{{\mathrm{SNR}}_{S_h}^2}}{{(\overline{{\mu }_a\left(E_l\right)}\overline{{\mu }_g\left(E_h\right)}-\overline{{\mu }_g\left(E_l\right)}\overline{{\mu }_a\left(E_h\right)})}^2},$$ (8)

$${\sigma }_{t_g{t}_a}=\frac{\frac{\overline{{\mu }_a\left(E_h\right)}\overline{{\mu }_g\left(E_h\right)}}{{\mathrm{SNR}}_{S_l}^2}+\frac{\overline{{\mu }_a\left(E_l\right)}\overline{{\mu }_g\left(E_l\right)}}{{\mathrm{SNR}}_{S_h}^2}}{-{(\overline{{\mu }_a\left(E_l\right)}\overline{{\mu }_g\left(E_h\right)}-\overline{{\mu }_f\left(E_l\right)}\overline{{\mu }_a\left(E_h\right)})}^2},$$ (9)

where ${\mathrm{SNR}}_{S_i}^2$ is the squared signal to noise ratio of the detector signal S_i and $\overline{{\mu }_j\left(E_i\right)}$ is the mean attenuation of material j for detector signal i. Combining all of the above terms, the breast density measurement uncertainty can be written in final form as

$${\sigma }_D^2=\left(\frac{1}{{(\overline{{\mu }_a\left(E_l\right)}\overline{{\mu }_g\left(E_h\right)}-\overline{{\mu }_a\left(E_h\right)}\overline{{\mu }_g\left(E_l\right)})}^2}\right){\left(\frac{1}{{(t_a+t_g)}^2}\right)}^2[{\left(t_a\right)}^2(\frac{\overline{{\mu }_a^2\left(E_h\right)}}{{\mathrm{SNR}}_{S_l}^2}+\frac{\overline{{\mu }_a^2\left(E_l\right)}}{{\mathrm{SNR}}_{S_h}^2})+{(-t_g)}^2(\frac{\overline{{\mu }_g^2\left(E_h\right)}}{{\mathrm{SNR}}_{S_l}^2}+\frac{\overline{{\mu }_g^2\left(E_l\right)}}{{\mathrm{SNR}}_{S_h}^2})\left(2t_a{t}_g\right)(\frac{\overline{{\mu }_g\left(E_h\right)}\overline{{\mu }_a\left(E_h\right)}}{{\mathrm{SNR}}_{S_l}^2}+\frac{\overline{{\mu }_g\left(E_l\right)}\overline{{\mu }_a\left(E_l\right)}}{{\mathrm{SNR}}_{S_h}^2})].$$ (10)

Given a known breast density, D, it is possible to express the percent relative standard deviation (%RSD) as

$$\%{\mathrm{RSD}}_D=\frac{{\sigma }_D}{D}\times 100.$$ (11)

MATERIALS AND METHODS

Simulation input functions and parameters

Detector signals

The detector signal S is given by

$$S=\int f^2{N}_0\left(E\right)e^{-\left({\mu }_f\left(E\right)t_f\right)}{e}^{-({\mu }_g\left(E\right)t_g+{\mu }_a\left(E\right)t_a)}W\left(E\right)Q\left(E\right)G\left(E\right)dE,$$ (12)

where f is the aperture size. The square of the aperture is the effective measurement area and was set at 0.0049 mm² to correspond with an aperture size of 70 μm, which is the same as one aperture used in digital mammography (Selenia, Hologic Inc., Bedford, MA). The fill factor was set to be unity.

N₀(E) is the incident x-ray spectrum (photon fluence per energy). For the case of two monoenergetic beams, beam spectra were simulated from 10 to 150 keV.

For the case of two polyenergetic beams, the XCOMP5R code of Nowotny and Hoofer⁴⁵ was used to simulate x-ray photons generated from a tungsten anode x-ray tube. A typical effective anode angle in mammography is 24 deg.⁴⁶ This effective angle was also used as the inherent anode angle for simulations. A comparison of the XCOMP5R, at an anode angle of 24 deg, and TASMIP (Ref. ⁴⁷) spectral models showed only a small difference (<3%) in incident mean beam energy. Typically, however, the inherent anode angle is between 0 and 16 deg with the remaining angulation provided by titling the x-ray tube. The x-ray tube filtration was set at 1 mm Be. Beam spectra were simulated from 20 to 150 kVp.

The term e^{−(μ_f(E)t_f)} corresponds to the prepatient filtration. Spectra from the tungsten anode x-ray tube were filtered by 50 μm rhodium for the low energy image and 300 μm copper for the high energy image. The filter in the low energy image corresponds to what would be expected in a screening mammogram. The purpose of a high energy filter is to increase the mean beam energy. Numerous options spanning the periodic table are available yielding similar increases. The best choice is a compromise between increasing beam energy and minimizing tube loading. The selection of a 300 μm copper filter provides excellent beam filtration and does not increase the resultant tube loading to prohibitively high levels.

μ_j(E_i) is the attenuation coefficient of material j at energy E. Elemental attenuation coefficients were obtained from a previous report by Boone.⁴⁸ Values spanned the full periodic table and energies extended below and above the range necessary for applications in medical imaging. The chemical compositions of glandular and adipose tissues were from the data of Hammerstein.⁴⁹ Combined, the data defined the functions μ_g(E) and μ_a(E).

t_j is the corresponding tissue thickness. Breast thicknesses were considered in a range of 2–10 cm.

W(E) is an energy weighting factor used to describe the detector type, and Q(E) is the quantum detection efficiency of the detector. An ideal photon counting detector was simulated in the first case and, for this case, W(E) and Q(E) were both set to 1. The second case simulated the detection properties of the amorphous selenium photoconductor in a digital mammography system. W(E) in this case was set to E and Q(E) was calculated for a 200 μm selenium absorber (mass thickness of 85.6 mg∕cm²).

G(E) is the absorption due to the presence of the cellular x-ray scatter grid. The transmission of the grid was measured at several energies and the data were empirically fit and extrapolated for all remaining higher energies. The grid has 30 μm copper septa with 640 μm air interspaces.^{50, 51}

Noise sources

Noise was considered similar to other cascaded system models⁵² but due to the size of the whole breast, frequency dependent effects were ignored and the propagation of noise was considered in the spatial domain. When considering the ideal detector, only quantum x-ray noise was included. When considering the detector in the digital mammography system, variances of quantum x-ray noise, gain (i.e., Swank) noise, digitization error, additive electronics noise, and the additional noise imparted due to x-ray scatter were included:

$${\sigma }_S^2={\sigma }_Q^2+{\sigma }_G^2+{\sigma }_{DQ}^2+{\sigma }_E^2+{\sigma }_{SC}^2,$$ (13)

where ${\sigma }_Q^2$ is the quantum x-ray noise. The quantum noise was calculated from the mean number of photons per unit area per energy. After transmission through material and absorption in the detector, the noise is expressed as

$${\sigma }_Q^2=\int f^2{N}_0\left(E\right)e^{-\left({\mu }_f\left(E\right)t_f\right)}{e}^{-({\mu }_g\left(E\right)t_g+{\mu }_a\left(E\right)t_a)}{W}^2\left(E\right)Q\left(E\right)G\left(E\right)dE.$$ (14)

The gain noise, ${\sigma }_G^2$, was modeled with an energy dependent Swank factor with data from previous work on amorphous selenium.⁵³ The gain noise is itself proportional to the quantum noise and not a completely independent term.

The digitization error, ${\sigma }_{DQ}^2$, was estimated given the mean entrance exposure necessary to generate one gray level. The additive electronics noise, ${\sigma }_E^2$, was determined by a logarithmic fit of noise as a function of signal. The offset of the fit corresponded to the additive electronics noise in pixel counts. These last two values were determined, in part, with data provided by the manufacturer of our digital mammography system.⁵⁴

The noise due to x-ray scatter, ${\sigma }_{SC}^2$, was estimated from measurements of scatter-to-primary ratio (SPR) with the digital mammography system using lead beam stops at BR12 phantom thicknesses of 0.5, 1, 2, 4, 6, and 8 cm at three different energies. The data were empirically fit and extrapolated for all higher energies. The added noise variance due to x-ray scatter was equal to the calculated SPR.

Mean glandular dose

Values for the mean glandular dose (MGD) per photon were calculated with Monte Carlo simulations.^{55, 56} Dose data were available for breast thicknesses of 2–10 cm, densities of 0%, 50%, and 100%, and energies of 5–150 keV.

THE OPTIMIZATION PROBLEM

The breast was modeled as a semicircle 10 cm in radius and composition was set to 50% glandular and 50% adipose tissue by volume (homogenous equal thicknesses of adipose and glandular tissues), consistent with the FDA definition of the standard breast.⁴⁶ A thickness of 4.2 cm was selected to be representative of the set. The size of the breast is inversely related to the total required dose due to statistical pixel averaging and occupies an area equivalent to 3 205 704 pixels (at a pixel pitch of 70 μm). We require the precision of greater than 99% of all breast density measurements to fall within 1%. Thus, for a normal distribution, a particular simulation was considered a success if the %RSD for the whole breast was less than 1∕3%. For a given beam pair and breast thickness, the %RSD was calculated at a particular dose and dose ratio (i.e., the relative allocation of available dose for the low and high energy images). The dose ratio was varied from 0 to 1 with a step size of 0.1. If no ratio passed the tested %RSD criteria, the particular dose was incremented and the process repeated until success. In addition, to test the effect of glandularity on the required dose, compositions of 10% and 90% glandularity were also simulated at 4.2 cm for the tungsten anode beam. To test the effect of heterogeneity, two samples, each 1000 points in length, were compared. The first had a heterogeneous distribution, uniformly distributed, of glandularities evenly spaced from 0% to 100% with an effective mean glandularity of 50%. The second was a completely homogenous distribution, with the glandularity fixed at 50%. The mean variances were compared for the two distributions at an equal fixed mean glandular dose for the tungsten anode beam.

RESULTS

Two monoenergetic beams

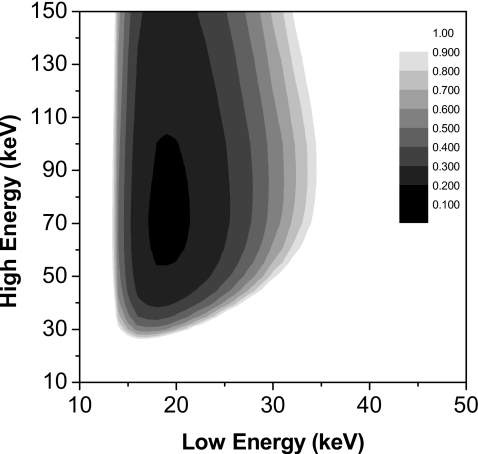
Shown in Fig. 2 is a dose contour plot for the two monoenergetic beams at a breast thickness of 4.2 cm. The minimal required MGD of 0.183 μGy was obtained at low and high beam energies of 19 and 71 keV. The optimal relative dose allocation between the low and high energy images was 0.6:0.4.

Figure 2.

Dose contour plot expressing the required MGD as a function of the two monoenergetic beams and a 4.2 cm breast. Minimal MGD was 0.183 μGy at 19 and 71 keV.

Tungsten anode spectra

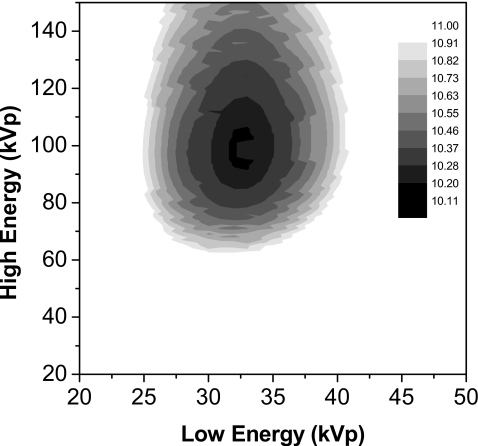
The dose contour plot for the dual energy case using x-ray beam spectra from a tungsten anode for a 4.2 cm breast is shown in Fig. 3. The minimal required MGD was 9.85 μGy and obtained at beam spectra of 32 and 96 kVp. The optimal dose allocation ratio was 0.7:0.3.

Figure 3.

Dose contour plot expressing the required MGD as a function of the two polyenergetic tungsten anode beam spectra and a 4.2 cm breast. Minimal MGD was 9.85 μGy at 32 and 96 kVp.

Additionally, the minimal required MGD for glandularities of 10% and 90% were 39.90 and 7.52 μGy, respectively. The relative increase in the mean variance for the heterogeneous data set relative to the homogenous data set was 6.6%.

The effect of dose allocation

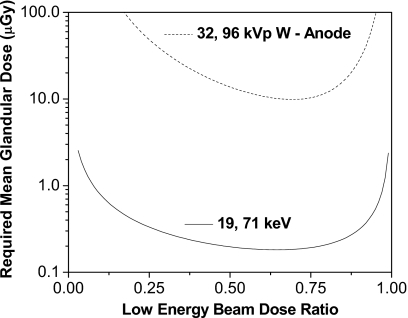
The effect of varying the dose allocation ratio is seen in Fig. 4, where the required dose is shown as a function of the low energy dose ratio for the two configurations: at 19 and 71 keV and at 32 and 96 kVp beam pair for a 4.2 cm breast.

Figure 4.

Required MGD as a function of the relative low energy dose for the two configurations and a 4.2 cm breast. Energies were 19 and 71 keV, and 32 and 96 kVp.

Summary of results

Optimal beam energies, dose ratios, and required MGD data for each technique and all thicknesses are shown in Table 1.

Table 1.

Minimal dose values, dose allocation ratios and energies for each technique, and thickness.

Breast thickness (cm)	Beam configuration
	Monoenergetic beams			Polyenergetic beams (W anode)
	Beam energy (keV) (low, high)	Dose ratio (low:high)	MGD (μGy)	Beam spectra (kVp) (low, high)	Dose ratio (low:high)	MGD (μGy)
2	16, 70	0.6:0.4	0.301	29, 87	0.6:0.4	10.39
3	17, 70	0.6:0.4	0.218	29, 86	0.7:0.3	9.33
4	19, 71	0.6:0.4	0.186	31, 94	0.7:0.3	9.59
5	20, 74	0.6:0.4	0.172	33, 102	0.7:0.3	10.36
6	21, 74	0.7:0.3	0.167	35, 110	0.7:0.3	12.10
7	22, 79	0.7:0.3	0.167	37, 116	0.7:0.3	13.64
8	23, 79	0.7:0.3	0.172	37, 103	0.7:0.3	16.12
9	24, 84	0.7:0.3	0.179	37, 104	0.7:0.3	19.48
10	25, 85	0.7:0.3	0.189	41, 137	0.7:0.3	22.66

DISCUSSIONS

The major limitation of dual energy application for microcalcification detection has been the low signal to noise ratio of the desired signal in the subtracted image.⁵⁷ This is in part due to the small area occupied by the object of interest. On the other hand, this is not the case for breast density quantification as the whole breast is used for measurement. This suggests that dual energy imaging is well suited to quantify breast density with respect to mean glandular dose.

Of the cases considered, as expected, the use of two monoenergetic beams showed the lowest dose requirement. The simulation of monoenergetic beams also provides physical insight and sets upper limits on the theoretical peak performance. In Fig. 2, for the 4.2 cm breast thickness, the ideal low energy beam was centered at 19 keV, coinciding with the first simulation study of dual energy mammography for imaging calcium by Johns and Yaffe²⁵ while the ideal high energy of 71 keV was slightly higher than the previously reported 68 keV. However, as the imaging tasks were different, it was not expected that the energies would be the same. The result for the ideal low beam energy is convenient as it is near the mean energy of most clinical mammographic spectra and suggests that a dual energy measurement of breast density can make use of an existing mammogram as the low energy image. This is further substantiated by the fact that the optimal low energy beam for tungsten anode is 32 kVp, which is within the clinical range. The tungsten anode beam spectra, however, did require substantially more dose than the monoenergetic beams. It is clear, however, that regardless of the technique, the overall predicted required dose is relatively low when compared to the dose of 1.6 mGy for a standard screening mammogram.⁵⁸ As an example, consider the case of spectra from the tungsten anode and a 4.2 cm breast thickness. The required dose is only 9.85 μGy, which is a small fraction of the dose from a standard screening mammogram. Furthermore, it is possible to use the standard screening mammogram itself as the low energy image. In this case, the relative dose allocation between the low and high energy image would not be optimal as the dose in the low energy image would far exceed what is required. However, this is not a hindrance as the required additional dose from the high energy image would remain low. The added dose for the tungsten spectra would be 2.96 μGy. Currently, the optimal kVp predictions are outside the range of current clinical mammography systems. However, the x-ray tube simulated in this study is based on a tungsten anode. Standard tungsten anode x-ray tubes are capable of imaging at high kVps and it is not difficult to conceive that a tungsten tube designed for mammography could be modified for usage at higher kVps. Alternatively, it is still possible to measure breast density if the system is limited to a certain maximum kVp, which will increase the required dose. Our digital mammography system is limited to maximum beam energy of 49 kVp. In this case the added dose from the high energy image would increase to 3.93 μGy for a 4.2 cm breast. In either case, the expected added dose from the additional high energy image is less than 1% of the dose for one view in the case of standard mammography (1.6 mGy).

The first breast DXA reported that the technique was highly repeatable. The mean energies for the 100 and 140 kVp broad beam spectra used in the DXA system were estimated to be approximately 52 and 64 keV, respectively.⁵⁹ The 100 kVp low energy beam is far above the optimal beam energy predicted in this study for quantifying breast density.

The study indicated that the clinical value of the DXA images was limited for quantifying breast tissue densities and choosing alternative (i.e., lower) beam energies might improve the tissue selectivity of the technique. As seen from Eqs. 7, 8, 9, 10 above, the noise variance in dual energy imaging is a strong function of the two materials’ combined attenuation coefficient separation and a reduction in dose for a given SNR is, in general, possible by increasing the spectral separation between the two beams.⁶⁰ At energies of 52 and 64 keV, the combined differential attenuation was relatively low.

An important source of error in quantification of breast density is x-ray scatter. It causes both random and systematic error in breast density measurements. The random error, which is caused by the additive stochastic noise due to x-ray scatter, has been included in the noise analysis. However, the systematic error, which is caused by the offset to the pixel signal due to x-ray scatter, has not been included in this simulation. Previous simulation studies involving dose requirements in dual energy imaging have also not included x-ray scatter in the simulation.^{25, 31, 36} Therefore, scatter correction in the low and high energy images is necessary for accurate breast density measurement. There are a number of previously reported scatter correction techniques that can be used for this purpose.^{61, 62, 63} Future experimental implementation of the technique will address the systematic error caused by x-ray scatter. The current study has focused on the minimum required patient dose for reliable breast density measurement assuming that the systematic error due to x-ray scatter can be corrected.

For the model used in this study, the effect of heterogeneity was determined to yield a relatively small increase in the average variance, and hence required mean glandular dose. This increase is likely due to reduced x-ray transmission and a loss of quantum statistics in regions of high breast density. It will be useful to include further simulations of different mean glandularities and heterogeneous breast tissue distributions in future studies.

The data presented here suggest that a new technique can be developed to reliably measure breast density. The technique can optionally make use of a standard screening mammogram in conjunction with a second high energy image exposure. In either case, a relatively small amount of dose would be imparted to the patient in comparison to a standard screening mammogram. A recent report⁶⁴ has called into question the validity of any areal measure of breast density and a technique like the one presented here is able to incorporate the needed three-dimensional information when determining breast density.

APPENDIX: DUAL ENERGY NOISE PROPAGATION

Using propagation of errors, the variance of function in Eq. 6 can be written as

$${\sigma }_{t_g}^2={\left(\frac{\partial t_g}{\partial S_l}\right)}^2{\sigma }_{S_l}^2+{\left(\frac{\partial t_g}{\partial S_h}\right)}^2{\sigma }_{S_h}^2,$$ (A1)

$${\sigma }_{t_a}^2={\left(\frac{\partial t_a}{\partial S_l}\right)}^2{\sigma }_{S_l}^2+{\left(\frac{\partial t_a}{\partial S_h}\right)}^2{\sigma }_{S_h}^2,$$ (A2)

$${\sigma }_{t_g{t}_a}=\left(\frac{\partial t_g}{\partial S_l}\right)\left(\frac{\partial t_a}{\partial S_l}\right){\sigma }_{S_l}^2+\left(\frac{\partial t_g}{\partial S_h}\right)\left(\frac{\partial t_a}{\partial S_h}\right){\sigma }_{S_h}^2,$$ (A3)

and rewritten⁶⁵, ⁶⁶, ⁶⁷ as

$${\sigma }_{t_g}^2=\frac{1}{J^2}({\left(\frac{\partial S_h}{\partial t_a}\right)}^2{\sigma }_{S_l}^2+{\left(\frac{\partial S_l}{\partial t_a}\right)}^2{\sigma }_{S_h}^2),$$ (A4)

$${\sigma }_{t_a}^2=\frac{1}{J^2}({\left(\frac{\partial S_h}{\partial t_g}\right)}^2{\sigma }_{S_l}^2+{\left(\frac{\partial S_l}{\partial t_g}\right)}^2{\sigma }_{S_h}^2),$$ (A5)

$${\sigma }_{t_g{t}_a}=\frac{-1}{J^2}(\left(\frac{\partial S_h}{\partial t_g}\right)\left(\frac{\partial S_h}{\partial t_a}\right){\sigma }_{S_l}^2+\left(\frac{\partial S_l}{\partial t_g}\right)\left(\frac{\partial S_l}{\partial t_a}\right){\sigma }_{S_h}^2),$$ (A6)

where J², the squared Jacobian determinant, is equal to

$$J^2={(\left(\frac{\partial S_h}{\partial t_g}\right)\left(\frac{\partial S_l}{\partial t_a}\right)-\left(\frac{\partial S_l}{\partial t_g}\right)\left(\frac{\partial S_h}{\partial t_a}\right))}^2.$$ (A7)

The partial derivatives are calculated according to the following with an added step of defining the final quantity as the product of the mean attenuation and detector signal from Eq. 12:

$$\frac{\partial S_i}{\partial t_j}=\frac{\partial }{\partial t_j}(\int d^2{N}_0\left(E\right)e^{-\left({\mu }_f\left(E\right)t_f\right)}{e}^{-({\mu }_g\left(E\right)t_g+{\mu }_a\left(E\right)t_a)}W\left(E\right)Q\left(E\right)dE)\equiv -\overline{{\mu }_j\left(E_i\right)}{S}_i.$$ (A8)

J² can then be written as

$$J^2={\left(S_l{S}_h\right)}^2{(\overline{{\mu }_a\left(E_l\right)}\overline{{\mu }_g\left(E_h\right)}-\overline{{\mu }_g\left(E_l\right)}\overline{{\mu }_a\left(E_h\right)})}^2.$$ (A9)

Combining the above terms and rewriting expressions with the form $S_i^2∕{\sigma }_{S_i}^2$ as ${\mathrm{SNR}}_{S_i}^2$, ${\sigma }_{t_f}^2$, ${\sigma }_{t_a}^2$, and σ_tatf reduce to

$${\sigma }_{t_g}^2=\frac{\frac{{\left(\overline{{\mu }_a\left(E_h\right)}\right)}^2}{{\mathrm{SNR}}_{S_l}^2}+\frac{{\left(\overline{{\mu }_a\left(E_l\right)}\right)}^2}{{\mathrm{SNR}}_{S_h}^2}}{{(\overline{{\mu }_a\left(E_l\right)}\overline{{\mu }_g\left(E_h\right)}-\overline{{\mu }_g\left(E_l\right)}\overline{{\mu }_a\left(E_h\right)})}^2},$$ (A10)

$${\sigma }_{t_a}^2=\frac{\frac{\overline{{\mu }_g^2\left(E_h\right)}}{{\mathrm{SNR}}_{S_l}^2}+\frac{\overline{{\mu }_g^2\left(E_l\right)}}{{\mathrm{SNR}}_{S_h}^2}}{{(\overline{{\mu }_a\left(E_l\right)}\overline{{\mu }_g\left(E_h\right)}-\overline{{\mu }_g\left(E_l\right)}\overline{{\mu }_a\left(E_h\right)})}^2},$$ (A11)

$${\sigma }_{t_g{t}_a}=\frac{\frac{\overline{{\mu }_a\left(E_h\right)}\overline{{\mu }_g\left(E_h\right)}}{{\mathrm{SNR}}_{S_l}^2}+\frac{\overline{{\mu }_a\left(E_l\right)}\overline{{\mu }_g\left(E_l\right)}}{{\mathrm{SNR}}_{S_h}^2}}{-{(\overline{{\mu }_a\left(E_l\right)}\overline{{\mu }_g\left(E_h\right)}-\overline{{\mu }_g\left(E_l\right)}\overline{{\mu }_a\left(E_h\right)})}^2}.$$ (A12)

Details here are consistent with previous derivations that have been presented elsewhere in the literature.⁶⁰, ⁶⁵, ⁶⁶, ⁶⁷, ⁶⁸, ⁶⁹, ⁷⁰