Skip to main content
PMC home page
Medical Physics logoLink to Medical Physics
. 2008 Nov 11;35(12):5434–5439. doi: 10.1118/1.3006353

Technical note: Heterogeneity dose calculation accuracy in IMRT: Study of five commercial treatment planning systems using an anthropomorphic thorax phantom

Scott E Davidson 1,a), Richard A Popple 2, Geoffrey S Ibbott 3, David S Followill 3
PMCID: PMC2736720  PMID: 19175103

Abstract

The purpose of this study was to determine the accuracy of five commonly used intensity-modulated radiation therapy (IMRT) treatment planning systems (TPSs), 3 using convolution superposition algorithms or the analytical anisotropic algorithm (CSA∕AAAs) and 2 using pencil beam algorithms (PBAs), in calculating the absorbed dose within a low-density, heterogeneous region when compared with measurements made in an anthropomorphic thorax phantom. The dose predicted in the target center met the test criteria (5% of the dose normalization point or 3 mm distance to agreement) for all TPSs tested; however, at the tumor-lung interface and at the peripheral lung in the vicinity of the tumor, the CSA∕AAAs performed better than the PBAs (85% and 50%, respectively, of pixels meeting the 5%∕3-mm test criteria), and thus should be used to determine dose in heterogeneous regions.

Keywords: anthropomorphic phantom, heterogeneity dose calculation, film, TLD, measurement

INTRODUCTION

Treatment planning system (TPS) dose calculation algorithms that incorporate 3D density computed tomography (CT) information for electron transport [such as convolution superposition algorithms and the analytical anisotropic algorithm (CSA∕AAAs)]1, 2 provide better dose estimates than those relying on an attenuation correction method3, 4, 5 [such as pencil beam algorithms (PBAs)],6, 7, 8 especially in low-density heterogeneous regions.9 When the planning target volume (PTV) is adjacent to or within a low-density region, treatment plans that use an attenuation-corrected PBA tend to overestimate the dose in the PTV and underestimate the broadening of the beam penumbra. Various studies have been done in an attempt to understand the differences between CSA∕AAAs and PBAs for intensity-modulated radiation therapy (IMRT).10, 11, 12, 13, 14, 15, 16, 17, 18, 19 Some of these studies have examined the accuracy of dose calculations along the central axis and penumbral regions based on simple beam geometries using slab phantoms of unit density and low-density layers.11, 15, 18 Others have compared the accuracy of TPS dose calculations relative to Monte Carlo calculations.10, 12, 13, 16, 17, 20, 21 The goal of the current study was to present a technical note on the dose calculation accuracy within a low-density region of five common IMRT TPSs, three using CSA∕AAAs and two using PBAs, by combining results of previous work that compared two IMRT TPSs with measurements in an anthropomorphic thorax phantom19 with similar measurements for 3 more commercial IMRT TPSs. To our knowledge, the present work represents the most complete anthropomorphic measurement-based study to date of the accuracy of many of the commonly used commercial IMRT TPSs under well-defined clinically relevant conditions as recommended by the American Association of Physicists in Medicine Task Group 65 report on heterogeneity corrections.9

METHODS AND MATERIALS

Of the five TPSs we tested, three use CSA∕AAAs and two use PBAs. The CSA∕AAA TPSs were the Eclipse AAA version 7.5.18.0 (Varian Medical Systems, Palo Alto, CA), the TomoTherapy version 2.2.1.2 (TomoTherapy, Inc., Madison, WI), and the Pinnacle version 7.6c (Philips Medical Systems, Andover, MA). The two PBA TPSs were the Eclipse PBA version 7.5.18.0 (Varian Medical Systems) and Corvus version 5.0 (Best Medical International, Inc., Springfield, VA). While these five TPSs are in wide use, there are other commonly used TPSs, such as XiO’s PBA and CSA (Computerized Medical Systems, Inc., St. Louis, MO), that were not included in this study. The TPSs were tested at two institutions: The Eclipse (AAA), Eclipse PBA, and TomoTherapy systems were tested at The University of Alabama at Birmingham, and the Pinnacle and Corvus systems were tested at The University of Texas M. D. Anderson Cancer Center. The TomoTherapy system was tested using the 6 MV photon beam from the TomoTherapy Hi-Art accelerator; all other TPSs were tested using 6 MV photons from Varian Clinac 21EX linear accelerators. Because we used Varian accelerators from two institutions and a TomoTherapy Hi-Art accelerator, a total of three beam models were used. The four plans for the Varian accelerator used the same beam geometry, while, because of the TomoTherapy Hi-Art helical delivery technique, the beam geometry for the TomoTherapy plan was not the same as it was for the other four plans. Finally, since the IMRT process is driven by an optimization process to meet the design constraints, each plan’s multileaf collimator (MLC) segmentation was unique, except in the case of the Eclipse CSA and PBA, which were calculated based on a common dynamic MLC leaf sequence.

An evaluation of the accuracy of the dose calculation of the Pinnacle and Corvus TPSs in lung density material is described elsewhere where the design approach and measurement method taken are identical to those described herein.19 To measure the delivered dose, we used the Radiological Physics Center anthropomorphic thorax phantom (Fig. 1) previously described in detail by Followill et al.22 Briefly, this water-fillable phantom contains synthetic heart, lungs, and spinal cord similar in density to their human counterparts and thus mimics heterogeneous thoracic anatomy. In the current study, an ellipsoid shaped nylon target, representing a tumor, was located off-center within the phantom’s left lung in the medial-anterior direction to simulate the position relative to the pulmonary hilum at which bronchogenic tumors are commonly found. Two types of dosimeters were housed within the thorax phantom: Thermoluminescent detectors (TLDs) (Radiation Detection Company, Gilroy, CA) and radiochromic film (International Specialty Products, Wayne, NJ). The TLDs were used as an absolute dosimeter and reported point doses found in the center of the target, heart, and spinal cord. The target TLD was used to normalize the 2D film dose distributions. The film used in this study was EBT radiochromic film, whereas that described in the previous work19 was MD-55 radiochromic film. Both films are nearly energy independent.23, 24, 25 To reduce the standard error of the mean and to evaluate the repeatability of the measurements, the phantom was irradiated three times for each treatment plan.

Figure 1.

Figure 1

Open in a new tab

Anthropomorphic thorax phantom, frontal view. S: Superior; LL: Left lateral; A: Anterior. Inset: CT image of the axial cross section through the center of the tumor. (Tumor is located medially within the left lung.)

The Eclipse IMRT plans, which consisted of four coplanar beams and one noncoplanar beam, were the same as that described by Davidson et al.19 in terms of the prescription, target definitions, constraints, gantry, collimator, and couch positions. Unlike in the aforementioned previous study, the optimization in this analysis is based on a dynamic MLC configuration rather than a static MLC configuration. The Eclipse optimization engine created optimal fluence maps which were converted to dynamic MLC leaf sequences. The dose delivered by the resulting leaf sequences was calculated using both the CSA∕AAA and the PBA with a modified Batho effective pathlength correction.4 In this case, both types of calculation methods (CSA∕AAA and PBA) were based on the same MLC segmentation. The dose grid spacing for both algorithms was 2.5 mm in the transverse plane and was the CT image spacing, 3 mm, in the longitudinal direction.

We used the same constraints and prescription dose as those in the Eclipse, Pinnacle, and Corvus TPSs to create the TomoTherapy plan. The TomoTherapy dose calculation grid was based on the CT image matrix, which was down sampled from the original 512×512-pixel matrix to a 256×256-pixel matrix. The pixel spacing of the down sampled matrix was 1.95 mm. As with the Eclipse algorithms, the spacing in the longitudinal direction was the CT image spacing, 3 mm.

Each institution followed its own phantom IMRT quality assurance (QA) procedures. The University of Alabama’s QA procedure for the Eclipse systems used an acrylic slab phantom and a PTW model 31010 ion chamber (PTW Freiburg GmbH, Freiburg, Germany); for the TomoTherapy system, a cylindrical water equivalent plastic phantom was used similar to the one described by Thomas et al.26 and an Exradin A1SL thimble ion chamber (Standard Imaging, Middleton, WI). At M. D. Anderson, an in-house water phantom and a model CC04 ion chamber (Scanditronix Wellhofer, Bartlett, TN) comprised the IMRT QA equipment. Ion chamber measurements were made in a high-dose, low-gradient region; this method, typical of the IMRT QA process used before treating a patient, resulted in the analysis of the TPS dose calculation algorithm without regard to heterogeneities. In order to be consistent with the methods previously reported,19 the calculation from each TPS was adjusted by the ratio of ion chamber measurement value to the calculation value in response to the IMRT QA procedure. In situations where large differences occur, this method can help to separate possible errors between the heterogeneous calculation or setup and those related to the specific plan or beam modeling. However, this method only considers a point measurement made in a high dose low gradient region and does not explicitly consider the penumbra and low dose regions.

Each dose calculation algorithm was evaluated by comparing it based on the criteria set forth by Task Group 53.27 The criterion applied to test the accuracy of each TPS dose calculation algorithm were ±7% of the measured normalization dose or ±7 mm distance to agreement of the measured dose distribution. A second, more stringent (and perhaps more clinically relevant) criterion (±5% of the normalization dose or ±3 mm distance to agreement) was also tested.

The analysis included point dose comparisons, profile dose comparisons, and 2D dose comparisons. The point dose comparisons were made using the TLDs located in the target, heart, and spinal cord. The dose profiles and 2D dose distribution comparisons were made using radiochromic films normalized to TLD. The films were positioned in all three anatomical planes and intersected the center of the target. The films extended into the low-density regions of the lung. The dose profiles compared the calculated and measured values and were made in the lateral, anterior posterior, and superior posterior directions in the center of the target. The 2D dose distribution comparisons, referred to as binary agreement maps (BAMs), depicted regions of agreement and disagreement and were generated to compare measured and calculated dose values using the two sets of test criteria.28 These maps are similar to the commonly used gamma index method,29, 30 but the BAMs do not provide detail of those regions that may be near or far from a specified criterion as do the gamma maps. The measured and calculated data sets were interpolated and registered as 255×255-pixel arrays having 0.5-mm pixel sizes. The BAMs showed regions of agreement within the ±5%∕3-mm criteria level, regions of agreement between the criteria levels, and regions of disagreement beyond the ±7%∕7-mm criteria level. The results of testing at two criteria levels, ±5%∕3 mm and ±7%∕7 mm, were plotted together on single figures. The proportion of pixels meeting a specific criterion was determined and compared among the five algorithms we tested.

RESULTS

The estimated uncertainty for the dose determined for the EBT film at one standard deviation was between 2.6% and 3.6%. This estimate included the uncertainty of the TLD dose,31 the film uniformity, the film-to-film variation, and the fit of the dose response curve.32 The TLD uncertainty is included here because the film is normalized to the adjacent TLD housed within the phantom. The TLD is known to be a very accurate dosimeter and negates any variation that may occur between the film calibration process and the actual film used in the phantom at the time of irradiation.

Table 1 presents the results of the IMRT QA process showing the correction factors applied to each TPS dose calculation matrix. The variation in the IMRT QA correction factor is due to variations in the TPSs and differences between the specific treatment plans and not due to the different QA methods that were used. It is not uncommon to observe differences between the measurement and calculation of the patient IMRT QA process. Dong et al.33 studied the results of IMRT QA on 751 patient plans that were planned on the Corvus TPS and, in general, found good consistency. However, they did report a greater than 3.5% difference between measurement and calculation in 3% of the cases studied. Note that small corrections for the Eclipse plans (PBA and AAA) and the TomoTherapy plan were applied. Normally such corrections would not be applied in a clinical setting, but due to the procedure previously followed19 the plans were corrected accordingly. Table 1 also shows the results for the point dose comparisons between the calculation algorithms and measurement means. The results showed agreement in the target to be less than 5% for both the CSA∕AAAs and PBAs. Regardless of which dose calculation algorithm was used, the dose calculated in the center of the target met the ±5%∕3-mm criterion as compared to measurement. However, we observed greater variation (from an underestimation of 3.6% to an overestimation of 11.2%) in the low-dose critical structure regions of the heart and spinal cord, with the exception of the Pinnacle CSA (<4%). The PBA and CSA∕AAA performed similarly in these homogeneous regions.

Table 1.

Point-dose ratio comparisons between calculations and TLD measurements for all TPSs. Note: Corrections to the calculated data have been made in response to the IMRT QA process (Ref. 19).

TPS IMRT QA correction multiplier Ratio of TPS calculation (corrected) to TLD measurement
Tumor Heart Cord
Pinnacle (CSA) 1.027 0.992 1.021 0.964
Corvus (PBA) 1.055 1.050 1.093 1.090
Eclipse AAA (CSA) 1.007 1.036 1.112 1.099
Eclipse (PBA) 0.993 1.049 1.065 1.042
TornoTherapy (CSA) 0.994 1.021 0.974 0.851
Open in a new tab

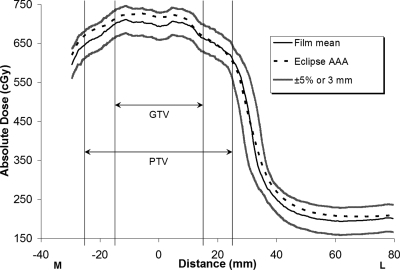
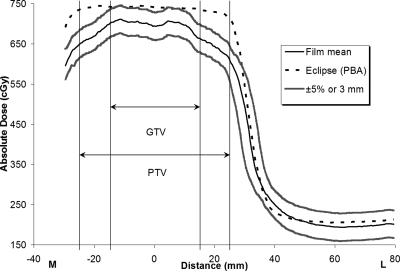
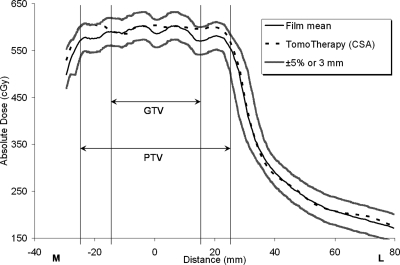
Figures 234, respectively, show the medial-to-left lateral profiles from the Eclipse AAA plan, Eclipse PBA plan, and TomoTherapy plan. Each profile includes the average measured film profile generated from the three repeated irradiations, the TPS calculated profiles, and the acceptance criterion boundaries (±5%∕3 mm). The gross tumor volume (GTV) and PTV regions are indicated in the figures. Figures 24, respectively, show that the measured and calculated data for the Eclipse AAA and TomoTherapy plans along the one-dimensional profile were in good agreement, even in the penumbral region. The Eclipse PBA calculation agreed fairly well with the actual delivered dose in the high-dose target region (Fig. 3), but failed to predict the extent of penumbral broadening by overestimating the dose, as seen in a similar report21 and in other PBA calculations.19

Figure 2.

Figure 2

Open in a new tab

Eclipse AAA IMRT calculation and measurement, medial-to-left lateral profile. GTV: Gross tumor volume; PTV: Planning target volume. The measured film values are means from three irradiations. The ±5%∕3-mm criterion bands show how well the calculated data compare to the measured data.

Figure 3.

Figure 3

Open in a new tab

Eclipse PBA IMRT calculation and measurement, medial-to-left lateral profile. The measured film values are means from three irradiations. The ±5%∕3-mm criterion bands indicate that the predicted dose underestimates the extent of penumbral broadening.

Figure 4.

Figure 4

Open in a new tab

TomoTherapy IMRT calculation and measurement, medial-to-left lateral profile. The measured film values are means from three irradiations. The ±5%∕3-mm criterion bands show how well the calculated data compare to the measured data.

The BAMs for the axial planes from a single irradiation from the Eclipse AAA plan, Eclipse PBA plan, and TomoTherapy plan are shown in Figs. 5a, 5b, 5c, respectively. In general, the CSA∕AAAs showed good agreement within the PTV and surrounding lung regions, while the PBAs disagreed in the PTV portion of the lung and penumbral regions surrounding the target. Based on the BAM data for the three irradiations for the CSA∕AAAs, it appeared that the Eclipse TPS showed better agreement with the measurements than the TomoTherapy algorithm, especially in the penumbra region. In general, the CSA∕AAAs performed in a similar manner in terms of the percentage of pixels meeting the criteria as described in Fig. 6. We observed no differences in performance related to the beam-shaping technology used—dynamic MLC (Eclipse), static MLC (Pinnacle and Corvus), or helical tomotherapy (TomoTherapy).

Figure 5.

Figure 5

Open in a new tab

IMRT calculation and measurement BAMs of the axial plane from a single irradiation. White regions indicate where the agreement criterion was met, gray regions show areas of disagreement beyond ±5%∕3 mm but within ±7%∕7 mm, and black regions reveal disagreement beyond ±7%∕7 mm.

Figure 6.

Figure 6

Open in a new tab

Percentage of pixels meeting criteria at both levels tested for all TPSs.

Figure 6 shows the percentages of pixels that met the two criterion levels (±5%∕3 mm and ±7%∕7 mm) as analyzed from the BAMs of the three anatomical film planes from the three repeated irradiations for each TPS algorithm combination. The CSA∕AAAs’ performance was superior to the PBAs’ performance. For the CSA∕AAAs, greater than 96% of the pixels met the criterion at the ±7%∕7-mm agreement level; furthermore, even when the criterion was tightened to ±5%∕3 mm, more than 85% of the pixels still met it. Conversely, the agreement for the PBAs using the more generous ±7%∕7-mm criterion showed that fewer than 60% of the pixels met it. With only 50% of the pixels meeting the ±5%∕3-mm criteria, the Eclipse PBA showed the worst agreement.

DISCUSSION AND CONCLUSION

Based on our analysis of comparisons between two types of dose calculation algorithms using TLD and radiochromic film measurements in an anthropomorphic thorax phantom, we conclude that CSA∕AAAs perform consistently and more accurately than PBAs when applied to IMRT planning involving low-density regions. Numerous studies have indicated that CSA∕AAAs are more accurate than PBAs in low-density regions.9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 21 Using Monte Carlo calculations, Jeraj et al.10 showed a systematic error in a lung tumor of approximately 1% for the Pinnacle CSA and approximately 5% for the Corvus PBA. Sterpin et al.21 compared the Eclipse AAA and Eclipse PBA in Monte Carlo simulations and found that the AAA showed better overall accuracy than the PBA; they also reported that the Eclipse PBA overestimated dose in regions where lung tissue was encompassed within the PTV. Thus, their findings are consistent with our evaluation of the Eclipse TPSs.

Our use of BAMs instead of the presently common use of the gamma index method to test the agreement between measurement and calculation at a specified criterion was made, in part, to remain consistent with our prior publication.19 Additionally, using the same anthropomorphic phantom system, Alvarez et al.34 evaluated the calculation performances of the CSA∕AAA and PBA algorithms from 33 institutions using the gamma index method and found results consistent with ours. The BAMs do not provide the level of detail of those regions that may be near or far from a specified criterion as do the gamma maps. However, unique to the BAM implementation of testing at two different criteria levels, ±5%∕3 mm and ±7%∕7 mm, allowed for their interpretation on a single figure.

While this study was limited to a lung plan with specified constraints, it brought together a large set of data to compare the performance of several common commercial TPS∕algorithm combinations with actual measurements in an anthropomorphic thorax phantom. We demonstrated that TPSs that employ a CSA∕AAA perform well both in the target region and surrounding low-density regions. As institutions adjust dose prescriptions to correct for heterogeneities, a realistic and complete set of evaluations in an anthropomorphic phantom can be used to help make this transition.9

Regardless of the type of dose calculation algorithm, it remains difficult to determine the dose in regions distal to the PTV. Our results reflect this: In such regions (e.g., the heart or spinal cord) we found that differences in dose varied between underestimations of 3.6% to overestimations of 11.2%. Estimates of dose in low-dose regions outside the PTV tend to have high uncertainty partly because radiation scatter, which is not modeled as well as the primary beam, is the main cause of dose in these regions.1 In addition, the measurement setup uncertainty may increase in these regions due to the greater radial distances from the PTV isocenter location. The low dose regions of the heart and cord easily met their dose constraints and did not affect the understanding of algorithm accuracy in low-density heterogeneous regions.

In regions of low density, we found that TPSs that use CSA∕AAAs consistently meet the 5%∕3-mm performance criterion, while correction-based TPSs that use PBA consistently overestimate dose in a PTV and underestimate penumbral broadening and thus fail to meet the criterion in these regions. This pattern of disagreement reflects the inherent limitation of one-dimensional correction-based algorithms: These algorithms consider only the density along the primary photon path and do not account for scatter conditions within heterogeneities. In contrast, the CSA∕AAAs account for lateral scatter and electron transport. Therefore, CSA∕AAAs should be used to determine the dose in heterogeneous regions such as the tumor-lung interface and lung tissue surrounding a tumor.

ACKNOWLEDGMENTS

This work was supported by Public Health Services Grant Nos.CA 10953 and CA 81647 awarded by the National Cancer Institute, Department of Health and Human Services.

References

  1. Mackie T. R., Scrimger J. W., and Battista J. J., “A convolution method of calculating dose for 15-MV x rays,” Med. Phys. 10.1118/1.595774 12(2), 188–196 (1985). [DOI] [PubMed] [Google Scholar]
  2. Ulmer W. and Harder D., “A triple Gaussian pencil beam model for photon beam treatment planning,” Z. Med. Phys. 5, 25–30 (1995). [Google Scholar]
  3. Batho H. F., “Lung corrections in cobalt 60 beam therapy,” J. Can. Assoc. Radiol. 15, 79–83 (1964). [PubMed] [Google Scholar]
  4. Sontag M. R. and Cunningham J. R., “Corrections to absorbed dose calculations for tissue inhomogeneities,” Med. Phys. 10.1118/1.594329 4(5), 431–436 (1977). [DOI] [PubMed] [Google Scholar]
  5. Sontag M. R. and Cunningham J. R., “The equivalent tissue-air ratio method for making absorbed dose calculations in a heterogeneous medium,” Radiology 129(3), 787–794 (1978). [DOI] [PubMed] [Google Scholar]
  6. Bourland J. D. and Chaney E. L., “A finite-size pencil beam model for photon dose calculations in three dimensions,” Med. Phys. 10.1118/1.596772 19(6), 1401–1412 (1992). [DOI] [PubMed] [Google Scholar]
  7. Storchi P. and Woudstra E., “Calculation models for determining the absorbed dose in water phantoms in off-axis planes of rectangular fields of open and wedged photon beams,” Phys. Med. Biol. 10.1088/0031-9155/40/4/003 40(4), 511–527 (1995). [DOI] [PubMed] [Google Scholar]
  8. Storchi P. and Woudstra E., “Calculation of the absorbed dose distribution due to irregularly shaped photon beams using pencil beam kernels derived form basic beam data,” Phys. Med. Biol. 10.1088/0031-9155/41/4/005 41(4), 637–656 (1996). [DOI] [PubMed] [Google Scholar]
  9. Papanikolaou N., Battista J. J., Boyer A. L., Kappas C., Klein E. E., Mackie T. R., Sharpe M., and Van Dyk J., “Tissue inhomogeneity corrections for megavoltage photon beams,” AAPM Task Group #65 Radiation Therapy Committee (2004).
  10. Jeraj R., Keall P. J., and Siebers J. V., “The effect of dose calculation accuracy on inverse treatment planning,” Phys. Med. Biol. 10.1088/0031-9155/47/3/303 47(3), 391–407 (2002). [DOI] [PubMed] [Google Scholar]
  11. Jones A. O. and Das I. J., “Comparison of inhomogeneity correction algorithms in small photon fields,” Med. Phys. 10.1118/1.1861154 32(3), 766–776 (2005). [DOI] [PubMed] [Google Scholar]
  12. Knoos T., Wieslander E., Cozzi L., Brink C., Fogliata A., Albers D., Nystrom H., and Lassen S., “Comparison of dose calculation algorithms for treatment planning in external photon beam therapy for clinical situations,” Phys. Med. Biol. 10.1088/0031-9155/51/22/005 51(22), 5785–5807 (2006). [DOI] [PubMed] [Google Scholar]
  13. Ma C. M., Pawlicki T., Jiang S. B., Li J. S., Deng J., Mok E., Kapur A., Xing L., Ma L., and Boyer A. L., “Monte Carlo verification of IMRT dose distributions from a commercial treatment planning optimization system,” Phys. Med. Biol. 10.1088/0031-9155/45/9/303 45(9), 2483–2495 (2000). [DOI] [PubMed] [Google Scholar]
  14. McDermott P. N., He T., and DeYoung A., “Dose calculation accuracy of lung planning with a commercial IMRT treatment planning system,” J. Appl. Clin. Med. Phys. 10.1120/1.1623172 4(4), 341–351 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Metcalfe P. E., Wong T. P., and Hoban P. W., “Radiotherapy x-ray beam inhomogeneity corrections: The problem of lateral electronic disequilibrium in lung,” Australas. Phys. Eng. Sci. Med. 16(4), 155–167 (1993). [PubMed] [Google Scholar]
  16. Pawlicki T., and Ma C. M., “Monte Carlo simulation for MLC-based intensity-modulated radiotherapy,” Med. Dosim. 26(2), 157–168 (2001). [DOI] [PubMed] [Google Scholar]
  17. Vanderstraeten B., Reynaert N., Paelinek L., Madani I., Wagter C. D., Gersem W. D., Neve W. D., and Thierens H., “Accuracy of patient dose calculation for lung IMRT: A comparison of Monte Carlo, convolution∕superposition, and pencil beam computations,” Med. Phys. 10.1118/1.2241992 33(9), 3149–3158 (2006). [DOI] [PubMed] [Google Scholar]
  18. Carrasco P., Jornet N., Duch M. A., Weber L., Ginjaume M., Eudaldo T., Jurado D., Ruiz A., and Ribas M., “Comparison of dose calculation algorithms in phantoms with lung equivalent heterogeneities under conditions of lateral electronic disequilibrium,” Med. Phys. 10.1118/1.1788932 31(10), 2899–2911 (2004). [DOI] [PubMed] [Google Scholar]
  19. Davidson S. E., Ibbott G. S., Prado K. L., Dong L., Liao Z., and Followill D. S., “Accuracy of two heterogeneity dose calculation algorithms for IMRT in treatment plans designed using an anthropomorphic thorax phantom,” Med. Phys. 10.1118/1.2727789 34(5), 1850–1857 (2007). [DOI] [PubMed] [Google Scholar]
  20. Knoos T., Ahnesjo A., Nilsson P., and Weber L., “Limitations of a pencil beam approach to photon dose calculations in lung tissue,” Phys. Med. Biol. 10.1088/0031-9155/40/9/002 40(9), 1411–1420 (1995). [DOI] [PubMed] [Google Scholar]
  21. Sterpin E., Tomsej M., De Smedt B., Reynaert N., and Vynckier S., “Monte Carlo evaluation of the AAA treatment planning algorithm in a heterogeneous multilayer phantom and IMRT clinical treatments for an Elekta SL25 linear accelerator,” Med. Phys. 10.1118/1.2727314 34(5), 1665–1677 (2007). [DOI] [PubMed] [Google Scholar]
  22. Followill D. S., Evans D. R., Cherry C., Molineu A., Fisher G., Hanson W. F., and Ibbott G. S., “Design, development, and implementation of the radiological physics center’s pelvis and thorax anthropomorphic quality assurance phantoms,” Med. Phys. 10.1118/1.2737158 34(6), 2070–2076 (2007). [DOI] [PubMed] [Google Scholar]
  23. Meigooni A. S., Sanders M. F., Ibbott G. S., and Szeglin S. R., “Dosimetric characteristics of an improved radiochromic film,” Med. Phys. 10.1118/1.597747 23(11), 1883–1888 (1996). [DOI] [PubMed] [Google Scholar]
  24. Alvarez P., Hernandez N., Followill D., Tailor R., and Ibbott G., “TU-FF-A1-01: Characterization of EBT versus MD55 Gafchromic[registered sign] films for relative dosimetry measurements,” Med. Phys. 33(6), 2217–2218 (2006). [Google Scholar]
  25. Chiu-Tsao S.-T., Ho Y., Shankar R., Wang L., and Harrison L. B., “Energy dependence of response of new high sensitivity radiochromic films for megavoltage and kilovoltage radiation energies,” Med. Phys. 10.1118/1.2065467 32(11), 3350–3354 (2005). [DOI] [PubMed] [Google Scholar]
  26. Thomas S. D., Mackenzie M., Field G. C., Syme A. M., and Fallone B. G., “Patient specific treatment verifications for helical tomotherapy treatment plans,” Med. Phys. 10.1118/1.2134929 32(12), 3793–3800 (2005). [DOI] [PubMed] [Google Scholar]
  27. Fraass B., Doppke K., Hunt M., Kutcher G., Starkschall G., Stern R., and Van Dyke J., “American Association of Physicists in Medicine Radiation Therapy Committee Task Group 53: Quality assurance for clinical radiotherapy treatment planning,” Med. Phys. 10.1118/1.598373 25(10), 1773–1829 (1998). [DOI] [PubMed] [Google Scholar]
  28. Harms W. B., Low D. A., Wong J. W., and Purdy J. A., “A software tool for the quantitative evaluation of 3D dose calculation algorithms,” Med. Phys. 10.1118/1.598363 25(10), 1830–1836 (1998). [DOI] [PubMed] [Google Scholar]
  29. Low D. A., Harms W. B., Mutic S., and Purdy J. A., “A technique for the quantitative evaluation of dose distributions,” Med. Phys. 10.1118/1.598248 25(5), 656–661 (1998). [DOI] [PubMed] [Google Scholar]
  30. Low D. A. and Dempsey J. F., “Evaluation of the gamma dose distribution comparison method,” Med. Phys. 10.1118/1.1598711 30(9), 2455–2464 (2003). [DOI] [PubMed] [Google Scholar]
  31. Kirby T. H., Hanson W. F., and Johnston D. A., “Uncertainty analysis of absorbed dose calculations from thermoluminescence dosimeters,” Med. Phys. 10.1118/1.596797 19(6), 1427–1433 (1992). [DOI] [PubMed] [Google Scholar]
  32. Devic S., Seuntjens J., Hegyi G., Podgorsak E. B., Soares C. G., Kirov A. S., Ali I., Williamson J. F., and Elizondo A., “Dosimetric properties of improved GafChromic films for seven different digitizers,” Med. Phys. 10.1118/1.1776691 31(9), 2392–2401 (2004). [DOI] [PubMed] [Google Scholar]
  33. Dong L., Antolak J., Salehpour M., Forster K., O’Neill L., Kendall R., and Rosen I., “Patient-specific point dose measurement for IMRT monitor unit verification,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/S0360-3016(03)00197-4 56(3), 867–877 (2003). [DOI] [PubMed] [Google Scholar]
  34. Alvarez P., Molineu A., Hernandez N., Hall F., Followill D., and Ibbott G., “TU-C-AUD B-03: A comparison of heterogeneity correction algorithms,” Med. Phys. 35(6), 2888 (2008) [Google Scholar]

Articles from Medical Physics are provided here courtesy of American Association of Physicists in Medicine

RESOURCES