Postnatal development of sound pressure transformations by the head and pinnae of the cat: Monaural characteristics

Abstract

Although there have been many anatomical, physiological, and psychophysical studies of auditory development in cat, there have been no comparable studies of the development of the sound pressured transformations by the cat head and pinnae. Because the physical dimensions of the head and pinnae determine the spectral and temporal transformations of sound, as head and pinnae size increase during development, the magnitude and frequency ranges of these transformations are hypothesized to systematically change. This hypothesis was tested by measuring directional transfer functions (DTFs), the directional components of head-related transfer functions, and the linear dimensions of the head and pinnae in cats from the onset of hearing (∼1.5 weeks) through adulthood. Head and pinnae dimensions increased by factors of ∼2 and ∼2.5, respectively, reaching adult values by ∼23 and ∼16 weeks, respectively. The development of the spectral notch cues to source location, the spatial- and frequency-dependent distributions of DTF amplitude gain (acoustic directionality), maximum gain, and the acoustic axis, and the resonance frequency and associated gain of the ear canal and concha were systematically related to the dimensions of the head and pinnae. These monaural acoustical properties of the head and pinnae in the cat are mature by 16 weeks.

INTRODUCTION

The head and the pinnae are fundamental in shaping the spatial-location dependence of the spectral and temporal aspects of sounds that ultimately arrive at the tympanic membrane (Ruggero and Temchin, 2002; Kuhn, 1987). An important consequence of the acoustic directionality of the head and pinnae is their role in establishing the cues to sound source location. The three primary cues for location are generated by the spatial- and frequency-dependent reflection and diffraction of the propagating sound waves by the head and pinnae. Interaural time differences (ITDs) arise because the distance of the path of sound to the two ears differs. Interaural level differences (ILDs) result jointly from the amplification effects of the pinna ipsilateral to the source and the acoustic shadowing effect of the head and contralateral pinna that occurs primarily for high-frequency sounds. Finally, monaural spectral shape cues arise from differential reflection and diffraction of pressure waveforms from sounds originating from different directions by the head, torso, and pinnae.

The spatial and frequency dependences of the monaural and binaural cues to location are well documented in the adult cat (Wiener et al., 1966; Middlebrooks and Pettigrew, 1981; Calford and Pettigrew, 1984; Irvine, 1987; Martin and Webster, 1989; Musicant et al., 1990; Rice et al., 1992; Young et al., 1996; Xu and Middlebrooks, 2000; Phillips et al., 1982). Moreover, the magnitudes of the cues to location and the manner in which they change with location are dependent on the physical size and dimensions of the head and pinnae (Shaw, 1974; Middlebrooks, 1999; Xu and Middlebrooks, 2000; Schnupp et al., 2003; Maki and Furukawa, 2005). Interindividual differences in head and pinnae size and morphology are the basis for individual differences in the cues to location. These facts also create a challenge during development where the growing size of the head and pinnae in mammals increases dramatically from birth, thus also changing not only the magnitude of the acoustical transformations but also the relationship between the cues and sound location.

Cats have been a common model for anatomical, physiological, and behavioral studies of auditory system development [see reviews by Kitzes (1990) and Walsh and McGee (1986)]. Their auditory system is relatively immature at birth and their physical size relative to other species (e.g., rat, mouse, and gerbil) permits good access to the neural structures of interest. A wealth of knowledge exists on the anatomy, physiology, and behavior of the adult cat binaural auditory system to which developmental data can be compared (Irvine, 1986). However, aside from some spatially and spectrally sparse measurements of the development of the ILD cues in kittens by Moore and Irvine (1979) there has been no systematic study of the development of the complete complement of acoustical cues and their relationship to the development of the linear dimensions of the head and pinnae. In this paper we investigate the development of the physical dimensions of the head and pinnae in the cat from the onset of hearing through adulthood and the concomitant changes in the monaural acoustical transformations of sound pressure at the ear.

METHODOLOGY

Animal preparation

Twenty nine domestic short-hair cats (Liberty Research, Waverly, NY) were used in this study. Most animals were female (5∕29 were male). All animals had clean external ears and ear canals. The weight and linear measurements of head diameter and pinnae height and width of each animal were taken immediately before each experiment [see insets, Figs. 1A, 1C]. A digital micrometer was used for the linear measurements. Head diameter was taken at the widest part of the head, occurring a few millimeters rostral to the meatus at the points of the zygomatic process (the bizygomatic breadth) of the temporal bone (Gilbert, 1981); this is the maximum transverse diameter of the cat head (Latimer, 1931). Pinnae heights were measured on the inside (medial, 1-3 in Fig. 1C inset) and outside (lateral, 1-2 in Fig. 1C inset) from the tip of the pinna to where the pinna edges intersected the skin covering the skull; this intersection is well defined in the cat pinna. Finally, pinna width CD was measured as the linear distance across the pinna opening from one edge to the other at one-half the pinna height (this does not include the depth of the pinna). In 16 (12 of which acoustic data were collected) animals, these dimensions were measured nearly every day beginning at 1 week of age up through 16–20 weeks in order to construct growth curves for these structures (Fig. 1).

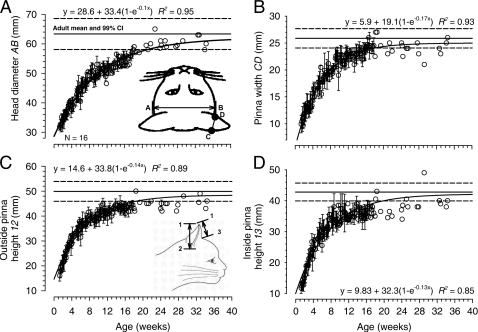
Figure 1.

Developmental growth of the head and pinnae of the cat. The four measured dimensions are shown in the insets of (A) and (C). (A) Head diameter AB. (B) Pinna width at half-height CD. (C) Outside pinna height 1-2. (D) Inside pinna height 1-3. The measured data are from 16 animals. Data points with error bars indicate the across-animal mean±SD of the measured dimension at that age. Data points without error bars indicate single animal measurements at that age. In each panel, the solid and dashed horizontal lines indicate the mean 99% confidence interval, respectively, of the measured dimension taken from nine adult animals. The parameters of the best-fitting growth curve for each measured dimension are displayed in each panel along with the coefficient of determination (R²) for the fit.

The acoustic measurement procedure detailed below lasted approximately 1–2 h during which the animals remained anaesthetized and kept in areflexia. In preparation for acoustical measurements, cats were anaesthetized with ketamine hydrochloride (20 mg∕kg) along with acepromazine (0.1 mg∕kg). Atropine sulfate (0.05 mg∕kg) was also given to reduce mucous secretions, and a tracheal cannula was inserted. Supplemental doses of sodium pentobarbital (3–5 mg∕kg) were administered intravenously into the femoral vein as needed to maintain areflexia. Heart rate was continuously monitored as was core body temperature (with a rectal probe), the latter maintained with a heating pad at 37°C (model TC 100, CWE, Inc., Ardmore, PA). Additionally, blood-oxygen levels, respiratory rate, and end-tidal CO₂ were measured continuously via a capnograph (Surgivet V90040, Waukesha, WI). A small hole was made in the wall of the posterior and ventral aspect of ear canal as near as possible to where the ear canal enters the skull (just medial to where the ear canal makes a nearly 90° turn into the skull) by advancing a slightly curved 14-gauge needle through the canal and skin from inside the canal to outside the skin so that the sharp tip of the needle is outside. A 50-mm-long (Bruel and Kjaer, part no. AF-0555, 1.65 mm outer diameter) or 76-mm-long (Etymotic ER7-14C probe tube) flexible probe tube was then inserted into the needle. The needle was then extracted so as to leave the tip of the probe tube well within the ear canal. Using an otoscope the location of the probe tube tip was adjusted by slightly extracting the probe tube until the desired location of the tip was achieved. The probe tube was fixed in place with cyanoacrylate glue.

Animals were placed on a platform in the center of the sound-attenuating room (see below) and secured in place via a custom bite bar (modeled directly after that used by Musicant et al., 1990) with its interaural axis aligned in the boom of loudspeakers using three lasers, two at the poles and one at (0°,0°). No part of the bite bar∕head holder interfered with the direct propagation of sound to the pinnae. However, for some source locations behind and below the animal the platform impeded the propagation of sound to the contralateral ear; data from these sources were not used. This platform and bite bar ensured the orientation of the head so that the Horsley–Clarke plane was nearly horizontal in all animals. A scaled version of the bite bar was used for the infant animals. To examine the role of the pinna, after taking the first set of acoustic measurements, the pinnae of one animal was completely removed and the measurements repeated. Removal of the pinnae did not alter the position of the probe tube microphone in the ear canal and animals remained centered in the loudspeaker boom. All surgical and experimental procedures complied with the guidelines of the University of Colorado Health Sciences Center Animal Care and Use Committees and the National Institutes of Health.

Experimental setup

All experiments were performed in an ∼3×3×3 m³ (interior dimensions) double-walled sound-attenuating room (IAC, Bronx, NY); the walls and equipment were lined with 4-in.-thick reticulated wedged acoustic foam (Sonex Classic). Stimuli were presented in one of two different experimental setups. Although we could not make any direct comparisons between the two setups, results from adult animals measured in the different setups were consistent and comparable to previous literature. In one setup stimuli were presented from 25 loudspeakers (Morel MDT-20) attached to a custom-built horizontally oriented [i.e., “single-pole” coordinate system (Middlebrooks and Pettigrew, 1981; Leong and Carlile, 1998)] semicircular boom. The 25 loudspeakers were spaced in azimuth along the boom at 7.5° spacing, from −90° (left) to +90° (right). The axis of rotation of the boom was aligned with the interaural axis of the animal (i.e., through the ears). The radius of the boom was 1 m. The 25 loudspeakers were selected from a larger set (∼100) on the basis of best-matching frequency responses. A stepper motor (Advanced Micro Systems AMH34-1303-3) and motor controller∕power supply (Advanced Micro Systems CMAX-810) under computer control could position the boom in elevation with a precision of <1°. The semicircular boom was moved in steps of 7.5° along the elevation using the stepper motor controlled via personal computer (PC) by custom written software in MATLAB (Mathworks, Natick, MA). Stimuli were presented from a total of 625 different locations selected to evenly sample azimuth and elevation (i.e., the pole locations were not overly sampled). The elevation spanned from −45° to +225°. In some experiments, a second setup was used where stimuli were presented from nine frequency-response matched loudspeakers (Morel MDT-20) spaced in elevation from −30° to +90° in 15° steps on a fixed boom (1 m radius), the ends of which were attached to the chamber directly above and directly below the animals’ head. In this setup, instead of moving the loudspeaker boom, a stepper motor was used to rotate the platform holding the animal about the interaural axis in steps of 10°. 289 different locations were sampled (8 elevations×36 azimuths, plus the overhead position). For this latter setup, the interaural axis of the cat was placed in the center of the boom supporting the speakers using the system of three lasers as described earlier. This centering was important as the cat was then rotated about this point. As one test of the validity of the recordings at each rotational angle, the responses to the speaker placed directly overhead were compared. If the cat was perfectly aligned the acoustic responses should not depend on the rotation angle since the two ears would always be equidistant from the overhead speaker. For animals tested in this setup, the acoustic responses measured from this position differed little with azimuth; the standard deviation in acoustic gain at each frequency was <1.0 dB versus 10–25 dB at 0° elevation. In order to treat the data collected in each of these two setups in the same way, all data were expressed in a vertical pole coordinate system in which “azimuth” is the angle around the vertical axis and “elevation” is the angle above or below the horizontal plane.

The general measurement stimuli consisted of 11th order maximum length sequences (MLSs) (Rife and Vanderkooy, 1989) repeated without interruption 128 times from each loudspeaker. The MLS was presented at full 24 bit resolution at a rate of 97 656.25 Hz [Tucker-Davis Technologies (TDT), RP2.1, Alachua, FL]. In some of the very first experiments using the second setup described above, the stimuli consisted of trains of 10.24 μs clicks presented 300–1000 times (e.g., Musicant et al., 1990; Rice et al., 1992). In both setups, loudspeakers for stimulus presentation were selected via two daisy-chained TDT multiplexers (TDT PM2R power multiplexer) and the stimulus amplified (TDT SA1 stereo power amplifier) before being presented to the loudspeaker. The resulting acoustic waveforms in the ear canals of the left and right ears were simultaneously recorded through two probe tube microphones (Bruel and Kjaer, type 4182), amplified (TDT MA2), and collected at 24 bits using two analog to digital converter channels at 97 656.25 Hz (TDT RP2.1). All the stimulus presentation, acquisition, analysis, and movement of the speaker boom were controlled by custom written software in MATLAB. The recorded signals were stored on a PC hard disk for later processing. In all experiments a calibration measurement was also made in the absence of the animal by placing the tips of the probe tubes so that they corresponded to the location where the center of the head of the cats would be located. The calibration measurements capture the spectral characteristics of the loudspeakers and microphones for later processing.

Data processing and data analysis

For data collected in the first experimental setup, the impulse response for each ear and each location was calculated by circular cross-correlation of the original 11th order MLS stimulus and the in-ear recording from the probe tube microphone (Rife and Vanderkooy, 1989). For data collected in the second setup, the impulse response for each ear and location was computed from the average of the responses to the train of clicks. In both cases, the impulse responses were then truncated to 512 points (5.12 ms duration) by a 512-point Hanning window where the center of the window was set to coincide approximately with the point of maximum amplitude in the impulse response. This windowing procedure removes the small-amplitude reflections that may be contained in the impulse response. Next, the head related transfer functions (HRTFs) were derived by dividing the frequency response of the in-ear recording by that of appropriate loudspeaker calibration measurement. This procedure removes the loudspeaker and microphone frequency response from each in-ear measurement. The resulting function is referred to as the HRTF, as it represents the acoustical gain and delay introduced by the head and the pinnae. However, the resulting HRTF can be highly dependent on the exact placement of the tip of the probe tube microphone in the ear canal relative to the tympanic membrane (Middlebrooks et al., 1989). To reduce the confounding effects of the probe tube placement in the ear canal, for each ear the directional transfer functions (DTFs) were then calculated from the HRTFs by dividing the HRTF made at each spatial location by the geometrical mean of all the measured HRTFs across all measurement locations for that ear. The spectral features resulting from the exact placement of the probe tube microphone in the ear canal are expected to be similar for all measurement locations (i.e., they are not dependent on spatial location), so this “common” spectral feature is removed from the HRTFs, resulting in the DTFs (Middlebrooks and Green, 1990). In essence, the DTFs are the sound source direction-dependent components of HRTFs.

The amplitude spectra of the DTFs were calculated after the spectra were passed through a bank of 351 bandpass filters; the center frequencies of which were spaced at intervals of 0.0143 octave spanning from 1 to 32 kHz. The 3 dB bandwidth of filters was held constant across all frequencies at 0.12 octaves, and the upper and lower slopes of the filters fell off at ∼105 dB∕octave. These filters have properties similar to the bank of bandpass filters that have been used elsewhere to filter DTFs (Middlebrooks, 1999; Xu and Middlebrooks, 2000; Schnupp et al., 2003). Only data up to 32 kHz were used here as the signal-to-noise ratio was poor for higher frequencies in some animals.

For spatial plotting purposes, the data were displayed as Mollweide projections. In each of these projections the nose of the animal is considered to be projecting out of the page at 0° azimuth and 0° elevation, as if the animal were looking at the reader. The Mollweide projections were plotted for elevations from −30° to +90° and all azimuths from −180° to +180°.

RESULTS

Results are based on data from 29 animals (5∕29 were male). Acoustical measurements were obtained in 20 of these animals, 9 of which were adults and 11 were animals at different ages ranging from 1.3 to 22.1 weeks (for convenience, the age in days was converted to weeks by dividing by 7 and the quotient rounded to the nearest 1∕10th of a week. For example, 9 days divided by 7 is equivalent to 1.3 weeks). The latter 11 animals came from five different litters. Nine additional adults were used only for measurements of head and pinnae dimensions. Adult acoustic measurements were obtained in conjunction with physiological experiments that utilized the acoustical measurements for virtual space stimulus presentation. In this paper we show detailed data from three animals from different age groups spanning development: 1.3 weeks (K009), 5 weeks (K008), and adult (Adult). Summary data, when shown, were computed from all animals.

Growth of the head and pinnae

Figure 1 shows linear measurements of head diameter AB, pinna width CD, and inside 1-3 and outside 1-2 pinnae height as a function of age in weeks for 16 cats starting at 1.3 weeks. The horizontal lines represent the mean and 99% confidence interval for these values in 12 adults (>52 weeks). To quantify the growth rate a three-parameter exponential rise to maximum function was fitted to the data of the form y=y_o+a(1−e^−bx), where x is the age in weeks, y_o is the extrapolated dimension at birth (0 week), a is the amount by which that dimension increases during development, (y_o+a) is the asymptotic value at full development, and b is the rate of growth. This equation accurately characterized the growth of each dimension (based on F-testP<0.0001 for all fitted equations; coefficients of determination R² are reported on the figure). Solving the growth equation for the age parameter x, we can compute the age at which the curve reaches any arbitrary proportion of the maximum value; given a proportion (e.g., 0.9), the equation reduces to −ln(1-proportion)∕b. We use a proportion of 0.9 (90%) to indicate “adult” values because this proportion produced values of the dimensions that first fell within the 99% confidence intervals for adult dimensions. The fitted parameters of the equations are shown in each panel in Fig. 1.

Based on the fitted growth curve, head diameter increases from 28.6 mm at birth to 62 mm, reaching 90% of adult value by 23 weeks. In contrast, the growth of the pinnae was much more rapid. Inside pinnae height 1-3 increased from 9.8 to 42.1 mm, reaching 90% at 18 weeks. Outside pinnae height 1-2 increased from 14.6 to 48.4 mm, reaching 90% at 16 weeks. And pinnae width CD increased from 5.9 to 25.0 mm, reaching 90% at 14 weeks. Bodyweight (not shown) increased from 0.2±0.06 kg at ∼1.5 weeks and asymptotes at 2.6±1.1 kg by ∼18 weeks. Although not shown as a figure, we also measured the interocular distance (i.e., the distance between the center of the pupils) resulting in the equation y=13.3+20.4(1−e^−0.11x) (R²=0.83, n=16). Interocular distance reached 90% of adult size by 21 weeks, which was comparable to the growth of the head.

During development, the dimensions of the head and pinnae were highly and significantly correlated with the weight and age of the animal (mean R²=0.91±0.05, n=15 pairwise comparisons). These correlations were not surprising and not particularly useful. However, as shown in the correlation matrix in Table 1, even in a group of 18 adults we found significant correlations: outside pinna height 1-2 and pinna width CD were significantly correlated with weight (p<0.01), but the head diameter AB was not. We did not track gender differences in development because the five males in the study were utilized for the acoustical measurements at very young ages.

Table 1.

Pearson correlation coefficients. N=18 adult cats. Bold and italic values indicate correlation coefficients that were significant at p<0.01 and p<0.05, respectively. Values for AB, 1-3, 1-2, and CD correspond to the head and pinna dimensions, as shown in Fig. 1.

	Weight	Head AB	Pinna 1-3	Pinna 1-2	Pinna CD
Weight	1.00
Head AB	0.41	1.00
Pinna 1-3	0.39	0.48	1.00
Pinna 1-2	0.62	0.45	0.79	1.00
Pinna CD	0.66	0.36	0.66	0.70	1.00

Frequency range and spatial-location dependence of broadband spectral notches

We observed a systematic change in the frequency of the first (i.e., lowest frequency) broadband spectral notch [i.e., first notch frequency (FNF), Rice et al. (1992)] with changes in source location in the frontal hemisphere in animals of all ages. The depths of the spectral notches were ∼10–15 dB in the youngest animals increasing to 15–20 dB in adults. Figure 2A shows the DTFs for the right ear (ipsilateral ear, +90°) of three animals of different ages, 1.3 weeks, 5 weeks, and adult, for elevations ranging from −30° to 90° in 15° steps at 0° azimuth. Prominent broadband spectral notches were observed for most source locations in the frontal hemisphere particularly toward the ipsilateral ear but for different frequency ranges depending on source location and age [Fig. 2B]. The FNF was easily detectable and moved systematically with elevation and azimuth for sources in the frontal hemisphere [e.g., Figs. 2A, 2B], except in the youngest animal (1.3 weeks). The iso-FNF contours [Fig. 2B] reveal that as the source was moved up in elevation and in azimuth toward the ipsilateral ear, the FNFs generally increased. However, for a given source location, FNF decreased with age [Figs. 2B, 2C]. For example, for a source at (0°,0°), FNFs were 20, 14, and 10.5 kHz at 1.3 weeks, 5 weeks, and adult. This developmental aspect of FNF is illustrated in Fig. 2C where FNFs at 0° azimuth and changing elevation for animals at nine ages are shown. At all ages, FNF increases with elevation, but the range of FNFs shifts progressively lower during development.

Figure 2.

Development of the monaural broadband spectral notch cues. (A) DTF gain for seven different elevations from −30° to 60° at 0° azimuth for cats of three different ages (upper left in each panel). (B) Plots of the isofrequency contours of the first (lowest frequency) notch frequencies, or FNF, for sources in the frontal hemispheres for the same three animals as in (A). (C) FNFs plotted as a function of elevation at 0° azimuth for animals of nine different ages. (D) Development of the first notch frequency range as a function of the development of the outside pinnae height 1-2 (n=18 animals). Symbols indicate FNF at (0°,0°) while the error bars indicate the range of FNFs observed in the frontal hemisphere. Solid line indicates the best-fitting function relating FNFs at (0°, 0°) to pinna height 1-2. Hatched region indicates the range of FNFs observed in the frontal hemisphere in adult animals.

Given the developmental changes in the linear dimensions of the pinnae [Figs. 1B, 1C, 1D] and the finding that the FNFs for a given spatial location decrease systematically with age, we hypothesized that the developmental change in FNF range is determined by the development of pinnae size. To test this hypothesis, Fig. 2D shows the FNF for a single source location (0°,0°) as a function of the outside pinnae height 1-2 in 19 animals (8 were adults); the error bars show the overall range of detectable FNFs observed in the frontal hemisphere for 13 of the animals used in the developmental phase of the studies. The remaining data points for adults had FNFs in encompassing a range from ∼8 to 16 kHz [hatched area, Fig. 2D], which is typical of FNF ranges reported for adult cats (Musicant et al., 1990; Rice et al., 1992; Xu and Middlebrooks, 2000). The data show that FNFs did not fully encompass the adult range in all animals until sometime after 10 weeks (Figs. 2C, 2D). Recall in Fig. 1C that the outside pinnae dimension 1-2 reached 90% of adult size, or ∼44 mm, by ∼16 weeks. Figure 2D shows that the ranges of FNFs observed in animals with pinnae dimensions >44 mm were all adultlike while those <44 mm were not. A three-parameter exponential decay function accurately describes the development of the FNF at 0° as a function of the outside pinnae height 1-2 (R²=0.89, P<0.0001, and y=7.42+25.82e^−0.039x) supporting the hypothesis that the linear dimensions of the pinnae determine the FNFs. In further support, in one animal (K013, 2.86 weeks) the pinnae on both sides were removed and the acoustic measurements repeated. Pinnae removal eliminated the spectral notches in both ears (not shown). The spectral notch cues are adult by 16 weeks consistent with the development of the pinnae.

Spatial distribution of DTF amplitude gain

The DTF gain at a given frequency varied with source direction and with the age of the animal. Figure 3 shows the distribution of DTF gains for 1, 2, 4, 8, 12, 16, and 20 kHz for sources in the frontal hemisphere for right ears (i.e., −180° is ipsilateral) for the same three animals as in Figs. 2A, 2B. Here DTF gain is plotted only for the right ear as it was almost mirror symmetric with that of the left ear in most of the animals. Each of the gain plots was normalized by the maximum DTF gain (upper left side of each panel) observed at that frequency and −3 dB contours were plotted. For a given frequency, the maximum gain tended to increase and the area of gain (i.e., the area bound by the −3 dB contour) tended to decrease with the age of the animal.

Figure 3.

Spatial distribution of DTF gains for seven frequencies for the right ears (e.g., −90° is ipsilateral) of three animals aged 1.3 weeks, 5 weeks, and adult. DTF gains for each animal have been normalized by the maximum gain (indicated at the upper left of each panel) at the indicated frequency (upper right of panels in last column). The contours are plotted at −3 dB intervals from the maximum gain. Color bar (bottom) indicates the relative gain with respect to the maximum gain.

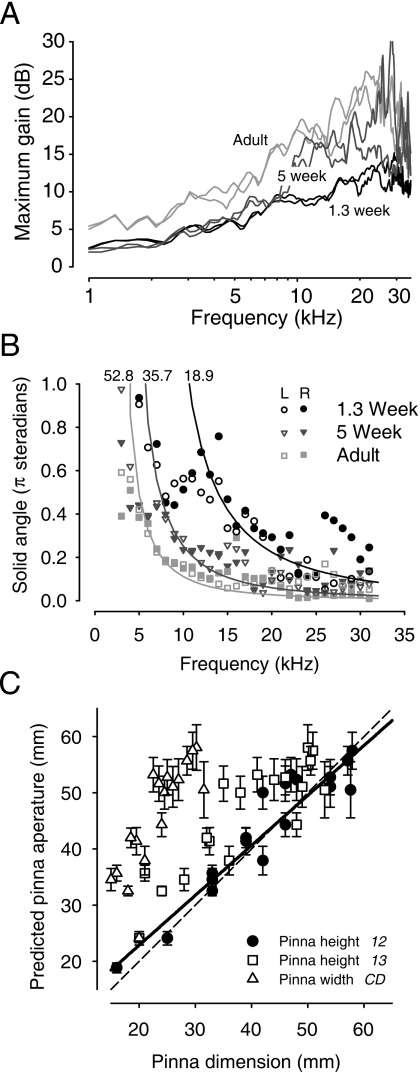
Figure 4A plots the maximum gain in the DTFs (which does not include the canal resonance gain) as a function of frequency for animals of three different ages from Fig. 3. Maximum gain occurs at the acoustic axis for a given frequency. In all animals, the maximum gain tended to increase with frequency, at least up to ∼20–30 kHz. However, for frequencies >5 kHz there was a systematic increase in the maximum gain with age. In adults, maximum gains of 20–25 dB were achieved and occurred at higher frequencies. In the youngest animals, maximum gains only achieved 10–15 dB over this same range of frequencies. The gain curves appear to be simply shifted toward lower frequencies with age, consistent with the increase in the linear dimensions of the pinnae and head (Fig. 1). Since DTFs were computed in this paper, any acoustical gains (e.g., ear canal resonance) that were nondirectional were removed from the data. Estimates of canal and concha gain and resonance frequency and their development are discussed in Sec. 3F.

Figure 4.

(A) Maximum acoustical gain of the head and pinnae as a function of frequency for animals aged 1.3 weeks, 5 weeks, and adult. (B) Solid angle area (in units of π sr) enclosed by the −3 dB contour from the DTF gain plots (Fig. 3) as a function of frequency. Data are shown for the left (open) and right (filled) ears of the same animals as in (A). Solid lines indicate the best-fitting circular aperture model (see text) to the data corresponding to each animal; the aperture diameter from the best-fitting function is indicated at the top of each line. (C) Scatter plot of the predicted aperture diameter from the circular aperture model fitted to the data as a function of the pinnae dimension in 19 animals. Data are shown for the three pinnae dimensions: CD, 1-2, and 1-3 in Figs. 1B, 1C, 1D, respectively. Error bars show 95% confidence intervals. Solid line shows linear regression of predicted aperture and pinnae height 1-2. Dashed line indicates line of equality.

Acoustic directionality of the head and pinnae and relationship to pinnae dimensions

The spatial distributions of DTF gain (Fig. 3) were quantified in two ways. The first measured the acoustic axis, the spatial location for a given frequency of highest acoustical gain, which will be reported in Sec. 3D. Second, the directionality of the pinnae and head was obtained by computing the solid angle contained by the −3 dB contour at frequencies from 2 to 32 kHz in 1 kHz frequency steps. Figure 4B shows the −3 dB contour area (in π sr; here 2π sr equals 1∕2 hemisphere) with frequency for left and right ears for the three animals of different ages in Figs. 23. For frequencies <∼4–5 kHz, the area covered more than one hemisphere (2π sr, not shown in figures). At higher frequencies, the −3 dB contour area systematically decreased with frequency for all animals.

We hypothesized that for a given frequency the solid area enclosed by the −3 dB contour should decrease with the age of the animal because the linear dimensions of the external ear increase during development [Figs. 1B, 1C, 1D]. To test this hypothesis the equation describing the frequency dependence of the solid angle for a −3 dB contour for acoustic diffraction through a circular aperture for a given aperture diameter [equation derived in Calford and Pettigrew (1984) and Coles and Guppy (1986)] was fitted to the acoustical data (e.g., Fig. 4) for 19 animals (8 adults and 11 at different ages). In the fitting the aperture diameter was the only free parameter (MATLAB Version 7.1 robust nonlinear least-squares trust-region method). We noticed that the empirical data at lower frequencies were poorly fitted by the model, so only data for solid angles <∼0.5 were used for the fitting resulting in frequencies >∼7–15 kHz (depending on the age of the animal) although all empirical data are shown in Fig. 4B. The best-fitting functions describing the solid angle are shown for three animals in Fig. 4B; the predicted diameters of the circular aperture for these animals were 18.9, 35.7, and 52.8 mm, respectively (R² equals 0.63, 0.5, and 0.5, respectively). Coefficients of determination (R²) for the population averaged 0.52±0.19 with a median of 0.5 and a range of 0.18–0.85. In cases where the fit was poor, the fitting error tended to occur at the lower frequency end of the curve [e.g., Fig. 4B, 1.3 week].

There were some data points in Fig. 4B that deviated substantially from the predictions. The deviations occurred at low frequencies for all animals, at high frequencies for the 1.3 week animal, and ∼15 and 25 kHz in adults. These deviations occur due to a splitting of the spatial area of highest gain, the acoustical axis. Examples of this splitting are beginning to be apparent at 20 kHz in the 1.3 week animal and at 16 kHz in the adult in Fig. 3. This phenomenon has been reported previously in adult cats for frequencies around 14 and around 28 kHz, consistent with our findings here (Musicant et al., 1990).

To test the hypothesis that the increasing linear dimensions of the pinnae during development determine the directionality as computed by the −3 dB area as a function of frequency [e.g., Fig. 4B], the predicted pinnae aperture from the fitted function was plotted in Fig. 4C as a function of the three empirically measured linear dimensions of the pinnae [Figs. 1B, 1C, 1D]. The pinna dimension that described most of the variance in the predicted aperture diameter was the outside pinnae height 1-2; the linear regression of predicted pinnae aperture diameter on the empirical pinna height 1-2 was significant (R²=0.92, P<0.0001, y=5.1+0.89x, and n=19). The linear regressions with the other pinnae dimensions were also significant (P<0.0001), but the coefficients of determination and the slopes of the regression functions were not as close to 1.0 (R² and slope 0.87 and 0.85, and 0.77 and 1.75 for pinnae dimensions 1-3 and CD, respectively). These data support the hypothesis that the linear dimensions of the pinnae, in particular, the outer height 1-2, determine the development of the frequency dependence of the −3 dB area of the acoustical directivity.

Broadband head and pinnae directionality

Figure 5 shows the directionality of the head and pinnae computed across the entire stimulus bandwidth considered here (1–30 kHz). Note that because DTFs were computed here, the gain at frequencies <∼2 kHz was quite small (<5 dB), as can be seen in Fig. 3. Thus, the broadband gain shown here is largely due to the gains for frequencies >2 kHz. Figure 5A shows the spatial distribution of broadband directionality and the associated −3 dB area (in π sr, upper left) for animals of three different ages corresponding to those in Figs. 234. Figure 5B summarizes the −3 dB spatial area for the left and right ears for 20 (9∕20 were adults) animals as a function age. In Fig. 5B the −3 dB areas were normalized by the average area obtained in nine adults. These data can be thought of as a general characterization of the development of head and pinnae acoustic directionality with age (see Mrsic-Flogel et al., 2003). A three-parameter exponential was fitted to the data (R²=0.91, P<0.0001, and y=1.04+24.3e^−0.74x). The −3 dB area decreased from ∼1∕4 of the frontal hemisphere (∼1π sr) at 1.3 weeks by a factor of 10 during development and fully asymptotes to adult values (i.e., 1.0) by ∼14 weeks. Recall that by 16 weeks, the outside pinnae height 1-2 was 90% of adult size. The computation of the broadband acoustic directionality was motivated in part by some experimental data on the development of neural coding of acoustical space in the cat and other species, which will be detailed in Sec. 4.

Figure 5.

(A) Broadband DTF gain for animals aged 1.3 weeks, 5 weeks, and adult. Each plot has been normalized by the maximum DTF gain and −3 dB contours with respect to the maximum gain are plotted. The area (in units of π sr) enclosed by the −3 dB contour is indicated in the upper left of each panel. (B) The development of the −3 dB area as a function of the age of cats for the left (filled symbols) and right (open symbols) ears (n=19 animals). The −3 dB area has been normalized by the average broadband gain area in 8 (8∕19) adult animals. Solid line indicates best-fitting function to all of the data (see text).

The acoustical axis

The spatial location of the DTF gain maximum (and minimum) varied as a function of frequency. The direction of maximum acoustical gain at a given frequency is known as the acoustical axis (Middlebrooks and Pettigrew, 1981; Phillips et al., 1982). Figure 6 shows the spatial location of the acoustic axis for azimuth (top) and elevation (bottom) as a function frequency for one ear in animals of four different ages (age indicated in upper left). Two general patterns emerged upon examination of the acoustic axis for these animals as well as the others. First, in all except the youngest animal (1.3 weeks, Fig. 6), with increasing frequency the location of the axis in azimuth revealed patterns that tended to move from medial to lateral locations interspersed by discrete jumps back toward the midline. Vertical dashed lines mark the approximate frequency of these transitions in Fig. 6. In the adult, the azimuth of the acoustic axis begins at ∼40°–50° at 3 kHz, then makes an abrupt transition toward the midline at ∼14 kHz, moves laterally again to ∼50° by 25 kHz, with yet another transition toward midline at 28 kHz. Qualitatively similar patterns were seen in each of the younger animals. For example, the data for the 7.1 and 5 week animals [see also data for 3.9 weeks in Fig. 8A] show similar movements and transitions of the azimuthal acoustic axis, but the transitions occurred at systematically higher frequencies than the adult. The movements of the acoustic axis in the youngest animal (1.3 weeks) were different than for the older animals; here the azimuthal acoustic axis moved from lateral to medial and with abrupt transitions back toward lateral locations.

Figure 6.

The elevation (top panels) and azimuth (bottom panels) corresponding to the acoustic axis as a function of frequency in four animals aged 1.3, 5, and 7.1 weeks as well as adult (age indicated in upper left of each panel). The acoustic axis is the spatial location corresponding to the maximum DTF gain [Fig. 4A] at a particular frequency (see Fig. 3). Vertical dashed lines indicate frequencies where discrete transitions appear to occur in the acoustic axis.

Figure 8.

Estimated development of the resonance frequency, acoustic gain, and the length of the ear canal and concha. The gain (filled) and resonance frequency (open) of the ear canal∕concha (labeled simply “canal” in the figure) were estimated from the nondirectional common components of the DTFs (see Sec. 2) in 16 animals (5∕16 were adults). Solid line shows the best-fitting three-parameter exponential decay function relating the canal∕concha resonance frequency to age in weeks. Dashed line indicates the canal∕concha length (in millimeters) estimated from the fitted resonance frequency function and assuming that the canal∕concha can be modeled as a simple cylinder of a given length and closed at one end (see text).

The acoustic axis in elevation in all animals tended to move from lower to higher elevations with increases in frequency that were interrupted by transitions again to lower elevations. For example, in the adult, the elevation axis increases from −30° to 30° for frequencies from 4 to 12 kHz, and then shifts back down to 0° by 14 kHz increasing to +30° or more by 20 kHz. In the 5 week animal, the first downward transition occurs at ∼17 kHz while in the youngest animal (1.3 weeks) this transition does not appear to occur until ∼28 kHz. By 7.1 weeks, the first transition occurs at ∼14 kHz, which was comparable to adult values. These transitions are indicated with vertical dashed lines. The elevation acoustical axis was more difficult to interpret in the youngest animals.

The frequencies where the transitions occurred in the azimuth and elevation acoustic axes revealed a rough correspondence with the frequency ranges where the first spectral notch cues occurred (Fig. 2). Recall that the ranges of FNF move systematically toward lower frequencies during development [Fig. 2D] and so too do the acoustic axes transition frequencies (Fig. 6).

Contribution of the pinnae to DTF gain, directivity, and acoustic axis

Spatial directivity

While it is typically assumed that the pinnae are a major determinant of the spatial and frequency dependences of acoustical gain, directivity, and the acoustic axis, few experiments have actually tested this hypothesis directly (see Koka et al., 2008). None of these studies has examined the role of the pinnae in developing animals. Here, in one animal (K013, 2.9 weeks) we assessed the contribution of the pinnae in the developing animal to the DTF gain and the associated directivity by measuring DTFs before and after the removal of both pinnae. Figure 7A shows for the right ear (−180° corresponds to the ipsilateral ear) the spatial pattern of DTF gain for three frequencies with (left) and without (right) pinnae. The maximum gain for these conditions is listed at the top left of each panel. Two major findings were apparent. The pinnae increased the overall acoustical gain by as much as 6 dB for the example frequencies and also vastly increased the acoustical directivity. This latter finding is illustrated in Fig. 7B where the solid angle encompassing the −3 dB contour for the left and right ears is plotted as a function of frequency. Predictions of −3 dB area based on the circular aperture model (see Sec. 3C) are plotted for aperture diameters of 40, 15, and 10 mm. The −3 dB area prediction corresponding to a 24.13 mm aperture is the best-fitting function to the data in the intact animal (R²=0.7; although note the substantial deviations from the prediction <∼10 kHz). The 24.13 mm predicted value compares favorably with the 25 mm empirical measurement of the outer pinna height 1-2 for this animal [e.g., Fig. 4C]. For virtually all frequencies, the solid angle was substantially increased upon removal of the pinnae [Fig. 7A]. Data from the pinnaeless animal could not be accounted for by the circular aperture model. This result shows that the pinnae in developing cats are critical for increasing the acoustical gain and the overall acoustic directivity.

Figure 7.

The contribution of the pinnae to the spatial distributions of DTF gain (A), the frequency dependence of the −3 dB area of the DTF gain (B), the azimuth and elevation of the acoustic axis (C), and the maximum gain as a function of frequency (D). All data are from one animal aged 2.9 weeks. (A) DTF gain for three frequencies (upper right, left panels) with (left column) and without (right column) the pinnae. Maximum gain indicated in upper left of each panel. Axes and lines as in Fig. 3. (B) Solid angle area (in π sr) enclosing the −3 dB contours as a function of frequency for the left (open) and right (closed) ears with (black symbols) and without (red symbols) the pinnae. Solid lines indicate the predicted areas based on the circular aperture model (see text) with the diameter given at the top of each respective line. A diameter of 24.13 mm fitted the intact data the best. (C) The elevation (top) and azimuth (bottom) of the acoustic axis for the right ear with (black symbols) and without (red symbols) the pinnae. The values of the axis without pinnae have been shifted by −3° to prevent overlap. (D) Maximum gain as a function of frequency with (black) and without (red) the pinnae. The gain due to the pinnae (gray line) was computed from the difference in the gains with and without the pinnae. The two different lines for each condition in (D) correspond to the left and right ears.

The acoustic axis

The pinnae are a major determinant of the acoustic axis, particularly at high frequencies. Figure 7C shows the acoustic axis in elevation (top) and azimuth (bottom) with and without the pinnae for the left ear. Results for the right ear were comparable. Changes in the elevation axis were not readily apparent. The axis in azimuth was substantially altered by pinnae removal with the axis located predominantly toward the far lateral azimuths. Moreover the pattern of acoustic axis movement with frequency was altered. After pinnae removal the axis moved from lateral to medial azimuths, beginning ∼17 kHz with an abrupt transition again to lateral azimuths at ∼23 kHz. In the pinnae intact condition, the azimuth axis moved from medial to lateral with a transition back to medial azimuths at ∼25 kHz consistent with general trends shown in Fig. 6 for developing animals.

Acoustical gain due to the pinnae

The pinnae contribute substantially to the overall acoustical gain. Figure 7D shows the maximum gain for the left and right ears as a function of frequency both with and without the pinnae. The maximum gain occurs at the acoustic axis. With the pinnae, the maximum gain increased systematically with frequency, approaching 25 dB at high frequencies. After pinnae removal, the gain also increased with frequency, but much less so than with the pinnae. The gain due to the pinnae was computed by taking the difference of the gains produced with and without the pinnae. In this young animal, the pinnae do not become directional until ∼8 kHz. Above this, the maximum gain increased with frequency reaching a maximum 9.6 dB at 16.4 kHz, then falling somewhat for higher frequencies.

Development of ear canal and concha resonance and gain

Because DTFs were computed in this paper, any acoustical gains that were nondirectional are not present in the data. However, a major source of nondirectional gain is the resonance of the ear canal and concha (Rosowski et al., 1988). The resonance of the canal and concha is a large source of the overall acoustical gain of the auditory periphery. During development the dimensions of the ear canal and concha (length and diameter) increase, which would be expected to lower the frequency of the resonance. Unfortunately, we did not measure ear canal or concha dimensions. However, the nondirectional gain and resonance frequency of the canal∕concha can be estimated from the common components of the HRTFs [see Sec. 2 and Koka et al. (2008) and Rosowski et al. (1988)]. The common component had a gain of ∼0 dB as frequency approached 0 Hz, but exhibited a prominent peak in the gain at midfrequencies consistent with expected resonance frequency of the canal and concha. The peak gains and frequencies were remarkably consistent in the left and right ears of each animal, so the results here represent the average gain and corresponding frequency across the left and right ears. The gain and frequency associated with this peak were computed and are plotted in Fig. 8 as a function of age for 16 animals (5∕16 were adults). In the youngest animal (1.3 weeks) the estimated resonance frequency was 8.58 kHz producing a gain of 15.6 dB. With development, the resonance frequency decreased rapidly averaging 3.3±0.3 kHz in five adults. To quantify the development of the canal resonance frequency an exponential decay function was fitted to the data. The fitted function y=3.58+12.04e^−0.67x accurately described the data (R²=0.91, P<0.0001, and n=16). There was no systematic change in the gain with development, averaging 13.6±3 dB in the five adults and 13.6±2 dB in the 11 developing animals. The linear regression relating canal gain to age was not significant (R=0.08, P=0.77). In terms of the resonance frequency, the ear canal of the cat appears to be adultlike in its acoustical properties by 14 weeks when the fitted function asymptotes fully.

DISCUSSION

Cats have been a common model system for general studies of the development of auditory system function including anatomy, physiology, and behavior. Although there has been one brief report of the development of the acoustics of the head and external ear in cats, that study was limited to measurements of the ILD cue to sound location (Moore and Irvine, 1979) in animals older than 5 weeks. To fill this void, we measured here the DTFs in cats from the onset of hearing (∼1.5 weeks) from which the monaural acoustical spectral transformations could be computed. Our data reveal that there is considerable development of both the dimensions of the head and pinnae and the resultant acoustical transformations before 5 weeks in the cat and that the monaural acoustical cues are adult by ∼16 weeks.

Development of the linear dimensions of the head and pinnae

We studied the development of head and pinnae dimensions in 16 animals beginning at 1.3 weeks after birth. Growth curves were fitted to the head and pinnae measurements to provide a quantitative measure of the general growth of these structures in a population of cats. The head and the pinnae of the cats increased in size substantially during development from birth to adult. Based on the growth curves, head diameter increased by a factor of 2.17 from 28.6 mm at birth to 62 mm in adults and reached 90% of adult value by 23 weeks. These compare favorably with values of 29 and 63.02 mm measured in 35 newborn (Latimer, 1931) and 54 adult female cats (Latimer, 1936), respectively. Head diameter in adult males averages 5.5% larger (Latimer, 1936). Interocular (or interpupillary) distance increased by a factor of 2.53 from 13.3 to 33.6 mm, reaching 90% of adult value by 21 weeks. While our measured growth rate for interocular distance was comparable to that reported by Timney (1988) our asymptotic value was ∼15% less. The growth of the pinnae dimensions was much more rapid. Inside pinnae height 1-3 increased by a factor of 4.3 from 9.8 to 42.1 mm, reaching 90% at 17.7 weeks. Outside pinnae height 1-2 increased by a factor of 3.31 from 14.6 to 48.4 mm, reaching 90% at 16.4 weeks. And pinnae width CD increased by a factor of 4.23 from 5.9 to 25.0 mm, reaching 90% at 13.5 weeks. Bodyweight (not shown) increased from 0.2±0.06 kg at ∼1.5 weeks and asymptotes at 2.6±1.1 kg by ∼18 weeks. Newborn weights in kittens average 0.15±0.03 kg (n=35, Latimer, 1967).

As expected, weight was positively and significantly correlated with all head and pinnae measurements during development, but some correlations remained even in adults (see Table 1). The significant correlation between pinnae dimension and weight in adults found here provides a potential explanation for the observation by Xu and Middlebrooks (2000) that optimal frequency scaling factors for DTFs between different cats were significantly correlated with their weight.

Because the behavioral onset of hearing in cats is ∼1.5 weeks (Ehret and Romand, 1981; Villablanca and Olmstead, 1979), the acoustical consequences of the increasing size of the head and pinnae are functionally relevant only for ∼1.5 weeks and older. Beginning at 1.5 weeks instead of birth the average head diameter increases by a factor of 1.9 and pinnae dimensions CD, 1-3 and 1-2 increased by factors of 2.5, 2.7, and 2.3, respectively. Thus, from the onset of hearing in the cat the dimensions of the head and pinnae change substantially.

The rate of growth of the pinnae (given by parameter b in the equations in Fig. 1) was 30%–70% greater than that of the head. As such, the pinnae reach adult dimensions much sooner than the head diameter. The major dimension of the pinnae, the outside height 1-2, reached 90% of adult size by 16 weeks while head diameter took 23 weeks. One implication of the rapid development of the pinnae is that the acoustic transformations that are heavily determined by the pinnae, such as the spectral notches (Fig. 2), the acoustic gain (Figs. 3578), and the acoustic axis (Figs. 367), would be expected to become adultlike before the acoustical transformations that depend on head diameter, such as the binaural cues to sound location, ITDs, and ILDs. (The development of the binaural cues to location will be detailed in a separate paper.) The empirical acoustical measurements discussed below support this hypothesis.

Development of the broadband spectral notch cues to location

The spectral notch cues were found to be present in the cat primarily for source locations in the frontal hemisphere. First notch frequencies (e.g., Rice et al., 1992) in animals of all ages were found to increase systematically from lower to higher frequencies as source elevation increased and as source azimuth moved toward the ipsilateral ear [Figs. 2A, 2B, 2C]. However, the frequency ranges of FNFs in the frontal hemisphere were highly dependent on age, with high FNFs ranging from 18 to 25 kHz in the youngest animals to lower FNFs of ∼8–16 kHz in adults. In other words, for a given source location, the FNF associated with that position systematically decreased with age. Removal of the pinnae in one animal eliminated the spectral notch cues, supporting the hypothesis that even in developing animals with smaller pinnae these cues are created exclusively by the pinnae, as has been demonstrated in other species (rat: Koka et al., 2008; bat: Wotton et al., 1995 and Aytekin et al., 2004; cat: Musicant et al., 1990; and ferret: Parsons et al., 1999). Our data on the spatial dependence of FNFs in adult cats are comparable to that reported in prior studies on cats (Musicant et al., 1990; Rice et al., 1992; Young et al., 1996; Xu and Middlebrooks, 2000).

The developmental changes in FNFs and their ranges were determined by the linear dimensions of the pinnae [Fig. 2D]. As the outside height 1-2 of the pinnae increased, the FNF range systematically decreased. Although the ranges of FNFs began to overlap with adult range by 3.9–5 weeks, it was not until >10 weeks that the range fully encompassed the adult range. Outside pinnae height 1-2 was essentially adult by 16 weeks with a value of 44 mm. FNF ranges were fully adult for pinnae heights >44 mm but were not adult for values less than that. The pinnae dimensions determine directly the functional range of FNFs during development and their final range as adults.

Development of the spatial distribution of DTF amplitude gain

Development of acoustical gain and directionality

The maximum acoustical gain produced by the head and pinnae increased with frequency and age. Regardless of age, a gain of ∼3–5 dB was observed at low frequencies <∼3 kHz and far lateral angles [e.g., Figs. 4A, 6] and was likely due to the so-called obstacle effect of the head (Kinsler et al., 1982). However, at higher frequencies the maximum gains increased considerably, reaching values of 10–15 dB in the youngest animals increasing to 20–25 dB in adults [Fig. 4A], at least over the range of frequencies examined here. The adult values of gain are comparable with the ∼25 dB maximum gain at higher frequencies reported previously in cat (Musicant et al., 1990). The increase in gain with age is likely due to the developing amplification capabilities of the pinnae as it increases in size (Coles and Guppy, 1986). Already by 2.9 weeks, the pinnae, by themselves, in the cat can produce nearly 10 dB of gain [Fig. 7D]. This is consistent with prior reports of frequency-dependent pinna-only gains of 3–18 dB, with the higher gains occurring at higher frequencies in cat (Phillips et al., 1982), ferret (Carlile and King, 1994 and Schnupp et al., 1998), wallaby (Coles and Guppy, 1986), guinea pig (Palmer and King, 1985), bat (Jen and Chen, 1988 and Obrist and Wenstrup, 1998), and rat (Koka et al., 2008). In a behavioral study by Flynn and Elliot (1965) thresholds for detection in cats were increased when the pinnae were removed by 11 dB at 4 kHz increasing to 17 dB at 16 kHz.

DTF gain directionality and its development were quantified by computing the area of the −3 dB (with respect to maximum gain) contour. In animals of all ages, with increasing frequency the DTF amplitude gain became more directional in that the −3 dB area systematically decreased [Figs. 34B]. The hypothesis that the developmental increase in acoustic directionality was determined by the increasing dimensions of the pinnae was tested here by modeling the pinnae as a circular aperture (see Calford and Pettigrew, 1984 and Coles and Guppy, 1986) and comparing the outputs of the model to our empirical measurements. The frequency dependence of the diffraction of sound into a circular aperture has been shown to account qualitatively for the area of acoustic directionality in a variety of species (Calford and Pettigrew, 1984; Coles and Guppy, 1986; Carlile and Pettigrew, 1987; Musicant et al., 1990; Carlile, 1990; Obrist and Wenstrup, 1998). Here we fitted the circular aperture model to the −3 dB area data for each animal, where the diameter of the aperture was the only free parameter. While the pinnae of the cat are certainly not circular, this simple model did provide an adequate description of the directionality, accounting on average for 50% of the variance in the data. Fits were very poor at low frequencies [Figs. 4B, 7B] and at a few discrete frequencies near 14 and 28 kHz [see Musicant et al. (1990) and Carlile (1990) for a discussion of this phenomenon].

A plot of the best-fitting circular aperture diameter as a function of the three empirically measured pinnae dimensions (Fig. 1) revealed significant linear relationships. However, only the outside pinnae height 1-2 accounted for the most variance (92%) and yielded a regression slope nearest 1.0 (0.89). That the empirical acoustical data can be accounted for by the simple aperture model and that the best-fitting aperture diameter is significantly correlated with the empirical pinnae dimensions (with a slope near 1.0) support the hypothesis that the increasing pinnae dimensions during development are responsible for the increasing acoustical directionality. The pinnae themselves were a critical determinant to directionality as demonstrated in the experiment where both pinnae were removed [Figs. 7A, 7B, 7C, 7D], supporting an earlier finding by Phillips et al. (1982) in cat where pinnae removal abolished the pinna directionality at high frequencies.

Development of the acoustic axis

The acoustic axis is the spatial direction for each frequency that produces the largest gain relative to all other directions (Middlebrooks and Pettigrew, 1981; Phillips et al., 1982). In animals of all ages, the acoustic axis in azimuth exhibited a general dependence on frequency where the axis began to migrate from medial to lateral azimuths with increasing frequency (Fig. 6). This trend was interrupted with jumps back toward the midline at particular frequencies followed again by migrations toward lateral azimuths. Sometimes another jump back toward the midline would occur at higher frequencies. Similar trends were observed in elevation where initially the axis migrates from low to high elevations with increasing frequency, transitions back to lower elevations, and then continues to increase in elevation. While the qualitative patterns of acoustic axis movements with frequency were similar in all animals (expect the youngest, 1.3 weeks), the frequencies of the transitional jumps decreased with increasing age. The values of the frequencies of transitions in a given animal were comparable to the ranges of FNFs observed in that animal [Fig. 2D]. Given that the FNFs were shown to be dependent on the linear dimensions of the pinnae, which increase with age, we hypothesize that the discrete frequency transitions in the movements of the acoustic axis are determined by the size of the pinnae. While our data are qualitatively consistent with this hypothesis, we did not formally test it. That the pattern of acoustic axis migration with frequency was similar in animals of all ages (and sizes) but that the frequency ranges of these patterns were systematically shifted toward higher frequencies in the younger, smaller animals support our hypothesis. In further support, when the pinnae were removed in one animal, these transitions were substantially disrupted [see also Carlile and Pettigrew (1987)]. These general patterns in the acoustic axis are similar to those reported in other species [cat: Musicant et al. (1990), this paper, wallaby: Coles and Guppy (1986), ferret: Carlile (1990), and rat: Koka et al. (2008)].

We should note that the acoustic axes in the youngest animal (1.3 weeks, Fig. 6) displayed trends that were different than observed in the older animals, particularly in azimuth. In this animal, the azimuthal axis shifted from lateral to medial azimuths, with discrete jumps back to lateral azimuths, with increasing frequency. This pattern was observed in both ears of this animal and was not observed in any of the other animals (or the other species listed above). Rather, these data were similar to that seen in the guinea pig (Carlile and Pettigrew, 1987). We do not know the exact explanation for this, but the morphology of the pinnae in the youngest cats (at least <2.9 weeks) was rounded, stumpy, and protruded directly away from the meatus and was quite different than that in juveniles or adults where the pinnae take a more triangular and upright shape. The infant cat pinnae that produce the anomalous acoustic axes may be more similar to that in guinea pig.

Development of the ear canal and concha resonance frequency and gain

A major factor in the acoustical transformation of sound by the external ear is the resonance created by the ear canal and concha. In our measurements we could not separate the different effects of canal and concha (see Rosowski et al., 1988). For each animal we estimated the canal∕concha resonance frequency and gain from the common components of the DTFs. Figure 8 shows that the resonance frequency decreased from 8.58 kHz at 1.3 weeks to an average of 3.3 kHz in adult cats; the asymptote of the fitted curve in Fig. 8 was 3.6 kHz. The resonance frequency was adult by ∼14 weeks. The acoustical gain associated with this frequency was essentially constant over development, averaging 13.6 dB. Our estimate of resonance frequency and gain of 3.6 kHz and 13.6 dB is comparable to other measurements of canal∕concha resonance in adult cats, which occur between 3 and 4 kHz with gains of ∼15 dB (Wiener et al., 1966; Phillips et al., 1982; Rosowski et al., 1988; Musicant et al., 1990; Rice et al., 1992). The acoustic effects of the ear canal are often modeled as a cylinder closed at one end by the tympanic membrane (Shaw, 1974; Rosowski et al., 1988). In this model the wavelength of the resonance is equal to 1∕4 of the length of the canal. Using this equation, we estimate that the length of the ear canal and concha increased from ∼10.2 mm at 1.3 weeks and asymptotes to a value of 23.6 mm in adults. Unfortunately we did not measure canal or concha lengths. The latter value of 23.6 mm compares favorably with the concha length of 25.4 mm measured in cats by Rosowski et al. (1988). In their study of the development of auditory capabilities in kittens, Olmstead and Villablanca (1980) measured canal and concha length from birth through ∼2 weeks. At 1 week the length was 10 mm increasing to 15 mm by 2 weeks. The 10 mm empirical measurement is comparable to our 10.2 mm estimate based purely on acoustical measurements. From the fitted function to our data, at 2 weeks the length is estimated to be 13.3 mm, comparable to the 15 mm measured by Olmstead and Villablanca (1980). Given the correspondence between our estimated canal∕concha lengths in these latter young ages and in adults, we believe that the length of the developing ear canal and concha in cats can be accurately described using the fitted function describing the resonance frequency and the model of the canal [e.g., length=(343 m∕s)∕(4×(3.58+12.04e^−0.67x))] which is plotted also in Fig. 8.

Implications for physiological and behavioral development

There have been many anatomical, physiological, and behavioral studies in the cat for which our data may be relevant [see reviews by Kitzes (1990) and Walsh and McGee (1986)]. Because the acoustical properties of the outer and middle ears are major determinants in establishing the frequency range of hearing (Ruggero and Temchin, 2002), we suggest that the general development of the physiology of the ascending auditory pathway and of behavior in general will also be influenced to a large degree by the development of the outer and middle ears. For example, the development of behavioral (Ehret and Romand, 1981) and physiological (Litovsky, 1998) absolute auditory thresholds measured in the free field requires knowledge of the spatial- and frequency-dependent peripheral acoustical transformations reported here, such as the gain and resonance frequency of the ear canal (Fig. 8) and the frequency dependence of maximum acoustical gain of the head and pinnae [Fig. 4A]. These acoustical data along with the development of the middle ear transfer function will ultimately determine the effective input to the cochlea [see review by Ehret (1990)].

These data also have implications for the concomitant development of the acoustical cues to sound source location, the neural encoding of these cues, and their ultimate use by the animal for the perception of source location. We shall discuss at length the development of the primary binaural cues to location, ITDs, and ILDs, and how they relate to the growing dimensions of the head and pinnae in a separate paper. Behaviorally, adult cats localize sounds quickly and accurately with performance nearing that of humans (Moore et al., 2008; Tollin et al., 2005; Huang and May, 1996; Populin and Yin, 1998). And even kittens can approach sounds by around 24 days of age, although with much less precision (Clements and Kelly, 1978; Olmstead and Villablanca, 1980; Villablanca and Olmstead, 1979; Norton, 1974). The ability of kittens to make overt orienting responses to sounds suggests that the basic organization of the binaural system may be established early in development. But physiological (Pujol and Hilding, 1973) and simple behavioral (Ehret and Romand, 1981) responses to sound are seen much earlier, a few days after birth. The apparent delay in directional responding might be related to a slower rate of development of the binaural hearing mechanism, the specific cues for location, or simply motor control.

Another contributing factor for poor localization in infant cats may be that the acoustical cues to location are not yet mature. And this would be reflected in the neural coding and subsequent perceptual interpretation of the cues. There is only one study known to the authors that potentially addresses this issue. Wallace and Stein (1997) reported that the size of the auditory spatial receptive fields measured for broadband stimuli in the superior colliculus in the developing cat decreased in size substantially, by more than a factor of 5 beginning from 2 weeks of age, with adult sizes being reached by ∼15–16 weeks [see Fig. 4A in Wallace and Stein (1997)]. The rate of development of the physiological spatial receptive fields they reported was virtually identical to the rate of development of the broadband −3 dB acoustical areas we measured here in Fig. 5. We compared our broadband acoustical data because many superior colliculus neurons in cat exhibit fairly broad selectivity for sound frequency (Hirsch et al., 1985). We fitted a three-parameter exponential function to the receptive field size data of Wallace and Stein (1997) which yielded y=1.26+28.3e^−0.78x (R²=0.95, P<0.0001). The 95% confidence intervals for the three fitted parameters encompassed all three of the parameters of the function that was fitted to our acoustical data in Fig. 5B (y=1.04+24.3e^−0.74x). In other words, the two functions were not significantly different (P<0.05). That the physiological spatial receptive field areas and the −3 dB acoustical areas measured here developed at the same rate strongly suggest that it was the development of the acoustics of the cat head and pinnae that determined the spatial receptive field sizes observed by Wallace and Stein (1997) and not necessarily a development of the physiological receptive field properties of the neurons themselves. Thus, a parsimonious explanation for the development of the spatial receptive fields observed by Wallace and Stein (1997) is that the neural receptive fields in the developing cat may be already adultlike in their physiological properties and that the changing spatial receptive field size with age was a simple consequence of the development of the acoustical properties of the head and external ears. A similar finding was shown directly in the auditory cortex of ferret (Mrsic-Flogel et al., 2003).

We demonstrated here that one monaural cue to source location, the spectral notch (Fig. 2), develops considerably from the onset of hearing through ∼16 weeks. These spectral notch cues have been shown to be used by cats for the localization of sounds varying primarily in elevation (Huang and May, 1996; Tollin and Yin, 2003). The range of FNFs decreases by 1–1.5 octaves over ∼16 weeks raising interesting, but as yet unanswered, questions as to how cats compensate for these changes. Is there plasticity in the central auditory system during this period that effectively recalibrates mapping of the spectral notch cues (the FNFs) and source location [see Moore and King (2004)]? Or is the internal mapping in the developing animals fixed genetically at or near the onset of hearing with an adultlike mapping?

Studies in the barn owl have revealed a sensitive period early in development where normal acoustical input to the two ears, and thus normal cues to source location, must be present for normal sound localization behavior to develop (Knudsen et al., 1984a, 1984b). The duration of this sensitive period was shown to be correlated with the time course over which the head and facial ruff (like pinnae) dimensions reach maturity, ∼8 weeks (Knudsen et al., 1984a). These studies revealed that owls reared with altered acoustical cues (e.g., ear plug) prior to 8 weeks were able to adapt and regain normal sound localization abilities despite the altered cues; however, when the cues were altered in owls after 8 weeks no adaptation was found. Thus, for a period of ∼8 weeks, the internal mapping of the ensemble of acoustical cues to location and spatial location itself remains plastic. To the extent to which a similar sensitive period for the development of sound localization in cats exists, our present data detail the developmental constraints on when the peripheral acoustical transformations reach maturity. Here, the monaural spectral transformations are mature by 16 weeks, in line with the development of the linear dimensions of the head and pinnae. We hypothesize that a critical or sensitive period for the consolidation of sound localization in the cat for the monaural cues to location will occur within 16 weeks. Because the head dimensions and the associated binaural cues to location do not reach maturity until ∼23 weeks, the sensitive period may be somewhat longer.