Maximum proton kinetic energy and patient-generated neutron fluence considerations in proton beam arc delivery radiation therapy

Abstract

Several compact proton accelerator systems for use in proton therapy have recently been proposed. Of paramount importance to the development of such an accelerator system is the maximum kinetic energy of protons, immediately prior to entry into the patient, that must be reached by the treatment system. The commonly used value for the maximum kinetic energy required for a medical proton accelerator is 250 MeV, but it has not been demonstrated that this energy is indeed necessary to treat all or most patients eligible for proton therapy. This article quantifies the maximum kinetic energy of protons, immediately prior to entry into the patient, necessary to treat a given percentage of patients with rotational proton therapy, and examines the impact of this energy threshold on the cost and feasibility of a compact, gantry-mounted proton accelerator treatment system. One hundred randomized treatment plans from patients treated with IMRT were analyzed. The maximum radiological pathlength from the surface of the patient to the distal edge of the treatment volume was obtained for 180° continuous arc proton therapy and for 180° split arc proton therapy (two 90° arcs) using CT# profiles from the Pinnacle™ (Philips Medical Systems, Madison, WI) treatment planning system. In each case, the maximum kinetic energy of protons, immediately prior to entry into the patient, that would be necessary to treat the patient was calculated using proton range tables for various media. In addition, Monte Carlo simulations were performed to quantify neutron production in a water phantom representing a patient as a function of the maximum proton kinetic energy achievable by a proton treatment system. Protons with a kinetic energy of 240 MeV, immediately prior to entry into the patient, were needed to treat 100% of patients in this study. However, it was shown that 90% of patients could be treated at 198 MeV, and 95% of patients could be treated at 207 MeV. Decreasing the proton kinetic energy from 250 to 200 MeV decreases the total neutron energy fluence produced by stopping a monoenergetic pencil beam in a water phantom by a factor of 2.3. It is possible to significantly lower the requirements on the maximum kinetic energy of a compact proton accelerator if the ability to treat a small percentage of patients with rotational therapy is sacrificed. This decrease in maximum kinetic energy, along with the corresponding decrease in neutron production, could lower the cost and ease the engineering constraints on a compact proton accelerator treatment facility.

INTRODUCTION

Recently there has been debate regarding the cost-effectiveness of proton therapy.^{1, 2} Proton therapy has the potential to improve sparing of normal tissue as compared to x-ray therapy because of the finite and well-defined proton range. However, current estimates show that proton therapy is 2.4 times more costly than intensity-modulated x-ray therapy (IMRT).³ Opponents of proton therapy claim that the benefits of proton therapy relative to IMRT do not merit the additional cost of protons, and, in particular, the use of proton radiotherapy for prostate cancer has been called into question, especially for older patients. Proponents of proton therapy claim that there is a clinical benefit of protons over IMRT. Furthermore, they claim that proton therapy is a relatively new treatment modality, and the promise of technological advancements could serve to reduce the cost of proton therapy relative to IMRT, lowering the cost increase factor to as low as 1.7 within the next 5 years.³

All currently operable proton facilities are large, high-cost (∼$100 million) facilities that use a cyclotron or synchrotron to accelerate the particles and then split the beam into several different beam lines that travel to large proton gantries mounted in different treatment rooms. However, there have recently been proposals for low-cost proton treatment facilities where the accelerator is mounted on a gantry and contained in a single room, similar to current x-ray therapy treatment rooms. Some prospects for producing compact designs include laser-induced plasma wakefield accelerators,^{4, 5} miniaturized cyclotrons,⁶ and the dielectric wall accelerator (DWA).⁷

Of paramount importance to the design of all of these accelerators is the maximum proton kinetic energy that must be achieved. Higher proton energies lead to increased volume of the apparatus, increased magnet current for beam transport, and increased cost of the entire facility due to neutron shielding. The generally accepted values defining the range of kinetic energy that must be reached by a medical proton therapy accelerator is 230 to 250 MeV.^{6, 8} The range of 250 MeV protons in water is about 38 cm.⁹ However, there have only been two studies published that quantitatively evaluate the necessary proton range or energy for treatment.^{10, 11} One of these studies is specific to the treatment of choroidal melanoma,¹⁰ and the other is specific to prostate cancer.¹¹ Neither article provides comprehensive proton range or energy requirements that include all patients eligible for proton therapy. Proton therapy is currently administered at five centers in the United States: The University of Texas M.D. Anderson Cancer Center, the Loma Linda University Medical Center, the Massachusetts General Hospital Cancer Center, the University of Florida Proton Therapy Institute, and the Midwest Proton Radiotherapy Institute. These centers use cyclotrons or synchrotrons to accelerate protons to maximum kinetic energies of 250, 250, 235, 230, and 208 MeV, respectively.^{6, 12, 13, 14, 15} Most of these centers use a passive scattering technique, where scattering foils are used to enlarge the beam laterally and create a broad treatment field. Due to these beam interactions prior to the beam entering the patient, the maximum kinetic energy of the clinically useful proton beam, immediately prior to entry into the patient, at existing passive scattering facilities in the U.S. is less than the maximum energy achievable by the accelerator.

This article will examine the maximum kinetic energy of protons, immediately prior to entry into the patient, required for arc therapy by examining treatment plans from patients that were treated with x-ray therapy. Proton kinetic energy requirements given in this article were calculated with a proton treatment system based around the DWA in mind. The objective of this article is not to give a detailed description of the DWA treatment system, but a brief description of the proposed design is included to clarify the assumptions made in this study. It is assumed that a DWA-based proton therapy treatment system would have the ability to deliver radiation in a rotational fashion over an arc between 180 and 360 degrees. There would be onboard CT imaging for daily patient setup and proton pathlength corrections. The DWA treatment system would be able to modulate the energy of the beam on a pulse-by-pulse basis, with energy resolution less than 1 MeV. Energy modulation would be achieved by electronic control of accelerator components, and the beam would not pass through a range shifter. It is assumed that the system would employ spot scanning (SS), distal edge tracking (DET), and distal gradient tracking (DGT) to deliver dose. In SS delivery, many proton beam spots of varying intensities are distributed over the entire treatment volume to create the desired dose distribution. DET and DGT are described below. For a DWA-based proton therapy system, the maximum proton kinetic energy achievable by the accelerator is almost exactly equal to the maximum beam energy immediately prior to entry into the patient, because the beam will only interact with the thin walls of the monitor chamber before entering the patient. Nonetheless, the proton kinetic energy requirements given in this article are still applicable to proton therapy systems other than the DWA, including passive scattering systems, as long as it is clear that these energy requirements refer to the beam energy immediately prior to entry into the patient. That is, these kinetic energy requirements apply to the beam after it has passed through all range modulating and scattering material, and are less than the energy requirements for the accelerator alone in a passive scatting system.

Distal edge tracking (DET) is a refinement of the SS delivery method that places Bragg peak spots only on the distal edge of the tumor.¹⁶ Multiple intensity modulated beams are used to deliver a homogeneous dose to the tumor, as long as the size of the target volume is not too large. It has recently been shown that rotations of only 180° are sufficient for DET to homogeneously irradiate most tumors.¹⁷ DET has the advantage of lowering the integral dose relative to SS because more of the high-dose region proximal to the Bragg peak stays in the tumor.¹⁶ However, DET also requires more accuracy concerning depth to the tumor and beam transport calculations. A recent refinement to DET is distal gradient tracking (DGT). DGT places Bragg peak spots along high dose gradient regions within the treatment volume in addition to the spots placed along the distal edge of the treatment volume. DGT is capable of making the dose homogeneous to arbitrarily large target volumes and nonuniform dose distributions.¹⁷

A Monte Carlo study of neutron production in a water phantom representing a patient is also described. The patient-generated neutron fluence that could be produced by a proton therapy treatment system is strongly dependent on the maximum proton kinetic energy achievable by the accelerator. If a treatment unit has a higher available proton energy, then more patients may be eligible for treatment and use of higher energy protons will create a higher energy neutron spectrum for those patients. For a specific patient, the neutron production in the patient is a function only of the treatment plan, and depends strongly on field size, beam angle selections, and required proton penetration depth, which determines the required beam energy. However, a treatment system that can produce 250 MeV protons must provide adequate neutron shielding for neutrons produced by interactions of a beam of this energy in the treatment head and in a patient. In contrast, a treatment system that could, for example, only produce protons of energies up to 200 MeV would not need as much shielding against neutron production in patients because the maximum treatment depths are necessarily less for such a system.

Although neutron production within a patient is fixed by a specific treatment volume and set of beam angles, it is possible to minimize neutron production within a patient by selecting beam angles that minimize the penetration depth required to reach the target. If the required penetration depth is very large for a specific beam angle, then it is very likely that the exit pathlength beyond the treatment volume is short. For such cases, some of the benefit of protons over photons is lost because the dose deposited in normal tissue by a photon beam beyond the treatment volume is smaller than for shallow treatment sites. Furthermore, the lateral penumbra of a proton pencil beam becomes larger with depth, reducing the ability to create a sharp dose gradient between the treatment volume and an adjacent critical structure. Protons still gain an advantage over photons on the entrance dose due to their Bragg peak, but in general, very deep penetration depths minimize the benefit of protons over photons, especially for small treatment volumes. Thus, selecting beam angles that minimize the required proton penetration, within the constraints imposed by critical normal tissue avoidance objectives, has the dual advantage of maximizing the benefit of protons over photons and minimizing the neutron production in the patient.

METHODS

Proton kinetic energy calculations

Two main goals in the development of the DWA system are to increase the number of proton treatment sites available to patients and to decrease the cost of proton therapy. The group of patients currently treated at proton therapy centers is a specific subset of all patients treated with radiation therapy. In particular, the majority of proton therapy patients are prostate and head and neck patients. The results presented in this article are aimed at a more general set of patients that better represents the total population of patients receiving radiation therapy. This choice was made under the assumption that, as proton therapy becomes more widely available, the group of patients receiving proton therapy will have a makeup similar to that of the total population of radiation therapy patients. One hundred randomly selected treatment plans from patients treated at the University of Wisconsin Carbone Cancer Center during June and July of 2007 were studied. The patient population was selected completely at random, and no restrictions were made based on the patients’ treatment history, disease site, or any other qualifications, other than those listed below. In order to randomize the types of patients and diseases included in the study, 100 consecutive patients receiving their first fraction, beginning on or after 1 June 2007, were selected. Any patient beginning treatment on any of the TomoTherapy or Varian units at the UW clinic were included in the study. A summary of the target locations included in the study is given in Table 1. Cranial stereotactic radiosurgery or brachytherapy patients were not included, but extracranial stereotactic patients were included. The treatment location “abdomen and pelvis” includes all tumor sites in the abdomen and pelvis, except the prostate, such as the colon, kidney, ovary, rectum, stomach, urinary bladder, etc. The location “brain, head, and neck” includes cranial, ocular, and oral cavity tumors.

Table 1.

Summary of treatment site occurrence rates in the U.S., treatment sites included in this study, and patients in this study treatable at a proton kinetic energy of 200 MeV.

Treatment location	U.S. proportion of sites	Number of patients in study	Number of patients in study treatable at 200 MeV
Breast	19	12	12
Brain, head, and neck	21	28	28
Lung and bronchus	14	20	19
Abdomen and pelvis	12	20	15
Prostate	34	20	17
Total	100	100	91

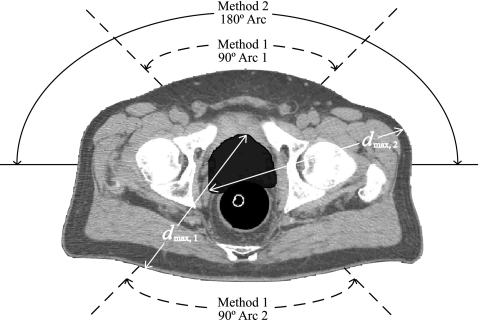
Treatment plans for each patient were examined using the Pinnacle treatment planning system to determine the maximum proton kinetic energy necessary to treat the patient using two methods. Method 1 used two 90° treatment arcs, and method 2 used one continuous 180° treatment arc. Delivery with only coplanar arcs was presumed. All treatment plans included CT image sets of the relevant patient volume and contours showing the prescribed treatment volume. A sample patient analysis is shown in Fig. 1. It was assumed that DGT (Ref. ¹⁷) would be used for proton dose delivery; thus, the maximum required depth of penetration, d_max, is equal to the maximum pathlength from the surface of the patient to the distal edge of the treatment volume, where the maximum is taken over the selected 180° treatment arc and all CT slices. The treatment arcs were selected to minimize d_max, and no restrictions were placed on the angles through which the treatment arcs could fall for either method. Selections of the treatment arcs were based entirely on the proton pathlengths, and the possibility of previous treatments through these arcs was not considered. These selections were made using standard measurement tools included in the Pinnacle treatment planning software.

Figure 1.

Sample analysis of a prostate cancer patient. The planning treatment volume (PTV) is shaded dark gray surrounding the prostate. Optimal treatment angles for split arc 180° proton therapy using two 90° arcs (method 1) are shown by the dashed curves. The optimal continuous 180° arc (method 2) is shown by the solid curve. The maximum pathlength from the surface of the patient to the distal edge of the treatment volume, d_max, is shown for both methods 1 and 2.

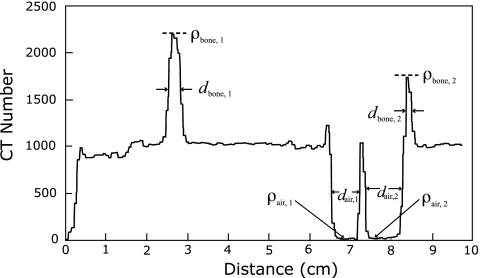
A profile of CT number along the pathlength defined by d_max was then created. A sample analysis of one such plot is shown in Fig. 2. All tissues along d_max with a CT number between 800 and 1200 were considered to be water with unit density. Any peaks (considered as bone∕water mixtures) or valleys (considered as air∕water mixtures) extending above a CT number of 1200 or below 800, respectively, were treated as corrections to the initial water-equivalent radiological pathlength, given in cm²∕g by d_max. The total radiological pathlength through bone∕water is given by

$$d_{\text{bone},\mathrm{tot}}=\sum _{i=1}^n{d}_{\text{bone},i}{\rho }_{\text{bone},i},$$ (1)

where d_bone,1,d_bone,2,…,d_bone,n are the widths of the peaks extending above a CT number of 1200, taken at full width at half-maximum (FWHM), and ρ_bone,1,ρ_bone,2,…,ρ_bone,n are the corresponding densities of the peaks, taken at the maximum value of the peak in order to make a conservative estimate of the density. Densities were calculated from CT number to density conversion tables created during the commissioning of the Pinnacle treatment planning software using phantoms of known compositions. The average bone∕water density is given by

$${\overline{\rho }}_{\text{bone}}=\frac{{\sum }_{i=1}^n{d}_{\text{bone},i}{\rho }_{\text{bone},i}}{{\sum }_{i=1}^n{d}_{\text{bone},i}}.$$ (2)

The bone fraction was defined as

$$f_{\text{bone}}=\frac{{\overline{\rho }}_{\text{bone}}-1}{{\rho }_{\mathrm{ICRP}}-1},$$ (3)

where ρ_ICRP is the density of ICRP cortical bone. This assumes that the density above unity is attributable to cortical bone. A similar calculation was done for the air∕water valleys on the CT# histogram by substituting all bone subscripts with air and replacing ρ_ICRP with ρ_air, to yield the total radiological pathlength through air∕water, d_air,tot, the average air∕water density, ${\overline{\rho }}_{\text{air}}$, and the air fraction, f_air. The total distance through water-equivalent tissue is given by

$$d_{\text{water},\mathrm{tot}}=d_{\max }-(\sum _{i=1}^n{d}_{\text{bone},i}+\sum _{j=1}^m{d}_{\text{air},j}),$$ (4)

and the total radiological pathlength to the distal edge of the treatment volume was then calculated using

$$d_{\mathrm{tot}}=d_{\text{water},\mathrm{tot}}+d_{\text{bone},\mathrm{tot}}+d_{\text{air},\mathrm{tot}}.$$ (5)

Figure 2.

Sample analysis of a CT number profile taken along the maximum distance from the edge of the patient to the distal edge of the treatment volume, d_max, in a lung cancer patient. The widths d_i of each peak (valley) were measured at the full width at half-maximum (minimum). All density values ρ_i were calculated from the corresponding CT number using CT number to density conversion tables found in the Pinnacle treatment planning system.

This information was then used to calculate the proton kinetic energy necessary to traverse this radiological pathlength. Differences in the stopping power of protons in air, bone, and water were accounted for in the following manner. All bone∕water and air∕water mixtures along d_max were assumed to fall halfway along the pathlength d_max. The error introduced by this assumption is small and will be addressed at the end of this section. Let E₁ be the kinetic energy necessary for a proton to travel a radiological distance of d_water,tot∕2. This value was obtained from proton range tables developed by the ICRU.⁹ Now, define R_1,water to be the range (in cm²∕g) of protons in water and define R_1,bone to be the range in ICRP cortical bone. Next, define E_2,bone to be the kinetic energy necessary for a proton to traverse a radiological pathlength of f_boneR_1,bone+(1−f_bone)R_1,water in bone and E_2,water to be the kinetic energy necessary for a proton to traverse the same pathlength in water. Finally, define

$$E_2=f_{\text{bone}}{E}_{2,\text{bone}}+(1-f_{\text{bone}})E_{2,\text{water}},$$ (6)

which is the kinetic energy necessary to for a proton to travel through the bone∕water mixture followed by half of the water-equivalent tissue. This exact procedure can now be repeated for the pathlength through air by substituting E₂ back in for E₁ and replacing all variables with the subscript bone by the corresponding air values. This will then yield E₃, the kinetic energy necessary to travel through air∕water, bone∕water, and half of the water-equivalent tissue. Finally, the procedure can be repeated a third time, substituting E₃ back in for E₁, setting R_1,water=d_water,tot∕2, and setting f_bone=0. This will yield E_tot, the total kinetic energy necessary for a proton to enter the patient and travel to the distal edge of the treatment volume.

The procedure described above was used on each patient to calculate the maximum proton kinetic energy necessary for treatment for both method 1 and method 2. It was noted earlier in this section that error was introduced when it was assumed that the bone and air cavities were exactly in the middle of the pathlength defined by d_max. This error was quantified by performing a similar energy calculation for each patient, but placing the bone∕water and air∕water regions either at the very beginning or very end of the pathlength defined by d_max. The mean error introduced in E_tot was only 0.06% and the maximum error introduced for a single patient was 0.30%. Another potential source of error in this pathlength calculation comes from the conversion of CT number to density, stopping power ratios, and ultimately proton range. The final proton range calculation is quite insensitive to changes in the material stopping power used, be it tissue, bone, lung, air, or some combination. This is due to the fact that the (Z∕A) value of materials found in patients is relatively constant. Furthermore, in a region near 200 MeV on the curve that converts proton range in water to proton kinetic energy, the gradient is approximately 4.5 MeV∕cm. Thus, a range error of 1 cm in a proton pathlength calculation, which is relatively large by the standards of most proton treatment facilities, results in an energy error of only 4.5 MeV in the energy range of interest to this article.

For each patient included in the study, a calculation was done where only the tissue density relative to water along the pathlength was considered, and no stopping power corrections were made. That is, the radiological pathlength was scaled according to the tissue densities, but the entire pathlength was assumed to have a stopping power value equal to that of water. This method thus used stopping powers that were incorrect at some locations along the pathlength by more than 13%. The resultant energies obtained with this method varied by an average of 0.4% from the full energy calculation. The maximum percent difference for a single patient was 1.9%. This demonstrates that, as long as the converted stopping powers are accurate to within 10%, which ICRU stopping power tables certainly are, then the proton energy calculations in this study are accurate to within 2%. At 200 MeV, this corresponds to an energy uncertainty of 4 MeV. The range uncertainty used in the only other published study of a similar nature to the present work was 3.5% of d_max,¹¹ which corresponds to an energy uncertainty of 4 MeV for protons with an initial kinetic energy of 200 MeV and agrees very well with energy uncertainties presented in this article. The previous calculation is intended to give an upper limit on the range calculation error. Other proton range error analyses have been performed and have set an upper limit on the stopping power error of more sophisticated range calculation algorithms at 1.8% in bone and 1.1% in soft tissue.¹⁸ This corresponds to an error in proton kinetic energy of well less than 1%.

Monte Carlo neutron production simulations

Monte Carlo simulations were performed using Los Alamos National Laboratory’s code MCNPX version 2.5.0 to determine the neutron production as a function of the incident proton beam kinetic energy due to the interactions of the proton beam within a water phantom representative of a the patient. MCNPX is a well-established code used for modeling neutron production in a wide variety of circumstances. MCNPX has been benchmarked with experimental measurements for proton therapy and for other physics applications.^{19, 20, 21, 22, 23, 24, 25, 26, 27} It is important to note that in such codes as MCNPX, the accuracy of the result depends directly on the underlying neutron production cross sections and the nuclear physics models used when measured cross sections are not available. MCNPX uses the LANL extensively evaluated LA150 nuclear cross sections below 150 MeV neutron energy and well-established nuclear models above this energy.

For the simulations presented in this article, protons were transported and neutrons were created as the proton beam interacted with a water phantom. The neutrons created in the simulations came from (p,Xn) and (n,Xn^′) interactions. MCNPX version 2.5.0 does not include neutron production cross-section data from light ions such as alphas, deuterons, and tritons that may have been created by the primary protons.²⁸ The nuclear interactions in MCNPX are given by a combination of evaluated data and theoretical models. As mentioned, from 0 to 150 MeV, the code uses evaluated nuclear data files that come from experimental measurements and measured data normalized nuclear models. For energies above 150 MeV, physics models are used. For nucleon interactions, the model of choice is the Bertini intranuclear cascade model.²⁹ Extensive cross-section measurements have been done to collect the necessary data to create the evaluated nuclear libraries and implement them in MCNPX. A detailed explanation of the evaluation of the nuclear data implemented in MCNPX is available.³⁰

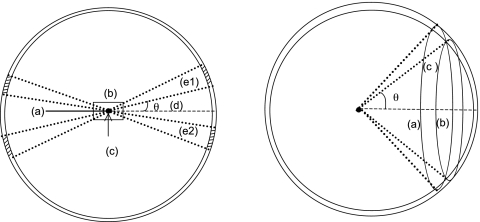
Several simulations were performed for proton beam energies ranging from 100 to 250 MeV. For these simulations, the physical DWA accelerator was not included in the geometry, as it is not considered a source of neutrons because energy degraders and scattering foils are not necessary during treatment delivery. Only a monoenergetic, monodirectional pencil beam (zero area) interacting with a water phantom was simulated. The simulated geometry consisted of a water phantom and several detecting volumes used to score the neutron fluence around the phantom, as shown in Fig. 3. The phantom was made of a right circular cylinder with a thickness and diameter of 400 mm such that the beam stops completely in the phantom. The detecting volumes were made by the intersection of cones with a spherical shell 1 m in radius concentric with the phantom. The cone angles were defined with respect to the geometry central axis along which the proton pencil beam traveled. The cones used to intercept the scoring shell started with a 5° cone in the forward direction and 165° in the backward direction. A total of 34 cones were defined: 17 forward and 17 backward in 5° increments. The neutron flux was integrated over the 5° arc between each cone, with the exception of a cone defined from 5 to 15°. This was the region of interest in the forward direction, and the flux was integrated along 10° to increase the scoring volume region and thus improve the statistics. Also, the total neutron flux in each detecting volume was integrated over energies from 1×10⁻⁵ MeV up to the primary proton beam incident kinetic energy. With these simulations it was possible to determine the neutron angular distribution, their energy spectra, and the neutron production dependency on the primary proton beam kinetic energy. Currently these simulations have not been benchmarked against experimental measurements, but the neutron production observed agrees with what others reported previously.^{31, 32, 33}

Figure 3.

Left: Geometry used to determine the neutron production by the intersection of a proton beam with a water phantom. (a) incident monoenergetic proton pencil beam; (b) water phantom; (c) cones’ vertex and shell’s center; (d) cone angles defined with respect to the central axis; (e1) and (e2) volume segments from the same cone-spherical shell intercept. Right: Additional view of the detecting volume created by the intercept of the cones with the spherical shell. The detecting volume is the region between the intercept of (a) and (b), labeled (c).

RESULTS AND DISCUSSION

Proton kinetic energy thresholds

The results of the proton pathlength analysis described in Sec. 2A are shown in Fig. 4. The locations of the prostate and brain, head, and neck patients were marked on top of the curves representing all patients, as these treatment sites are those most commonly treated with proton therapy today. It is important to note that, although it does indeed require 240 MeV protons to treat 100% of patients in the study, a high percentage of patients can be treated with a much lower maximum kinetic energy. Ninety percent of this sample of patients could be treated by a maximum proton kinetic energy of 198 MeV, and 95% of patients could be treated at a maximum kinetic energy of 207 MeV, using arc splitting (method 1). Relaxing the maximum kinetic energy requirement for a new proton therapy system from 250 to 200 MeV could produce an important decrease in size, cost, and neutron production of the system. As indicated in Table 1, all of the breast, brain, head, and neck cases could be treated with one of the arc methods with a 200 MeV beam kinetic energy, immediately prior to beam entry into the patient. Furthermore, 19∕20 of the lung and bronchus, 15∕20 of the abdominal and pelvis (excluding prostate), and 17∕20 of the prostate patients could be treated with 200 MeV protons. The only other study published on this subject was specific to prostate patients, and concluded that 97.5% of prostate treatment fields could be treated with a kinetic energy of 209 MeV, and 100% of prostate fields could be treated at 213 MeV.¹¹ This study showed excellent agreement, concluding that 95% of prostate patients could be treated at 207 MeV, and 100% of prostate patients could be treated at 216 MeV.

Figure 4.

Maximum proton kinetic energy necessary to treat patients. Data are representative of a set of 100 randomly selected radiotherapy patients treated at the UW Carbone Cancer Center (Madison, WI). The dashed curve represents continuous 180° arc proton therapy, while the solid curve allowed splitting of the 180° arc into two 90° arcs if doing so would decrease the necessary proton kinetic energy for treatment. The two disease sites most commonly treated with proton therapy, prostate and head and neck, are shown explicitly on the curve to highlight their separation in energy. The uncertainty in energy is less than 2%, and error bars were omitted for readability.

As mentioned previously, the issue of reducing the maximum energy of a proton accelerator is one of cost versus benefit. The cost of decreasing the maximum attainable proton kinetic energy is the loss of the ability to treat the largest patients with deep-seated tumors. The benefit is a relaxation on constraints for a new accelerator. It is important to note the shape of the curve shown in Fig. 4. There is a well-pronounced shoulder at about 200 MeV, and this is exactly where it would be most cost-beneficial to truncate the proton kinetic energy. Due to the decreased slope of the curve after this shoulder, increasing the maximum kinetic energy above the shoulder gives a much smaller gain in treatable patients versus kinetic energy increase.

Also of interest in Fig. 4 is the similarity of the solid (method 1) and dashed (method 2) curves. Most of the divergence of the two curves comes at high proton energies. This is due to the fact that prostate, abdominal, and pelvic cases, which generally require the highest proton kinetic energies, benefit most from splitting the proton arc into two 90° segments. However, even at high proton kinetic energies, the difference between the two curves is not that large. Using method 2, 201 MeV protons would be necessary to treat 90% of the patients in this study. This kinetic energy value is only decreased to 195 MeV when arc splitting is allowed as in method 1.

Currently, many proton therapy patients have failed previous radiation therapy treatments, and some of these patients have metal support appliances implanted, which can increase the required energy for treatment if the beam passes through these metal implants. Such patients were not included in this study. Although this study is not aimed at examining the current class of proton therapy patients but rather a more general class of patients, this issue in nonetheless worth addressing. It is apparent from Fig. 4 that the majority of head and neck patients fall on the low energy end of the curve, while the high energy end of the curve is dominated by prostate patients. In fact, 28 out of 28 head and neck patients studied required an energy less than 200 MeV for treatment, and 26 of them fell below 180 MeV. Thus, although metal implants can increase the energy requirements for certain head and neck patients, it is unlikely that this effect would increase the estimated maximum energy requirement of the accelerator, as most of these patients fall well below the maximum energy cutoff. However, metal hip implants on prostate patients could potentially increase the proton kinetic energy requirements if treatment beams are chosen such that they pass through the implants. Such a situation is not desirable due to the inaccuracy of CT number to stopping power conversions for high-Z materials, and treatment through metal hip implants would most likely be avoided in most cases. In addition to potentially having metal implants, previously treated patients can limit the beam angles that can be used for treatment due to dose previously received by normal tissue. Since the proposed treatment system will deliver radiation over 180 degrees or more, constraints can be imposed on the optimizer to avoid delivering radiation from angles which would cause the beam to pass through metal support structures or in cases where normal tissue tolerances would be exceeded due to previous treatments. Furthermore, it is not necessarily true that metal implants or previously treated tissue will fall within the arcs that are selected for treatment.

Neutron production

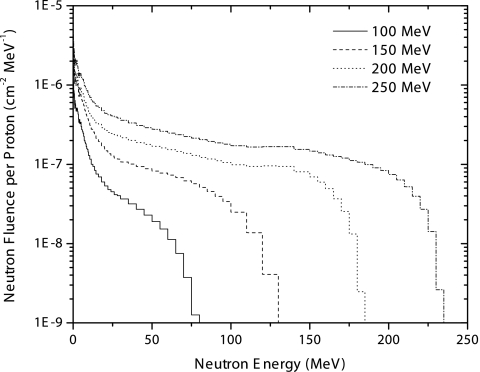
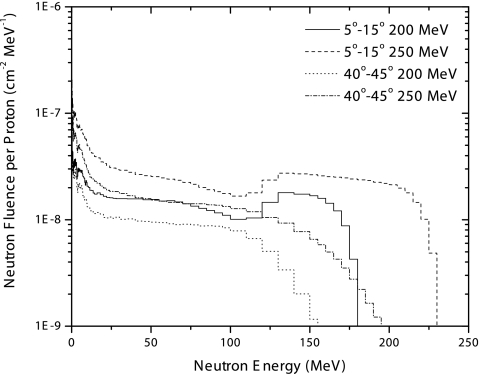
The neutron production as a function of proton beam kinetic energy and the neutron angular distribution were investigated for a monoenergetic proton pencil beam incident on a water phantom. Figure 5 presents the neutron energy spectra for four of the proton energies studied. These spectra show the neutron production by the interaction of the beam with the phantom, integrated over all angles. As can be seen in Fig. 5, as the proton beam kinetic energy increases, the neutron production increases as well. For all proton energies, a large contribution to the fluence from low energy neutrons can be observed. These low energy neutrons are mainly evaporation neutrons and their contribution is nearly isotropic. For the higher proton energies, 200 and 250 MeV, there is a nearly constant neutron production for neutron energies above 30 MeV up to energies close to the incident proton kinetic energy.

Figure 5.

Neutron energy spectra produced in a water phantom by incident monoenergetic proton pencil beams of varying energies. Spectra correspond to integrating the fluence over all emission angles. Data shown are the result of Monte Carlo simulations using the MCNPX transport code.

Figure 6 presents the neutron energy spectra for two of the angular regions studied at 200 and 250 MeV proton kinetic energy. The production of neutrons is mainly forward directed and peaked at angles between 5 and 15°. For angles smaller than 5°, the neutron production at energies above 30 MeV is nearly constant and lower than from 5 and 15°. Notice that in the forward direction there is an increment of high energy neutrons that is not observed at larger angles, which is attributed to knock-on reactions. This increment becomes larger and occurs over a much broader energy range as the proton kinetic energy increases. This behavior is especially important in terms of the shielding considerations that have to be taken into account at the time of facility construction to assure minimal exposure to personnel as well as to the general public. As the angle increases, the production of high energy neutrons diminishes, and the spectrum becomes dominated by neutron emission over a broad range of energies.

Figure 6.

Neutron energy spectra produced in a water phantom by incident monoenergetic proton pencil beams of varying kinetic energies. Spectra are shown for two different angular scattering regions and two different incident proton beam energies, as specified in the legend. Data shown are the result of Monte Carlo simulations using the MCNPX transport code.

Most of the simulations and measurements previously reported in the literature are used for shielding evaluations, where protons interact with a stopping target producing neutrons. The neutron production and their energy spectra have been investigated for various proton energies and target materials.^{34, 35} The neutron energy spectra results presented here are similar to what others have reported for a proton beam stopping in a thick water and tissuelike target.^{31, 32, 33}

In the present work, the proposed DWA treatment system does not require any passive beam modification devices such as scattering foils, range modulators, or other devices used to deliver the proton beam to the patient. Hence, neutron production occurs principally in the stopping media. For passive scattering proton treatment systems, neutron production in the treatment head is the dominant source of unwanted neutron dose to the patient. Neutron dose can be further reduced by selecting pathlengths through the patient that minimize the proton penetration depth.

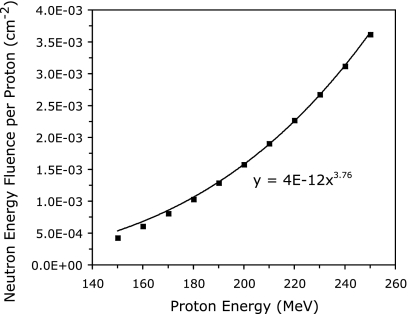
In a system where almost all neutron production occurs in the patient, the fluence produced by proton beams in all patients can be used as a first order indication of the neutron shielding necessary for a compact proton treatment facility. The total neutron energy fluence, integrated over all scattering angles, was calculated for proton beam energies ranging from 150 to 250 MeV in increments of 10 MeV. The results of these calculations are shown in Fig. 7. The total neutron energy fluence increases with the 3.76th power of the proton kinetic energy. Reducing the maximum proton kinetic energy from 250 to 200 MeV decreases the total neutron energy fluence produced by a factor of 2.29. However, this reduction factor only applies to a direct comparison between two patients treated at 200 and 250 MeV. The difference in the total neutron energy fluence produced by two treatment systems of maximum energies of 200 and 250 MeV, integrated over a large patient population representative of the patient load seen by the machines, is significantly less. A rough estimate assuming that about 10% of eligible patients will be treated with energies between 200 and 250 MeV on the higher energy system predicts that the total neutron energy fluence produced by the 200 MeV system would be reduced by a factor of about 1.2 to 1.4.

Figure 7.

Total neutron energy fluence produced in a water phantom as a function of the kinetic energy of the incident monoenergetic proton pencil beam. The solid curve is a power fit of the data, showing the dependence of neutron production on incident proton kinetic energy. Data shown are the result of Monte Carlo simulations using the MCNPX transport code.

CONCLUSIONS

Despite some opposition, the use of proton therapy is growing rapidly. There have been several proposed accelerator systems for single-room, compact proton treatment facilities, and some hospitals have already placed orders for such facilities. One of the primary goals of these compact facilities is to decrease the cost of proton therapy and allow more patients access to this modality. The maximum kinetic energy requirement for the accelerator system is an important factor in the cost and feasibility of a compact proton accelerator. Many articles have cited a value of 250 MeV as the accepted maximum kinetic energy needed for an accelerator to treat patients with proton therapy. This article has shown that 90%–95% of patients can be treated by a proton therapy system that provides a clinically useful beam with a maximum kinetic energy of about 200 MeV. It is clear that decreasing the maximum energy of the accelerator in a proton treatment system will decrease the cost of production. However, this advantage must be weighed against the disadvantage of having to turn away a small percentage of patients. The availability of proton therapy centers is increasing rapidly, and a DWA-based proton treatment system would aim to further increase the availability and decrease the cost of proton therapy. In the future, designing a facility to treat 90%, 95%, 98%, or 100% of patients might be more of a marketing decision than a scientific one. In addition to easing the engineering and cost constraints on a compact proton accelerator system, decreasing the maximum proton kinetic energy decreases the patient-generated neutron fluence of the treatment system. Lowering the neutron production reduces unwanted dose to the patient and could also reduce the amount of neutron shielding necessary for a compact proton treatment facility.