Accuracy in the localization of thoracic and abdominal tumors using respiratory displacement, velocity, and phase

Abstract

Current four dimensional (4D) computed tomography (CT) reconstruction techniques are retrospectively created based on either the phase or displacement of the respiratory signal. Both techniques have known limitations which cause clinically significant motion artifacts in 4D CT images. These artifacts, which appear as undefined or irregular boundaries in the 4D CT images, cause systematic errors in patient contouring and dose calculations. The aim of this work was to evaluate the reproducibility of tumor position as a function of displacement, phase, and velocity of the respiratory signal, respectively, in order to determine the optimum parameter or combination of parameters to use in order to minimize artifacts in 4D CT images or to accurately deliver radiation to relevant structures during treatment. Method and materials: Estimated tumor centroid position and respiratory signal data were acquired with the Cyberknife Synchrony system for 26 thoracic radiotherapy patients (52 fractions). A reference respiratory cycle was calculated for each patient. Displacement, phase, and velocity of ten data points were calculated from this reference respiratory cycle, where each point represents an image bin. The corresponding tumor position was then sorted into these image bins if the phase, displacement, simultaneous displacement and phase, or simultaneous displacement and velocity of the respiratory signal were within tolerances of 0.5 mm for displacement and 0.5 mm∕s for velocity, respectively, from the corresponding data of the reference cycle for each image bin. Results: The mean of the standard deviations of tumor positions over all bins and all fractions for the superior-inferior direction were 2.13±1.01 mm for phase sorting, 1.20±0.76 mm for displacement sorting, 1.20±0.71 mm for simultaneous displacement and phase sorting, and 1.10±0.71 mm for simultaneous displacement and velocity sorting, with maximum deviations of 43.0, 16.1, 15.5, and 14.1 mm for each scenario, respectively. The same trend was observed for the anterior-posterior and left-right directions. A linear dependence was observed between the mean of the standard deviations of tumor positions over all fractions as a function of the velocity of the respiratory signal at each bin for all the sorting scenarios. A substantially larger gradient for the phase sorting scenario, compared to the other scenarios, suggests that tumor localization will become increasingly less accurate as the velocity of the tumor increases during a breathing cycle, e.g., if the amplitude of motion increases while the period of the respiratory cycle stays constant or during mid inhale or exhale phases of the respiratory cycle. Conclusion: This study illustrates that position of a tumor can be determined more accurately if displacement and velocity are used simultaneously as sorting parameters for 4D CT images or during treatment. A real-time displacement and velocity based 4D CT image sorting method may therefore produce fewer and smaller artifacts in 4D CT images than current retrospective sorting methods.

INTRODUCTION

Current 4D CT reconstruction techniques are retrospectively based on phase or displacement of the respiratory signal. Mismatches in displacement or phase of a patient’s respiratory signal corresponding to two dimensional (2D) images taken at subsequent couch positions are caused by cycle to cycle variations in the respiratory motion. These mismatches become visible as artifacts in reconstructed 4D CT images.^{1, 2, 3, 4, 5, 6, 7, 8} These artifacts appear as undefined or irregular boundaries in the 4D CT images and cause systematic errors in patient contouring and dose calculations. Various studies have shown that the magnitude of artifacts resulting from retrospective displacement sorting is less severe than those resulting from retrospective phase sorting.^{1, 3, 5, 7} Recently it was found that at least one artifact appeared in retrospectively phase sorted 4D CT images for 45 out of 50 patients.⁹ The problem with retrospective displacement sorting is, on the other hand, that data may be insufficient at some couch positions because of variations in the respiratory motion. Images with the nearest displacement to the displacement used for the image bin could then be used, although this is not optimal because artifacts may again be introduced because of resulting mismatches. A solution to this problem is to do image sorting in real-time, in order to ensure that sufficient data exist for each couch position to reconstruct the 4D CT. Parameters of the respiratory signal that can be used are either phase, displacement (inhale and exhale separately, i.e., displacements with the same magnitude, but different signs for the temporal derivative are treated separately), simultaneous displacement and phase, or simultaneous displacement and velocity of the respiratory signal. Here velocity is the temporal derivative of the respiratory signal. The method used here to do sorting of the respiratory signal in real-time by using either displacement or simultaneous displacement and velocity as sorting parameters is discussed in detail by Langner and Keall.¹⁰

The rationale for using velocity as sorting parameter comes from the analogy of viewing respiration as a damped driven harmonic model. With the simultaneous use of displacement and velocity of the respiratory signal as sorting parameters, image sorting is essentially done in a five dimensional parameter space, where displacement and the sign of the velocity (representing inhale or exhale) are used for temporal sorting and velocity as a separate parameter, correlating to some additional parameter of the system, e.g., the airflow rate.^{11, 12} This is illustrated by the assuming that respiratory motion can be modeled as damped, driven harmonic oscillating motion, given by

$$m\frac{d^{2}x}{d{t}^2}+r\frac{dx}{dt}+kx=F_{\text{driving}},$$ (1)

where m is the mass of, e.g., a tumor with a trajectory correlating to the respiratory motion, x is the displacement of the tumor centroid from its equilibrium position, t is the time, F_driving is the driving force (predominantly the diaphragm), kx is the restoring force of the oscillator (caused by anatomical elasticity), and r (dx∕dt) is the damping (predominantly density changes in the tumor environment because of, e.g., perfusion, organ motion, etc.), with k and r arbitrary constants. The general solution to this equation is a sum of a transient (the solution for a damped undriven harmonic oscillator) that depends on initial conditions, and a steady state that depends only on driving frequency, driving force, restoring force, and damping force. For 4D CT, a three dimensional tumor trajectory is inferred from its correlation with a one dimensional respiratory trace modeled by Eq. 1. This implies that in order to acquire artifact free 4D CT images, the same anatomical “state” must be sampled for different respiratory cycles for each image bin, respectively. This is also true for accurate tumor localization during treatment. It is important to note that displacement s(t), as used for image sorting, is given by

$$s\left(t\right)=k+x\left(t\right),$$ (2)

where x(t) is the displacement from an equilibrium position from Eq. 1 and k is an arbitrary transient constant for each cycle. Drift of the respiratory trace is therefore implicitly incorporated in s(t), but not in x(t). Therefore, if phase is used as a sorting parameter, s(t) associated with each phase may differ for different respiratory cycles, resulting in different magnitudes of displacement even if the phase is the same. If a periodic driving force is assumed for the respiratory motion, e.g., F_driving=F₀ cos(ωt) with F₀ an arbitrary constant and ω the driving frequency, it is evident that phase of the respiratory trace can be used to uniquely determine the spatial position of a non-deformable isotropic body, e.g., a tumor, in a homogeneous isotropic medium if the trajectory of the tumor is fixed and correlates with respiratory motion. Alternatively, s(t) and the sign of the velocity (to distinguish between inhale and exhale) can be used concurrently, to uniquely determine the spatial position of the tumor. Both these methods use parameters of the respiratory cycle as temporal sorting parameters to sort the 2D CT images in order to construct a 4D CT image. This is true even if the frequency of the respiratory motion varies from cycle to cycle, which implies that the body will traverse the same fixed trajectory at a faster rate, although the velocity and acceleration of the tumor for the two cycles might be different for the same phase or same displacement.

However, human anatomy cannot always be assumed to be homogeneous and isotropic and a tumor may be deformable, i.e., there might be slight density imbalances in the tumor volume¹² as well as in its immediate environment, which may cause significant changes in its trajectory (hysteresis), which is dependent on the forces on the tumor. The driving force is also a superposition of sinusoidal solutions, which may vary from cycle to cycle. The amplitude and periodicity of the driving force also change from cycle to cycle, which may cause changes in the initial displacement of the respiratory trace and hysteresis in the tumor trajectory, e.g., residual tension in muscles can differ, air volume in the lungs can differ, involuntarily motion can occur, etc. These changes invalidate the assumption of a fixed tumor trajectory for certain anatomical sites, e.g., the lungs. For other regions of the anatomy, e.g., in the breast, a fixed trajectory for tumor motion, and thus phase sorting, may be a reasonable assumption, if changes in k from Eq. 2 are small from cycle to cycle. From Eq. 1 it then follows that if the trajectory of the tumor is changing from cycle to cycle, then the use of phase as a sorting parameter from respiratory trace may not be sufficient to uniquely sample the tumor’s spatial position and deformation inside the anatomy from respiratory cycle to cycle, because even if the displacement and phase of the respiratory signal match instantaneously during two subsequent respiratory cycles, the driving forces may differ, implying different instantaneous forces acting on the tumor. This is also evident from the inability of retrospective phase sorting methods to produce artifact-free 4D CT images.^{1, 3, 5, 7} However, it is assumed here that if the displacement and velocity of the respiratory trace match for two different cycles, it can also be assumed that the acceleration, and therefore the instantaneous force on the tumor, is equal or nearly equal, resulting in the same deformation and trajectory. It is therefore hypothesized that this method can produce accurate reconstructed 4D CT images in five dimensional parameter space, by sorting 2D CT images not only by using a temporal parameter, but also an “anatomical state” parameter.

Another advantage in using velocity as a sorting parameter is that online phase estimation is avoided. Online phase estimation is strongly dependent on the reproducibility of the respiratory signal and is prone to significant errors if the predicted period of the respiratory cycle is not the same as the true period.^{8, 13}

In this work the validity of the hypothesis that respiratory displacement and velocity can be used as sorting parameters for 4D CT images to accurately sample the “state” of the anatomy is studied. The aim of this work is therefore to quantify the variation in estimated tumor position based on different sorting parameters or combinations of sorting parameters of the respiratory signal, and to demonstrate the clinical significance of these respective sorting parameters.

METHOD

Evaluating clinical significance of respective sorting parameters

If the hypothesis that respiratory displacement and velocity can be used as sorting parameters for 4D CT images or during treatment to accurately sample the state of the anatomy is true, images acquired at the same couch position, i.e., the same subset of the anatomy, for this state should be exactly the same. To illustrate this, images acquired at the same couch position with similar parameters of the respiratory signal were selected from a 4D data set. These images were then subtracted from each other in order to determine if they are indeed similar. These images are illustrated in Fig. 2 for the different sorting scenarios. The parameters of the respiratory signal corresponding to each image are illustrated in Fig. 1.

Figure 2.

Two images acquired at the same couch position (top and middle panels) for similar values of the parameters of the respiratory signal (see Fig. 1 and Table 1) for different sorting scenarios: (a) Retrospective phase sorting, (b) simultaneous displacement and phase sorting, and (c) simultaneous displacement and velocity sorting. In the bottom panel the subtraction image of the two top images are shown.

Figure 1.

Respiratory displacement as function of (a) time, (b) phase, and (c) velocity, respectively. The images of Fig. 2 were acquired for the respiratory parameters indicated, i.e., gray triangles for retrospective phase sorting, gray squares for simultaneous displacement and phase sorting, and gray diamonds for simultaneous displacement and velocity sorting. The dark gray symbols indicate the mid scan time for each image.

Table 1 summarizes the root mean square (RMS) values for the displacement, velocity, and phase between images used for each sorting scenario.

Table 1.

Root mean square values for the differences in displacement, phase, and velocity between two arbitrary images acquired at the same couch position. These images are shown in Fig. 2 and the corresponding positions relative to the respiratory signal in Fig. 1.

Sorting method	RMS displacement difference (mm)	RMS phase difference (%)	RMS velocity difference (mm∕s)
Retrospective phase sorting	1.5	1.4	0.7
Simultaneous displacement and phase sorting	0.8	0.5	3.5
Simultaneous displacement and velocity sorting	0.2	14.2	0.4

Tumor position assessment for different sorting scenarios

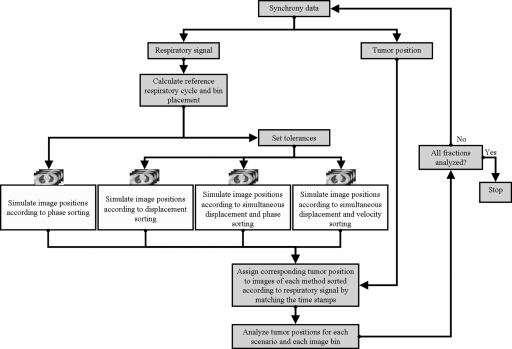
Respiratory signal data and the corresponding estimated tumor position were acquired with the Cyberknife Synchrony system¹⁴ for 26 thoracic and abdominal radiotherapy patients (52 fractions).¹⁵ The tumor locations were lung (24 patients) and liver (2). Data were selected from the original set¹⁵ for patients with mean respiratory amplitude of at least 0.5 cm. These respiratory signals were then sorted according to one of the sorting scenarios given below. The corresponding tumor positions were then assessed to determine the quality of each sorting scenario. The accuracy of the tumor motion data was computed to be 1.5±0.8 mm.¹⁶ Similar values for the Synchrony model using different data were obtained by Seppenwoolde et al.¹⁷ The tumor position error in the Synchrony data will be contained as a systematic error of the same magnitude in all the sorting methods. This process, as illustrated in Fig. 3, is described below. To accurately calculate the phase and velocity of the respiratory data retrospectively, it was first smoothed by applying a three-point running average recursively to the measured respiratory signal.

Figure 3.

Methodology for comparing different sorting scenarios for 4D CT images.

Successive maxima of the respiratory trace were placed at 0 rad (0%) and 2π rad (100%) phase, respectively. Phase was then linearly assigned for each point between the maxima. A reference respiratory cycle was calculated for each fraction from samples of the respiratory signal by determining the weights of the five most significant Fourier components in a least squares fit to the respiratory sample.¹⁸ Displacement, phase, and velocity of ten data points were calculated from this reference respiratory cycle, where each point represents an image bin. Image bins were placed at equal time intervals with the first bin placed at the maximum (end inhale −0% phase) of the reference cycle and the bin closest to the minimum (end exhale −∼50% phase) of the reference cycle shifted to coincide with it. The tumor position temporally corresponding to the respiratory signal was then sorted into these image bins each time that the phase, displacement, simultaneous displacement and phase, or simultaneous displacement and velocity of the respiratory signal were within tolerances of 0.5 mm and 0.5 mm∕s, respectively, for displacement and velocity corresponding to the data points of the image bins. For phase sorting and simultaneous displacement and phase sorting, the phase closest to the reference phase for each bin was sorted into the image bins if the corresponding respiratory displacement was within a tolerance of 0.5 mm. Standard deviations of the tumor centroid positions for each bin were then calculated for anterior-posterior (AP), left-right (LR), and superior-inferior (SI) motion, respectively.

RESULTS AND DISCUSSION

Mean standard deviations of the tumor centroid position over all fractions and all bins are given in Table 2 for each spatial direction and for each sorting scenario. It can be seen that sorting of the tumor position according to displacement and velocity of the respiratory signal produced the smallest mean standard deviations, which indicate better reproducibility of the tumor position for different respiratory cycles. The mean standard deviation for sorting according to phase alone was increased by approximately a factor of 1.8 with a larger error for all spatial directions, when compared to the other scenarios. The sorting according to displacement alone and simultaneous displacement and phase produced markedly similar results, i.e., the addition of phase to the displacement sorting method does not add useful information to increase the accuracy of the sorting process. However, the addition of velocity to displacement as sorting parameter decreased the mean standard deviation of the tumor position in all three directions. The maximum differences for all the fractions and all the bins in Table 2 are a factor of ∼12.9 larger than the mean value for simultaneous displacement and velocity sorting in the SI direction, a factor of ∼13.4 larger for displacement sorting, and a factor of ∼20.2 larger for phase sorting, respectively. Even though these maximum values are large for simultaneous displacement and velocity sorting, they are a factor of ∼3 smaller than for phase sorting. Localization errors caused by irregular respiratory motion can thus be markedly reduced by using both the displacement and velocity of the respiratory trace as sorting parameters instead of just the phase.

Table 2.

The mean of the standard deviations of the tumor centroid position over 26 thoracic radiotherapy patients (52 fractions) and all the bins in each spatial direction for different scenarios of parameters of the respiratory trace used for sorting. The maximum differences for all the fractions and all the bins are also shown for each spatial direction.

Sorting method	Mean standard deviation over all fractions and all bins			Maximum difference for all fractions and all bins
	SI (mm)	LR (mm)	AP (mm)	SI (mm)	LR (mm)	AP (mm)
Phase sorting	2.13±1.01	0.82±0.71	1.08±0.63	43.0	21.0	24.8
Displacement sorting	1.20±0.76	0.55±0.39	0.70±0.44	16.1	6.5	8.8
Simultaneous displacement and phase sorting	1.20±0.71	0.55±0.40	0.70±0.45	15.5	7.6	9.7
Simultaneous displacement and velocity sorting	1.10±0.71	0.52±0.38	0.62±0.41	14.1	6.9	8.9

In Fig. 4 histogram plots are shown which compare the mean standard deviations of the tumor centroid position over all bins and for all fractions for each spatial direction and each sorting scenario. From these plots it can be seen that more fractions have a mean standard deviation less than 0.6 mm for simultaneous displacement and velocity sorting in all three spatial directions than for the other scenarios: ∼34% for the SI direction, ∼71% for the AP direction, and ∼79% for the LR direction of all the fractions are ⩽0.6 mm, while ∼65% for the SI direction, ∼92% for the AP direction, and ∼87% for the LR direction are ⩽1.0 mm. For the displacement sorting scenario, the fractions below 1.0 mm are ∼60% for the SI direction, ∼83% for the AP direction, and ∼88% for the LR direction. For the simultaneous displacement and phase sorting scenario, the fractions ⩽1.0 mm are ∼56% for the SI direction, ∼87% for the AP direction, and ∼69% for the LR direction. For the phase sorting scenario, the fractions ⩽1.0 mm are ∼12% for the SI direction, ∼60% for the AP direction, and ∼75% for the LR direction. For the scenario where only phase sorting was performed, the mean standard deviations were >1 mm in all spatial directions, except the LR direction.

Figure 4.

Histogram plots of the mean standard deviations of the tumor centroid positions over all bins and for all fractions for the superior-inferior (SI), anterior-posterior (AP), and left-right (LR) directions for phase sorting, displacement sorting, simultaneous displacement and phase sorting, and simultaneous displacement and velocity sorting, respectively. Histograms are drawn for each sorting scenario at intervals of 0.02 cm.

Even though the differences in the results in Table 2 appear to be insignificant, it must be noted that they give the mean standard deviation of the tumor centroid position. The mean peak-to-trough variation of the tumor centroid position in the SI direction is ∼4.0 mm for all fractions while the mean peak-to-trough variation of the respiratory signal is ∼10.0 mm for all fractions. This gives a diaphragm motion which is on average a factor of 2.5 larger than the tumor motion for this data set, assuming that the diaphragm motion has a similar motion magnitude to the abdominal wall motion.¹⁹ It follows then that if the amplitude of an anatomical structure is increased for the same waveform, i.e., the period stays the same, the velocity will increase accordingly. Therefore, the velocity can be used as an indirect measurement to determine the effect on the standard deviation of the tumor centroid position if the amplitude increases. This is illustrated in Fig. 5, where the mean standard deviations of the tumor centroid position for each bin over all the fractions as a function of the absolute mean velocity for each bin are shown. A linear dependence was observed for each of the sorting scenarios between the mean standard deviations of the tumor centroid position for each bin over all the fractions and the absolute mean velocity with gradients of 4.13 for phase sorting, 0.39 for displacement sorting, 0.92 for simultaneous displacement and phase sorting, and 0.07 for simultaneous displacement and velocity sorting. Sorting done by simultaneously using the displacement and velocity of the respiratory signal therefore results in a mean standard deviation of the tumor centroid position that is almost constant as a function of velocity. This indicates that the error in tumor localization will stay almost constant as a function of the velocity, i.e., the position of the tumor can be determined with an accuracy of approximately 1.2 mm at any of the bins of the reference cycle, which enhances the duty cycle of this method if it is used during treatment. For the phase sorting scenario the accuracy on the tumor localization will decrease as the velocity increases, i.e., if the amplitude of the respiratory motion increases while the period stays constant. Therefore, for the phase sorting scenario, only bins with velocities below 1 mm∕s can be used with confidence during treatment if an accuracy of less than 2 mm is required, i.e., only data acquired during end exhale. Even though the differences between displacement sorting and simultaneous displacement and phase sorting are insignificant, it must be noted that phase was calculated retrospectively and it is then used as an online method here with accurate phase. This will not be the case if the phase of the respiratory signal is calculated in real-time during image acquisition or treatment of the patient. Mismatches in tumor localization may therefore increase because of incorrect online phase assignment. Online phase sorting is therefore currently not a viable option and any retrospective sorting with displacement will inherit the problems of insufficient data, discussed earlier, for image acquisition.

Figure 5.

Mean standard deviations of the tumor centroid position for each bin over all the fractions as a function of the absolute mean velocity for each bin for the phase sorting (top left), displacement sorting (top right), simultaneous displacement and phase sorting (bottom left), and simultaneous displacement and velocity (bottom right) scenarios. Note the scale difference between the figures.

In Fig. 2 two images are shown for each sorting scenario acquired at the same couch position for similar values of the parameters of the respiratory signal. Each point of the respiratory signal parameters corresponding to each image set is illustrated in Fig. 1 where the displacement as function of time, phase, and velocity, respectively, are shown. From the differences between the RMS values of all the respiratory data corresponding to each image given in Table 1 and Fig. 1 it is clear that the image set in the first column of Fig. 2 is similar to images sorted according to phase, the second set of images sorted according to simultaneous displacement and velocity, and the third set of images sorted according to simultaneous displacement and phase. From the subtraction images in Fig. 2 it follows that the images acquired for the simultaneous displacement and velocity sorting scenario are more similar than those for the other scenarios, even though there is a 14% RMS difference in phase between the parameters of the respiratory trace corresponding to the two images. For images acquired for simultaneous displacement and phase sorting, the differences are markedly larger compared to the other scenarios, although the RMS difference in phase is only 0.5% of the mean respiratory cycle. This suggests that velocity of the respiratory trace, not phase, may be a more appropriate parameter to use for image sorting together with displacement. The importance of displacement mismatches is stressed in the image set acquired for phase sorting. There the RMS differences in phase and velocity are small, although the displacement difference in the respiratory trace is 1.5 mm. Substantial differences can be seen at the boundary of the diaphragm for these images.

CONCLUSIONS

From the reproducibility of the centroid of the tumor positions for subsequent respiratory cycles, if both the displacement and velocity of the respiratory signal are used as sorting parameters, it follows that fewer and smaller artifacts may be present in 4D CT images reconstructed with these parameters, because images will be acquired with the tumor in approximately the same anatomical position at each respiratory cycle. For example, for phase sorting this might not be true and differences in the tumor position for subsequent respiratory cycles will result in motion artifacts in 4D CT images. The mean standard deviation of the tumor centroid position as a function of the velocity of the respiratory cycle increases faster for phase sorting, displacement sorting, and simultaneous displacement and phase sorting than for simultaneous displacement and velocity sorting. This indicates that the reproducibility of the tumor position will be approximately independent of the velocity for the last scenario, e.g., if the amplitude of the tumor motion increases while the period of the tumor stays the same as for structures closer to the diaphragm. This is not true for the other scenarios where, e.g., for phase sorting, the tumor position is reproduced most accurately for bins where the velocity of the respiratory motion is small, e.g., during the end exhale phases of the respiratory motion.

In this study the phase was calculated retrospectively and is therefore accurate, which might not be true for online phase estimation. If any of these sorting methods is used during a gated treatment, the phase estimation must be done online. Therefore, the results shown here for simultaneous displacement and velocity sorting will give a best case scenario for the mean standard deviation of the tumor centroid position. Using velocity of the respiratory signal instead of phase as a parameter for sorting also avoids the problem of online phase estimation.