Abstract
The experiments presented in this paper explore the hypothesis that cochlear gain is reduced, in a frequency-specific manner, over the course of a sound (called a “precursor”) which was designed to activate the medial olivo-cochlear reflex (MOCR). Psychophysical tuning curves (PTCs) and off-frequency growth of masking (GOM) functions were measured with two precursors. The on-frequency precursor condition, which was hypothesized to activate the MOCR at the signal frequency, produced a PTC with a lower best frequency in all subjects consistent with less gain. This same condition produced a GOM function with less gain and an elevated compression breakpoint. The data were analyzed with two models. The gain-reduction model, which assumed a change in the basilar membrane input-output function, was superior at predicting the data relative to a model of additivity of masking.
INTRODUCTION
The auditory system, like other sensory systems, adjusts to stimuli in the environment. Some adjustments may protect the ear from harm (such as the stapedial reflex), while others may facilitate perception of a signal of interest. For example, Dean et al. (2005) showed that rate-level functions in the inferior colliculus adjust to the statistical characteristics of the input waveform intensity. Such an adjustment may facilitate perception by optimizing auditory dynamic range and avoiding the deleterious effects of saturation. In humans, it may be possible to study how the auditory system adjusts to sound through perceptual experiments involving auditory masking. For example, under certain conditions the detection of a short signal, presented simultaneously with a masker, improves when preceded by a sound (often called a “precursor”) rather than silence. This improvement in detection threshold has been referred to as “overshoot” (Zwicker, 1965) or the “temporal effect” (Hicks and Bacon, 1992) and has been a source of study for over 40 years. For generality, the term precursor may be regarded as a separate sound or an extension of the masker’s duration.
Overshoot may occur as a result of an adjustment in the auditory system over the course of the precursor. Although the hypothesized mechanisms of this adjustment are still a matter of debate, recent psychophysical experiments suggest that it may be related to a decrease in cochlear gain (von Klitzing and Kohlrausch, 1994; Strickland, 2001, 2004; Strickland and Krishnan, 2005; Strickland, 2008). Such a decrease in gain may be mediated by the medial olivo-cochlear reflex (MOCR) (Schmidt and Zwicker, 1991). Efferent fibers from the MOCR connect directly to the outer hair cells in the cochlea. These hair cells, which are associated with the cochlear amplifier, amplify soft sounds (i.e., provide “gain”) and sharpen tuning (or “frequency selectivity”) by feeding energy into the cochlea’s basilar membrane (BM). In addition, they help determine the BM’s input∕output (I∕O) function, which describes how much gain is applied to a stimulus of a given intensity. Animal studies report a frequency-specific reduction in BM gain and frequency selectivity when the MOCR is elicited (Guinan and Gifford, 1988; Cooper and Guinan, 2006). The current study explored whether similar reductions in frequency selectivity and gain could be observed in humans through perceptual experiments involving precursors in forward masking.
The hypothesis that gain reduction explains overshoot seems counterintuitive because for some overshoot conditions, frequency selectivity increases when a precursor is present (Bacon and Viemeister, 1985; Bacon and Moore, 1986; Kimberley et al., 1989; Bacon et al., 2002; Strickland, 2004). Although a broadband precursor has been shown to decrease frequency selectivity (Strickland, 2001), a notched precursor, having the same spectrum as the masker, increases frequency selectivity. Strickland (2004) hypothesized that suppression may account for this dichotomy. This hypothesis was supported by showing that the data were consistent with a BM I∕O model which assumed gain decreased in cochlear regions overlapping with the frequency spectrum of the precursor. The author argued that at wide notch widths, suppressive masking largely determined thresholds and reasoned that suppression may decrease over the course of the precursor. If this were the case, masking due to suppression would also decrease. Such an effect would require higher masker levels at wide masker notch widths and produce higher estimates of frequency selectivity.
If the opposing findings regarding frequency selectivity in overshoot are related to a reduction in suppression, it may be possible to control for suppression by using a forward masking technique. Although precursor studies related to forward masking and frequency selectivity are limited, insight may be garnered from studies on forward masker duration. Unfortunately, these studies are inconclusive. For example, Kidd et al. (1984) reported a slight broadening of tuning as masker duration increased while Bacon and Jesteadt (1987) reported a slight sharpening of tuning when measuring psychophysical tuning curves (PTCs) and masking patterns (MPs), respectively. This failure to show a consistent effect may be understood by considering a conceptual model of forward masking that assumes two underlying masking mechanisms which differ in their time-course of influence. The first mechanism has a short time-course and masks the signal by virtue of a continuation of masker-related neural activity (Oxenham, 2001). This mechanism is theoretically similar to the temporal window model (Moore et al., 1988) and is assumed to be effective for short maskers (or parts of longer maskers) existing 20–30 ms prior to the signal’s onset (i.e., neural activity “persists” for at least 20–30 ms). The second mechanism, which has a longer time-course, produces masking by reducing the gain of the cochlear amplifier. This mechanism is assumed to be effective for maskers existing at least 40–70 ms prior to the signal’s onset. Specifically, the masking effect of this second mechanism is assumed to follow the time-course of the MOCR as described by Backus and Guinan (2006). Under the assumption that forward masking is a mix of neural persistence and gain reduction, the PTC and MP data discussed above become difficult to interpret because neither masking mechanism is under experimental control. In other words, for a given masker frequency and duration, the relative contribution of each mechanism is unknown.
Krull and Strickland (2008) described a precursor-based technique that may control or isolate the masking effects of the gain-reduction mechanism. This technique took advantage of the “sluggishness” of the MOCR by restricting the masker duration and the masker-signal interval such that gain-reduction effects from the masker should be minimal (i.e., gain-reduction effects were primarily from the precursor). The study by Krull and Strickland (2008) was limited to estimating cochlear gain via growth of off-frequency masking; however, if the MOCR were involved, frequency selectivity may also change in a manner consistent with less cochlear-amplifier gain. The current set of experiments adopts the technique described by Krull and Strickland (2008) to test this hypothesis. Behavioral estimates of frequency selectivity and gain were measured using PTCs and off-frequency growth of masking (GOM) functions, respectively. Within each experiment, data were measured for two conditions which differed by the frequency of the precursor. In the on-frequency precursor condition, the precursor was the same frequency as the signal and was assumed to elicit the MOCR at the signal place. Conversely in the off-frequency precursor condition, the precursor’s frequency was fixed well below the signal frequency and was assumed to have little to no effect on the cochlear amplifier at the signal place. Under the assumption of MOCR-induced gain reduction, the on-frequency precursor condition may result in a broader PTC and a GOM function consistent with less gain. In the general discussion, a model is described that tests the assumption of MOCR-induced gain reduction. An additional model based on additivity of masking is also tested.
METHODS
Subjects and procedures
Four normal-hearing subjects were recruited for the experiment. All were clinically normal on measures of acoustic immittance, distortion-product otoacoustic emissions, and pure-tone audiometry (thresholds were below 15 dB HL at audiometric frequencies between 250 and 4000 Hz). Subjects were between 24 and 27 years of age and were recruited among the students and staff at Purdue University and citizens of the Greater Lafayette community. All were inexperienced with psychoacoustic tasks and paid for their time except subject 3, who is the first author. Prior to data collection, the subjects were given 2–3 h of practice on each experiment to minimize learning effects.
In both of the experiments, masker level at threshold was measured using a three-interval forced-choice task. Subjects listened to the stimuli in a double-walled sound-attenuating booth. For a given trial, the listener pressed a button to indicate the interval in which the signal was perceived. Visual stimuli marked the observation intervals and feedback was provided to indicate a correct or an incorrect response. If the response was incorrect, the masker level decreased. If the response was correct over two successive trials, the masker level increased. This stepping rule converged on the level where the subject achieved 70.7% correct (Levitt, 1971). A run consisted of 50 trials. An even number of reversals, excluding the first two, were averaged to estimate the threshold for a run. The step size was 5 dB until the second reversal, after which it decreased to 2 dB. At least two and often three runs were averaged for the final threshold estimate of each condition. Runs with a standard deviation greater than 5 dB were excluded. If performance improved appreciably over successive runs, measurement continued until performance stabilized, after which only the last two or three measurements were averaged. Each experimental session was limited to 1–1.5 h in length.
Stimuli
The digitally-generated stimuli were presented through four separate D∕A channels (TDT DA 3-4), low-pass filtered at 10 kHz (TDT FT5 and TDT FT6-2), and adjusted by programmable attenuators (TDT PA4). The stimuli were then mixed (TDT SM3), passed through a headphone buffer (TDT HB6), and presented to the listener’s left ear via an ER-2 insert earphone.
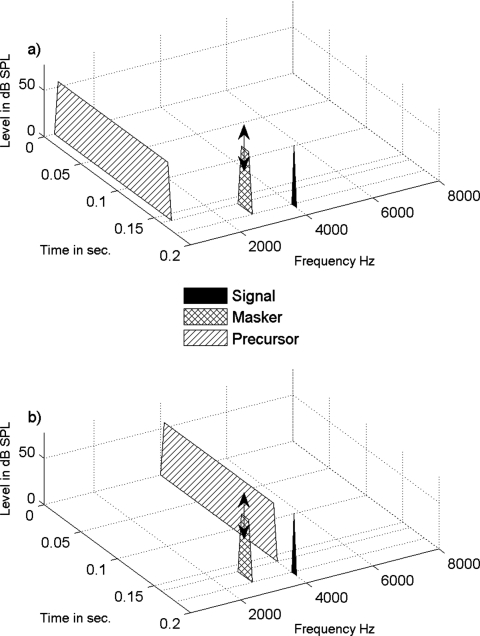
The stimulus paradigm used for the GOM and PTC experiments is depicted in Fig. 1. This paradigm contains the following three components: (1) a fixed-level tonal precursor, (2) a variable-level tonal masker, and (3) a fixed-level 4 kHz signal. In all conditions, the total durations (including onset∕offset ramps) of the precursor, masker, and signal were 160, 20, and 6 ms, respectively. Each had 5 ms cos2 onset and offset ramps except the signal, where this value was 3 ms. There was no delay between the offset of one component (i.e., precursor, masker, or signal) and the onset of the next. High-pass noise (cutoff frequency=1.2×signal frequency) was gated 50 ms before precursor onset and 50 ms after signal offset at a spectrum level 40 dB below the signal level to restrict off-frequency listening. Within each experiment, data were collected for two precursor frequencies. The 4 kHz precursor (“on-frequency precursor”) was designed to elicit the MOCR at the signal place, while the 0.8 kHz precursor (“off-frequency precursor”) functioned as a control. This stimulus paradigm attempted to restrict MOCR-induced gain reduction to cochlear regions at and near the signal by (1) fixing the level, frequency, and duration of the on-frequency precursor across all conditions and (2) minimizing masker duration and masker-signal delay such that MOCR-induced gain reduction from the masker was minimal during the presentation of the signal.
Figure 1.
Three dimensional representation of the stimuli used in the experiments. Temporal and spectral parameters of the signal and precursor are shown for the off-frequency (a) and on-frequency precursor (b) conditions. Masker level at threshold was the dependent variable in all conditions. In experiment 1, thresholds were measured for a series of masker frequencies (Note: only one frequency is displayed in the figure) to construct two PTCs, one for each precursor frequency. In experiment 2, thresholds for an off-frequency masker were measured for a series of signal levels to construct two GOM functions, one for each precursor frequency.
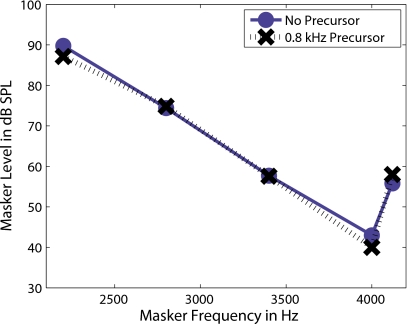
In addition to attempting to control for the MOCR, this stimulus paradigm minimized any attention-related effects by including a precursor in all conditions rather than comparing measurements with and without a precursor. Data from a pilot experiment (Fig. 2) found that thresholds for the 0.8 kHz precursor condition were nearly identical to thresholds without a precursor. These pilot data are from S3 and involve a slightly longer masker (40 ms) than the experiments described below.
Figure 2.
Data comparing PTCs measured without a precursor and with the 0.8 kHz control precursor. Note that these conditions produce similar thresholds and suggest the 0.8 kHz control precursor is an appropriate approximation of thresholds without a precursor.
Thresholds for the signal were measured in quiet for all subjects and are displayed in Table 1. Also displayed is the level of the signal in the PTC experiment, the level of the precursor (LPE), and the level of the precursor needed to just mask the signal in the absence of the masker (LPA).
Table 1.
Threshold data and model parameter estimates.
| Subject | Signal threshold in quieta | Signal level (PTC)a | Precursor level (LPE) a | Precursor masking level (LPA) a | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | 27.30 | 50.00 | 60.00 | 70.58 | |||||||||
| S2 | 38.14 | 55.00 | 60.00 | 74.90 | |||||||||
| S3 | 35.08 | 52.00 | 60.00 | 94.00 | |||||||||
| S4 | 35.03 | 55.00 | 50.00 | 71.01 | |||||||||
| Roex filter parameters | GOM parameters | ||||||||||||
| Subject | Precursor | BF (kHz) | LBFa | pl | wl | tl | pu | rmsb | Q10 | Gainb | c | BP1a | rmsb |
| S1 | Off-frequency | 4.00 | 53.8 | 42.8 | 7.0×10−3 | 12.2 | >500 | 0.5 | 9.72 | 40 | 0.17 | 42.83 | 1.3 |
| On-frequency | 3.53 | 40 | 33.7 | 4.6×10−3 | 8.2 | 34.7 | 1.8 | 4.22 | 13.3 | 0.62 | 70 | 2.2 | |
| S2 | Off-frequency | 4.12 | 57.3 | 21.3 | NA | NA | 224.9 | 2.2 | 4.92 | 25.62 | 0.07 | 64.13 | 0.8 |
| On-frequency | 3.74 | 50.4 | 25.8 | NA | NA | 27.1 | 0.6 | 3.36 | ⋯ | 0.34 | 56.75 | 0.3 | |
| S3 | Off-frequency | 4.08 | 57.0 | 26.0 | NA | NA | >500 | 0.5 | 6.68 | 32.99 | 0.42 | 55 | 1.5 |
| On-frequency | 3.92 | 47.1 | 30.0 | NA | NA | 110.7 | 1.7 | 5.89 | 19.32 | 0.55 | 67.42 | 3 | |
| S4 | Off-frequency | 4.10 | 48.3 | 26.0 | NA | NA | >500 | 1.2 | 6.36 | 22.20 | 0.32 | 62.72 | 1.5 |
| On-frequency | 3.91 | 39.3 | 33.5 | 1.0×10−4 | 0.16 | 105.7 | 6.44 | 5.3 | 14.00 | 0.54 | 68.6 | 1.7 | |
Units in dB SPL.
Values in dB.
Experiment 1: Psychophysical tuning curves
Experiment 1 estimated frequency selectivity at the signal place. The signal level was fixed at 17–23 dB SL (i.e., approximately 20 dB SL). The masker level was adjusted to find threshold for a series of masker frequencies ranging from approximately 2000 to 5000 Hz. Data were collected in steps of approximately 400 and 80 Hz for masker frequencies below and above the signal frequency, respectively. The precursor level was fixed at 60 dB SPL for all subjects except subject 4, who was unable to perform the task at this level. For this subject, the precursor level was lowered to 50 dB SPL.
Experiment 2: Growth of masking functions
Experiment 2 estimated the I∕O function at the signal frequency using the GOM technique first described by Oxenham and Plack (1997). This technique often involves comparing on and off-frequency GOM data to account for any non-linearities in forward masking (Oxenham and Plack, 2000; Oxenham and Bacon, 2004); however, for short masker-stimulus intervals (0–10 ms) the on-frequency GOM function is linear with a slope of 1. This suggests that the off-frequency GOM function can be directly interpreted as an estimate of the I∕O function without measuring on-frequency GOM. The masker frequency was fixed at 2.8 kHz. A similar experiment (Oxenham and Plack, 1997) reported using a masker frequency one octave below the signal frequency. Initial data collection revealed that it was not possible to measure threshold for such a low masker frequency without exceeding the limits of the equipment (95 dB SPL). Therefore, the masker’s frequency was raised sufficiently to measure threshold and maintain a reasonable assumption of linear growth at the signal place. Thresholds were obtained for a series of fixed signal levels from near threshold to 40–60 dB SL in 3 or 5 dB steps.
RESULTS AND DISCUSSION
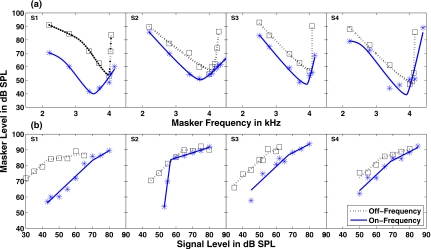
Figure 3 displays the individual data for the PTC and GOM experiments in the top and bottom rows, respectively. Squares and asterisks are data for the off-frequency and on-frequency precursors. Dashed and solid lines are model fits to the data and are discussed below.
Figure 3.
PTC (a) and GOM (b) results. The data are presented for each subject individually (S1–S4). Squares and asterisks represent the off-frequency and on-frequency precursor data, respectively. Dotted and solid lines are model fits to the data (see text).
PTC data
Masker level is plotted as a function of masker frequency for the PTC data. Error bars were omitted for clarity [the average standard deviations by subject number for the off- and on-frequency data were 2.38, 3.82 (S1), 3.00, 2.60 (S2), 1.34, 2.51 (S3), 3.18, 2.11 (S4)]. Roex (p,w,t) filter shapes were fitted to the data as described by Yasin and Plack (2003) and represent the data reasonably well (see Table 1 for rms error values). The filter parameters were allowed to vary independently for the upper and lower skirts of the filter. In order to fit the roex functions, two additional free parameters were added (“BF” and LBF). Parameter estimates were obtained using a least-squares minimization procedure using the MATLAB function “fminsearch.” The equations which described the output of the roex filter for the lower and upper skirts were
| (1) |
| (2) |
where BF is the filter’s best frequency, LBF is the estimated output at BF, p (“pl” or “pu”) and tl determine the filter slopes for the tip and tail, respectively, and wl delineates the intersection of pl and tl.
Table 1 presents the parameter estimates of the fitting procedure. The cells marked “NA” denote when a parameter did not appreciably improve the fit. Filter sharpness (Q10) was estimated by dividing BF by the filter bandwidth at 10 dB above LBF.
Three general patterns emerged from the PTC data. First, masker levels at threshold were lower in the on-frequency precursor condition at all masker frequencies (except for S4 at 4 kHz). Second, the estimated Q10 was reduced in all subjects in the on-frequency precursor condition; however, this effect was not significant (t[3]=1.57, p(one-tailed)=0.106). Finally, the estimated BF was consistently lower in the on-frequency precursor condition (t[3]=4.32, p(one-tailed)=0.011).
GOM data
The GOM results are plotted on the bottom row of Fig. 3. Masker level is plotted as a function of signal level. Error bars were omitted for clarity [the average standard deviations for the off and on-frequency data were 0.98, 2.57 (S1), 2.27, 3.13 (S2), 1.11, 0.81 (S3), 0.65, 1.64 (S4)]. Two lines were simultaneously fitted to the GOM data for each condition using a minimization procedure with three free parameters (G, c, and “BP1”). This procedure was modified from Yasin and Plack (2003). The first line was fitted to the lower leg of the data and was constrained to have a slope of 1. The y-intercept of this line was a free parameter (G) and can be interpreted as an estimate of gain. The second line was fitted to the upper leg of the data and its slope (c) can be interpreted as an estimate of compression. The lower breakpoint (BP1) delineated the end of the first line and the beginning of the second line. An additional breakpoint (“BP2”) was initially a free parameter; however, it did not improve the fitting procedure so its value was fixed at 100 dB. The two-line model fits were given by
| (3) |
| (4) |
| (5) |
where Lin is the input signal level, BM(Lin) is the estimated masker level at threshold, and the “internal breakpoints” are IBP1=G+BP1 and IBP2=IBP1+c(BP2−BP1). For one subject (S2), the lowest data point resulted in a poor model fit and an incorrect characterization of the breakpoint. The poor fit was largely due to the steep slope of the lower leg of the data. A similar steep slope was also observed in some subjects by Strickland (2008) and Krull and Strickland (2008) and may be related to the absolute threshold effects discussed by Plack and Skeels (2007). For this subject, the slope of the line fit to the lower leg of the data was allowed to vary. As a result of this minor change in the model, S2’s data were not included in the statistical tests for gain.
The parameter estimates of the GOM fitting procedure are displayed in Table 1. The on-frequency precursor condition produced lower estimates of gain (t[2]=2.95, p(one-tailed)=0.049) and higher estimates of the compression slope (t[3]=−3.97, p(one-tailed)=0.028) compared to the off-frequency precursor condition. There was no significant effect with respect to the breakpoint (t[3]=−2.74, p(one-tailed)=0.138). This was unexpected considering a previous study by Krull and Strickland (2008) that reported an increase in breakpoint under similar conditions. Three of the four subjects in the current study exhibited a fairly large increase in breakpoint, while the other (S2) showed a decrease. This reversal in the direction of the breakpoint for S2 may explain why this effect was not significant.
The estimates of compression slope are similar to previous studies with respect to the off-frequency precursor data. For example, Rosengard et al. (2005) reported values between 0.20 and 0.37 compared to a range of 0.07–0.46 in the current study. The slightly elevated values of compression slope in subjects 3 and 4 are likely a result of insufficient data above BP1 to obtain an accurate estimate. This is also true for the compression estimates in the on-frequency precursor condition for subjects 1 and 3.
Oxenham and Plack (1997) reported that the off-frequency GOM function became “more linear” between 40–50 dB, which can be interpreted as an estimate of BP1. The present study’s estimates are somewhat higher than this range for three out of four of the subjects; however, similar high breakpoints have been observed in individual subjects in previous studies. For example, two subjects in Moore et al. (1999) (i.e., subjects JP and AG in Fig. 4) appear to have breakpoints between 55 and 60 dB SPL. Similarly, subject 2 in Oxenham and Plack (2000) showed no definable breakpoint up to the maximum signal threshold obtained (approximately 55 dB SPL). Finally, consistent with the current study, Krull and Strickland (2008) reported breakpoints above 60 dB SPL for two of their three subjects.1
Figure 4.
Schematic representation of the additivity model using estimated BM I∕O functions. The dotted line represents the I∕O function fit to the GOM data in the off-frequency precursor condition [BMunadapted(in)], while dashed lines represent a linear I∕O function for the off-frequency masker. Panel (a) displays threshold for the signal (circle) in the presence of the masker (squares) alone. The data from this condition determined the signal-to-masker ratio at threshold. Panel (b) displays the threshold for the signal in the presence of the precursor (triangle) alone at LPA. The constant γ represents the decay of the precursor energy during the silent interval between the signal and precursor. The value of γ was determined in panel (b) and assumed to be the same in panels (c) and (d). Panels (c) and (d) display how the precursor (at LPE) and masker outputs (solid dashes on the y-axis) might add to produce an additivity-of-masking effect for the tip and tail frequencies. The horizontal line labeled “TE” represents the total energy needed to mask the signal (i.e., the addition of the masker and precursor outputs equal TE). The leftward pointing arrows represent the decrease in masker input needed to maintain a constant signal-to-masker+precursor ratio at the output of the BM I∕O function. The open squares [and filled triangles in (c) and (d)] are the input(s) to the model and the closed squares are the predicted output.
Comparing the current data across experiments reveals a pattern that is consistent with a decrease in cochlear-amplifier gain in the on-frequency precursor condition. This pattern is characterized by lower estimates of gain, frequency selectivity, and BF. A similar pattern was noted by Strickland (2001), who measured frequency selectivity in simultaneous masking with and without a broadband precursor. The author interpreted these data as a reduction in cochlear gain and supported this interpretation using a simple BM I∕O function model. Although frequency selectivity was measured, Strickland (2001) would not have been able to observe a decrease in BF due to the measurement method (i.e., notched-noise method). In a recent forward masking study, Krull and Strickland (2008) estimated the BM I∕O function using the off-frequency GOM technique. They reported a 5–20 dB reduction in gain across subjects when a 60 dB SPL precursor was present. This range is similar to Strickland (2008) and the current study, where a similar precursor produced 9–27 dB of gain reduction. It is noteworthy that physiological studies on the MOCR have observed reductions in BM gain of the same magnitude (Murugasu and Russell, 1996).
GENERAL DISCUSSION AND MODELING
Although the pattern of results discussed above is consistent with a decrease in gain in the on-frequency precursor condition, there are other potential interpretations, the most prominent of which involves the additivity of masking (Oxenham and Moore, 1994; Plack and O’Hanlon, 2003; Plack et al., 2006, 2007). Under this interpretation, the precursor and masker are viewed as two maskers whose intensities add after being processed by the auditory periphery. A typical additivity-of-masking experiment consists of two phases. During the first phase, the signal level is fixed and thresholds are measured for each masker individually. In the second phase, the maskers are presented together at the levels measured in the first phase, and the signal level at threshold is then measured. In a linear system, this approach should lead to a 3 dB increase in signal level relative to the first phase; however, threshold shifts are often much larger. This phenomenon is referred to as “excess masking” and has been interpreted as evidence of compression (Penner et al., 1980). Under the additivity-of-masking assumption, the magnitude of excess masking is related to the amount of compression and the relative input levels of the two maskers for a given signal level. In experiment 2, the precursor level was fixed; therefore, as the signal level increases, any partial (or additive) masking from the precursor decreases. This argument suggests that excess masking should be largest at low signal levels where the partial masking from the precursor is highest. Qualitatively, this appears to be the case in all four subjects.
A modeling approach was used to evaluate the additivity-of-masking hypothesis. The experimental design in the current study differs from typical additivity-of-masking experiments; therefore, the model (hereafter referred to as the “additivity model”) also differs and involves a few more assumptions. To compare the hypotheses of additivity and gain reduction, a “gain-reduction” model was tested as well. This model was also evaluated by predicting data from a previous study that was interpreted in terms of additivity of masking (Plack et al., 2006).
For the current data set, the purpose of modeling was to predict the on-frequency precursor data (solid lines Fig. 3) by using the off-frequency precursor data (dotted lines Fig. 3) as a reference. For the PTC predictions, two masker frequencies were modeled, one at the signal frequency (4000 Hz) and the other well below the signal frequency (≈2200 Hz). These frequencies will be referred to as the “tip” and “tail” frequencies, respectively. They were chosen because their BM I∕O functions were either measured in experiment 2 (tip frequency) or reasonably assumed to be linear with a slope of 1 (tail frequency). For the GOM predictions, only the additivity model was evaluated. Both additivity and gain-reduction models assumed no effect from the off-frequency precursor; therefore, in subsequent sections the term precursor will be reserved for the on-frequency precursor, unless otherwise stated.
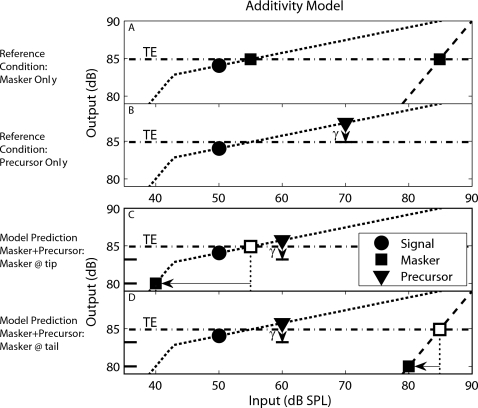
Additivity model
Under the additivity-of-masking assumption, the effective intensities of the masker and precursor add internally at the output of the auditory periphery. Two thresholds were used as reference conditions and are shown schematically in Figs. 4a, 4b.2 These thresholds describe the individual internal representations of the precursor and masker when presented individually with the signal. Specifically, the precursor reference condition [Fig. 4b] was the threshold for the signal in the presence of the precursor at a 20 ms precursor-signal interval and is represented by the column LPA in Table 1. The masker reference condition [Fig. 4a] was the threshold measured for the off-frequency PTC at the tip and tail frequencies. All reference thresholds were assumed to be a function of the BM I∕O function and a constant signal-to-masker ratio (or signal-to-precursor ratio for the case of the precursor alone) at the output of the auditory periphery. An estimate of this ratio was obtained from the reference threshold for the masker alone and can be interpreted graphically as the vertical distance between the filled circle and filled squares in Fig. 4a. For each listener, the fitted GOM function in experiment 2 (off-frequency precursor condition) served as the estimate of the BM I∕O function [BMunadapted(in)]. The internal representation of the precursor when presented alone with the signal (IRPreference) was estimated by
| (6) |
in decibels, where LPA is level of the precursor needed to mask the signal in the absence of the masker and γ is a constant representing the decrease in precursor output during the 20 ms silent interval between the precursor and signal. For the combined masker-precursor case, it was assumed that the signal was detected at a constant signal-to-masker+precursor ratio after peripheral processing; therefore, the total energy (TE) needed to mask the signal at threshold was described by
| (7) |
where IRPmodel is Eq. 6 evaluated at LPE and IRMmodel is the predicted internal representation of the masker in the on-frequency precursor condition. IRMmodel was solved from Eq. 7:
| (8) |
and then passed into the inverse of the BM I∕O function to predict the masker threshold for the on-frequency precursor condition.
Gain-reduction model
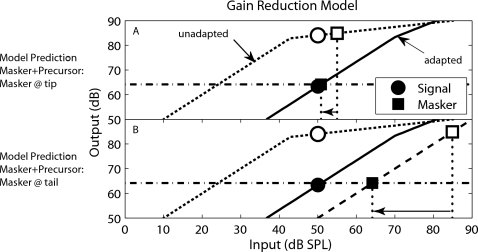
In contrast to the additivity model, the gain-reduction model (Fig. 5) did not assume energetic masking from the precursor. Rather, it assumed that the precursor reduced the gain of the BM I∕O function, after which the signal was detected at a constant signal-to-masker ratio. For each listener, the fitted GOM function in experiment 2 (on-frequency precursor condition) served as an estimate of the BM I∕O function [BMadapted(in)]. Note that for this model, the signal-to-masker ratio was determined solely by the masker (i.e., the precursor intensity did not add to the masker intensity before detection).
Figure 5.
Schematic representation of the gain-reduction model. This model assumed the on-frequency precursor reduced BM gain (or equivalently “adapted” the on-frequency I∕O function). Two masker frequencies are schematized, one at the same frequency as the signal (a) and the other far below the signal frequency (b). Within each panel, the masker (squares) and signal (circles) are plotted for the masker alone condition (open symbols), or for the masker+precursor condition (closed symbols). Notice that the masker alone condition assumes that the signal and on-frequency masker operate on the unadapted I∕O function [BMunadapted(in), dotted lines], while the masker+precursor condition assumes that the signal and on-frequency masker operate on the adapted I∕O function [BMadapted(in), solid lines]. The dashed line in (b) represents the linear I∕O function for the off-frequency masker. The horizontal line represents the masker output needed to maintain a constant signal-to-masker ratio at the output of the adapted I∕O function.
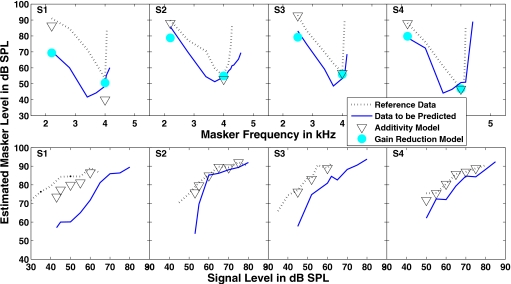
Model predictions and discussion
The predictions of the additivity and gain-reduction models are presented in Fig. 6. The PTC (top row) and GOM (bottom row) data were replotted. Dashed and solid lines represent the reference data (i.e., the input to the models) and the data to be predicted, respectively. Accurate model predictions lie near the solid line for a given listener. First consider the PTC predictions. The triangles and circles represent the additivity and gain-reduction model predictions, respectively (rms error: additivity model=8.17 dB; gain-reduction model=3.40 dB). As expected both models predicted a reduction in masker level at threshold relative to the reference data. At the tip frequency, the models are nearly equally accurate (except for S1, where the additivity model is poor). In contrast, a deviation between models is observed at the tail frequency, where the gain-reduction model is more accurate.3Krull and Strickland (2008) reported a similar finding when attempting to model precursor effects on off-frequency GOM under the additivity assumption. Their additivity model underestimated the effect of the precursor in all three of their subjects. Consistent with their findings, the current additivity simulations involving off-frequency masking (i.e., the tail frequency condition of the PTC experiment and the entire GOM experiment) underestimated the effect of the precursor. These results suggest that although additivity of masking explains data for two consecutive forward maskers with energy at the signal frequency, it may not explain data for two consecutive forward maskers having energy at and well below the signal frequency [however, see Arifianto and Plack (2008)].
Figure 6.
Model prediction for the PTC (top row) and GOM (bottom row) experiments. The predictions of the additivity (PTC and GOM data) and the gain-reduction (PTC data only) models are displayed as open triangles and filled circles, respectively. The models were intended to predict the on-frequency precursor data (asterisks in Fig. 3), which are replotted as a solid line. The dashed lines are the off-frequency data replotted and serve as a reference.
It is important to note that the gain-reduction model does not to attempt to predict the shift in BF observed in the data. In order to predict this shift, the model would need an estimate of the BM I∕O function at each masker frequency. Given the current data, such estimates are not available; however, a decrease in BF is often associated with an excitation pattern dominated by the passive mechanics of the BM (Ruggero et al., 1997). This domination may occur as a result of high input levels (Moore et al., 2002) or due to a decrease in the active process. For example, Yasin and Plack (2003) observed a decrease in BF in their PTC data when a suppressor was present, which is consistent with suppression functioning as an instantaneous decrease in the active process. The decrease in BF observed in the current experiment may also reflect a decrease in the active process given the low signal level used to measure the PTCs.
Modeling previous data
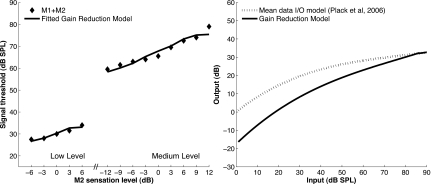
To further test the gain-reduction model, predictions were obtained for the mean data in Plack et al. (2006). This study involved measuring signal threshold in the presence of one or two temporally non-overlapping on-frequency forward maskers (M1 and M2). Using an additivity-of-masking model, Plack et al. (2006) were able to predict signal thresholds for the combined masker condition (M1+M2), by referencing signal thresholds from the separate masker conditions (M1 or M2 alone) and assuming a constant signal-to-masker ratio. A similar approach was taken in the current study; however, it was assumed that M1 reduced the gain of the I∕O function rather than adding with M2 at the output of the BM. Figure 7 displays the predictions of the gain-reduction model and the I∕O function which minimized the error of these predictions. The equation for this I∕O function was similar to that used in Plack et al. (2006), except in units of decibels and with the additional constant d:
| (9) |
where x is the input signal level (dB SPL) and a, b, and c are coefficients. The assumptions of the model were as follows: (1) The signal was detected at a constant signal-to-masker ratio at the output of the auditory periphery, (2) signal thresholds for M2 alone were a result of an I∕O function with high gain (dotted line in Fig. 7), and (3) signal thresholds for M1+M2 were a result of an I∕O function with relatively lower gain (solid line in Fig. 7). The coefficients for the “high-gain” I∕O function were fixed at the values measured for the mean data in Plack et al. (2006) (a=4.3×10−5, b=−9.9×10−3, c=0.913, and d=0). Gain reduction was simulated by allowing the parameter d to vary, while constraining the output to be equal to the high-gain model above a certain input level (xeq). This constraint produced the following relationship for the coefficient c:
| (10) |
where f(xeq) is the output of the high-gain polynomial model at xeq. The values of a and b were constrained to be equal to those of the high-gain model; therefore, the three free parameters in the gain-reduction model were d, xeq, and the threshold signal-to-masker ratio (k). As shown in Fig. 7, the gain-reduction model captures the data reasonably well. These results support the previous observation that additivity and gain-reduction models are equally accurate when the maskers (or the masker and precursor) have the same frequency.4
Figure 7.
Gain-reduction model predictions of Plack et al. (2006) (mean data) and the I∕O function which minimized the error of the predictions. Parameter estimates of the gain-reduction model were d=−17.48, xeq=85.47, and k=−9.81
SUMMARY AND CONCLUSIONS
The experiments and model simulations presented in this study support the hypothesis that a reduction in gain can account for the effects of a precursor (or second masker) in the current study and at least one previous study. This conclusion is consistent with previous studies in forward and simultaneous masking which have also modeled masking data as a reduction in gain (Strickland, 2001; Oxenham, 2001; Strickland, 2004; Strickland and Krishnan, 2005; Strickland, 2008; Krull and Strickland, 2008). This study also showed that additivity of masking can account for some of the data in the experiments; however, for much of the data the size of the precursor effect was larger than predicted by additivity.
An interesting dichotomy emerges when comparing simultaneous and forward masking in terms of precursor effects. In simultaneous masking, a precursor usually improves detectability relative to thresholds without a precursor, while the opposite is true in forward masking. This dichotomy suggests that the human auditory system is designed for optimal performance in simultaneous masking tasks. Such a design seems appropriate given that most “everyday” listening tasks involve detecting and understanding signals embedded in background noise. In such environments, the MOCR may adjust gain to reduce the influence of competing signals and their effects on neural adaptation and transmitter depletion (Guinan, 2006). Similarly, such an adjustment may help to shift the rate-level functions of auditory neurons to optimize encoding of the signal of interest (Dean et al., 2005).
ACKNOWLEDGMENTS
We would like to thank the associate editor Magdalena Wojtczak and reviewers Chris Plack and Andrew Oxenham for their helpful comments and suggestions on previous versions of this manuscript. Similarly, we would like to thank Vidya Ganesh for her comments on the revised manuscript. This work was funded in part by NIH (NIDCD) Grant Nos. RO1-DC008327 and T32-DC00030.
Footnotes
The frequency response of the ER-2 headphones used in the current study may contribute to the high breakpoints. These headphones produce a flat frequency response at the level of the eardrum. Many of the previous studies have used circumaural headphones such as the Sennheiser HD580 (Rosengard et al., 2005), which may produce a slightly higher output in the 2–6 kHz region (the frequency region of our signal) when calibrated in a similar manner.
This schematic is based on the data from S1 with a slight modification to add visual clarity. This modification involved slightly increasing the masker level at threshold, as well as slightly decreasing the value of LPA.
It is not surprising that the gain-reduction model predicts the data at the tail frequency since the estimated I∕O functions used in the model were derived under similar stimuli conditions as the data being predicted. These data could have been equally well predicted by a BM model where gain varied as a parameter; however, to limit the number of the parameters to the model, the GOM functions were used instead.
The model simulations were limited to the M1+M2 data. Although the model could be revised to include M1 predictions, such a revision would require adding additional assumptions and parameters. In an effort to reduce the model’s parameters and assumptions, we limited our predictions to the M1+M2 data.
References
- Arifianto, D., and Plack, C. J. (2008). “Behavioral evidence for off-frequency compression at 4 kHz,” J. Acoust. Soc. Am. 10.1121/1.2935709 123, 3858. [DOI] [Google Scholar]
- Backus, B. C., and Guinan, J. J. (2006). “Time-course of the human medial olivocochlear reflex,” J. Acoust. Soc. Am. 10.1121/1.2169918 119, 2889–2904. [DOI] [PubMed] [Google Scholar]
- Bacon, S. P., and Jesteadt, W. (1987). “Effects of pure-tone forward masker duration on psychophysical measures of frequency selectivity,” J. Acoust. Soc. Am. 10.1121/1.395688 82, 1925–1932. [DOI] [PubMed] [Google Scholar]
- Bacon, S. P., and Moore, B. C. (1986). “Temporal effects in masking and their influence on psychophysical tuning curves,” J. Acoust. Soc. Am. 10.1121/1.394328 80, 1638–1645. [DOI] [PubMed] [Google Scholar]
- Bacon, S. P., Repovsch-Duffey, J. L., and Liu, L. (2002). “Effects of signal delay on auditory filter shapes derived from psychophysical tuning curves and notched-noise data obtained in simultaneous masking,” J. Acoust. Soc. Am. 10.1121/1.1485972 112, 227–237. [DOI] [PubMed] [Google Scholar]
- Bacon, S. P., and Viemeister, N. F. (1985). “The temporal course of simultaneous tone-on-tone masking,” J. Acoust. Soc. Am. 10.1121/1.392891 78, 1231–1235. [DOI] [PubMed] [Google Scholar]
- Cooper, N. P., and Guinan, J. J. (2006). “Efferent-mediated control of basilar membrane motion,” J. Physiol. (London) 10.1113/jphysiol.2006.114991 576, 49–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dean, I., Harper, N. S., and McAlpine, D. (2005). “Neural population coding of sound level adapts to stimulus statistics,” Nat. Neurosci. 10.1038/nn1541 8, 1684–1689. [DOI] [PubMed] [Google Scholar]
- Guinan, J. J. (2006). “Olivocochlear efferents: Anatomy, physiology, function, and the measurement of efferent effects in humans,” Ear Hear. 10.1097/01.aud.0000240507.83072.e7 27, 589–607. [DOI] [PubMed] [Google Scholar]
- Guinan, J. J., Jr., and Gifford, M. L. (1988). “Effects of electrical stimulation of efferent olivocochlear neurons on cat auditory-nerve fibers. III. Tuning curves and thresholds at CF,” Hear. Res. 10.1016/0378-5955(88)90075-5 37, 29–45. [DOI] [PubMed] [Google Scholar]
- Hicks, M. L., and Bacon, S. P. (1992). “Factors influencing temporal effects with notched-noise maskers,” Hear. Res. 10.1016/0378-5955(92)90174-L 64, 123–132. [DOI] [PubMed] [Google Scholar]
- Kidd, G., Mason, C. R., and Feth, L. L. (1984). “Temporal integration of forward masking in listeners having sensorineural hearing loss,” J. Acoust. Soc. Am. 10.1121/1.390558 75, 937–944. [DOI] [PubMed] [Google Scholar]
- Kimberley, B. P., Nelson, D. A., and Bacon, S. P. (1989). “Temporal overshoot in simultaneous-masked psychophysical tuning curves from normal and hearing-impaired listeners,” J. Acoust. Soc. Am. 10.1121/1.397954 85, 1660–1665. [DOI] [PubMed] [Google Scholar]
- Krull, V., and Strickland, E. A. (2008). “The effect of a precursor on growth of forward masking,” J. Acoust. Soc. Am. 10.1121/1.2912440 123, 4352–4357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt, H. (1971). “Transformed up-down methods in psychoacoustics,” J. Acoust. Soc. Am. 10.1121/1.1912375 49, 467–477. [DOI] [PubMed] [Google Scholar]
- Moore, B. C., Alcantara, J. I., and Glasberg, B. R. (2002). “Behavioural measurement of level-dependent shifts in the vibration pattern on the basilar membrane,” Hear. Res. 10.1016/S0378-5955(01)00390-2 163, 101–110. [DOI] [PubMed] [Google Scholar]
- Moore, B. C., Glasberg, B. R., Plack, C. J., and Biswas, A. K. (1988). “The shape of the ear’s temporal window,” J. Acoust. Soc. Am. 10.1121/1.396055 83, 1102–1116. [DOI] [PubMed] [Google Scholar]
- Moore, B. C., Vickers, D. A., Plack, C. J., and Oxenham, A. J. (1999). “Inter-relationship between different psychoacoustic measures assumed to be related to the cochlear active mechanism,” J. Acoust. Soc. Am. 10.1121/1.428133 106, 2761–2778. [DOI] [PubMed] [Google Scholar]
- Murugasu, E., and Russell, I. J. (1996). “The effect of efferent stimulation on basilar membrane displacement in the basal turn of the guinea pig cochlea,” J. Neurosci. 16, 325–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oxenham, A. J. (2001). “Forward masking: Adaptation or integration?” J. Acoust. Soc. Am. 10.1121/1.1336501 109, 732–741. [DOI] [PubMed] [Google Scholar]
- Oxenham, A. J., and Bacon, S. P. (2004). in Compression: From Cochlea to Cochlear Implants, edited by Bacon S. P., Fay R. R., and Popper A. N. (Springer, New York: ), pp. 62–106. [Google Scholar]
- Oxenham, A. J., and Moore, B. C. (1994). “Modeling the additivity of nonsimultaneous masking,” Hear. Res. 10.1016/0378-5955(94)90014-0 80, 105–118. [DOI] [PubMed] [Google Scholar]
- Oxenham, A. J., and Plack, C. J. (1997). “A behavioral measure of basilar-membrane nonlinearity in listeners with normal and impaired hearing,” J. Acoust. Soc. Am. 10.1121/1.418327 101, 3666–3675. [DOI] [PubMed] [Google Scholar]
- Oxenham, A. J., and Plack, C. J. (2000). “Effects of masker frequency and duration in forward masking: Further evidence for the influence of peripheral nonlinearity,” Hear. Res. 10.1016/S0378-5955(00)00206-9 150, 258–266. [DOI] [PubMed] [Google Scholar]
- Penner, M. J., Shiffrin, R. M., and Shiffrin, R. M. (1980). “Nonlinearities in the coding of intensity within the context of a temporal summation model,” J. Acoust. Soc. Am. 10.1121/1.383885 67, 617–627. [DOI] [PubMed] [Google Scholar]
- Plack, C. J., Carcagno, S., and Oxenham, A. J. (2007). “A further test of the linearity of temporal summation in forward masking,” J. Acoust. Soc. Am. 10.1121/1.2775287 122, 1880–1883. [DOI] [PubMed] [Google Scholar]
- Plack, C. J., and O’Hanlon, C. G. (2003). “Forward masking additivity and auditory compression at low and high frequencies,” J. Assoc. Res. Otolaryngol. 4, 405–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plack, C. J., Oxenham, A. J., and Drga, V. (2006). “Masking by inaudible sounds and the linearity of temporal summation,” J. Neurosci. 10.1523/JNEUROSCI.1134-06.2006 26, 8767–8773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plack, C. J., and Skeels, V. (2007). “Temporal integration and compression near absolute threshold in normal and impaired ears,” J. Acoust. Soc. Am. 10.1121/1.2769829 122, 2236–2244. [DOI] [PubMed] [Google Scholar]
- Rosengard, P. S., Oxenham, A. J., and Braida, L. D. (2005). “Comparing different estimates of cochlear compression in listeners with normal and impaired hearing,” J. Acoust. Soc. Am. 10.1121/1.1883367 117, 3028–3041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruggero, M. A., Rich, N. C., Recio, A., Narayan, S. S., and Robles, L. (1997). “Basilar-membrane responses to tones at the base of the chinchilla cochlea,” J. Acoust. Soc. Am. 10.1121/1.418265 101, 2151–2163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt, S., and Zwicker, E. (1991). “The effect of masker spectral asymmetry on overshoot in simultaneous masking,” J. Acoust. Soc. Am. 10.1121/1.400656 89, 1324–1330. [DOI] [PubMed] [Google Scholar]
- Strickland, E. A. (2001). “The relationship between frequency selectivity and overshoot,” J. Acoust. Soc. Am. 10.1121/1.1357811 109, 2062–2073. [DOI] [PubMed] [Google Scholar]
- Strickland, E. A. (2004). “The temporal effect with notched-noise maskers: Analysis in terms of input-output functions,” J. Acoust. Soc. Am. 10.1121/1.1691036 115, 2234–2245. [DOI] [PubMed] [Google Scholar]
- Strickland, E. A. (2008). “The relationship between precursor level and the temporal effect,” J. Acoust. Soc. Am. 10.1121/1.2821977 123, 946–954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strickland, E. A., and Krishnan, L. A. (2005). “The temporal effect in listeners with mild to moderate cochlear hearing impairment,” J. Acoust. Soc. Am. 10.1121/1.2074787 118, 3211–3217. [DOI] [PubMed] [Google Scholar]
- von Klitzing, R., and Kohlrausch, A. (1994). “Effect of masker level on overshoot in running- and frozen-noise maskers,” J. Acoust. Soc. Am. 10.1121/1.408679 95, 2192–2201. [DOI] [PubMed] [Google Scholar]
- Yasin, I., and Plack, C. J. (2003). “The effects of a high-frequency suppressor on tuning curves and derived basilar-membrane response functions,” J. Acoust. Soc. Am. 10.1121/1.1579003 114, 322–332. [DOI] [PubMed] [Google Scholar]
- Zwicker, E. (1965). “Temporal effects in simultaneous masking and loudness,” J. Acoust. Soc. Am. 10.1121/1.1909588 38, 132–141. [DOI] [PubMed] [Google Scholar]