Abstract
At least two modes of pitch perception exist: in one, the fundamental frequency (F0) of harmonic complex tones is estimated using the temporal fine structure (TFS) of individual low-order resolved harmonics; in the other, F0 is derived from the temporal envelope of high-order unresolved harmonics that interact in the auditory periphery. Pitch is typically more accurate in the former than in the latter mode. Another possibility is that pitch can sometimes be coded via the TFS from unresolved harmonics. A recent study supporting this third possibility [Moore et al. (2006a). J. Acoust. Soc. Am. 119, 480–490] based its conclusion on a condition where phase interaction effects (implying unresolved harmonics) accompanied accurate F0 discrimination (implying TFS processing). The present study tests whether these results were influenced by audible distortion products. Experiment 1 replicated the original results, obtained using a low-level background noise. However, experiments 2–4 found no evidence for the use of TFS cues with unresolved harmonics when the background noise level was raised, or the stimulus level was lowered, to render distortion inaudible. Experiment 5 measured the presence and phase dependence of audible distortion products. The results provide no evidence that TFS cues are used to code the F0 of unresolved harmonics.
INTRODUCTION
Many sounds in our environment, such as voiced speech, musical tones, and some animal vocalizations, are harmonic, comprising frequencies that are all at, or close to, integer multiples of a fundamental frequency (F0). We tend to hear a pitch corresponding to the F0, even when there is no energy at the F0 itself. This phenomenon has various terms, including the “pitch of the missing fundamental,” periodicity pitch, and residue pitch (e.g., Schouten, 1940; Licklider, 1954).
The mechanisms of pitch perception have been the subject of numerous studies over the past century and are still being debated today (Plack et al., 2005). There is broad consensus on certain aspects of pitch perception. For instance, low-numbered harmonics (<10) typically produce a more salient pitch and more accurate F0 discrimination than do high-numbered harmonics. The transition from strong to weak pitch with increasing lowest harmonic number (N) within a complex corresponds reasonably well with the transition from resolved to unresolved harmonics, as estimated by the dependence of F0 difference limens (F0DLs) on the phase relationships between components (Houtsma and Smurzynski, 1990; Shackleton and Carlyon, 1994; Bernstein and Oxenham, 2006a, 2006b), although it does not appear to be peripheral resolvability per se that determines the changes in percept with increasing N (Houtsma and Goldstein, 1972; Bernstein and Oxenham, 2003, 2008).
Resolved harmonics (such as isolated pure tones) may be coded by their tonotopic (place) representation (e.g., Wightman, 1973), by phase-locking to the temporal fine structure (TFS) in the auditory nerve (e.g., Meddis and O’Mard, 1997), or by a combination of both (Shamma and Klein, 2000; Oxenham et al., 2004). In so-called “pattern recognition” models of pitch, the estimates of the individual frequencies are combined to derive the overall F0 (Goldstein, 1973; Terhardt, 1974).
For unresolved harmonics, which interact within the passband of single peripheral auditory filters, the F0 may be extracted via phase-locking to the temporal envelope of the complex waveform after peripheral filtering, by phase-locking to TFS peaks located near envelope peaks, or both. Early evidence in favor of the use of TFS to derive the F0 from unresolved harmonics came from experiments using sinusoidally amplitude-modulated (SAM) tones (e.g., de Boer, 1956; Schouten et al., 1962). A SAM tone has three tonal components, the carrier frequency (fc) and two side bands, one above and one below the carrier, with the frequency spacing between the components corresponding to the modulation frequency (fm). When fc is an integer multiple of fm, the waveform is periodic and consists of three consecutive harmonics with an F0 equal to fm. When fc is not an integer multiple of fm, the temporal envelope is still periodic, with a frequency fm; however the TFS no longer shares the same F0. The fact that listeners heard a shift in pitch when the fc was shifted, even when fm remained the same, was taken as evidence that listeners were sensitive to the TFS of complex waveforms (de Boer, 1956; Schouten et al., 1962). One potential confound in these early experiments was that the spectral centroid of the complex shifted with the fc, leaving open the possibility that listeners were responding to a change in the spectrum of the three-tone complex rather than to a change in the TFS. Moore and Moore (2003) addressed this issue by using stimuli with more components, which were either harmonically related or were all shifted upward by the same amount in Hertz, and filtering them such that the spectral envelope of the stimuli remained constant. When the lowest harmonic number (N) present was about 14 or higher, no pitch shifts were heard when the frequencies of the components were shifted, suggesting that listeners were only sensitive to the temporal envelope and not to the TFS. At low values of N a pitch shift was heard, but this may have been due to the frequency shifts of the individual resolved harmonics. At intermediate N values of around 9, significant pitch shifts were found. Moore and Moore (2003) concluded that the results at intermediate values of N could be interpreted in two ways: First, if the harmonics were partially resolved, listeners may have been able to extract the individual frequencies of some of the harmonics and thus perceived a pitch shift by way of a shift in the individual harmonic frequencies; second, if the harmonics were unresolved, listeners may have been sensitive to the TFS of the complex waveform, in line with the theories of de Boer (1956) and Schouten et al. (1962). In a follow-up study, Moore et al. (2006a) attempted to distinguish between these two possibilities.
Moore et al. (2006a) measured F0DLs for three-component harmonic complexes centered at 2000 Hz as a function of F0 or, equivalently, the lowest harmonic number present. Either the three components were all in cosine phase (COS) or the middle component was shifted by 90° to produce what is often referred to as alternating phase (ALT). It was assumed that accurate F0 discrimination, as reflected by low F0DLs, implied that listeners were able either to access resolved harmonics or to process the TFS information from unresolved harmonics. Moore et al. (2006a) proposed to distinguish between these two possibilities by assessing whether or not F0DLs were dependent on the component phase relationships: if the components were resolved, then F0DLs should be independent of phase, whereas if they were unresolved, the components would interact within the auditory periphery and F0DLs might be phase-dependent. When N was 6 or 7, Moore et al. (2006a) found that F0DLs were low, and there was no effect of component phase, consistent with the harmonics being resolved. When N was 8, mean F0DLs in the COS condition were still as low as those when N was 6 or 7, but now mean F0DLs in the ALT condition were about a factor of 2 higher. The combination of low F0DLs and a phase effect led Moore et al. (2006a) to conclude that listeners were indeed using TFS to code the F0 from unresolved harmonics for values of N between about 8 and 10.
The conclusions of Moore et al. (2006a) have important theoretical implications. They suggest that listeners are able to use TFS for extracting not only information about the frequencies of individual resolved harmonics or the center frequency of a narrowband sound but also information about the F0 of a complex tone. Although the idea stems from early pitch research (e.g., Schouten, 1940; de Boer, 1956), more recent approaches have tended to consider pitch perception as originating from two cues [or possibly two mechanisms—see Carlyon and Shackleton (1994)], one that involves the individual frequencies of resolved harmonics (coded via place and∕or TFS) and one that involves the F0 of the unresolved harmonics (coded via temporal envelope cues) (e.g., Shamma and Klein, 2000). The suggestion that TFS may play another role for unresolved harmonics in the “intermediate” range of harmonic numbers (for N between 8 and 11) can be interpreted as adding a third pitch mechanism, which has implications for models of pitch processing. Another important implication of the results of Moore et al. (2006a) relates to the current debate regarding the role of TFS encoding in relation to the listening difficulties experienced by hearing-impaired individuals. Recent studies have extended the work of Moore et al. (2006a) to hearing-impaired listeners (Moore et al., 2006b; Hopkins and Moore, 2007) and have shown that in most of these listeners, there was no evidence for this intermediate region, where phase effects are found despite good (low) F0DLs. This has been interpreted as evidence that hearing-impaired listeners have reduced access to TFS cues (Moore et al., 2006b; Hopkins and Moore, 2007). The idea that hearing-impaired listeners have difficulties extracting TFS information in a way that cannot be simply explained by poorer frequency selectivity (and fewer resolved harmonics) has also been extended to studies of speech reception (e.g., Lorenzi et al., 2006; Hopkins et al., 2008). Because of their theoretical importance and their influence on subsequent research on TFS coding, the results of Moore et al. (2006a) deserve closer consideration.
One puzzling aspect of the results of Moore et al. (2006a) is that they found a strong phase effect even when there was no increase in the F0DLs for the COS complex. Although this is crucial to their interpretation that TFS coding is involved, it does not seem consistent with earlier studies. For instance, Houtsma and Smurzynski (1990) used complexes that were either in sine phase, which is thought to produce a highly modulated temporal envelope after auditory filtering, or in negative Schroeder phase (Schroeder, 1970), which is thought to produce a much less modulated temporal envelope (e.g., Kohlrausch and Sander, 1995; Oxenham and Dau, 2001). Houtsma and Smurzynski (1990) found that phase affected performance only once F0DLs in the sine-phase complex were elevated. Similar results were obtained in studies by Bernstein and Oxenham (2005, 2006b) when comparing sine-phase and random-phase complexes. Moore et al. (2006a) suggested that the difference might be due to the possibility that random and Schroeder phases do not produce the “optimally” flat temporal envelope produced by ALT-phase complexes and that the earlier studies had used complexes with more components.
Another difference between the study of Moore et al. (2006a) and the previous ones is the level of background noise used to mask distortion products. Houtsma and Smurzynski (1990) used a pink noise and presented their tones 20 dB above masked threshold; Bernstein and Oxenham (2003, 2005, 2006b) used a noise that produced roughly equal pure-tone detection thresholds at all frequencies (e.g., Moore et al., 2000), and presented their tones on average between 10 and 15 dB above masked threshold. In contrast, Moore et al. (2006a) used threshold equalizing noise at a level of 30 dB∕ERBN, where ERBN refers to the average value of the equivalent rectangular bandwidth of the auditory filter for young normal-hearing listeners at moderate levels (Glasberg and Moore, 1990). Because their complexes were presented at a level of 60.2 dB SPL (sound pressure level) per component, the tones were likely to have been 30–35 dB above their masked threshold.
The level of distortion products induced by two-, three-, and multitone complexes has been the subject of much research (e.g., Goldstein, 1967; Smoorenburg, 1972a, 1972b; Buunen et al., 1974; Pressnitzer and Patterson, 2001). The effective level of the distortion products is influenced by a number of variables, but it is not unusual to find distortion products at levels as high as 20 dB below the level of the primary components. The level and phase of distortion products have been shown to vary with the phase relations of the (three or more) primary components (Buunen et al., 1974; Pressnitzer and Patterson, 2001), and a number of researchers have proposed that some phase effects found in pitch perception can be ascribed to changes in the levels of distortion products (Goldstein, 1973; Buunen et al., 1974; Fleischer, 1976; for an early review, see Moore, 1977). Thus, it appears that the noise level used by Moore et al. (2006a) may not have been sufficient to mask distortion products. This in turn implies that changes in the relative levels of the distortion products with changes in phase may have influenced their results. The present study was designed to repeat the study of Moore et al. (2006a) with the same level of noise used in the original study and with a higher level of background noise to assess the extent to which their results and conclusions were affected by the audibility of distortion products.
EXPERIMENT 1: REPLICATION WITH LOW BACKGROUND NOISE LEVEL
Methods
Subjects
Four listeners (aged 18–22 yr) took part. All four had normal hearing, defined as having audiometric thresholds of 20 dB HL (hearing level) or less at octave frequencies between 250 and 8000 Hz. Following pure-tone audiometry, the listeners were given the opportunity to familiarize themselves with the stimuli and task. In all experiments in this study, all listeners had some musical education and had played a musical instrument at some point in their life. In addition, most of them had already participated in pitch discrimination experiments prior to this study. Therefore, they had no difficulty understanding the instructions, and by the end of the first 2-h session, their thresholds already fell within the same range as those obtained by one of the authors, who had extensive experience in pitch discrimination tasks, and they showed no clear signs of further improvement. In this and all subsequent experiments, elevated thresholds, obtained at first in a few of the listeners (mostly those with the least amount of musical training or prior experience in pitch discrimination tasks), were discarded before actual data collection began.
Procedure
This experiment measured F0DLs using a two-interval two-alternative forced-choice method with a 3-down 1-up adaptive procedure that tracks the 79% correct point on the psychometric function (Levitt, 1971). The two intervals contained complex tones with F0s that differed by an amount of ΔF0, expressed as a percentage of the F0 around which the two interval F0s were geometrically centered (F0c). The initial value of ΔF0 was 20%, which was initially varied (increased or decreased, according to the adaptive procedure) by a factor of 1.414 for the first four reversals in the adaptive rule. The factor was reduced to 1.189 for the final four reversals. Threshold was defined as the geometric mean value of ΔF0 at the last four reversals. At least four threshold estimates were obtained for each subject in each condition. The reported threshold was taken as the geometric mean of all estimates.
Stimuli
The stimuli were the same as those used by Moore et al. (2006a). Each complex tone consisted of three consecutive harmonics, each with a level of 60.2 dB SPL (65 dB SPL overall). The nominal number of the lowest harmonic, N, ranged from 4 to 14. The nominal frequency of the center component was 2000 Hz, which was roved by ±10% on each trial to encourage listeners to base their judgments on comparisons within each trial, rather than on any long-term memory representations. To reduce the effectiveness of spectral cues (as opposed to F0 cues), the value of N was roved across intervals, such that the actual lowest harmonic for each stimulus could be N−1, N, or N+1. The roved value was selected independently (with replacement) in each interval. The three components were added either in cosine phase (COS condition) or in alternating phase (ALT condition), where the phase of the center component lagged by 90° (sine phase). Each complex tone had a total duration of 480 ms, gated on and off with 20-ms raised-cosine ramps. The two complex tones within each trial were separated by an interstimulus interval of 300 ms.
A background threshold equalizing noise (Moore et al., 2000) was added, which was gated on 400 ms before the first interval and gated off 400 ms after the second interval. The noise was generated in the spectral domain and contained energy between 50 and 3000 Hz. The level of the noise was set to 30 dB SPL∕ERBN, so that the individual tones were about 30–35 dB above their masked thresholds in the noise.
Results and discussion
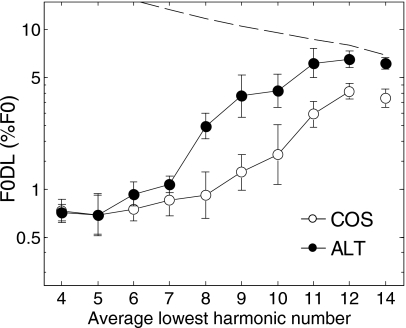
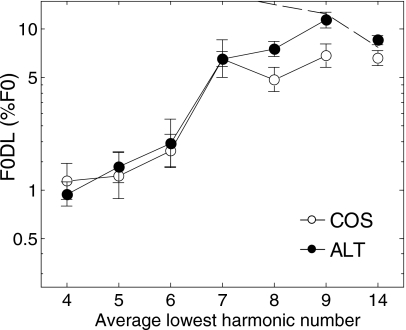
The mean results across the four listeners are shown in Fig. 1, where F0DLs are plotted as a function of the lowest harmonic number (N) of the three-tone complex for COS (open symbols) and ALT (filled symbols) complexes. Despite inter-individual variability, as also found by Moore et al. (2006a), the mean data obtained in this experiment replicated the main findings from the experiment of Moore et al. (2006a): for low values of N, F0DLs were low and similar in COS and ALT phases; at high values of N, F0DLs were higher and were generally higher in ALT than in COS phase.
Figure 1.
Mean F0DLs for three-component complexes as a function of the lowest harmonic number present (N). Filled symbols represent results for stimuli in ALT phase; open symbols represent results for stimuli in COS phase. Error bars represent ±1 standard error of the mean. The level of the threshold equalizing noise was set at 30 dB∕ERBN, meaning that the components were about 30–35 dB above their masked thresholds in noise. The dashed line shows the predicted thresholds based solely on spectral, rather than F0, information.
According to the reasoning of Moore et al. (2006a), if TFS can be used to code the F0 of unresolved harmonics, then some conditions should exist where (a) F0DLs are small, implying accurate coding using TFS, and (b) a phase effect is found, implying that the harmonics are unresolved. Such conditions can be seen in Fig. 1 for values of N between 8 and 10, where F0DLs are still relatively small in the COS condition but not in the ALT condition. To test this more formally, we established a “cutoff” F0DL, at the mid-point between the “asymptotic” low and high F0DLs, estimated using the geometric mean of the F0DLs in the COS condition at the lowest and highest value of N tested. We then took the highest value of N at which the F0DL in the COS condition fell below the cutoff value for the F0DL; this represented the condition for which the harmonics were most likely to be unresolved and still produce low F0DLs. Finally, we performed a paired t-test comparing the (log-transformed) F0DLs in the COS and ALT conditions for the selected value of N.
For the data in Fig. 1, the cutoff F0DL value was 1.64%. The highest N value for which the mean COS F0DLs fell below the cutoff was 10. A paired t-test at this value of N produced a significant effect of phase [paired t(3)=2.93, one-tailed p=0.031]. This finding of significant phase interactions for conditions in which the F0DLs are low is consistent with the results and conclusions of Moore et al. (2006a). In other words, these data show that a phase effect can occur, even when F0DLs are low, in line with the idea that TFS can be used to code the F0 of unresolved harmonics.
As the value of ΔF0 increases, the roving of lowest harmonic number by ±1 ceases to rule out the use of spectral (as opposed to F0) cues. The dashed curve in Fig. 1 shows the prediction of performance based solely on the (perfect or noiseless) frequency discrimination of the lowest component in each complex, as described in detail by Moore et al. (2006a). It can be seen that the mean F0DLs at the highest values of N approached this limit in the ALT, but not the COS, condition.
Experiment 1a: Using a different roving technique
As discussed by Moore et al. (2006a), their roving technique (also used here in experiment 1) leads to a listener obtaining 67% correct responses at small values of ΔF0, even if all responses are based solely on the increase in the frequency of the lower spectral edge of the stimulus and not on the change in F0. This is because with the three possible values of the lowest harmonic number in each interval (NINT), the probability that the N of the interval with the higher F0 will be the same as or greater than the N of the interval with the lower F0 is 67% (or 6 out of 9). Although 67% is lower than the tracking percent correct of 79%, it is still considerably higher than the 50% value of chance in a more typical two-alternative forced-choice experiment. Also, for two out of the nine possible combinations of N, the difference in N between the intervals was 2, producing a very large change in timbre, which listeners may have found distracting. Both these factors may have led subjects to lend more weight to the spectral pitch of the stimuli, rather than the desired periodicity pitch. Experiment 1a was designed to avoid these potential confounds by restricting the difference in NINT between the two intervals within a trial to 1 and by ensuring that at small values of ΔF0, listeners would only achieve 50% correct by using spectral edge cues. We achieved this goal by ensuring that the lowest harmonic number in the two intervals was always different and always differed by only 1. In other words, the possible combinations of the lowest harmonic number in the two intervals were (N−1,N), (N,N−1), (N,N+1), and (N+1,N). All other details in the experiment were the same as in the main experiment, except that the background noise was now broadband (extending from 50 Hz to 19.2 kHz) instead of being lowpass filtered at 3 kHz. Seven normal-hearing subjects took part in this experiment. Two of these listeners also took part in experiment 1. The ages of the subjects ranged from 19 to 33. The different roving paradigm led to some different predictions for thresholds based only on the frequency of the lowest harmonic. Briefly, the frequency of the lowest harmonic is a consistently reliable cue when (N−1)F0H>NF0L, where F0H and F0L are the F0s of the higher- and lower-F0 interval within a trial, respectively. Given that F0H=F0L(1+ΔF0∕100), where ΔF0 is the difference between F0H and F0L in percent, the inequality can be solved for ΔF0, such that spectral cues are reliable under the following condition:
| (1) |
This prediction is shown as a dashed curve in Fig. 2, along with the mean results from experiment 1a. It can be seen that F0DLs were somewhat higher overall than in experiment 1. This is consistent with the prediction that a higher sensitivity (d′) is required to achieve 79% correct when performance based on spectral cues is 50%, as opposed to 67%, although part of the difference may simply be due to inter-subject variability. Other than that, the pattern of results was similar to that found in the main experiment.
Figure 2.
As in Fig. 1, except that the noise was broadband, instead of lowpass filtered at 3 kHz, and that the roving of the N followed a different procedure (see text for details). As in Fig. 1, error bars in this and following figures represent ±1 standard error of the mean. In this and all following figures, the dashed line shows predicted thresholds based on spectral rather than F0 information. These predictions differ slightly from those shown in Fig. 1 due to the use of a different lower-harmonic-number randomization rule.
Using the same analysis that was used for experiment 1, the cutoff F0DL (i.e., the geometric mean of the lowest and highest group F0DLs) was 2.37%, and the highest value of N with an F0DL below that cutoff in the COS condition was 7. For this value of N, a paired t-test revealed a significant effect of phase [paired t(6)=2.92, one-tailed p=0.014]. Thus, consistent with the results from experiment 1, conditions existed in which F0DLs were low but a phase effect was observed. The similarity in the pattern of results between experiments 1 and 1a was supported by a mixed-model analysis of variance (ANOVA), with experiment as a between-subjects variable and N and phase as within-subject variables.1 The ANOVA revealed a significant main effect of experiment [F(1,9)=8.44, p=0.017], in line with F0DLs being somewhat higher in experiment 1a, but no interactions of the other variables (N and phase) with experiment (p>0.1 in all cases).
EXPERIMENT 2: REDUCING THE AUDIBILITY OF DISTORTION PRODUCTS WITH BROADBAND NOISE
Rationale
Both experiments 1 and 1a were successful in replicating the basic results of Moore et al. (2006a), in particular the finding that low F0DLs, implying TFS processing, were found in conjunction with phase dependencies, implying unresolved harmonics, at intermediate values of N. However, as discussed in Sec. 1, the background noise level was not sufficient to rule out the audibility of distortion products, the amplitudes of which may have varied with the phase relationships and may have influenced the results. This possibility was tested here by raising the level of the background noise to 50 dB SPL∕ERBN, which led to the individual components of the complex being between 10 and 15 dB above their masked thresholds.
Methods
The stimuli and procedure were the same as in experiment 1a, with the exception that the level of the background noise was increased by 20 dB. The roving paradigm was the same as that used in experiment 1a, so that at small values of ΔF0 listeners would obtain only 50% correct by basing their judgments on the frequency of the lowest harmonic present, rather than on the F0. Nine normal-hearing listeners (aged 18–33) took part in this experiment. Seven of them also participated in either experiment 1 or experiment 1a, or both. The experiments were not run systematically in the order in which they are described in this article. In fact, those listeners who took part in both experiment 2 and experiment 1 or 1a had completed experiment 2 first.
Results and discussion
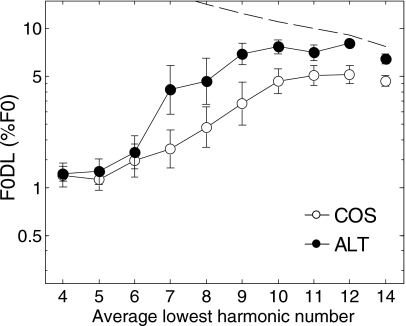
The mean F0DLs across the nine listeners are plotted in Fig. 3. Again, filled symbols represent thresholds for ALT phase, and open symbols represent thresholds for COS phase. The dashed line represents predictions based solely on the frequency of the lowest harmonic, as described in experiment 1a. Many trends in the data are similar to those observed in experiments 1 and 1a. In particular, F0DLs are low at low values of N and increase at higher values of N, and differences between COS and ALT conditions only emerge at higher values of N. However, some differences between these and the earlier results are also apparent. Most importantly, for our purposes, is the apparent lack of a phase effect at values of N for which F0DLs were low. Using the same analysis that was used for experiment 1, the cutoff F0DL (i.e., the geometric mean of the lowest and highest group F0DLs) was 3.40%, and the highest value of N with an F0DL below that cutoff in the COS condition was 6. In contrast to experiments 1 and 1a, no significant phase effect was found for this value of N [paired t(8)=0.219, one-tailed p=0.416].
Figure 3.
As in Fig. 2, except that the level of the background noise was 20 dB higher, which should have been sufficient to mask distortion products.
This pattern is not consistent with the results of Moore et al. (2006a), as replicated in experiments 1 and 1a, but it is consistent with the earlier studies of Houtsma and Smurzynski (1990) and Bernstein and Oxenham (2005, 2006a). It seems that increasing the level of the noise to ensure that distortion products were masked was sufficient to eliminate the phase effects when F0DLs were small. The results therefore suggest that the phase effects found by Moore et al. (2006a) in conjunction with small F0DLs may have been produced by distortion products, rather than by the coding of F0 via the TFS of unresolved harmonics.
At least one puzzle remains. In the studies of Houtsma and Smurzynski (1990) and Bernstein and Oxenham (2003), the transition between good and poor performance occurred for N values between about 9 and 12, whereas in the present study the transition occurs between N values of 6 and 7. One possible reason is that the present study used only three harmonics, whereas the earlier studies used 12 or 13 consecutive harmonics. At face value, the larger number of harmonics does not provide a very satisfactory explanation if (as often assumed) it is the lowest harmonics present that primarily determine performance. On the other hand, the larger number of harmonics may provide more spectral (and timbral) stability, making the rove of the lowest harmonic less perceptually distracting. Another possibility relates to the range of F0s tested. In the present experiment, when N=6, the nominal F0 of the complex was about 286 Hz. This is higher than the F0s used by either of the earlier studies. In fact, a more recent study by Oxenham and Keebler (2007) found that even when 12 harmonics were present, the transition from good to poor performance occurred for values of N between 9 and 12 only when the F0 was either 100 or 200 Hz; for F0s of 300 Hz or higher, the transition occurred for values of N between 6 and 9, more in line with the current results. Thus, it may be that the apparent discrepancy between the present results and those of earlier studies is related more to the underlying F0 than to the number of harmonics presented. This conjecture should be explicitly tested by studying the effects of the number of harmonics present on the transition point between low and high F0DLs.
EXPERIMENT 3: REDUCING THE AUDIBILITY OF DISTORTION PRODUCTS WITH LOWPASS NOISE
Rationale
The results of experiment 2 showed that the effect of phase on F0DLs only became apparent when F0DLs were poor, consistent with the idea that unresolved harmonics are coded by the temporal envelope and not TFS. It was suggested that the effect of the background noise was to mask distortion products. Another possibility is that the higher noise level used in experiment 2 interfered with the ability of listeners to use the TFS cues, via some form of direct masking of the stimulus components, rather than the distortion products. The aim of the present experiment was to test this hypothesis by using a lowpass-filtered noise with a cutoff frequency below the frequency of the lowest component present. The predictions were as follows: if the effect of the noise was to interfere with TFS processing, then reducing the on-frequency noise by lowpass filtering should result in an improvement in performance and a restoration of the phase effects observed by Moore et al. (2006a); on the other hand, if the main effect of the noise was to mask the distortion products, then lowpass filtering the noise should have little effect on the pattern of results, so long as the cutoff frequency is set such that the noise still masks the distortion products.
Methods
The stimuli and procedure were the same as those used in experiment 2, with the exception that the high-frequency cutoff of the background noise was varied from trial to trial and was set such that it was 0.5F0 Hz lower than the lowest component presented in the two intervals of each trial. In this way, the noise energy did not directly overlap with any of the stimulus frequency components, but the cutoff frequency was always higher than the nearest distortion product in the spectrally lower of the two complexes (corresponding to the 2f1-f2 distortion product, where f1 and f2 are the frequencies of the lower two components of the complex). Nine normal-hearing listeners participated in this experiment (aged between 18 and 22 yr); four of the subjects had also taken part in at least one of the previous experiments.
Results and discussion
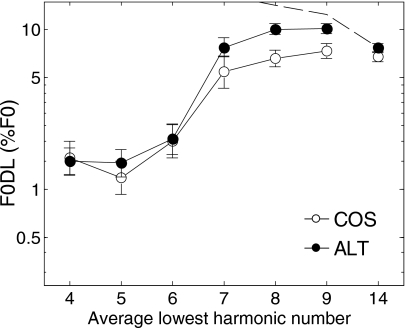
The mean results across the nine listeners are shown in Fig. 4. Thresholds were somewhat lower overall than in experiment 2, suggesting that removing the “on-frequency” background noise had some effect. However, the overall pattern of results was very similar to that found in experiment 2 (Fig. 3), with low F0DLs for values of N up to 6 and higher F0DLs beyond that.
Figure 4.
As in Fig. 3, except that the noise was lowpass filtered with a cutoff frequency below the stimulus components but above the frequency of the likely distortion products.
The search for low F0DLs in conjunction with significant phase effects was carried out in the same way as was done in experiments 1 and 2. The cutoff F0DL was found to be 2.42%, and the highest value of N for which the COS F0DL fell below the cutoff was again 6. At this value of N a paired t-test revealed no significant effect of phase [t(8)=1.63, one-tailed p=0.071].
Overall, neither experiment 2 nor experiment 3 provides support for the idea that phase effects can occur when F0DLs are small if potential distortion products are masked.
EXPERIMENT 4: F0DLS FOR COMPLEXES AT LOW SENSATION LEVELS
Rationale
This experiment provided a further test of whether the background noise was interfering with TFS processing, rather than just masking distortion products, by presenting the stimuli in quiet. To reduce the possibility that listeners could detect and use distortion products, the stimuli were presented at the relatively low sensation level of 20 dB above absolute threshold (20 dB SL). This low level should be sufficient to render distortion products inaudible but should nevertheless be sufficient for good pitch perception. For instance, Hoekstra (1979) showed that F0DLs for complex tones in noise approach an asymptotic value at around 20 dB above masked threshold.
Methods
The stimuli and procedure were the same as those used in experiment 2, with the following two differences: (1) there was no background noise present; (2) the three-tone complexes were presented at a level 20 dB above detection threshold in quiet. Detection thresholds in quiet were measured for three-component complexes, with the frequency of the middle component fixed at 2 kHz and the lowest harmonic number set to 6, 8, or 10 (corresponding to F0s of 285.71, 222.22, and 181.82 Hz). The overall level of the complex was varied adaptively, following a 3-down 1-up rule, which tracked thresholds corresponding to 79.4% correct. After thresholds had been estimated by taking the average of three adaptive runs for each subject for each of the three test conditions, the level of the test stimuli was set to 20 dB above the estimated threshold value for each subject individually. Five normal-hearing listeners participated in this experiment (aged between 18 and 22 yr). All of these subjects had also taken part in at least one of the previous experiments.
Results and discussion
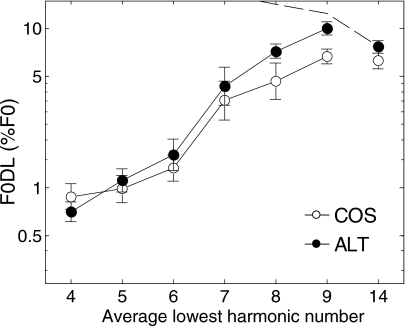
The results are shown in Fig. 5. Despite the lack of background noise and the lower absolute level, the pattern of results was very similar to that found in experiments 2 (Fig. 3) and 3 (Fig. 4). In this case, the cutoff F0DL was 3.92%, and the highest value of N for which the COS F0DL fell below the cutoff was again 6. At this value of N a paired t-test revealed no significant effect of phase [paired t(4)=0.49, one-tailed p=0.325]. Overall, the results from this experiment in the absence of background noise were consistent with those from experiments 2 and 3, suggesting that the lack of a phase effect when F0DLs are low cannot be ascribed to direct masking or interference by the noise. A parsimonious interpretation of the results from all five experiments so far is that distortion products can affect F0DLs when audible (experiments 1 and 1a); when distortion products are not audible, no effects of phase are observed in conditions producing low F0DLs.
Figure 5.
As in Fig. 3, except that no background noise was present and that the complexes were presented at 20 dB SL.
All three experiments in which distortion products were deemed inaudible (experiments 2–4) yielded very similar patterns of results. The trends observed between and within each of three experiments were further studied using a mixed-model ANOVA, with experiment as a between-subjects variable and N and phase as within-subject variables.2 The results of this analysis revealed a significant main effect of phase [F(1,20)=24.73, p<0.0005], a significant main effect of harmonic number [F(5.38,107.76)=123.48, p<0.0005], and a significant interaction between these two factors [F(4.51,90.24)=5.02,p=0.001]. Post hoc comparisons (paired t-tests) between COS and ALT thresholds pooled across all three experiments for each value of N showed a phase effect emerging at N=8 [t(22)=5.25, one-tailed p<0.005; for higher N’s: 4.20<t(22)<14.66, one-tailed p<0.005] but not below [for 4≤N≤7:−2.00<t(22)<2.01, one-tailed p≥0.2].3 This pattern of results is consistent with the hypothesis that when distortion products are inaudible, phase effects are only observed in conditions where F0DLs are poor and are likely to be determined by temporal envelope cues. All three experiments showed a significant phase effect emerging at N=8, rather than at N=7, even though F0DLs were already high for N=7 (see Figs. 345). This outcome may be related to how resolvability affects pitch and phase effects differently: for tones to be unresolved, at least two must interact, but for a phase effect to be observed between tones that are not in an octave relationship, at least three components must interact. This might account for why a phase effect emerged at a value of N that was 1 higher than the value of N for which F0DLs became poor.
EXPERIMENT 5: EFFECTS OF PHASE ON THE RELATIVE LEVEL OF DISTORTION PRODUCTS
Rationale
The results of the current study suggest that distortion products may play an important role in explaining the results of Moore et al. (2006a). However, all the evidence presented so far is indirect in that it is inferred that the primary effect of the broadband noise (experiment 2), lowpass noise (experiment 3), and low-level stimuli (experiment 4) was to render distortion products inaudible. To explain the phase effects observed by Moore et al. (2006a) (and replicated here in experiment 1) at lower values of N, it must be assumed not only that distortion products were audible but that they were more audible (or had a greater effect on F0DLs) when the components were in COS phase than when they were in ALT phase. The results of Pressnitzer and Patterson (2001), using multitone complexes, suggest that this may indeed occur under certain conditions. They measured the distortion produced by harmonics 15–25 of a 100-Hz F0, with a level of 54 dB SPL per component. Using a beat-suppression technique, these authors estimated that a tone at the F0 had to be presented at between about 40 and 44 dB SPL to match the level of the distortion product when the complex was in COS phase, but when the complex was in ALT phase the level of the matching tone was found to be less than 35 dB SPL in one subject and was unmeasurable in the other subject. Although the level of their components was comparable to ours, the number of components and the N used were not, making direct predictions for our situation difficult. The stimuli of Buunen et al. (1974) were closer to those used in the present study. They measured distortion products for a three-component complex with an F0 of 200 Hz, centered at 2000 Hz, corresponding to our N=9 condition. Their stimuli were presented at a sensation level of 40 dB, and the lowest component was presented at a level 10 dB below that of the upper two components to maximize the relative level of the distortion products. They found clearly audible distortion products at the frequencies corresponding to one and two harmonics below N. Using a method of cancellation, they also found that the relative phase of the center component strongly affected the level of distortion products, as well as affecting the pitch strength of the F0. However, the relationship between the complex’s phase and the level of the distortion products varied between the three subjects tested. Our final experiment attempted to estimate the relative levels of some distortion products in the presence of both the COS and ALT complexes. Our prediction was that the COS complex would produce higher-level distortion products than the ALT complex, thereby leading to a lower effective N in the COS than in the ALT case, even when the actual component frequencies were the same.
The technique used to provide an estimate of the relative levels of the distortion products involves presenting the three-tone complex along with an additional tone that was mistuned from the frequency of an expected distortion product by 4 Hz to produce an audible beating sensation with the distortion product, which should be maximal when the additional tone and the distortion product were at comparable effective levels. Listeners were asked to adjust the level of the additional tone to the level at which the beats were most prominent.
Methods
Subjects
Seven normal-hearing listeners participated in this experiment (ages ranged from 20 to 38). One of these listeners also took part in experiment 1.
Stimuli
Three-component complexes similar to those used in experiment 1 were used in this experiment. One difference was that the F0 of the complexes was fixed instead of roved across trials. The value of N was fixed at 8, and the F0 was 222.22 Hz, so that the frequency of the center harmonic was equal to 2000 Hz. The other stimulus difference with experiment 1 was that each complex lasted for 1150 ms, instead of 400 ms, to allow for multiple beat cycles. Each complex was accompanied by a “probe” pure tone with a frequency that was 4 Hz below the frequency of a potential distortion product. This probe tone was gated on 200 ms after the onset of the complex and off 200 ms before the offset of the complex. The total duration of the probe was therefore 750 ms (three cycles of the 4-Hz beat modulation), and it was gated on and off with 20-ms raised-cosine ramps. The distortion products tested were the three consecutive harmonic frequencies below the complex (2f1−f2,3f1−2f2,4f1−3f2), as well as the F0 itself (the difference tone; f2−f1), where f1 and f2 denote the frequencies of the lowest and center harmonics in the complex, respectively. The 4-Hz deviation between the frequency of the probe tone and the frequency of the targeted distortion product was chosen based on informal pilot tests, which revealed that the depth of beats at 4 Hz was relatively easy to judge. No background noise was used in this experiment.
Procedure
Listeners were instructed to adjust the level of the probe tone until they found the level at which the 4-Hz beating sensation was most salient. The level of the probe tone could be adjusted after each stimulus presentation by three pairs of buttons on the computer screen. The upper, middle, and lower pairs of buttons adjusted the test-tone level by steps of 6, 3, and 1 dB, respectively. Listeners were instructed to try a wide range of levels on each run and to bracket the point of maximum saliency, first using largest step sizes and then the smaller ones. At the beginning of a match, the level of the probe tone was drawn randomly from a uniform discrete range including values between −25 and +25 dB around 50.2 dB SPL in 5-dB steps. The level of the probe tone was not allowed to exceed the limits of this 50-dB range. Each listener produced six matches in each condition.
Results and discussion
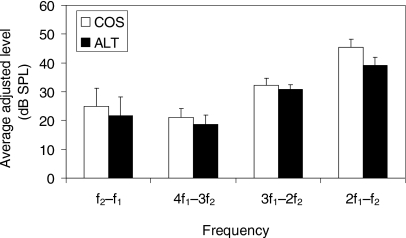
Beating was heard by subjects at all the test frequencies considered. The mean levels of the probe tones that were judged by subjects to produce the most salient beats are shown in Fig. 6. Overall, there was a small but significant trend for the level of the matching tone to be higher for the COS condition than for the ALT condition [F(1,6)=96.67, p<0.0005]. In the original experiment of Moore et al. (2006b), the background noise was set to 30 dB SPL∕ERBN, which would have resulted in masked thresholds of between 25 and 30 dB SPL. This suggests that only the 2f1−f2 distortion product would have been reliably above masked threshold in the noise; no other average effective distortion product level fell above 33 dB SPL. Interestingly, the most audible (2f1−f2) distortion product also showed the largest mean difference between probe-tone levels in the COS and ALT conditions of about 6 dB (paired t-test: t=4.29, df=6, p=0.005).
Figure 6.
Mean levels (in dB SPL) to which the matching probe tone was adjusted to produce the most salient beating sensation with the distortion products at different frequencies. Error bars represent ±1 standard error of the mean. See text for details of the different conditions.
The results suggest that at least the distortion product closest to the stimulus would have been audible in our experiment 1, which replicated that of Moore et al. (2006b). The higher level of the distortion product in the COS condition may have made it more salient and may therefore have lowered the effective value of N by 1 in the COS condition but not in the ALT condition. This in turn may have led to the effects of phase that were observed at intermediate values of N where the F0DLs were low.
GENERAL DISCUSSION
Experiments 1 and 1a replicated the findings of Moore et al. (2006a) that F0DLs with three-tone harmonic complexes could be small, suggesting the use of TFS cues, and yet still be dependent on the component phase relationships, suggesting that the components were unresolved. However, experiments 2–4 showed that the results were different when distortion products were rendered inaudible, either by increasing the background noise level (experiment 2 and 3) or decreasing the overall stimulus level (experiment 4). Under these conditions, phase effects only emerged once F0DLs were high, implying the use of temporal envelope cues. The results from experiment 5 provided more direct evidence that the cubic distortion product just below the primary components would have been audible in the Moore et al. (2006a) experiment and may have been lower in amplitude in the ALT-phase than in the COS-phase conditions. The differences between the ALT and COS conditions found in their experiment (and our experiment 1) at intermediate values of N may have been due to the differential audibility of distortion rather than to differences in the TFS representations.
Overall, the results from the present study (experiments 2–4) are consistent with earlier studies using more harmonics (Houtsma and Smurzynski, 1990; Bernstein and Oxenham, 2006b; a) in showing that no phase effect is observed for conditions that produce small F0DLs. Based on these results, some of the conclusions from Moore et al. (2006a) require re-examination. As outlined in Sec. 1, one rationale of the experiment of Moore et al. (2006a) was to distinguish between two interpretations of the earlier results of Moore and Moore (2003), involving the pitch of frequency-shifted harmonic complexes. Moore et al. (2006a) interpreted their finding of small F0DLs in conjunction with phase sensitivity as indicating that listeners had access to TFS within the waveform of unresolved harmonics. As phase sensitivity is not found when distortion products are rendered inaudible, the results of Moore et al. (2006a) can no longer be taken as evidence that listeners have access to TFS to code the F0 of unresolved harmonic tone complexes.
Another implication of the present results relates to studies of pitch perception and TFS processing in hearing-impaired listeners (e.g., Moore et al., 2006b; Hopkins and Moore, 2007). These studies have shown that hearing-impaired listeners often do not exhibit low F0DLs for low or intermediate values of N. If, as suggested by Moore et al. (2006a), normal-hearing listeners can use TFS information from unresolved harmonics to code F0, poorer performance in hearing-impaired listeners might be interpreted as implying that they have a selective deficit in processing TFS. Similar claims have been made with regard to hearing-impaired listeners’ ability to use TFS information in speech (e.g., Lorenzi et al., 2006; Hopkins et al., 2008). An alternative explanation is that the limited benefit of TFS information for hearing-impaired listeners relates to the well-known effect of broadened auditory filters, poorer frequency selectivity, and lower-amplitude (or absent) distortion products (Moore, 2007). For instance, Bernstein and Oxenham (2006b) found that the transition between good and poor F0DLs in hearing-impaired listeners corresponded well with other measures of frequency selectivity, suggesting that reduced frequency selectivity and fewer resolved harmonics may account for the poorer F0 discrimination associated with hearing impairment. Broader filters have been proposed as one reason for poorer TFS sensitivity in hearing-impaired listeners (Moore, 2008). However, given the lack of conclusive evidence that normal-hearing listeners use TFS to code F0 using unresolved harmonics, it may not be necessary to posit any deficits beyond frequency selectivity in order to explain the results found for hearing-impaired listeners in tests that have been designed so far to probe potential TFS deficits.
As mentioned in the discussion of experiment 2, the fact that the transition between good and poor F0DLs seems to occur when the average N is between 6 and 7 does not appear to be consistent with earlier studies, which found the transition to occur between N values of 9 and 12 (e.g., Houtsma and Smurzynski, 1990; Bernstein and Oxenham, 2003). Whether this is due to the number of harmonics in each complex or to the value of F0 remains to be determined. In either case, it presents a challenge to the view that the transition between good and poor F0DLs is intimately linked to auditory filter bandwidths. Such questions have been raised before, but primarily in conjunction with the lower limit of pitch perception (e.g., Krumbholz et al., 2000). This question leads to a more general note of caution regarding the definition of resolved and unresolved components. The present study used the rationale forwarded by Moore et al. (2006a) to distinguish between resolved and unresolved harmonics, as well as between temporal envelope and temporal fine structure. However, this approach should not be interpreted as implying that the distinction between resolved and unresolved harmonics, or between temporal envelope and fine structure, is always clear cut (Shackleton and Carlyon, 1994). For instance, it is possible that situations exist in which stimulus components may be sufficiently resolved for one purpose (such as estimating the frequencies of individual components) and yet sufficiently unresolved for another purpose (such as perceiving interactions between neighboring components). One example of such a situation is the perception of beats between two tones a semitone apart, where the individual frequencies can be heard, but where the interactions (beats) are also audible. Similarly, stimuli that are not spectrally resolved (in terms of producing large peaks in a spectral excitation pattern) may nevertheless be resolved via a temporal code that involves phase-locking to the component frequency (e.g., Sachs et al., 1983). In summary, it is unlikely that resolvability is a binary variable, and caution should be used in generalizing across different measures of resolvability.
ACKNOWLEDGMENTS
This work was supported by a grant from the National Institutes of Health (Grant No. R01 DC 05216). We thank Brian Moore, Daniel Pressnitzer, one anonymous reviewer, and the associate editor, Richard Freyman, for numerous helpful comments on previous versions of this paper.
Footnotes
For the purposes of analysis, the two subjects who participated in both experiments were treated as independent subjects in each experiment. However, the conclusions remained the same if the two subjects were excluded from experiment 1a to maintain completely independent samples (and more equal sample sizes) in each experiment.
The design of this analysis was complicated by the fact that some of the listeners took part in more than one experiment. As listeners who had lower thresholds on average (compared to other listeners) in one experiment also tended to have lower thresholds in another experiment, the data were not uncorrelated across experiments. In order to overcome this problem, we subtracted from each (log-transformed) threshold measured in a given listener the mean of the (log-transformed) thresholds measured in this same listener across all experiments and conditions in which the listener took part. This transformation left the effects of phase and harmonic number within each listener unchanged, but reduced across-experiment correlations in the data. Following this transformation, no significant main effect of experiment [F(2,20)=3.32, p=0.057] or interactions with experiment and other factors were observed [experiment×N interaction: F(10.78,107.76)=1.03, p=0.423; experiment×phase interaction: F(2,20)=0.03, p=0.970; three-way interaction: F(9.02,90.24)=0.439, p=0.911]. These conclusions remained unchanged when the ANOVA was performed directly on the measured thresholds, without first subtracting the mean from each listener’s data. Here and in the main text, non-integer degrees of freedom in the reported F statistics reflect the application of the Huynh–Feldt correction.
These p values include Bonferroni’s correction for multiple comparisons.
References
- Bernstein, J. G., and Oxenham, A. J. (2003). “Pitch discrimination of diotic and dichotic tone complexes: Harmonic resolvability or harmonic number?” J. Acoust. Soc. Am. 10.1121/1.1572146 113, 3323–3334. [DOI] [PubMed] [Google Scholar]
- Bernstein, J. G., and Oxenham, A. J. (2005). “An autocorrelation model with place dependence to account for the effect of harmonic number on fundamental frequency discrimination,” J. Acoust. Soc. Am. 10.1121/1.1904268 117, 3816–3831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein, J. G., and Oxenham, A. J. (2006a). “The relationship between frequency selectivity and pitch discrimination: Effects of stimulus level,” J. Acoust. Soc. Am. 10.1121/1.2372451 120, 3916–3928. [DOI] [PubMed] [Google Scholar]
- Bernstein, J. G., and Oxenham, A. J. (2006b). “The relationship between frequency selectivity and pitch discrimination: Sensorineural hearing loss,” J. Acoust. Soc. Am. 10.1121/1.2372452 120, 3929–3945. [DOI] [PubMed] [Google Scholar]
- Bernstein, J. G., and Oxenham, A. J. (2008). “Harmonic segregation through mistuning can improve fundamental frequency discrimination,” J. Acoust. Soc. Am. 10.1121/1.2956484 124, 1653–1667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buunen, T. J. F., Festen, J. M., Bilsen, F. A., and van den Brink, G. (1974). “Phase effects in a three-component signal,” J. Acoust. Soc. Am. 10.1121/1.1914501 55, 297–303. [DOI] [PubMed] [Google Scholar]
- Carlyon, R. P., and Shackleton, T. M. (1994). “Comparing the fundamental frequencies of resolved and unresolved harmonics: Evidence for two pitch mechanisms?” J. Acoust. Soc. Am. 10.1121/1.409971 95, 3541–3554. [DOI] [PubMed] [Google Scholar]
- de Boer, E. (1956). On the “Residue” in Hearing (University of Amsterdam, Amsterdam: ). [Google Scholar]
- Fleischer, H. v. (1976). “Über die Wahrnehmbarkeit von Phasenänderungen (On the perception of phase changes),” Acustica 35, 202–209. [Google Scholar]
- Glasberg, B. R., and Moore, B. C. J. (1990). “Derivation of auditory filter shapes from notched-noise data,” Hear. Res. 10.1016/0378-5955(90)90170-T 47, 103–138. [DOI] [PubMed] [Google Scholar]
- Goldstein, J. L. (1967). “Auditory nonlinearity,” J. Acoust. Soc. Am. 10.1121/1.1910396 41, 676–689. [DOI] [PubMed] [Google Scholar]
- Goldstein, J. L. (1973). “An optimum processor theory for the central formation of the pitch of complex tones,” J. Acoust. Soc. Am. 10.1121/1.1914448 54, 1496–1516. [DOI] [PubMed] [Google Scholar]
- Hoekstra, A. (1979). Frequency Discrimination and Frequency Analysis in Hearing (Institute of Audiology, University Hospital, Groningen, The Netherlands: ). [Google Scholar]
- Hopkins, K., and Moore, B. C. J. (2007). “Moderate cochlear hearing loss leads to a reduced ability to use temporal fine structure information,” J. Acoust. Soc. Am. 10.1121/1.2749457 122, 1055–1068. [DOI] [PubMed] [Google Scholar]
- Hopkins, K., Moore, B. C. J., and Stone, M. A. (2008). “Effects of moderate cochlear hearing loss on the ability to benefit from temporal fine structure information in speech,” J. Acoust. Soc. Am. 10.1121/1.2824018 123, 1140–1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houtsma, A. J. M., and Goldstein, J. L. (1972). “The central origin of the pitch of complex tones: Evidence from musical interval recognition,” J. Acoust. Soc. Am. 10.1121/1.1912873 51, 520–529. [DOI] [Google Scholar]
- Houtsma, A. J. M., and Smurzynski, J. (1990). “Pitch identification and discrimination for complex tones with many harmonics,” J. Acoust. Soc. Am. 10.1121/1.399297 87, 304–310. [DOI] [Google Scholar]
- Kohlrausch, A., and Sander, A. (1995). “Phase effects in masking related to dispersion in the inner ear. II. Masking period patterns of short targets,” J. Acoust. Soc. Am. 10.1121/1.413097 97, 1817–1829. [DOI] [PubMed] [Google Scholar]
- Krumbholz, K., Patterson, R. D., and Pressnitzer, D. (2000). “The lower limit of pitch as determined by rate discrimination,” J. Acoust. Soc. Am. 10.1121/1.1287843 108, 1170–1180. [DOI] [PubMed] [Google Scholar]
- Levitt, H. (1971). “Transformed up-down methods in psychoacoustics,” J. Acoust. Soc. Am. 10.1121/1.1912375 49, 467–477. [DOI] [PubMed] [Google Scholar]
- Licklider, J. C. R. (1954). “‘Periodicity’ pitch and ‘place’ pitch,” J. Acoust. Soc. Am. 26, 945. [Google Scholar]
- Lorenzi, C., Gilbert, G., Carn, H., Garnier, S., and Moore, B. C. J. (2006). “Speech perception problems of the hearing impaired reflect inability to use temporal fine structure,” Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0607364103 103, 18866–18869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meddis, R., and O’Mard, L. (1997). “A unitary model of pitch perception,” J. Acoust. Soc. Am. 10.1121/1.420088 102, 1811–1820. [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J. (1977). “Effects of relative phase of the components on the pitch of three-component complex tones,” in Psychophysics and Physiology of Hearing, edited by Evans E. F. and Wilson J. P. (Academic, London: ), pp. 349–358. [Google Scholar]
- Moore, B. C. J. (2007). Cochlear Hearing Loss: Physiological, Psychological and Technical Issues (Wiley, Chichester: ). [Google Scholar]
- Moore, B. C. J. (2008). “The role of temporal fine structure in normal and impaired hearing,” in Auditory Signal Processing in Hearing-Impaired Listeners: First International Symposium on Auditory and Audiological Research (ISAAR 2007), edited by Dau T., Buchholz J. M., Harte J. M., and Christiansen T. U. (Centertryk A∕S, Helsingor, Denmark: ), pp. 249–262.
- Moore, B. C. J., Glasberg, B. R., Flanagan, H. J., and Adams, J. (2006a). “Frequency discrimination of complex tones; assessing the role of component resolvability and temporal fine structure,” J. Acoust. Soc. Am. 10.1121/1.2139070 119, 480–490. [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J., Glasberg, B. R., and Hopkins, K. (2006b). “Frequency discrimination of complex tones by hearing-impaired subjects: Evidence for loss of ability to use temporal fine structure,” Hear. Res. 10.1016/j.heares.2006.08.007 222, 16–27. [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J., Huss, M., Vickers, D. A., Glasberg, B. R., and Alcantara, J. I. (2000). “A test for the diagnosis of dead regions in the cochlea,” Br. J. Audiol. 34, 205–224. [DOI] [PubMed] [Google Scholar]
- Moore, G. A., and Moore, B. C. J. (2003). “Perception of the low pitch of frequency-shifted complexes,” J. Acoust. Soc. Am. 10.1121/1.1536631 113, 977–985. [DOI] [PubMed] [Google Scholar]
- Oxenham, A. J., Bernstein, J. G. W., and Penagos, H. (2004). “Correct tonotopic representation is necessary for complex pitch perception,” Proc. Natl. Acad. Sci. U.S.A. 10.1073/pnas.0306958101 101, 1421–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oxenham, A. J., and Dau, T. (2001). “Towards a measure of auditory-filter phase response,” J. Acoust. Soc. Am. 10.1121/1.1414706 110, 3169–3178. [DOI] [PubMed] [Google Scholar]
- Oxenham, A. J., and Keebler, M. V. (2007). “Pitch perception: Frequency selectivity and temporal coding,” in Auditory Signal Processing in Hearing-Impaired Listeners (ISAAR 2007), edited by Dau T., Buchholz J. M., Harte J. M., and Christiansen T. U. (Centrik A/S, Helsingor, Denmark: ), pp. 273–279. [Google Scholar]
- Plack, C. J., Oxenham, A. J., Popper, A. N., and Fay, R., eds. (2005). Pitch: Neural Coding and Perception (Springer Verlag, New York. [Google Scholar]
- Pressnitzer, D., and Patterson, R. D. (2001). “Distortion products and the pitch of harmonic complex tones,” in Physiological and Psychophysical Bases of Auditory Function, edited by Breebaart J., Houtsma A. J. M., Kohlrausch A., Prijs V. F., and Schoonhoven R. (Shaker, Maastricht: ), pp. 97–103. [Google Scholar]
- Sachs, M. B., Voigt, H. F., and Young, E. D. (1983). “Auditory nerve representation of vowels in background noise,” J. Neurophysiol. 50, 27–45. [DOI] [PubMed] [Google Scholar]
- Schouten, J. F. (1940). “The residue and the mechanism of hearing,” Proc. K. Ned. Akad. Wet. 43, 991–999. [Google Scholar]
- Schouten, J. F., Ritsma, R. J., and Cardozo, B. L. (1962). “Pitch of the residue,” J. Acoust. Soc. Am. 10.1121/1.1918360 34, 1418–1424. [DOI] [Google Scholar]
- Schroeder, M. R. (1970). “Synthesis of low peak-factor signals and binary sequences with low autocorrelation,” IEEE Trans. Inf. Theory 10.1109/TIT.1970.1054411 16, 85–89. [DOI] [Google Scholar]
- Shackleton, T. M., and Carlyon, R. P. (1994). “The role of resolved and unresolved harmonics in pitch perception and frequency modulation discrimination,” J. Acoust. Soc. Am. 10.1121/1.409970 95, 3529–3540. [DOI] [PubMed] [Google Scholar]
- Shamma, S., and Klein, D. (2000). “The case of the missing pitch templates: How harmonic templates emerge in the early auditory system,” J. Acoust. Soc. Am. 10.1121/1.428649 107, 2631–2644. [DOI] [PubMed] [Google Scholar]
- Smoorenburg, G. F. (1972a). “Audibility region of combination tones,” J. Acoust. Soc. Am. 10.1121/1.1913151 52, 603–614. [DOI] [Google Scholar]
- Smoorenburg, G. F. (1972b). “Combination tones and their origin,” J. Acoust. Soc. Am. 10.1121/1.1913152 52, 615–632. [DOI] [Google Scholar]
- Terhardt, E. (1974). “Pitch, consonance, and harmony,” J. Acoust. Soc. Am. 10.1121/1.1914648 55, 1061–1069. [DOI] [PubMed] [Google Scholar]
- Wightman, F. L. (1973). “The pattern-transformation model of pitch,” J. Acoust. Soc. Am. 10.1121/1.1913592 54, 407–416. [DOI] [PubMed] [Google Scholar]