Abstract
This study addressed how manipulating certain aspects of the envelopes of high-frequency stimuli affects sensitivity to envelope-based interaural temporal disparities (ITDs). Listener’s threshold ITDs were measured using an adaptive two-alternative paradigm employing “raised-sine” stimuli [John, M. S., et al. (2002). Ear Hear. 23, 106–117] which permit independent variation in their modulation frequency, modulation depth, and modulation exponent. Threshold ITDs were measured while manipulating modulation exponent for stimuli having modulation frequencies between 32 and 256 Hz. The results indicated that graded increases in the exponent led to graded decreases in envelope-based threshold ITDs. Threshold ITDs were also measured while parametrically varying modulation exponent and modulation depth. Overall, threshold ITDs decreased with increases in the modulation depth. Unexpectedly, increases in the exponent of the raised-sine led to especially large decreases in threshold ITD when the modulation depth was low. An interaural correlation-based model was generally able to capture changes in threshold ITD stemming from changes in the exponent, depth of modulation, and frequency of modulation of the raised-sine stimuli. The model (and several variations of it), however, could not account for the unexpected interaction between the value of raised-sine exponent and its modulation depth.
INTRODUCTION
In 1997, van de Par and Kohlrausch (1997) introduced a new class of high-frequency signals that they termed “transposed stimuli.” They created transposed stimuli in an effort to provide high-frequency auditory channels with envelope-based neural timing information that would mimic waveform-based neural timing information naturally available only in low-frequency channels. van de Par and Kohlrausch (1997) reported data showing that transposed stimuli enhanced high-frequency binaural processing in that they yielded NoSπ thresholds of detection that were comparable to the much lower thresholds of binaural detection routinely obtained at low center frequencies. Following that, Bernstein and Trahiotis specifically showed that transposed stimuli enhanced the processing of envelope-based interaural temporal disparities (ITDs) conveyed by high-frequency channels. They reported that transposed stimuli yielded smaller threshold ITDs (Bernstein and Trahiotis, 2002), larger extents of ITD-based laterality (Bernstein and Trahiotis, 2003), and substantial resistance to binaural interference effects produced by the addition of simultaneously presented, diotic low-frequency energy (Bernstein and Trahiotis, 2004, 2005). Furthermore, physiological studies have also revealed “enhanced” processing in that the neural timing information conveyed by the envelopes of high-frequency transposed stimuli can approximate that conveyed by the fine-structure of low-frequency waveforms (Griffin et al., 2005; Dreyer and Delgutte, 2006).
At this time, it remains an open question just which aspect(s) of the envelopes of any high-frequency stimuli, be they transposed or conventional (e.g., sinusoidally amplitude-modulated (SAM) tones, two-tone complexes, and bands of Gaussian noise), lead to efficient processing of ongoing ITDs. To begin to answer this question, we conducted the first of a series of studies employing “raised-sine” stimuli that were recently described by John et al. (2002) in their study of steady state auditory evoked potentials. The algorithm used to generate raised-sine stimuli allows one to vary independently the frequency of modulation, the depth of modulation, and the exponent of the raised-sine. (Varying the exponent affects the “peakedness” or “sharpness” of the envelope of a raised-sine waveform.) These are features that cannot be varied independently with conventional stimuli such as SAM tones, repeated Gaussian clicks (e.g., Buell and Hafter, 1988; Stecker and Hafter, 2002), or the transposed tones used in our previous studies. As will be shown in Sec. 1A, the use of raised-sine stimuli allows one to generate high-frequency signals having envelopes with temporal features that “fall in between” those of SAM tones and those of transposed stimuli while having spectral content restricted to a relatively narrow range. The purpose of this study was to determine how the discriminability of ongoing ITDs is affected by systematic and graded changes in the temporal features of such stimuli. To that end, two experiments were conducted. One focused on determining how varying the exponent of the raised-sine affects threshold ITDs for stimuli having frequencies of modulation ranging from 32 to 256 Hz. The second focused on determining how parametric changes in both the exponent and its depth of modulation affect threshold ITDs for a raised-sine stimulus. Together, the results of the experiments provide initial insights regarding how particular features of the temporal signatures of the envelopes of high-frequency stimuli and their interaction affect sensitivity to changes in ongoing ITDs.
Generating raised-sine stimuli
The generation of raised-sine stimuli entails raising a dc-shifted sine-wave to a power greater than or equal to 1.0 prior to multiplication with a carrier. The equation used to generate such stimuli is
| (1) |
where fc is the frequency of the carrier, fm is the frequency of the modulator, m is the modulation index, and n is the exponent denoting the power to which the dc-shifted modulator is raised.1
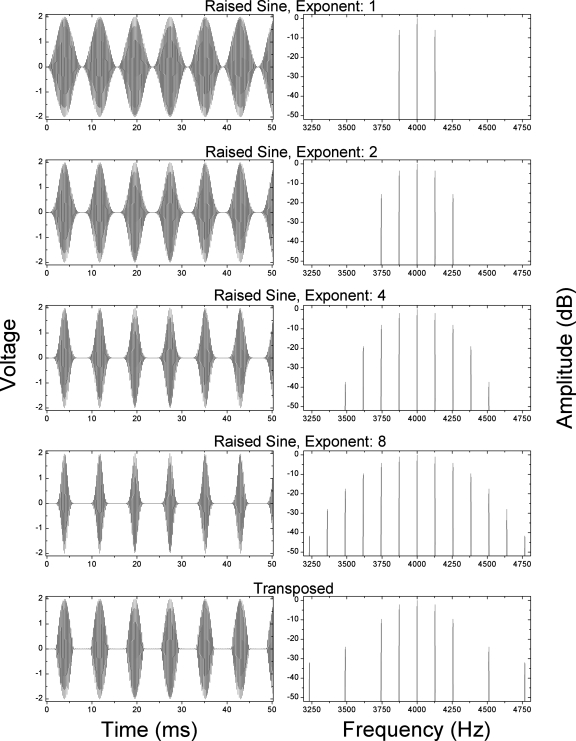
The left side of Fig. 1 depicts the time-waveforms for cases in which a 128 Hz modulating tone was raised using exponents of 1, 2, 4, or 8 prior to multiplication with a 4-kHz carrier. In all cases, m=1.0. The bottom row of the figure depicts a 128-Hz tone transposed to 4 kHz. Note that an exponent of 1.0 yields a conventional SAM waveform. Examination of the figure reveals that the peakedness or sharpness of the envelope increases directly with the value of the exponent to which the modulator is raised. Simultaneously, for these 100%-modulated signals, the “dead-time” or “off-time” between individual lobes of the envelope also increases with increasing values of the exponent. The right side of the figure displays the long-term spectrum of each stimulus. Note that increasing the value of the exponent also increases the number of “sidebands” and their spectral extent. It is important to note that, for each of the stimuli depicted, the vast majority of its energy falls within the approximately 500-Hz wide auditory filter centered at 4 kHz (see Moore, 1997).
Figure 1.
Left-hand panels: 50 ms epochs of the time-waveforms of 4-kHz-centered raised-sine stimuli modulated at 128 Hz and having exponents of 1, 2, 4, and 8 (rows 1–4, respectively) and of a 4-kHz-centered transposed stimulus modulated at the same rate (bottom row). Right-hand panels: Each row depicts the corresponding long-term power spectrum of the time-waveform shown immediately to its left.
EXPERIMENT I
Procedure
Threshold ITDs were measured for raised-sine stimuli having exponents of 1.0 (equivalent to a SAM tone), 1.5, 2.0, 4.0, and 8.0 and for transposed tones. All stimuli were centered at 4 kHz. For each of the six types of “targets,” thresholds were measured at rates of modulation ranging between 32 and 256 Hz. Targets were generated digitally using a sampling rate of 20 kHz (TDT AP2), were low-pass filtered at 8.5 kHz (TDT FLT2), and were presented via Etymotic ER-2 insert earphones at a level of 70 dB sound pressure level (SPL). The duration of the targets was 300 ms including 20-ms cos2 rise-decay ramps. A continuous diotic noise, low-passed at 1.3 kHz (spectrum level equivalent to 30 dB SPL) was presented to preclude listeners’ use of low-frequency distortion products arising from normal, non-linear peripheral auditory processing (e.g., Nuetzel and Hafter, 1976; Bernstein and Trahiotis, 1994).
Threshold ITDs were measured using a two-cue, two-alternative, forced choice, adaptive task. Each trial consisted of a warning interval (500 ms) and four 300-ms observation intervals separated by 400 ms. Each interval was marked visually by a computer monitor. Feedback was provided for approximately 400 ms after the listener responded. The stimuli in the first and fourth intervals were diotic. The listener’s task was to detect the presence of an ongoing ITD (left-ear leading) that was presented with equal a priori probability in either the second or the third interval. The remaining interval, like the first and fourth intervals, contained diotic stimuli. Ongoing ITDs were imposed by applying linear phase-shifts to the representation of the signals in the frequency domain and then gating the signals destined for the left and right ears coincidentally, after transformation to the time-domain. The starting phases of the envelopes and carriers of the targets were chosen randomly for each observation interval both within and across trials. The ITD for a particular trial was determined adaptively in order to estimate 70.7% correct (Levitt, 1971). The initial step-size for the adaptive track corresponded to a factor of 1.584 (equivalent to a 2-dB change of ITD) and was reduced to a factor of 1.122 (equivalent to a 0.5-dB change of ITD) after two reversals. A run was terminated after 12 reversals and threshold was defined as the geometric mean of the ITD across the last 10 reversals.
Four normal-hearing adults served as listeners. Particular stimulus combinations were chosen pseudo-randomly and three consecutive estimates of threshold were obtained for each of the 24 stimulus combinations (six types of target×four frequencies of modulation) before moving on to the next one. Then, three more thresholds were obtained by re-visiting the same stimulus conditions in reverse order. The entire procedure was repeated, yielding 12 estimates of threshold for each stimulus condition. The final values of threshold for each listener and stimulus condition were obtained by computing the median of the 12 estimates.
Results and discussion
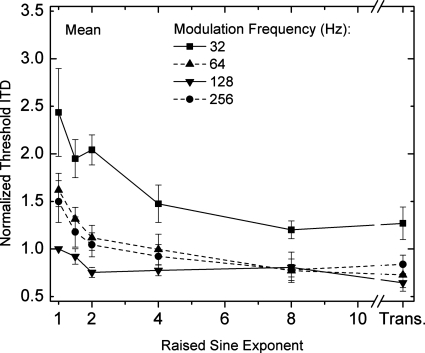
Figure 2 displays the mean “normalized” threshold ITDs, calculated across the four listeners as a function of the exponent of the raised-sine stimulus. For purposes of comparison, normalized threshold ITDs obtained with the transposed stimuli are plotted at the far right. The parameter of the plot is the frequency of modulation. Normalized thresholds are shown in order to remove the differences in absolute sensitivity to ITD that are commonly found across listeners with high-frequency, complex stimuli (e.g., Bernstein et al., 1998). The goal was to remove such inter-listener variability in order to reveal more precisely the changes in threshold ITDs that occur across conditions. The normalization was accomplished by dividing an individual listener’s threshold ITDs by that listener’s threshold ITD obtained with a SAM tone (raised-sine exponent equal to 1.0) having a frequency of modulation of 128 Hz. The individual threshold ITDs for that “reference” stimulus were 128, 271, 113, and 217 μs. The error bars in Fig. 2 represent ±1 standard error of the mean normalized thresholds.
Figure 2.
Mean normalized threshold ITDs, calculated across the four listeners as a function of the exponent of the raised-sine stimulus. Normalized threshold ITDs obtained with the transposed stimuli are plotted at the far right. The normalization was accomplished by dividing an individual listener’s threshold ITDs by that listener’s threshold ITD obtained with a SAM tone (raised-sine exponent equal to 1.0) having a frequency of modulation of 128 Hz. The individual threshold ITDs for that reference stimulus were 128, 271, 113, and 217 μs. The parameter of the plot is the frequency of modulation. Error bars represent ±1 standard error of the mean normalized thresholds.
Visual inspection of the patterning of the normalized thresholds reveals three general outcomes. First, for all four rates of modulation, threshold ITDs decreased with increases in the exponent of the raised-sine and approximated threshold ITDs obtained with transposed stimuli when the exponent was 8.0. Intuitively, this outcome appears to be consistent with the notion that, for a given rate of modulation, graded changes in the amounts of peakedness∕sharpness of the envelope of 100%-modulated stimuli lead to graded changes in sensitivity to ongoing envelope-based ITDs.2 Such changes appear to be largest for the rate of modulation of 32 Hz, where threshold ITDs are generally largest, and smallest for the rate of modulation of 128 Hz, where threshold ITDs are generally smallest. Second, threshold ITDs decreased with increases in rate of modulation from 32 to 128 Hz and then increased slightly when the rate of modulation was increased to 256 Hz. The latter trend was found previously with SAM and transposed tones by Bernstein and Trahiotis (2002). Third, the relatively small standard errors about each mean indicate that the relative changes in threshold ITD as a function of changes in either rate of modulation of the exponent of the raised-sine were homogeneous across listeners.
The data obtained with the raised-sine stimuli in Fig. 2 were subjected to a two-factor (four modulation frequencies ×five exponents), within-subjects analysis of variance (ANOVA). The error terms for the main effects and for the interactions were the interaction of the particular main effect (or the particular interaction) with the subject “factor” (Keppel, 1973). In addition to testing for significant effects, the proportions of variance accounted for (ω2) were determined for each significant main effect and interaction (Hays, 1973).
Consistent with visual inspection of the data, the main effect of frequency of modulation was significant (assuming an α of 0.05) [F(3,9)=22.2, p<0.001] and accounted for 43% of the variability of the data. This significant main effect reflects the fact that, on average, threshold ITDs were lower for higher modulation frequencies. The main effect of the raised-sine exponent was also significant [F(4,12)=52.0, p<0.001] and accounted for 22% of the variability in the data. This significant main effect reflects the fact that, on average, threshold ITDs decreased with increases in the value of the exponent. The interaction between frequency of modulation and value of raised-sine exponent was also significant [F(12,36)=2.5, p<0.02] and accounted for 6% of the variability in the data. This reflects the finding that the magnitudes of the relative changes in threshold ITD produced by changes in the raised-sine exponent depended on the frequency of modulation. Overall, the ANOVA reveals that 71% of the variability in the relative magnitudes of the threshold ITDs calculated across the four listeners is accounted for by the stimulus variables.
EXPERIMENT 2
The new data obtained in experiment 1 revealed that, in general, increasing the exponent of the raised-sine led to decreases in threshold ITD. It occurred to us that it would be fruitful to measure threshold ITDs while manipulating depth of modulation of raised-sine stimuli. The motivation for doing so follows directly from the fact that sensitivity to ITDs conveyed by the envelopes of high-frequency two-tone complexes and SAM tones has been shown to vary directly with their depths of modulation (e.g., McFadden and Pasanen, 1976; Nuetzel and Hafter, 1981). In addition, by varying, in a parametric fashion, both the exponent and the depth of modulation of the raised-sine stimuli, one could assess not only the separate influences of those variables on ITD-discrimination but also any interactive influences between them.
Procedure
Threshold ITDs were obtained for 4-kHz-centered raised-sine stimuli having exponents of 1.0, 1.5, and 8.0 at a rate of modulation of 128 Hz. For each of the three raised-sine exponents, thresholds were measured at indices of modulation (m) of 0.25, 0.5, 0.75, and 1.0. The 128-Hz rate of modulation was chosen because (as shown in Fig. 2) it yielded the smallest values of threshold ITD and, therefore, would provide the largest “dynamic range” for observing the expected increases in threshold ITD that would result from reductions in depth of modulation from 1.0. The general procedures were those described under experiment 1. For this experiment, however, thresholds were collected in pairs (rather than in triplets) and a total of 10 thresholds was collected for each listener and condition.3
Results and discussion
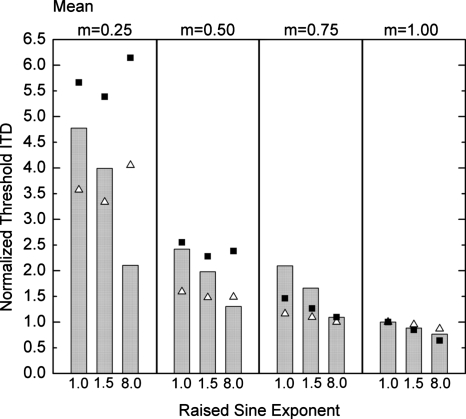
Figure 3 displays the mean normalized threshold ITDs, calculated across four listeners, three of whom participated in experiment 1. Once again, the normalization was accomplished by dividing an individual listener’s threshold ITDs by that listener’s threshold ITD obtained with a SAM tone (raised-sine exponent equal to 1.0) having a frequency of modulation of 128 Hz. The error bars represent +1 standard error of the mean. One of the four listeners was unable to consistently perform the task when the raised-sine exponent was 1.0 and the index of modulation was 0.25. When thresholds could be obtained from this listener and condition, they were in the region of 1 ms. For purposes of computing the normalized threshold ITDs, this listener’s threshold for that condition was coded as 1 ms. The time-waveforms corresponding to four of the stimuli are depicted atop their corresponding bars.
Figure 3.
Mean normalized threshold ITDs. Each of the four sections of the figure contains data obtained with a single depth of modulation and raised-sine exponents having values of 1.0, 1.5, or 8.0. Error bars represent +1 standard error of the mean. The time-waveforms corresponding to four of the stimuli are depicted atop their corresponding bars.
Each of the four sections of the figure contains data obtained with a single depth of modulation and raised-sine exponents having values of 1.0, 1.5, or 8.0. Consistent with the results of experiment 1, threshold ITDs decreased with increases in the exponent of the raised-sine. In addition, threshold ITDs increased as the index of modulation was decreased from 1.00 to 0.25. Finally, it appears that changes in the exponent of the raised-sine stimuli produced the largest changes in normalized threshold ITD when the index of modulation was 0.25. The data were subjected to the same type of two-factor (four indices of modulation ×three exponents), within-subjects ANOVA described earlier. In accord with visual inspection of Fig. 3, the main effect of raised-sine exponent was significant (again assuming an α of 0.05) [F(2,6)=74.4, p<0.001] and accounted for 17% of the variability of the data. The main effect of index of modulation was also significant [F(3,9)=28.6, p<0.001] and accounted for 62% of the variability in the data. Finally, the interaction between raised-sine exponent and index of modulation was also significant [F(6,18)=8.1, p<0.001] and accounted for 9% of the variability in the data. Overall, the ANOVA reveals that 86% of the variability in the relative magnitudes of the threshold ITDs calculated across the four listeners is accounted for by the stimulus variables.
The two significant main effects were not unexpected. First, the results of experiment 1 showed that threshold ITDs decreased with increases in the exponent of the raised-sine, and the new data in Fig. 3 indicate that general relation held across different depths of modulation. Second, several studies employing SAM tones have demonstrated that threshold ITDs increase with decreases in the index of modulation when ITDs are conveyed by the envelopes of high-frequency stimuli (e.g., McFadden and Pasanen, 1976; Nuetzel and Hafter, 1981; Bernstein and Trahiotis, 1996a). The data in Fig. 3 indicate that the same general relation also holds for raised-sine stimuli having exponents of 1.5 and 8.0.
The significant interaction between the two main effects reflects the fact that the degree to which increases of the exponent of the raised-sine led to decreases in normalized threshold ITDs depended on the index of modulation. Specifically, when the raised-sine exponent was increased from 1.0 to 8.0, normalized threshold ITDs decreased by 2.7, 1.1, 1.0, and 0.2 for indices of modulation of 0.25, 0.5, 0.75, and 1.00, respectively. This type of outcome, which could not have been discovered without varying parametrically the exponent and depth of modulation of the raised-sine stimuli, was not expected. That is, a priori, we had no reason to suspect that increasing the exponent of the raised-sine stimuli would enhance sensitivity to changes in ITD to a greater extent for stimuli having a low index of modulation as compared to stimuli having a high index of modulation.
QUANTITATIVE ACCOUNTS OF THE DATA
Predictions of the threshold ITDs in Fig. 2 were obtained via a cross-correlation-based model that incorporated an initial stage of gammatone-based bandpass filtering at 4 kHz (see Patterson et al., 1995), “envelope compression” (exponent=0.23), square-law rectification, and low-pass filtering at 425 Hz to capture the loss of neural synchrony to the fine-structure of the stimuli that occurs as the center frequency is increased (Weiss and Rose, 1988). As discussed below, the model also includes a second stage of low-pass filtering designed to attenuate spectral components of the envelope above 150 Hz. The reader is referred to Bernstein and Trahiotis (2002) for further details.4
In order to account for the data, it was assumed that the listener’s threshold ITDs reflect a constant change of the normalized interaural correlation (the value of the cross-correlation at “lag-zero”) from 1.0 (the interaural correlation of each diotic reference stimulus). This type of general model and strategy has provided accurate predictions regarding binaural detection and extents of ITD-based laterality for data obtained with a wide variety of complex, high-frequency stimuli (e.g., Bernstein and Trahiotis, 1996b, 2002, 2003; Bernstein et al., 1999).
In order to make the predictions, it was necessary to determine functions relating ITD to normalized interaural correlation. This was done separately for each stimulus used in the experiments (i.e., for each particular combination of frequency of modulation, depth of modulation, and exponent). Numerical measures were obtained by implementing the peripheral stages of the model in MATLAB© and then computing the normalized interaural correlation between the model’s “left” and “right” outputs for a wide range of ITDs. Then, using a least-squares criterion, polynomials were fitted to the paired values of normalized correlation and ITD. In order to arrive at predicted mean normalized threshold ITDs, we sought the criterion value of normalized interaural correlation that maximized the amount of variance accounted for between predicted and obtained values.
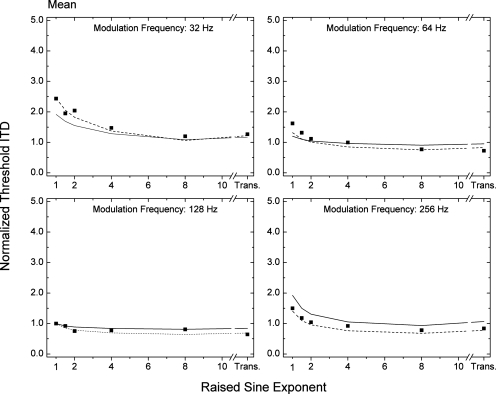
In order to facilitate visual comparisons between data and predictions, the data in Fig. 2 have been re-plotted in Fig. 4 in four separate panels, one panel for each of the four frequencies of modulation. The squares represent the obtained normalized threshold ITDs. The solid and dashed lines represent two sets of predictions that differ only in terms of the order of the 150-Hz low-pass filter applied to the processed stimuli. The predictions represented by the solid lines were generated using the same second-order (12 dB∕octave) Butterworth low-pass filter that was employed in our previous studies. Those predictions account for 71% of the variance in the data obtained across the four frequencies of modulation.5 Note, however, that there are systematic overestimates of normalized threshold ITD for the frequencies of modulation of 128 and 256 Hz. The more accurate predictions represented by the dashed lines were generated using a first-order (6 dB∕octave) Butterworth low-pass filter like the one originally used by Kohlrausch et al. (2000) and Ewert and Dau (2000) in order to account for temporal modulation transfer functions using sinusoidally amplitude-modulated stimuli. Those predictions account for 93% of the data. This indicates that the interaural correlation-based model captures quite precisely the values of normalized threshold ITDs measured as a function of the value of the exponent of raised-sine stimuli for the range of rates of modulation from 32 to 256 Hz.
Figure 4.
A re-plotting of the normalized threshold ITDs from Fig. 2 (squares). Each panel contains the data obtained with one of the four frequencies of modulation. The solid lines represent predictions obtained from an interaural correlation-based model incorporating a final stage of second-order (12 dB∕octave) low-pass filtering at 150 Hz. The dashed lines represent predictions obtained from the same model but with a final stage of first-order (6 dB∕octave) low-pass filtering at 150 Hz.
The choice of a second-order low-pass filter was originally made by Bernstein and Trahiotis (2002) while attempting to fit threshold ITDs obtained at center frequencies of 4, 6, and 10 kHz with both SAM and transposed tones. Employing a second-order filter provided a better fit than did a first-order filter when the data obtained at all three center frequencies were fitted simultaneously. When the data obtained at the three center frequencies were considered separately, however, predictions made using the first-order filter accounted for 86% of the variance in the data at 4 kHz, while the use of a second-order filter accounted for 83% of the variance. Therefore, it appears that it is neither ad hoc nor unreasonable to use a first-order, 150-Hz low-pass filter to account better for threshold ITDs obtained with raised-sine stimuli centered at 4 kHz.
Figure 5 contains the normalized threshold ITDs re-plotted from Fig. 3 along with two sets of predictions. One set, represented by the closed squares, was calculated via the model using a first-order low-pass filter and the same criterion change in interaural correlation (0.0005) that provided the best-fitting (dashed-line) predictions shown in Fig. 4. Those predictions lead to three important generalizations. First, when the index of modulation is 1.0, the model captures very accurately the changes in normalized threshold ITD that occur when changing the exponent of the raised-sine stimulus from 1.0 to 1.5 to 8.0. The predictions account for 73% of the variance across those three normalized threshold ITDs. It is important to note that the three thresholds shown in Fig. 5 for m=1.0 are replications of normalized threshold ITDs included in Fig. 4. The excellent fit to both sets of measures attests to both the consistency of the behavioral thresholds and to the accuracy of the model.
Figure 5.
Normalized threshold ITDs re-plotted from Fig. 3 (bars) along with two sets of predictions (symbols). The predictions were generated via the interaural correlation-based model using a final stage of first-order low-pass filtering at 150 Hz. Predictions represented by the closed squares were calculated using same criterion change in interaural correlation that provided the best-fitting (dashed-line) predictions shown in Fig. 4. Predictions represented by the open triangles were calculated using the criterion correlation that yielded the model’s best fit to those thresholds.
Second, considering only the SAM stimuli (raised-sine exponent of 1.0, left-most bar in each section of Fig. 5), the model captures fairly well the increases in threshold ITD that occur as the index of modulation is reduced from 1.0 to 0.25. The model accounts for 79% of the variance across those four measures. This is logically consistent with the analysis of Bernstein and Trahiotis (1996a). They showed that a quantitative account based on normalized interaural correlation could account for the threshold ITDs, taken as a function of the depth of modulation, for high-frequency SAM tones (Nuetzel and Hafter, 1981) and high-frequency two-tone complexes (McFadden and Pasanen, 1976).
Third, and perhaps most important for our purposes, is the fact that the model fails to capture the monotonic decrease in thresholds with increases in the exponent of the raised-sine found at indices of modulation of 0.25 and 0.5. In fact, calculation of the variance accounted for yielded a negative value, indicating that the mean of all of the data provided better predictions than did the model. This failure results mostly because, at those two indices, the model appears consistently to overestimate the normalized threshold ITDs obtained with raised-sine stimuli having an exponent of 8.0.
In order to determine whether this “failure” of the model results from the use of the criterion correlation that best described the data in Fig. 4, new predictions were made for all of the data in Fig. 5 using the criterion correlation that yielded the model’s best fit to those thresholds. Those predictions are represented by the open triangles in Fig. 5. Quantitatively, they show an improvement in that the amount of variance in the data accounted for by using the model increased to 54%. This improvement notwithstanding, there are two reasons to evaluate those predictions as problematic. The first is that they also fail to capture the data and their trends at the lowest index of modulation. Accounting for those data was the primary motivation for generating these additional predictions. Second, the criterion change in correlation required to fit the data was an order of magnitude smaller than the criterion changes required to fit the data in Fig. 4 and the threshold ITDs obtained at a center frequency of 4 kHz by Bernstein and Trahiotis (2002).
Several analyses were conducted in attempts to understand why the model failed to predict threshold ITDs obtained with low indices of modulation and a high value of the raised-sine exponent. These included generating predictions after altering the form of the model in the following ways: (1) removing all stages designed to incorporate peripheral auditory processing and then considering only the envelopes calculated via the Hilbert transforms of the stimuli in each channel; (2) increasing the frequency of the low-pass filter designed to attenuate higher spectral components of the envelope of the stimuli; (3) combining the outputs of a series of gammatone filters surrounding the gammatone filter centered at 4 kHz; (4) replacing the gammatone filters by gammachirp filters (e.g., Irino and Patterson, 1997; Unoki et al., 2006; Irino and Patterson, 2006) and conducting analyses using either a single filter centered at 4 kHz or a series of them surrounding 4 kHz [as in (3)]; (5) incorporating values of “modulation gain” reported by Joris and Yin (1992) who measured how changes in the indices of modulation of SAM tones were reflected in indices of modulation of the responses of eighth-nerve units in the cat; (6) changing the type of rectification (linear half-wave vs square-law) and degree of compression (including none).
While none of these manipulations redressed the fundamental shortcomings of the model discussed above, the enterprise proved to be enlightening in one respect. The only way to capture even the trends in the data obtained with the lowest index of modulation was both to increase “operational bandwidth” while simultaneously increasing the cutoff frequency of the low-pass “envelope” filter to at least 200 Hz. This modest success, unfortunately, came at the expense of poorer predictions of normalized threshold ITDs obtained at the higher indices of modulation. Finally, we considered the possibility that the cutoff frequency of the envelope low-pass filter might somehow effectively increase with decreases in the index of modulation. This ad hoc notion was rejected because the behavioral data used by Kohlrausch et al. (2000) and Ewert and Dau (2000) to place the cutoff frequency of the low-pass filter at 150 Hz were obtained when listeners discriminated between stimuli having no modulation and stimuli having depths of modulations that were just large enough to be detected. That is, the very same 150 Hz low-pass filter that we have shown that enables accurate prediction of threshold ITDs for 100% modulated stimuli was, itself, derived from data obtained with stimuli having very low indices of modulation.
Prompted by a suggestion made by Dr. Wes Grantham, we investigated whether the failure of the model to account for the interaction could be redressed by considering the displacements and patterning of interaural correlation functions rather than only its value at lag-zero (i.e., the normalized interaural correlation). To do so, we evaluated changes in the “mean-to-sigma” properties along the delay axis of raised-sine stimuli having exponents of either 1.0 or 8.0. In order to evaluate whether this type of mean-to-sigma approach would account for the observed interaction, we determined the relative increase in the width (variance) of the peak of each function that resulted from decreasing depth of modulation from 1.0 to 0.25. We then compared those relative increases across the two stimuli, one having an exponent of 1.0, the other having an exponent of 8.0 and found them to be, for all practical purposes, identical. This suggests that, within the experiment, in order to overcome the reduction in depth of modulation, the same relative increase in interaural delay would be required to reach threshold for raised-sine stimuli having exponents of 1.0 (SAM) or 8.0. Consequently, the interaural correlation-based model fails to predict the interaction between the value of the exponent and the depth of modulation of raised-sine stimuli independent of whether one considers only activity at lag-zero (the normalized correlation) or mean-to-sigma displacements of the peak of the correlation function along the delay axis. At this time, we can offer no satisfactory way to either change or augment the general interaural correlation-based model in a manner that allows it to capture the interaction in the data between changes in index of modulation and raised-sine exponent.
SUMMARY AND CONCLUSIONS
The purpose of this study was to determine how the discriminability of ongoing ITDs is affected by systematic and graded changes in temporal features of such stimuli. To that end, two experiments were conducted. One focused on determining how varying the exponent of raised-sine stimuli affects threshold ITDs. In both experiments, the set of raised-sine stimuli included conventional SAM tones (i.e., raised-sine stimuli having an exponent of 1.0). Overall, the data indicate that graded increases in the exponent led to graded decreases in envelope-based threshold ITDs. The improvements were found to be largest for raised-sine stimuli having a rate of modulation of 32 Hz where thresholds were, overall, the highest. Second, threshold ITDs decreased with increases in rate of modulation from 32 to 128 Hz and then increased slightly when the rate of modulation was increased to 256 Hz. The latter trend was found previously with SAM and transposed tones by Bernstein and Trahiotis (2002).
The second experiment assessed how parametric changes in both the exponent of the raised-sine and changes in its depth of modulation affect threshold ITDs for raised-sine stimuli having a rate of modulation of 128 Hz. The results showed that threshold ITDs decrease with increases in the exponent of the raised-sine for depths of modulation ranging from 0.25 to 1.0. Second, as reported in previous studies concerning discriminability of envelope-based ITDs, threshold ITDs increased with decreases in the index of modulation. One unexpected finding was an interaction between the value of raised-sine exponent and its depth of modulation such that increasing the exponent of the raised-sine stimuli enhanced sensitivity to changes in ITD to a greater extent for stimuli having a low index of modulation than it did for stimuli having a high index of modulation.
Predictions of the data were generated from an interaural correlation-based model. The model was generally able to capture changes in threshold ITD stemming from changes in the exponent, depth of modulation, or frequency of modulation of raised-sine stimuli. The only aspect of the data for which satisfactory predictions of threshold ITD could not be made (even with a variety of major changes in the nature of the model) was the unexpected interaction between the value of raised-sine exponent and its depth of modulation. This failure of the model suggests to us that some, additional, unknown factor or strategy influences how efficiently listeners process envelope-based ITDs for such stimuli. We believe that this finding is potentially important especially because, for only those stimuli, the listeners’ sensitivity to envelope-based ITDs is remarkably greater than can be explained either by a generally successful model interaural correlation-based model or several of its variants.
ACKNOWLEDGMENTS
The authors thank Dr. Toshio Irino for his assistance in implementing the gammachirp filterbank. The authors also thank Dr. Richard Freyman, Dr. Wes Grantham, and one anonymous reviewer whose helpful and insightful comments on an earlier version of the manuscript resulted in an improved presentation. This research was supported by research Grant Nos. NIH DC-04147 and DC-04073 from the National Institute on Deafness and Other Communication Disorders, National Institutes of Health.
Footnotes
Equation 1 differs from the one published by John et al. (2002) in that we have corrected a typographical error concerning where their parentheses were placed. The corrected equation produces stimuli identical to the ones they used to illustrate the method.
This should not be taken to mean that we are suggesting that it is the peakedness∕sharpness of the envelopes of our stimuli, per se, that determines sensitivity to differences in ITD. It should be recognized that the relative peakedness∕sharpness of the envelopes of these 100%-modulated stimuli covaries with other characteristics of their temporal signatures, including: 1) the “dead-time” between individual lobes of the envelopes and 2) the slope of the transition from dead-time to the re-emergence of the envelope’s positive voltage. Analyses of normalized threshold ITDs plotted against measures of peakedness (defined as the “width” of an individual lobe at 50% or 80% of its peak value) or dead-time revealed that, while either variable could account for variations in those thresholds at a given rate of modulation, neither could account for them across rates of modulation. Said differently, neither similar values of peakedness∕sharpness nor similar values of dead-time led to similar threshold ITDs. In any case, one would not expect dead-time to be generally useful because that metric would not vary in a systematic fashion where depth of modulation also varied. This is so because decreasing the depth of modulation from 100% would eliminate any straightforwardly defined meaning of dead-time. As will be seen when the data from experiment 2 are discussed, graded decreases in depth of modulation lead to graded increases in threshold. It does not appear that this outcome can be straightforwardly captured by only considering either measures of peakedness∕sharpness or dead-time. Part of our ongoing program of research is directed toward discovering useful metrics of the temporal signatures of envelopes of high-frequency stimuli having predictive power that is robust against simultaneous changes in several relevant parameters of the stimuli.
These data were collected in the context of another, larger, set of experimental conditions for which no continuous 1.3-kHz low-pass noise was present. Subsequent to the collection of the data reported here, several “spot-checks” were conducted by repeating the measurements in the presence of continuous 1.3-kHz low-pass noise. The presence or absence of the low-pass noise produced no substantial or systematic affects on the measured thresholds. As will be seen when the data from experiment 2 are discussed, threshold ITDs for conditions that overlap with those measured in experiment 1 were essentially identical.
As discussed in detail by van de Par and Kohlrausch (1998) and by Bernstein et al. (1999), the characteristics of the compression observed in the response of the basilar membrane are appropriately modeled by applying compression to the time-varying magnitude (i.e., the envelope) of the stimulus. In accord with the procedures detailed by Bernstein et al. (1999), this was accomplished within the model employed here by compressing the Hilbert envelope of the stimulus subsequent to bandpass filtering. Note that after the compressed waveform was passed through the subsequent stages of the model (i.e., square-law rectification and low-pass filtering), the resulting envelope function was not equivalent to the compressed Hilbert envelope.
The formula used to compute the percentage of the variance for which our predicted values of threshold accounted was , where Oi and Pi represent individual observed and predicted values of threshold, respectively, and represents the mean of the observed values of threshold (e.g., Bernstein and Trahiotis, 1994).
References
- Bernstein, L. R., and Trahiotis, C. (1994). “Detection of interaural delay in high-frequency SAM tones, two-tone complexes, and bands of noise,” J. Acoust. Soc. Am. 10.1121/1.409973 95, 3561–3567. [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (1996a). “The normalized correlation: Accounting for binaural detection across center frequency,” J. Acoust. Soc. Am. 10.1121/1.417237 100, 3774–3784. [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (1996b). “The normalized correlation: Accounting for binaural detection across center frequency,” J. Acoust. Soc. Am. 10.1121/1.417237 100, 3774–3784. [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2002). “Enhancing sensitivity to interaural delays at high frequencies by using ‘transposed stimuli’,” J. Acoust. Soc. Am. 10.1121/1.1497620 112, 1026–1036. [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2003). “Enhancing interaural-delay-based extents of laterality at high frequencies by using ‘transposed stimuli’,” J. Acoust. Soc. Am. 10.1121/1.1570431 113, 3335–3347. [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2004). “The apparent immunity of high-frequency ‘transposed’ stimuli to low-frequency binaural interference,” J. Acoust. Soc. Am. 10.1121/1.1791892 116, 3062–3069. [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., and Trahiotis, C. (2005). “Measures of extents of laterality for high-frequency ‘transposed’ stimuli under conditions of binaural interference,” J. Acoust. Soc. Am. 10.1121/1.1984827 118, 1626–1635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein, L. R., Trahiotis, C., and Hyde, E. L. (1998). “Inter-individual differences in binaural detection of low-frequency or high-frequency tonal signals masked by narrow-band or broadband noise,” J. Acoust. Soc. Am. 10.1121/1.421378 103, 2069–2078. [DOI] [PubMed] [Google Scholar]
- Bernstein, L. R., van de Par, S., and Trahiotis, C. (1999). “The normalized correlation: Accounting for NoSπ thresholds obtained with Gaussian and ‘low-noise’ masking noise,” J. Acoust. Soc. Am. 10.1121/1.428051 106, 870–876. [DOI] [PubMed] [Google Scholar]
- Buell, T. N., and Hafter, E. R. (1988). “Discrimination of interaural differences of time in the envelopes of high-frequency signals: Integration times,” J. Acoust. Soc. Am. 10.1121/1.397050 84, 2063–2066. [DOI] [PubMed] [Google Scholar]
- Dreyer, A., and Delgutte, B. (2006). “Phase locking of auditory-nerve fibers to the envelopes of high-frequency sounds: Implications for sound localization,” J. Neurophysiol. 10.1152/jn.00326.2006 96, 2327–2341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewert, S. D., and Dau, T. (2000). “Characterizing frequency selectivity for envelope fluctuations,” J. Acoust. Soc. Am. 10.1121/1.1288665 108, 1181–1196. [DOI] [PubMed] [Google Scholar]
- Griffin, S. J., Bernstein, L. R., Ingham, N. J., and McAlpine, D. (2005). “Neural sensitivity to interaural envelope delays in the inferior colliculus of the guinea pig,” J. Neurophysiol. 10.1152/jn.00794.2004 93, 3463–3478. [DOI] [PubMed] [Google Scholar]
- Hays, W. L. (1973). Statistics for the Social Sciences (Holt, Rinehart, and Winston, New York: ). [Google Scholar]
- Irino, T., and Patterson, R. D. (1997). “A time-domain, level-dependent auditory filter: The gammachirp,” J. Acoust. Soc. Am. 10.1121/1.417975 101, 412–419. [DOI] [Google Scholar]
- Irino, T., and Patterson, R. D. (2006). “A dynamic compressive gammachirp auditory filterbank,” IEEE Trans. Audio, Speech, Lang. Process. 14, 2222–2232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- John, M. S., Dimitrijevic, A., and Picton, T. (2002). “Auditory steady-state responses to exponential modulation envelopes,” Ear Hear. 23, 106–117. [DOI] [PubMed] [Google Scholar]
- Joris, P. X., and Yin, T. C. (1992). “Responses to amplitude-modulated tones in the auditory nerve of the cat,” J. Acoust. Soc. Am. 10.1121/1.402757 91, 215–232. [DOI] [PubMed] [Google Scholar]
- Keppel, G. (1973). Design and Analysis: A Researchers Handbook (Prentice-Hall, Englewood Cliffs, NJ: ). [Google Scholar]
- Kohlrausch, A., Fassel, R., and Dau, T. (2000). “The influence of carrier level and frequency on modulation and beat-detection thresholds for sinusoidal carriers,” J. Acoust. Soc. Am. 10.1121/1.429605 108, 723–734. [DOI] [PubMed] [Google Scholar]
- Levitt, H. (1971). “Transformed up-down methods in psychoacoustics,” J. Acoust. Soc. Am. 10.1121/1.1912375 49, 467–477. [DOI] [PubMed] [Google Scholar]
- McFadden, D., and Pasanen, E. G. (1976). “Lateralization at high frequencies based on interaural time differences,” J. Acoust. Soc. Am. 10.1121/1.380913 59, 634–639. [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J. (1997). in “Frequency analysis and pitch perception,” Handbook of Acoustics, edited by Crocker M. (Wiley, New York: ), Vol. III, pp. 1447–1460. [Google Scholar]
- Nuetzel, J. M., and Hafter, E. R. (1976). “Lateralization of complex waveforms: Effects of fine-structure, amplitude, and duration,” J. Acoust. Soc. Am. 10.1121/1.381227 60, 1339–1346. [DOI] [PubMed] [Google Scholar]
- Nuetzel, J. M., and Hafter, E. R. (1981). “Discrimination of interaural delays in complex waveforms: Spectral effects,” J. Acoust. Soc. Am. 10.1121/1.385690 69, 1112–1118. [DOI] [Google Scholar]
- Patterson, R. D., Allerhand, M. H., and Giguere, C. (1995). “Time-domain modeling of peripheral auditory processing: A modular architecture and a software platform,” J. Acoust. Soc. Am. 10.1121/1.414456 98, 1890–1894. [DOI] [PubMed] [Google Scholar]
- Stecker, G. C., and Hafter, E. R. (2002). “Temporal weighting in sound localization,” J. Acoust. Soc. Am. 10.1121/1.1497366 112, 1046–1057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Unoki, M., Irino, T., Glasberg, B., Moore, B. C. J., and Patterson, R. D. (2006). “Comparison of the roex and gammachirp filters as representations of the auditory filter,” J. Acoust. Soc. Am. 10.1121/1.2228539 120, 1474–1492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van de Par, S., and Kohlrausch, A. (1997). “A new approach to comparing binaural masking level differences at low and high frequencies,” J. Acoust. Soc. Am. 10.1121/1.418151 101, 1671–1680. [DOI] [PubMed] [Google Scholar]
- van de Par, S., and Kohlrausch, A. (1998). “Diotic and dichotic detection using multiplied-noise maskers,” J. Acoust. Soc. Am. 10.1121/1.421356 103, 2100–2110. [DOI] [PubMed] [Google Scholar]
- Weiss, T. F., and Rose, C. (1988). “A comparison of synchronization filters in different auditory receptor organs,” Hear. Res. 10.1016/0378-5955(88)90030-5 33, 175–180. [DOI] [PubMed] [Google Scholar]