Abstract
Scatter correction is crucial to the quality of reconstructed images in x-ray cone-beam computed tomography (CBCT). Most of existing scatter correction methods assume smooth scatter distributions. The high-frequency scatter noise remains in the projection images even after a perfect scatter correction. In this paper, using a clinical CBCT system and a measurement-based scatter correction, the authors show that a scatter correction alone does not provide satisfactory image quality and the loss of the contrast-to-noise ratio (CNR) of the scatter corrected image may overwrite the benefit of scatter removal. To circumvent the problem and truly gain from scatter correction, an effective scatter noise suppression method must be in place. They analyze the noise properties in the projections after scatter correction and propose to use a penalized weighted least-squares (PWLS) algorithm to reduce the noise in the reconstructed images. Experimental results on an evaluation phantom (Catphan©600) show that the proposed algorithm further reduces the reconstruction error in a scatter corrected image from 10.6% to 1.7% and increases the CNR by a factor of 3.6. Significant image quality improvement is also shown in the results on an anthropomorphic phantom, in which the global noise level is reduced and the local streaking artifacts around bones are suppressed.
INTRODUCTION
In x-ray computed tomography (CT), scatter causes severe distortions and contrast loss in the reconstructed images.1, 2 Scatter magnitude increases as the x-ray illuminated volume size increases.3 In an x-ray system with a large area detector, such as a cone-beam CT (CBCT) system, the scatter-to-primary ratio (SPR) can be as high as 8 in certain areas of the projection images.4, 5
CBCT is being commonly used in many applications for its large volume coverage. However, the high SPR severely deteriorates the quality of CBCT image and hampers its clinical usage. Many scatter correction methods have been proposed in the literature, and research in this field is still very active.4, 6, 7, 8, 9 There are two major types of scatter removal techniques. The first type performs scatter suppression during the acquisition of projection data, based on the difference between the incident angles of primary photons and scatter photons. Typical examples include the antiscatter grid method and the air gap method.10, 11 Although instant scatter suppression is achieved using these methods, their efficacy is usually limited. Siewerdsen et al., for example, showed that an antiscatter grid was effective only in improving the contrast-to-noise ratio (CNR) of low resolution CT images.11 Kyriakou et al. also reported that if an antiscatter grid is used and the scatter is high, the imaging dose need to be increased significantly to compensate for the primary loss due to the insertion of the grid.12 An improved scatter correction capability has been demonstrated using the scatter correction methods in the second category, where the scatter is corrected using postprocessing techniques on the scatter contaminated projection images.9, 13, 14, 15 Due to the randomness of scattering events, however, these methods implicitly or explicitly assume smooth scatter distributions and tacitly ignore the existence of high-frequency scatter noise. The scatter noise is therefore left in the image after scatter correction, resulting a degradation of CNRs in the reconstructed images.16 So far, the noise due to scatter in the x-ray projection image is generally considered as a low-dose imaging problem, and little attention has been paid in the literature to reduce the noise due to scatter correction. As the scatter correction techniques become more successful, this issue is becoming increasingly important.
The purpose of this paper is to investigate the role of high-frequency noise in the CB projection image after scatter correction and to provide a practical solution to noise suppression in scatter corrected reconstructed images. We first study the noise property of the projection images after scatter correction according to Poisson statistics. A penalized weighted least-squares (PWLS) algorithm is then applied to effectively suppress the image noise.17 The algorithm is evaluated using phantom experiments on a clinical CBCT system.
METHOD
Noise in x-ray projections with and without scatter correction
There are two major types of noise in x-ray projection images. One is the image independent noise due to the electrical and roundoff error, which can be considered as Gaussian noise; the other is the image dependent noise due to the statistical fluctuation of the x-ray photons that exit an object, which can be considered as Poisson noise.18 We assume the noise of the first type is small and consider only the Poisson noise here.
Denote variables s and p as the detected scatter and primary signals with mean values S and P, respectively. s and p are Poisson distributed, i.e., s∼Poisson(S) and p∼Poisson(P). From the fact that the point spread function of the scatter is broad and smooth,19 we assume s is independent of p, and therefore, (s+p)∼Poisson(S+P). Denote ns and np as the statistical noises of the scatter and primary, respectively, and one obtains
| (1) |
Due to Poisson statistics,
| (2) |
Denoting I0 as the incident photon intensity and q as the line integral image without scatter correction, we have
| (3) |
The last step uses Taylor’s expansion at (S+P).
Since I0 is typically very large, the noise associated with log(I0) can be ignored. Assume (ns+np) is small and ignore the high order term, then the noise of q, nnc, and its variance are approximated as
| (4) |
| (5) |
When an effective scatter correction algorithm is applied, the scatter mean value S is removed, while the high-frequency noise ns is left in the corrected image. Similarly, the scatter corrected line integral image qc can be written as
| (6) |
The associated noise nc and its variance is approximated as
| (7) |
Therefore, the ratio of the variances of nc and nnc is
| (8) |
Equation 8 shows that the noise is magnified after a scatter correction is applied on the projection image. Since the noise-free scatter signal S is spatially much smoother than the noise-free primary signal P, the spatial distribution of SPR (S∕P) is typically nonuniform. In a projection image on a human chest, for example, the SPR value is very low around the object boundary (less than 0.2) and can be larger than 8 in areas of small primary signals (e.g., behind bones). As a result, the noise variance magnification across the projection image ranges from below 1.5 to more than 80. As will be shown in Sec. 3, the nonuniform noise magnification not only increases the noise level in the reconstructed image but also results in local streaking artifacts.
The noise suppression algorithm
Based on the noise property of the scatter corrected image as derived in Eq. 7, we modify and implement a previously developed penalized weighted least-squares (PWLS) method20 to suppress the image noise. The PWLS method is a statistics-based algorithm that aims to estimate the ideal linear integrals by minimizing the PWLS objective function. The PWLS objective function models the first and second moments of the projection data. Mathematically, the PWLS cost function is written as
| (9) |
The first term in Eq. 9 is a weighted least-squares criterion. The variable qc is the vector of the scatter corrected line integral data as shown in Eq. 6; the variable is the vector of noise suppressed line integral data to be estimated. The symbol T denotes the transpose operator. The matrix Σ is diagonal matrix and its ith element is the variance of qc at detector pixel i. From Eq. 7, we approximate the variance of qc based on the following equations:
| (10) |
| (11) |
where pm is the measured projection data before scatter correction and logarithm operation; se is the scatter estimate obtained from scatter correction algorithms. With the nonuniform weights included in the least-squares criterion, the data with lower signal-to-noise ratios (SNR) contribute less for estimation of the noise suppressed line integrals.
The second term in Eq. 9 is a smoothness penalty or a prior constraint, where β is the smoothing parameter which controls the degree of agreement between the estimated and the measured data. A quadratic function as used in the previous publications21 is adopted here,
| (12) |
where n represents four nearest neighbors around pixel i and win is the weight for neighbor n. To preserve the edge information, anisotropic weights are used as win. The weight of the neighbor is determined by the magnitude of difference between neighbors and the pixel of concern,
| (13) |
where δ is another user-defined parameter which controls the strength of edge preservation.
In our implementations, the parameter δ was chosen as such a value that 90% of the sinogram pixels in the projection images to be processed has a gradient magnitude smaller than δ.22 The cost function 9 is minimized efficiently using an iterative Gauss–Seidel updating strategy.21 If standard CBCT imaging parameters are used, the algorithm converges to an optimal solution typically after about 20 iterations. On a 3.0 GHz PC, the process takes about 3 s on each projection image.
Scatter estimation
In this work, we use a measurement-based method for scatter estimation. In each experiment, a lead strip was inserted between the x-ray source and the object, resulting in a horizontal strip shadow on the detector with a width of approximately 2 cm. Since the lead strip attenuates almost all the incident photons, the signal detected inside the strip shadow only contains scatter. Assuming that the scatter distributions with and without the insertion of the lead strip are approximately the same, we consider the measured scatter signals using a lead strip as the scatter signals in a conventional scan at the same location. To get rid of the noise in the measurement, the detected signals inside the 2 cm strip shadow were first averaged in the longitudinal direction and then smoothed laterally using a moving average filter. The resultant signal was used as the scatter estimate in a following conventional scan.
Evaluation
The proposed method is evaluated using experiments on a Varian Acuity CT simulator (Varian Medical Systems, Palo Alto, CA). This CBCT imaging system is commonly used in radiation therapy for verifying the patient geometry. A standard protocol as used in clinic was used in the experiments. The x-ray tube operated at 125 kVp voltage and 80 mA with the pulse width at each projection angle of 25 ms. Data of a 360° scan consist of about 680 projections with an angle interval of about 0.5°. The dimension of each acquired projection image was 397.3×298.0 mm2, containing 1024×768 pixels. The source-to-axis distance (SAD) was 1000 mm and the source-to-imager distance (SID) was 1500 mm. To increase the field of view (FOV), a half-fan mode was used, with the flat-panel detector shifted by approximately 160 mm.
Two phantoms were used in the experiments. The first was an evaluation phantom which consisted of a Catphan©600 phantom in the middle with a radius of 10 cm and an oval body annulus in the periphery to expand the phantom to an elliptical cylinder with a major axis of 38 cm and a minor axis of 30 cm. The uniform oval annulus is made of the same material as that of the CTP 486 uniformity test module inside the standard Catphan©600 phantom, and it has an estimated CT number of ∼15 Hounsfield Units (HU). Due to the increased volume size, scatter was high in the scan and the image quality was much worse than that when only the Catphan©600 phantom was imaged. No bow-tie filter was used in the experiments. The second phantom was an anthropomorphic chest phantom. A bow-tie filter as used in clinic was placed on in order to maintain a more uniform photon statistics across the FOV. The reconstructed images are presented in HU, i.e., with a CT number of −1000 HU for air and a CT number of 0 HU for water-equivalent materials.
Images are reconstructed using the standard FDK algorithm,23 without scatter correction and noise suppression, with scatter correction but without noise suppression, and with scatter correction and the proposed noise suppression using different β values. The same filters are used in all the reconstructions. To demonstrate the advantage of the proposed algorithm on noise suppression, two more reconstructions of the Catphan©600 phantom are carried out with the same scatter correction. For a fair comparison, the noise suppression parameters in these reconstructions are adjusted such that the corresponding modulation transfer functions (MTF) approximately match, indicating a similar spatial resolution performance. The first reconstruction uses a standard low-pass Hamming filter in the filtering step in the FDK algorithm to suppress the projection noise. The second reconstruction assumes zero scatter in the noise suppression step after the scatter correction and directly uses the previously developed PWLS algorithm for the noise suppression, i.e., assuming se=0 in Eq. 11. The tungsten carbide inside the Catphan©600 phantom with a diameter of 0.28 mm is used for the MTF measurements.
Side-by-side comparisons of reconstructed images are provided to illustrate the performance on noise reduction in the proposed algorithm as well as its effect on the image resolution. Difference images before and after noise suppression are also presented. In the quantitative analysis, besides image noise levels, image contrasts and CNRs in selected regions of interest (ROI) with relatively uniform reconstructed values are used. The image contrast is defined as
| (14) |
where μr is the mean reconstructed value inside the ROI and μb is the mean reconstructed value in the surrounding area. The CNR is defined as
| (15) |
where is the variance inside the ROI and is the variance in the surrounding area.
RESULTS
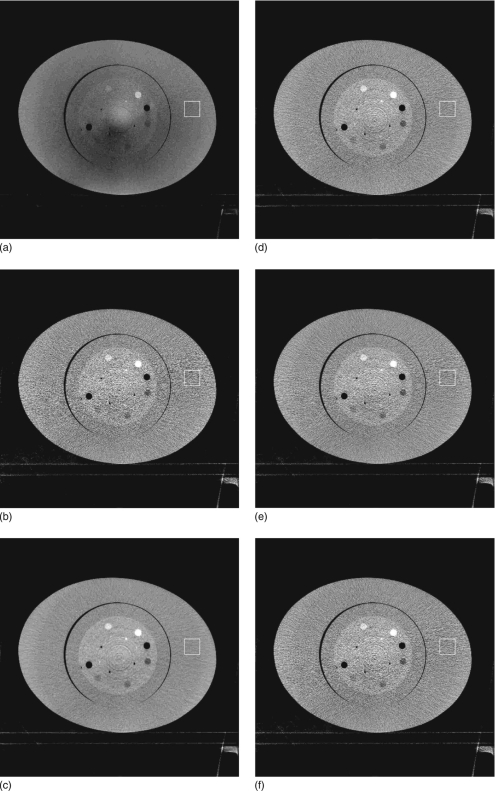
Figure 1 shows the reconstructed images of the Catphan©600 phantom with an oval annulus. The image distortion is obvious in Fig. 1a, where no scatter correction is applied. Most of the shading artifacts due to scatter are eliminated using the measurement-based scatter correction, as shown in Fig. 1b. However, the noise is magnified in the scatter corrected image and the image quality is degraded. Figures 1c, 1d are the images with noise suppressed using the proposed method. To investigate the performance of the algorithm on noise reduction and image resolution, two different β values are used. The first value is relatively large, and generates an image [Fig. 1c] with approximately the same noise level in the selected ROI as that in the image without scatter correction and noise suppression. The improvement of image quality is significant. A small β value is used in the second implementation of the noise suppression algorithm. This value achieves a less smoothed image as seen in Fig. 1d. Figure 1e is the result using a standard Hamming filter on the projection images for noise suppression. Figure 1f is the result using the previously developed PWLS algorithm. Equivalently, we assume se=0 in Eq. 11 of the proposed algorithm. The MTFs of the six reconstructions are measured and shown in Fig. 2. Note that we adjust the noise suppression parameters such that Figs. 1d, 1e, 1f have approximately the same MTF curves. With similar performances on image resolution, Hamming filtering and the previously developed PWLS method reduce the noise standard deviation in the selected ROI from 191 HU to approximately 150 HU, and the proposed algorithm is able to further reduce the noise standard deviation down to 108 HU. An improved image quality using the proposed algorithm is also evident in the comparison shown in Fig. 1. Figure 3 shows the difference images of the same slice as in Fig. 1 before and after noise suppression using different algorithms as described above.
Figure 1.
Reconstructed images of the Catphan©600 phantom with an oval body annulus. Display window: [−500 500] HU. The mean and standard deviation (std) inside the white squares in the images are measured as mean+std HU. (a) No scatter correction and no noise suppression; CT number in the selected ROI (white square): −117±51 HU. (b) Scatter correction without noise suppression; CT number in the ROI: 17±191 HU. (c) Scatter correction using the proposed noise suppression algorithm, β=0.0009; CT number in the ROI: 18±52 HU. (d) Scatter correction using the proposed noise suppression algorithm, β=0.0001; CT number in the ROI: 16±108 HU. (e) Scatter correction with noise suppression using the standard Hamming filter; CT number in the ROI: 18±152 HU. (f) Scatter correction using the proposed noise suppression algorithm, assuming se=0; CT number in the ROI: 18±151 HU.
Figure 2.
Measured MTFs using the Catphan©600 phantom. The algorithm parameters are tuned such that the last three curves as shown in the legend match.
Figure 3.
Difference images after applying noise suppression on Fig. 1b using different algorithms. Display window: [−150 150] HU. (a) Scatter correction using the proposed noise suppression algorithm, β=0.0009. [Fig. 1c–Fig. 1b]. (b) Scatter correction using the proposed noise suppression algorithm, β=0.0001. [Fig. 1d–Fig. 1b]. (c) Scatter correction with noise suppression using the standard Hamming filter [Fig. 1e–Fig. 1b]. (d) Scatter correction using the proposed noise suppression algorithm, assuming se=0. [Fig. 1f–Fig. 1b].
Figure 1f indicates that it is important to include the scatter estimate in the proposed noise suppression algorithm. Although scatter estimation∕correction algorithms are now becoming more and more successful, it is still challenging to achieve an accurate scatter estimate in many applications. Another reconstruction is carried out to study the sensitivity of the proposed algorithm performance with respect to the accuracy of the scatter estimation. When scatter correction is inaccurate, residual scatter artifacts are dominant as compared to the image noise. For a better illustration of the algorithm performance on noise suppression, we use an accurate scatter estimate for the scatter correction. In the noise suppression step using the proposed algorithm, we assume that scatter is uniform over the whole field and it equals a constant fraction of the smallest intensity in each projection. The algorithm parameters are tuned such that the corresponding MTF curve matches those of Figs. 1d, 1e, 1f. The reconstructed image and its difference image as compared to the result without noise suppression [Fig. 1b] are shown in Fig. 4. The inaccurate scatter estimation not only significantly compromises the noise suppression capability of the proposed algorithm [the noise standard deviation in the selected ROI of Fig. 4a is 183 HU] but also results in additional streaking artifacts which are evident in the difference image [Fig. 4b]. It is interesting to note that the proposed algorithm with a zero scatter estimate [Fig. 1f] performs better than that with a uniform scatter estimate [Fig. 4a]. The main reason is that the performance of the proposed algorithm is determined by the estimation accuracy of the spatial distribution of the image noise, instead of the total magnitude. Using a constant fraction of the smallest intensity in each projection as the scatter estimate gives a better estimate on the total image noise magnitude than using zero scatter estimates. However, it results in a spatial distribution of noise variance more different from the truth. More discussion on this issue will follow in a later section.
Figure 4.
Reconstruction of the Catphan©600 phantom using the proposed algorithm with an accurate scatter estimate in the scatter correction but an inaccurate scatter estimate in the noise suppression. (a) Noise suppression using the proposed algorithm, assuming scatter to be a constant fraction of the smallest intensity in each projection; CT number in the ROI: 15±183 HU. Display window: [−500 500] HU. (b) Difference image [Fig. 4a–Fig. 1b]. Display window: [−150 150] HU.
To further investigate the image resolution with respect to the β values, Fig. 5 shows the reconstructed slices with the resolution gauges. Note that a display window different from that in Fig. 1 is used for a better display of the line pairs. Zoom-in images of the line pairs from resolvable to irresolvable are provided at the lower-left corner of each image. Figure 6 shows 1D profiles that pass through the centers of the line pairs indicated by dashed white arcs in Fig. 5. With β values properly chosen, the proposed method is able to significantly reduce the noise of the reconstructed image with a negligible resolution loss.
Figure 5.
Reconstructed images of the Catphan©600 phantom with an oval body annulus. Display window: [−500 1700] HU. A different slice from Fig. 1 is shown to investigate the resolution performance. A zoom-in image of the line pairs inside the dashed rectangle is shown at the lower left corner in each image. The dashed arcs indicate the sets of line pairs, of which 1D profiles passing through the center are compared in Fig. 6. (a) No scatter correction and no noise suppression. (b) Scatter correction without noise suppression. (c) Scatter correction using the proposed noise suppression algorithm, β=0.0009. (d) Scatter correction using the proposed noise suppression algorithm, β=0.0001.
Figure 6.
Comparison of 1D profiles passing through the center of the line pairs indicated by the dashed arcs shown in Fig. 5.
For a quantitative analysis of the image quality, another scan was carried out on the Catphan©600 phantom without the oval body annulus. A narrow collimator was used to further reduce the scatter. The reconstructed image, as shown in Fig. 7, is considered as a benchmark image. Seven ROIs as indicated in Fig. 7 are used to calculate the contrasts, and the results are summarized in Table 1. The error relative to the contrasts of the benchmark image is provided in parentheses. The scatter correction greatly reduces the reconstruction errors. The average reconstruction error is reduced from 65.9% to 10.6% when the scatter correction is applied. Using the proposed noise suppression algorithm, the average error is further reduced to 5.8% when a small β is used and 1.7% when a large β is used. The comparison also shows that when the image resolution is matched, the proposed algorithm is superior to the standard method using a Hamming filter and the previously developed PWLS algorithm.
Figure 7.
Catphan image without the oval body annulus used as the benchmark. A narrow collimator was also used to further reduce the scatter artifacts. Seven ROIs are used in the quantitative analysis.
Table 1.
Contrast comparison of the selected ROIs (HU). The values in parentheses are the relative errors in percentage (absolute values) with respect to the benchmark image shown in Fig. 7.
| ROI | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| No scatter correction [Fig. 1a] | 83 (66.1%) | 302 (65.0%) | −421 (60.7%) | −98 (64.2%) |
| Scatter correction only [Fig. 1b] | 283 (15.7%) | 998 (13.3%) | −1131 (5.5%) | −279 (2.2%) |
| Proposed algorthum, β=0.0009 [Fig. 1c] | 261 (6.4%) | 873 (1.1%) | −1069 (0.2%) | −272 (0.5%) |
| Proposed algorithm, β=0.0001 [Fig. 1d] | 267 (9.3%) | 876 (1.5%) | −1067 (0.5%) | −270 (1.3%) |
| Using a Hamming filter [Fig. 1e] | 284 (15.9%) | 958 (11.0% | −1123 (4.8%) | −282 (3.0%) |
| Proposed algorithm, se=0 [Fig. 1f] | 281 (14.9%) | 956 (10.8%) | −1123 (4.8%) | −279 (1.9%) |
| Benchmark (Fig. 7) | 245 | 863 | −1072 | −273 |
| ROI | 5 | 6 | 7 | mean error |
| No scatter correction [Fig. 1a] | −61 (67.6%) | −37 (70.0%) | −334 (67.9%) | 65.9% |
| Scatter correction only [Fig. 1a] | −213 (12.6%) | −96 (22.8%) | −1058 (1.9%) | 10.6% |
| Proposed algorithm, β=0.0009 [Fig. 1c] | −190 (0.7%) | −121 (2.8%) | −1037 (0.1%) | 1.7% |
| Proposed algorithm, β=0.0001 [Fig. 1d] | −202 (6.7%) | −102 (18.3%) | −1010 (2.7%) | 5.8% |
| Using a Hmming filter [Fig. 1e] | −209 (10.4%) | −116 (6.9%) | −1075 (3.5%) | 7.9% |
| Proposed algorithm, se=0 [Fig. 1f] | −209 (10.8%) | −104 (16.9%) | −1065 (2.5%) | 8.9% |
| Benchmark (Fig. 7) | −189 | −125 | −1038 |
Table 2 shows the CNRs for different ROIs. After scatter correction, although the reconstruction error is greatly reduced and image contrast is increased, the average CNR decreases from 3.14 to 2.55 due to the image noise magnification. Using the proposed noise suppression algorithm, the average CNR increases to 4.10 for a small β and 9.16 for a large β.
Table 2.
CNR comparison of the selected ROIs.
| ROI | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Average |
|---|---|---|---|---|---|---|---|---|
| No scatter correction [Fig. 1a] | 1.37 | 4.57 | 6.57 | 1.68 | 1.28 | 0.74 | 5.78 | 3.14 |
| Scatter correction only [Fig. 1b] | 1.29 | 3.94 | 5.58 | 1.15 | 0.99 | 0.38 | 4.54 | 2.55 |
| Proposed algorithm, β=0.0009 [Fig. 1c] | 4.12 | 14.16 | 17.14 | 4.87 | 3.28 | 2.09 | 18.47 | 9.16 |
| Proposed algorithm, β=0.0001 [Fig. 1d] | 1.86 | 6.07 | 8.37 | 2.08 | 1.57 | 0.74 | 8.02 | 4.10 |
| Using a Hamming filter [Fig. 1e] | 1.60 | 4.90 | 6.86 | 1.42 | 1.21 | 0.57 | 5.81 | 3.19 |
| Proposed algorithm, se=0 [Fig. 1f] | 1.58 | 4.97 | 6.98 | 1.43 | 1.14 | 0.48 | 5.59 | 3.17 |
Figure 8 shows the reconstruction results of the anthropomorphic phantom. Note that a bowtie filter was used in the scan, which made the SPR more uniform. However, along the projection lines which pass through highly attenuating objects, such as bones, the SPR can still be very high (around 8) due to the extremely low primary signals. After the logarithm operation, the noise in those projection data boosts up after an effective scatter correction and results in streaking artifacts in the reconstruction, which is obvious in Fig. 8b. As shown in Figs. 8c, 8d, these artifacts are effectively suppressed using the proposed algorithm, and the image noise is also reduced. Figure 9 shows the difference images before and after the proposed noise suppression. Figure 10 compares 1D central vertical profiles of the images shown in Fig. 8.
Figure 8.
Reconstructed images of the anthropomorphic phantom. Display window: [−500 500] HU. The mean and standard deviation (std) inside the white squares in the images are measured as mean±std HU. (a) No scatter correction and no noise suppression; CT number in the selected ROI (white square): −291±43 HU. (b) Scatter correction without noise suppression; CT number in the selected ROI: 1±146 HU. (c) Scatter correction using the proposed noise suppression algorithm, β=0.001; CT number in the selected ROI: 17±46 HU. (d) Scatter correction using the proposed noise suppression algorithm, β=0.0001; CT number in the selected ROI: 18±89 HU.
Figure 9.
Difference images after applying noise suppression on Fig. 8b using different algorithm parameters. Display window: [−150 150] HU. (a) Scatter correction using the proposed noise suppression algorithm, β=0.001 [Fig. 8c– Fig. 8b]. (b) Scatter correction using the proposed noise suppression algorithm, β=0.0001. [Fig. 8d–Fig. 8b].
Figure 10.
Comparison of 1D central vertical profiles of the images shown in Fig. 8. The results using the proposed noise suppression algorithm with different β values have a relatively large difference only in the noisy areas.
DISCUSSION
Majority of the existing scatter correction methods use postprocessing techniques on the scatter contaminated projection images to improve the reconstruction accuracy. These methods only partially solve the problem caused by scatter and leave the high frequency components of the scatter signal intact, which often leads to degraded CNRs and image quality. In this work, both theoretical analysis and physical experiments show the effect of noise magnification in the reconstructed image due to scatter correction. Experiments were carried out on a clinical CBCT system with a commonly used protocol on phantoms with a human size. The results indicate that an effective scatter correction alone does not provide satisfactory images in CBCT because the gain from the scatter reduction is inevitably accompanied with overwhelming noise-related artifacts. One traditional method to deal with the noise problem is to increase the dose. However, the results on both the evaluation phantom and the anthropomorphic phantom show that the noise variance increases by a factor of more than 10 when scatter correction is applied. Since noise variance of a CT image is roughly inversely proportional to the total number of incident photons,24 the dose needs to be increased by a factor of more than 10 in order to make the noise level of the scatter corrected image comparable to that without scatter correction. This excessive dose increase is hardly acceptable in clinical practice.25
An improved PWLS algorithm is implemented in this work to suppress the noise in reconstructed images. The PWLS objective function models the first-order and second-order statistics of the measurements and it is equivalent to the penalized maximum likelihood (pML) or maximum a posteriori (MAP) criterion for the independent Gaussian distributed noise. Indeed, the noise of CT line integrals can be well approximated by Gaussian noise based on an experimental study.26 Therefore, the minimization of the PWLS objective function gives an optimal solution in a statistical sense. In the previous work, we have shown that the performance of the PWLS algorithm is better than those low-pass filters during image reconstruction or noise reduction filters based on local statistics of measurements.17 In this paper, both results on the evaluation phantom and the anthropomorphic phantom show effective reduction in global image noise as well as local streaking artifacts around high attenuating objects, such as bones. While a measurement-based scatter correction method is used to demonstrate the nature of the noise magnification problem incurring in the process of scatter removal, the developed noise suppression algorithm is expected to work effectively with other scatter correction algorithms as long as they can provide accurate scatter estimates.
One concern about a noise suppression algorithm is the possible resolution loss due to smoothing. We compare the proposed algorithm with the standard noise suppression method using a Hamming filter on the projection images. The comparison shows that when a similar image resolution is achieved, the proposed algorithm is superior on noise suppression. Our results also show that using a conservative smoothing strategy, significant noise reduction is still achievable with negligible resolution loss. The choice of parameter β in the PWLS algorithm is a tradeoff between reconstruction accuracy and resolution loss. In adaptive radiation therapy using CBCT, for example, the CBCT images are used for dose calculation and the CT number accuracy is more important than the image resolution. In such an application, an aggressive noise suppression strategy (a large β) should be used.
The proposed algorithm is based on the previously developed PWLS algorithm. To show the significance of including the scatter estimate se in the the noise estimation formula [Eq. 11], we compare the results using the proposed new algorithm and the previously developed PWLS algorithm. The latter is equivalent to the proposed algorithm with a zero scatter estimate. Similar to the comparison with the result using Hamming filtering, the proposed algorithm achieves lower noise when the same image resolution is maintained. Note that this degraded ability of noise suppression using the previously developed PWLS algorithm is not due to the underestimation of total noise magnitude by assuming zero scatter signals, since such an underestimation can always be compensated for using a larger β in the algorithm. The essence of the PWLS algorithms is to equalize the noise variance of different pixels by assigning different weights. The presence of scatter greatly changes the spatial distribution of the noise variance. Since the noise variance is proportional to (1+SPR)2 according to Eq. 10, and SPR spatially varies from values close to zero to those larger than 8, the true spatial distribution of the noise variance is quite different from that if the scatter is assumed to be zero. The misestimation of scatter results in incorrect estimation of noise spatial distribution, and the corresponding weighting in the PWLS algorithm is not able to equalize the noise variance of each projection pixel. The noise suppression ability is therefore significantly compromised. To illustrate the importance of accurate scatter estimation for a superior noise suppression performance, we also compare the result using the proposed algorithm with a uniform scatter estimate. Since uniform scatter estimation results in an estimate of SPR distribution much less accurate than that using a zero scatter estimate, the noise suppression performance is also much worse. Finally, we want to emphasize that the inaccuracy in scatter estimation compromises the performance of noise suppression using the proposed method, however, it does not make reconstruction less accurate than that without noise suppression. We can always tune the β value based on the tradeoff between the noise suppression capability and the image artifacts caused by inaccurate scatter estimation.
CONCLUSION
Scatter correction methods based on postprocessing fall short in eliminating the high-frequency scatter noise and are incapable of providing satisfactory CBCT image quality. Using a clinical CBCT system with conventional imaging settings, we have shown that after scatter correction, the noise variance in selected ROIs of the reconstructed image can be increased by a factor of more than 10. We argue that a scatter correction algorithm should be used together with a noise suppression algorithm to achieve a satisfactory image. A PWLS algorithm is proposed for the noise suppression. The phantom experiments indicate that the algorithm is able to further reduce the reconstruction error in a scatter corrected image without noise suppression from 10.6% to 1.7%, and the average CNR in selected ROIs is also increased by a factor of 3.6. The improvement in image quality is critical in many clinical applications of CBCT, such as accurate dose calculation and tumor target delineation in radiation therapy planning.
ACKNOWLEDGMENTS
This project was supported in part by grants from Department of Defense (W81XWH-08-1-0127), Komen Foundation (BCTR 0504071) and National Cancer Institute (1R01 CA98523 and CA104205). The authors also thank Triple Ring Technology for providing the anthropomorphic phantom.
References
- Glover G. H., “Compton scatter effects in CT reconstructions,” Med. Phys. 10.1118/1.595197 9, 860 (1982). [DOI] [PubMed] [Google Scholar]
- Joseph P. M. and Spital R. D., “The effects of scatter in x-ray computed tomography,” Med. Phys. 10.1118/1.595111 9, 464 (1982). [DOI] [PubMed] [Google Scholar]
- Fox T. R., Nisius D. T., Aradate H., and Saito Y., “Practical x-ray scatter measurements for volume CT detector design,” Proc. SPIE 10.1117/12.430948 4320, 808 (2001). [DOI] [Google Scholar]
- Zhu L., Bennett N. R., and Fahrig R., “Scatter correction method for x-ray CT using primary modulation: theory and preliminary results,” IEEE Trans. Med. Imaging 10.1109/TMI.2006.884636 25, 1573 (2006). [DOI] [PubMed] [Google Scholar]
- Ning R., Tang X., and Conover D., “X-ray scatter correction algorithm for cone beam CT imaging,” Med. Phys. 10.1118/1.1711475 31, 1195 (2004). [DOI] [PubMed] [Google Scholar]
- Siewerdsen J. H., Daly M. J., Bakhtiar B., Moseley D. J., Richard S., Keller H., and Jaffray D. A., “A simple, direct method for x-ray scatter estimation and correction in digital radiography and cone-beam CT,” Med. Phys. 10.1118/1.2148916 33, 187 (2006). [DOI] [PubMed] [Google Scholar]
- Jarry G., Graham S. A., Moseley D. J., Jaffray D. J., Siewerdsen J. H., and Verhaegen F., “Characterization of scattered radiation in kV CBCT images using Monte Carlo simulations,” Med. Phys. 10.1118/1.2358324 33, 4320 (2006). [DOI] [PubMed] [Google Scholar]
- Rinkel J., Gerfault L., Estve F., and Dinten J.-M., “A new method for x-ray scatter correction: first assessment on a cone-beam CT experimental setup,” Phys. Med. Biol. 10.1088/0031-9155/52/15/018 52, 4633 (2007). [DOI] [PubMed] [Google Scholar]
- Kyriakou Y., Riedel T., and Kalender W. A., “Combining deterministic and Monte Carlo calculations for fast estimation of scatter intensities in CT,” Phys. Med. Biol. 10.1088/0031-9155/51/18/008 51, 4567 (2006). [DOI] [PubMed] [Google Scholar]
- Persliden J. and Carlsson G. A., “Scatter rejection by air gaps in diagnostic radiology calculations using a monte carlo collision density method and consideration of molecular interference in coherent scattering,” Phys. Med. Biol. 10.1088/0031-9155/42/1/011 42, 155 (1997). [DOI] [PubMed] [Google Scholar]
- Siewerdsen J. H., Moseley D. J., Bakhtiar B., Richard S., and Jaffray D. A., “The influence of antiscatter grids on soft-tissue detectability in cone-beam computed tomography with flat-panel detectors,” Med. Phys. 10.1118/1.1819789 31, 3506 (2004). [DOI] [PubMed] [Google Scholar]
- Kyriakou Y. and Kalender W., “Efficiency of antiscatter grids for flat-detector CT,” Phys. Med. Biol. 10.1088/0031-9155/52/20/013 52, 6275 (2007). [DOI] [PubMed] [Google Scholar]
- Lo J. Y., Floyd C. E., Baker J. A., and Ravin C. E., “Scatter compensation in digital chest radiography using the posterior beam stop technique,” Med. Phys. 10.1118/1.597388 21, 435 (1994). [DOI] [PubMed] [Google Scholar]
- Seibert J. A. and Boone J. M., “X-ray scatter removal by deconvolution,” Med. Phys. 10.1118/1.596208 15, 567 (1988). [DOI] [PubMed] [Google Scholar]
- Honda M., Kikuchi K., and Komatsu K., “Method for estimating the intensity of scattered radiation using a scatter generation model,” Med. Phys. 10.1118/1.596710 18, 219 (1991). [DOI] [PubMed] [Google Scholar]
- Engel K. J., Herrmann C., and Zeitler G., “X-ray scattering in single- and dual-source CT,” Med. Phys. 10.1118/1.2820901 35, 318 (2008). [DOI] [PubMed] [Google Scholar]
- Wang J., Li T., Lu H., and Liang Z., “Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose x-ray computed tomography,” IEEE Trans. Med. Imaging 10.1109/TMI.2006.882141 25, 1272 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kak A. C. and Slaney M., Principles of Computerized Tomography (IEEE, Piscataway, NJ, 1987). [Google Scholar]
- Boone J. and Seibert J., “An analytical model of the scattered radiation distribution in diagnosticradiology,” Med. Phys. 10.1118/1.596186 15, 721 (1998). [DOI] [PubMed] [Google Scholar]
- Wang J., Li T., Lu H., and Liang Z., “Noise reduction for low-dose single-slice helical CT sinograms,” IEEE Trans. Nucl. Sci. 10.1109/TNS.2006.874955 53, 1230 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., Li T., Liang Z., and Xing L., “Dose reduction for kilovoltage cone-beam computed tomography in radiation therapy,” Phys. Med. Biol. 10.1088/0031-9155/53/11/009 53, 2897 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perona P. and Malik J., “Scale-space and edge detection using anisotropic diffusion,” IEEE Trans. Pattern Anal. Mach. Intell. 10.1109/34.56205 12, 629 (1990). [DOI] [Google Scholar]
- Feldkamp L. A., Davis L. C., and Kress J. W., “Practical cone-beam algorithm,” J. Opt. Soc. Am. 1, 612 (1984). [Google Scholar]
- Riederer S. J., Pelc N. J., and Chesler D. A., “The noise power spectrum in computed x-ray tomography,” Phys. Med. Biol. 10.1088/0031-9155/23/3/008 23, 446 (1978). [DOI] [PubMed] [Google Scholar]
- Brenner D. J. and Hall E. J., “Computed tomography—an increasing source of radiation exposure,” N. Engl. J. Med. 10.1056/NEJMra072149 357, 2277 (2007). [DOI] [PubMed] [Google Scholar]
- Wang J., Lu H., Eremina D., Zhang G., Wang S., Chen J., Manzione J., and Liang Z., “An experimental study on the noise properties of x-ray CT sinogram data in the radon space,” Phys. Med. Biol. 10.1088/0031-9155/53/12/018 53, 3327 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]