Design of optimal collimation for dedicated molecular breast imaging systems

Abstract

Molecular breast imaging (MBI) is a functional imaging technique that uses specialized small field-of-view gamma cameras to detect the preferential uptake of a radiotracer in breast lesions. MBI has potential to be a useful adjunct method to screening mammography for the detection of occult breast cancer. However, a current limitation of MBI is the high radiation dose (a factor of 7–10 times that of screening mammography) associated with current technology. The purpose of this study was to optimize the gamma camera collimation with the aim of improving sensitivity while retaining adequate resolution for the detection of sub-10-mm lesions. Square-hole collimators with holes matched to the pixilated cadmium zinc telluride detector elements of the MBI system were designed. Data from MBI patient studies and parameters of existing dual-head MBI systems were used to guide the range of desired collimator resolutions, source-to-collimator distances, pixel sizes, and collimator materials that were examined. General equations describing collimator performance for a conventional gamma camera were used in the design process along with several important adjustments to account for the specialized imaging geometry of the MBI system. Both theoretical calculations and a Monte Carlo model were used to measure the geometric efficiency (or sensitivity) and resolution of each designed collimator. Results showed that through optimal collimation, collimator sensitivity could be improved by factors of 1.5–3.2, while maintaining a collimator resolution of either ≤5 or ≤7.5 mm at a distance of 3 cm from the collimator face. These gains in collimator sensitivity permit an inversely proportional drop in the required dose to perform MBI.

INTRODUCTION

Mammography is currently the most widely used method for breast imaging and is the only modality shown to reduce the mortality rate due to breast cancer when used in regular screening programs.¹ While the overall sensitivity of mammography for detecting breast cancers has been reported as ranging from 71% to 96%,¹ mammography has a lowered sensitivity ranging between 48% and 63% in women with mammographically dense breasts.^{2, 3, 4} Mammography relies on differences in the attenuation of low-energy x rays to distinguish cancer from normal breast tissue. In areas of fatty breast tissue, these differences are observable; however, in areas of dense tissue on a mammogram, cancerous lesions can be obscured. This limitation of mammography is particularly important due to the fact that women with dense breasts are also at an increased risk of developing breast cancer.⁵

Scintimammography is a functional imaging method that detects the uptake of a radiotracer in the breast with a gamma camera. This method has the advantage that uptake of the radiotracer does not appear to be affected by mammographic breast density. Unfortunately, breast positioning with a conventional gamma camera is suboptimal, resulting in poor spatial resolution and limited ability to reliably detect tumors smaller than 1 cm in size.⁶

During the past decade, several laboratories have reported on the use of small field-of-view gamma cameras specifically designed for breast imaging.^{7, 8, 9, 10, 11} These systems permit the breast to be placed in close proximity to the detector, leading to greatly improved spatial resolution over conventional systems. We have been studying several dedicated cameras with detectors comprised of the semiconductor cadmium zinc telluride (CZT). To distinguish breast imaging with these new solid-state systems from the scintillating technology of scintimammography, we have named the technique molecular breast imaging (MBI).

Previous work from our laboratory has shown MBI to have a high sensitivity for the detection of small breast lesions.^{12, 13} More recently, we have reported a significant increase in sensitivity with the use of a dual-head MBI system comprising two opposing dedicated gamma cameras,¹⁴ and have shown this technique to be superior to screening mammography for the detection of breast cancer in women who have a mammographically dense breast pattern and are at increased risk of developing breast cancer. Interim results from a 1000-patient study have shown MBI to detect approximately three times as many cancers as screening mammography, while maintaining an equivalent specificity.¹⁵ Based on these findings, MBI appears to have tremendous potential as an adjunct technique to mammography in women with dense breasts and∕or increased risk.

A key consideration for any annual or biennial screening procedure based on MBI is the radiation dose delivered to the patient from the radiotracer. The current screening MBI research protocol at our institution utilizes a dose of 20 mCi of Tc-99m sestamibi, which delivers an effective dose to the body of 6.7 mSv.¹⁶ This is approximately seven to ten times the effective dose to the body from screening mammography. In order to reduce the effective dose of MBI, we are studying several approaches that would permit MBI to be performed using a lower administered dose of the radiotracer. These approaches include optimization of the collimator design, reduction in image noise by combining opposing images acquired with a dual-head system, use of noise-reducing postprocessing methods, and developments in CZT detector technology. We believe that with the combination of these technical improvements, along with the development of alternative radiotracers for MBI, a reduction of a factor of 10 or more in the effective radiation dose associated with MBI may be achievable.

In this work, we report on one approach to improve system sensitivity—optimization of the collimator. For general nuclear medicine studies, optimization is a relatively straightforward trade-off between resolution and sensitivity. However the imaging geometry of MBI presents a specialized situation compared to most other nuclear medicine procedures. During MBI, the breast is lightly compressed between the two opposing detectors and the object of interest, i.e., the breast lesion, is in very close proximity to the collimator face (typically within 3–4 cm of either of the opposing detectors). Hence detector intrinsic resolution is an important factor and the rate of drop off in resolution with distance is not as critical as in conventional nuclear medicine studies. In addition, the pixilated nature of these small dedicated detectors allows matched collimator designs, in which the collimator holes directly align with pixel elements. This allows for innovative collimator designs not practical or relevant for conventional nuclear medicine.

Previous studies done in our laboratory and by Gruber et al. evaluated several existing collimator designs for dedicated breast imaging and determined that high-sensitivity collimation was more optimal than high resolution collimation in the context of detecting small lesions at a distance of 6 cm or less from the collimator face.^{17, 18} In this study, we have expanded on previous work by optimizing all parameters affecting collimator design, including collimator hole dimensions, collimator material, detector pixel size, source-to-collimator distance, desired spatial resolution, and septal penetration. We examined various low-energy, parallel-hole collimator designs and compared the geometric efficiency and resolution of each design through both theoretical calculations and Monte Carlo simulations. Our objective was to improve the MBI system sensitivity while maintaining subcentimeter resolution throughout the breast.

MATERIALS AND METHODS

General collimator theory

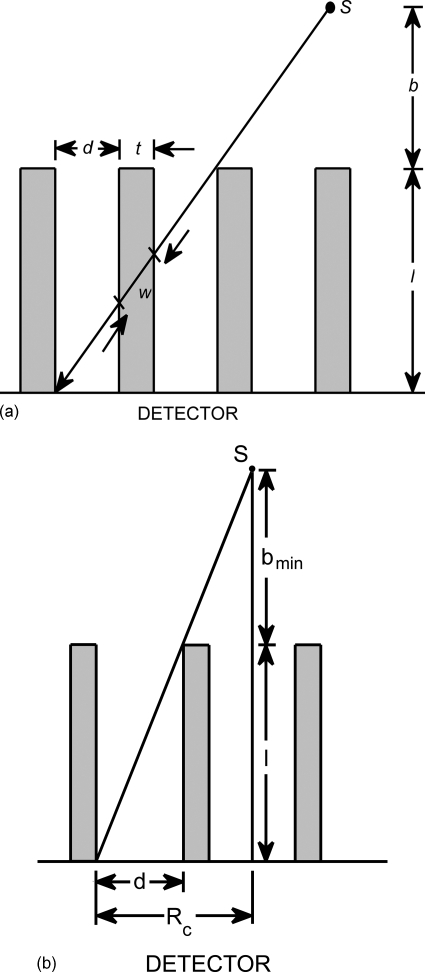
The performance of a collimator is characterized by its hole shape, hole dimensions (length and diameter), septal thickness, and collimator material. These adjustable hole dimensions—hole length l, hole diameter (parallel-to-parallel side distance) d, and septal thickness t (shown in Fig. 1)—determine the two main measures of collimator performance: geometric efficiency and collimator resolution.

Figure 1.

(a) Schematic of the side view of a collimator. Holes of length l and diameter d are separated by septa with thickness t. A point source S exists at distance b from the collimator surface. The shortest path an emitted gamma ray may travel through a septa is a distance w. (b) The general equations for a collimator’s sensitivity and resolution require that a source can be detected by more than one collimator hole. The distance b_min is the minimum source-to-collimator distance for which the classic equations still apply. At a distance less than b_min, a source is detected by only a single hole, and special considerations must be taken, especially regarding where the source is relative to the collimator septa.

The geometric efficiency of a parallel-hole collimator is described by the equation¹⁹

$$g=\frac{A_{\text{open}}}{4\pi l_e^2}\frac{A_{\text{open}}}{A_{\text{unit}}},$$ (1)

where A_open and A_unit are the open area of the hole and area of the lattice cell unit, respectively, and l_e is the effective hole length, which can be expressed as l_e=l−2μ⁻¹.²⁰ The constant μ is the linear attenuation coefficient of the collimator material at the energy of interest, which is 140 keV for Tc-99m. Equation 1 is essentially identical to a commonly used equation^{21, 22} that involves an approximated coefficient K to describe the hole arrangement, though Eq. 1 retains the exact geometric relationship and can be applied to any hole shape and array. Two common hole arrangements were considered in this study: hexagonal holes in a hexagonal array and square holes in a square array. For hexagonal holes in a hexagonal array, where

$$A_{\text{open}}=\left(\sqrt{3}∕2\right)d^2\text{and}{A}_{\text{unit}}=\left(\sqrt{3}∕2\right){\left(d+t\right)}^2,$$

Eq. 1 may be written

$$g_{\text{hex}}=\frac{\sqrt{3}}{8\pi l_e^2}\frac{d^4}{{\left(d+t\right)}^2}.$$ (2)

Also for square holes in a square array, where

$$A_{\text{open}}=d^2\text{and}{A}_{\text{unit}}={\left(d+t\right)}^2,$$

Eq. 1 becomes

$$g_{\text{sq}}=\frac{1}{4\pi l_e^2}\frac{d^4}{{\left(d+t\right)}^2}.$$ (3)

Geometric efficiency is unitless and, in order to be more clinically relevant, is often converted to sensitivity with units of cpm∕μCi using the equation²³

$$S=2.2x{10}^6\eta g,$$ (4)

where η is the number of gamma rays emitted per nuclear decay.

The resolution of a collimator R_c is determined by its hole dimensions and the distance of the source from the collimator and is defined as²¹

$$R_c=\frac{d\left(l_e+b\right)}{l_e},$$ (5)

where b is the distance from the source to the collimator surface (Fig. 1). For a conventional gamma camera which utilizes a single scintillating crystal coupled to photomultiplier tubes, the collimator resolution combines with the intrinsic resolution of the detector to produce a system resolution that is worse than either resolution component. The system resolution of a conventional gamma camera, R_S, is defined as

$$R_S=\sqrt{R_c^2+R_I^2},$$ (6)

where R_I is the intrinsic detector resolution.

Molecular breast imaging with dedicated detectors

Gamma camera systems

Two different types of MBI systems, previously described in detail,^{17, 24, 25} are currently used in our laboratory. One MBI system comprises of two opposing prototype CZT detectors (G.E. Medical Systems, Haifa, Israel). Each detector utilizes an 80×80 array of CZT elements with dimensions of 2.5×2.5×5 mm³, giving a field of view (FOV) of 20×20 cm². These detectors are currently equipped with a matched square-hole general purpose (GP) lead collimator with hole dimensions of 2.3×2.3×35 mm³ and septal thickness of 0.2 mm. The energy resolution of this system is 7.8% at the photopeak of Tc-99m (140 keV).

The second MBI system utilizes two LumaGem detectors (Gamma Medica-Ideas, Northridge, CA). Each detector utilizes a 96×128 array of CZT elements with dimensions of 1.6×1.6×5 mm³, giving a 15 cm×20 cm FOV. The LumaGem detectors are equipped with high-sensitivity hexagonal-hole lead collimators with a parallel-to-parallel hole diameter of 2.54 mm, hole length of 25 mm, and septal thickness of 0.3 mm. This system has an energy resolution of 3.9% at 140 keV.

Both MBI systems are configured such that the breast is placed between the two detectors and light, pain-free compression is applied to both reduce breast thickness and reduce patient motion during imaging. With the dual-head design, simultaneous opposing views of the breast are acquired without requiring any additional imaging time or dose. The main advantage of this design is that by providing opposing views from two detector heads, the ability to detect small cancers is increased by ensuring that no lesion is more than half the thickness of the compressed breast from either detector face.¹⁴

Choosing parameters for collimator optimization

The specifications of the two systems described above and knowledge of typical patient-related variables, such as breast thickness and tumor size, guided the selection of collimator material, pixel size, source-to-collimator distance, and desired resolution.

Two collimator materials were considered: lead (μ=26.32 cm⁻¹ at 140 keV), which is currently used in both systems, and tungsten (μ=34.48 cm⁻¹ at 140 keV), another common option that provides a greater linear attenuation of gamma rays than lead due to its higher density. The two pixel sizes of the systems, 2.5 and 1.6 mm, were investigated in depth. Additionally, custom pixel sizes were explored, ranging from 1.0 to 3.5 mm.

From measurement in over 1000 MBI studies, the average compressed breast thickness was ∼6 cm (range of 2.5–11.5 cm).^{12, 13, 14, 15} With a dual-head MBI system, the maximum distance from a breast lesion to the collimator surface is half the total breast thickness. Hence source-to-collimator distances of 3 and 6 cm were selected as being representative of the average midbreast and total breast thicknesses, respectively. Setting the average source-to-collimator distance, b=3 cm, collimator optimization was performed to achieve system resolutions of ≤5.0 and ≤7.5 mm at this 3 cm depth. System resolutions close to 5 mm at a 3 cm depth have been employed in clinical studies to date;^{12, 13, 14, 15} however, a slight degradation in resolution up to 7.5 mm, with the corresponding large increase in sensitivity may be worth evaluating in screening applications.

Collimator optimization

Optimization using general equations

At a desired resolution limit, collimator geometric efficiency can be maximized by expressing g as a function of l, then setting dg∕dl=0.²⁶ This approach was performed using Eqs. 2, 3 to find the hole length which gives maximum efficiency for hexagonal-hole and square-hole collimators, respectively. Equations 2, 3 may be expressed in terms of l by substituting the equations for collimator resolution, Eq. 5, and septal thickness, Eq. 7,

$$t=\frac{2dw}{l-w}$$ (7)

into Eq. 1. In Eq. 7, w is the shortest path length for gamma rays to travel from one hole to another (Fig. 1), and it is related to the septal penetration β by e^−μw≤β. These substitutions yield Eq. 8 for a hexagonal-hole collimator and Eq. 9 for a square-hole collimator,

$$g_{\text{hex}}=\frac{\sqrt{3}}{8\pi }\frac{R_c^2}{{\left(l-2{\mu }^{-1}+b\right)}^2}{\left(\frac{l\mu +\text{ln}\beta }{l\mu -\text{ln}\beta }\right)}^2,$$ (8)

$$g_{\text{sq}}=\frac{1}{4\pi }\frac{R_c^2}{{\left(l-2{\mu }^{-1}+b\right)}^2}{\left(\frac{l\mu +\text{ln}\beta }{l\mu -\text{ln}\beta }\right)}^2.$$ (9)

The optimal hole length l_opt, which gives the maximum geometric efficiency for hexagonal-hole and square-hole collimators, is found by setting dg∕dl=0. For both Eqs. 8, 9, this yields

$$l_{\text{opt}}=-\frac{\text{ln}\beta }{\mu }+{\left[2{\left(\frac{\text{ln}\beta }{\mu }\right)}^2+4\frac{\text{ln}\beta }{{\mu }^2}-2b\frac{\text{ln}\beta }{\mu }\right]}^{1∕2}.$$ (10)

The other hole dimensions, d and t, were optimized by rearranging Eqs. 5, 7,

$$d_{\text{opt}}=R_c\frac{l_{\text{opt}}-2u^{-1}}{l_{\text{opt}}-2u^{-1}+b},$$ (11)

$$t_{\text{opt}}=-\frac{2d_{\text{opt}}\text{\hspace{0.17em}ln}\beta }{l_{\text{opt}}\mu +\text{ln}\beta }.$$ (12)

Together, Eqs. 10, 11, 12 describe the hole dimensions of an optimized collimator. Using the input parameters described in Sec. 2B2 of μ=26.32 cm⁻¹ or 32.48 cm⁻¹, b=3 or 6 cm, a threshold of either 5.0 or 7.5 mm for R_c and a septal penetration β of 0.05, the optimal hole length, diameter, and septal thickness for each unique set of parameters was found. Sensitivity of these optimized collimator designs in cpm∕μCi was then calculated according to Eq. 4.

This optimization is useful for conventional cameras; however, these equations do not account for the effects of coupling a collimator to a pixilated detector. With pixilated detectors, a matched collimator design is possible in which each collimator hole directly aligns with each detector element. Given the theoretical advantages in the design of a matched collimator as described below and the current use of pixilated gamma cameras in MBI, this study focused on the optimization of a matched collimator design.

Optimization of matched collimators using constraints

In the case of a pixilated camera with a matched collimator, the pixels are matched exactly to the collimator holes so each hole and its corresponding pixel is independent of other holes and pixel units. Therefore, the system resolution is determined solely by the collimator resolution (R_s=R_c), offering improved spatial resolution over traditional hexagonal-hole designs.²⁴ The collimator resolution equation for a matched collimator with a pixilated detector is expressed slightly differently. A correction factor ρ is incorporated and the classic collimator resolution equation is adjusted, giving²⁷

$$R_c=\rho \frac{d\left(l+b-{\mu }^{-1}\right)}{l-2{\mu }^{-1}}.$$ (13)

The correction factor ρ accounts for several factors, such as hole shape, angular averaging, and the ratio of detector-to-source distance to hole length. Wieczorek and Goedicke²⁷ plotted the value of the correction factor as a function of this ratio for various hole shapes. For a source to collimator distance of 3 cm, correction factor ρ had values of 0.938 and 0.867 for square and hexagonal-hole collimators, respectively. This equation was used to calculate the theoretical collimator resolution of matched collimators.

In addition to improved system resolution, another potential advantage of using a matched collimator with a pixilated system is that the small inactive portions at the edge of each detector element are covered by the collimator septa rather than being exposed in the area of the holes, so that optimal geometric efficiency should be achieved.²⁸ Also, the alignment of the septa with detector elements eliminates any possible aliasing patterns that can arise due to mismatch of hexagonal collimator holes and square pixels.¹⁷

One constraint necessary for a matched collimator design is that the size of a collimator lattice unit, d+t, must equal the size of each detector element, or the pixel size p. When this requirement is introduced, solving for the optimal hole dimensions becomes an iterative procedure. This was handled by creating a MATLAB algorithm to perform two tasks: first determine the possible combinations of hole dimensions, then evaluate which combinations have the best geometric efficiency or sensitivity.

First, the algorithm stepped through the possible hole dimensions l and d, and calculated t such that it met the pixel constraint. The variables μ, b, and p were fixed at the following values as given in Sec. 2B2: μ=26.32 or 32.48 cm⁻¹, b=3 or 6 cm, and p=1.0–3.5 mm.

Another constraint on the possible sets of hole dimensions was in regard to septal penetration. Septal penetration can degrade the quality of an image by causing starlike patterns and loss of contrast. A collimator is free from such penetration artifacts if it meets the University of Chicago penetration criterion:²³

$$P\le \mu l\left[1-\frac{A_{\text{hole}}}{A_{\text{unit}}}\right],$$ (14)

where P is a penetration parameter dependent on hole pattern. For square holes in a square array, P=12.57±0.53,²³ and Eq. 10 becomes

$$P_{\text{sq}}\le \mu l\left[1-{\left(\frac{d}{d+t}\right)}^2\right].$$ (15)

By using this inequality to determine the minimum and maximum values of l and d, it was assured that all sets of hole dimensions met this constraint as well.

One final condition was that the resultant collimator resolution R_c calculated for a set of hole dimensions had to be equal to or better than the threshold resolution of either 5.0 or 7.5 mm. Because of the trade-off between sensitivity and resolution, the resolution was fixed and the geometric efficiency was calculated for that specific resolution.

When this algorithm was completed, a list of the possible combinations of hole dimensions for the variable input parameters of μ, b, p, and R_c which met the imposed constraints was generated. The geometric efficiency of each collimator was determined and converted to a measure of collimator sensitivity. The design that maximized sensitivity without exceeding the required collimator resolution was then determined.

Monte Carlo simulation

In order to validate the theoretical collimator calculations, a Monte Carlo simulation program—the Monte Carlo n-particle (MCNP) code, Version 5, developed by Los Alamos National Laboratory²⁹—was used to measure the sensitivity and spatial resolution of each collimator design considered. The MCNP model used by this laboratory for simulating MBI gamma camera systems has been described previously.^{30, 31}

A MCNP model was created to simulate (1) the collimators currently used by our laboratory and their respective pixilated detectors and (2) each optimal matched collimator design determined above with a detector with the appropriate pixel size to satisfy the constraint p=d+t. For each simulated collimator, the model simulated a Tc-99m line source in air placed at a distance of 3 or 6 cm from the collimator face. The line source was tilted 30° to provide oversampling of pixel intensity profiles through the source.

During each simulation, 75×10⁶ gamma rays were simulated, which produced at least 10 000 counts (<1% uncertainty) for the collimator with the lowest sensitivity. The number of counts acquired was recorded as a measure of sensitivity for each simulated collimator.

Collimator resolution was measured from the full width at half maximum (FWHM) of the sum of profiles through the line source after accounting for the line source’s angular offset. The line source profile was fit with a Gaussian curve to determine the Gaussian FWHM (FWHM_GHA). The collimator resolution was obtained from the Gaussian FWHM by rearranging the equation,²³

$${\text{FWHM}}_{\text{GHA}}=\sqrt{2\text{\hspace{0.17em}ln}2}\frac{d\left(l+b\right)}{l},$$ (16)

where FWHM_GHA is the Gaussian hole approximation of the aperture function and the quantity d(l+b)∕l is the baseline expression for collimator resolution. This equation is derived for a traditional collimator, but since it is an approximation based on a single hole, the relationship also exists for matched collimators. With a matched collimator, the response is non-Gaussian, and the collimator resolution is equal to FWHM_GHA divided by $\sqrt{2\ln 2}$.

The number of counts acquired (sensitivity) and the resolution of each of the modeled collimators were compared to the theoretical calculations of sensitivity and resolution.

Collimator near-field considerations

Classical collimator theory assumes that the geometric efficiency is independent of the source position and the distance from the collimator face, as is evident in Eq. 1. However, this assumption is invalid for a source very close to the collimator face.

The collimator’s field of view and the equations governing collimator performance only apply at distances beyond which a source can be detected in adjacent holes. This minimum distance is indicated as b_min in Fig. 1b and from the simple geometry in Fig. 1b, can be calculated from the equation

$$b_{\text{min}}=\frac{l}{2}+\frac{lt}{d}.$$

For distances <b_min, the geometric efficiency and collimator resolution will be highly dependent on source location relative to the collimator septa. If a source is directly over a single hole, the geometric efficiency will decrease as 1∕(b+l)² and the collimator resolution will be independent of the distance and will be determined only by the hole diameter with no contribution from the hole length. For a source located directly over the septa, geometric efficiency may increase with distance, whereas resolution will be degraded at distances <b_min.²³ This dependence of geometric efficiency and collimator resolution on b_min and source position relative to the hole and septa was simulated using the Monte Carlo code.

RESULTS

Optimized collimator design without constraints

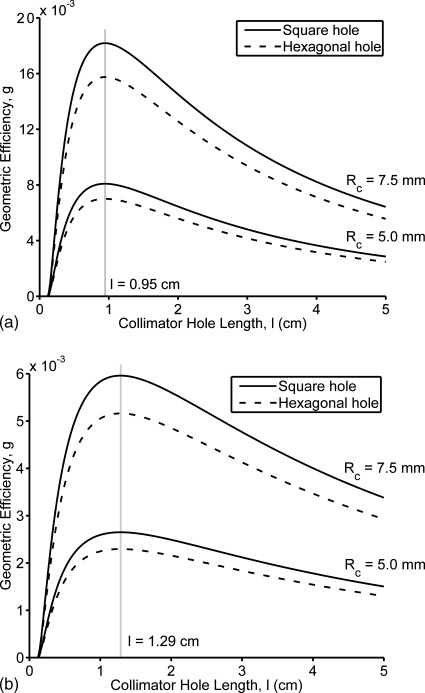
Using the general equations describing collimator characteristics, optimal collimator designs were calculated. Figure 2 plots the geometric efficiency as a function of hole length as described by Eqs. 8, 9 for the resolutions of interest, 5.0 and 7.5 mm, and for source-to-collimator distances of 3 cm [Fig. 2a] and 6 cm [Fig. 2b]. These results (shown for a lead collimator) indicate that there is an optimum hole length l_opt of either 0.95 or 1.29 cm (for b=3 cm or b=6 cm, respectively) which yields the maximum geometric efficiency that is independent of the collimator resolution at a given source-to-collimator distance. As given in Table 1, the corresponding optimal hole lengths for a tungsten design were 0.81 and 1.11 cm. Figure 2 also shows the greater geometric efficiency of a square-hole collimator compared to a hexagonal-hole collimator due to the higher ratio of (A_open)² to A_unit.

Figure 2.

Calculated geometric efficiency as a function of collimator resolution, hole length, and hole shape. A lead collimator (μ=26.32 cm⁻¹, 140 keV) was assumed, with a conventional septal penetration of β=0.05. Two subcentimeter resolutions were examined. The distances from the source to the collimator surface are within the range necessary for dual-head MBI systems: (a) b=3 cm and (b) b=6 cm.

Table 1.

Optimal hole dimensions—hole length, hole diameter, and septal thickness—for varying input parameters using general collimator equations without constraints. Septal penetration was approximately 0.05 for all collimators.

Input parameters			Optimized hole dimensions				S [×103 (cpm∕μCi)]
Desired Rc (mm)	b (cm)	μ (cm−1)	l (cm)	d (mm)	t (mm)	bmin (mm)
5.0	3	26.32	0.946	1.12	0.31	7.35	1.82
5.0	3	34.48	0.813	1.01	0.24	6.00	2.04
5.0	6	26.32	1.29	0.840	0.16	8.91	0.595
5.0	6	34.48	1.11	0.747	0.13	7.48	0.649
7.5	3	26.32	0.946	1.69	0.46	7.30	4.09
7.5	3	34.48	0.813	1.51	0.36	6.00	4.59
7.5	6	26.32	1.29	1.26	0.24	8.91	1.34
7.5	6	34.48	1.11	1.12	0.19	7.43	1.46

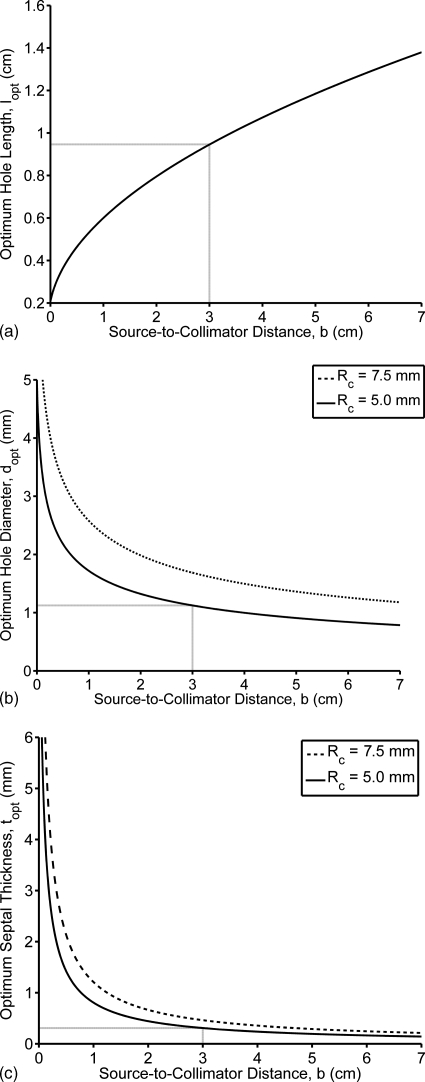
The hole dimensions l_opt, d_opt, and t_opt of an optimized lead collimator as a function of source-to-collimator distance b and collimator resolutions of 5.0 and 7.5 mm, and septal penetration of 5% are plotted in Fig. 3. Using these relationships, the optimal hole dimensions for b=3 or 6 cm, and a R_c of either ≤5.0 or ≤7.5 mm at this distance were calculated and are given in Table 1. This table lists the optimal hole dimensions and the resultant sensitivity for both lead collimators (μ=26.32 cm⁻¹) and tungsten collimators (μ=32.48 cm⁻¹). At b=3 cm, the highest sensitivity lead collimator for R_c=5.0 mm had hole dimensions of l=0.946 cm, d=1.12 mm, and t=0.31 mm, and had a value of b_min=0.73 cm.

Figure 3.

Optimized hole dimensions as a function of source-to-collimator distance for a lead collimator: (a) Optimal hole length, (b) optimal hole diameter, and (c) optimal septal thickness. Hole dimensions are optimized to produce the greatest geometric efficiency at a given collimator resolution and source-to-collimator distance.

Optimized design of matched collimators with constraints

By using the MATLAB algorithm to solve for the possible collimator designs that would meet the imposed constraints for a matched collimator design and would meet the University of Chicago penetration criterion for septal penetration, 23 different sets of input parameters were created (Table 2).

Table 2.

Collimator dimensions—hole length, hole diameter, and septal thickness—for two currently used collimators and 23 optimized collimator designs determined by the MATLAB algorithm using constraints. [L=LumaGem hexagonal-hole, low-energy high-sensitivity collimator and P=prototype cadmium zinc telluride, matched square-hole general purpose collimator.]

Collimator (mm)	Input parameters				Optimal collimator dimensions
	Desired Rc (mm)	b (cm)	p (mm)	μ (cm−1)	l (cm)	d (mm)	t (mm)	bmin
L	⋯	3	1.6	26.32	2.50a	2.54a	0.30a	15.45
P	⋯	3	2.5	26.32	3.47a	2.26a	0.24a	21.03
1	≤5.0	3	1.6	26.32	0.94	1.12	0.48	8.79
2	≤5.0	3	1.6	34.48	1.03	1.28	0.32	7.73
3	≤5.0	3	2.5	26.32	2.13	2.19	0.31	13.67
4	≤5.0	3	2.5	34.48	2.23	2.27	0.23	13.41
5	≤5.0	3	Custom: 1.9	26.32	1.27	1.50	0.40	9.74
6	≤5.0	3	Custom: 1.7	34.48	1.15	1.40	0.30	8.21
7	≤5.0	6	1.6	26.32	2.28	1.42	0.18	14.29
8	≤5.0	6	1.6	34.48	2.37	1.47	0.13	13.95
9	≤5.0	6	2.5	26.32	4.73	2.37	0.13	26.24
10	≤5.0	6	2.5	34.48	4.77	2.39	0.11	26.05
11	≤5.0	6	Custom: 1.3	26.32	1.69	1.10	0.20	11.52
12	≤5.0	6	Custom: 1.2	34.48	1.58	1.05	0.15	10.16
13	≤7.5	3	1.6	34.48	0.67	1.08	0.52	6.58
14	≤7.5	3	2.5	26.32	0.98	1.79	0.71	8.79
15	≤7.5	3	2.5	34.48	1.12	2.05	0.45	8.06
16	≤7.5	3	Custom: 3.0	26.32	1.40	2.43	0.57	10.28
17	≤7.5	3	Custom: 2.6	34.48	1.19	2.16	0.44	8.37
18	≤7.5	6	1.6	26.32	1.24	1.25	0.35	9.67
19	≤7.5	6	1.6	34.48	1.34	1.36	0.24	9.06
20	≤7.5	6	2.5	26.32	2.44	2.24	0.26	15.03
21	≤7.5	6	2.5	34.48	2.52	2.31	0.19	14.67
22	≤7.5	6	Custom: 2.1	26.32	1.88	1.81	0.29	12.41
23	≤7.5	6	Custom: 1.7	34.48	1.46	1.47	0.23	9.58

^aCollimator specifications of existing collimators in our laboratory.

Table 3 presents the sensitivity and resolution of the 23 matched designs and the two existing clinical designs generated from both the theoretical calculations and the Monte Carlo model. The resolutions found with the model, using Eq. 16, and the calculated resolutions, using Eq. 13, were compared as absolute values. Because the Monte Carlo model simulated the number of counts acquired rather than sensitivity in units of cpm∕μCi, the calculated sensitivity of each collimator was converted to counts acquired by normalizing to the collimator currently used on the LumaGem system. Results from the calculations and the Monte Carlo simulation were in close agreement; the average percent difference in resolution was 1.50±1.03%, and the average percent difference in counts or sensitivity was 1.56±1.27%. When comparing collimator designs, the average of the calculated and Monte Carlo results was used.

Table 3.

Sensitivity, resolution, and septal penetration values of collimators from Table 2 found through theoretical calculations and MCNP modeling. [L=LumaGem hexagonal-hole, low-energy high-sensitivity collimator and P=prototype cadmium zinc telluride, matched square-hole general purpose collimator.]

	Calculations				MCNP Model		Difference (MCNP−calculated)
Collimator	Rc (mm)	S [×103 (cpm∕μCi)]	Normalized counts×104	% Septal penetration	FWHM (mm)	Counts×104	FWHM (%)	Counts (%)
L	5.72	1.34	3.85	0.025	5.97	3.85	4.3	N∕A
P	3.92	0.640	1.83	0.010	4.00	1.83	1.9	0.4
1	4.84	1.45	4.17	0.013	4.80	4.16	0.8	0.2
2	5.02	1.96	5.62	0.019	4.98	5.58	0.8	0.8
3	5.04	1.54	4.42	0.025	5.00	4.44	0.8	0.6
4	5.04	1.59	4.56	0.025	5.01	4.55	0.5	0.1
5	5.02	1.74	4.98	0.020	4.93	4.98	1.9	0.1
6	5.01	1.97	5.64	0.022	4.96	5.59	1.0	0.9
7	5.04	0.578	1.65	0.028	5.08	1.70	0.9	2.8
8	5.02	0.603	1.73	0.031	5.06	1.77	0.7	2.4
9	5.04	0.411	1.18	0.036	5.00	1.20	0.8	2.1
10	5.04	0.415	1.19	0.025	4.99	1.20	0.9	0.5
11	5.01	0.588	1.68	0.025	4.96	1.69	1.0	0.6
12	5.02	0.644	1.84	0.026	5.01	1.85	0.2	0.1
13	6.23	2.51	7.18	0.011	6.17	7.00	1.1	2.6
14	7.45	3.55	10.2	0.014	7.31	9.85	2.0	3.2
15	7.50	4.43	12.7	0.022	7.24	12.2	3.5	3.6
16	7.54	3.90	11.2	0.021	7.26	10.8	3.8	3.9
17	7.52	4.44	12.7	0.023	7.44	12.2	1.1	4.1
18	7.53	1.24	3.56	0.018	7.42	3.50	1.5	1.9
19	7.53	1.44	4.12	0.024	7.38	4.05	2.0	1.5
20	7.53	1.27	3.65	0.030	7.40	3.59	1.7	1.7
21	7.53	1.33	3.80	0.032	7.37	3.74	2.2	1.6
22	7.53	1.32	3.79	0.025	7.45	3.72	1.1	1.8
23	7.53	1.45	4.16	0.026	7.43	4.18	1.4	2.0
Mean							1.5±1.0	1.5±1.3

The optimal matched collimator for dual-head MBI was selected as the one that provided the greatest gain in sensitivity while maintaining a collimator resolution of ≤5 mm at a distance of 3 cm. Six collimators (1–6) met these criteria, and the one with the greatest sensitivity was collimator 6 which was made of tungsten, required a detector pixel size of 1.7 mm, and had hole dimensions of l=1.15 cm, d=1.40 mm, and t=0.30 mm. The calculated sensitivity of this collimator was 1.97×10³ cpm∕μCi, which produced an average gain in sensitivity of 1.46 times that of the LumaGem LEHS collimator while improving collimator resolution by 0.86 mm at a distance of 3 cm.

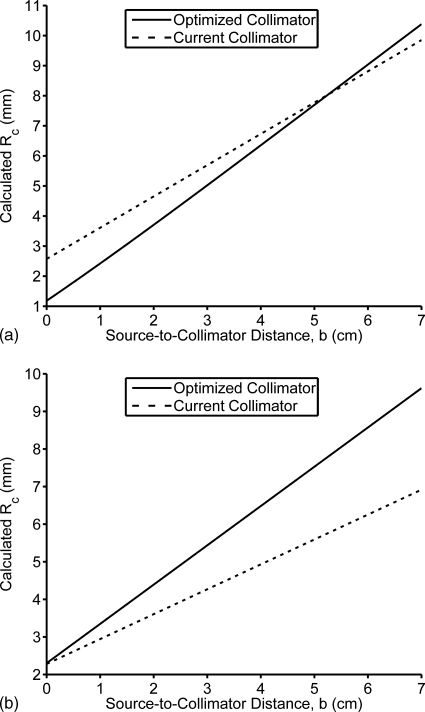
With the constraint of a pixel size=1.6 mm (as used in the LumaGem system), collimator 2 provided almost identical sensitivity to collimator 6, with hole dimensions of l=1.03 cm, d=1.28 mm, and t=0.32 mm. The sensitivity with collimator 2 increased by a factor of 1.45 over the current hexagonal-hole LumaGem LEHS collimator. The resolution of this collimator also improved by 0.85 mm at 3 cm. In addition there was a reduction in b_min from 15 to 8 mm. Figure 4a shows the resolution of collimator 2 as a function of source-to-collimator distance relative to the current LumaGem LEHS collimator.

Figure 4.

Calculated R_c as a function of source-to-collimator distance for the collimator currently used by the laboratory and the matched square-hole collimator optimized for a resolution of 5.0 mm at a distance of 3 cm. The collimators are optimized according to the pixel size of detectors currently used by the laboratory: (a) pixel size of 1.6 mm, showing the currently used hexagonal-hole LumaGem LEHS collimator and collimator 2; and (b) pixel size of 2.5 mm, showing the currently used matched square-hole prototype CZT GP collimator and collimator 4.

When a pixel size of 2.5 mm (as used in the prototype CZT system) was considered, the best collimator with resolution of ≤5.0 mm at a distance of 3 cm was collimator 4. This collimator was made of tungsten and had hole dimensions of l=2.23 cm, d=2.27 mm, and t=0.23 mm, and had a b_min=13.41 mm. This collimator resulted in a sensitivity of 1.59 cpm∕μCi, which represents a 1.18-fold average increase over the LumaGem LEHS collimator and a 2.49-fold average increase in sensitivity over the current prototype CZT GP collimator. However, this gain in sensitivity was accompanied by a 1.11 mm loss in resolution (from 3.92 mm to an average of 5.03 mm) at a distance of 3 cm. Collimator 3, which was a lead collimator, also produced very similar sensitivity and resolution results to the tungsten collimator 4. Figure 4b shows collimator resolution as a function of source-to-collimator distance for the current matched GP collimator and an optimal collimator for pixel size of 2.5 mm and resolution ≤5.0 mm at a distance of 3 cm.

Degrading resolution from ∼5 to ∼7.5 mm resulted in a greater than twofold increase in sensitivity. Highest sensitivity overall was achieved with collimator 17, a tungsten collimator with a custom pixel size of 2.6 mm and hole dimensions of l=1.19 cm, d=2.16 mm, and t=0.44 mm. This collimator had a calculated sensitivity of 4.44×10³ cpm∕μCi, representing a 3.24 gain in sensitivity over the LumaGem LEHS collimator and a 6.81 gain in sensitivity over the GP collimator for the prototype CZT camera. However, this gain in sensitivity over the two existing collimators is accompanied by a significant loss in resolution (at a distance of 3 cm) from 5.72 mm (LumaGem LEHS), and 3.92 mm (prototype CZT GP), to an average of 7.48 mm. Figure 5 demonstrates the effect of using collimation with slightly poorer resolution in order to improve sensitivity on the ability to image lesions less than 10 mm in size.

Figure 5.

Images of three simulated lesions acquired with different collimation are shown. For all images, the lesions (as drawn in the schematic) have diameters of 5.0, 7.5, and 10 mm, have a ratio of lesion to background activity of 20:1, and are located 3 cm from the collimator in a 6 cm breast. Panels (a) and (b) show images obtained with matched tungsten collimators designed for 1.6 mm pixels; panels (c) and (d) used matched tungsten collimators for 2.5 mm pixels. [Panel (a)] Collimator 2, R_c at b=3 cm was 5.02 mm and sensitivity was 1.96×10³ cpm∕μCi. [Panel (b)] Collimator 13, R_c at b=3 was 6.23 mm and sensitivity was 2.51×10³ cpm∕μCi. [Panel (c)] Collimator 4, R_c at b=3 cm was 5.04 mm and sensitivity was 1.59×10³ cpm∕μCi. [Panel (d)] Collimator 15, R_c at b=3 cm was 7.50 mm and sensitivity was 4.43×10³ cpm∕μCi.

Collimator near-field considerations

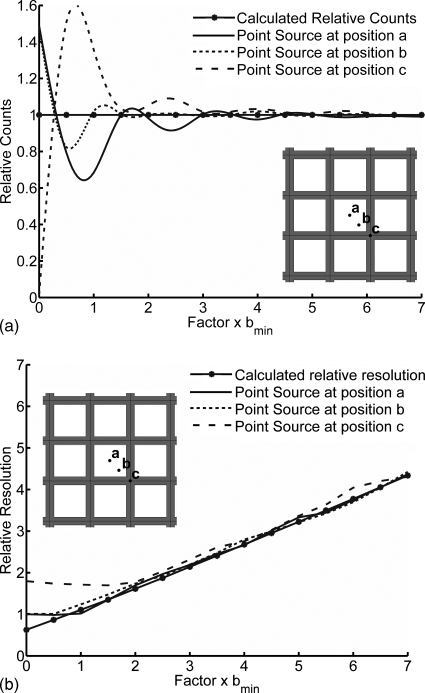
Figure 6a shows the effects of variation in source location and distance b on the collimator sensitivity calculated using MCNP simulations. A source positioned over the septal junction (position c) will have a gain of approximately 2.5 in sensitivity relative to a source located over the center of a hole (position a) at distances close to b_min. For sources located over the hole center, count sensitivity decreases according to the inverse square law as the source is moved from the surface to b_min. Past a distance of b_min, the count sensitivity periodically increases and decreases as the source interacts with an increasing number of adjacent holes and septa. Sources located over the septal junction will register no counts when placed at the collimator surface. As b is increased, sensitivity initially sharply increases because the source is immediately detected in four surrounding holes; as b is further increased, a periodic relationship between sensitivity and b that is inverse the relationship for a source over the hole is established.

Figure 6.

Sensitivity and resolution as a function of source position and distance from the collimator relative to b_min. In (a), relative counts are shown as a measure of sensitivity for sources at position a, centered above a collimator hole; b, at the midpoint between the hole center and septal junction; and c, centered above the septal junction. In (b), relative resolution is shown for sources placed at the same positions.

Figure 6b likewise demonstrates the changes in spatial resolution as a function of source location relative to the collimator holes. For a source directly over a collimator hole, resolution is equivalent to the pixel size at distances <b_min. When a source directly over a septal junction is considered, the source is detected by the four holes adjacent to the junction, giving a degraded resolution for distances <2×b_min, These near-field effects on resolution do impact small objects located at distances less than b_min, as illustrated in Fig. 7. Here, using the Monte Carlo simulation, a 3 mm lesion placed 4 mm from the collimator face was imaged using collimator 2, which has a b_min of 7.7 mm. The ability to detect this lesion decreases dramatically when the lesion is located directly over a septal junction compared to when it is located directly over a collimator hole.

Figure 7.

Images of a simulated lesion acquired with collimator 2 are shown. For both images, the lesion is 3 mm in diameter, has a ratio of lesion to background activity of 20:1, and is located 4 mm from the collimator in a 6 cm breast. The lesion is more clearly seen in panel (a), where the lesion is placed directly over a collimator hole, than in panel (b), where the lesion is placed directly over a septal junction.

Therefore, because of the fluctuations in collimator sensitivity and resolution at near-field distances, a collimator design that minimizes b_min while maintaining high sensitivity is desirable.

DISCUSSION

In this work, the optimal collimation for a dedicated dual-head MBI system was studied. The unique geometry of this system allows the breast to be lightly compressed between two opposing cameras, thereby creating a much shorter imaging distance with an average object-to-collimator range of about 0–3 cm. Optimization of collimator characteristics was performed to maximize sensitivity given a range of specific desired resolutions at a certain distance from the collimator. To perform this optimization, a re-evaluation of collimator theory was required in order to address the limitations that arise in its applications to newly developed small field-of-view gamma cameras.

Application of collimator theory to MBI systems

A collimator optimization method for conventional gamma camera systems was initially proposed by Keller in the 1960s.²⁶ Although this method was a simple but effective technique for maximizing efficiency as a function of hole dimensions, it has not been appreciated in modern collimator design. Using this method, results indicated that a square-hole collimator design is slightly preferable to a hexagonal-hole collimator design with regard to sensitivity.

The optimal hole dimensions determined using general collimator equations are not wholly applicable to a collimator designed specifically for a pixilated gamma camera, however, because they were derived based on a continuous detector system. In order to design a collimator for MBI, several modifications were made. Two important constraints were applied on the hole dimensions so that holes of the matched collimator aligned with pixels of the detector and so an acceptable level of septal penetration was maintained. In addition, a correction factor ρ was applied to measurements of collimator resolution to more accurately reflect the resolution of a matched square-hole collimator.

Taking these factors into account, matched square-hole collimators for a pixilated dual-head MBI system were designed. In general, the optimized matched designs (Table 2) had longer hole lengths, larger diameters, and thicker septa than the optimal designs calculated with the general equations. The thicker septa was necessary to satisfy a stricter septal penetration criterion than the conventional 5%, and the larger hole diameters were used to match the hole size to the pixel size. As a result of these two changes, longer hole lengths were necessary for the matched designs.

Very early work in collimator design indicated that a septal penetration of 5% was tolerable.²² This was the value used in computing the general equations for collimator resolution and sensitivity in this study. However, a more exact method of ensuring acceptable septal penetration has been developed by Gunter²³ using extensive ray tracing techniques and has produced an empirical formula for the penetration threshold. This formula, the University of Chicago penetration criterion, depends on the hole shape and array pattern. In requiring that the various collimator designs meet this criterion, we found that the penetration values ranged from 1.1% to 3.6% with a mean of 2.3±0.61%. Greater septal penetration could have been allowed to further increase collimator sensitivity; however, it would increase the likelihood of decreased image contrast and∕or star artifacts.

Lastly, results demonstrated that the general collimator equations become invalid for sources very close to the collimator face. While a discussion of collimator performance for distances <b_min is irrelevant for general nuclear medicine studies, it is important for MBI as a lesion lie easily within b_min. The average distance b_min for the collimators considered in this paper ranged from 0.66 to 2.62 cm, with an average of 1.20±0.51 cm, meaning that for a dual-head system with a camera separation of 6 cm, an average of 40% of the breast tissue in the field of view can lie within the range <b_min of both collimator faces.

Hence, as the results in Figs. 67 indicate, the minimization of b_min is important so that the large variations in both sensitivity and resolution that occur between the collimator and b_min do not adversely impact the detection of a breast lesion or the accurate assessment of radiotracer uptake in a lesion.

Optimal matched designs

For the LumaGem detector (pixel size of 1.6 mm), the optimal collimation was a tungsten, matched square-hole design (Table 3, collimator 2) that resulted in improvements in both sensitivity and resolution over the existing lead hexagonal-hole collimator. The results showed that a tungsten collimator provided a 35% gain in sensitivity over the equivalent lead collimator.

For the prototype CZT system (pixel size of 2.5 mm), the optimal design resulted in a small loss in resolution relative to the existing collimator; however, this was considered acceptable since the desired resolution of ≤5 mm at a distance of 3 cm was maintained and sensitivity was increased by more than a factor of 2. Results showed that both lead and tungsten designs provided a similar gain in sensitivity for a pixel size of 2.5 mm; hence, a change to a tungsten material would not yield any significant benefits in this case.

When pixel size was allowed to vary from the 1.6 or 2.5 mm sizes in our current detectors, the greatest gain in collimator sensitivity (while maintaining 5 mm resolution at 3 cm) was observed for a pixel size of 1.7 mm. However, the slight difference in sensitivity and resolution between collimators designed for 1.6 and 1.7 mm pixel sizes (collimators 2 and 6) suggests that the high cost of manufacturing a detector with custom pixel sizes is not justified for this application.

For our purposes, we focused on obtaining a 5 mm resolution or better at a distance of 3 cm. These parameters were chosen based on our need to detect lesions as small as 5 mm throughout the breast. Although the average compressed breast thickness in our MBI studies is 6 cm, the use of a dual-head system requires that we achieve the desired spatial resolution at half that distance. Lesions beyond this distance will be detected by the opposing detector. Without a dual-head configuration, the requirement of a 5 mm resolution at a distance of 6 cm would result in a significant loss in sensitivity with all of the proposed collimator designs.

If a 7.5 mm resolution at 3 cm was considered adequate, collimation with even greater gains in sensitivity could be produced. This type of collimation may be appropriate for some low-dose MBI screening settings in which a very high resolution is not essential. As done with mammography, additional diagnostic views could be performed if a screening MBI was suspicious. The diagnostic MBI study could be performed using a higher resolution collimator and longer acquisition times as necessary to acquire the desired number of counts. However, one important consideration here is the potential drop in the ability to detect small (5–10 mm) lesions because some resolution would be lost as a trade-off to gains in sensitivity, as illustrated in Fig. 5.

Future work to allow-dose reduction

The gains in sensitivity obtained with these optimized design will contribute to ongoing work in our laboratory to reduce the necessary dose administered for MBI studies. For example, by implementing the optimal matched collimator design on the LumaGem system (collimator 2), count sensitivity could be increased by a factor of ∼1.5, permitting a reduction in the administered dose of 20–13.3 mCi, while also improving spatial resolution.

By combining optimal collimation with other dose reduction approaches currently under study in our laboratory, we anticipate that this dose could be further reduced by a significant amount to at most 5 mCi and possibly as low as 2 mCi. One critical dose reduction method will be the combination of two breast views acquired with the dual-head MBI system along with various noise-reducing image processing algorithms to permit images with less counts to be acquired. Further advancements in the CZT technology and the development of alternative radiotracers to sestamibi for MBI may also contribute to dose reduction.

CONCLUSION

This study demonstrated that the absolute count sensitivity of a dual-head MBI system could be increased by as much as 1.5–3.2 times by using a tungsten collimator with matched square holes. The optimal hole dimensions were determined by maximizing geometric efficiency for a desired collimator resolution of either ≤5 or ≤7.5 mm throughout the breast while maintaining acceptable septal penetration. These findings will be used as part of an ongoing study to reduce the administered dose of Tc-99mm sestamibi for MBI, thereby permitting its use as a regular screening test.