Abstract
The purpose of this study is to evaluate the performance of an antiscatter grid and its potential benefit on image quality for a full-field digital mammography (FFDM) detector geometry at energies typical for temporal subtraction contrast-enhanced (CE) breast imaging. The signal intensities from primary, scatter, and glare were quantified in images acquired with an a-Si∕CsI(Tl) FFDM detector using a Rh target and a 0.27 mm Cu filter at tube voltages ranging from 35 to 49 kV. Measurements were obtained at the center of the irradiation region of 20–80 mm thick breast-equivalent phantoms. The phantoms were imaged with and without an antiscatter grid. Based on these data, the performance of the antiscatter grid was determined by calculating the primary and scatter transmission factors (TP and TS) and Bucky factors (Bf). In addition, glare-to-primary ratios (GPRs) and scatter-to-primary ratios (SPRs) were quantified. The effect of the antiscatter grid on the signal-difference-to-noise ratio (SDNR) was also assessed. It was found that TP increases with kV but does not depend on the phantom thickness; TP values between 0.81 and 0.84 were measured. TS increases with kV and phantom thickness; TS values between 0.13 and 0.21 were measured. Bf decreases with kV and increases with phantom thickness; Bf ranges from 1.4 to 2.1. GPR is nearly constant, varying from 0.10 to 0.11. SPR without an antiscatter grid (SPR−) ranges from 0.35 to 1.34. SPR− decreases by approximately 9% from 35 to 49 kV for a given phantom thickness and is 3.5 times larger for an 80 mm thick breast-equivalent phantom than for a 20 mm thick breast-equivalent phantom. SPR with an antiscatter grid (SPR+) ranges from 0.06 to 0.31. SPR+ increases by approximately 23% from 35 to 49 kV for a given phantom thickness; SPR+ is four times larger for an 80 mm breast-equivalent phantom than for a 20 mm breast-equivalent phantom. When imaging a 25 mm PMMA plate at the same mean glandular dose with and without an antiscatter grid, the SDNR is 4% greater with a grid than without. For an 75mm PMMA plate, the SDNR is 20% greater with a grid. In conclusion, at the higher x-ray energy range used for CE-DM and CE-DBT, an antiscatter grid significantly reduces SPR and improves SDNR. These effects are most pronounced for thick breasts.
Keywords: Scatter, glare, antiscatter grid performance, SDNR, contrast-enhanced digital mammography, contrast-enhanced digital breast tomosynthesis
INTRODUCTION
The recent development of contrast-enhanced digital mammography (CE-DM)1, 2, 3, 4, 5, 6 and CE digital breast tomosynthesis (CE-DBT)7, 8, 9, 10 has made it possible to produce high-resolution, low-dose functional x-ray images of breast tumor vascularity and tissue perfusion. In temporal subtraction CE breast x-ray imaging, high-energy images using an x-ray spectrum with energies predominantly above the K edge of iodine (33.2 keV) are acquired before and after the administration of an iodinated vascular contrast agent. Mo, Rh, and W targets operated between 41 and 55 kV with up to 0.3 mm Cu filtration (Fig. 1) have been used for this application.1, 2, 6, 7, 10 Iodine-enhanced images are produced by subtracting the logarithm of the pre- and postcontrast series, yielding images in which the signal intensities (SIs) are proportional to the iodine concentration. Analogous to CE-MRI, it is anticipated that clinical diagnosis using CE-DM and CE-DBT will rely on a combined analysis of morphological enhancement features and quantitative measurements of the vascular lesion enhancement kinetics.11, 12, 13, 14
Figure 1.
Mass attenuation coefficients of iodine and ICRU-44 breast tissue. Typical spectrum for temporal subtraction CE-DM from a Rh target exposed at 49 kV using a 0.27 mm Cu filtration. The spectrum was simulated by extrapolating the Boone model (Ref. 7).
X-ray scatter (originating in the x-ray tube, collimator, air, compression paddle, breast, breast support, and detector) and optical glare (the scatter of optical photons within the phosphor layer of the detector) degrade image quality by reducing image contrast, signal-difference-to-noise ratio (SDNR), and the effective dynamic range of the digital detector. In addition, in CE x-ray imaging, scatter and glare affect the measurement accuracy of the x-ray transmission of the iodine contrast agent, resulting in erroneous iodine concentration quantification.7, 15, 16, 17, 18 The effects of scatter and glare on iodine quantification are well known and have been described for dual-energy cardiac imaging and digital subtraction angiography,15, 16, 17 as well as for CE breast x-ray imaging.7, 18 Within the conventional low x-ray energy range used in full-field digital mammography (FFDM), the scatter-to-primary-ratio (SPR) exiting the breast can range from approximately 0.1 to 1.3, depending on breast size and other parameters.19, 20, 21 These ratios are similar for the higher x-ray energy range used for CE breast x-ray imaging.21
Experimental20, 22, 23 and theoretical studies24, 25 have demonstrated that scatter reduction improves image quality of full-field mammography at conventional x-ray energies; typically scatter is reduced before the detector by using an antiscatter grid.20, 22, 23, 24, 26 Although antiscatter grids are also used in full-field CE-DM, only one study has evaluated their performance for these higher energies.25 That study evaluated the performance of antiscatter grids as a function of the incidence angle of monoenergetic x rays using Monte Carlo techniques. The results of that study, however, do not directly translate to grid performance for practical conditions such as varying breast thickness and the polyenergetic x-ray beams encountered in CE-breast imaging.
Antiscatter grids are generally not applicable to DBT because in DBT the x-ray tube rotates over a limited angular range, while the detector typically remains stationary, preventing the use of an antiscatter grid. Mammographic antiscatter grids contain fixed lamellas parallel to the anode-cathode axis. Rotation of the x-ray tube relative to the detector would result in a significant cutoff of the primary x-ray beam. A preliminary theoretical study investigating the effectiveness of an antiscatter grid for full-field DBT at conventional x-ray energies has shown improved SDNR when using a grid.27 The actual performance of antiscatter grids in higher-energy CE-DBT has not yet been investigated.
Two studies have assessed the contribution of glare at mammographic x-ray energies and both used a narrow x-ray beam geometry.28, 29 These studies define glare as the optical and x-ray scatter arising in the detector when a breast-equivalent phantom is distant from the detector; i.e., it is present for beam-hardening only. Using that definition, it was shown that in a narrow beam geometry, glare accounts for up to 2.6% of the total signal intensity in the detector, with little spectral dependence.28, 29 However, no data are available on glare for full-field irradiation.
The purpose of this current study is to quantify the performance of an antiscatter grid for a full-field detector geometry using high-energy x-ray spectra typical for CE-breast imaging. Measurements were performed in projection images acquired with and without an antiscatter grid for various breast-equivalent phantom thicknesses and typical irradiated areas. Based on these measured data, the primary and scatter transmission factors (TP and TS) and Bucky factors (Bf) were estimated. In addition, SPRs and glare-to-primary ratios (GPRs) were quantified. By using the x-ray detector to measure scatter and glare, it is impossible to distinguish the contribution of x-ray scatter originating in the detector from optical glare. For the purpose of this paper, we define scatter (S) as the x-ray and optical scatter that arises from the addition of the breast (or phantom) on top of the breast support, while glare (G) refers to the x-ray and optical scatter arising with the phantom positioned close to the x-ray tube; i.e., it is present for beam-hardening only. These definitions are consistent with prior published work.28, 29 The measurements were used to investigate the benefit of an antiscatter grid on image quality in CE-DM and CE-DBT projection images.
MATERIAL AND METHODS
Imaging system
Experiments were performed with a modified FFDM system (Senographe 2000D, General Electric Medical Systems, Milwaukee, WI). The Senographe 2000D has an x-ray tube with Mo and Rh targets and 30 μm Mo and 25 μm Rh filters. Three target-filter combinations are allowed: Mo–Mo, Mo–Rh, and Rh–Rh. The Mo target can be used with a voltage between 22 and 36 kV and the Rh target can be operated at a maximum potential of 49 kV. Since the x-ray beam energies used in CE breast x-ray imaging can only be obtained with the Rh target, the experiments were restricted to the Rh target. A new filter wheel was installed in which the Rh filter was replaced with a 0.27 mm thick Cu filter (Puratomic® 99.999% Cu, Alfa Aesar, Ward Hill, MA). The Cu filter will produce an x-ray spectrum with higher mean energy than can be obtained with a Rh filter. The half value layer (HVL) of the Rh target beam filtered with 0.27 mm Cu was 3.06 mm Al at 49 kV.
The Senographe 2000D x-ray detector consists of a CsI(Tl) phosphor coupled to an array of photodiodes and thin-film transistors arranged as a matrix on a flat panel. The pixel size is 100 μm, and 14 bit images are produced. The source-to-detector distance is 66 cm and the distance between the tabletop and the surface of the detector is approximately 1.5 cm. The 1.4 mm thick compression plate is made of Lexan 141R. Two breast supports are available including one containing a reciprocating linear antiscatter grid (Smit Röntgen, Eindhoven, The Netherlands) and one without a grid. The antiscatter grid consists of 0.020 mm thick Pb lamellas with 0.30 mm fiber interspacing; it has 31 lines∕cm and a 5:1 grid ratio.
Assessment of glare, primary, and scattered radiation
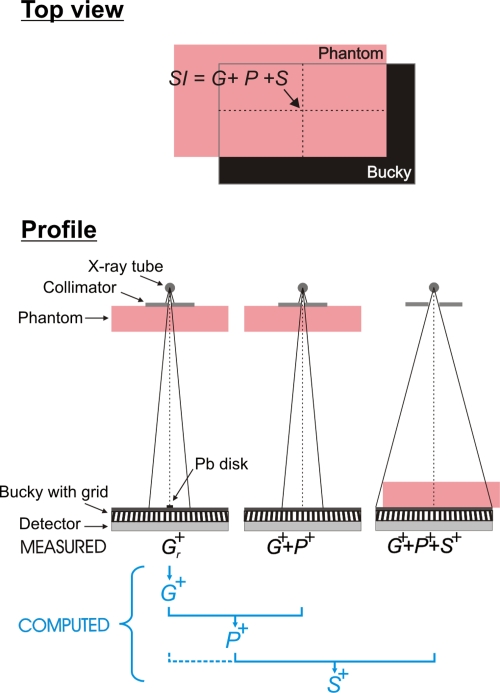
The SI in a clinical x-ray image of a breast is the sum of the glare (G), primary radiation (P), and scattered radiation (S). We assessed the magnitudes of these three components at the center of the irradiated area of a breast-equivalent phantom positioned on top of the breast support to mimic the mediolateral oblique view (MLO) (Fig. 2). G, P, and S were evaluated using 50% fat–50% glandular breast-equivalent phantoms with 20, 40, 60, and 80 mm thickness and an area 24 cm wide by 30 cm long (CIRS, Norfolk, VA). The phantoms were exposed with and without the antiscatter grid at 35, 40, 45, and 49 kV. All SIs were measured in linear images after flat-field and offset corrections were applied by the manufacturer. Image analysis was performed with MATLAB (Version R2006a, 170 Mathworks, Natick, MA).
Figure 2.
(Top) Illustration of the breast tissue equivalent phantom positioned on top of the Bucky so as to simulate the MLO view. The contributions of glare (G), primary (P), and scatter (S) to the SI at the center of the irradiated phantom area were assessed. (Bottom) Illustration of the geometry for assessing G+, P+, and S+ in the presence of the antiscatter grid. G and S were extrapolated from signal intensities behind Pb disks of various radii r. All measurements were performed with the same mA s. G−, S−, and P− without antiscatter grid were acquired in a similar way.
Glare
As stated above, G is defined as the signal arising from either x-ray scatter or optical glare when the phantom is placed distant from the detector for the sole purpose of beam hardening.29 The magnitude of G was assessed experimentally using the Pb-blocker method28, 29 (Fig. 2). A series of Pb disks of various radii was imaged consecutively, each centered at the same location on the breast support. The SI in a region of interest (ROI) behind a Pb disk with radius r is defined as Gr. Gr at zero Pb-disk radius, G, was obtained by extrapolating Gr to zero disk radius. Accurate positioning of the Pb disks was obtained through a pattern printed on a transparency slide that was fixed to the top of the breast support, with a matching pattern fixed to the top of each Pb disk.
The theoretical form of the function for extrapolation of Gr to G is not known. Prior reports in literature have applied linear or logarithmic least-squares fits to Gr as a function of the imaged Pb-disk radius28, 29 and it is clear that different results are obtained with these two methods. In our study, logarithmic fits were used. This choice was based on preliminary experiments performed in our laboratory in which the logarithmic fit yielded superior results,30 with approximately 17% smaller standard deviation in the estimate of G.
The Pb disks were 1.8 mm thick, resulting in a primary transmission of less than 10−6 for the 49 kV Rh–Cu spectrum. Gr measurements will be inaccurate if the size of the measurement ROI is incommensurate with the Pb-disk diameter or if the ROI is too small. Because of geometric unsharpness (finite focal spot size), the edges of the image of the Pb disk will be blurred; thus, the ROI must be chosen in the uniform portion of the image of the Pb disk. Due to noise, however, accurate measurement of Gr requires that the SI be averaged over a large number of pixels. The Pb-disk radii were chosen so that the G measurements were not biased by the above factors. The values chosen for r were 2.0, 2.4, 3.2, 4.8, 6.4, and 11.3 mm. A circular ROI was used with radius equal to 0.4 times the radius of the imaged Pb disk. These choices were determined in preliminary experiments to produce the most robust estimates of G; i.e., those which had the highest Pearson correlation coefficients for the logarithmic fit and the smallest standard deviations in the fit of G.
Preliminary experiments were performed to investigate the dependence of G on FOV size. These preliminary experiments were performed at 49 kV with an antiscatter grid. The estimate of G should increase with irradiated FOV size up to a FOV size where the contribution from the tails of the point spread function of G is negligible. Thereafter, the estimate of G should remain constant. Thus, to obtain an accurate estimate of G the FOV needs to be large enough to measure the full extent of G and yet narrow enough so that scattered radiation arising outside the detector does not substantially bias the G measurement.
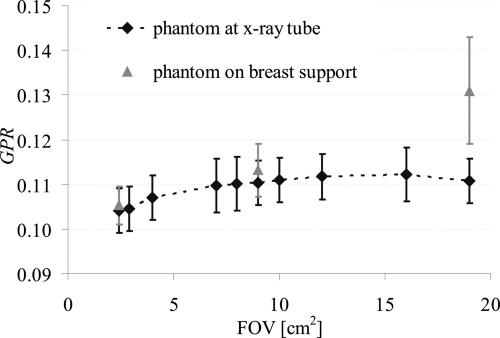
G was assessed with x-ray field sizes from 2.3×2.3 to 19×19 cm2. The preliminary measurements were performed without a phantom in the beam to ensure that the measured SI was virtually scatter-free. G was expressed as the GPR. P was obtained by subtracting the estimates of G from the SI in an image obtained using the same geometry but without a Pb disk in the beam. Figure 3 shows GPR as a function of FOV size. Note that GPR does not increase beyond a FOV of 7×7 cm2.
Figure 3.
GPR as a function of the irradiated FOV. The black symbols are GPR values with the breast-equivalent phantom positioned close to the x-ray tube; the gray symbols are GPR values assessed with the breast-equivalent phantom positioned on top of the breast support. GPR was assessed at 49 kV with antiscatter grid.
Next, the effect of beam hardening and scatter contamination were investigated by repeating the above experiment using a 2.3×2.3, 9×9, and 19×19 cm2 FOV with an 8 cm thick breast-equivalent phantom positioned as close as possible to the x-ray tube. The phantom served to filter the x-ray beam to match the primary x-ray spectrum incident on the detector when the phantom is positioned on top of the breast support, but with substantially reduced scatter. G was again expressed as GPR. P was obtained by subtracting the estimates of G from the SI in an image assessed using the same geometry but without a Pb disk in the beam. Figure 3 shows that when using a 2.3×2.3 cm2 FOV, GPR assessed with the phantom in the beam differs by 1% from the GPR assessed without phantom, suggesting that beam hardening does not significantly alter G and that scatter is insignificant at this field size. Again when using a 9×9 cm2 FOV, no significant difference is observed between G assessed using the two experimental conditions. The slight increase observed can be attributed to the slight increase in scatter recorded in this larger FOV. However, GPR with the phantom is 19% higher when using a 19×19 cm2 FOV. This measurement of G is thus clearly biased with scattered radiation when using such a large FOV.
From these preliminary experiments, it can be concluded that a 9×9 cm2 irradiated FOV size is large enough to estimate G accurately with appropriate beam hardening, while minimizing the contribution from scattered radiation arising outside the detector. Thus, a 9×9 cm2 FOV was used for the remainder of the G measurements.
Primary
P was assessed from the estimate of G and from an image of G+P acquired without a Pb disk in the beam. G+P was measured as the SI in an image of the phantom positioned as close as possible to the x-ray tube using an x-ray beam collimated to a 9×9 cm2 field of view (Fig. 2). G+P was measured at the center of the irradiated phantom area to ensure that magnitude of G was the same in the G and G+P measurements. P was calculated by subtracting the estimate of G from P+G.
Scatter
S was assessed from images of G+P and G+P+S.G+P+S was measured with the phantom positioned on top of the breast support so as to mimic the MLO view (Fig. 2). To acquire these images, the entire detector was irradiated.G+P+S was measured at the center of the irradiated phantom area. S was calculated by subtracting G+P from G+P+S. Note that this definition of S accounts for the difference in the nonprimary signal between the phantom absent and the phantom present conditions, with similar beam hardening of the primary spectrum. Thus, the predominant contribution to S is from x-ray scatter arising in the phantom. However, this method does include the effects of shielding of air scatter (and other scatter sources above the phantom), as well as contributions from any scatter and glare arising in the detector from the x-ray scatter originating in the phantom. This method is chosen to be consistent with prior related work.28, 29
The magnitude of S varies with the irradiated breast area,21, 31 therefore S was evaluated for two irradiated phantom areas simulating a large and a small area breast. For the large irradiated phantom area, 11.5×21 cm2 of the detector was covered by the phantom. For the small irradiated phantom area, 7.5×16 cm2 of the detector was covered by the phantom. Note that the small phantom area exceeds 7×7 cm2, the minimum size needed to ensure that the contribution of G is estimated without bias. The portion of the phantom outside of the irradiated field was intended to mimic the higher-order scatter from the chest and the arm.
Antiscatter grid performance
The antiscatter grid was characterized in terms of three parameters: the transmission of primary x rays TP, the transmission of scattered x rays TS, and the Bucky factor Bf. TP, TS, and Bf were measured as
| (1) |
| (2) |
| (3) |
where P+, S+, and G+ refer to the magnitude of P, S, and G with the antiscatter grid in place, and P−, S−, and G− are the magnitude of P, S, and G in the absence of the antiscatter grid. TP, TS, and Bf were evaluated for 20, 40, 60, and 80 mm thick breast-equivalent phantoms at 35, 40, 45, and 49 kV.
Glare-to-primary ratio
The magnitude of G was expressed as the glare-to-primary ratio (GPRk). GPRk is defined as GPRk=Gk∕Pk, where k refers to the presence (+) or absence (−) of the antiscatter grid. GPR+ and GPR− were evaluated for 20, 40, 60, and 80 mm thick breast-equivalent phantoms at 35, 40, 45, and 49 kV.
Scatter-to-primary ratio
The magnitude of S was expressed as the scatter-to-primary ratio (SPRk). SPRk is defined as SPRk=Sk∕Pk. SPR+ and SPR− were evaluated for 20, 40, 60, and 80 mm thick phantoms using the large irradiated phantom area at 35, 40, 45, and 49 kV. SPR+ was also assessed for all the phantom thicknesses using the small phantom area at 49 kV.
Signal-difference-to-noise ratio
To measure the effect of the antiscatter grid on image quality, the SDNR between an iodine-enhanced region I and the surrounding homogenous background B was used. The SDNR was defined per pixel as
| (4) |
where and are the average detected SI per pixel in the iodine-enhanced region and the background in the presence (k=+) or absence (k=−) of an antiscatter grid; is the standard deviation in . SDNR calculations were repeated with and without the grid using the same mean glandular dose to the phantom for each condition; thus, for each phantom thickness, the same mA s was applied with and without the antiscatter grid. The ratio of the SDNR values with and without the grid, KSDNR=SDNR+∕SDNR−, was then calculated and evaluated as a function of GPR−+SPR−. KSDNR values were assessed both experimentally and using a theoretical model of the imaging system.
The evaluation of the effect of the antiscatter grid on image quality was performed using polymethyl methacrylate (PMMA) as a phantom material instead of the breast tissue equivalent phantoms used for the previously described measurements. We were required to use a PMMA phantom because it was the only phantom available to us that contained cylindrical iodine disks. In the experiments, a 25 mm thick PMMA phantom containing iodine disks of various known areal concentrations was imaged alone or together with 25 or 50 mm thick homogeneous PMMA plates. The phantoms covered 11.5×21 cm2 of the radiation field, equivalent to the large irradiated phantom area used to assess S from the breast tissue equivalent materials (Sec. 2B). Images were acquired with and without the antiscatter grid at 49 kV. SDNR values were calculated in the raw images (processed only with the manufacturer’s gain, offset, and defective pixel correction) according to Eq. 4. SII values were measured in a circular ROI behind the 2 mg∕cm2 iodine disk; and were derived in a neighboring circular ROI behind PMMA only. The 2 mg∕cm2 iodine disk was positioned at the center of the irradiated phantom area where S is highest. GPR− and SPR− were measured for 25, 50, and 75 mm thick PMMA plates using the methods described in Secs. 2B, 2E.
For the theoretical derivation of KSDNR, the signal intensities were calculated as and. The standard deviation in the noise was calculated as , where m and q were obtained experimentally. The factors m and q were measured as follows. A 50 mm thick PMMA plate was exposed using the Rh–Cu spectrum at 49 kV with mA s values from 4 to 160. The average SI and standard deviations per pixel were computed in a 2×2 cm2 reference ROI in the raw images. The standard deviations per pixel were then plotted as a function of the average SI. A power-law least-squares fit (i.e., minimizing the χ2 value) was then applied through the data points to determine m and q.
For the condition in which the phantom entrance exposure level is the same with and without the antiscatter grid, SDNR+ and SDNR− were calculated as
| (5) |
| (6) |
where KSDNR can then expressed as
| (7) |
In this derivation, it is assumed that the difference in the scatter and glare between the iodine and background regions is negligible. In other words, the calculation of KSDNR only requires knowledge of q, GPR−, GPR+, SPR−, TP, and TS.
KSDNR was calculated for a broad continuum of GPR− and SPR− values, including the experimentally derived values for 25, 50, and 75 mm PMMA. The KSDNR calculations were repeated for the condition using no antiscatter grid (TP=1, TS=1), an ideal antiscatter grid (TP=1, TS=0), and the experimental TP and TS values derived as described in Sec. 2A for the tissue equivalent materials. In a separate experiment (not shown), TP and TS for PMMA were measured to be equivalent for tissue equivalent material and PMMA. This finding is consistent with the results of Elbakri et al.32
RESULTS
Antiscatter grid performance
Figures 4a, 4b, 4c show TP, TS, and Bf for the various breast-equivalent phantom thicknesses as a function of kV. TP increases nearly linearly as a function of kV and is independent of the phantom thickness. TP range from 0.81 (at 35 kV) to 0.84 (at 49 kV). The largest value of TS is 0.26 for an 80 mm thick phantom at 49 kV. For a given phantom thickness, TS increases nearly linearly as a function of kV. Depending on the phantom thickness, 32%–40% more scattered radiation is transmitted through the grid at 49 kV than at 35 kV. At a given kV, TS increases with phantom thickness. TS is between 12% and 27% higher for an 80 mm thick phantom than for a 20 mm thick phantom.
Figure 4.
(a) TP, (b) TS, and (c) Bf as a function of kV for various thicknesses of 50% adipose–50% glandular breast-equivalent phantoms. To assess S, 11.5×21 cm2 of the detector was covered by the phantom, while the entire detector was irradiated. The error bars show the standard error in the mean; they are representative of all TP and TS values. Error bars for Bf are negligible and are not shown.
For a given phantom thickness, Bf decreases as a function of kV. For instance, for a 40 mm thick phantom, the Bf is 1.76 at 35 kV and 1.59 at 49 kV. At a given kV, Bf increases as a function of the phantom thickness. As an example, at 35 kV the Bf is 1.52 for a 20 mm thick phantom and 2.12 for an 80 mm thick phantom.
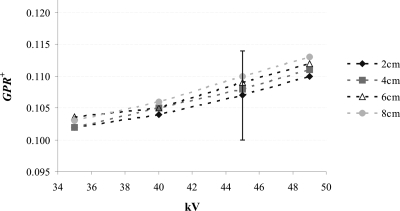
Glare-to-primary ratio
Figure 5 shows GPR+ for the 20, 40, 60, and 80 mm breast-equivalent phantoms as a function of kV. GPR+ values range between 0.10 (20 mm thick phantom at 35 kV) and 0.11 (80 mm thick phantom at 49 kV). GPR+ shows little spectral dependence, increasing approximately 8% from 35 to 49 kV. At a given kV, GPR+ values are slightly higher for thicker phantoms. Note, however, that none of these differences are statistically significant. The GPR− values are similar to GPR+ values. GPR− demonstrates trends similar to GPR+ as a function of kV and phantom thickness (results not shown).
Figure 5.
GPR+ as a function of kV for various thicknesses of 50% adipose–50% glandular breast-equivalent phantoms. The error bars represent the standard error in the mean; they are representative of all GPR+ values.
Scatter-to-primary ratio
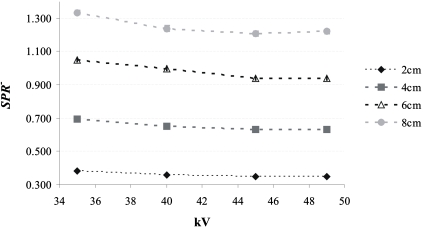
Figure 6 shows SPR− for the 20, 40, 60, and 80 mm thick breast-equivalent phantoms and the large irradiated phantom area as a function of kV. The largest SPR− is 1.34 for an 80 mm thick phantom at 35 kV. For a given phantom thickness, SPR− is approximately 9% smaller at 49 kV than at 35 kV. SPR− increases linearly as a function of the phantom thickness (Pearson correlation >0.99); SPR− for an 80 mm thick phantom is approximately 3.5 times higher than that for a 20 mm thick phantom.
Figure 6.
SPR− as a function of kV for various thicknesses of 50% adipose–50% glandular breast-equivalent phantoms. To assess S, 11.5×21 cm2 of the detector was covered by the phantom, while the entire detector was irradiated. The SPR− was calculated at the center of the irradiated region of the phantom. The error bars correspond to the standard deviation in SPR−.
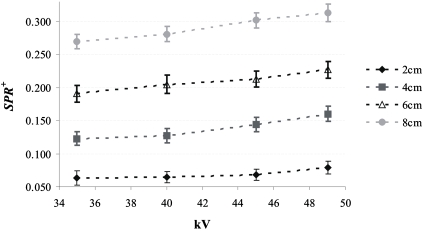
Figure 7 shows SPR+ for the 20, 40, 60, and 80 mm breast-equivalent phantoms and the large irradiated phantom area as a function of kV. The largest SPR+ is 0.31 for an 80 mm thick phantom at 49 kV. For a given phantom thickness, SPR+ increases as a function of kV; SPR+ was between 16% and 30% higher at 49 kV than at 35 kV. This result is expected as the antiscatter grid is more transmissive at 49 kV. SPR+ increases linearly as a function of the phantom thickness (Pearson correlation >0.99); SPR+ for an 80 mm thick phantom is approximately 4 times higher than that for a 20 mm thick phantom.
Figure 7.
SPR+ as a function of kV for various thicknesses of 50% adipose–50% glandular breast-equivalent phantoms. To assess S, 11.5×21 cm2 of the detector was covered by the phantom, while the entire detector was irradiated. SPR+ was calculated at the center of the irradiated region of the phantom. The error bars correspond to the standard deviation in SPR+.
Table 1 shows SPR+ at 49 kV for the 20, 40, 60, and 80 mm thick breast-equivalent phantoms as a function of the irradiated phantom area. As expected, SPR+ increases with increased irradiated phantom area. The increase in SPR+ with the irradiated phantom area is larger for thicker phantoms. When the irradiated phantom area is increased from 7.5×16 to 11.5×21 cm2, SPR+ increases by 53% for 20 mm thick phantoms and 67% for 80 mm thick phantoms.
Table 1.
SPR+ as a function of irradiated phantom area for various thicknesses of 50% adipose–50% glandular breast-equivalent phantoms exposed at 49 kV. SPR+ is calculated at the center of irradiated region of the phantom. The mean and standard deviation are given.
| Thickness (cm) | SPR+ | |
|---|---|---|
| (16×7.5 cm2)a | (21×11.5 cm2)a | |
| 2 | 0.052±0.009 | 0.079±0.010 |
| 4 | 0.100±0.009 | 0.160±0.011 |
| 6 | 0.142±0.009 | 0.227±0.013 |
| 8 | 0.187±0.009 | 0.313±0.013 |
Irradiated phantom area.
Signal-difference-to-noise ratio
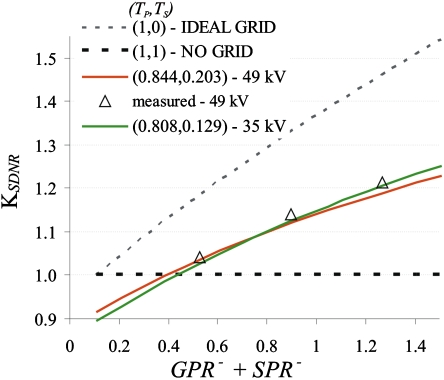
Figure 8 shows KSDNR values as a function ofGPR−+SPR−. Theoretical KSDNR values are shown for 35 and 49 kV, and experimental values are shown for 49 kV. For the theoretical calculation GPR−=GPR+=0.11, the average experimentally measured GPR− value. For the theoretical KSDNR, the measured value of q in the power curve fit, σ=m⋅SIq, is 0.5316 (χ2=0.145). In Fig. 8SPR− is varied from 0 to 1.4. TP and TS values averaged over phantom thickness, at 35 and 49 kV, respectively, were used since they change little as a function of phantom thickness.
Figure 8.
KSDNR as a function of GPR−+SPR−. The lines are theoretical KSDNR values for various antiscatter grids. The symbols represent experimentally derived KSDNR.
The experimental KSDNR values are very similar to the theoretical KSDNR values at 49 kV; they differ by a maximum of 1.3%. Note also that the theoretical KSDNR shows little energy dependence. The difference in KSDNR at 35 and 49 kV is at most 2.2%. For the two breast areas and the four breast thicknesses analyzed, SPR− is greater than 0.36, indicating that the use of an antiscatter grid will improve image quality without an increase in dose for all breast thicknesses.
DISCUSSION AND CONCLUSION
The purpose of this study was to investigate the performance of an antiscatter grid and its effect on image quality for full-field CE-DM and CE-DBT projection images. We observed that the use of the studied grid results in superior image quality (higher SDNR) for all breast-equivalent phantom thicknesses. Thus, for the same dose to the breast, CE x-ray projection imaging with the antiscatter grid benefits greatly from the reduction in S and is not deleteriously affected by the reduction in P.
It is not possible to compare directly the antiscatter grid performance found in our study with other studies; to the best of our knowledge, no studies have evaluated the antiscatter grid in the Senographe 2000D FFDM at energies that might be applied for temporal subtraction CE-DM and CE-DBT. However, the trends in the performance of the antiscatter grid studied in this paper are similar to those found by Rezentes et al.22 and Shen et al.,29 who studied the performance of the same antiscatter grid at conventional mammography energies. Shen et al.29 studied the antiscatter grid performance for a slot-scanning geometry using x-ray beams between 26 and 40 kV generated with a W-target tube and filtered with Al. Rezentes et al.22 examined the antiscatter grid performance for a large area conventional screen-film detector using x-ray beams between 25 and 35 kV generated with a Mo-target tube and filtered with Mo.
It was found that TP increases almost linearly with kV. This is analogous to the findings of Shen et al. The observed trend is most likely attributable to the lower attenuation of the carbon fiber interspace material at higher energies. In addition, coherent scatter is more forward peaked at higher energies33 and, as a consequence, more coherent scatter may be included in the primary signal measurement. The current TP values are similar to those found by Shen et al. The TP values in the current study ranged from 0.81 to 0.85, while they ranged between 0.76 and 0.85 in the study of Shen et al. The difference in Tp values in the two studies arise from the difference in the average energy of the spectra and the difference in the methods used to derive TP. As in the current work, Shen et al. used the Pb-beam stop as an intermediate step in the calculation of TP; however, Shen et al. used Pb disks with smaller radii than in the current study and this could account for the observed difference in TP.
It was found that TS increases linearly with kV. This is analogous to the results of Shen et al. However, we cannot directly compare the TS values from the current study with those of Shen et al. because of the energy dependence in TS and the different detector geometries used in the two studies. Shen et al. reported TS values between 0.19 and 0.30, while in the current work TS ranges between 0.13 and 0.22. For the slot-scan geometry considered by Shen et al., TS reflects the transmission of forward directed scatter parallel to the short axis of the detector and the transmission of scatter in all directions parallel to the long axis of the detector. For the large area geometry applied in this study, TS reflects the transmission of scatter propagating in all directions in both dimensions of the detector.
It was observed that Bf decreases as a function of kV and increases for larger phantom thicknesses. This observation is similar to the findings of Rezentes et al.22 Rezentes reported Bf values that were higher because their spectra had lower energy than in our study. We found Bf values between 1.41 and 2.12, while the Bf values found by Rezentes et al. ranged from 1.70 to 2.23.
It was observed that GPR is almost energy independent; this is similar to the findings of Shen et al.29 The presented G values, however, are higher than the values reported by Shen et al. We found that G as a percentage of G+P+S varied from 7.8% to 8.8%, while Shen et al. found that G as a percentage of G+P+S varied from 2.2% to 2.6%. The discrepancy can be attributed to three factors. First, Shen et al. used a slot detector geometry with only a partial contribution from large angle glare in the direction parallel to the long axis of the detector. Second, in contrast to Shen et al., the x-ray beam energy used in this study exceeds the K edge of the CsI(Tl) phosphor (36.0 keV for Cs and 33.2 keV for I); the interaction of x rays with the K shell of either Cs or I will generate K-fluorescence x rays which contribute additional glare34, 35 (note that the definition of glare used in the current paper and by Shen et al. includes reabsorption of scattered and fluorescence x rays). Third, Shen et al. used smaller Pb-disk radii than we did to calculate G, and the size of the Pb disks is known to affect the measurement outcome. Our GPR values agree with earlier findings by Shen et al.36 where they observed a 9% low-frequency drop (LFD) in the modulation transfer function (MTF) of the Senographe 2000D, measured by placing an opaque edge on top of the breast support. The LFD represents optical and x-ray scatters arising in the detector under a similar measurement geometry as ours.
In the current work, SPR− values decrease slightly with energy. This is similar to other work showing little energy dependence of SPR− for large area detectors.21 The SPR− values are larger than the simulated scatter-to-primary ratios exiting the breast reported by Boone et al.21 for W–Al spectra between 30 and 120 kV and various breast thicknesses. This result can be attributed to the larger irradiated phantom area used in the current experimental setup and also because our S measurements include x-ray and optical scatters in the detector arising from x-ray scatter originating in the phantom.
The effect of scatter and glare on the quantification of iodinated vascular contrast agent was beyond the scope of this paper. However, in earlier work, we showed that failure to correct for scatter and glare will result in a significant underestimation of the iodine concentration.7 For instance, for a 40 mm breast thickness, the iodine concentration will be underestimated by 40% without a grid and by 22% with a grid.7 The antiscatter grid thus improves the accuracy of iodine concentration estimation. However, scatter and glare correction algorithms are likely to be necessary for accurate iodine quantification.
The current study has the following limitations. Due to technical constraints, the impact of the antiscatter grid on image quality was only investigated in the central projection image. We anticipate that antiscatter grids, in similar fashion to conventional DBT images,27 will improve image quality in reconstructed CE-DBT images. However, additional studies are needed to fully characterize their effect on reconstructed CE-DBT images. In addition, the benefits of an antiscatter grid for CE breast x-ray imaging have only been determined for a linear carbon fiber interspaced grid with 5:1 grid ratio and these benefits may not be directly applicable to all grid technologies.
In conclusion, at the higher x-ray energy range used for CE-DM and CE-DBT, the antiscatter grid significantly reduces SPR and improves SDNR. These effects are most pronounced for thicker breasts. The results obtained in this study support the use of an antiscatter grid to improve for CE-breast image quality.
ACKNOWLEDGMENTS
The authors acknowledge the financial support from Philips Medical Systems∕RSNA Research Seed Grant 2005, the Department of Defense for the Concept Award No. BC052803, and the National Cancer Institute Grant No. PO1-CA85484. The authors thank Beverly Collins for editing this manuscript.
References
- Skarpathiotakis M., Yaffe M. J., Bloomquist A. K., Rico D., Muller S., Rick A., and Jeunehomme F., “Development of contrast digital mammography,” Med. Phys. 10.1118/1.1510128 29, 2419–2426 (2002). [DOI] [PubMed] [Google Scholar]
- Jong R. A., Yaffe M. J., Skarpathiotakis M., Shumak R. S., Danjoux N. M., Gunesekara A., and Plewes D. B., “Contrast-enhanced digital mammography: Initial clinical experience,” Radiology 10.1148/radiol.2283020961 228, 842–850 (2003). [DOI] [PubMed] [Google Scholar]
- Lewin J. M., Isaacs P. K., Vance V., and Larke F. J., “Dual-energy contrast-enhanced digital subtraction mammography: Feasibility,” Radiology 10.1148/radiol.2291021276 229, 261–268 (2003). [DOI] [PubMed] [Google Scholar]
- Bornefalk H., Hemmendorff M., and Hjarm T., “Contrast-enhanced dual-energy mammography using a scanned multislit system: Evaluation of a differential beam filtering technique,” J. Electron. Imaging 10.1117/1.2727497 16, 023006-1–023006-7 (2007). [DOI] [Google Scholar]
- Puong S., Bouchevreau X., Patoureaux F., Iordache R., and Muller S., “Dual-energy contrast enhanced digital mammography using a new approach for breast tissue canceling,” Proc. SPIE 6510, 65102H-1–65102H-12 (2007). [Google Scholar]
- Ullman G., Sandborg M., Dance D., Yaffe M., and Alm Carlsson G., “A search for optimal x-ray spectra in iodine contrast media mammography,” Phys. Med. Biol. 10.1088/0031-9155/50/13/012 50, 3143–3152 (2005). [DOI] [PubMed] [Google Scholar]
- Carton A. -K., Li J., Albert M., Chen S., and Maidment A. D., “Quantification for contrast-enhanced digital breast tomosynthesis,” Proc. SPIE 6142, 61420D-1–61420D-11 (2006). [Google Scholar]
- Carton A. K., Lindman K., Ullberg C. K., Francke T., and Maidment A. D. A., “Dual-energy subtraction for contrast enhanced digital breast tomosynthesis,” Proc. SPIE 10.1117/12.713703 6510, 651007-1–651007-12 (2007). [DOI] [Google Scholar]
- Puong S., Patoureaux F., Iordache R., and Muller S., “Dual-energy contrast enhanced digital breast tomosynthesis: Concept, method, and evaluation on phantoms,” Proc. SPIE 6510, 65100U-1–65100U-12 (2007). [Google Scholar]
- Chen S. C., Carton A. -K., Albert M., Conant E. F., Schnall M. D., and Maidment A. D. A., “Initial clinical experience with contrast-enhanced digital breast tomosynthesis,” Acad. Radiol. 14, 229–238 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nunes L. W., Schnall M. D., Siegelman E. S., Langlotz C. P., Orel S. G., Sullivan D., Muenz L. A., Reynolds C. A., and Torosian M. H., ““Diagnostic performance characteristics of architectural features revealed by high spatial-resolution MR imaging of the breast,” AJR, Am. J. Roentgenol. 169, 409–415 (1997). [DOI] [PubMed] [Google Scholar]
- Kuhl C. K., Mielcareck P., Klaschik S., Leutner C., Wardelmann E., Gieseke J., and Schild H. H., “Dynamic breast MR imaging: Are signal intensity time course data useful for differential diagnosis of enhancing lesions?,” Radiology 211, 101–110 (1999). [DOI] [PubMed] [Google Scholar]
- Hylton N. M., “Vascularity assessment of breast lesions with gadolinium-enhanced MR imaging,” Magn. Reson. Imaging Clin. N. Am. 9, 321–331 (2001). [PubMed] [Google Scholar]
- Schnall M. D., Blume J., Bluemke D. A., DeAngelis G. A., DeBruhl N., Harms S., Heywang-Köbrunner S. H., Hylton N. M., Kuhl C. K., Pisano E. D., Causer P., Schnitt S. J., Thickman D., Stelling C. B., Weatherall P. T., Lehman C., and Gatsonics C. A., “Diagnostic architectural and dynamic features at breast MR imaging: Multicenter study,” Radiology 238, 42–53 (2006). [DOI] [PubMed] [Google Scholar]
- Shaw C. -G., Ergun D. L., Myerowitz P. D., Van Lysel M. S., Mistretta C. A., Zarnstorff W. C., and Crummy A. B., “A technique of scatter and glare correction for videosensitometric studies in digital subtraction videoangiography,” Radiology 142, 209–213 (1982). [DOI] [PubMed] [Google Scholar]
- Shaw C. -G. and Plewes D. B., “Quantitative digital subtraction angiography: Two scanning techniques for correction of scattered radiation and veiling glare,” Radiology 157, 247–253 (1985). [DOI] [PubMed] [Google Scholar]
- Molloi S. Y. and Mistretta C. A., “Quantification techniques for dual-energy cardiac imaging,” Med. Phys. 10.1118/1.596418 16, 209–216 (1989). [DOI] [PubMed] [Google Scholar]
- Carton A. -K., Li J., Chen S. C., Conant E. F., and Maidment A. D. A., “Optimization of contrast-enhanced digital breast tomosynthesis, ” Lect. Notes Comput. Sci. 4046/2006, 183–189 (2006). [Google Scholar]
- Dance D. R. and Day G. J., “The computation of scatter in mammography by Monte Carlo methods,” Phys. Med. Biol. 10.1088/0031-9155/29/3/003 29, 237–247 (1984). [DOI] [PubMed] [Google Scholar]
- Fahrig R., Mainprize J. G., Robert N., Rogers A., and Yaffe M. J., “Performance of glass fiber antiscatter devices at mammographic energies,” Med. Phys. 10.1118/1.597236 21, 1277–1282 (1994). [DOI] [PubMed] [Google Scholar]
- Boone J. M., Lindfors K. K., V. N.CooperIII, and Seibert J. A., “Scatter∕primary in mammography: Comprehensive results,” Med. Phys. 10.1118/1.1312812 27, 2408–2416 (2000). [DOI] [PubMed] [Google Scholar]
- Rezentes P. S., de Almeida A., and Barnes G. T., “Mammography grid performance,” Radiology 210, 227–232 (1999). [DOI] [PubMed] [Google Scholar]
- Gennaro G., Katz L., Souchay H., Klausz R., Alberelli C., and di Maggio C., “Grid removal and impact on population dose in full-field digital mammography,” Med. Phys. 10.1118/1.2426402 34, 547–555 (2007). [DOI] [PubMed] [Google Scholar]
- Dance D. R., Persliden J., and Carlsson G. A., “Calculation of dose and contrast for two mammographic grids,” Phys. Med. Biol. 10.1088/0031-9155/37/1/017 37, 235–248 (1992). [DOI] [PubMed] [Google Scholar]
- Boone J. M., Seibert J. A., Tang C. M., and Lane S. M., “Grid and slot scan scatter reduction in mammography: Comparison by using Monte Carlo techniques,” Radiology 10.1148/radiol.2222010491 222, 519–527 (2002). [DOI] [PubMed] [Google Scholar]
- Boone J. M., Makarova O. V., Zyryanov V. N., Tang C. M., Mancini D. C., Moldovan N., and Divan R., “Development and Monte Carlo analysis of antiscatter grids for mammography,” Technol. Cancer Res. Treat. 1, 441–447 (2002). [DOI] [PubMed] [Google Scholar]
- Wu G., Mainprize J. G., Boone J. M., and Yaffe M. J., “Evaluation of scatter effects on image quality for breast tomosynthesis,” Proc. SPIE 6510, 65101T-1–65101T-9 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aslund M., Cederstrom B., Lundqvist M., and Danielsson M., “Scatter rejection in multislit digital mammography,” Med. Phys. 10.1118/1.2179122 33, 933–940 (2006). [DOI] [PubMed] [Google Scholar]
- Shen S., Bloomquist A. K., Mawdsley G. E., and Yaffe M., “Effect of scatter and an antiscatter grid on the performance of a slot-scanning digital mammography system,” Med. Phys. 10.1118/1.2184445 33, 1108–1115 (2006). [DOI] [PubMed] [Google Scholar]
- Bevington P. R., Data Reduction and Error Analysis for the Physical Sciences (McGraw-Hill, New York, 1969). [Google Scholar]
- Fritz S. L., Chang C. H. J., and Livingston W. H., “Scatter∕primary ratio for x-ray spectra modified to enhance iodine contrast in screen-film mammography,” Med. Phys. 10.1118/1.595350 10, 866–870 (1983). [DOI] [PubMed] [Google Scholar]
- Elbakri I. A., Shen S., Bloomquist A., Tesic M. M., Mawdsley G., and Yaffe M., “One-dimensional scatter grid for the SenoScan slot-scanning digital mammography system,” Proc. SPIE 5745, 1103–1111 (2005). [Google Scholar]
- Johns P. C. and Yaffe M. J., “Coherent scatter in diagnostic radiology,” Med. Phys. 10.1118/1.595443 10, 40–50 (1983). [DOI] [PubMed] [Google Scholar]
- Rowlands J. A. and Taylor K. W., “Absorption and noise in cesium iodide x-ray image intensifiers,” Med. Phys. 10.1118/1.595357 10, 786–795 (1983). [DOI] [PubMed] [Google Scholar]
- Luhta R. and Rowlands J. A., “Origins of flare in x-ray image intensifiers,” Med. Phys. 10.1118/1.596447 17, 913–921 (1990). [DOI] [PubMed] [Google Scholar]
- Shen S., Mawdsley S., Bloomquist A. K., Mainprize J. G., and Yaffe M. J., “Interpreting system MTF and NPS measured on clinical digital mammography systems,” Proceedings of the Workshop on IWDM, Bremen, Germany, 2002. (unpublished), pp. 123–127.