Adapting liver motion models using a navigator channel technique

Abstract

Deformable registration can improve the accuracy of tumor targeting; however for online applications, efficiency as well as accuracy is important. A navigator channel technique has been developed to combine a biomechanical model-based deformable registration algorithm with a population motion model and patient specific motion information to perform fast deformable registration for application in image-guided radiation therapy. A respiratory population-based liver motion model was generated from breath-hold CT data sets of ten patients using a finite element model as a framework. The population model provides a biomechanical reference template of the average liver motions, which were found to be (absolute mean±SD) 0.12±0.10, 0.84±0.13, and 1.24±0.18 cm in the left-right (LR), anterior-posterior (AP), and superior-inferior (SI) directions, respectively. The population motion model was then adapted to the specific liver motion of 13 patients based on their exhale and inhale CT images. The patient motion was calculated using a navigator channel (a narrow region of interest window) on liver boundaries in the images. The absolute average accuracy of the navigator channel to predict the 1D SI and AP motions of the liver was less than 0.11, which is less than the out-of-plane image voxel size, 0.25 cm. This 1D information was then used to adapt the 4D population motion model in the SI and AP directions to predict the patient specific liver motion. The absolute average residual error of the navigator channel technique to adapt the population motion to the patients’ specific motion was verified using three verification methods: (1) vessel bifurcation, (2) tumor center of mass, and (3) MORFEUS deformable algorithm. All three verification methods showed statistically similar results where the technique’s accuracy was approximately on the order of the voxel image sizes. This method has potential applications in online assessment of motion at the time of treatment to improve image-guided radiotherapy and monitoring of intrafraction motion.

INTRODUCTION

Advances in online soft-tissue imaging, including kV fluoroscopy, MV CT, MV cone-beam CT (CBCT), and kV CBCT enable daily imaging of the target tissue for improved tumor targeting.^{1, 2, 3, 4, 5, 6, 7, 8, 9} Daily target localization has the potential to increase the precision and accuracy of radiation delivery by reducing the treatment margins. Reducing treatment margins, and therefore the volume of normal tissue irradiated can reduce complications, while permitting local dose escalation at the tumor.^{10, 11} High precision radiation treatments, such as stereotactic body radiation therapy (SBRT), benefit from this increase in precision, allowing the technique to deliver high doses in fewer fractions to a conformal target around the tumor, which has numerous benefits for the patient.

SBRT for primary and metastatic liver cancer is currently being investigated in clinical trails.^{12, 13, 14} Radiation treatment of liver cancer is challenging, as the liver and neighboring organs such as the stomach, small bowel, and esophagus are dose limiting organs. Tumor localization at the time of treatment is important for assessing the potential dose difference from planning for both the tumor and the normal surrounding tissue. This localization is complicated by the changing liver anatomy due to stomach filing, daily patient positioning, and respiration motion.

Respiration motion of the liver, which can vary from day to day, can be quantified at the time of treatment through fluoroscopy or respiration correlated CBCT imaging.^{15, 16} Measuring the motion at the time of treatment ensures that the planning target volume (PTV) is adequate to assure coverage during treatment. Precise treatment of liver tumors is difficult as the tumor is typically not visible in x-ray generated images without the use of IV contrast. Surrogates such as the liver can be used in place of the tumor to register online images to planning for treatment assessment and delivery. If volumetric images are available, the entire liver boundary can be used as a surrogate for tumor localization, and when only low contrast images are available, the diaphragm is the most easily identifiable liver edge to determine motion and positional differences.^{1, 2, 3} Quantifying respiratory motion must first register baseline shifts of the liver with respect to the surrounding bony anatomy. Studies have shown that the reference liver position can change daily across a fractionated treatment;² therefore it is important to initially localize the reference respiratory position of the liver (e.g., the end-exhale position) at the time of treatment to the corresponding respiratory position at planning to ensure that there is not a systematic error in the treatment delivery. Image registration can be used to correlate treatment day images with planning images to compensate for image differences and to quantify the respiratory motion for tumor localization.

Rigid image registration is commercially available; however, research has shown that residual errors may exist due to deformation.^{1, 4, 5} Research is currently being conducted to investigate the geometric and dosimetric benefits of deformable image registration. Currently, the majority of the studies are focused on treatment planning images, which have substantially more soft-tissue contrast. The application of deformable registration for image-guided liver radiotherapy is currently still under investigations with narrow-band,⁶ B-splines,^{7, 8, 9} thin-plate splines,^{10, 11} optical flow,¹² fluid flow,¹³ deformation field map,¹⁴ demons,¹⁵ free-form,¹⁶ and finite element modeling (FEM)-based^{17, 18, 19} approaches. Implementation of deformable registration in the clinic is often limited in part due to potentially long computation times, uncertainties in accuracy due to reduced contrast available on in-room imaging, or the need for the time consuming process of manual segmentation, such as contouring.

FEM deformable registration using a biomechanical-based platform, MORFEUS, as described by Brock et al.²⁰ has been shown to provide accurate results in deforming the liver within the image voxel sizes, where the slice thickness is 0.25 cm. This deformable registration technique has applications in predicting tumor localization at the time of treatment and in assessing treatment response with dosimetric quantifications; however it requires segmentation of the liver on each image. Therefore, this investigation proposes to use a novel technique to predict liver motion using population models to incorporate the FEM deformable registration technique within the clinical restraints by eliminating manual segmentation and reducing the computational time.

Models are a common tool in scientific method which bring together observations and measurements of a system into a parametric function to act as a template for any possible occurrences.²¹ Using a priori knowledge and patient information, organ models can be generated to describe general and patient specific organ shape, motion, and deformation at specific time frames and across a treatment. Patient motion models can be a useful tool in patient treatment planning and assessing organ specific conditions during and as a response to therapies for a single patient or across a population.^{22, 23, 24, 25, 26, 27, 28, 29, 30, 31} This investigation proposes to generate a population liver motion FEM model that can be used to assess differences in motion variations across a liver cancer patient population in statistical application and as a template to derive patient specific motion models. The latter application will be investigated in this paper using a novel proposed protocol.

An early investigation has explored a population model, developing a navigator channel 1D motion detector, and determining the accuracy of adapting population motion models.³² The purpose of this study is to develop and validate an efficient workflow of performing the biomechanical model-based deformable registration for use with 4D images to predict patient specific respiratory motion and deformation for liver cancer cases. This is achieved by (1) generating a population model describing the average motion of the liver across a population, (2) developing a technique to automatically detect patient specific motion of the liver on patient images, and (3) using the detected motion to adapt the population motion to become patient specific.

Through these three means, this investigation will attempt to eliminate the dependence on manual segmentation and decrease computational times. In addition, the use of a population motion model will enable this technique to be applied in clinics that do not have a biomechanical model-based deformable registration algorithm. The accuracy of the technique will be assessed for both the motion detection and the adapted motion methods. Motion detection will be compared to the corresponding point motion defined using the validated full FEM deformable algorithm, MORFEUS, while the adapted motion will be compared to vessel bifurcations, tumor center-of-mass (COM) motions, and the MORFEUS deformable algorithm.²⁰

METHODS

Patient data

Treatment planning images from 13 patients treated under an institutional review board-approved protocol phase I of high precision radiotherapy for unresectable liver cancer were obtained.³³ Each patient had an abdominal CT scan (GE Lightspeed∕Discovery, GE Medical Systems, Milwaukee, WI) in the supine position with their arms above their head in an immobilization bag (Vac-Lok, Bionix, Toledo, OH) prior to treatment planning. Patients were imaged using one of the three available breathing protocols depending on their compliance and capability to perform the procedure: free-breathing (FB), abdominal compression plate (COMP),^{34, 35} or at breath-hold (BH) using the active breathing device (ABC) (Elekta Oncology Systems, Crawley, UK).^{2, 33} FB and COMP patients had a 4D CT scan (RPM, Varian Medical Systems, Palo Alto, CA) and their respiratory-sorted exhale and inhale images were used in this investigation. ABC patients had end-exhale and inhale BH CT scans (Elekta Oncology Systems, Crawley, UK), which were then used directly in this investigation. These images were acquired within 1 BH, which was approximately 15 s. Previous investigations^{2, 36} have shown that images acquired with the ABC device are highly reproducible and contain no artifacts which will affect this investigation. Table 1 outlines the statistical numbers of the patients in this investigation and their treatment protocols.

Table 1.

Characteristics of the patients and treatment protocols.

	No. of patients (N=13)
Gender
Male	6 (46.2%)
Female	7 (53.8%)
Age	66.4±10.2 (51–81)
Cancer type
Primary	6 (46.2%)
Metastatic	7 (53.8%)
Breathing protocol
Free-breathing (FB)	6 (46.2%)
Compression plate (Comp)	4 (30.8%)
Active breathing coordinator (ABC)	3 (23%)
Prescribed radiation dose	3655±863 cGy (3000–5400)

Image data

The main application for this study is to perform deformable registration between a planning CT image at a reference breathing state and a CBCT image at the same reference state or between inhale and exhale images of a 4D CBCT image. However, the main goal of this manuscript is to validate the proposed workflow (development of a population model, identification of the liver boundary, and adaptation of the population motion model). Development and adaptation of the population motion model are independent of the imaging modality used, but the quantitative accuracy, which is challenging, must be assessed. Identification of the liver boundary will be slightly more difficult on a 4D CBCT image compared to a 4D CT image, as the contrast is not as clear. Since the goal of this manuscript is to describe the feasibility of the process, 4D CT images will be used, as it would enable quantification of the accuracy using naturally occurring fiducials (e.g., vessel bifurcations), motion of the tumor COM, and comparison to a full deformable algorithm, MORFEUS, which has been previously validated. By using 4D CT images at this initial step, feasibility of the technique is established and accuracy is assessed. The substitution of 4D CBCT images for 4D CT images will only require subsequent validation of the algorithm’s ability to detect the boundary of the liver on the CBCT image. This validation can be performed through precise manual contouring of the liver on the 4D CBCT images, which is the subject of ongoing investigations.

MORFEUS: FEM based deformation registration algorithm

Exhale and inhale breath-hold data sets or exhale and inhale respiration-sorted data sets were imported into a commercial treatment planning system (PINNACLE³ v6.4 or v7.6b, Philips Radiation Oncology Systems, Madison, WI) and manual delineations of the liver was performed on each image. These contours were exported as binary masks and converted into triangular-element surface meshes using the IDL software (ITT, Boulder, CO), for use in MORFEUS, a biomechanical model-based deformable registration algorithm.

MORFEUS,²⁰ which has been described in detail in literature, will be briefly described below. MORFEUS integrates commercially available FEM pre- and post-processes (HYPERMESH v7.0, Altair Engineering, Troy, MI), Finite element analysis (FEA) software packages (ABAQUS, ABAQUS Inc., Pawtucket, RI), and the treatment planning system. The surface meshes are converted to tetrahedral-element volume meshes to represent the 3D volume. A rigid registration is initially performed using a COM translation. After rigid registration a surface projection of the two FEMs will provide boundary constraints relating the surface of the liver between exhale and inhale, which is then applied to the FEMs. In this study, the liver is assumed to undergo linear, isotropic, elastic, small deformations only and was modeled with biomechanical properties of Young’s modulus (7.8 kPa) and Poisson’s ratio (0.45).³⁷ Finally, the deformation of each node was calculated using the FEA and a deformation map of the liver’s respiratory deformation was produced. The average time required for this process depends on the number of nodes used in the mesh model, the complexity of the model, and the speed of the computer. In this study, the average computational time for MORFEUS per patient ranged between 5 and 10 min for 1724 nodes and 8819 volumetric elements (average size element is approximately 0.75 cm) from the population liver model to deform into each patient’s exhale and subsequent inhale liver model on a 2.8 GHz Pentium 4 processor with 2 GB of RAM. The output deformation map for each patient will be used to verify the accuracy of the proposed technique, which is described in Sec. 2G

4D population motion deformation model

Data sets from 10 of out 13 patients were randomly selected to formulate the basis of the population model. The exhale livers were rigidly registered to each other using rigid registration of translation based on the COM. This procedure eliminates patient positioning variations and aligns the different livers to a common spatial coordinate using a simple computation algorithm. The translation transformations were applied to the patients’ exhale liver binary mask. The binary masks were then combined into one binary mask using a logical OR function and converted into a triangular-element surface mesh, producing a population exhale liver model. This liver FEM mesh was smoothed to remove the discontinuous edges caused by the voxel summation procedure. The method generated a population model of the liver, which is larger in volume than the average liver. This is advantageous for the deformation of this population model to each patient specific liver (described below) as deformation from a large volume to a smaller volume reduces the risk of element distortion. Distortions occur when a smaller FEM model deforms into a larger FEM model. Elements are stretched during the surface projection and can lead to nodes producing large spikes in the model. However, a deformation from a large to smaller FEM model reduces these distortions and was a motivation in generating a large population model. The population model is important in assigning corresponding nodes to the same liver regions.

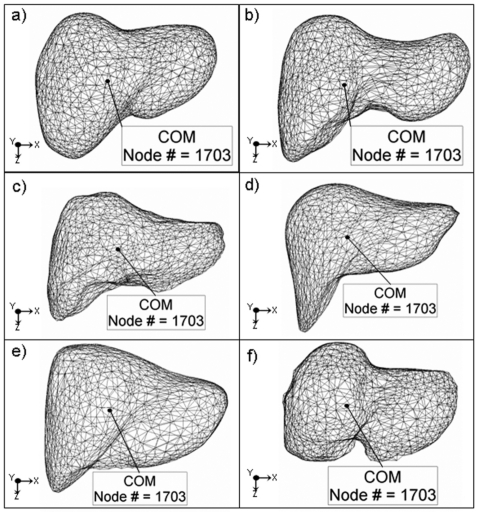
The population exhale liver model was then rigidly registered to the ten patients’ exhale liver FEMs using a principal component analysis (PCA) method to eliminate the large rotational and translational motion differences between the population and the ten patients’ specific exhale livers. PCA determines the distribution of the nodes from the mesh volumes and creates orthogonal axes for each of the patients’ exhale and the population exhale liver model. It then maps the population exhale liver model’s orthogonal axis onto each of the patients’ exhale liver model axes. The resulting rigidly registered population exhale liver model was then deformed into each patient exhale liver to generate patient specific exhale liver models using the deformable registration algorithm, MORFEUS. This result in a series of population-patient specific liver exhale models, each with a consistent mesh representation (i.e., same number of nodes, with corresponding node numbers, and with each node in approximately the same anatomical region of the liver). To show the consistency in node liver region coverage when deforming the population model to patient exhale, the COM was calculated on the population liver and on each of the patient specific FEM liver models independently. A node closest to the COM was identified and it was found that the same FEM node was consistent in the population model and across all patients (see Fig. 1).

Figure 1.

FEM mesh models of the population and five example patient exhale livers. The COM was calculated and the COM node number was highlighted on each liver showing the consistent COM node representation.

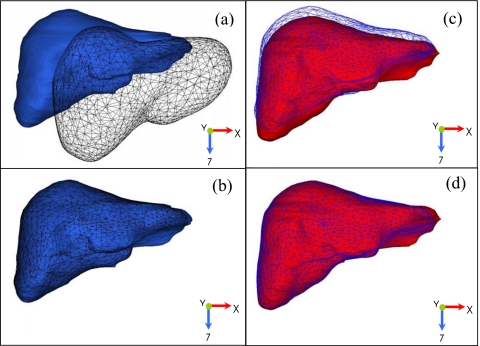
The population exhale liver model (black mesh) and a patient specific exhale liver model (black solid volume) are shown before and after both rigid and deformable registration in Figs. 2a, 2b, respectively. The resulting population-patient exhale liver model meshes (the population liver at the patient specific exhale) for each patient, shown in a light mesh in Figs. 2c, 2d, were then deformed into the patient’s respective inhale liver model (light solid volume) to obtain a deformation map of the population-patient specific respiratory liver motion for each of the ten patients. An outline of all the rigid and deformation registration processes from the population to patient model is shown in Fig. 3. The respiratory deformation maps for the ten patient population was averaged across the left-right (LR), anterior-posterior (AP), and superior-inferior (SI) directions from the exhale to inhale transformation of each node in the population-patient meshes and applied to the population exhale liver model to generate a population liver motion model. Figure 4 shows the resulting population motion model.

Figure 2.

A patient example of the liver population model deforming into the patient specific exhale and inhale liver using MORFEUS deformable algorithm to generate the liver population motion model. [(a) and (b)] The liver population exhale model (black mesh) is deformed into the patient’s exhale model (black solid volume). [(c) and (d)] The resulting population-patient exhale liver model (light mesh) is deformed into the patient’s inhale liver (light solid volume). This process generated patient specific deformation maps from the exhale to inhale respiratory states using a common mesh representation for statistical and verification analysis.

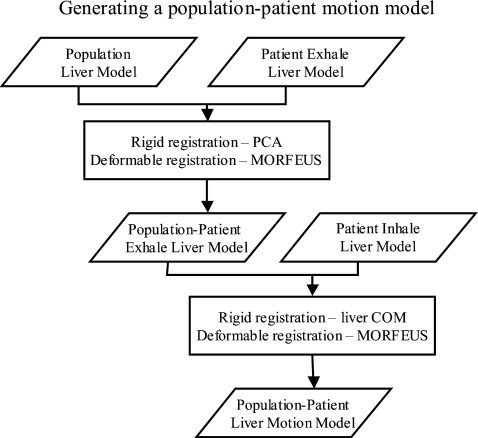
Figure 3.

A flowchart outlining the rigid and deformable registration techniques used to deform the population liver model into the patient specific exhale and then subsequently inhale liver model to generate patient specific liver motion models for validation of the proposed method.

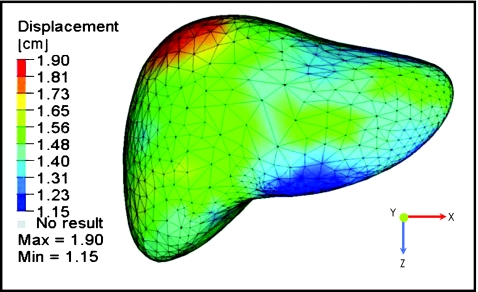
Figure 4.

Deformation color map of the liver population exhale to inhale liver motion model.

Quantification of motion using navigator channels

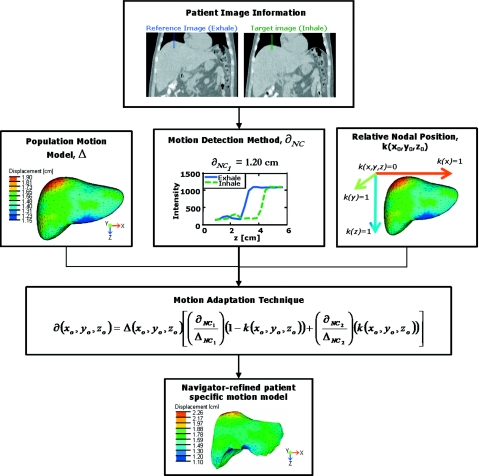
To quickly adapt the population liver motion to become patient specific without the dependence of a finite element modeling and analysis software, patient motion was quantified at four liver boundaries at the superior dome, inferior tip, anterior, and posterior edges on the patient’s exhale and inhale abdominal images and applied to the population liver motion to derive the patient specific motion. Motion in the left-right direction of the liver models was not investigated as the population motion model showed small variations less than the image voxel sizes. To quantify the motion, a navigator channel technique was developed and its process is displayed in Fig. 5. The term “navigator” originated from McConnell et al.,³⁸ defining a specific region of interest on an image to measure the diaphragm displacement. This investigation proposes a new term “navigator channel” to define a rectangular region of interest on an image, which captures the intensity values within the region and quantifies the organ edge motions as shifts in the intensity edge gradients.

Figure 5.

A schematic diagram displaying the navigator channel technique process. The motion adaptation technique utilizes the population motion model information, motion information obtained from patient specific images, and the relative nodal position to adapt the population motion model into a navigator-adapted patient specific motion. Here, the adapted motion is applied to a patient exhale FEM model for illustrative purpose.

In this study, motion was determined by placing a navigator channel at a manually chosen location along the boundary of the liver in a manually selected coronal or sagittal slice reconstruction of the exhale CT. The CT slice was selected to be approximately the middle of the liver. The channel can be adjusted in width, length, and angle along a selected sagittal or coronal slice according to the structure of interest. The navigator channel used in this initial investigation was approximately 0.5×5.0 cm² (width×length) and was placed at 0° (horizontal channel in the sagittal image) and 90° (vertical channel in the coronal image) with the image dimensions at the specified liver boundaries. The navigator channel was initially placed on the primary exhale image at the superior dome of the liver (the diaphragm) capturing the lung-liver interface; at the tip of the inferior region of the liver, capturing the liver-bowl interface; and at the anterior and the posterior liver boundaries capturing the liver-muscle interfaces. A corresponding navigator channel was then automatically placed on the secondary inhale image at the same spatial coordinates as the exhale navigator channel, capturing the intensity of the inhale image to determine the inhale positional difference at the specified liver boundary. The pixel intensities across the width of the navigators were averaged to give a 1D intensity plot function along the length of the navigator channel and to improve signal-to-noise ratio. Two intensity plots were derived, one for the exhale image and one for the inhale image, which were then fitted to a Gaussian error function by least-squares curve fitting for boundary identification. The error function is defined in Eq. 1, where x is the pixel positions along the navigator channel and I is the intensity value at each pixel positions,

$$\text{erf}\left(x\right)=\frac{2}{\sqrt{\pi }}{\int }_0^x{e}^{-I^2}dI.$$ (1)

Organ motion ∂_NC was then automatically determined (t∼10 s) as the shift required to move the primary exhale error-fitted intensity plot onto the secondary inhale error-fitted intensity plot functions. The motion detection method was tested on the four liver edges (superior, inferior, anterior, and posterior) on manually determined central slices of 4D CT planning images for all 13 liver cancer patients.

Patient specific motion and the adaptation of the population motion model

Patient specific motion was derived from the population liver motion model after adaptation using the following described technique and the 1D navigator channel motion information. The population model’s motion and deformation at each node ∂(x₀,y₀,z₀) was corrected for each patient specific motion by a linear weighting equation of the detected patient specific motion and the node’s relative distance within the liver model,

$$\partial \left(x_0,y_0,z_0\right)=\Delta \left(x_0,y_0,z_0\right)\left[\left(\frac{{\partial }_{{\text{NC}}_1}}{{\Delta }_{{\text{NC}}_1}}\right)\left(1-k\left(x_0,y_0,z_0\right)\right)+\left(\frac{{\partial }_{{\text{NC}}_2}}{{\Delta }_{{\text{NC}}_2}}\right)\left(k\left(x_0,y_0,z_0\right)\right)\right].$$ (2)

Here, Δ(x₀,y₀,z₀) represents the population motion model’s predicted deformation at that particular node. It is adjusted by the relative differences between the navigator channel’s calculated motion at two liver edges (SI or AP) (∂_NC1) and (∂_NC2) of the liver to the population’s predicted motion at those relative spatial coordinate points (Δ_NC1) and (Δ_NC2), respectively. Each node is also corrected by the specified node’s relative distance k(x₀,y₀,z₀) within the liver. This weighting function is a linear interpolation of the influences of each navigator channel’s detected patient motion across the liver volume,

$$k\left(x_0,y_0,z_0\right)=\left(\frac{{\left(x,y,z\right)}_{{\text{edge}}_1}-\left(x_0,y_0,z_0\right)}{{\left(x,y,z\right)}_{{\text{edge}}_1}-{\left(x,y,z\right)}_{{\text{edge}}_2}}\right).$$ (3)

The nodal relative distance k(x₀,y₀,z₀) is the node’s distance within the liver (x,y,z)_edge1−(x₀,y₀,z₀) between the largest liver lengths [(x,y,z)_edge1−(x,y,z)_edge2] in each cardinal direction (i.e., k=0 at the superior, right, and anterior edges of the liver and 1 at the inferior, left, and posterior edges). Equation 2 was applied to all nodes on the population volume mesh model for all 13 patients to derive patient’s specific deformation. This describes the patients’ liver exhale to inhale respiratory nodal displacement. This is effectively normalizing the population motion model based on the breathing amplitude of the patient.

A leave-one-out method was used to recalculate the population motion. The navigator channel adaptation technique was reapplied to each of the ten patients used in the generation of the population motion map to verify that there is no bias of the accuracy results to the ten patients selected.

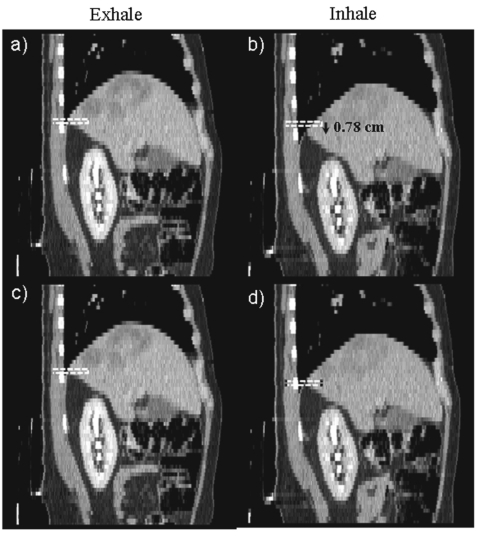
The adaptation technique was first computed in the SI direction and the resulting adapted motion was then used to help position the AP inhale navigator channel. The SI motion calculated at the location of the AP navigator channel was applied to the navigator channel on the inhale image so that the navigator channels were matched at the same anatomical position (see Fig. 6). This allowed the technique to account for the larger SI respiration motion to ensure accurate motion detection of corresponding liver edges. The complete navigator channel motion detection and the adaptation process as shown in Fig. 5, took approximately 1–2 min for each patient on a 2.8 GHz Pentium 4 processor with 2 GB of RAM.

Figure 6.

Sagittal images of a patient example showing the SI-adapted motion shifting the inhale navigator channel on the image before calculating the AP patient specific motion. (a) and (c) show the navigator channel on the patient exhale sagittal image. (b) shows the initial position of the navigator channel on the inhale sagittal image. (c) shows the shifted position of the navigator channel on the inhale sagittal image. Note that the navigator channel on images (c) and (d) are on the same anatomic position of the liver, which will ensure accurate assessment of the motion at this position.

Accuracy

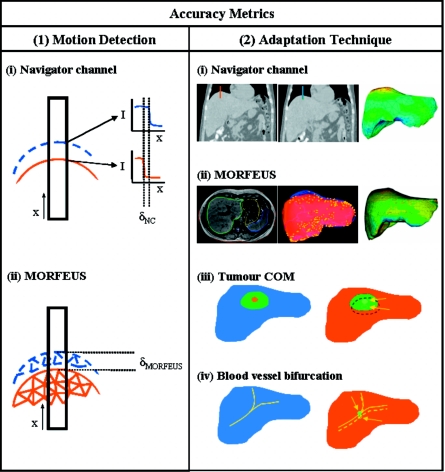
Accuracy of the navigator channel technique was assessed using several methods, which are illustrated in Fig. 7. The accuracy can be broken down into two main components: the accuracy of the navigator channel to detect the motion and the accuracy of the adapted population motion model to describe the patient specific motion.

Figure 7.

An illustration depicting the various accuracy metrics used to validate the two methods used in the navigator channel technique. To validate (1) the motion detection method, (i) the navigator channel technique was compared to (ii) MORFEUS’ motion at spatially corresponding location. An illustration of an example of a navigator channel placed on the superior dome of the liver at exhale (solid line) and at inhale (dashed line) liver boundaries. Intensity plots of the two respiratory liver edges along the navigator channel show the calculated motion as the shift between the two gradients. The navigator channel motion is compared to the node motion calculated from the population-patient FEM model generated using MORFEUS. The right box (2) shows a representation of (i) navigator channel adaptation technique and the three comparison methods used for accuracy verification. (ii) shows an axial slice image of contours of the liver, which are used to generate a FEM mesh to calculate a deformation map across the liver volume. (iii) shows an illustration of the exhale (blue and solid) and inhale (red and dashed) livers with a representative spherical tumor from which the tumor COM is calculated and their displacement is determined. (iv) shows an illustration of an enhanced vessel bifurcation from the exhale (blue and solid line) and the inhale (red and dashed) from which the point of bifurcation from both is used to calculate the bifurcation motion.

The accuracy of the navigator channel’s ability to determine the motion of the liver boundaries was determined by comparing the navigator channel’s measurement with the motion measured by the deformable registration algorithm, MORFEUS, at the corresponding position of the navigator channel. The MORFEUS technique determines its surface motion through a projection of the primary organ’s FEM surface nodes onto the secondary organ’s FEM surface and interpolates interior motion from this boundary condition restrained by the organ’s biomechanical properties. Therefore by definition of surface projection the MORFEUS technique matches the contour of the liver at exhale to the contour of the liver at inhale. This allows for MORFEUS to be an accurate comparison method for the navigator channel technique in predicting liver boundary motion, allowing for simple correlation between the image edge and the image edge determined by contours, within the contour variability.

The accuracy of the adaptation of the population motion model to predict the patient specific motion was assessed through three methods: (1) bifurcation motion, (2) tumor COM motion determined from images, and (3) (a) tumor COM motion determined from MORFEUS and (b) comparison to MORFEUS node displacement (N=number of patients; n=number of points∕tumors).

A subset of patients was administered IV iodized CT contrast agent (N=3) prior to their 4D CT scan, allowing for vessel bifurcation points within the liver to be identified on both the exhale and inhale patient images. Vessel bifurcation points are natural landmarks within organs that can be identified with contrast enhancements at spatial coordinates. With contrast enhancement and precise timing, the same vessel bifurcation can be identified in the exhale and inhale respiratory phases. Therefore, vessel bifurcation displacements can be used in determining the true motion of an organ at specified point locations (N=3, n=16). The reproducibility of identifying these vessel bifurcations has been studied and shown to have errors less than a millimeter.²⁰ The actual displacement of each bifurcation was calculated from the change in position determined from the images. The residual error of the navigator channel technique was defined as the difference between the actual and the predicted displacement. These vessel bifurcations are typically limited to the liver and are difficult to localize within the disorderly vessel system of the tumors.

Tumor COM displacements can also be determined from the patients’ images. Tumors can be delineated in patient’s 4D CT images with contrast (N=3) and in a few patient cases (N=4), where sufficient contrast remained in the tumor at the inhale BH scan. From the tumor contours, the COM can be calculated for both the exhale and inhale breathing phases to determine its motion (N=7, n=14). The navigator channel technique was applied to the exhale tumor COM positions and the calculated tumor COM displacement was compared to the tumor COM displacement determined from the images to quantify the accuracy of the technique.

For the remaining patient cases (N=6, n=18), the tumors were only visible in the exhale image. The exhale tumor contours were delineated and included in the FEM, enabling the tumor inhale position to be determined using MORFEUS.¹⁷ The tumor motion was calculated from the change in the COM motion of the tumor. The navigator channel technique was applied to the exhale tumor COM positions and the calculated tumor COM displacements were compared to the MORFEUS determined tumor COM displacement to determine the accuracy of the technique.

To compare the two tumor COM methods (image-based and MORFEUS-based), the subset of patients (N=7) with visible tumors in the exhale and inhale images (n=14) was evaluated using the MORFEUS deformable algorithm to determine the MORFEUS predicted tumor COM motion. A paired student’s t-test was conducted to determine if there is a significant difference (P<0.05) in accuracy assessment for the same patients and tumors (N=7, n=14) calculated from the image COM and the MORFEUS COM calculations.

To calculate the accuracy of the liver motion across the whole liver, the full MORFEUS method was used for comparison for all patients (N=13). MORFEUS uses finite element modeling to calculate the displacement at all points in an organ and has been previously validated to give accurate displacement information with an average 0.20 cm error.¹⁷ Pixel coordinates of the images were correlated with the CT spatial location and attached to nodes defined in the deformable registration algorithm. This allowed for comparison between the benchmark deformable registration algorithm²⁰ and the technique evaluated in this investigation at each corresponding node (n=1724 nodes for each patient). The displacements at these points were calculated and compared to the predicted displacement points in the adapted patient motion model.

RESULTS

Population model of liver motion

Qualitative assessment of the agreement of the surface deformation of the population adapted mesh to each of the patient specific exhale and subsequent inhale meshes showed good spatial agreement [Fig. 2d]. The average absolute motions (mean±SD) of the population liver motion model in the LR, AP, and SI direction were 0.12±0.10, 0.84±0.13, and 1.24±0.18 cm, respectively. Figure 4 depicts the population liver motion model at the exhale position with a color map representing the motion and deformation to the population average inhale position. The process of deforming the population exhale liver into each of the patient’s exhale and subsequent inhale liver models using the MORFEUS technique took, on average, approximately 20 min.

Accuracy of the motion detection technique

The motion detection capability of the technique was assessed at four liver boundaries: the superior dome of the liver, the inferior tip of the left lobe, the anterior liver edge, and the posterior liver edge. An approximate median coronal and sagittal slice was chosen from each patient’s liver CT images and the navigator channels were placed at the farthest extent of the liver in the slice. For the coronal slice, the superior and inferior edges were tested and for the sagittal slice, the anterior and posterior edges were tested. The accuracy of the motion detection technique was assessed by comparing the measured motion to the motion determined by the full patient specific deformable registration by MORFEUS at the navigator channel central position along the liver edge. An illustration of the motion calculation from the two techniques is shown in the left panel of Fig. 7. The average absolute accuracies (mean±SD) for the four liver boundaries at the superior dome, inferior tip, anterior edge, and posterior edge were 0.10±0.09, 0.11±0.04, 0.11±0.07, and 0.10±0.07 cm, respectively, as shown in Table 2. These values are comparable to the respective CT voxel resolution of 0.10×0.10×0.25 cm³ and the computational time took less than 1 min.

Table 2.

The average absolute accuracy of patient motion detection using the navigator channel at the four liver boundaries compared to the corresponding locations in the full deformable registration algorithm. (MORFEUS motion—navigator channel motion).

Liver boundary	Mean (cm)	SD (cm)	Max (cm)	Min (cm)
Superior dome	0.10	0.09	0.31	0.01
Inferior tip	0.11	0.04	0.20	0.04
Anterior edge	0.11	0.07	0.21	0.01
Posterior edge	0.10	0.07	0.26	0.00

Accuracy of the adapted-population motion models

The population motion model was adapted to each patient using the 1D motion calculated from the navigator channel at the four liver boundaries for SI and AP direction adaptation to account for the differences in patient specific motion from their CT images. The accuracy of the adaptation of the population motion to the patient specific was compared using the three different methods described above and are shown in Table 3. The LR residual error between the population motion without adaptation and the patient specific motion was also compared and showed similar results to the SI and AP residual errors in all three types of verification methods.

Table 3.

The average absolute accuracy of patient motion prediction of the adapted motion model compared to the three different verification metrics: (1) MORFEUS deformable algorithm, (2) tumor COM, and (3) vessel bifurcations. (Comparison method motion—adapted motion). There are 13 patient data sets in total, which were all tested using the MORFEUS deformable registration algorithm. A subset of the patients (N=3) had contrast administration, where bifurcations and tumors were identifiable. An additional subset of patients (N=4) had visible tumor shadows in their images, which allowed for tumor COM comparison as well as the contrast patients. The remaining patients (N=6=13−7) where the inhale tumor was not visible in the CT images derived the tumor COM motion using the MORFEUS deformable algorithm.

Verification method	SI	AP	LR	Vector
	Mean (cm)	Mean (cm)	Mean (cm)	Mean (cm)
Bifurcations (N=3, n=16)	0.26	0.13	0.15	0.33
Tumor COM (N=7, n=14)
MORFEUS tumor COM	0.19	0.15	0.20	0.33
Image tumor COM	0.14	0.13	0.21	0.29
MORFEUS (N=13, n=1724)	0.25	0.24	0.23	0.43
MORFEUS tumor COM (N=6, n=18)	0.20	0.22	0.24	0.38

Corresponding vessel bifurcations identified on the patient’s exhale and inhale image were used to compare the accuracy of the adapted-population motion at the specified point locations. The absolute average accuracies (mean±SD) at the vessel bifurcation points were 0.26±0.16 and 0.13±0.13 cm in the SI and AP directions, respectively.

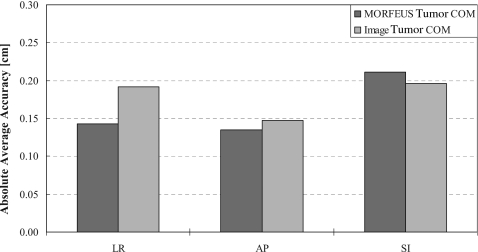
The adapted-population motion accuracies were also verified using tumor COM using two methods: (1) from the images directly and (2) using the MORFEUS deformation algorithm. The absolute average differences in the calculated displacement of the tumor COM motion between the adapted-population motion and the image determined COM motion for the tumor visible patients (N=7, n=14) were 0.14±0.13 and 0.13±0.11 cm in the SI and AP directions, respectively. The absolute average differences in the calculated displacement of the tumor COM motion between the adapted-population motion and the MORFEUS determined COM motion for the remaining patients (i.e., patients where the tumor was not visible on the inhale image, N=6, n=18) were 0.19±0.17 and 0.15±0.09 cm in the SI and AP directions, respectively. The two tumor COM accuracy methods were compared by performing the MORFEUS deformable algorithm on the tumor visible patients (N=7, n=14). A paired student’s t-test showed no significant difference (P>0.05, P=0.32, 0.79, 0.73) in all three directions, LR, AP, and SI, respectively (Fig. 8).

Figure 8.

A bar graph illustrating the absolute average accuracy of the navigator channel adaptation technique using the two tumor COM methods: MORFEUS (dark gray) and image derived (light gray).

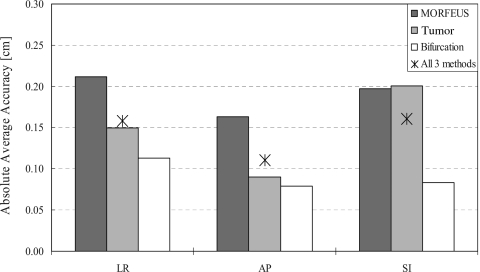
The accuracy was assessed across all node displacements in the adapted volumetric mesh by comparison to the corresponding node displacements calculated from the full population-patient specific deformation using the MORFEUS algorithm to determine the relative accuracy across the entire liver volume. The absolute average accuracies (mean±SD) across N=13 patients were 0.25±0.19 and 0.24±0.16 cm in the SI and AP directions, respectively. For the subset of patients (N=3) where all three accuracy metrics were applicable, the analysis showed similar results for all three verification methods (see Fig. 9).

Figure 9.

A bar graph illustrating the absolute average accuracies across the contrast enhanced subset of patients (n=3), which were verified using all three verification methods. A star is drawn showing the average of all three verification methods in each of the cardinal directions.

DISCUSSION

This research introduces several new concepts to improve current deformable registration techniques for online applications. The objective of this investigation was to develop a technique that utilizes a priori information and updated patient-specific limited information to quickly adapt patient specific motion information. Population motion models were introduced as a priori templates of patient respiratory motion, liver deformation, and subsequently surrogate tumor motions during treatment. The updated patient-specific limited information studied was 1D motion information acquired from patient images. A navigator channel technique was developed, which brought together these new concepts, to incorporate and update FEM deformable registration to describe patients’ specific motion within online restraints for applications in image-guided radiotherapy (IGRT) such as SBRT.

The adaptation accuracy was verified through three different methods. Vessel bifurcations are natural landmarks within organs that can be defined with contrast enhancement. Bifurcation points identified in all patients used in this study would be ideal in verifying the motion accuracy of the technique; however this is currently difficult to obtain. Standard contrast enhanced imaging is time sensitive, requiring precise timing to capture the contrast. 4D CT images can be obtained after the administration of contrast; however only a moderate amount of visible vessels in both the exhale and inhale sorted data sets is identifiable. Optimization of IV contrast for 4D CT and 4D CBCT is still under investigation. Currently this investigation has investigated three contrast patients. Therefore, other validation methods were investigated for comparison.

The tumor and the internal motions and deformations are important treatment-based measurements that should be considered. While the vessel bifurcation points were assessed to identify the error precision at specific points, the deformation algorithm was used to verify the accuracy at points in all regions of the liver, including the tumor. There are several factors, which make MORFEUS a suitable accuracy metric for this investigation. The accuracy of MORFEUS has been previously validated with bifurcation points and tumor COM and publications have shown an absolute average accuracy of 0.20 cm across the volume of the liver for the largest motion direction, SI.²⁰ The maximum error of MORFEUS has also been studied and shown as 0.40, 0.66, and 0.31 cm in the LR, AP, and SI directions, respectively.³⁹ The same accuracy was seen in this study’s patient motion model results. The accuracy of the navigator channel technique using MORFEUS as a comparison showed similar results to the other three types of verification methods. In particular, for a subset of patients with visible tumors, the tumor COM verification method was compared using the images directly and also using the MORFEUS deformable algorithm. The results of the two methods had no significant difference, enabling MORFEUS to be a surrogate for accuracy when patient specific tumor motion is not available.

A subset of patients that had contrast administration (N=3) was verified using all the verification methods: (1) MORFEUS deformable registration algorithm, (2) tumor COM, and (3) vessel bifurcations. A comparison of the navigator channel technique’s accuracy from all three verification methods shows similar results across the methods (Fig. 9). For therapeutic applications, the tumor area is of particular interest to assess treatment response for online image-guided applications of the liver region (defined by MORFEUS and bifurcation points) for treatment complication assessment.

The overall accuracy results of the navigator channel technique show a similar error to the MORFEUS deformable algorithm, which can validate this technique’s ability to substitute MORFEUS for online applications. The technique retains the advantages of a biomechanical FEM motion model generated from MORFEUS through the incorporation of the population motion model in the adaptation technique. Yet the navigator channel technique has the advantage of a shorter computation time of less than 2 min and is independent of manual segmentations, which is of interest for online low contrast images such as CBCT.

One of the proposed benefits of using a biomechanical model-based technique is the inclusion of different material properties between the liver and the tumor. The population motion model provides a reference to the internal motion of the liver based on inherent biomechanics, which is incorporated into the adaptation method by Eq. 2. This is advantageous over a simple linear interpolation of the detected navigator channel edge motion as it provides a template to the biomechanical motion of the internal liver motion. A simple comparison of the adapted population motion model technique to a simple 1D linear interpolation was tested on the tumor COM and showed that 3 out of 13 patients had errors of >0.50 cm with linear interpolation, where the adaptation technique with the population motion model had errors of <0.25 cm. The population motion model adaptation technique described here currently does not include the variation in the material properties between the tumor and the liver, as this is different for each patient. Future work will investigate the benefit of approximating the local changes resulting in tumor stiffness on the accuracy of the method. Using a patient specific motion model, as opposed to the population motion model, would enable this variation in materials to be included in the adaptation at each treatment fraction.

Using a patient specific motion model and adapting based on the information obtained at their individual treatment is the primary and ideal application for this technique. However, a population motion model and adaptation was investigated for two reasons. First, a population motion model can provide a common template for describing the variations in motion across a population in treatment assessment. The common nodes and liver motion for specific liver regions provides a reference template of the expected motion in the area that is then adapted to the patient specific motion. Second, to enable general clinical implementation, a population motion model was generated for use in any clinic with the navigator channel technique to derive the patient’s specific motion without the need for an in-house finite element modeling and analysis algorithm. The complete navigator channel motion detection and adaptation method takes approximately 1–2 min to perform with the population motion model, which is still within the online time constraint and can be used in adaptive treatment planning to adjust PTV margins for daily respiratory motion changes.

The liver population motion model was shown to accurately adapt to patient specific motion using SI and AP patient motion information. The SI and AP motions were studied in this investigation as they had the greatest motion variations in the patient population used in this study. The navigator channel technique currently utilizes a voxel-by-voxel analysis of the image intensity and is currently limited to the image resolutions of 0.10×0.10×0.25 cm³ for the 4D CT images. Detection and adaptation of the model in the LR direction were ignored as the difference between patient and population motion was on the order of the voxel size for all three accuracy metrics, as seen in Table 3. Future investigation on interpolating the image intensity values between the voxel lengths will increase the accuracy of the navigator channel detection and adaptation technique and allow for LR direction adaptation.

This investigation evaluated the accuracy of developing and adapting a population motion model based on 4D images. This consisted of three steps, each of which requires validation: (1) generation of the population motion model, (2) detection of the motion at the organ boundaries, and (3) refinement of the population motion model. Steps 1 and 3 are independent of the images used in the analysis and step 3 is arguably the most novel, with the highest demand for validation. For these reasons, 4D CT images were used to enable validation of the population refinement using anatomical features in the 4D CT images, which are not visualized in 4D CBCT images, which is the target application. Future work will focus on validating the detection of motion at the organ boundaries based on 4D CT images; however the accuracy presented here provides an estimation of the accuracy that may be expected.

Applying the navigator channel technique to all phases of 4D CT or 4D CBCT is another exciting future application. Continuous respiratory motion model can be a valuable tool for future investigation of irregularities in a patient’s breathing pattern. A continuous respiratory motion model can be generated at treatment planning using 4D CBCT. Then with the navigator channel technique, the motion model can be adapted to daily CBCT images to account for the changing patient anatomy. For this initial investigation, the aim was to validate the application of the navigator channel technique to the current clinical practice of assessing two respiratory phases, the exhale and inhale phase, in determining the patient’s treatment motion. Therefore the navigator channel technique was tested from these breathing states to predict the accuracy of this method’s ability to account for the large differences in breathing motion.

The motion was captured with a rectangular region of interest to reduce computational time in this investigation. The motion detection technique uses an edge detection that is not sensitive to the tissue’s slight variations in specific voxel intensities at the tissues. At these boundaries, gradients of intensity value differences between soft tissues (lung∕liver or liver∕intestinal tract) are fitted to a Gaussian error function, which is then used to calculate the edge motion regardless of the intensity magnitudes. The 1D calculation allows the motion technique to be fast, within seconds, for online applications. Future investigation will look at adapting this technique to cine MR and fluoroscopy as in-room real time imaging modality offers the possibility of online tracking or gating of treatment delivery with this technique to ensure complete coverage of the tumor throughout the duration of the treatment.^{40, 41}

This investigation has shown that the navigator channel technique has the capability to provide motion information in limited image data by reducing the need for time-consuming steps required in some deformable registration such as contouring to quantify online patient motion for verification and assessment of treatment delivery. This technique is not restrained by the need for volumetric data and can be applied to real-time imaging modalities such as cine MR or fluoroscopy. Its application can further expand to other important anatomical sites, which exhibit intrafraction motion, such as prostate or lung. The navigator channel technique is a promising method to apply quick and accurate deformable registration with visual aids of motion models to verify, assess, and adapt treatment delivery for multiple sites which experiences intrafraction motion.