Abstract
Several Monte Carlo systems were benchmarked against published measurements of bremsstrahlung yield from thick targets for 10–30 MV beams. The quantity measured was photon fluence at 1 m per unit energy per incident electron (spectra), and total photon fluence, integrated over energy, per incident electron (photon yield). Results were reported at 10–30 MV on the beam axis for Al and Pb targets and at 15 MV at angles out to 90° for Be, Al, and Pb targets. Beam energy was revised with improved accuracy of 0.5% using an improved energy calibration of the accelerator. Recently released versions of the Monte Carlo systems EGSNRC, GEANT4, and PENELOPE were benchmarked against the published measurements using the revised beam energies. Monte Carlo simulation was capable of calculation of photon yield in the experimental geometry to 5% out to 30°, 10% at wider angles, and photon spectra to 10% at intermediate photon energies, 15% at lower energies. Accuracy of measured photon yield from 0 to 30° was 5%, 1 s.d., increasing to 7% for the larger angles. EGSNRC and PENELOPE results were within 2 s.d. of the measured photon yield at all beam energies and angles, GEANT4 within 3 s.d. Photon yield at nonzero angles for angles covering conventional field sizes used in radiotherapy (out to 10°), measured with an accuracy of 3%, was calculated within 1 s.d. of measurement for EGSNRC, 2 s.d. for PENELOPE and GEANT4. Calculated spectra closely matched measurement at photon energies over 5 MeV. Photon spectra near 5 MeV were underestimated by as much as 10% by all three codes. The photon spectra below 2–3 MeV for the Be and Al targets and small angles were overestimated by up to 15% when using EGSNRC and PENELOPE, 20% with GEANT4. EGSNRC results with the NIST option for the bremsstrahlung cross section were preferred over the alternative cross section available in EGSNRC and over EGS4. GEANT4 results calculated with the “low energy” physics list were more accurate than those calculated with the “standard” physics list.
Keywords: Monte Carlo, radiotherapy, bremsstrahlung, megavoltage x-ray spectra
INTRODUCTION
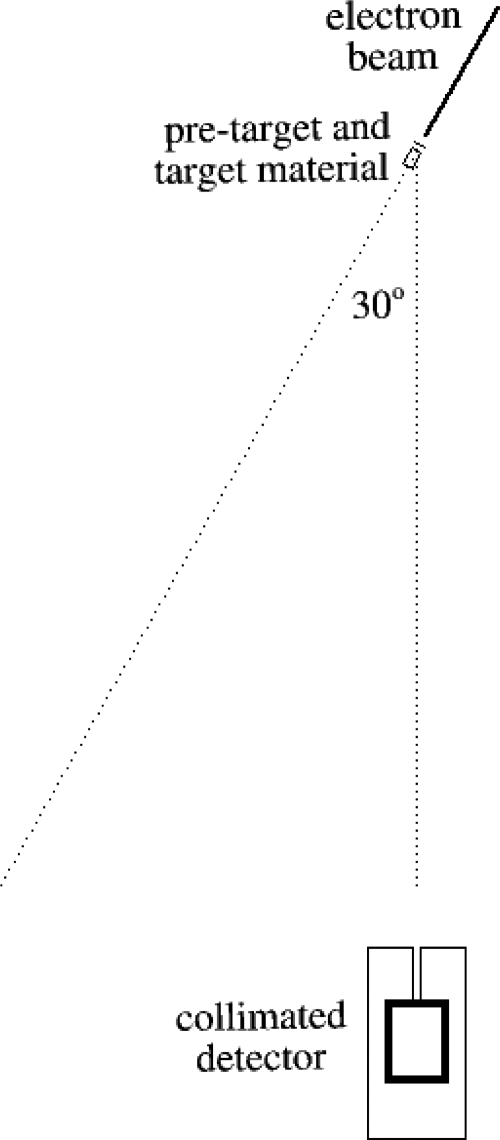
The objective of this work was to use published experimental benchmarks to evaluate the accuracy of thick-target bremsstrahlung calculated with current Monte Carlo systems. The measurements of photon yield and spectra from thick targets by Faddegon et al.1, 2 are the most accurate and comprehensive published benchmarks of thick-target bremsstrahlung for beam energies used in radiotherapy. In these experiments, depicted in Fig. 1, thick targets of Be, Al, and Pb were irradiated with electrons ranging in energy from 10 to 30 MeV in 5 MeV increments. Photon fluence was measured differential in energy. Measurements were done on the beam axis for 10–30 MV x-ray beams and at angles out to 90° from the beam axis for the 15 MV x-ray beams.
Figure 1.
Experimental geometry, drawn to scale. Electron beam incident on pretarget material and the Be target, with the collimated NaI detector placed at an angle of 30° to the incident beam direction.
Three of the most commonly used Monte Carlo systems for treatment head simulation in radiotherapy were evaluated against these benchmarks: EGSNRC,3GEANT4,4, 5 and PENELOPE,6, 7 (see, for example, the review article by Verhaegen and Seuntjens8). The codes are ordered alphabetically without regard for preference of one code over another.
It is time to revisit this benchmark. EGS4, benchmarked against these measurements in the original publications,1, 2 has undergone refinements up to and including the release of EGSNRC that may have impacted the result.9PENELOPE has only been benchmarked against the 15 MV measurements.10GEANT4 has not been benchmarked against these measurements. Computer processor speeds have increased dramatically since the EGS4 benchmark results were first published. This made it practical to calculate fluence, differential in energy and angle, with a calculational precision well below the experimental uncertainty, resulting in a more accurate comparison.
Radiation transport parameters were chosen for accuracy in favor of speed. Simulations done using the different codes were run on the computers available to the experts performing the simulation to take advantage of their knowledge of the code. Therefore, a comparison of speed was not done. A meaningful comparison of calculation efficiency requires selection of radiation transport parameters for speed and accuracy with the different codes run on the same computer with optimal compiler settings.
MATERIALS AND METHOD
Measurement
The benchmarks are published measurements1, 2 made at the National Research Council of Canada on a Vickers linear accelerator. The published details of the experiment needed for simulation are repeated here. The beam energies used in the simulations are more accurate than those previously reported.
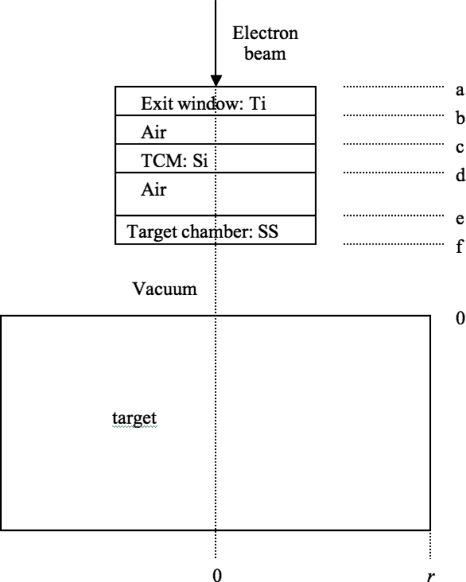
A 0.35-cm-diam electron beam was normally incident on a high purity Ti exit window, passing into air and through a transmission current monitor (TCM) and into the target, as shown in Fig. 2. An evacuated target chamber with a stainless-steel (SS) window was used at small measurement angles (0°–10°) to keep noise down for measuring low beam currents in the target. At larger angles, beam currents were high enough for measurement with the TCM, and the target chamber was removed for the measurements (30°–90°).
Figure 2.
Source of photons in the published experimental benchmark. The target chamber with the stainless steel (SS) entrance window was removed for the measurements at 30°–90°, with the vacuum between the TCM and target replaced by air. Letters on the side refer to the positions of the different components shown in Table 1.
Individual photons were detected and energy resolved with a 20 cm×25 cm NaI scintillator. The detector was placed with the central axis of the 2.4-cm-diam, 20-cm-thick Pb collimator aligned with the point on the upstream surface of the target on the beam axis. The detector surface was 318–361 cm from the upstream surface of the target. The fluence of photons that would reach the surface of the detector with only vacuum between the target and detector was determined. To do so, the raw counts from the detector were corrected for the presence of the detector and other material downstream of the target. The main corrections were for attenuation by the target chamber (when present) and air, the collimator effect, pulse pile-up, detector response, and detector efficiency. It was assumed that charged particle fluence was reduced sufficiently with scatter in the over 3 m of air and subsequent collimation to have a negligible effect on the photon count and spectra.
The corrected photon count included photons from the target and material upstream of the target. Results were published as photon fluence per unit energy per incident electron (spectra) and total fluence of photons above a lower energy cutoff per incident electron (photon yield). Photon yield was measured with an accuracy of 5% on the beam axis, 5%–7% off axis. Relative fluence for different energies on the same target, or different angles from the beam axis for the same beam energy, was measured to 3% out to and including 30°, with uncertainty as high as 6% at 90°. Uncertainties are 1 s.d. and include both random and systematic errors.
The first set of published benchmarks1 was made on the beam axis for 10–30 MV x-ray beams. The photon yield was limited to energies above 0.22 MeV. The second set2 was made at angles out to 90° for the 15 MV beam. The photon yield was limited to energies above 0.145 MeV. A detailed uncertainty analysis is given in these papers.
The positions of the different components (Fig. 2) relative to the target are shown in Table 1. The 10–30 MV measurements were made with a 0.15-mm-thick TCM and the target chamber window between the exit window and target. The angular distribution measurements at 15 MV were made using a 0.1-mm-thick TCM with the target chamber present for measurements out to and including 10°.
Table 1.
Positions of the different components used in the thick-target bremsstrahlung yield measurements shown in Fig. 2, from the target surface. Units are centimeters.
| Point | 10–30 MV on beam axis | 15 MV angular distribution | ||
|---|---|---|---|---|
| Al | Pb | Be and Al | Pb | |
| a | 2.613 | 3.313 | 2.613 | 3.313 |
| b | 2.6 | 3.3 | 2.6 | 3.3 |
| c | 2.215 | 2.915 | 2.21 | 2.91 |
| d | 2.2 | 2.9 | 2.2 | 2.9 |
| e | 0.9051 | 1.6051 | 0.9051 | 1.6051 |
| f | 0.9 | 1.6 | 0.9 | 1.6 |
| r | 3.63 | 1.583 | 3.63 | 1.583 |
The electron beam from the Vickers accelerator was transported through a 90° bending magnet consisting of two 45° dipole magnets. At the time of the measurements the energy calibration was based largely on a measurement of the photoneutron threshold in 16O. Since then, a more detailed energy calibration was carried out using an independent magnetic spectrometer. The standard uncertainty on the new calibration curve was estimated to be 0.2%. During that work, it was noted that changes in the position and angle at which the beam entered the analyzing magnet could lead to changes in the electron energy of up to 1%. A new slit system to better define the beam as it entered the analyzing magnet was added. The beam energies used in the thick-target bremsstrahlung measurements, made without the new slit system, were determined from the new calibration curve to be 10.09, 15.18, 20.28, 25.38, and 30.45 MeV. Changes in the beam entrance geometry done prior to the calibration could have led to changes in the beam energy of ±0.5%, leading to a 0.5% uncertainty estimate in the quoted beam energies. The energy spread was limited to 1.5% with slits in the bending magnet.
Simulation
The source was simulated as a 0.35-cm-diam circle (EGSNRC and GEANT4) or a 0.35×0.35 cm square (PENELOPE) of constant fluence normally incident on the exit window. The beam energies were those listed earlier, from the latest calibration of the bending magnet.
The simulation geometry from the exit window through to the target was the same as the experimental geometry, shown in Fig. 2. The targets were cylinders with radii given in Table 1. They were simulated as pure Be, Al, and Au, using the measured density of 1.848 g∕cm3 for Be, 2.699 g∕cm3 for Al, and 11.34 g∕cm3 for Pb. Target thicknesses (from measurement) with energy increasing from 10 to 30 MV for the Al target were 6.48, 9.73, 11.63, 15.14, and 16.21 g∕cm2 and for the Pb target were 6.85, 9.13, 11.43, 11.43, and 13.68 g∕cm2. The Be target, used only at 15.18 MeV, was 11.67 g∕cm2 thick. The exit window was composed of pure titanium of density 4.54 g∕cm3, the TCM of pure Si of density 2.33 g∕cm3. Air was close to room temperature, simulated as density 0.001205 g∕cm3 of C, N, O, and Ar in proportion of 0.000124, 0.756, 0.232, 0.0128 by weight. Stainless steel was simulated as density 8.06 g∕cm3, consisting of C, Si, Cr, Mn, Fe, and Ni in proportion of 0.001, 0.007, 0.18, 0.01, 0.712, 0.09 by weight. The region downstream of the target was simulated as vacuum as the measurements were corrected for material between the target and the detector, including air, and the wall of the target chamber, when present.
Fluence was scored either in a 0.1-cm-thick region on the surface of a 176.7 cm radius cylinder with the flat end 100 cm from the upstream surface of the target (EGSNRC) or on the surface of a 100 cm radius sphere centered on the point at the intersection of the beam axis and the upstream surface of the target (GEANT4 and PENELOPE). The widths of the energy bins were 0.01 MeV, sufficiently small to allow rebinning without adding significantly to the uncertainty in the comparison.
Each code offers different parameters for the radiation transport. Parameters were selected to give an accurate calculation of photons emitted from the target. Some options were chosen to speed up the simulation without loss of accuracy. The parameters chosen for each code follow.
EGSNRC
The simulation utilized EGSNRC3 version 1.41 of 13 February, 2007 with the FLURZ user code, version V1 Rev 1.31 of 12 March, 2003. Both codes were downloaded from the web site of the Ionizing Radiation Standards group of the National Research Council of Canada at www.irs.inms.nrc.ca. Details of the radiation transport and cross sections are given on that web site.
The multiple scattering algorithm in EGSNRC is based on the Goudsmit and Saunderson theory,11, 12 as formulated in Kawrakow and Bielajew13 with a single elastic scattering cross section from partial wave analysis calculations.14 This results in more accurate scattering than the algorithm used in EGS4. The default total and differential bremsstrahlung cross section in EGSNRC is the Born approximation Bethe-Heitler cross sections with an empirical correction factor below 50 MeV from Koch and Motz,15 with the angular distribution based on formula 2BS in the same paper. There is an option to select only the leading term of this distribution, but this can lead to differences of a few percent in the angular distribution at 10° off axis.16
Transport parameters included electron lower energy cut-offs ECUT and AE of 0.7 MeV, and photon lower energy cut-offs PCUT and AP of 1 keV, with the boundary crossing algorithm set to EXACT and the electron-step algorithm set to PRESTA-II. The maximal fractional energy loss per step ESTEPE was 0.25, maximum first elastic moment per step XIMAX of 0.5, and skin depth for BCA 3.0 mean free paths. PEGS4 cross sections were generated using the EPSTFL=1 and IAPRIM=1 for more accurate collisional and radiative stopping powers. Bremsstrahlung and pair angular sampling were from Koch and Motz (KM). Spin effects, bound Compton scattering, Rayleigh scattering, and atomic relaxations were turned on. Photoelectron angular sampling, triplet production, radiative Compton corrections, and electron impact ionization were turned off. Uniform bremsstrahlung splitting, a technique originally implemented in EGS4 by Bielajew,1 was used with Russian Roulette of the secondary charged particles, with 100 photons generated for each bremsstrahlung event.
Four sets of simulations of the experimental benchmarks were done to assess the effect of different cross sections. Option set 1 used the above-mentioned transport parameters and cross sections with bremsstrahlung from the Bethe–Heitler (BH) cross section (EGSNRC option of BH) and Storm and Israel photon cross sections17 from PEGS4. Option set 2 used the NIST differential bremsstrahlung cross-section database,18 which is the basis for ICRU recommended radiative stopping powers (EGSNRC option NIST). Option sets 3 and 4 used the NIST bremsstrahlung cross sections with different photon cross sections: Option set 3 the XCOM cross-sections,19 option set 4 the EPDL20 cross sections. Results shown in the figures are for option set 4 (EPDL) unless otherwise stated.
GEANT4
The GEANT4 Simulation Toolkit version 4.9.0p01 of 28 August, 2008 was used. Details of the radiation transport methods and cross-section data are given in the GEANT4 Physics Reference Manual available at the web site http:∕∕geant4.web.cern.ch∕. All material definitions were taken from the NIST material definitions built into GEANT4, with the exception of stainless steel, which was defined as compositions of appropriate NIST elements.
The list of processes to simulate (“physics list” in GEANT4 terminology) was taken from the “low energy” physics list “PhysListEmLivermore,” taken from the standard examples distributed with GEANT4, example TestEM7. Results were compared to simulations done using the “standard” physics list “PhysListEMStandard,” taken from the same example as the low energy physics list, TestEM7.
The multiple-scattering model used in GEANT4 with either physics list belongs to the class of condensed simulations. It uses model functions (described in the reference manual for GEANT4.9 of 14 December, 2007, in Chap. 3, “Electromagnetic Interactions,” Sec. 3, “Common to All Charged Particles”), to determine the angular and spatial distributions after a step. The functions have been chosen in such a way as to give the same moments of the angular and spatial distributions as the Lewis theory.21 The model incorporates correlations between lateral displacement and scattering angle and provides several options for limiting the step size near geometry boundaries.22 For the present study, the default option was used such that after entering a volume the step size cannot be larger than the distance to the next boundary over 2.5.
The low energy physics processes, designed for best accuracy at energies where atomic shell structure is important, use cross section data extracted from a set of publicly distributed evaluated data libraries: EPDL97 (Evaluated Photons Data Library),20 EEDL (Evaluated Electrons Data Library),23 and EADL (Evaluated Atomic Data Library).24 The standard processes, optimized for high energy physics applications, rely on parametrizations of these data.
For bremsstrahlung above a given threshold energy with either physics list, the energy loss is simulated by the explicit production of photons. Below the threshold the emission of soft photons is treated as a continuous energy loss.22, 23 The energy of the final state photons is sampled according to the spectra of Seltzer and Berger.24 They have calculated the bremsstrahlung spectra for materials with atomic numbers Z=6, 13, 29, 47, 74, and 92 in the electron kinetic energy range 1 keV–10 GeV. The angular distribution is based on the distribution of Tsai.25
The range cut parameter was set to 0.1 mm. The correspondence between range cut and energy cut for the different targets is shown in Table 2. Simulations done for the 15 MV beam for the different targets with the range cut set to 1 mm agreed with the results for the 0.1 mm range cut to 1% for the angular range of the measurements. The range cut parameter had a larger effect when using the standard physics list. Changing the cut from 0.1 to 1 mm resulted in an increase of the photon yield of up to 3%–5% at 15 MV at certain angles.
Table 2.
Energy cuts in GEANT4, corresponding to the different range cuts and targets used.
| Range cut (mm) | Material | Energy cut for photons (keV) | Energy cut for electrons (keV) |
|---|---|---|---|
| 0.1 | Be | 1.03 | 108 |
| 0.1 | Al | 2.31 | 130 |
| 0.1 | Pb | 29.3 | 240 |
| 1.0 | Be | 1.99 | 467 |
| 1.0 | Al | 6.89 | 597 |
| 1.0 | Pb | 101 | 1361 |
Uniform bremsstrahlung splitting, as implemented in EGSNRC (see earlier), was implemented in GEANT4, with Russian Roulette of the secondary charged particles.26 Each bremsstrahlung event generated 100 photons.
Penelope
The simulations were carried out with version 2006.6, 7 The bremsstrahlung cross-section differential in the energy of the emitted photon is obtained from published tables.18, 27 To sample the angular distribution of the emitted photons, PENELOPE relies on a semiempirical fit to the partial-wave shape functions of Kissel et al.28 for electron energies below 500 keV. Above this value the shape function is approximated by a classical dipole distribution.
Charged particles are transported using a mixed scheme, in which hard interactions (involving energy losses or angular deflections above certain cutoffs) are simulated in detail, that is, one by one. Soft collisions occurring between two hard interactions, in turn, are grouped together and described with a single artificial soft event. Its spatial position is determined according to the so-called random hinge scheme. The angular and energy loss distributions associated with these artificial soft events reproduce the first and second moments of the differential cross-section models employed for each interaction mechanism (i.e., elastic, inelastic, and bremsstrahlung). Further details are given by Salvat et al.6
Individual elastic collisions of charged particles are described by using the database of numerical differential cross sections of ICRU Report No. 77,29 which was generated with the relativistic partial-wave code ELSEPA30 using the static-field approximation. According to the ICRU, this database provides the most reliable theoretical description available of elastic scattering by neutral atoms for energies higher than about 10 keV.
Material definitions were taken from the PENELOPE database, which in turn was built from the database of the ESTAR program of Berger,31 with the only exception of stainless steel. The latter material was defined according to the chemical composition and mass density given earlier.
Simulation parameters were set for all materials as follows. The absorption energies, at which the simulation of a particle is terminated and the remaining kinetic energy assumed to be locally deposited, were set to 200 and 10 keV for electrons (or positrons) and photons, respectively. The parameters C1 and C2 were set to 0.05. These parameters determine the maximum average path length between consecutive hard interactions of electrons and positrons in such a way that the average angular deflection (defined as 1 -cos θ, where θ is the average deflection angle) and the average fractional energy loss along each step are less than C1 and C2, respectively. The corresponding cutoffs for inelastic and bremsstrahlung interactions, called WCC and WCR in PENELOPE, were chosen as 200 and 10 keV, respectively. The maximum allowed step lengths, named DSMAX, were set to 1∕10 of the thickness of each material layer present in the geometry.
Benchmark comparisons
Photon yield was calculated in angular bins of 0.5°–1° for energies greater than 0.22 MeV for the 10–30 MV benchmarks, 0.145 MeV for the 15 MV benchmarks, corresponding to the lowest energy in the published measured data. Fluence was scaled using the inverse square law to 1 m from the target and reported in SI units (∕m2), numerically the same as fluence per steradian, reported in the earlier publications. Fluence ratios are the calculated result divided by the measured result.
Spectra are reported in energy bins with the same energies and widths as the published measured spectra, binned to give approximately the same fluence and statistical precision in each bin. Energy fluence is plotted, as the range in energy fluence is much less than the range in fluence over the same energy range, making the plots more compact, with differences between curves easier to see.
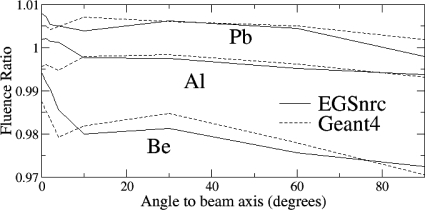
In the experiment, the target chamber was removed for measurements made at 30° and greater. The process of benchmarking Monte Carlo codes was simplified by applying small, calculated correction factors to the fluence measured at wide angles such that only the experimental geometry with the target chamber needs to be simulated. The effect of removal of the target chamber window on the photon yield is shown in Fig. 3, calculated with EGSNRC and GEANT4. The window increases bremsstrahlung for the Be and Al targets, as these have lower atomic number than stainless steel, and decreases bremsstrahlung for the higher atomic number Pb target. The measured fluence at 30, 60, and 90 was corrected by the average effect from Fig. 3: 0.983, 0.977, and 0.971 for Be, 0.998, 0.996, and 0.993 for Al, and 1.006, 1.005, and 1.000 for Pb. The shapes of the calculated spectra were not significantly affected by removal of the target chamber window.
Figure 3.
Ratio of photon yield calculated without the stainless steel window of the target chamber to that with the window. Results from simulations with EGSNRC (solid lines) and GEANT4 (dashed lines).
Uncertainties
Only experimental uncertainties are used in the comparisons. The calculational precision of each simulation was small compared to experimental uncertainty and safely neglected. Uncertainties in the measured spectra are comparable to the fluctuations seen in the plots.
Errors introduced by source, geometry, and scoring differences between the simulations and measurements were ignored. The geometry was accurately known. The source was accurately represented in the simulations as a normally incident monoenergetic beam with a uniformly distributed circular or square focal spot. The uncertainty in the beam energy of 0.5% contributes a 1% uncertainty to the photon yield. The approximation of the source as a circle or square of constant fluence compared to the actual source distribution (which was not measured) had minimal impact on the calculated photon yield. This was quantified by comparing results of GEANT4 simulation with a point source, constant fluence in a 0.35-cm-diam circle and a Gaussian distribution with a 0.35 cm full width at half maximum.
Scoring differences between simulation and measurement included rebinning spectra in energy, scaling fluence by the inverse square law, and using different angular bin widths in the measurement and calculation. Rebinning spectra from the 10 keV bins of the simulated spectra to the variable-width bins of the measured spectra resulted in less than a 1% error in the calculated photon yield. Simulations with EGSNRC for the 15 MV beam on the Pb target showed use of the inverse-square law to scale fluence from a plane at 100 cm to a plane at 300 cm resulted in an overestimate of fluence of close to 3% on the beam axis, dropping rapidly to under 0.5% at angles of 4° or more. Angular bins of 1°, although much larger than the measurement, added no more than a 2% error to the photon yield, based on the measured dependence of photon yield on beam angle.
RESULTS AND DISCUSSION
Photon yield
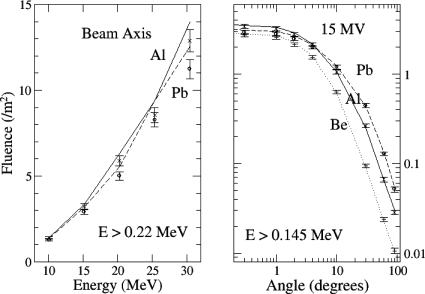
Photon yields from the published experimental benchmark are shown with calculated yields from one of the codes (GEANT4) in Fig. 4. Photon yield on the beam axis increases with the square of the energy and drops two orders of magnitude or more over the angular range. Photon yield on the beam axis is similar for the different targets, as the electron scattering power and bremsstrahlung yield scale in a similar manner with atomic number. The increase in scattering power results in a broader angular distribution with increasing atomic number.
Figure 4.
Photon yield for 10–30 MV x rays on the beam axis and for 15 MV x rays out to the right angle from the beam axis. The published experimental benchmark is shown with error bars for Be (plus signs), Al (crosses), and Pb (circles), compared to results of Monte Carlo simulation with GEANT4 for Be (dotted line), Al (solid line), and Pb (dashed line).
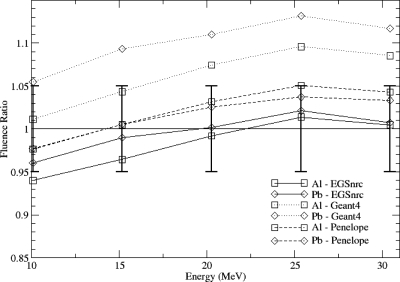
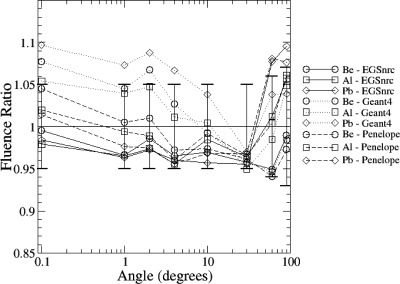
The ratios of the photon yields, calculation to measurement, are shown in Figs. 56. Experimental uncertainty shown in the plots includes the significant systematic uncertainty in the measurement of the beam current. The values of photon yields calculated by the different codes are the product of the plotted photon yield ratios with the published measured values. GEANT4 results are for the low energy physics list.
Figure 5.
Ratio of calculated to measured photon yield on the beam axis from Al and Pb targets for 10–30 MV beams for photons above 0.22 MeV. The error bars are 1 s.d. experimental uncertainty from unity.
Figure 6.
Ratio of calculated to measured photon yield out to 90° from Be, Al, and Pb targets for 15 MV beams for photons above 0.145 MeV. The error bars are 1 s.d. experimental uncertainty from unity.
Calculated photon yields on axis from 10–30 MV beams from Al and Pb targets were within 1 s.d. experimental uncertainty of the measurements for PENELOPE and EGSNRC, and 3 s.d. for GEANT4. The EGSNRC results for Al were a closer match to the benchmark than EGS4 results.1 Photon yield at angles out to a right angle from the beam axis for 15 MV for Be, Al, and Pb targets were within 2 s.d. deviations for all codes, including EGS4.2
In radiotherapy it is desirable to have an uncertainty under 3% in the calculated dose, relative to a standard field.32, 33 The treatment field is generally confined to an angle of 15° or less. For fluence based dose calculation codes such as those using the Monte Carlo method, this requires calculation of the fluence off-axis relative to the fluence on the beam axis with an accuracy of 1%–2%. The uncertainty of the measured relative fluence for beam angles out to and including 10° is 3%. This uncertainty is lower than for photon yield as the relative beam current is known to higher accuracy than the absolute beam current. The ratio of calculated to measured photon yield at 15 MV in this angular range relative to the ratio at 2° (from Fig. 6) is as high as 2% for EGSNRC, 4% for PENELOPE, and 5% for GEANT4 (7% for Be at 10°), within 2 s.d. of the experimental uncertainty.
Errors in the calculation of the photon yield are attributed to errors in the electron transport, in particular, the multiple scattering, or errors in bremsstrahlung cross sections. For example, an overestimate of photon yield on the beam axis would result from the electron scattering power being to low or the bremsstrahlung production in the forward direction being too high. Other aspects of the radiation transport such as electron energy loss and photon attenuation and scatter are handled with sufficient accuracy with these codes for calculation of the photon yield.
The measured photon yield drops more slowly with angle than the calculated result, regardless of Monte Carlo code. This could be due to a common problem with the simulations such as the different distance from the target to detector in the simulations and measurement. The trend is within experimental uncertainty. Therefore, a more accurate experimental benchmark is needed to establish whether this trend is real.
Photon energy distributions
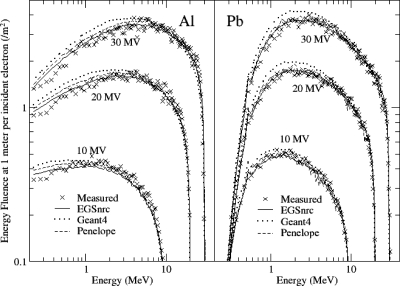
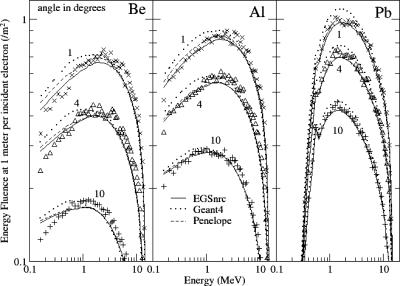
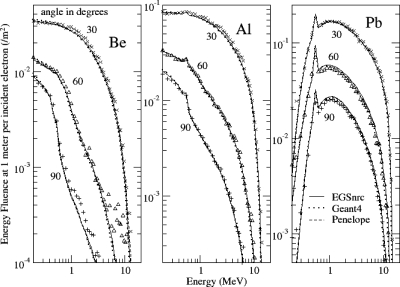
Calculated and measured energy distributions are compared in Fig. 7 on the beam axis for beam energies of 10, 20, and 30 MV and in Figs. 89 at 15 MV for angles of 1°, 4°, 10°, 30°, 60°, and 90°. Similar results were obtained for the other energies and beam angles. The calculated spectra are generally in close agreement with the measured spectra.
Figure 7.
Photon energy fluence distributions on the beam axis at 10–30 MV from Al and Pb targets. Measurements compared to calculations with EGSNRC, GEANT4, and PENELOPE. Results are representative of those at 15 and 25 MV.
Figure 8.
Photon energy fluence distributions at small angles at 15 MV from Be, Al, and Pb targets. Measurements compared to calculations with EGSNRC, GEANT4 and PENELOPE. Results are representative of those at 0° and 2°.
Figure 9.
Photon energy fluence distributions at large angles at 15 MV from Be, Al, and Pb targets. Measurements compared to calculations with EGSNRC, GEANT4, and PENELOPE.
Results for all of the codes for photon energies over 5 MeV are in close agreement with measurement for the Pb target at all angles and the Be and Al target at the larger angles. There is a large discrepancy in the high-energy tail of the energy distribution at large angles for the Be target, discussed shortly. Fluence from the lower atomic number targets at photon energies of around 5 MeV was overestimated at the smaller angles by as much as 10% by all of the codes. The fluence of photons (per incident electron) below 2–3 MeV for the lower atomic number targets at small angles was overestimated by EGSNRC and PENELOPE by as much as 15% and by GEANT4 by as much as 20%. An overestimate at low energies is apparent for the Pb target as well with GEANT4. The differences from the measured spectra are attributed to errors in the bremsstrahlung cross section, with too few high-energy photons and too many low-energy photons generated in the simulation at small beam angles.
There are large differences between measurement and simulation for the Be target at 60° and 90° in the higher energy region where the measurement suffers from low counting statistics. The discrepancy suggests an error in the measured fluence on the higher energy side of the spectrum at the two largest angles, possibly associated with problems with background measurement, noise, unfolding the detector response or the contribution of charged particles to counted events in the NaI detector.
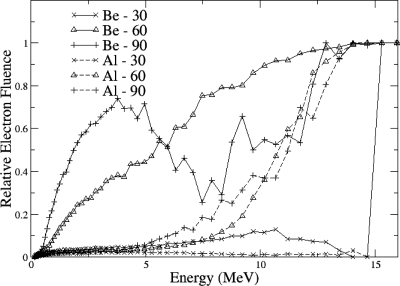
The excess counts at large angle from the Be target could be high energy electrons that leaked from the target and managed to make it to the detector through the collimator (Fig. 1). Since the bremsstrahlung fluence at wide angles is very low for the Be target, due to the low bremsstrahlung yield and electron scattering power, the contribution of the electron contamination from the pretarget material would be highest for this case, which could explain why the effect is most apparent for the Be target. The contribution of electron fluence to the total fluence was calculated with EGSNRC in a simulation of the 15 MV beam incident on the pretarget and target material without the target chamber, with no bremsstrahlung splitting but ten times the number of source electrons, to emphasize the electron contamination. Results shown in Fig. 10 show significant electron fluence in the 2–10 MeV energy range for the Be target, corresponding to the energy range of the discrepancy between measurement and simulation. The effect was much less for the Al target, as expected. From the simulation with the Be target, the electron fluence at 60° (integrated over energy) was only 25% of the total fluence. A prominent peak at 14.7 MeV due to scatter from the pretarget material constituted 8% of the fluence and could be responsible for a significant portion of the excess counts if most of those electrons made it to the detector. A separate simulation of a narrow beam of 14.7 MeV electrons normally incident on 380 cm of air followed by the 20-cm-thick, 2.54-cm-diam detector collimator of Pb showed that the collimator did little to degrade the energy of the peak and only 0.5% of the electrons reached the detector. This rules out the possibility that these excess counts are due to electron contamination.
Figure 10.
Electron fluence in energy bins relative to total fluence in the energy bin (electrons and photons), in geometry with air between target and scoring surface for 15 MV beams from Be and Al targets at the widest angles, calculated with EGSNRC, options set 1. There was no collimator in the simulation.
Cross-section data
Both EGSNRC and GEANT4 were run with different sets of cross section data to determine whether one data set is preferred over another to match the experimental benchmark. The photon yield was insensitive to the photon cross sections used, as the targets were relatively thin, having transmission around 30%. For example, the EGSNRC results calculated with the Storm and Israel or XCOM photon cross sections were within 1% of the photon yield calculated with the EPDL photon cross sections. The energy distributions were all within 2%.
The Bethe–Heitler bremsstrahlung cross section (BH) available with EGSNRC gave somewhat different results than the NIST cross section. The 10–30 MV photon yield on the beam axis calculated with BH compared to those calculated with NIST were low by 0.3%–0.8% for Al and high by 1.0%–1.7% for Pb. Significant differences in the 15 MV photon yield from 0° to 90° was limited to photon energies below 1 MeV where the photon yield was underestimated at the lowest energies in the spectrum (0.15–0.2 MeV) by up to 20% for Be, 7% for Al. This resulted in a photon yield that was 2%–4% low for Be, 0.8%–1.2% low for Al, and 0.2%–1.5% high for Pb, depending on angle.
Sarfehnia et al.9 reported EGSNRC results were accurate to “better than three orders of magnitude as compared to the old EGS4 code.” Their statement is inconsistent with the results shown in their Fig. 5 and the close agreement between published EGS4 results2 and those calculated with EGSNRC, shown in Fig. 9.
GEANT4 simulations were done to determine whether photon yield is overestimated when using the standard physics list, as suggested in a recent publication.34 The yield of photons over 0.145 MeV for the 15 MV beams calculated with GEANT4 using the standard physics list and a 0.1 mm range cut were 8%–11% higher than those calculated with the low energy physics list at small angles out to and including 4°. The yield at angles of 30° and over was up to 16% higher for the Be target, 9%–12% higher for the Al target, and 5% higher for the Pb target. There was a trend of an overestimate of fluence of photons with energies below 2–4 MeV at the larger beam angles, below 5 MeV or so at the smaller beam angles.
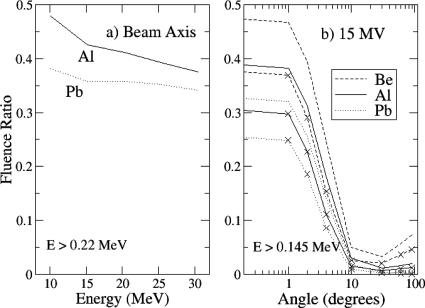
Pretarget material
The energy and angular distributions of photon yield are not impacted much by the small amount of material upstream of the target, as shown for the removal of the target chamber window in Fig. 3. At small angles, this is due to an approximately even trade-off between the influence of the increase in scattering power and bremsstrahlung yield with atomic number. At wide angles, photons are mostly from bremsstrahlung from widely scattered electrons in the target and photon scatter in the target. This argument was used in the past to justify the small amount of material upstream of the target. However, a quarter to half the photon yield near the beam axis is from material upstream of the target, even when the target chamber is removed (Fig. 11). The results shown are for normal incidence. The beam will have a certain amount of angular spread that could reduce the contribution from the pretarget material. However, simulations done with a 1° angular spread, a reasonable maximum for the beams used in the measurement, gave comparable results. Therefore, the benchmark would be improved by reducing the amount of pretarget material, or by placing the target in vacuum.
Figure 11.
Proportion of photons from the material upstream of the target, with energies greater than the threshold in the measurement, calculated with EGSNRC, option set 1: (a) 10–30 MV results on the beam axis, and (b) 15 MV results showing dependence on angle. Plots are fluence from the pretarget material relative to total fluence. Results of simulations with the target chamber removed have the points marked with crosses.
CONCLUSIONS
The results reported are the most accurate and comprehensive benchmarking of Monte Carlo codes for thick-target bremsstrahlung at radiotherapy energies to date. The energy used in the simulations was more accurate than used in previous publications. The simulations were run using the latest revisions of codes widely used in radiotherapy.
Differences in the results obtained with the different codes were due to a combination of differences in radiation transport methodology, techniques employed for efficiency gain, cross-section data used in the simulations, and details of the implementation (coding). A sufficient number of source particles were simulated so that statistical precision did not play a significant role.
Monte Carlo simulation is capable of calculation of thick-target bremsstrahlung yield to 5%, the angular distribution of fluence to 3%, and fluence differential in energy to 10% at intermediate energies, 15% at lower energies, for angles out to 30°. EGSNRC and PENELOPE were the most accurate of the codes tested, when using the specified radiation transport parameters. The codes were close to indistinguishable in their calculation of the yield of photons at energies over 2–3 MeV. Fluence in the low-energy part of spectra from the lower atomic number targets was overestimated with all of the codes. In all cases the spectra were calculated with sufficient accuracy for a wide variety of applications in radiotherapy where the result is insensitive to the relatively small amount of energy carried by these low energy photons. Care needs to be taken in calculations sensitive to the relative fluence of low energy photons in the spectrum, such as the response of a flat panel detector to an unflattened beam produced by a low atomic number target.
The measured angular distribution of fluence, with an uncertainty of 3%, is not as accurate as the 1%–2% desired in radiotherapy. A more accurate measurement of relative fluence profiles would be a useful benchmark for thick-target bremsstrahlung simulation. Applications that could benefit from the benchmark include radiotherapy dose calculation in regions with inhomogeneities, a steep dose gradient, or low transmission, detector response calculation, activation analysis, and calculation of leakage. Benchmarks of bremsstrahlung yield on the beam axis would be further improved by reducing the amount of material upstream of the target.
One might argue that the fluence benchmark used in this work is sufficiently accurate since an error in the simulation of the angular distribution of fluence may be compensated by adjustment of source and geometry parameters in the treatment head simulation. However, the possibility of an error in the fluence profile of a few percent may significantly impact the accuracy of the calculated quantity of interest. Lacking an accurate benchmark, this would need to be rigorously evaluated for the calculated quantities for all expected variations in the geometry (beam modifiers, patient, detectors, etc.).
Simulation parameters were chosen to give the most accurate radiation transport available for each code for the calculation of photon yield in the experimental geometry. Radiation transport and cross-section parameter choices other than the ones used in this study could improve calculation efficiency without loss of accuracy. Results can be calculated by users of the different Monte Carlo codes with the parameters used here and compared to results calculated with a modified parameter set to determine more optimal parameters for a particular geometry and endpoint.
ACKNOWLEDGMENTS
This work is supported in part by the National Institute of Health under R01 CA104777-01A2 and the U.S. Department of Energy under Contract No. DE-AC02-76SF00515. J.S. also acknowledges partial financial support from the Spanish Ministerio de Educacion y Ciencia, Project No. FIS2006-07016 and from the Spanish Ministerio de Sanidad y Consumo, CIBER-BBN. We are grateful to Tsukasa Aso for providing scoring routines for the GEANT4 simulations.
References
- Faddegon B. A., Ross C. K., and Rogers D. W. O., “Forward-directed bremsstrahlung of 10–30 MeV electrons incident on thick targets of Al and Pb,” Med. Phys. 10.1118/1.596560 17, 773–785 (1990). [DOI] [PubMed] [Google Scholar]
- Faddegon B. A., Ross C. K., and Rogers D. W. O., “Angular distributions of bremsstrahlung from 15 MeV electrons incident on thick targets of Be, Al and Pb,” Med. Phys. 10.1118/1.596667 18, 727–739 (1991). [DOI] [PubMed] [Google Scholar]
- Kawrakow I., “Accurate condensed history Monte Carlo simulation of electron transport. I. EGSnrc, the new EGS4 version,” Med. Phys. 10.1118/1.598917 27, 485–498 (2000). [DOI] [PubMed] [Google Scholar]
- Agostinelli S. et al. , “Geant4–A Simulation Toolkit,” Nucl. Instrum. Methods Phys. Res. A 10.1016/S0168-9002(03)01368-8 506, 250–303 (2003). [DOI] [Google Scholar]
- Allison J. et al. , “Geant4 developments and applications,” IEEE Trans. Nucl. Sci. 10.1109/TNS.2006.869826 53, 270–278 (2006). [DOI] [Google Scholar]
- Salvat F., Fernandez-Varea J. M., and Sempau J., “PENELOPE-2006: A code system for Monte Carlo simulation of electron and photon transport,” OECD Nuclear Energy Agency, Issy-les-Moulineaux, France, 2006, available in pdf at http://www.nea.fr.
- Sempau J., Acosta E., Baro J., Fernandez-Varea J. M., and Salvat F., “An algorithm for Monte Carlo simulation of coupled electron-photon transport,” Nucl. Instrum. Methods Phys. Res. B 10.1016/S0168-583X(97)00414-X 132, 377–390 (1997). [DOI] [Google Scholar]
- Verhaegen F. and Seuntjens J., “Monte Carlo modelling of external radiotherapy photon beams,” Phys. Med. Biol. 10.1088/0031-9155/48/21/R01 48, R107–R164 (2003). [DOI] [PubMed] [Google Scholar]
- Sarfehnia A., Jabbari K., Seuntjens J., and Podgorsak E. B., “Experimental verification of beam quality in high-contrast imaging with orthogonal bremsstrahlung photon beams,” Med. Phys. 10.1118/1.2745243 34, 2896–2906 (2007). [DOI] [PubMed] [Google Scholar]
- Sempau J., Fernandez-Varea J. M., Acosta E., and Salvat F., “Experimental benchmarks of the Monte Carlo code PENELOPE,” Nucl. Instrum. Methods Phys. Res. B 10.1016/S0168-583X(03)00453-1 207, 107–123 (2003). [DOI] [Google Scholar]
- Goudsmit S. A. and Saunderson J. L., “Multiple scattering of electrons,” Phys. Rev. 10.1103/PhysRev.57.24 57, 24–29 (1940). [DOI] [Google Scholar]
- Goudsmit S. A. and Saunderson J. L., “Multiple scattering of electrons. II,” Phys. Rev. 10.1103/PhysRev.58.36 58, 36–42 (1940). [DOI] [Google Scholar]
- Kawrakow I. and Bielajew A. F., “On the representation of electron multiple elastic-scattering distributions for Monte Carlo calculations,” Nucl. Instrum. Methods Phys. Res. B 10.1016/S0168-583X(97)00723-4 134B, 325–336 (1998). [DOI] [Google Scholar]
- Kawrakow I. and Rogers D. W. O., “The EGSnrc Code System: Monte Carlo simulation of electron and photon transport,” NRC Report No. PIRS-701, Ottawa, Canada, 2003.
- Koch H. W. and Motz J. W., “Bremsstrahlung cross-section formulas and related data,” Rev. Mod. Phys. 10.1103/RevModPhys.31.920 31, 920–955 (1959). [DOI] [Google Scholar]
- De Smedt B., Reynaert N., Flachet F., Coghe M., Thompson M. G., Paelinck L., Pittomvils G., De Wagter C., De Neve W., and Thierens H., “Decoupling initial electron beam parameters for Monte Carlo photon beam modeling by removing beam-modifying filters from the beam path,” Phys. Med. Biol. 10.1088/0031-9155/50/24/012 50, 5935–5951 (2005). [DOI] [PubMed] [Google Scholar]
- Storm E. and Israel H. I., “Photon cross sections from 1 keV to 100 MeV for elements Z=1 to Z=100,” At. Data Nucl. Data Tables 7, 565–681 (1970). [Google Scholar]
- Seltzer S. M. and Berger M. J., “Bremsstrahlung spectra from electron interactions with screened atomic nuclei and orbital electrons,” Nucl. Instrum. Methods Phys. Res. B 10.1016/0168-583X(85)90707-4 12, 95–134 (1985). [DOI] [Google Scholar]
- Berger M. J. and Hubbell J. H., “XCOM: Photon cross sections on a personal computer,” Report No. NBSIR87-3597, NIST, Gaithersburg, 1987.
- Cullen D., Hubbell J. H., and Kissel L., “EPDL97: The Evaluated Photon Data Library, ’97 version,” UCRL–50400, Vol. 6, Rev.5, Lawrence Livermore National Laboratory, Livermore, CA, 1997.
- Lewis H. W., “Multiple scattering in an infinite medium,” Phys. Rev. 10.1103/PhysRev.78.526 78, 526–529 (1950). [DOI] [Google Scholar]
- Perl J., “Changes in Geant4 electromagnetics from Release 4.6.1 to 4.9.1,” SLAC Technical Report No. SLAC-TN-08-002, 2008.
- Perkins S. T., Cullen D. E., and Seltzer S. M., “Tables and graphs of electron-interaction cross sections from 10 eV to 100 GeV derived from the LLNL Evaluated Electron Data Library (EEDL), Z=1–100,” Lawrence Livermore National Laboratory, Livermore, CA, Report No. UCRL-50400, 1991, Vol. 31.
- Cullen D. E.et al. , “Tables and graphs of atomic subshell and relaxation data derived from the LLNL Evaluated Atomic Data Library (EADL), Z=1–100,” UCRL-50400, Vol. 30, Lawrence Livermore National Laboratory, Livermore, CA, 1991.
- Tsai Y.-S., “Pair production and bremsstrahlung of charged leptons,” Rev. Mod. Phys. 10.1103/RevModPhys.46.815 46, 815–851 (1974). [DOI] [Google Scholar]
- Tinslay J., Faddegon B., Perl J., and M Asai, “Verification of bremsstrahlung splitting in Geant4 for radiotherapy quality beams, SU-FF-T-447,” Med. Phys. 34, 2504 (2007). [Google Scholar]
- Seltzer S. M. and Berger M. J., “Bremsstrahlung energy spectra from electrons with kinetic energy 1 keV–10 GeV incident on screened nuclei and orbital electrons of neutral atoms with Z=1–100,” At. Data Nucl. Data Tables 10.1016/0092-640X(86)90014-8 35, 345–418 (1986). [DOI] [Google Scholar]
- Kissel L., Quarles C. A., and Pratt R. H., “Shape functions for atomic-field bremsstrahlung from electrons of kinetic energy 1–500 keV on selected neutral atoms 1<=Z<=92,” At. Data Nucl. Data Tables 10.1016/0092-640X(83)90001-3 28, 381–460 (1983). [DOI] [Google Scholar]
- ICRU Report 77, “Elastic scattering of electrons and positrons,” J. ICRU 7(1) (2007). [DOI] [PubMed] [Google Scholar]
- Salvat F., Jablonski A. and Powell C. J., “ELSEPA—Dirac partial-wave calculation of elastic scattering of electrons and positrons by atoms, positive ions and molecules,” Comput. Phys. Commun. 10.1016/j.cpc.2004.09.006 165, 157–190 (2005). [DOI] [Google Scholar]
- Berger M. J., “ESTAR, PSTAR and ASTAR: Computer programs for calculating stopping-power and range tables for electrons, protons and helium ions,” National Institute of Standards and Technology, Report No. NISTIR 4999, Gaithersburg, MD, 1992.
- Van Dyk J., Barnett R. B., Cygler J. E., and Shragge P. C., “Commissioning and quality assurance of treatment planning computers,” Int. J. Radiat. Oncol., Biol., Phys. 26, 261–273 (1993). [DOI] [PubMed] [Google Scholar]
- Fraas B., Doppke K., Hunt M., Kutcher G., Starkschall G., Stern R., and Van Dyke J., “American Association of Physicists in Medicine Radiation Therapy Committee Task Group 53: Quality assurance for clinical radiotherapy treatment planning,” Med. Phys. 10.1118/1.598373 25, 1773–1829 (1998). [DOI] [PubMed] [Google Scholar]
- Faddegon B. A., Perl J., and Asai M., “Monte Carlo simulation of large electron fields,” Phys. Med. Biol. 10.1088/0031-9155/53/5/021 53, 1497–1510 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]