Hydration and Conformational Mechanics of Single, End-Tethered Elastin-like Polypeptides

Abstract

We investigated the effect of temperature, ionic strength, solvent polarity, and type of guest residue on the force—extension behavior of single, end-tethered elastin-like polypeptides (ELPs), using single molecule force spectroscopy (SMFS). ELPs are stimulus-responsive polypeptides that contain repeats of the five amino acids Val-Pro-Gly-Xaa-Gly (VPGXG), where Xaa is a guest residue that can be any amino acid with the exception of proline. We fitted the force—extension data with a freely jointed chain (FJC) model which allowed us to resolve small differences in the effective Kuhn segment length distributions that largely arise from differences in the hydrophobic hydration behavior of ELP. Our results agree qualitatively with predictions from recent molecular dynamics simulations and demonstrate that hydrophobic hydration modulates the molecular elasticity for ELPs. Furthermore, our results show that SMFS, when combined with our approach for data analysis, can be used to study the subtleties of polypeptide—water interactions and thus provides a basis for the study of hydrophobic hydration in intrinsically unstructured biomacromolecules.

Introduction

Hydration is essential for proteins to maintain a functional, three-dimensional structure and thus to maintain biological activity. Protein conformation and flexibility is thus intimately linked to the hydration water structure, in which the hydrogen-bonded hydration water network transmits information around the protein and controls its dynamics.¹ The interaction of water with hydrophobic protein surfaces (hydrophobic hydration) is typically manifest in a change in the clustering of water in the vicinity of the hydrophobic solute surface rather than in changes in water—solute interactions. Hydrophobic hydration generally produces a reduction in water density and an increase in heat capacity, both of which are consequences of more ordering in the solvent which also causes a negative entropy change. The interaction of water with hydrophobic groups is important in protein folding/unfolding^2-8 and intra and intermolecular interactions^9-11 and profoundly affects the mechanochemical properties of biomacromolecules.^12-14 While computer simulations^15-20 provide insights into temperature,²¹ size,^17,22 and cosolvent effects^23-25 on hydrophobic hydration, experimental studies that address the mechanical consequences of changes in hydrophobic hydration on the molecular level are largely missing.

Our research is motivated by the desire to understand the mechanochemical and hydration properties of elastin-like polypeptides (ELPs) at the single molecule level. ELPs are stimuli-responsive polypeptides²⁶ that consist of repeats of the pentapeptide sequence Val-Pro-Gly-X-Gly (VPGXG) (X is any amino acid except Pro),^27,28 and undergo, in solution, a lower critical solution temperature (LCST) transition. Below their LCST, ELPs are soluble in water, but when the temperature is raised above their LCST, a sharp phase transition occurs that leads to desolvation and aggregation of the polypeptides. Changes in the ambient temperature, ionic strength, or pH can trigger this reversible, inverse transition.²⁸ ELPs are attractive for different applications that require molecular level control of polymer structure because they are genetically encodable and can be synthesized easily by heterologous overexpression from a synthetic gene, with precise control over their composition and chain length.^26,29 Furthermore, the LCST of ELPs can be tuned precisely to a temperature of interest between 0—100 °C, which is difficult to achieve with other synthetic polymers that exhibit LCST behavior.

We previously showed that ELPs that are chemically grafted onto self-assembled monolayers (SAMs) on gold, exhibit an interfacial hydrophilic—hydrophobic phase transition in response to increased temperature or ionic strength.^30-32 Understanding the mechanochemical properties of ELPs is important because ELPs can be exploited for force generation³³ and as molecular switches with tunable properties³⁴ and can provide the building blocks for engineered protein elastomers.²⁶

Although waters of hydrophobic hydration are thought to play an important role in the elasticity of elastin,^14,35 details of their conformational mechanics on the molecular level remain largely unexplored.^36,37 Three main models have been proposed to explain elastin's elasticity: (1) The model by Flory and Hoeve³⁸ considers elastin to behave like a random chain polymer with entropic (configurational) elasticity. While this model can explain the high mobility of the elastin backbone, it neglects the details of solvent—polypeptide interactions. These are, however, important, as elastin only shows elasticity in the presence of solvents.¹⁴ (2) An alternative model, proposed by Urry,^28,39 suggests that elasticity arises from “librational” entropy afforded by the relatively large kinetic mobility of peptide segments between the more rigid type II β-turn segments (Pro2-Gly3; Val1-COHN-Val4 H-bond) of a β-spiral, in which the β-turns function as spacers between the turns of the helix. (3) The two-phase model by Weis-Fogh and Anderson¹² considers elastin to be composed of globular protein regions in an aqueous diluent. In this model, stretch-induced elastic stresses were qualitatively accounted for in two ways, (i) by a decrease in the configurational entropy of elastin chains, and (ii) by changes in the interfacial free energy associated with hydrophobic hydration of elastin side groups upon extension. The latter model is supported by recent molecular dynamics (MD) simulations of elastin with explicit water.¹⁴ These simulations showed that an ELP molecule in water behaves more as an amorphous polymer chain, with only local secondary structure.²⁸ Furthermore, these simulations showed that interaction of water with hydrophobic side chains of ELP modulates the elasticity of the ELP molecule significantly.

Single molecule force spectroscopy (SMFS) by AFM and optical tweezers have enabled the study and manipulation of single macromolecules attached to surfaces.^40-44 SMFS experiments with globular proteins, DNA, and synthetic macromolecules have largely focused on the analysis of molecular “fingerprints” that arise from force-induced changes in secondary and tertiary structures^40,45-48 and changes in intrachain hydrogen bonding.^44,49 Nevertheless, systematic experiments on the single molecule level that link differences in the elastic behavior of polypeptides to changes in their hydration behavior are missing.

Force-induced molecular stretching of polypeptides in SMFS experiments causes a change in the equilibrium conformation of the macromolecule and potentially increases its solvent-accessible surface area by exposing previously solvent-inaccessible regions. Especially for hydrophobic polypeptides, such as ELPs, molecular-level stretching likely leads to hydrophobic hydration of the molecule as increasingly more hydrophobic surface is exposed.¹³ We argue that the force required to stretch a single ELP molecule in an aqueous solvent thus primarily reflects two components: (1) the restoring force that arises from the stretch-induced entropic elasticity of the polypeptide backbone, and (2) the force that arises from changes in the solvent—polypeptide interactions. The polypeptide conformation is intimately linked to the hydration water structure, as waters of hydrophobic hydration form a hydrogen-bonded network around the polypeptide surface; i.e., the hydration water network transmits information around the polypeptide and controls its dynamics.

Here we describe the effect of solvent quality, temperature, and type of guest residue on the force—extension behavior (elasticity) of ELPs at large molecular extensions (60—80% of the contour length) in terms of an effective Kuhn segment length. Our results suggest that SMFS can be used to study subtleties of polypeptide—water interactions. Although in this research we studied ELPs, we believe that our work provides a basis for future SMFS studies of hydrophobic hydration for a range of intrinsically unstructured biomacromolecules.

Experimental Section

ELP Synthesis

Three different ELP polypeptides containing repeats of the five amino acids Val-Pro-Gly-Xaa-Gly (VPGXG), where Xaa is a guest residue, were used in this study (Scheme 1). Each construct contained the N-terminal leader sequence Ser-Lys-Gly-Pro-Gly and a C-terminal trailer with Trp-Pro. ELP1—180 consists of 180 pentapeptide repeats, with a total molecular weight of 71.9 kDa and includes Val, Ala, and Gly at the guest residue positions in a 5:2:3 ratio. ELP4—120 has a molecular weight of 50 kDa and includes Val at every guest residue position of the pentapeptide, and ELP2—160 has a molecular weight 60 kDa and contains Val, Gly, Ala at the guest residue position in a 1:7:8 ratio. A table listing the transition temperatures of these ELPs is provided in the Supporting Information. The transition temperature is defined at the maximum in the turbidity gradient while heating at 1 °C/min for an ELP concentration of 25 μM in PBS.

Scheme 1.

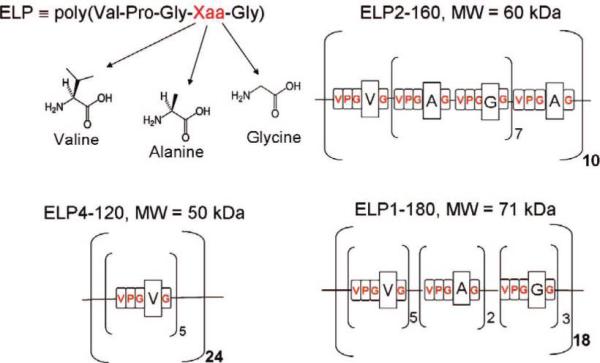
Schematic Representation of the Different ELP Constructs Studied Here

The ELPs were synthesized by overexpression of a plasmidborne synthetic gene of the ELP in E. coli to synthesize the ELP.^29,50 In brief, cells harboring a plasmid that encodes for the ELP were grown in 50 mL of CircleGrow culture media (Bio101, CA) supplemented with 100 μg/mL ampicillin, with shaking at 300 rpm at 37 °C. Cell growth was monitored by the optical density (OD) at 600 nm (OD₆₀₀). Isopropyl β-thiogalactopyranoside (IPTG) was added to a final concentration of 1 mM at an OD₆₀₀ of 1.0 to induce protein expression. After incubation for 3 h at 37 °C, the cells were recovered from the culture medium by centrifugation (2500g, 4 °C, 15 min) and resuspended in 5 mL of phosphate-buffered saline solution (PBS, 140 mM NaCl). The cells were lysed by sonication and centrifuged at 16 000g for 20 min, and the supernatant containing the ELP was collected for purification. The ELPs were purified by inverse transition cycling, as described elsewhere.^26,51

Sample Preparation

We prepared gold thin films with an average Au grain diameter of 30 nm on glass cover slides by thermal evaporation of a chromium adhesion layer (10 nm), followed by gold (100 nm), at a pressure of 4 × 10⁻⁷ torr. Before deposition, the glass surfaces were cleaned for 20 min in a 1:3 (v:v) Piranha etch of H₂O₂ and H₂SO₄ at 80 °C (extreme caution must be exercised when using Piranha etch). A mixed SAM of COOH- and CH₃-terminated oligoethylene glycol-functionalized alkanethiols was prepared on the gold surfaces to attach the ELP covalently to the substrate surface via its amine-terminal end. Specifically, an EG₆ thiol, with a COOH terminal group (Prochimia, cat. no: TH 011-01) was chosen to attach the ELP via amine coupling, while an EG₃thiol with a CH₃ terminal group, synthesized in our laboratory, was chosen as a diluent thiol with good protein resistance.⁵² By changing the ratio of EG₃ and EG₆thiols in the mixture, we were able to adjust the surface density of ELP molecules. In the experiments we used a ratio of 10 vol % COOH-terminated EG₆ and 90 vol % CH₃-terminated EG₃ thiol. More detailed protocols for SAM functionalization and ELP grafting can be found in the Supporting Information.

Force Spectroscopy

Force spectroscopy experiments were carried out by AFM (MultiMode with Nanoscope IIIa controller, DI, Veeco) in phosphate-buffered saline (PBS) solutions, using a fluid cell attachment. Rectangular Si₃N₄ cantilevers (TM Microscopes) were used for all experiments and their spring constants (typically 20—25 pN/nm) were estimated before an experiment from the power spectral density of the thermal noise fluctuations.⁵³ We used the MFP-3D (Asylum Research) AFM for cantilever calibration because of experimental convenience as the instrument provides a readily accessible thermal calibration routine. We checked the calibration with a Multimode AFM system where we used a National Instruments PCI-6052E data acquisition card in conjunction with Labview to collect the thermal noise spectrum of the cantilever deflections through the signal access box (Digital Instruments). We analyzed the data by a custom Matlab code. The values for the spring constants obtained from these two experimental setups were similar. The sensitivity of the photosensitive detector was determined from the constant compliance regime upon approach in the range between 1500 pN and 2000 pN. For force measurements, a set-point trigger force of 2000 pN and 2500 pN, and a constant pulling rate of 1 μm/s was used in all experiments. For experiments at different temperatures, the AFM was mounted in a thermostatted refrigerator for temperatures below room temperature (11 °C) and in a water-jacketed incubator for temperatures above RT. The AFM was equilibrated thermally in each of these environments for several hours prior to experiments. While the ELP was end-attached covalently to the substrate, we relied on unspecific interactions between the ELP and the AFM cantilever tip when “picking-up” an ELP for pulling experiments.

Data Reduction and Modeling

Force-extension curves are customarily interpreted using equilibrium statistical physics since the time scale of a force—extension experiment is sufficiently large so that a single polymer chain can adequately explore its many conformational degrees of freedom. Although the experiment involves a single macromolecule rather than an ensemble, a statistical description of entropy remains appropriate by the ergodic hypothesis which states that, given sufficient time, a single molecule in equilibrium will visit conformations in the same proportion as a molecular ensemble in any moment of time.

At extensions much smaller than the maximum length of the fully stretched molecule, the entropic force of extension is readily described by the random walk statistics of the random coil. While in this regime elongation depends linearly on force, it extends only to forces of about 8 pN for a polymer with a Kuhn length of 0.5 nm at room temperature;⁵⁴ i.e., smaller than the thermal noise-induced force fluctuations of a typical AFM cantilever. At larger forces, the freely jointed chain (FJC) model provides a useful description of the force—extension behavior.^38,55 This model represents a polymer chain by n rigid segments of length l_K connected by freely rotating joints with no long-range interactions:^43,44

$$x\left(F\right)=L\left(\coth \left(\frac{{\mathit{Fl}}_{\mathrm{K}}}{k_{\mathrm{B}}T}\right)-\frac{k_{\mathrm{B}}T}{{\mathit{Fl}}_{\mathrm{K}}}\right)$$ (1)

where L is the contour length, l_K is the Kuhn segment length, k_B is Boltzmann's constant, and T is absolute temperature.

Previous work showed that the value of the Kuhn segment length obtained by fitting the FJC model to the data depends on the force range considered in the fit.^42-44 In our analysis we consider a force window between 60 pN and 200 pN when fitting the FJC model to force—extension data (Figure 1). The lower force limit was selected to minimize the contribution from nonspecific interactions of ELPs with the surface and to ensure that the fit captured only sufficiently stretched ELPs. Above the upper force limit, the extended freely jointed chain model, which accounts for enthalpic force contributions due to bond angle torsion and bending,^43,50,56 is necessary to describe the data accurately. In the selected force window the simpler FJC model is sufficient to describe the data well. We note that in the chosen force range the molecular extension of ELP is typically in the range of 60—80% of the ELP contour length. To get more precise estimates for the effective Kuhn segment length, we selected only those force—extension curves from a large number of similar force pulls that showed a single force extension event and that could be normalized by contour length at a constant force (Figure 2). We subtracted the small, hydrodynamic drag force^45,57 on the cantilever in each of our experiments to further improve the FJC model fit (see Supporting Information). Since many force—distance curves are recorded during measurements under the same experimental conditions, and because each curve represents the same molecular sequence, each curve provides additional information for estimating the molecule's Kuhn length. We fitted the FJC parameters using a statistical procedure which combines data from these multiple curves to reduce variability and which accounts for increased variance in the measurements at lower forces using an iteratively reweighted least-squares procedure (see Supporting Information). We used a nonparametric Monte Carlo bootstrapping procedure to obtain sampling distributions and confidence intervals for the fitted parameters.⁵⁸ This quantification of the uncertainty in the estimated parameters is a critical aspect of comparing parameters obtained under different experimental conditions or from structural variants.

Figure 1.

Typical force—extension curve for ELP1—180 in PBS solution. The insets show the FJC model fit in the selected force window (60—200 pN).

Figure 2.

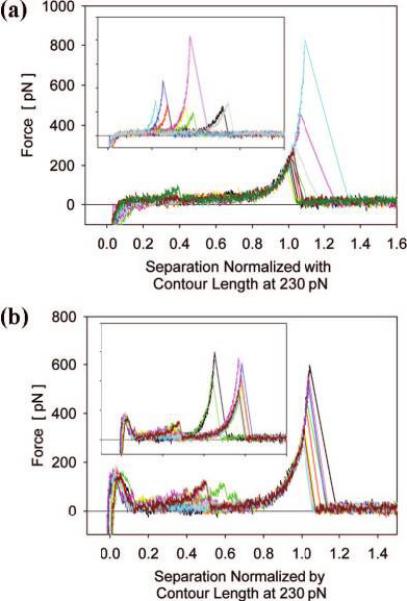
Typical force—extension curves for ELP1—180 normalized by the contour length at a force of 230 pN. Clear superposition demonstrates single molecule extension in (a) PBS and in (b) PBS + 1.5 M NaCl. Only at high ionic strength (poor solvent) appear significant unspecific adhesion forces at small extensions. Insert: force—extension curves before normalization.

Results and Discussion

To understand the mechanical properties of ELPs upon extension, and to explore the interaction of ELPs with the surrounding solvent, we analyzed ELP force—extension curves by fitting the data with the FJC model of the random coil, using the Kuhn segment length as a reporter. We found that the Kuhn segment length can be used to qualitatively interpret the effect of different guest residues and solvent quality on molecular elasticity of ELP (see below). Noting that the FJC model accounts for a force extension behavior of ideal chains,⁵⁴ we introduce an effective Kuhn length which implies that our FJC fits include contributions from both ELP backbone extension and contributions that result from entropic and enthalpic interactions of the solvent medium with the ELP molecule. The choice of the FJC model is justified by its good fit to the data over a large range of extensions. Furthermore, we have previously used the FJC model with good success in the interpretation of the force-induced prolyl cis—trans isomerization of ELP.³⁷

Effect of Solvent Temperature

It is well known that in solution below their LCST, ELPs are soluble in water, but when the temperature is raised above their LCST, they undergo a sharp phase transition, leading to desolvation and aggregation of the polypeptide. Many experimental observations suggest that the temperature-responsive properties of ELPs in solution occur via a mechanism involving three steps: (i) conformational change, (ii) association, and (iii) aggregation and that the first two are strongly interactive.⁵⁹ The notion of a LCST or transition temperature likely loses meaning when considering a single polypeptide, where one would expect a more gradual conformational change over a range of temperatures. To investigate the effect of temperature on hydration and elasticity of tethered, single ELP molecules during forced unfolding, we recorded force—extension curves for ELP1—180 at three different temperatures (T = 11 °C, 25 °C, and 42 °C). The choice of the temperature range was driven by the desire to have a reasonably large range that also brackets the transition temperature of about 41 °C for ELP1—180 in solution. For completeness we provide in the Supporting Information a table with the transition temperatures for all ELPs used in this work at a solution concentration of 25 μM. The corresponding Kuhn length distributions in Figure 3 show that the mean value for the distributions measured at 11 and 25 °C slightly increased (by ∼0.03 nm), while the mean Kuhn length increased considerably more (by ∼0.05 nm) upon increasing the temperature from 25 to 42 °C. We attribute the observed increase in Kuhn segment length with increasing temperature largely to changes in the entropic energy component associated with ELP hydrophobic hydration during unfolding, because the temperature effect on the entropic elasticity of the polypeptide backbone is already accounted for in the (k_BT) term of the FJC model.

Figure 3.

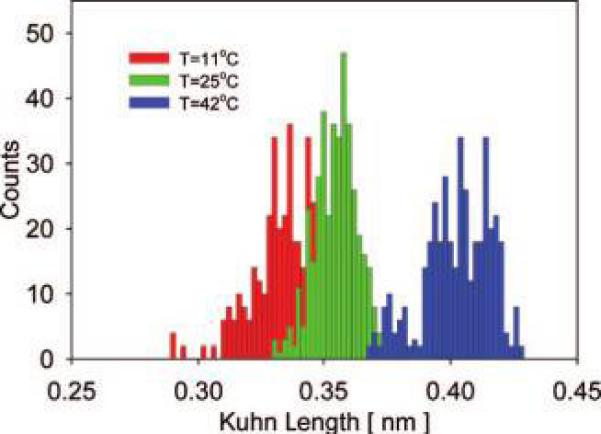
Distributions of the effective Kuhn segment lengths for ELP1—180 in MQ-grade water at three different temperatures. Left histogram: l̄_K = 0.33 ± 0.03 nm at T = 11 °C. Center histogram: l̄_K = 0.36 ± 0.02 nm at T = 25 °C. Right histogram: l̄_K = 0.41 ± 0.03 at T = 42 °C.

At low temperature, hydration waters are able to order around nonpolar groups of the polypeptide which results in a decrease of water's orientational entropy in the first solvation shell.^14,60 Although this is accompanied by a negative enthalpy that compensates energetically for the loss in solvent entropy, the entropy term is generally dominating and thus the free energy of hydrophobic hydration is positive. With increasing temperature, however, H-bonds within this hydration shell become increasingly more broken¹⁵ which results in increased melting of the structured waters around nonpolar groups of the polypeptide chain and causes an increase in solvent entropy.⁶⁰ This temperature-induced decrease in solvent ordering diminishes the entropic penalty that is caused by exposure of hydrophobic groups during molecular stretching and is reflected in an increase in the effective Kuhn segment length (Figure 3).

Our interpretation of the observed changes in effective Kuhn segment length with solvent temperature agrees with the theory for elastin's elasticity by Weis-Fogh et al.,¹² which suggested that increase in solvent-accessible nonpolar surface area upon extension contributes to elastomeric force. Furthermore, our interpretation is supported by the findings of recent MD simulations,^13,14 that gave detailed insight into molecular elasticity by modeling a single elastin molecule (VPGVG sequence with mw of ∼7000 Da) upon stretching in solution at different temperatures.^13,14 In these simulations, the number of ordered waters associated with elastin increased in response to stretching and decreased upon release of the molecule, respectively. The overall stretch-induced decrease in entropy caused a restoring contractile force.^13,14 Upon release of the molecule, the entropy of waters associated with hydrophobic side groups increased, and the entropy of waters associated with polar groups and with the polypeptide backbone decreased.

AFM force spectroscopy measurements thus yield an estimate for the energetic change associated with stretching a single ELP molecule from a relaxed to a highly extended state (i.e., increasing the accessible nonpolar surface area) and the energetic changes associated with the hydration of the solvent-accessible surface area.

Effect of Ionic Strength

Although directly increasing the ambient temperature is perhaps the simplest means to induce a hydrophobic folding of ELPs on surfaces³⁴ and in solution,²⁶ changing the ionic strength of the medium can also be used to trigger a conformational change in ELPs. It was previously shown that increasing the solution ionic strength induces hydrophobic folding of ELPs isothermally at the operating temperature; i.e., the temperature of the environment.^26,29

Force-extension curves for ELP1—180 in PBS and PBS with 1.5 M NaCl added (Figures 2a and 2b, respectively) show that in PBS mostly single, distinct force peaks with rupture forces of about 300—400 pN occurred, while in PBS + 1.5 M NaCl significantly larger nonspecific adhesion forces appear at small extensions, in addition to distinct force peaks at large extensions. These observations suggest that addition of NaCl increases the interactions between ELP and the substrate surface and also intramolecular interactions, likely due to hydrophobic interaction between hydrophobic segments within the polypeptide chain.

The effect of changes in the ionic strength of the solvent on the effective Kuhn length is shown in Figure 4. The Kuhn length increases slightly (by ∼0.01 nm) when solvent is exchanged from deionized water to PBS (∼0.14 M NaCl) and increases significantly more (by ∼0.05 nm) upon further increase of the ionic strength to 1.5 M NaCl. This increase in effective Kuhn segment length suggests that less energy is required to stretch the polypeptide at high ionic strength.

Figure 4.

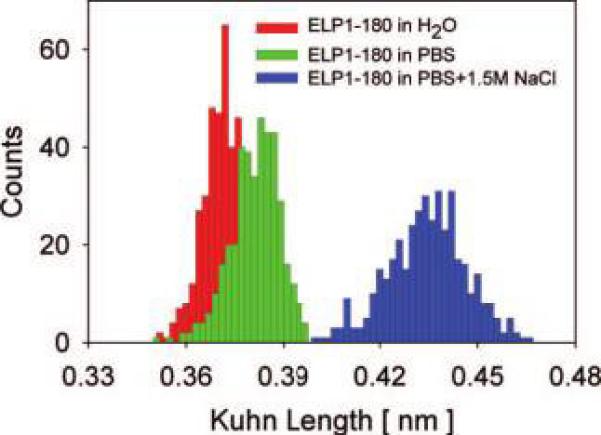
Distributions of the effective Kuhn segment lengths for ELP1—180 at different ionic strengths. Left histogram: l̄_K= 0.37 ±0.01 nm in MQ-grade water. Center histogram: l̄_K = 0.38 ± 0.02 nm in PBS solution. Right histogram: l̄_K = 0.43 ± 0.02 nm in PBS with 1.5 M NaCl added.

The interaction of ions with solvent and polypeptides can be complex and can, for different ion types, lead to different effects on the polypeptide hydration behavior. To interpret our results we make use of a recent study that measured the effect of ions on the water solubility of poly(N-isopropylacrylamide) (pNIPAAm).⁶¹ pNIPAAm, like ELP, is a stimulus-responsive macromolecule with LCST behavior and can be considered to be a synthetic analogue of ELP. The results of this recent study showed that addition of weakly chaotropic anions (such as Cl⁻) increases the surface tension of the water/hydrophobic interface in pNIPAAm in such a way that it destabilizes hydrophobic hydration and effectively lowers the LCST. Solvation effects due to the hydration entropy of the Cl⁻ anion and due to direct ion binding to the amide group in pNIPAAm were shown to be small. It also has long been known that for simple inorganic salts up to moderate concentrations, the surface tension of water at the hydrophobic/aqueous interface varies linearly with salt concentration.^61,62

Recent temperature-modulated differential scanning calorimetry (TMDSC) experiments by Reguera et al.⁶³ show that the enthalpy on heating an ELP solution in the presence of NaCl increases with increasing NaCl concentration. This interesting trend for ELPs is opposite that observed for other LCST polymers, such as pNIPAAm. In the latter, the enthalpy decrease has been associated with the disruption of ordered water surrounding the extended polymer chain with increases in the NaCl concentration (see above). Reguera et al.⁶³ argue that the opposite trend observed for ELP could be due, in part, to the formation of order in the polypeptide main chain with subsequent stabilization. We reconcile this apparent discrepancy by recalling that here we consider changes in hydrophobic hydration of ELP at large molecular extensions where ordered structures in the polypeptide main chain, that likely form in a force free state, are absent. We argue that in this regime an increase in ionic strength primarily leads to a disruption of ordered water surrounding the polypeptide chain, in analogy with observations for pNIPAam.

Taken together, these observations suggest that less energy will be required to stretch an ELP in solutions that contain higher concentrations of weak chaotropes, and this is reflected in the observed increase in Kuhn segment length with increasing NaCl concentration. Normal force measurements on end-grafted ELP in PBS solution with increasing NaCl concentrations further support this interpretation. In these experiments (see Supporting Information), the extent of the steric interaction distance, expressed conveniently by a decay length, decreased linearly with increasing ionic strength. This suggests that end-grafted ELPs adopt an increasingly more collapsed conformation with increasing salt concentration.

Effect of Solvent Polarity

The effect of increasing solvent polarity can be seen in Figure 5, where the average effective Kuhn segment length for ELP1–180 in deionized water is by 0.14 nm shorter than that in hexadecane. A smaller effective Kuhn length in water implies that more energy is required to extend the ELP in water compared to hexadecane. This is reasonable because hexadecane is an aprotic solvent, and a stretch-induced increase in the hydrophobic surface area of the ELP in this solvent does not likely entail significant changes in polypeptide–solvent interactions or solvent structure. It cannot, however, be discounted that there remains a small amount of water bound tightly to the ELP, even when experiments are performed in hexadecane, which could complicate the interpretation of these results.

Figure 5.

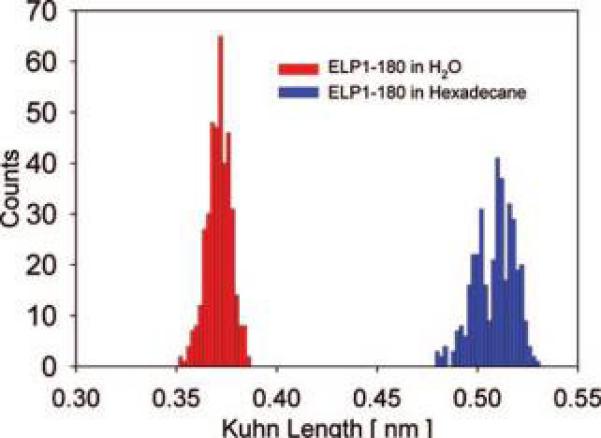
Distributions of the effective Kuhn segment lengths for ELP1–180 in MQ-grade water (l̄_K=0.37 ± 0.01 nm) and hexadecane (l̄_K = 0.51 ± 0.02 nm).

Effect of Guest Residue Type

Genetic engineering allows the synthesis of ELP constructs with a specific sequence of aliphatic amino acids at the guest residue position (Scheme 1). This provides us with molecular constructs of nearly identical molecular weight but significantly different side-group hydro-phobicity. The primary amino acid sequence determines the backbone mobility of proteins in the unfolded state.⁶⁴ The backbone mobility typically decreases with increasing size of the side group and entails an increase in the Kuhn length. For the ELP constructs studied here, the guest residues of ELP4 carry bulkier side groups than those of the guest residues in ELP1 or ELP2. This would suggest that flexibility is reduced for the ELP4 backbone and should result in a larger Kuhn length for ELP4 than for ELP2 or ELP1. Contrary to this hypothesis we find that the effective Kuhn length scales with the averaged hydrophobicity of the guest residues in the three different ELPs studied here: ELP4–120, the most hydrophobic ELP, which solely contains aliphatic Val guest residues, has the shortest Kuhn length of 0.30 nm, ELP1–180 with a 5:2:3 ratio of Val: Ala:Gly guest residues has an intermediate Kuhn length of 0.38 nm, and ELP2–160, the most hydrophilic ELP with a 1:8:7 ratio of Val:Ala:Gly guest residues, has the longest Kuhn length of 0.42 nm (Figure 6).

Figure 6.

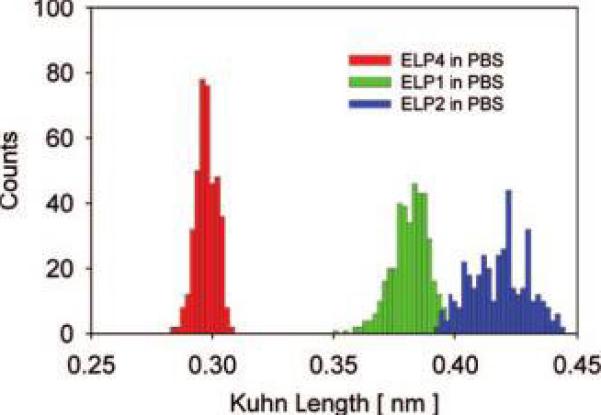
Distributions of the effective Kuhn segment lengths for three ELP constructs in PBS solution. Left histogram: l̄_K = 0.30 ± 0.01 nm for ELP4. Center histogram: l̄_K = 0.38 ± 0.02 nm for ELP1. Right histogram: l̄_K = 0.42 ± 0.02 nm for ELP2.

This apparent discrepancy in Kuhn length ordering can be resolved by considering the differences in the solvent-accessible surface area (ASA) of the nonpolar groups in the different ELPs.^6,65 The solvent-accessible surface area for a residue X in an extended standard state (ASA in Table 1) is taken to be the surface area of that residue in the extended tripeptide Gly-XGly. The values are calculated values for water as a solvent and taken from Rose et al.⁶⁵

Table 1.

	Gly		Ala		Val		Pro
	ASA (Å2)	total number	ASA (Å2)	total number	ASA (Å2)	total number	ASA (Å2)	total number	number of pentapeptides	ASA (Å2)/ pentapeptide
ELP4	88	240	118	0	164	240	146	120	120	645
ELP1	88	414	118	36	164	270	146	180	180	618
ELP2	88	390	118	80	164	170	146	160	160	594

In SMFS of ELP, the solvent-accessible nonpolar surface area increases as more and more hydrophobic groups are exposed to solvent upon stretching the molecule. On the basis of the surface-accessible nonpolar surface area of all the amino acids^65,66 that make up each of the ELP constructs, we expect that the total nonpolar surface area for a molecule of the same length is largest for ELP4 and smallest for ELP2 (Table 1). Thus, we expect that ELP4 has the largest contribution from hydrophobic hydration to the overall force required to stretch the molecule. Furthermore, a comparison of the molar volumes of the amino acids in the guest residue position shows that valine has the largest molar volume overall, relative to that expected from its molecular weight. Valine thus has an increased tendency to form ordered (clathrate) water if exposed to solvent, which entails larger entropic penalities when compared to the hydration of alanine or glycine. Our results agree with this qualitative explanation and show that the effective Kuhn lengths for ELPs apparently depend on the hydrophobicity of the amino acid sequence inserted at the guest residue position. Figure 6 shows that shorter Kuhn lengths are associated with ELPs with more hydrophobic guest residues; e.g., more force is required to hold ELP4 at the same extension as ELP2.

Discussion of the Approach

Here we chose to use an effective Kuhn segment length, obtained from fits of the FJC model to force–extension data, as a sensitive reporter of changes in ELP molecular elasticity and hydration. This approach is reasonable because the Kuhn segment length can be affected by molecular properties, such as conformational changes,⁵⁶ specific interactions between charge groups, the formation of supramolecular structures,^44,49 and changes in the solvent shell that is intimately linked with the polypeptide.^44,67,68 Uncertainty in the determination of cantilever spring constants^69-72 can, however, directly affect the value of the Kuhn segment length obtained from fits to the data and possibly compromise Kuhn length comparisons.⁵⁰ To estimate the effect of uncertainty in the spring constant on Kuhn length, we performed a sensitivity analysis, assuming that our cantilever calibration had an uncertainty of up to ±20% (see Figure S4, Supporting Information). We found that the mean, effective Kuhn lengths for each of our experimental conditions reported above were still different with statistical significance in all observed cases.

To explain mechanisms of elasticity in elastin, Urry et al.,^27,28,33,39 proposed the β -spiral model of elastin. Our experiments did not indicate the presence of such a secondary structural motif in the force–extension behavior. This, however, does not preclude the existence of such structures because our analysis (FJC model fits) concentrated on the molecular mechanics at large stretch ratios and was limited in the low force regime by thermal noise fluctuations of the AFM cantilever. Local hydrophobic interactions in denatured proteins can lead to formation of clusters that restrict the flexibility of a molecule's backbone motions;⁶⁵ however, in the high stretching regime used in our experiments (60% to 80% of the contour length) hydrophobic interactions are likely small and we thus do not expect them to affect the flexibility of the ELP backbone significantly (see Figure 2). Kuhn segment lengths will also differ if two or more molecules are pulled in parallel. Since our selection process included only those curves that could be normalized within experimental noise by contour length at constant force, we reasonably can exclude the contribution from parallel pulls. For example, a “double pull” would cause significant deviations from the majority of the normalized force extension curves, as the Kuhn length would be expected to be about 1/√2 that of the value for a single molecule.⁵⁴

Finally, specific interactions between charged molecular moieties and the presence of supramolecular structures can also affect the Kuhn segment length. We found that when an ELP was stretched for the first time, or after sufficient rest time, a deviation of the force–extension behavior from the FJC model occurred at forces in the range between 220–280 pN. We have shown elsewhere that this deviation arises from force-induced, prolyl cis–trans conformational transitions in the ELP molecule.³⁷ To ascertain that our experiments were performed at quasiequilibrium, we performed repeated stretch-release experiments for ELP1–180 in PBS, which showed that at the stretch-relaxation rate of the measurement, the folding and refolding paths were identical within measurement resolution. Here we only included force curves that did not show any such deviation; i.e., we used mechanically annealed ELPs.

To check the validity of our approach in which we use the effective Kuhn length as a reporter, we also performed a nonparametric curve fitting of SMFS force–extension data to estimate the areas under the force–extension curves without invoking a particular polymer elasticity model (see Supporting Information). The results from these nonparametric estimations qualitatively matched those obtained from FJC model fits, further justifying our use of the Kuhn segment length as a reporter for comparing different data sets.

Conclusions

We investigated the effect of temperature, ionic strength, solvent polarity, and type of guest residue on the force–extension behavior of single, end-tethered elastin-like polypeptides (ELPs), using single molecule force spectroscopy (SMFS). To improve the fits of polymer elasticity models to SMFS data we applied a novel statistical procedure. We applied this procedure to fit the FJC model to force–extension data obtained from stretching individual elastin-like polypeptide molecules, to infer effects of solvent quality and minor changes in molecular architecture on molecular elasticity. Our results show that subtle differences in the effective Kuhn segment lengths largely reflect energetic differences associated with hydrophobic hydration of ELPs upon forced unfolding and our experimental results are in good qualitative agreement with predictions from recent MD simulations. We believe this is the first experimental study that systematically explores the effect of solvent environment on the mechanics and hydration of elastin-like polypeptides at the single molecule level. In conclusion, SMFS, combined with our data analysis approach, could be used as a complementary tool to study the subtleties of polypeptide–water interactions in unstructured proteins on the single molecule level.