Abstract
The incompressibility and planar displacement assumptions were used to reduce the number of independent tissue parameters required for the characterization of a structural model of the vocal folds. The influence of these simplifying assumptions on the vibratory properties of the model was investigated. The purpose was to provide estimates of the error introduced by these assumptions. The variability in human tissue properties was accounted for through systematic variation of several material parameters. The modal properties of a vocal fold structural model were computed with each assumption and, in turn, were relaxed to determine their respective effects. The results indicated that the incompressibility assumption introduces little error. Errors introduced by the planar displacement assumption were found to depend on the ratio of the longitudinal stiffness and the transverse stiffness. Criteria for determining the compatibility of tissue property values from independent studies are also presented.
INTRODUCTION
Computational models are useful for the study of the mechanics of the vocal folds, in particular, their vibrations. Lumped element models (Flanagan and Landgraf, 1968; Ishizaka and Flanagan, 1972; Titze, 1988) capture the essential characteristics of vocal fold vibration during phonation, but they do not provide finer details associated with higher order vibration modes. Higher-order numerical modeling approaches, such as the finite element method, are better suited for a more detailed analysis and have been used for the study of biphonation (Tao et al., 2006b), impact stresses (Gunter, 2003; Tao et al., 2006a), and posturing (Hunter et al., 2004). Such studies require an accurate description of the local deformation of the tissue. One obstacle to accurate numerical simulations of human phonation is a lack of complete consistent vocal fold tissue property data.
The vocal folds may be idealized as consisting of three distinct tissue regions: the mucosa (or cover), the vocal ligament, and the thyroarytenoid muscle. As a first approximation, these tissues are often assumed to be linearly elastic, with the mucosa approximated as isotropic (Chan and Titze, 1999), and the remaining tissues modeled as transversely isotropic (Berry and Titze, 1996; Hunter et al., 2004). Three-layered linear elastic models would require 12 tissue parameters to unambiguously characterize tissue deformation. Only three of these parameters have been measured using human tissue. The shear modulus and Young’s modulus of the vocal fold mucosa were measured by Chan and Titze (1999) and Zhang et al. (2006), respectively. Young’s modulus of vocal fold ligament was measured by Min et al. (1995). These material parameters are summarized in Table 1, with measured human properties highlighted in bold. Canine tissue measurements have also been performed (Kakita et al., 1981; Alipour-Haghigni and Titze, 1985b; Hunter and Titze, 2007).
Table 1.
Tissue types and independent parameters required for linear elastic descriptions. Measured human tissue parameters indicated in bold.
| Tissue type | Independent parameters | Material type |
|---|---|---|
| Mucosa | Em, μm | Isotropic |
| Ligament | EL, , μL, , | Trans. isotropic |
| Thyroarytenoid | ETA, , μTA, , | Trans. isotropic |
Unfortunately, several material parameters required for continuum models of vocal folds tissue have not been measured due to the limitations inherent to current testing methods. The model behavior is determined in part by the chosen values. Alipour-Haghighi and Titze (1985a) observed that vocal fold vibration patterns were “highly affected by material parameters.” Unmeasured parameters must be estimated in order to obtain closure. Inaccurate estimates introduce errors in model predictions. A rigorous computationally expensive approach is to perform parametric variations (Berry and Titze, 1996) for each of the eight unknown parameters (, μL, , , ETA, μTA, , and ).
The purpose of the present study was to evaluate the consequences of two assumptions that can be used to reduce the number of independent parameters required for vocal fold models The first technique is the so-called planar displacement assumption which constrains vocal fold motion into coronal planes. This assumption is based on the observation that vocal fold motion occurs primarily in the coronal plane, and that motion perpendicular to this plane is much less substantial (Baer, 1981; Saito et al., 1985). The second assumption is that of incompressible (or nearly incompressible) tissue. This assumption is commonly applied to biological soft tissue, including the vocal folds (Pioletti and Rakotamanana, 2000; Berry and Titze, 1996; Hunter et al., 2004). While both assumptions are common in vocal fold models, neither has been thoroughly evaluated to determine their effects on the dynamic properties of vocal fold models.
METHODOLOGY
Justification for linear analysis
In general, a nonlinear relationship exists between stress and strain for most vocal fold tissues (Min et al., 1995; Chan and Titze, 1999; Zhang et al., 2006). Nonlinear stress-strain relationships are essential when large deformations occur (such as during posturing). However, linear approximations may be used for small amplitude deformations, such as vibrations about a given posture. Nonlinear vocal fold models require additional unmeasured tissue parameters, thus increasing the uncertainty of model outputs. It has been observed that laryngeal muscles exhibit a nearly linear stress-strain relationship when active muscular tension is present (Hast, 1966; Titze, 2006). Linear tissue models were used for all tissues in this study.
Modal analysis is a standard method for extracting the natural vibratory frequencies of a structure (Meirovitch, 2000). This technique is based on linear approximations and produces modal frequencies and modal vibration patterns. Modal vibration patterns have been hypothesized to be important in the self-oscillation of the vocal folds (Zhang et al., 2007; Berry et al., 1994). Continuum structures have, in principle, an infinite number of resonance frequencies, although only a few modal frequencies contribute significantly to phonation (Berry et al., 1994; Berry, 2001).
Planar displacement assumption
The motion of vocal fold vibration has been observed to be predominantly in coronal planes (Baer, 1981; Saito et al., 1985). By examining excised canine larynges, (Berry et al., 2001) quantified the anterior∕posterior motion of canine vocal folds as one order of magnitude smaller than motion in the coronal plane. Numerical simulations have yielded similar observations (Rosa et al., 2003). Based on such observations, the majority of computational vocal fold models have utilized the planar displacement assumption (Alipour-Haghigni et al., 2000; Alipour-Haghigni and Titze, 1988; Berry et al., 1994; Berry and Titze 1996; Tao et al., 2006a; Tao and Jiang, 2006c).
A transversely isotropic material generally requires five independent parameters (E, E′, v′, μ, and μ′—see Lekhnitskii, 1963). For either compressible or incompressible materials, the planar displacement assumption requires the value of v+ to be zero and that v be less than unity, while v′ has no effect on the material response. This is because the contribution of v′ to the material response is increasingly diminished as E′ becomes larger [see Eq. 3 below]. Poisson’s ratios of a material under the planar displacement condition are
| (1) |
| (2) |
The planar displacement assumption can be imposed in two ways. One approach is to remove the anterior∕posterior degree of freedom from numerical simulations (Alipour-Haghighi and Titze, 1985a; Berry and Titze, 1996). When using the finite element method, this approach causes artificial constraint forces to arise (Cook et al., 2001). The planar displacement may also be imposed by assuming an infinite longitudinal stiffness (Cook and Mongeau, 2007). While this approach does not require constraint forces, unusually high values of longitudinal stiffness are required.
For a linearly elastic material with transverse isotropy in the xz-plane, the stress-strain relations are expressed by Hooke’s law:
| (3) |
Taking the limit as E′→∞ causes all terms with E′ in the denominator to vanish. The condition of a symmetric compliance matrix (Lempriere, 1968) implies that v+ must also be zero. The resulting matrix has zeros in the second row and second column. Because the strain vector ε={0 1 0 0 0 0} is in the null space of the resulting compliance matrix, no anterior∕posterior strains (εyy) can develop, regardless of imposed loads (σ). This situation is equivalent to the planar displacement assumption. In practice, an infinitely large value of E′ is not amenable to computational methods. However, an extremely large value of E′ (∼104 times larger than E) was used in a previous study to demonstrate that this approach has the same effect as directly constraining anterior∕posterior degrees of freedom (Cook and Mongeau, 2007). The validity of the planar displacement condition is examined in Sec. 4B.
Incompressibility assumption
The incompressibility assumption is commonly applied to biological soft tissue (Humphrey, 2002). Total incompressibility causes a singularity in the compliance matrix of Eq. 3. Thus, the material is usually modeled as “nearly incompressible,” although the term “incompressible” is used in this paper for the sake of brevity. The incompressibility assumption has been justified based on the high water content of human tissue (Berry and Titze, 1996). This assumption has been applied to the vocal folds by Berry and Titze (1996), Rosa et al. (2003), Hunter et al., (2004), and Decker and Thomson, (2007). The incompressibility assumption leads to a reduction in the number of independent parameters needed for analysis.
For isotropic materials, Poisson’s ratio normally varies between 0 (completely compressible) and 1∕2 (totally incompressible). Values slightly less than 1∕2 are typically used to avoid singularities. If a material is assumed to be incompressible, Eq. 4 can be used to determine the shear modulus μ based on the measured values of Young’s modulus E or vice versa. Thus, only one independent parameter is required.
| (4) |
A similar approach can be used for transversely isotropic materials. Utilizing the incompressibility condition and the symmetry of the compliance matrix, all three Poisson’s ratios and the transverse shear modulus are expressed as functions of Young’s moduli, E and E′ (Itskov and Aksel, 2002):
| (5) |
| (6) |
| (7) |
and
| (8) |
Thus, an incompressible, linearly elastic, transversely isotropic material is characterized by three independent material properties {E,E′,μ′}. The above equations correspond to total incompressibility and a singular compliance matrix will result. This problem may be avoided by using a nearly incompressible formulation which relies on one additional parameter, the bulk modulus κ (Itskov and Askel, 2002). For near incompressibility, the values of Poisson’s ratios are weakly related to the choice of κ. Thus, κ is not considered as an independent parameter. The value for μ can be found by substituting Eq. 11 into Eq. 4, leading to
| (9) |
| (10) |
and
| (11) |
There are very few direct measurements of Poisson’s ratio of human tissue. There are no reported measurements of the compressibility of vocal fold tissues. Thus, Poisson’s ratio values for vocal fold simulation have been typically estimated from ad hoc arguments. In previous studies, the following values have been assumed for both longitudinal and transverse Poisson’s ratios (v and v′): {0, 0.3, 0.45, 0.66, 0.73, 0.76}. Values of v=0.9 and v′=0.99 have also been assumed. (Alipour-Haghigni et al., 2000; Tao et al., 2006a; Tao et al., 2006b; Tao et al., 2006c; Rosa et al., 2003; Berry and Titze, 1996). The sensitivity of modal property predictions to this parameter has not often been addressed. Berry and Titze (1996) reported that the second modal frequency increased as Poisson’s ratio increased, while the third mode decreased. The validity of the incompressibility assumption and its effects on the vibratory characteristics of the vocal folds are addressed in Sec. 4B.
Compatibility
Reported parameter values almost always correspond to different tissue samples. The selection of tissue parameters from independent studies may produce parameter sets that are mutually incompatible. For example, at zero strain, Zhang et al. (2006) reported Young’s modulus of the mucosa to vary between 4 and 20 kPa. Chan and Titze (1999) reported the (zero strain) shear modulus of the vocal fold cover within the range between 10 and 1000 Pa. Selection of average values within those ranges, for example, Ec=10 kPa and μc=500 Pa, would [by Eq. 4] lead to a nonphysical value for Poisson’s ratio (νc=9). The compatibility equations presented above can be used to avoid this situation. The incompressibility assumption (v=0.49) in conjunction with Eq. 4 and the choice Ec=4 kPa yield the value μc=1340 Pa. This value is reasonably close to the values reported by Chan and Titze (1999).
The compatibility conditions for an isotropic material are that ν<1∕2 and Eq. 4 is satisfied. For a transversely isotropic material, the conditions of a symmetric positive definite compliance matrix impose the following additional constraints on parameter values (see Lempriere, 1968):
| (12) |
| (13) |
| (14) |
and
| (15) |
These conditions can be used to verify that parameter values extracted from independent experimental studies are compatible with each other and do not violate fundamental assumptions.
NUMERICAL PROCEDURES
To quantify the errors introduced by the two assumptions discussed above, the incompressibility and planar displacement assumptions were applied to a structural model of the vocal folds. Modal analysis was used to compute the structure’s resonant mode shapes and frequencies in the absence of fluid loading. The incompressibility and planar displacement assumptions were then relaxed in turn by allowing varying amounts of compressibility and anterior∕posterior motion. The effects of these assumptions were determined by comparison between the relaxed and original cases.
The vocal fold structure was idealized as having a body and a cover, similar to the body-cover model of Titze (1988). The body-cover idealization considers the vocal ligament to be included in the cover region and reduces the number of parameters required to define the model. Since only the longitudinal stiffness of the vocal ligament has been measured experimentally, the remaining ligament parameters would necessarily be estimations, thus introducing additional uncertainty into the current study.
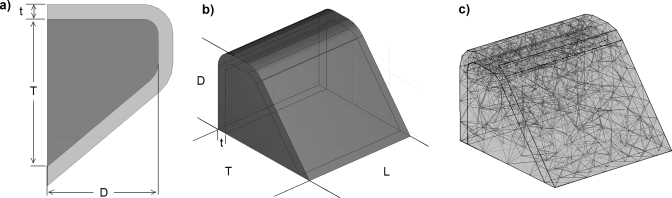
The model consisted of one vocal fold assumed to be symmetric in the anterior∕posterior direction. All materials were assumed to be linearly elastic. The body was represented by a transversely isotropic material. The cover was approximated by an isotropic material. The M5 geometry with an included angle of 0° (Scherer et al., 2001) was used to define the vocal fold profile. Geometric parameters are shown in Fig. 1 and Table 2. A length of 12 mm was chosen according to Berry and Titze (1996) and Cook and Mongeau (2007). The cover was formed by offsetting the standard M5 geometry by a constant distance t=0.8 mm from the body (Titze, 2006).
Figure 1.
Diagram of model geometry and mesh: (a) coronal cross section, (b) isotropic view, and (c) finite element mesh.
Table 2.
Geometric parameters of the body-cover model of Fig. 1.
| Parameter | Symbol | Value |
|---|---|---|
| Length | L | 12 mm |
| Depth | D | 7.5 mm |
| Thickness | T | 10 mm |
| Cover thickness | t | 0.8 mm |
The anterior, posterior, and lateral faces were fixed (zero displacement boundary conditions), while the remaining faces were free. The structure was meshed with approximately 3000 quadratic finite elements, for a total of approximately 15 000 degrees of freedom [see Fig. 1c]. This mesh was found to yield a mesh-converged solution since higher density meshes (∼20 000 degrees of freedom) produced identical results. Parametric modal analysis of the body-cover model was performed using COMSOL version 3.3 with MATLAB. Parametric variation of material parameters was accomplished via control loops executed in MATLAB. Model verification involved comparing modal analysis results predicted by COMSOL with those predicted by the commercial finite element code ADINA. Modal frequency differences were less than 2.5%, and similar mode shapes were predicted by both codes.
To relate unknown tissue properties to those previously measured, all tissues were first assumed to be incompressible (as in Sec. 2C). Accordingly, Poisson’s ratio of the cover was νc=0.499. Young’s modulus of the cover was chosen to be Ec=4 kPa (Zhang et al., 2006). Longitudinal Young’s modulus of the body was specified as (Titze, 2006). Poisson’s ratios and the shear modulus of the body were calculated according to equations of Sec. 2. Based on estimations used previously, the values Eb=10 kPa and were chosen (Berry and Titze, 1996; Cook and Mongeau, 2007). Equation 4 was used to determine the transverse shear modulus of the body. The resulting set of material properties is summarized in Table 3.
Table 3.
Nominal material properties of the body-cover model. Measured parameters indicated in bold.
| Property | Incompressibility | Incompressibility and planar displacement |
|---|---|---|
| Ec | 4 kPa | 4 kPa |
| 1340 kPa | 1340 kPa | |
| νc | 0.499 | 0.499 |
| 28 kPa (canine) | ∞ | |
| Eb | 10 kPaa | 10 kPaa |
| 10 kPaa | 10 kPaa | |
| μb | 2.7 kPaa | 2.5 kPa |
| νb | 0.82a | 0.999 |
Estimated or dependent on estimated properties.
The number of undetermined parameters was then further reduced by combining the incompressibility assumption with the planar displacement assumption. The techniques of Sec. 2 were used to eliminate the dependence of Poisson’s ratios on transverse stiffness (Eb). The assumption of planar displacement coupled with incompressibility thus reduced the number of unknown material properties from 5 to 2. The resulting parameter values are summarized in the final column of Table 3.
MODAL ANALYSIS RESULTS
Evaluation of the incompressibility assumption
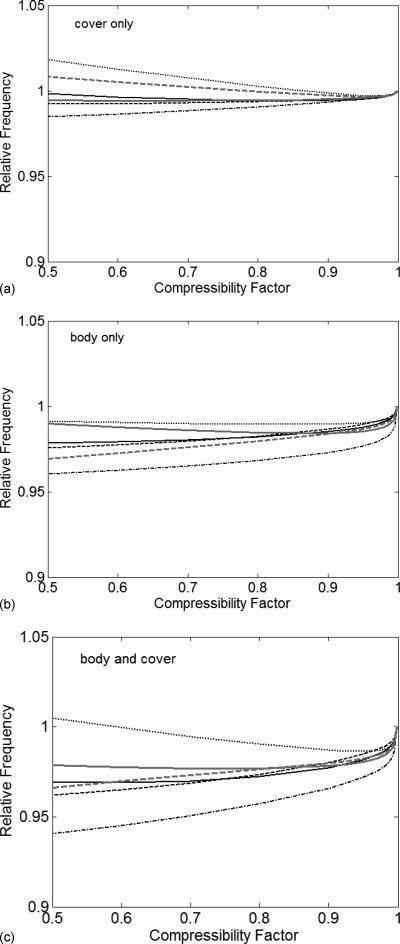
The errors introduced by the incompressibility assumption were determined by varying Poisson’s ratios of each tissue region independently as well as simultaneously. The results are presented in terms of the compressibility factor, which is defined here as the ratio between compressible (variable) and incompressible (fixed) Poisson’s ratios. For the isotropic cover layer, Poisson’s ratio was varied between 0.499 (incompressible) and 0.25. For the body layer, the bulk modulus was varied according to Eqs. 9, 10, 11 such that the compressibility factor was varied between unity (incompressible) and 0.5. For each set of tissue parameters, modal analysis produced the first six modes of vibration and their associated frequencies. The modal frequencies of all computed cases were normalized by dividing each modal frequency by the corresponding value obtained in the incompressible case. Figures 2a, 2b, 2c show the normalized modal frequencies as functions of the compressibility of the cover, the compressibility of the body, and the compressibility of both layers.
Figure 2.
Normalized modal frequencies as a function of compressibility and tissue region: (a) cover only, (b) body only, and (c) body and cover. Each curve normalized with the incompressible value as unity. (—–) mode 1; (---) mode 2; (-·-·-) mode 3; (·····) mode 4; (—) mode 5; (---) mode 6.
The vocal fold model was observed to be least sensitive to changes in cover compressibility. Each modal frequency changed by less than 3% for a 50% reduction in Poisson’s ratio of the cover. The model was more sensitive to changes in the compressibility of the body. Each modal frequency changed by less than 5% for a 50% reduction in the compressibility of the body. These results are influenced by the fact that the compressibility of only one tissue was modified while the remaining tissue was held as incompressible. When the compressibility of both body and cover was varied simultaneously, the maximum change in modal frequency was approximately 6% for a 50% reduction in compressibility. These changes are relatively small and would likely be negligible in most applications.
Wide variations in human tissue properties have been reported due to the male∕female differences, the age difference, and the experimental variability (Chan and Titze, 1999; Hammond et al., 2000; Zhang et al., 2006). To address this variability, the material properties of the above model were varied over the reported and estimated ranges of human tissue property values, listed in Table 4. For each series, one of the nominal model parameters of Table 3 was replaced by its corresponding value from Table 4. For each such replacement, the compressibility factor was assigned values of 0.50, 0.90, and 0.99. Modal analysis was performed for each unique set of tissue parameters. Six vibratory modes were calculated for each case. The mean and standard deviations of the differences between the results obtained using incompressible and compressible assumptions are presented in Table 5.
Table 4.
Parameter substitutions for parametric variation.
| Parameter values (kPa) | ||
|---|---|---|
| Ec | (Eb, ) pairs | |
| 1 | (0.57, 0.57) | 1 |
| 50 | (5.7, 5.7) | 100 |
| 100 | (4.5, 90) | |
| 200 | (9,90) | |
| (90,90) | ||
Table 5.
Discrepancies between incompressibility and partial compressibility for two values of compressibility factor.
| Mode | Compressibility factor | |||
|---|---|---|---|---|
| 0.5 | 0.9 | |||
| Mean diff | Std dev. | Mean diff | Std dev. | |
| 1 | −5% | 3% | −4% | 2% |
| 2 | −4% | 4% | −3% | 2% |
| 3 | −5% | 4% | −4% | 1% |
| 4 | −6% | 5% | −5% | 3% |
| 5 | −5% | 5% | −4% | 3% |
| 6 | −5% | 5% | −5% | 3% |
| All modes | −5% | 5% | −4% | 3% |
The mean difference between incompressible and 50% compressible tissues ranged between −4% and −6%. Greenleaf et al. (2003) reported the incompressibility levels between 98% and 99.8% for soft biological tissue. For a conservative estimate of 90% compressibility, the mean difference ranged between −3% and −5%, and the average difference for all six vibratory modes was −4% with a standard deviation of 3%. The actual variability would likely be considerably lower than these values.
Evaluation of the planar displacement assumption
The assumption of incompressibility was again used to reduce the number of undetermined parameters. The longitudinal stiffness was varied from (isotropy) to (planar displacement). All other parameters were either held constant or varied according to the equations of Sec. 2 (see Table 3 for resulting values).
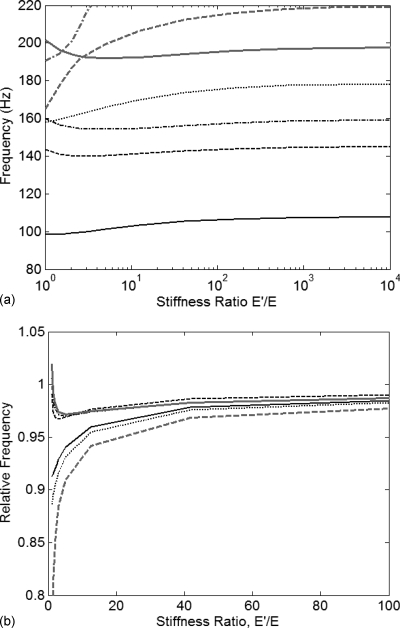
First, the body alone was subjected to the planar displacement assumption, as described in the preceding paragraph. The cover was assumed to be incompressible, with nominal tissue parameters. The resulting modal frequencies are shown in Fig. 3a as functions of longitudinal to transverse stiffness ratio. Very little variation was observed for stiffness ratio values greater than 100. The exception was the modal frequency of the seventh mode, observed at 190 Hz for a stiffness ratio of 1, but rising above 200 Hz for a stiffness ratio of 2. The seventh mode represents the lowest mode containing more than a single half-wavelength in the anterior∕posterior direction and exhibited primarily longitudinal motion. The behavior of this mode suggests that the planar displacement condition may have undesirable effects on modes containing two or more half-wavelengths in the anterior∕posterior direction since such modes are particularly sensitive to the longitudinal stiffness.
Figure 3.
Planar displacement condition imposed in the body layer only: (a) modal frequencies as a function of stiffness ratio; (b) normalized modal frequencies with the planar displacement value as unity (mode 7 omitted). (—–) mode 1; (---) mode 2; (-·-·-) mode 3; (·····) mode 4; (—) mode 5; (---) mode 6; (-·-·-) mode 7.
As with previous results, the modal frequencies of Fig. 3a were normalized by dividing each modal frequency by the corresponding prediction for planar displacement. Relative values are plotted in Fig. 3b. For stiffness ratios greater than 10, the maximum relative difference introduced by the planar displacement assumption was less than 10%. Differences were observed to consistently decrease with increasing stiffness ratio. The maximum relative difference was less than 5% for stiffness ratios greater than 30. This is consistent with previous results obtained using similar methods but a different structural model (Cook and Mongeau, 2007). The modal frequencies obtained for a stiffness ratio of 104 were found to differ by less than 1% from the frequencies obtained by eliminating the anterior∕posterior degree of freedom for every node in the body layer (absolute planar displacement).
The planar displacement condition was also applied to the body and cover simultaneously by eliminating the anterior∕posterior degree of freedom of every node in the computational model. In comparison with the results of Fig. 3, constraint of the entire structure increased modal frequencies by an average of 3%. Interestingly, constraint of the cover alone had nearly the same effect on modal frequencies as the constraint of the body alone. Constraint of either tissue region raised modal frequencies above the incompressible case by approximately 8%, and constraint of both regions raised modal frequencies by approximately 10%.
To account for human variability and experimental measurement errors, the independent parameters Ec, Eb, and were varied over wide ranges to determine the general applicability of the planar displacement assumption. The property ranges were the same as those given in Table 4, but values were controlled through the stiffness ratio. Since the planar displacement assumption does not reduce the number of independent parameters of the cover, only the stiffness ratio of the body was modified. For each unique parameter set, the stiffness ratio took on values (1,5, 30, 100, 10 000, 1 000 00).
As observed in Fig. 3, the variations introduced by the planar displacement assumption depend on the stiffness ratio. For stiffness ratios greater than 5, the relative difference decreased monotonically as a function of stiffness ratio. Table 6 shows the mean and standard deviations of the computed differences for the first six modal frequencies. The planar displacement assumption was found to yield reasonably accurate results for stiffness ratio values greater or equal to 30.
Table 6.
Influence of stiffness ratio on the relative differences between constrained and unconstrained modal frequencies.
| All modes | Stiffness ratio | |||
|---|---|---|---|---|
| 1 | 5 | 30 | 100 | |
| Mean difference | −9.0% | −6.7% | −4.0% | −2.3% |
| Std deviation | 11.8% | 6.1% | 3.6% | 2.2% |
DISCUSSION AND CONCLUSIONS
Two strategies may be followed to reduce the number of independent material properties. The first is to assume an infinite (or practically speaking, an extremely high) value for the longitudinal stiffness. This approach effectively forces v+ to zero and eliminates the influence of v′. Adjustment of v then allows control of the material’s level of compressibility. The second is to impose the condition of incompressibility. This allows Poisson’s ratios to be determined as functions of the longitudinal and transverse stiffness parameters. These assumptions can also be applied simultaneously for a further reduction in the number of independent parameters. Table 7 provides a summary of the above methods, identifying the independent material properties for each tissue type, and compares the reduced formulation to the 12 independent parameters required for a three-layer model of the vocal folds.
Table 7.
Summary of parameter reduction methods (measured properties indicated in bold).
| Assumption | Independent parameters | |||
|---|---|---|---|---|
| Mucosa (isotropic) | Ligament (transversely isotropic) | Muscle (transversely isotropic) | No. of independent parameters for a three-layer model | |
| None | Em, μm | EL, , μL, , | ETA, , μTA, , | 12 |
| Planar displacement | Em, μm | EL, , νL | ETA, , νTA | 8 |
| Incompressibility | Em or μm | EL, , | ETA, , | 7 |
| Planar disp. and incompressibility | Em or μm | EL, | ETA, | 5 |
The creation of computational vocal fold models often utilizes measured tissue parameter values which may be referred to as “uncorrelated” (i.e., each individual tissue property was obtained from a unique tissue sample). Natural variation between samples may therefore create a situation in which the measured values violate compatibility requirements. This undesirable situation may be avoided by ensuring that the chosen values obey the analytic relations of Sec. 2.
The discrepancies introduced by both assumptions were systematically investigated using a body-cover model of the vocal folds. The incompressibility assumption was found to be appropriate over a wide range of material properties. An upper limit for the mean error introduced through the incompressibility assumption was proposed. The planar displacement assumption introduced only minor errors for stiffness ratio values greater than 30. Significant errors (i.e., more than 10%) may be introduced for lower values of the stiffness ratio.
The present study highlights the need for additional measurements of the material constants of vocal fold tissues. Young’s modulus in the direction perpendicular to the fiber direction E appears as an independent parameter in all of the above cases. Unfortunately, this parameter has yet to be measured for either the thyroarytenoid muscle or the vocal ligament.
Both the incompressibility and the planar displacement assumptions significantly reduce (and in some cases eliminate) the role of Poisson’s ratios. Thus, experimental data for these constants may be less important than for the other more influential parameters such as E, μ, and μ′. The above assumptions can be implemented in numerical simulations with relative ease. In practice, finite element programs require users to enter nine parameters (five of which are independent) for transversely isotropic materials and two parameters for isotropic materials. The above relations can be used to calculate values for these constants as functions of the selected independent parameters. Furthermore, these methods ensure that the chosen values will be compatible with each other. Thus, by relating unmeasured parameters to measured parameters through a set of physiologically realistic assumptions and thermodynamic constraints, this approach reduces the number of independent parameters, decreases the cost of parametric studies, and produces models that are more directly based upon measured tissue properties.
ACKNOWLEDGMENTS
This study was supported by Grant Nos. R01 005788 and R01 008290 from the National Institute on Deafness and Other Communication Disorders, as well as by the Bilsland Strategic Initiatives Fellowship (Purdue University). The authors would like to thanks the Associate Editor and reviewers for their suggestions and assistance.
NOMENCLATURE
- L
length
- D
depth
- T
thickness
- t
cover thickness
- E
Young’s modulus (stiffness) in general or in the transverse plane
- E′
Young’s modulus (stiffness) in the longitudinal direction
- EMEc
Young’s modulus (stiffness) of the cover and mucosa, respectively
- ELETAEb
transverse Young’s modulus (stiffness) of the ligament, thyroarytenoid muscle, and body, respectively
longitudinal Young’s modulus (stiffness) of the ligament, thyroarytenoid muscle, and body, respectively
- μ
shear modulus
- μ′
shear modulus in one of two longitudinal planes
- μMμc
shear modulus of the cover and mucosa, respectively
- μLμTAμb
transverse shear modulus of the ligament, thyroarytenoid muscle, and body, respectively
longitudinal shear modulus of the ligament, thyroarytenoid muscle, and body, respectively
- υ
Poisson’s ratio (in a plane of symmetry)
- υij
Poisson’s ratio: passive strain in the i-direction induced by applied strain in the j-direction (note: some texts reverse these indices)
- υ′
applied longitudinal Poisson’s ratio: passive strain in the transverse direction induced by applied strain in the longitudinal direction
- υ+
passive longitudinal Poisson’s ratio: passive strain in the longitudinal direction induced by applied strain in the transverse direction
applied transverse Poisson’s ratio of the ligament and thyroarytenoid muscle, respectively
- υcυb
Poisson’s ratio of the cover and transverse Poisson’s ratio of the body
- κ
bulk modulus
References
- Alipour-Haghighi, F., and Titze, I. R. (1985a). “Simulation of particle trajectories of vocal fold tissue during phonation,” in Vocal Fold Phyisiology: Biomechanics, Acoustics, and Phonatory Control, edited by Titze I. and Scherer R. (Denver Center for the Performing Arts, Denver, CO: ). [Google Scholar]
- Alipour-Haghighi, F., and Titze, I. R. (1985b). “Viscoelastic modeling of canine vocalis muscle in relaxation,” J. Acoust. Soc. Am. 10.1121/1.392701 78, 1939–1943. [DOI] [PubMed] [Google Scholar]
- Alipour, F., and Titze, I. R. (1988) “A finite-element simulation of vocal fold vibrations,” in Proceedings of the 14th Annual Northeast Bioengineering Conference, edited by LaCourse (IEEE, New York: ), Catalog No.88-CH2666-6.
- Alipour, F., Berry, D., and Titze, I. R. (2000). “A finite-element model of vocal-fold vibration,” J. Acoust. Soc. Am. 10.1121/1.1324678 108, 3003–3012. [DOI] [PubMed] [Google Scholar]
- Baer, T. (1981). “Investigation of the phonatory mechanism,” Proceeding of the Conference on the Assessment of Vocal Pathology, ASHA Reports. 11, edited by Ludlow C. L. and Hart M. O. C. (ASHAA, Rockville, MD), pp. 38–46.
- Berry, D. A., Herzel, H., Titze, I. R., and Krischer, K. (1994). “Interpretation of biomechanical simulations of normal and chaotic vocal fold oscillations with empirical eigenfunctions,” J. Acoust. Soc. Am. 10.1121/1.409875 95, 3595–3604. [DOI] [PubMed] [Google Scholar]
- Berry, D. A., and Titze, I. R. (1996). “Normal modes in a continuum model of vocal fold tissues,” J. Acoust. Soc. Am. 10.1121/1.416975 100, 3345–3354. [DOI] [PubMed] [Google Scholar]
- Berry, D. A. (2001). “Mechanisms of modal and nonmodal phonation,” J. Phonetics 10.1006/jpho.2001.0148 29, 431–450. [DOI] [Google Scholar]
- Berry, D. A., Montequin, D. W., and Tayama, N. (2001). “High-speed digital imaging of the medial surface of the vocal folds,” J. Acoust. Soc. Am. 10.1121/1.1408947 110, 2539–2547. [DOI] [PubMed] [Google Scholar]
- Chan, R. W., and Titze, I. R. (1999). “Viscoelastic shear properties of human vocal fold mucosa: Measurement methodology and empirical results,” J. Acoust. Soc. Am. 10.1121/1.427947 106, 2008. [DOI] [PubMed] [Google Scholar]
- Cook, R. D., Malkus, D. S., Plesha, M. E., and Witt, R. J. (2001). Concepts and Applications of Finite Element Analysis, 4th ed. (Wiley, New York: ), p. 492. [Google Scholar]
- Cook, D. D., and Mongeau, L. (2007). “Sensitivity of a continuum vocal fold model to geometric parameters, constraints, and boundary conditions,” J. Acoust. Soc. Am. 10.1121/1.2536709 121, 2247–2253. [DOI] [PubMed] [Google Scholar]
- Decker, G., and Thomson, S. (2007) “Computational simulations of vocal fold vibration: Bernoulli versus Navier–Stokes,” J. Voice 21, 273–284. [DOI] [PubMed] [Google Scholar]
- Flanagan, J. L., and Landgraf, L. L. (1968). “Self-oscillating source for vocal tract synthesizers,” IEEE Trans. Audio Electroacoust. 10.1109/TAU.1968.1161949 AU-16, 57–64. [DOI] [Google Scholar]
- Greenleaf, J. F., Fatemi, M., and Insana, M. (2003). “Selected methods for imaging elastic properties of biological tissues,” Annu. Rev. Biomed. Eng. 10.1146/annurev.bioeng.5.040202.121623 5, 57–78. [DOI] [PubMed] [Google Scholar]
- Gunter, H. (2003). “A mechanical model of vocal-fold collision with high spatial and temporal resolution,” J. Acoust. Soc. Am. 10.1121/1.1534100 113, 994–1000. [DOI] [PubMed] [Google Scholar]
- Hammond, T. H., Gray, S. D., and Butler, J. E. (2000). “Age- and gender-related collagen distribution in human vocal folds,” Ann. Otol. Rhinol. Laryngol. 109, 913–920. [DOI] [PubMed] [Google Scholar]
- Hast, M. H. (1966) “Mechanical properties of the cricothyroid muscle,” Laryngoscope 76, 537–548. [Google Scholar]
- Humphrey, J. D. (2002). Cardiovascular Solid Mechanics, Cells, Tissues, and Organs (Springer-Verlag, New York: ), p. 89. [Google Scholar]
- Hunter, E. J., Titze, I. R., and Alipour-Haghigni, F. (2004). “A three-dimensional model of vocal fold abduction∕adduction,” J. Acoust. Soc. Am. 10.1121/1.1652033 115, 1747–1759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter, E. J., and Titze, I. R. (2007). “Refinements in modeling the passive properties of laryngeal soft tissue,” J. Appl. Phys. 103, 206–219. [DOI] [PubMed] [Google Scholar]
- Ishizaka, K., and Flanagan, J. L. (1972). “Synthesis of voiced sounds from a two-mass model of the vocal cords,” Bell Syst. Tech. J. 51, 1233–1267. [Google Scholar]
- Itskov, M., and Aksel, N. (2002). “Elastic constants and their admissible values for incompressible and slightly compressible anisotropic materials,” Acta Mech. 10.1007/BF01182156 157, 81–96. [DOI] [Google Scholar]
- Kakita, Y., Hirano, M., and Ohmaru, K. (1981). “Physical properties of the vocal fold tissue,” in Vocal Fold Physiology, edited by Stevens K. and Hirano M. (University of Tokyo, Tokyo, Japan: ). [Google Scholar]
- Lekhnitskii, S. G. (1963). Theory of Elasticity of an Anisotropic Body (Holden-Day, San Francisco: ), p. 25. [Google Scholar]
- Lempriere, B. M. (1968). “Poisson’s ratio in orthotropic materials,” Am. Inst. of Aero. and Astro. 6, 2226. [Google Scholar]
- Meirovitch, L. (2000). Principles and Techniques of Vibrations (Prentice-Hall, Upper Saddle River, NJ: ), pp. 469–485. [Google Scholar]
- Min, Y. B., Titze, I. R., and Alipour-Haghigni, F. (1995). “Stress-strain response of the human vocal ligament,” Ann. Otol. Rhinol. Laryngol. 104, 563–569. [DOI] [PubMed] [Google Scholar]
- Pioletti, E. P., and Rakotamanana, L. R. (2000). “Non-linear viscoelastic laws for soft biological tissues,” Eur. J. Mech. A∕Solids 10.1016/S0997-7538(00)00202-3 19, 749–759. [DOI] [Google Scholar]
- Rosa, M. O., Pereira, J. C., Grellet, M., and Alwan, A. (2003). “A contribution to simulating a three-dimensional larynx model using the finite element method,” J. Acoust. Soc. Am. 10.1121/1.1619981 114, 2893–2905. [DOI] [PubMed] [Google Scholar]
- Saito, S., Fukuda, H., and Kitahira, S. (1985). “Pellet tracking in the vocal fold while phonating: experimental study using canine larynges with muscle activity,” in Vocal Fold Physiology (Denver Center for the Performing Arts, Denver: ). [Google Scholar]
- Scherer, R. C., Shinwari, D., De Witt, K. J., Zhang, C., Kucinschi, B. R., and Afjeh, A. A. (2001). “Intraglottal pressure profiles for a symmetric and oblique glottis with a divergence angle of 10 degrees,” J. Acoust. Soc. Am. 10.1121/1.1333420 109, 1616–1630. [DOI] [PubMed] [Google Scholar]
- Tao, C., Jiang, J. J., and Zhang, Y. (2006a). “Simulation of vocal fold impact pressures with a self-oscillating finite-element model,” J. Acoust. Soc. Am. 10.1121/1.2197798 119, 3987–3994. [DOI] [PubMed] [Google Scholar]
- Tao, C., Jiang, J. J., and Zhang, Y. (2006b). “Anterior-posterior biphonation in a finite element model of vocal fold vibration,” J. Acoust. Soc. Am. 10.1121/1.2221546 120, 1570–1577. [DOI] [PubMed] [Google Scholar]
- Tao, C., and Jiang, J. J. (2007). “Mechanical stress during phonation in a self-oscillating finite-element vocal fold model,” J. Biomech. 40, 2191–2198. [DOI] [PubMed] [Google Scholar]
- Titze, I. R. (1988). “The physics of small-amplitude oscillation of the vocal folds,” J. Acoust. Soc. Am. 10.1121/1.395910 83, 1536–1552. [DOI] [PubMed] [Google Scholar]
- Titze, I. R. (2006). The Myoelastic Aerodynamic Theory of Phonation (National Center for Voice and Speech, Denver, CO: ), p. 84. [Google Scholar]
- Zhang, K., Siegmund, T., and Chan, R. W. (2006). “A constitutive model of the human vocal fold cover for fundamental frequency regulation,” J. Acoust. Soc. Am. 10.1121/1.2159433 119, 1050. [DOI] [PubMed] [Google Scholar]
- Zhang, Z., Neubauer, J., and Berry, D. A. (2007). “Physical mechanisms of phonation onset: A linear stability analysis of an aeroelastic continuum model of phonation,” J. Acoust. Soc. Am. 10.1121/1.2773949 122, 2279–2295. [DOI] [PubMed] [Google Scholar]