Dynamic regression hazards models for relative survival

SUMMARY

A natural way of modelling relative survival through regression analysis is to assume an additive form between the expected population hazard and the excess hazard due to the presence of an additional cause of mortality. Within this context, the existing approaches in the parametric, semiparametric and non-parametric setting are compared and discussed. We study the additive excess hazards models, where the excess hazard is on additive form. This makes it possible to assess the importance of time-varying effects for regression models in the relative survival framework. We show how recent developments can be used to make inferential statements about the non-parametric version of the model. This makes it possible to test the key hypothesis that an excess risk effect is time varying in contrast to being constant over time. In case some covariate effects are constant, we show how the semiparametric additive risk model can be considered in the excess risk setting, providing a better and more useful summary of the data. Estimators have explicit form and inference based on a resampling scheme is presented for both the non-parametric and semiparametric models. We also describe a new suggestion for goodness of fit of relative survival models, which consists on statistical and graphical tests based on cumulative martingale residuals. This is illustrated on the semiparametric model with proportional excess hazards. We analyze data from the TRACE study using different approaches and show the need for more flexible models in relative survival.

1. INTRODUCTION

In many cancer studies and also in population-based and clinical observational studies other than cancer, information on causes of death, remissions, etc. is sometimes unavailable, especially with a long follow-up. In some cases, this information is recorded on medical registries but it is incomplete or misleading, because death could be only partially due to the disease of interest and it is difficult to classify deaths due to other causes indirectly correlated with the disease of interest. For this reason the use of cause-specific survival in the framework of competing risks, where at least two distinct alternative causes need to be specified, is problematic. Moreover, many clinical studies aim at identifying prognostic factors for mortality due to the disease, differentiating whether their effects are also related to the natural mortality in the underlying population. In this case, problems arise in comparisons between studies based on different background populations.

Relative survival analysis provides a solution to these difficulties. It does not require information on cause of death, whereas it allows one to estimate patient survival corrected for the effect of other causes of death, using the natural mortality of the underlying population. Of course, the natural mortality encompasses also mortality from the disease of interest; however, when the latter is very small, and then negligible, the general population is commonly assumed to be unaffected by the disease of interest. Indeed, relative survival describes the excess mortality for patients diagnosed with the disease of interest, irrespective of whether the excess mortality is directly or indirectly attributable to the disease. In general, estimation of this corrected patient survival, a quantity that is hypothetically defined as the net survival in the competing risks setting, is the principal aim in relative survival. From population life tables theory, the estimate is given by the relative survival ratio between the observed survival of patients and the expected survival from the underlying population, with respect to the main factors affecting the natural mortality, such as age, sex and calendar time.

Thereby, a natural way of modelling relative survival through regression analysis consists in assuming the following additive form for the observed hazard at time t, conditional on covariates Z and X:

$$\lambda (t;Z,X)={\lambda }^{\ast }(t;Z)+\nu (t;X)$$ (1)

where Z and X are sets of covariates that are not necessarily all distinct. The total observed hazard is modelled by the sum of the expected hazard λ*(t; Z), which represents the background rate of mortality of the general population, and the excess hazard ν(t; X) due to the presence of an additional cause of mortality, such as cancer or other chronic diseases. The expected hazard is generally estimated from external data, i.e. mortality rates recorded in the public registries of the population underlying the patients’ sample under study. It is assumed to be known in the actual model and generally it depends on some characteristics Z of the population. The additional excess hazard follows a regression model based on the relevant risk factors X and can be modelled by a proportional or an additive form, according to the validity of the underlying assumptions. In general, the principal interest in regression analysis consists in evaluating possible prognostic factors that influence directly the excess risk, in the absence of the effect of competing causes of death. That is why only the excess risk is supposed to depend on the set of covariates observed in the exposed individuals.

Among different approaches to modelling relative survival, our attention is directed to models following the additive form in (1). Within this approach, various models and their extensions have been proposed recently and they can be classified as parametric, semiparametric or non-parametric models. Two basic methods that assume a multiplicative function of the covariates for the excess hazard, described by Hakulinen and Tenkanen [1] and Estve et al. [2], have been used in the parametric setting. Extensions of these models [3, 4] and handling time-dependent covariates [5] have also been developed in the literature. Although all these models are specified in continuous time, they assume a parametric function for the hazard, usually a constant hazard within pre-determined time intervals. In order to control for eventual non-proportional excess hazards, the standard solution used within these models consists of including time-dependent covariates as interaction terms (covariate by follow-up time intervals). More recently, some suggestions have used spline functions [6, 7] for modelling time-dependent hazard ratio and the baseline excess hazard, in order to yield more flexible and less restrictive additive models, in case of multiplicative scale for the excess hazard. In the semiparametric setting, these attempts can be seen as alternatives to the well-known proportional excess hazards model by Sasieni [8]. The semiparametric proportional excess hazards model considers an excess risk on Cox form and can easily handle time-dependent covariates, provided that the assumption of proportional hazards for the excess risk of individuals is verified. Zahl [9] considered the fully non-parametric additive hazards model [10] to model the excess hazard, where λ(t; X)=α₀(t)+α₁(t)X₁+···+α_p+1(t)X_p+1, overcoming problems about non-proportionality and non-positive excess hazards [11, 12].

We here study the additive hazard models and show how recent developments can be used to make inferential statements about the non-parametric additive excess hazards model. This makes it possible to test the key hypothesis that an excess risk effect is time varying in contrast to being constant over time. One problem with the fully non-parametric dynamic description is that the model might be too big, if some covariate effects are in fact constant with time. We therefore also show how the semiparametric additive risk model [13] can be considered in the excess risk setting. This model can provide a better and more useful summary of the data and makes a better bias/variance trade-off. We show how these two additive models are easy to fit with estimators on explicit form and how inference including tests for time-constant effects can be carried out based on a resampling scheme.

Our objective in this paper is to introduce and to assess the importance of time-varying effects for regression models in the relative survival framework. Their presence in the model shows directly how the influence of risk factors on the excess hazard may change over follow-up time, as regression coefficients are allowed to depend on time. No difficulties appear in handling time-dependent covariates, which are treated as commonly performed in the Aalen additive hazards model and in the Cox model.

Another aim of this paper is to describe a new suggestion for goodness-of-fit methods and graphical test for residuals in the relative survival setting. We do this by a straightforward way of using the cumulative martingale residuals proposed by Lin et al. [14], and we illustrate their use for testing the proportional hazards assumption in the proportional excess model by Sasieni [8]. This approach is very simple to implement and is known to work well in the standard survival setting. Even though our suggestion is related to the recent interesting proposal by Stare et al. [15], our approach has several important advantages. First, our method does not need any critical choice of smoothing parameters (or parametric assumptions) for the baseline. Secondly, our procedure is asymptotically justified and will thus lead to asymptotically correct p-values and this is not true in general for the Stare et al. procedure.

In Sections 2 and 3, we present the non-parametric additive regression model and the semi-parametric additive regression model for the excess hazard, respectively. To avoid confusion in terminology, we denominate them as the non-parametric and the semiparametric additive excess hazards models. We illustrate the estimators, their properties and tests of hypothesis about the time-varying regression coefficients. In Section 4, we describe the proportional excess model and the corresponding inference. Section 5 deals with new suggestions and discussion about goodness of fit within the relative survival analysis. Finally, in Section 6, we analyze data from the TRACE study using different models and we show the need for more flexible models in relative survival.

2. THE NON-PARAMETRIC ADDITIVE EXCESS HAZARDS MODEL

2.1. Model and estimators

An extension to the standard relative survival models is proposed when the excess hazard is modelled in additive form. The non-parametric additive excess hazards model, described also by Zahl [9], is

$$\lambda \left(t\right)=Y\left(t\right)[{\alpha }^{\ast }(t;Z)+X^{\mathrm{T}}\left(t\right)\beta \left(t\right)]$$ (2)

and contains only non-parametric terms. The excess rate follows the additive hazards model introduced by Aalen [10]. The function Y(t) is a risk indicator, which is 1 if the event or censoring has yet not occurred until t and 0 otherwise. The effects of risk factors on the excess mortality hazard ν(t; X)=Y(t)X^T(t)β(t) are expressed by the time-varying p-dimensional regression coefficient β(t)=(β₁(t), . . . ,β_p(t))^T.

The relative survival for the additive excess hazards model is equal to

$$r\left(t\right)=\exp \left\{-{\int }_0^t{X}^{\mathrm{T}}\left(s\right)\beta \left(s\right)\mathrm{d}s\right\}$$

which in general, for additive models, can be expressed as r(t)=S(t)/S*(t), where S(t) and S*(t) are the observed and expected survival, respectively.

The conditional intensity λ(t; Z, X) in (2) provides a model for its associated counting process N(t) that counts the observed failures in the observation period t ∈[0, τ], with τ<∞, of a subject with predictable covariates Z and X. We need a little notation to write out the estimators. Let (N_i(t), Y_i(t), Z_i(t), X_i(t)) for i =1, . . . ,n be n independent observations from the additive excess hazards model with intensity λ(t). Define N(t)=(N₁(t), . . . ,N_n(t))^T as the counting process of the n subjects and λ(t)=(λ₁(t), . . . ,λ_n(t))^T as the associated intensity. The n × p dimensional matrix X(t)=(Y₁(t)X₁(t), . . . ,Y_n(t)X_n(t))^T contains all information about the predictable covariates in the excess rate. The considered estimators have properties that rely on martingale theory, it is therefore suitable to introduce the n-dimensional zero-mean martingale M(t)= N(t)-Λ(t) associated with the counting processes N(t). The so-called compensator of the martingale, $\Lambda \left(t\right)={\int }_0^t\lambda \left(s\right)\mathrm{d}s$, is the total cumulative intensity. Define ${\lambda }^{\ast }\left(t\right)={(Y_1\left(t\right){\alpha }_1^{\ast }\left(t\right),\dots ,Y_n\left(t\right){\alpha }_n^{\ast }\left(t\right))}^{\mathrm{T}}$. We then have the increments dN(t)=λ(t)dt+dM(t)=λ*(t)dt+X(t)β(t)dt+dM(t) of the counting process using the excess additive regression model.

Inference is made by estimating the cumulative regression coefficients $B\left(t\right)={\int }_0^t\beta \left(s\right)\mathrm{d}s$, which give the cumulative effects of each covariate on the excess mortality rate. Estimators in the additive excess hazards model are very similar to the ones used for the standard additive hazards model. Let ${\Lambda }^{\ast }\left(s\right)={\int }_0^t{\lambda }^{\ast }\left(s\right)\mathrm{d}s$. The principal basic difference in working with relative survival consists in replacing the usual counting process N(t) with the modified counting process $\tilde{N}\left(t\right)=N\left(t\right)-{\Lambda }^{\ast }\left(t\right)$. Thus, from the increments of the martingale, we have

$$\mathrm{d}\tilde{N}\left(t\right)=\mathrm{d}N\left(t\right)-{\lambda }^{\ast }\left(t\right)\mathrm{d}t=\mathbf{X}\left(t\right)\beta \left(t\right)\mathrm{d}t=\mathrm{d}M\left(t\right)$$

which suggests the possibility to estimate the increments β(t)dt by least-squares methods for multiple linear regression. The increment in ${\tilde{N}}_i\left(t\right)$ thus gives the observed excess risk compared with the background mortality, among those under risk, since the martingale increment has mean zero. In other words, the expected number of deaths equals the expected number of background deaths plus the expected number of excess mortality deaths. The resulting estimator is

$$\mathrm{d}{\widehat{B}}^{\ast }\left(t\right)={\mathbf{X}}^{-}\left(t\right)\mathrm{d}\tilde{N}\left(t\right)$$ (3)

where the p × n matrix

$${\mathbf{X}}^{-}\left(t\right)={\left({\mathbf{X}}^{\mathrm{T}}\left(t\right)\mathbf{X}\left(t\right)\right)}^{-1}{\mathbf{X}}^{\mathrm{T}}\left(t\right)$$ (4)

is the generalized inverse of X(t). Therefore,

$${\widehat{B}}^{\ast }\left(t\right)={\int }_0^t{\mathbf{X}}^{-}\left(s\right)\mathrm{d}\tilde{N}\left(s\right)$$

is the estimator for the p-dimensional vector of cumulative regression coefficients.

The estimator in (4) can be expressed as

$${\widehat{B}}^{\ast }\left(t\right)=\widehat{B}\left(t\right)-{\int }_0^t{\mathbf{X}}^{-}\left(s\right){\lambda }^{\ast }\left(s\right)\mathrm{d}s$$

the difference of the standard Aalen estimator [10], $\widehat{B}\left(t\right)={\int }_0^t{\mathbf{X}}^{-}\left(s\right)\mathrm{d}N\left(s\right)$, and a predictable term depending on the known background rate and the observed covariates [11]. The second term represents the average expected hazard of the population at risk at each observed time, weighted with the observed covariate values. The Aalen estimator is incremented at each failure time (where a jump is observed) while it is constant between failures. Note that the estimator B̂* decreases systematically between failure times because of the Lebesgue integral in the second term. Consequently, even though the estimator B̂* is well defined by expression (3) and is an unbiased estimator of the excess mortality, some care has to be taken when implementing the Lebesgue integration. This aspect is also discussed in the related papers [8, 9, 16].

2.2. Properties of the estimators and inferential procedures

We observe that, if the matrix X(t) has full rank for all t,B̂*(t) is an unbiased estimator of B(t), because the second term in

$${\widehat{B}}^{\ast }\left(t\right)={\int }_0^t\mathrm{d}B\left(s\right)+{\int }_0^t{\mathbf{X}}^{-}\left(s\right)\mathrm{d}M\left(s\right)$$

is a martingale with zero mean. Moreover, using functional forms of the strong law of large numbers, under certain regularity conditions the following convergence in distribution can be proved [17]:

$$n^{1∕2}({\widehat{B}}^{\ast }-B)\stackrel{D}{\to }U\mathrm{for}n\to \infty$$

where U is a Gaussian martingale with covariance function $\Phi \left(t\right)={\int }_0^t\varphi \left(s\right)\mathrm{d}s$. An explicit expression for ϕ(t) can be found elsewhere [17]. These simple properties of the estimator B̂* are the fundamental elements for inference and are the same as those for the estimator B̂ for the standard non-parametric additive hazards model, since the asymptotic results are still based on the martingale M(t). The martingale in the additive excess model differs from the one in the standard additive model only for the expression of its compensator Λ(t). In fact, a component of this latter is constrained to be equal to the integrated expected mortality of the population.

Before describing inferential procedures, we present one of the possible estimators for the variance of B̂*,

$$\widehat{\Phi }\left(t\right)=n{\int }_0^t{\mathbf{X}}^{-}\left(s\right)\mathrm{diag}\left(\mathrm{d}N\left(s\right)\right){\left({\mathbf{X}}^{-}\left(s\right)\right)}^{\mathrm{T}}$$

the optional variation process of the martingale ${\int }_0^t{\mathbf{X}}^{-}\left(s\right)\mathrm{d}M\left(s\right)$ and it is uniformly consistent. Based on the jth diagonal element Φ̂_jj(t) of Φ̂(t), the pointwise confidence interval for B_j(t) is equivalent to

$${\widehat{B}}_j^{\ast }\left(t\right)\pm n^{-1∕2}{c}_{\alpha ∕2}{\widehat{\Phi }}_{jj}^{1∕2}\left(t\right)$$ (5)

where c_α/2 is the (1-α/2) quantile of the standard normal distribution. It is useful as a synthetic estimator but its use for a statistical test about the entire shape of the cumulative regression coefficients would lead to incorrect conclusions.

The two hypotheses $H_0^{\left(1\right)}:{\beta }_j\left(t\right)=0$ (or B_j(t)=0) and $H_0^{\left(2\right)}:{\beta }_j\left(t\right)=\gamma$ (or B_j(t)=λt), for all t in the range [0, τ], are of interest, each of them verifying, respectively, the assumption of no effect and the assumption of constant effect of the coefficient β_j. Tests are shown directly for the cumulative regression coefficient B_j(t). For testing the first hypothesis $H_0^{\left(1\right)}$, we consider the variance weighted test statistics

$$T_{1\mathrm{S}}=\underset{t\in [0,\tau ]}{\sup }\mid \frac{n^{1∕2}{\widehat{B}}_j^{\ast }\left(t\right)}{{\left({\widehat{\Phi }}_{jj}^{\ast }\left(t\right)\right)}^{1∕2}}\mid$$ (6)

based on the resampling approach for the additive Aalen model [18]. T_1S has the same asymptotic distribution as $\sup \mid {\Delta }_1\left(t\right)∕{\left({\widehat{\Phi }}_{jj}^{\ast }\left(t\right)\right)}^{1∕2}\mid$ under the null hypothesis, where Δ₁(t) is a resampling process, which depends only on standard normal random variables, conditional on the data (N_i(t),Y_i(t),Z_i(t),X_i(t)) for i =1, . . . ,n. The empirical distribution of the resampling process can be used to build confidence band for T_1S (see Appendix A). The observed test process can be plotted versus time together with its confidence band. Graphically, $H_0^{\left(1\right)}$ may be tested by observing whether the zero function, representing the null hypothesis, is contained within this confidence band.

In order to test the hypothesis $H_0^{\left(2\right)}$, the quantity ${\widehat{B}}_j^{\ast }\left(\tau \right)∕\tau$ may estimate the constant γ in the null hypothesis. Two possible test statistics are

$$T_{2\mathrm{S}}=n^{1∕2}\underset{t\in [0,\tau ]}{\sup }\mid {\widehat{B}}_j^{\ast }\left(t\right)-{\widehat{B}}_j^{\ast }\left(\tau \right)\frac{t}{\tau }\mid \text{and}{T}_{2\mathrm{I}}=n{\int }_0^{\tau }{\left({\widehat{B}}_j^{\ast }\left(t\right)-{\widehat{B}}_j^{\ast }\left(\tau \right)\frac{t}{\tau }\right)}^2\mathrm{d}t$$ (7)

Approximate p-values can be obtained by resampling from the process Δ₁(t)-Δ₁(τ)(t/τ). Note that these test statistics depend on the selected time interval [0, τ], and therefore different results may be obtained on smaller time intervals.

3. THE SEMIPARAMETRIC ADDITIVE EXCESS HAZARDS MODEL

3.1. Model and estimators

The semiparametric additive model is a submodel of the non-parametric additive model where some effects are allowed to be constant in time. We can specify a semiparametric model for relative survival with additive hazards

$$\lambda \left(t\right)=Y\left(t\right)\{{\alpha }^{\ast }(t;Z)+X^{\mathrm{T}}\left(t\right)\beta \left(t\right)+V^{\mathrm{T}}\left(t\right)\gamma \}$$ (8)

where X(t) and V(t) are, respectively, a p-dimensional and a q-dimensional covariates, Y(t) is the risk indicator, β(t) is the p-dimensional time-varying regression coefficient and γ is the q-dimensional time-invariant coefficient. After having tested whether effects are time varying or constant in the full additive model (2), the semiparametric additive model (8) could be fitted to better describe the right form of the regression coefficients. Moreover, the model is simpler and leads to easier estimators.

The estimators of the cumulative coefficient $B\left(t\right)={\int }_0^t\beta \left(s\right)\mathrm{d}s$ and γ can be obtained by least-squares methods, as for the non-parametric additive model. We consider the same setting as for the additive excess hazards model (2), where the counting process N(t) is now associated with the intensity λ(t) modelled by the semiparametric regression in (8). In addition to X(t), define the matrix V(t)=(Y₁(t)V₁(t), . . . ,Y_n(t)V_n(t))^T of dimension n × q. If we consider the martingale decomposition and the modified counting process $\tilde{N}\left(t\right)$, its corresponding increment can be expressed as

$$\mathrm{d}\tilde{N}\left(t\right)=\mathrm{d}N\left(t\right)-{\lambda }^{\ast }\left(t\right)\mathrm{d}t=\mathbf{X}\left(t\right)\beta \left(t\right)\mathrm{d}t+\mathbf{V}\left(t\right)\gamma \mathrm{d}t+\mathrm{d}M\left(t\right)$$

Since the martingale increments dM(t) are uncorrelated and with zero mean, least-squares methods can be applied. The estimator of γ is

$${\widehat{\gamma }}^{\ast }={\left({\int }_0^{\tau }{\mathbf{V}}^{\mathrm{T}}\left(t\right)\mathbf{H}\left(t\right)\mathbf{V}\left(t\right)\mathrm{d}t\right)}^{-1}{\int }_0^{\tau }{\mathbf{V}}^{\mathrm{T}}\left(t\right)\mathbf{H}\left(t\right)\mathrm{d}\tilde{N}\left(t\right)$$ (9)

where the inverse of the matrix H(t)=I-X(t)X^-(t) is assumed to exist. Plugging the estimator γ̂* into the estimating equation for dB̂*(t), the estimator of B(t) is given as

$${\widehat{B}}^{\ast }\left(t\right)={\int }_0^t{\mathbf{X}}^{-}\left(s\right)(\mathrm{d}\tilde{N}\left(s\right)-\mathbf{V}\left(s\right){\widehat{\gamma }}^{\ast }\mathrm{d}s)$$ (10)

This estimator can also be expressed as

$${\widehat{B}}^{\ast }\left(t\right)={\widehat{B}}^{\prime }\left(t\right)-{\int }_0^t{\mathbf{X}}^{-}\left(s\right){\widehat{\lambda }}^{\ast }\left(s\right)\mathrm{d}s+{\int }_0^t{\mathbf{X}}^{-}\left(s\right)\mathbf{V}\left(s\right)[{\widehat{\gamma }}^{\prime }-{\widehat{\gamma }}^{\ast }]\mathrm{d}s$$

depending on the estimated p-dimensional cumulative coefficient, ${\widehat{B}}^{\prime }\left(t\right)={\int }_0^t{\mathbf{X}}^{-}\left(s\right)[\mathrm{d}N\left(s\right)-\mathbf{V}\left(s\right){\widehat{\gamma }}^{\prime }\mathrm{d}s]$, and the estimated constant coefficient γ̂’ in a standard semiparametric additive hazards model. The estimator γ̂’ has the same expression of γ̂* in (9), except for the presence of N(t) instead of $\tilde{N}\left(t\right)$.

3.2. Properties of the estimators and inferential procedures

Asymptotic properties of the estimators B̂*(t) and γ̂* are of primary importance in testing hypotheses about B(t) and γ. Under some regularity conditions, as n→∞, n^1/2(γ̂*-γ) and n^1/2(B̂*-B) converge in distribution to a zero-mean normal and a zero-mean Gaussian process, respectively.

In order to test the hypothesis of no effect $({\mathbf{H}}_0^{\left(1\right)}:B_j\left(t\right)\equiv 0)$ and the hypothesis about an effect being time constant $({\mathbf{H}}_0^{\left(2\right)}:B_j\left(t\right)\equiv {\gamma }_{j}t)$, we suggest to use the confidence band for B_j(t) based on the resampling approach, similar to what was presented in Section 2.2. From the properties about asymptotic convergence previously described, we obtain the following test statistic for ${\mathbf{H}}_0^{\left(1\right)}$:

$$T_{1\mathrm{S}}=\underset{t\in [0,\tau ]}{\sup }\mid \frac{n^{1∕2}{\widehat{B}}_j^{\ast }\left(t\right)}{{\widehat{\Psi }}_{jj}^{1∕2}\left(t\right)}\mid$$ (11)

where Ψ̂_jj(t) is the jth diagonal element of Ψ̂(t), a consistent robust estimator of the variance n^1/2(B̂*-B) defined in Appendix A.

Similarly, for the hypothesis ${\mathbf{H}}_0^{\left(2\right)}$ the test statistics

$$T_{2\mathrm{S}}=n^{1∕2}\underset{t\in [0,\tau ]}{\sup }\mid {\widehat{B}}_j^{\ast }\left(t\right)-{\widehat{B}}_j^{\ast }\left(\tau \right)\frac{t}{\tau }\mid ,T_{2\mathrm{I}}=n{\int }_0^{\tau }{\left({\widehat{B}}_j^{\ast }\left(t\right)-{\widehat{B}}_j^{\ast }\left(\tau \right)\frac{t}{\tau }\right)}^2\mathrm{d}t$$ (12)

and their quantiles can be computed by resampling. For more details, see Appendix A. Graphical comparisons between the observed test process ${\widehat{B}}_j^{\ast }\left(t\right)-{\widehat{B}}_j^{\ast }\left(\tau \right)(t∕\tau )$ and the simulated processes under the null can show times of departure from this last hypothesis.

4. PROPORTIONAL EXCESS HAZARDS MODEL

The proportional excess model proposed by Sasieni [8] models the excess risk on a multiplicative scale. The statistical model is

$$\lambda \left(t\right)=Y\left(t\right)[{\alpha }^{\ast }(t;Z)+{\lambda }_0\left(t\right)\exp \left(X^{\mathrm{T}}\beta \right)]$$ (13)

where the p-dimensional regression coefficient β=(β₁, . . . ,β_p)^T is assumed to be time invariant. In a counting process setting, the intensity λ(t) is associated with the process N(t), with t ∈[0, τ], τ<∞. Referring to the same definitions of the previous models, we associate the compensated counting process ${\tilde{N}}_i=N\left(t\right)-{\Lambda }^{\ast }\left(t\right)$ with the usual martingale M(t) so that

$$M\left(t\right)=\tilde{N}\left(t\right)-{\int }_0^{t}Y\left(s\right)\exp \left(X^{\mathrm{T}}\beta \right)\mathrm{d}{\Lambda }_0\left(s\right)$$

with Y(t)=(Y₁(t), . . .,Y_n(t)).

Solving the unweighted score equations derived from the log likelihood for β and λ₀, up to all the observation period [0, τ], leads to the following estimator for the baseline cumulative excess hazard:

$${\widehat{\Lambda }}_0(t;\beta )={\int }_0^t\frac{\sum \mathrm{d}{\tilde{N}}_i\left(u\right)}{\sum Y_i\left(u\right){\mathrm{e}}^{X_i^{\mathrm{T}}\beta }}$$ (14)

with X_i equal to the p-dimensional vector of covariates of subject i. The substitution of this estimator in the score equation for β yields

$$U\left(\beta \right)=\sum _i\int \left\{X_i-\frac{\sum _j{Y}_j\left(t\right)X_j{\mathrm{e}}^{X_j^{\mathrm{T}}\beta }}{\sum _j{Y}_j\left(t\right){\mathrm{e}}^{X_j^{\mathrm{T}}\beta }}\right\}\mathrm{d}{\tilde{N}}_i\left(t\right)$$ (15)

which provides an estimator for the parameter β such that U(β̂)=0. Setting ${\lambda }_i^{\ast }\left(t\right)=0$ for i = 1, . . . ,n, the modified counting process ${\tilde{N}}_i$ is equal to N_i and the unweighted estimators are the solutions to the usual score equations for the Cox model. Properties of the estimators and conditions under which they are valid can be found in [8].

Note that some difficulties arise in exchanging summation with integration in equation (15), which depends on both the observed failure times and the observed censoring times, as the modified counting process ${\tilde{N}}_i$ changes at every censoring time, besides at every failure time.

5. GOODNESS OF FIT FOR RELATIVE SURVIVAL MODELS

There is a general lack of accomplished methodology for the regression diagnostics and assessment of goodness of fit of additive relative survival models. The existing theory is only sometimes implemented in public software. Some of the parametric models are estimated in the framework of generalized linear models, thereby enabling the use of standard regression diagnostics in this area. Recently, in the context of models with multiplicative excess rate, Stare et al. [15] proposed some diagnostics aimed at detecting time-varying effects of covariates on the excess risk and based on partial residuals defined similarly to the Schoenfeld residuals for Cox model, but as already mentioned their procedure relies heavily on the choice of a smoothing parameter that can be completely avoided by the procedure we suggest here. An additional problem with [15] is that it does not lead to the correct level even though it, in practice, tends to work well.

In this section, we propose a very straightforward procedure based on cumulative martingale residuals for testing goodness of fit of the proportional excess hazards model (13). Our approach can also be used to assess the fit of the additive hazards excess model, but we here illustrate the basic idea by looking at the proportional excess hazards model.

In the proportional excess hazards model, we are interested in checking whether the sub-model for the excess hazard is adequate. More specifically, in order to fulfill this objective, three aspects would need to be checked: Functional form of covariates, the form of the link function of the excess hazard, the assumption of proportional hazards. We show how the cumulative sums of martingale-based residuals [14] can be used to answer these problems.

The partial likelihood score function (15) for parameter β can also be expressed as a functional of the martingale process M_i(t) associated with individual i:

$$U\left(\beta \right)=\sum _i{\int }_0^{\tau }\{X_i-E(\beta ,t)\}\mathrm{d}{M}_i\left(t\right)$$

where we define E(β, t)=S₁(β, t)/S₀(β, t) and $S_k(\beta ,t)={\sum }_i{Y}_i\left(t\right)X_i^{\otimes k}\exp \left(X_i^T\beta \right)$, with k = 0, 1, 2. We have $X_i^{\otimes 0}=1$, $X_i^{\otimes 1}=X_i$ and $X_i^{\otimes 2}=X_i{X}_i^T$. X_i = (X_1i , . . . , X_pi)^T is the p-dimensional vector of covariates of individual i.

The martingale residuals for the proportional excess hazards model are defined as

$${\widehat{M}}_i\left(t\right)={\tilde{N}}_i\left(t\right)-{\int }_0^t{Y}_i\left(s\right)\exp \left(X_i^T\widehat{\beta }\right)\mathrm{d}{\widehat{\Lambda }}_0\left(s\right)$$ (16)

where Λ̂₀(s) is the estimator in (14). They are defined similarly to the martingale residuals for the standard proportional hazards model [19]. They verify the basic properties, i.e. their sum over the individuals is zero and they average to zero asymptotically. The cumulative martingale residuals are constructed by different partial-sum processes of the martingale residuals M̂_i(t). Processes can be over follow-up time or covariate values, in order to test, respectively, the proportional excess hazards assumption or the functional form of covariates and the link function. Then, tests about these aspects are made by using the processes to compare their observed behavior with their potential one under the assumption that the model is true.

The functional of the martingale residuals used to test the proportional excess hazards assumption is based on the observed score process in time, expressed as U(β̂, t)=Σ_i X_iM̂_i(t). Using the cumulative martingale residuals U_j(β̂, t)=Σ_i X_jiM̂_i(t), the proportional excess hazard assumption may be verified both by graphical plots and by hypothesis tests. A test statistics for each j (j=1, . . . , p) is given by the supremum of the standardized score process

$$\underset{t}{\sup }{\left(\widehat{\mathrm{Var}}\left(U_j(\widehat{\beta },t)\right)\right)}^{-1∕2}\mid U_j(\widehat{\beta },t)\mid$$ (17)

where

$$\widehat{\mathrm{Var}}\left(U_j(\widehat{\beta },t)\right)=\sum _i{\int }_0^t{\left(X_i-\frac{S_1(\widehat{\beta },s)}{S_0(\widehat{\beta },s)}\right)}^{\otimes 2}\mathrm{d}{N}_i\left(s\right)$$

is a consistent estimator of the variance of the observed score process. This supremum test for proportionality has the advantage that no specific functional form need to be chosen when looking for lack of fit of the model for a specific covariate j.

The distribution of n^-1/2U(β̂, t) is asymptotically equivalent to

$$n^{-1∕2}({\widehat{D}}_1\left(t\right)-\widehat{J}(\widehat{\beta },t){\widehat{J}}^{-1}(\widehat{\beta },\tau ){\widehat{D}}_1\left(\tau \right))$$ (18)

where ${\widehat{D}}_1\left(t\right)={\sum }_{i=1}^n{\int }_0^t(X_i-E(\widehat{\beta },s))\mathrm{d}{N}_i\left(s\right)G_i$ and G₁, . . . ,G_n independent standard normals. The matrix ĵ(β̂, t) represents minus the derivative of the score function with respect to β (15). Then, the asymptotic distribution of n^-1/2U(β̂, t) may be evaluated using a resampling procedure, by generating realizations from process (18), which depends only on the random variables G_i [17]. This is made by repeatedly generating normal random samples {G_i} while holding the observed {N_i, Y_i, X_i} fixed. The null distribution of the test statistics in (17) is then approximated by these simulations. A graphical test about proportionality may be obtained by plotting the observed score process U(β̂, t) over time together with the realizations we have simulated from process (18) in order to approximate the null distribution of U(β̂, t). If the observed score process diverges from the simulated processes under the model, which should randomly fluctuate around the zero axis, there is evidence of a lacking fit of the proportional excess hazards model due to the missing proportionality.

The key reasoning about the validity of these cumulative martingale in checking the current model consists in replacing the counting process N(t) with the modified counting process $\tilde{N}\left(t\right)$ when it is opportune. For more details, see Appendix A. Here, we underline the use of the estimator Λ̂₀ in (14), expressed as a function of $\tilde{N}\left(t\right)$. Finally, it is important to note that process (18) depends directly only on the original counting process N_i(t), but not on ${\tilde{N}}_i\left(t\right)$, as the variance of M_i(t) is equal to E(N_i), and therefore can be approximated by G_iN_i.

Graphical and statistical tests for checking the functional form of covariates and the link function in the proportional excess hazards model may be carried out very similarly to the ones proposed by Lin et al. [14] for the proportional hazards model and involve the same substitutions shown previously in this section. For investigation of the functional form of a certain covariate j, the tests are based on the cumulative residual process

$$M_c^j\left(x\right)=\sum _{i=1}^n{\int }_0^{\tau }I(X_{ji}\left(t\right)\le x)\mathrm{d}{\widehat{M}}_i\left(t\right)$$

where I(·) is the indicator function, x ∈R and M̂_i(t) are defined in (16). Resampling methods, as described previously, provide simulated realizations under the null, which approximate the asymptotic distribution of the latter process. Therefore, a graphical test is given by plotting the observed cumulative residuals $M_c^j\left(x\right)$ versus the continuous covariate with values x, together with random realizations under the model.

6. APPLICATION TO THE TRACE DATA

6.1. Description of the data

Data from the TRACE study are here illustrated. They provide a typical example of data exhibiting non-proportional excess hazards with respect to some covariates. The TRACE study [20], consisted in a cohort of 6676 patients with acute myocardial infarction who were screened in 27 Danish coronary-care units for entry between May 1990 and July 1992. Information on all patients survival was available from the Danish national registries. The follow-up period was from the day of diagnosis and onwards, during which the outcome under study was total death. The aim of the TRACE study group was to establish which risk factors had a prognostic importance on mortality of patients with acute myocardial infarction.

The actual data set analyzed in this section consists in a random sample of 1876 patients from the TRACE data. Models were fitted only in the follow-up period of the first 6 years from diagnosis, as most of the excess deaths for myocardial infarction occurred inside this time. Patients still alive after 6 years were considered right-censored. The total number of deaths after myocardial infarction during the follow-up period was 881, and of these, 221 took place within the first two months. The time scale was time since prognosis. The background control population mortality was obtained from the registry StatBank Denmark (http:www.statistikbanken.dk) during the 5-year period from 1986 to 1990. Information on the background mortality rates was collected by gender and age.

In our analysis, only the most relevant prognostic factors are taken into account as an example for fitting and comparing the different models. The recorded risk factors are age of patients during the follow-up time, gender (female=1), clinical heart pump failure (CHF)(presence =1), diabetes (presence=1) and ventricular fibrillation (VF) (presence=1). Some risk factors are expected to have very strongly time-varying effects, in particular VF. Previous studies [21] showed that VF was a very important risk factor for death due to myocardial infarction during the first short time period after diagnosis, but its adverse effect was exhausted approximately after two months.

6.2. Comparison of models and estimates

In this section, the non-parametric and semiparametric additive excess hazards models described in Sections 2 and 3 are analyzed on the TRACE data set and compared with the standard methods actually used for modelling relative survival. The total hazard would be expressed as the sum of the known background rate of mortality in the control population and the excess hazard associated with myocardial infarction.

In the first step, the non-parametric additive excess hazards model is applied to the TRACE data. Successively, we show how possible simplifications of the non-parametric model lead to the more parsimonious semiparametric hazards model. Excess risk for the TRACE data was also estimated through the proportional excess hazards model in Section 4.

Age was centered around its mean at the start of the study (defined as a‾₀) and considered as a time-dependent covariate. Results from the non-parametric additive excess hazards model are presented in Table I and Figure 1. For simulation-based tests, a number equal to 300 resampled processes was used. All covariates in the model had an effect significantly different from zero, according to the test T_1S in (6). Using the supremum test T_2S in (7), the effects of CHF, centered age and VF resulted to be time varying, while the effects of gender and diabetes turned out to be invariant in time (Table I). The same conclusions hold in case of using the alternative test statistics T_2I. The estimated cumulative regression coefficients B̂*(t) are shown in Figure 1 for each covariate, together with the 95 per cent pointwise confidence intervals (5) and the confidence band based on T_1S obtained by the resampling technique in Section 2.2. The regression function estimates β̂(t) are the slopes of the cumulative estimates. Interpretation of their patterns is explained later on in this paper.

Table I.

Non-parametric additive excess hazards model: 300 simulation-based tests for non-significant effects and for time-invariant effects

	Test for non-significant effects		Test for time-invariant effects
Covariate	T1S	p-Value	T2S	p-Value	T2I	p-Value
Intercept	2.74	0.147	0.061	0.060	0.006	0.073
CHF	10.20	<0.001	0.121	<0.001	0.043	<0.001
Agec	9.76	<0.001	0.006	0.003	1e-04	0.003
Sex (female=1)	4.67	<0.001	0.031	0.867	0.001	0.840
Diabetes	4.89	<0.001	0.066	0.763	0.003	0.890
VF	6.43	<0.001	0.459	<0.001	0.433	<0.001

Figure 1.

Estimated cumulative regression coefficients for the non-parametric additive hazards model, together with 95 per cent confidence intervals (dashed lines) and confidence bands based on 50 simulated processes under the null (solid lines).

Particular care needs to be taken in the interpretation of the intercept β₀(t) and its behavior in the model when compared with the horizontal zero line. In our application, the excess intensity for a male subject without CHF, diabetes and VF is ν_i(t)=Y_i(t)[β₀(t)+((a_0i+t)-a‾₀)β₁(t)], where a_0i is the age of subject i at the start of the study. In this case, the intercept needs to be interpreted together with the additional coefficient β₁. The excess base line hazard can then be represented by ν_i(t) for a subject with a_0i=a‾₀. In order to interpret correctly the coefficient β₀(t) on its own as the excess baseline hazard, the time-dependent age a_0i+t should be centered with respect to a‾₀+t. Thus, the additional term about age in the excess hazard would be null for a subject with mean age a‾₀+t at every t. In this second case, results from the application (not shown here) indicated that patients with acute myocardial infarction have an estimated decreasing relative survival during the whole follow-up period.

From Figure 1 it can be observed that the effects of gender and diabetes on the excess mortality rate are constant with time, as graphs of their estimated cumulative coefficients are approximately straight lines. The time invariance of these two covariate effects justifies a possible simplification of the model by reducing the number of non-parametric components. Therefore, the semiparametric additive excess hazards model is also applied to the TRACE data, where effects of gender and diabetes are assumed to be constant and the remaining covariate effects are allowed to be time varying.

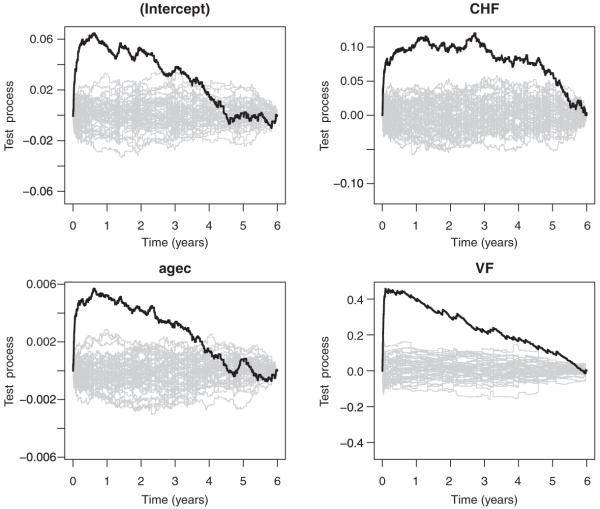
Results about the semiparametric excess hazards model are presented in Table II. The assumption of constant effects for gender and diabetes was confirmed by the results in the right-hand side of Table II. According to the tests T_2S and T_2I in (12), the remaining covariate effects were still significantly time varying, as in the previous non-parametric model. This reduced semiparametric model gives a better fit to the TRACE data, as it is simpler in the interpretation and able to discriminate between constant and time-varying effects. Moreover, going from the non-parametric to the semiparametric additive model, comparison of Tables I and II reveals that values of the supremum and squared tests are almost unchanged. Graphics about behavior of the estimated time-varying cumulative coefficients were also unchanged with respect to the non-parametric case, and thus they can be observed from the same Figure 1. Both the constant effects in Table II were significant (p-values<0.001) and positive: For patients with diabetes the estimated excess mortality rate was 8.3 per cent higher than for patients without diabetes and this increase was estimated to be constant within the 6 years follow-up; the female gender was associated with an estimated increased excess mortality rate of 4.3 per cent. Departure of the effects from the null hypothesis of time invariance may be observed easily looking at Figure 2, where each observed test process is shown along with 50 resampled processes under the null. The presence of a significant variation within the 6 years follow-up period is very evident for the VF coefficient: Behavior of its test process in Figure 2 reveals that the effect of VF is very strong initially, and thus the excess mortality rate has a very high increase within the first two months, but successively the effect seems to disappear in time. Increasing age had also a strongly time-varying effect, which was very high within approximately the first eight months. Similarly, the effect of CHF was increasing very fast initially, after two months it continued to be present but constant until the fourth year, finally the effect vanished during the last two years of follow-up.

Table II.

Semiparametric additive excess hazards model: 300 simulation-based tests for time-invariant effects and estimates of constant effects

Test for time-invariant effects					Constant effects
Covariate	T2S	p-Value	T2I	p-Value	Covariate	Coefficient γ	Robust SE
Intercept	0.065	0.003	0.008	0.003	Sex (female=1)	0.043	0.010
CHF	0.120	<0.001	0.043	<0.001	Diabetes	0.083	0.018
Agec	0.006	0.003	0.0001	0.003
VF	0.458	<0.001	0.432	<0.001

Figure 2.

Semiparametric additive excess hazards model: Observed test process for each covariate, along with 50 simulated processes under the null hypothesis of time-invariant effects.

We apply the proportional excess hazards model to the TRACE data, in order to verify whether the excess hazard associated with myocardial infarction could be described by a proportional form. The same set of covariates analyzed in the previous models is influencing significantly the proportional excess hazard by increasing it (Table III). CHF and VF seem to be very important risk factors in predicting the excess mortality rate due to myocardial infarction, as for patients with heart pump failure or with VF the excess hazard ratio is about 3.2 and 2.7, respectively. Nevertheless, these last results could be questionable because they are related to regression coefficients that are assumed to be invariant in time. If instead effects of CHF and VF were highly time varying (as it was in the semiparametric additive model), the assumption of proportional excess hazards would be violated, since it is strictly related to the invariance of the regression coefficients in the relative risk.

Table III.

Proportional excess hazards model: Tests for non-significant effects and 50 simulation-based tests for proportionality of the relative excess risk

Covariate	exp(β) (relative risk)	SE(β)	95 Per cent CI for relative risk	p-Value
Test for non-significant effects
CHF	3.158	0.130	(2.436-4.056)	<0.001
Age	1.046	0.005	(1.035-1.057)	<0.001
Sex (female=1)	1.689	0.117	(1.342-2.125)	<0.001
Diabetes	1.998	0.120	(1.579-2.529)	<0.001
VF	2.718	0.131	(2.109-3.522)	<0.001

Covariate j	Test-statistics supt |Uj(t)|	p-Value
Test for proportionality of the excess hazard
CHF	12.7	0.418
Agec	163.0	0.826
Sex (female=1)	22.1	0.176
Diabetes	19.4	0.086
VF	29.2	0.002

In order to test proportionality of the excess hazards of each covariate in the proportional model (13), we use the simple non-standardized version of the test statistics (17) based on cumulative martingale residuals. Results in Table III suggest that only the covariate VF contributes to violate the assumption of proportionality (p =0.002), whereas the proportional effect of CHF was correctly verified by the data.

Comparison of the model-based relative survival functions with the corresponding non-parametric estimated curves, underlines the possible violation of assumptions in the analyzed models. We considered the semiparametric additive excess hazards models and the proportional excess hazards model with sex and VF as the only risk factors. In Figure 3, the four estimated relative survival functions from each model are compared with the corresponding relative survival curves (relative survival ratios) estimated by using the Kaplan-Meier method for the observed and the Hakulinen method [22] for the expected survival. The choice of the alternative Edered II method [23] for the expected survival does not affect the final results, as our example concerns a short follow-up period. In panel (a) of Figure 3, it is observed that the proportional excess hazards model does not fit very well the data of patients with VF, neither for females nor for males. On the other hand, this model captures well the difference in relative survival between males and females. The current lack of fit of the proportional excess hazards model is due to the wrong assumption of proportional excess hazards for VF, which does not reflect a much higher excess risk of dying soon after admission in the study for patients with VF. Predictions in panel (b) of Figure 3 describe much better the excess mortality pattern for the different patients groups, since the presence of a time-varying coefficient for VF in the semiparametric model allows one to capture changes of the effect of VF with time.

Figure 3.

(a) Comparison between relative survival predictions based on the proportional excess hazards model (dashed lines) and non-parametric relative survival estimates based on the Kaplan-Meier and Hakulinen methods (solid lines) by sex and VF. (b) Comparison between relative survival predictions based on the semiparametric excess hazards model (dashed lines) and non-parametric relative survival estimates based on the Kaplan-Meier and Hakulinen methods (solid lines) by sex and VF.

The evidence of the wrong assumption about the proportionality for the VF effect within the additive model with excess risk as in (13), was also provided by the statistical and graphical tests proposed by Stare et al. [15], based on the maximum values of the Brownian bridge processes. The EM method for smoothed baseline excess hazards was chosen within the R package relsurv in order to fit the regression model. The effect of VF resulted to be time varying (maximum value was equal to 3.109 with p<0.001), whereas CHF and all the remaining covariates had time-constant effects. Therefore, the analyses of goodness of fit based on the test statistics (17) and on the tests by Stare reached the same conclusions about the TRACE study, stating that it is solely the covariate VF that ruins the proportional effects. Different results given by the models presented in this section are essentially due to modelling the excess risk on different scales, that is, the proportional or the additive scale. The effect for CHF, which resulted to be time varying when using the latter scale in the additive excess hazards models, but was time constant in models with the proportional scale, is an example of that.

7. DISCUSSION

The high flexibility of the additive non-parametric and semiparametric models for relative survival, together with the inferential aspects described in this paper, provides a very important alternative to the existing methods in this field, and on the other hand, a useful general extension of the more restrictive recent models. Indeed, the model fitting may fail both because the chosen link function for the excess hazard (multiplicative or additive function) is inappropriate, and because the time invariance of the hazard ratio does not hold, besides misspecification of the functional forms of covariates. The described additive excess hazards models overcome the critical problem of violating the proportional hazards assumption. The introduction of covariate-by-time interactions in the parametric relative survival models entails further assumptions that would need always to be carefully tested, in order to avoid neglecting possible associations between time-dependent covariates and excess mortality.

The TRACE example demonstrates the need of new flexible survival models for modelling the excess hazards, which can deal with time-varying dynamics of covariates effects. In this paper, we showed how the non-parametric and semiparametric versions of the additive excess hazard can easily handle these dynamics. We demonstrated when one or the other model is appropriate according to the responses of simulation-based graphical and statistical tests about variation of effects over time. Even though inferential procedures described here are complicated in their expressions, when they concern finding equivalent asymptotic distributions of Gaussian processes, the great advantage is a very easy interpretation of results. In this connection, the statistical software, e.g. the R packages used in our application and presented in Appendix B, is an essential instrument.

The graphical procedures for the additive excess hazards models presented in this paper, have the advantage of suggesting time points and sub-intervals where variation of the effects occurs in time with sufficient accuracy, whereas in the graphics about Brownian bridge processes [15] for the proportional excess models, this information is not clearly provided because of the implementation of smoothing procedures.

It would be of interest to extend other test methods about time-varying covariate effects and goodness-of-fit plots from the non-parametric and semiparametric additive hazards model to the relative survival case. Some starting points could be Aalen [24, 25] and Gandy et al. [26].

As for the non-parametric excess additive hazards model, also for the semiparametric model (8), approximate maximum likelihood estimators can be found, similar to what was done by McKeague and Sasieni [13] for the semiparametric additive hazards models. They are also asymptotically efficient in the case of consistent estimates of the weights. For the model by McKeague and Sasieni [13], there exist also other estimators, improved by their properties of robustness and consistency, which could be easily extended to the relative survival case when the replacement of $\mathrm{d}\tilde{N}\left(s\right)$ holds.

In choosing between a proportional or an additive form for the excess hazards, problems about non-proportionality and large number of covariates under study should always be faced. An additional crucial problem, which was not studied in this paper, concerns non-positive excess hazards in relative survival regression models. From a practical point of view, models on some situations as prevention studies, would need to allow the excess hazards to be negative, assuring however non-negative observed intensities. As pointed by Zahl [9], the non-parametric additive excess hazards model overcomes this problem. A proportional excess hazards model cannot be used in the case of negative excess intensities; however, it is still possible to consider an eventual excess intensity equal to zero [8].

Our suggestions about checking goodness of fit of the proportional excess hazards model and the additive excess models play an important role in a good model selection. An advantage of the supremum test described in Section 5 is that no specific deviations from proportionality need to be explicitly expressed. The drawback is, however, that the model is assumed to be correct with respect to all the other covariates when the proportionality assumption is investigated for a specific covariate. Nevertheless, this is a general problem faced also by the existing methods for goodness of fit of regression survival models. Then, important features of the data may be overlooked, and we might be unable to individuate where a possible lack of proportionality occurs during the follow-up time.

For these reasons, models that allow accommodating time-varying covariate effects are very interesting extensions to be considered in the relative survival scenario. In this paper, we studied such an extension for models with additive excess hazards and presented the usefulness of some inferential procedures about time-varying coefficients. A natural and important case to investigate, following the same lines of study presented here, would be allowing the presence of both time-varying and constant regression coefficients within the proportional excess hazards model (13).

APPENDIX A

A.1. Inferential procedures for the non-parametric and semiparametric excess hazards models

In order to explain the test statistics T_1S, T_2S and T_2I within the non-parametric additive hazards model, we consider the process

$${\Delta }_1\left(t\right)=n^{-1∕2}\sum _1^n{\widehat{\epsilon }}_i^{\ast }\left(t\right)G_i$$

which, conditional on the data (N_i(t), Y_i(t), Z_i(t), X_i(t)) for i = 1, . . . ,n and under some regularity conditions, has the same limit distribution as n^1/2(B̂*(t)-B(t)). The random variables G_i, for i = 1, . . . ,n, are independent and standard normal distributed and

$${\widehat{\epsilon }}_i^{\ast }\left(t\right)={\int }_0^t{\left(n^{-1}{\mathbf{X}}^{\mathrm{T}}\left(s\right)\mathbf{X}\left(s\right)\right)}^{-1}{X}_i\left(s\right)\mathrm{d}{\widehat{M}}_i\left(s\right)$$

with

$${\widehat{M}}_i\left(t\right)={\tilde{N}}_i\left(t\right)-{\int }_0^t{Y}_i\left(s\right)X_i^{\mathrm{T}}\left(s\right)\mathrm{d}{\widehat{B}}^{\ast }\left(s\right)$$

Moreover

$${\widehat{\Psi }}^{\ast }\left(t\right)=n^{-1}\sum _{i=1}^n{\widehat{\epsilon }}_i^{\ast }\left(t\right){\left({\widehat{\epsilon }}_i^{\ast }\left(t\right)\right)}^{\mathrm{T}}$$

is a consistent estimator of the asymptotic variance of n^1/2(B̂*(t)-B(t)).

Within the semiparametric additive hazards model, the test statistics T_1S, T_2S and T_2I are evaluated on the basis of the simple process Δ₃(t). From the properties about asymptotic convergence and martingale theory, it follows that

$${\Delta }_3\left(t\right)=n^{-1∕2}\sum _1^n{\widehat{\epsilon }}_{3i}^{\ast }\left(t\right)G_i$$

with G₁, . . . ,G_n independent standard normal, has the same asymptotic distribution as n^1/2(B̂*-B). The variance of this latter is consistently estimated by,

$${\widehat{\Psi }}^{\prime }\left(t\right)=n^{-1}\sum _1^n{\widehat{\epsilon }}_{3i}^{\ast }{\left({\widehat{\epsilon }}_{3i}^{\ast }\right)}^{\mathrm{T}}$$

with

$${\widehat{\epsilon }}_{2i}^{\ast }={\int }_0^{\tau }\{V_i\left(t\right)-\left(\mathbf{V}{\left(t\right)}^{\mathrm{T}}\mathbf{XX}\left(t\right)\right){\left(\mathbf{X}{\left(t\right)}^{\mathrm{T}}\mathbf{X}\left(t\right)\right)}^{-1}{X}_i\left(t\right)\}\mathrm{d}{\widehat{M}}_i\left(t\right)$$

$${\widehat{\epsilon }}_{3i}^{\ast }\left(t\right)={\widehat{\epsilon }}_{4i}^{\ast }\left(t\right)-P\left(t\right)C_1^{-1}{\widehat{\epsilon }}_{2i}^{\ast },{\widehat{\epsilon }}_{4i}^{\ast }\left(t\right)={\int }_0^t{\left(n^{-1}{\mathbf{X}}^{\mathrm{T}}\left(s\right)\mathbf{X}\left(s\right)\right)}^{-1}{X}_i\left(s\right)\mathrm{d}{\widehat{M}}_i\left(s\right)$$

Vectors C₁ and P(t) are predictable functions of the matrices V and X^- and they are defined as

$$C_1=n^{-1}{\int }_0^{\tau }{\mathbf{V}}^{\mathrm{T}}\left(t\right)\mathbf{H}\left(t\right)\mathbf{V}\left(t\right)\mathrm{d}t,P\left(t\right)={\int }_0^t{\mathbf{X}}^{-}\left(s\right)\mathbf{V}\left(s\right)\mathrm{d}s$$

The estimates M̂_i(t) of martingale residuals are

$${\widehat{M}}_i\left(t\right)={\tilde{N}}_i\left(t\right)-{\int }_0^t{Y}_i\left(s\right)(X_i^{\mathrm{T}}\left(s\right)\mathrm{d}{\widehat{B}}^{\ast }\left(s\right)+V_i^{\mathrm{T}}\left(s\right){\widehat{\gamma }}^{\ast }\mathrm{d}s)$$

A.2. Cumulative martingale residuals

In the process (18), Ĵ(β, t), i.e. the estimator minus the average of the derivative of the score function U(β) with respect to β, needs to be a function of $\tilde{N}\left(t\right)$ and it is evaluated as

$$\widehat{J}(\widehat{\beta },t)=\sum _i{\int }_0^t\left(\frac{S_2(\widehat{\beta },s)}{S_0(\widehat{\beta },s)}-E{(\widehat{\beta },s)}^{\otimes 2}\right)\mathrm{d}{\tilde{N}}_i\left(s\right)$$

APPENDIX B

We show the basic R code concerning the application of the models presented in this paper to the TRACE data. The R package timereg can be downloaded at http://staff.pubhealth.ku.dk/∼ts/timereg.html.

The data set is called TR and it is structured with multiple observations for each patient in order to fulfill the conditions for studying time-dependent variables. The function aalen.test fits both the non-parametric and semiparametric additive excess hazards models presented in Sections 2 and 3. Commands for the former model are

• library(timereg);

• dummy<-rnorm(nrow(TR));

• fit1 <-aalen.test(Surv(start,stop,status>=7) ∼ CHF+agec+sex+diabetes+VF+ +const(dummy),data=TR,n.sim=300,max.time=6,offsets=TR$rate,id=TR$id,fix.gam=1); summary(fit1)

In this example, the Surv(start,stop,...) setting is used for the time-dependent covariate agec, estimates are unweighted and summary of the output shows the tests T_1S for non-significant effects and the tests T_2S and T_2I for time-invariant effects. The offset TR$rate is the vector of expected mortality rates from the Danish population. The option fix.gam needs to be set equal to one in case of the non-parametric model. Further options are explained in the R help.

The following code:

• plot.aalen(fit1,pointwise.ci=2,sim.ci=1)

provides graphics about the behavior of the cumulative regression coefficients B(t). The arguments pointwise.ci ≥1 and sim.ci ≥1 show, respectively, the 95 per cent confidence intervals and the confidence bands based on 50 simulated processes under the null hypothesis.

The semiparametric additive excess hazard is given by

• fit2 <- aalen.test(Surv(start,stop,status>=7) ∼ CHF+agec+const(sex)+ +const(diabetes)+VF, data=TR,n.sim=300,max.time=6,offsets=TR$rate,id=TR$id);

• summary(fit2);

• plot.aalen(fit2,ylab=“Test process”,score=T)

The last plot, with the argument score, yields graphics about the observed processes used for computing T_2S and T_2I with 50 random realizations under the null hypothesis. Further options about plot.aalen are explained in the R help.

The function pe.sasieni fits the proportional excess hazards model described in Section 4 as follows:

• fit3 <- pe.sasieni(Surv(start,stop,status>=7) ∼ CHF+agec+sex+diabetes+VF, +data=TR,offsets=TR$rate,id=TR$id,max.time=6);

• summary(fit3)

The summary provides statistics about the regression coefficients and tests for non-significant effects. The non-standardized version of the test for the hypothesis of proportionality of the hazards, based on cumulative martingale residuals and presented in Section 5, is also given in the summary.