TRITONE: a Radio-Frequency Field (B1) Insensitive T1 Estimator for MRI at High Magnetic Fields.

Abstract

Fast, high resolution, longitudinal relaxation time (T₁) mapping is invaluable in clinical and research applications. It has been shown that two spoiled gradient recalled echo (SPGR) images acquired in steady state with variable flip angles is an attractive alternative to the multi-image sets previously acquired with inversion or saturation recovery. The known sensitivity of the two-point method to transmit radio-frequency field (B₁) inhomogeneity exacerbated at 3 Tesla and above, however, mandates its combination with an additional, time consuming and possibly SAR intensive B₁ measurement, preventing direct migration of the method to these fields. To address this we introduce a method designed to be free of systematic errors caused by B₁ inhomogeneity in which the value of T₁ is extracted from three SPGR images acquired with EPI readout. The precision of the T₁ maps produced is found to be comparable to the two-point method while the accuracy is greatly improved in the same time and spatial resolution. A welcome byproduct of the method is a map of B₁ that can be used to correct other acquisitions in the same session. Tables of the optimal acquisition protocols are provided for several total imaging times.

Introduction

The current most efficient strategy for obtaining T₁ maps within clinically acceptable time is based on acquiring two spoiled gradient recalled echo (SPGR) images in steady states with variable flip angles [1, 2]. Although the method's efficiency can be maximized by introducing various repetition times and number of averages used to acquires each image in the pair [3], its fundamental premise remains: The actual values of the flip angles experienced by the spins are necessary for accurate T₁ calculation. Fortunately, at 1.5 Tesla the imprecise knowledge of these angles caused by a combination of radio-frequency (RF) pulse imperfections, transmit coil profiles, standing wave effects, etc. results only in insignificant bias in T₁ [4]. At higher field strengths, however, the transmit RF inhomogeneity (B₁) becomes progressively worse. It leads to systematic errors in T₁ that can no longer be neglected, preventing direct migration of the two-point method to 3 T and above. For example, Cheng et. al. [5] considered the two-SPGR technique and showed that a ±15% deviation in flip angle, a level of non-uniformity often encountered in vivo and in vitro at 3 T [5-7], will cause a ±30% systematic error in T₁. This undermines the entire reason of T₁ determination, be it tissue segmentation, pathology identification or measurement of contrast agent uptake.

In order to take advantage of the increased sensitivity offered by high field scanners adiabatic pulses that deliver uniform excitation [8] can be employed. Specific absorption rate (SAR) limits, however, especially at high fields, may lower the efficiency or even preclude this approach. In general, given a particular hardware setup, the only way to cope with the SAR limit is to decrease or re-design the flip angles and/or increase the time intervals between them, rendering the SAR a sequence design restriction. An alternative approach to mitigate the B₁ inhomogeneity is to map it in situ using a separate B₁ measuring sequence [5, 7]. Unfortunately, it is time consuming and possibly SAR prohibitive in itself. In addition, B₁ measurement uncertainty propagates into the error of T₁ estimate, further reducing the overall efficiency of the scheme. Other solutions offered in the literature employ different sequences, requiring various RF power levels, imaging time and post processing needs [5, 7, 9-13]. Ultimately, regardless of the approach, the quality of T₁ estimation is given by its measurement error σ_T1 achieved in a given experimental time which includes the duration of calibration scans (if any) [3, 5, 7, 10, 14].

In the present paper, we introduce a new method based on three SPGR echo sequences for T₁ quantification that is insensitive to flip angle inhomogeneities and examine the sequence parameters that influence the precision of its T₁ estimation. Owing to the SPGR-triplet-for-T₁-estimation approach, we name this new method TRITONE. We show that despite the complication caused by flip angle non-uniformity, TRITONE attains precision of T₁ estimation comparable to that achieved by the two-SPGR methods [1-3] in the same time and spatial resolution and exceeds them in accuracy. If the two-SPGR methods are combined with B₁ measurement for accuracy, then TRITONE supersedes them in precision. The post processing step of TRITONE is straightforward and can be incorporated into on-line reconstruction.

Theory

Since we wish to develop a method for T₁ estimation to be used in clinical settings, we consider field of view (FOV), spatial resolution and total allocated examination time (T) as exogenous variables determined by the experimenter. The remaining SPGR sequence parameters: nominal flip angle (α), repetition time (TR), number of averages of a scan (N), echo time (TE) and readout duration (T_adc) are to be optimized for the highest quality in the resultant T₁ maps regardless of the unknown spatial flip angle non-uniformity. The observed SPGR intensity (S) in each pixel is a function of the sequence parameters, longitudinal (T₁) and transverse ($T_2^{\ast }$) relaxation times, flip angle inhomogeneity described by the actual-to-nominal flip angle ratio (B₁) and a factor proportional to the equilibrium magnetization (ρ₀):

$$S={\rho }_0\frac{1-e^{-TR∕T_1}}{1-e^{-TR∕T_1}\text{cos}\left(B_1\alpha \right)}\text{sin}\left(B_1\alpha \right)e^{-TE∕T_2^{\ast }}$$ (1)

From the structure of this equation it is clear that having three images S_m, m = 1, 2, 3, acquired with di erent TR's and/or flip angles is su cient to estimate T₁. Indeed, if the three share identical bandwidth, readout, FOV and spatial resolution (to ensure identical reconstruction artifacts and $T_2^{\ast }$ weighting), then the ratio of any two images depends only on the unknown T₁ and B₁ in a pixel. Therefore, a pair of such ratios, say S₁/S₃ and S₂/S₃, or equivalently a pair of spherical angles ϕ = arctan(S₃, S₁) and $\theta =\arccos \left(\frac{S_2}{\sqrt{S_1^2+S_2^2+S_3^2}}\right)$ are related to T₁ and B₁. Given sequence parameters, a two dimensional look-up table T₁(ϕ, θ) can be easily generated and then polled for fast, on-line, T₁ extraction. The precision of the result depends on the SNR of the raw images, sequence settings (TR_m, α_m, N_m, TE, T_adc) and on the actual values of T₁ and B₁ in that pixel.

The sequence parameter optimization will be performed with the goal of minimizing the standard deviation, σ_T1, of T₁ estimation in the vicinity of the “expected” relaxation time $T_1^{tune}$. Since ±15% variations in B₁ around the “expected” $B_1^{tune}=1.0$ are common at 3 Tesla [5-7] we will minimize the “average error” at $B_1=0.85B_1^{tune}$ and $B_1=1.15B_1^{tune}$:

$${\stackrel{‒}{\sigma }}_{T_1}=\sqrt{\frac{{\sigma }_{T_1,B_1=0.85}^2+{\sigma }_{T_1,B_1=1.15}^2}{2}}$$ (2)

The choice of TE and T_adc (T_adc ≤ 2TE) does not alter the spin excitation memory under investigation but a ects SNR and with it — the T₁ estimation precision. Their influence was considered in [3] where it was shown that the SNR due to $T_2^{\ast }$ decay is proportional to $\sqrt{T_{adc}}{e}^{-T_{adc}∕2T_2^{\ast }}$ (eq. (2) of [3]). Knowing that this function attains its maximum at $T_{adc}=T_2^{\ast }$, we consider SNR at this readout as a benchmark that is SNR at any other T_adc will be a fraction of the maximum given by:

$$\frac{\sqrt{T_{adc}}}{\sqrt{T_2^{\ast }}}\frac{e^{-T_{adc}∕2T_2^{\ast }}}{e^{-1∕2}}=\sqrt{\frac{T_{adc}}{T_2^{\ast }}}{e}^{\frac{1}{2}\left(1-\frac{T_{adc}}{T_2^{\ast }}\right)}$$ (3)

Since the SNR of the raw images also depends on the RF coil, receiver hardware, spatial resolution, spin density and its T₁, it is convenient to introduce a benchmark that would summarize all these properties and enable hardware and sample independent comparison of different sequences and protocols. One such measure that lends itself to the task is the maximum SNR attainable by running the SPGR sequence at the Ernst angle with the optimal readout in the same total imaging time as the proposed TRITONE experiment. Under these conditions the image intensity (Eq. 1) is given by ${\rho }_0\sqrt{\frac{1-e^{-TR∕T_1}}{1+e^{-TR∕T_1}}}={\rho }_0\sqrt{\tanh (TR∕2T_1)}$, so that the SNR achieved by averaging SPGR images over time T is given by $\frac{{\rho }_0}{{\sigma }_0}\sqrt{\frac{T}{2T_1}}\sqrt{\frac{\tanh (TR∕2T_1)}{TR∕2T_1}}$(see Eq. 4.3.26 in [15]) which increases monotonically as TR diminishes and approaches the maximum value of

$$SN{R}_{max}=\frac{{\rho }_0}{{\sigma }_0}\sqrt{\frac{T}{2T_1}}$$ (4)

where σ₀ is the standard deviation of the noise in a single image before averaging.

Using these results, χ² fitting [16] is executed to relate the standard deviation of T₁ to the three SPGR sequence parameters (see appendix A for full derivation):

$${\sigma }_{T_1}=\frac{T_1}{SN{R}_{max}}\cdot \sqrt{\frac{T_2^{\ast }}{T_{adc}}}{e}^{\frac{1}{2}\left(\frac{T_{adc}}{T_2^{\ast }}-1\right)}\cdot \sqrt{\frac{T}{2T_1}\sum _{m=1}^3\frac{1}{N_m}\frac{q_m^2}{T_1^2}}$$ (5)

where q_m's are defined in Eq. (A.3) in the appendix and SNR_max is the maximal SNR (Eq. 4) achievable in the time allocated: $T={\sum }_{m=1}^{3}T{R}_m{N}_m$.

Similar to the two-SPGR T₁ experiment [3], the error comprises three factors: (i) describing hardware and sample properties, (ii) accounting for signal decay and noise due to imaging readout and (iii) reflecting sensitivity of the sequence to T₁. It is thus the last two terms that are subject to optimization and, in fact, of interest. Following [3], we will use a dimensionless normalized coefficient of variation, ε_T1, as a sample- and hardware-independent measure of the precision of T₁ estimation:

$${\epsilon }_{T_1}=\frac{{\sigma }_{T_1}}{T_1}SN{R}_{max}$$ (6)

where smaller ε_T1 indicates more efficient use of the imaging time for T₁ estimation in addition to the usual “square root of time” law contained in SNR_max (Eq. 4). The normalized coefficient of variation corresponding to the average error to be minimized is then given by:

$${\stackrel{‒}{\epsilon }}_{T_1}=\sqrt{\frac{{\epsilon }_{T_1,B_1=0.85}^2+{\epsilon }_{T_1,B_1=1.15}^2}{2}}$$ (7)

Observing the structure of Eqs. (5), (6) and (7), the derivation of the expression for ${\stackrel{‒}{\epsilon }}_{T_1}$ entails only redefinition of q's to ${\stackrel{‒}{q}}^2=(q_{B_1=0.85}^2+q_{B_1=1.15}^2)∕2$, where q_B1's are the same q's defined by Eq. (A.3) but evaluated at the corresponding B₁'s.

Minimization of this metric yields optimal acquisition parameters for T₁ measurement in the vicinity of the assumed values of $T_1^{tune}$ and $B_1^{tune}$. Nevertheless, once a protocol is chosen Eqs. (5) and (6) can be used to evaluate ε_T1 for any combinations of T₁ and B₁. The map of ε_T1(T₁, B₁) can then be examined on how the precision degrades as T₁ and B₁ deviate from their tuning values. The wider the region over which the error remains small, i.e. the flatter the map, the better. Choosing to minimize the average error at ±15% rather than that simply at $B_1^{tune}$ helps this cause.

Materials and Methods

Minimization of the average normalized coefficient of variation was performed numerically using brute-force algorithm on a grid in the sequence-parameter space reported in Table 1. The value of $T_2^{\ast }$ needed for numerical minimization (since it enters Eq. (5)), was chosen to be $0.05T_1^{tune}$ as a good and practical approximation. It is however clear that if $T_2^{\ast }$ is substantially different, the minimization has to be repeated. The computation took several hours on a Pentium IV class workstation and yielded the set of acquisition parameters presented in Table 2. The granularity of the search grid is dictated by the numerical complexity of the problem. It is therefore possible that the absolute minimum was not reached. It is also possible that there are several minima. However, we are not interested in finding absolutely the best protocol per se, we only look for a protocol whose precision is as close to the absolute minimum as we can practically get.

Table 1.

Configuration of the brute-force search algorithm employed for sequence parameter optimization. The range of nominal flip angles was limited to (15°, 135°).

Experiment duration	Minimum TRm	Step in TRm	Step in αm, (°)
T ≤ 2.0T1	0.01T1	0.01T1	5
T > 2.0T1	0.1T1	0.1T1	5

Table 2.

Optimal SPGR sequence parameters for T₁ estimation for a given total imaging time T and $T_2^{\ast }=0.05T_1^{tune}$. The corresponding average normalized coefficient of variation ${\stackrel{‒}{\epsilon }}_{T_1}$ is also listed. Optimal readout duration: $(T_2^{\ast },T{R}_m)$.

$T∕T_1^{tune}$	${\stackrel{‒}{\epsilon }}_{T_1}$	$T{R}_1∕T_1^{tune}$	$B_1^{tune}{\alpha }_1,(°)$	N1	$T{R}_2∕T_1^{tune}$	$B_1^{tune}{\alpha }_2,(°)$	N2	$T{R}_3∕T_1^{tune}$	$B_1^{tune}{\alpha }_3,(°)$	N3
0.1	20.6648	0.03	15	1	0.03	35	1	0.04	135	1
0.2	14.1786	0.06	15	1	0.05	40	1	0.09	135	1
0.3	12.3081	0.09	15	1	0.04	35	2	0.13	135	1
0.4	11.3185	0.11	15	1	0.04	35	3	0.17	135	1
0.5	10.7166	0.13	15	1	0.05	40	3	0.22	135	1
0.6	10.3048	0.14	15	1	0.05	40	4	0.26	135	1
0.7	10.0273	0.16	15	1	0.05	40	5	0.29	135	1
0.8	9.8308	0.17	15	1	0.05	40	6	0.33	135	1
0.9	9.6718	0.21	15	1	0.05	40	6	0.39	135	1
1.0	9.5240	0.22	15	1	0.05	40	7	0.43	135	1
1.1	9.3959	0.22	15	1	0.05	45	8	0.48	135	1
1.2	9.2705	0.23	15	1	0.05	45	9	0.52	135	1
1.3	9.1371	0.30	20	1	0.05	40	9	0.55	135	1
1.4	8.9933	0.31	20	1	0.05	40	10	0.59	135	1
1.5	8.8622	0.32	20	1	0.05	40	11	0.63	135	1
1.6	8.7272	0.33	20	1	0.05	40	11	0.72	135	1
1.7	8.5948	0.34	20	1	0.05	40	12	0.76	135	1
1.8	8.4580	0.35	20	1	0.05	40	12	0.85	135	1
1.9	8.3222	0.34	20	1	0.05	45	13	0.91	135	1
2.0	8.1808	0.36	20	1	0.05	40	13	0.99	135	1
3.0	6.9789	0.4	20	1	0.1	55	9	1.7	135	1
4.0	6.0072	0.4	20	1	0.1	50	11	2.5	120	1
5.0	5.3975	0.6	25	1	0.1	50	15	2.9	120	1
6.0	5.0339	0.9	30	1	0.1	50	19	3.2	125	1
7.0	4.8082	1.1	30	1	0.1	50	23	3.6	125	1
8.0	4.6607	1.3	35	1	0.1	50	28	3.9	125	1
9.0	4.5709	1.6	40	1	0.1	50	32	4.2	125	1
10.0	4.5035	2.2	50	1	0.1	50	36	4.2	130	1
11.0	4.4396	3.1	65	1	0.1	50	39	4.0	135	1
12.0	4.3789	3.4	70	1	0.1	50	44	4.2	135	1
13.0	4.3370	3.8	75	1	0.1	50	49	4.3	135	1
14.0	4.3144	4.0	75	1	0.1	50	55	4.5	135	1
15.0	4.3055	4.4	80	1	0.1	50	60	4.6	135	1
16.0	4.3095	4.5	80	1	0.1	50	66	4.9	135	1
17.0	4.3248	4.7	80	1	0.1	50	74	4.9	135	1
18.0	4.3514	4.9	80	1	0.1	50	82	4.9	135	1
19.0	4.3885	4.9	80	1	0.1	50	92	4.9	135	1
20.0	4.4134	3.9	85	2	0.1	45	74	4.8	135	1

The experiments were done in a 3 T Trio whole body imager (Siemens AG, Erlangen, Germany) using its transmit-receive head coil, on a uniform 15cm diameter × 40cm length cylindrical water phantom and then in the brain of a volunteer. The volunteer was briefed on the procedure and gave institutional review board-approved written consent. Conventional 3D EPI data was acquired with 192 × 192 × 96mm³ field of view and 64 × 64 × 32 matrix on a phantom and with 224 × 224 × 64mm³ field of view and 224 × 224 × 64 matrix on a human head. As an example, we chose a $T=10T_1^{tune}$ protocol from Table 2 (underlined) and acquired data assuming $T_1^{tune}=300\mathrm{ms}$ in the phantom and $T_1^{tune}=1000\mathrm{ms}$ in vivo. In order to satisfy the shortest TR, as indicated in Table 2, 32 k-space lines were acquired after each excitation in the phantom experiment and 64 on the volunteer. The corresponding TEs were 13 and 45ms. After on-line image reconstruction, the three image values in each pixel were converted into the spherical angles that were used to look up the values of T₁ and B₁ from the precomputed tables. The look-up table approach replaces computationally expensive non-linear χ² fitting but is equivalent to it since the number of unknowns is equal to the number of images. Additional advantage of the approach is that the table can be generated during data acquisition while data is still unavailable dramatically reducing the postprocessing time.

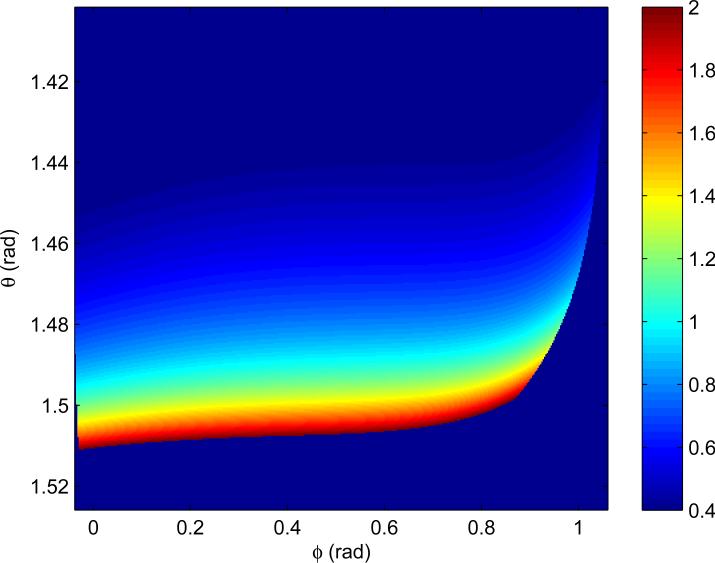
The look-up table (Fig. 1) is a 300 × 3000 array in the (ϕ, θ) plane. Each of its cells of is filled with the average value of T₁ whose underlying spherical angles fall within it. Entries into the cells are generated by computing the corresponding SPGR intensity triplet using Eq. (1) and then spherical angles for each combination of $T_1∕T_1^{tune}\in (0.4,6.0),B_1∕B_1^{tune}\in (0.7,1.4)$ in steps of 0.001. The cells where the maximum and the minimum entries differ by more than $0.005T_1^{tune}$ were marked as bad with a NAN (not-a-number). The table thus filled represents a single valued function T₁(ϕ, θ). In other words, for any measured intensity triplet, the spherical angles are computed and then the corresponding T₁ is unambiguously looked-up in the table (or NAN is assigned). The look up table B₁(ϕ, θ) (not presented) was generated in a similar fashion.

Fig. 1.

Lookup table for $T_1∕T_1^{tune}$ estimation as a function of ϕ = arctan(S₃, S₁) and $\theta =\arccos \left(\frac{S_2}{\sqrt{S_1^2+S_2^2+S_3^2}}\right)$ (See the Methods section). Sequence parameters are: $T{R}_1=2.2T_1^{tune}$, $T{R}_2=0.1T_1^{tune}$, $T{R}_3=4.2T_1^{tune}$, ${\alpha }_1=50°∕B_1^{tune}$, ${\alpha }_2=50°∕B_1^{tune}$, ${\alpha }_3=130°∕B_1^{tune}$ (Protocol of Table 2 with $T=10.0T_1^{tune}$).

After T₁ and B₁ in each pixel are determined, the $T_2^{\ast }$– and receive-B₁–weighted spin density, ρ₀, is extracted from Eq. (1). Since the receive/transmit coil was used, following the reciprocity principle [17] the B₁-corrected $T_2^{\ast }$-weighted spin density is obtained by dividing the extracted value by the corresponding B₁ in that pixel.

To illustrate the influence of the B₁ inhomogeneity on T₁ estimation we also acquired phantom data using optimal two-point 3D EPI of the same total imaging time and tuning ($T=10T_1^{tune},T_1^{tune}=300\mathrm{ms}$). The protocol was: TR₁ = 30ms, α₁ = 55°, N₁ = 55, TR₂ = 1440ms, α₂ = 85°, N₂ = 1 [3] with 32 k-space lines acquired after each excitation, as in TRITONE. This data was processed as described in [3].

Results

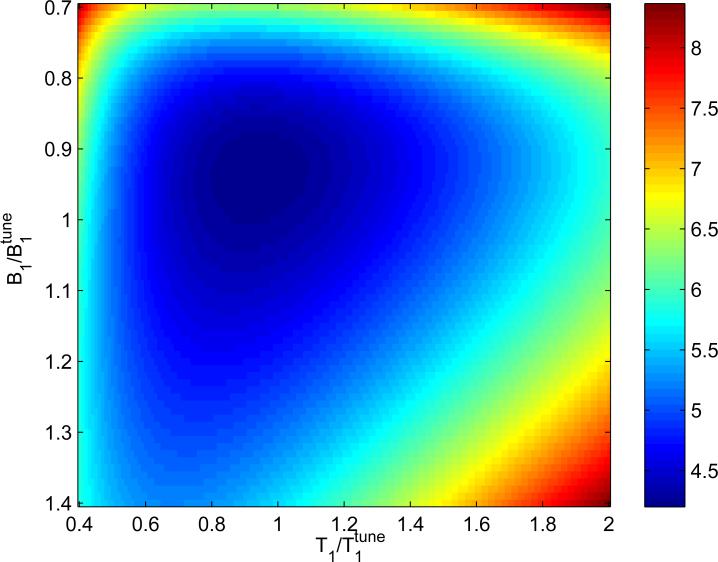
The theoretically expected performance of the T₁ estimation using selected protocol is demonstrated in Fig. 2 where the map of normalized coefficient of variation, ε_T1, is presented. Its minimal value is ${\epsilon }_{T_1}^{min}=4.2$. (Note that Table 2 lists the average coefficient, ${\stackrel{‒}{\epsilon }}_{T_1}$, which is larger than the minimum.) The surface of this plot is flat for a wide range of T₁'s and B₁'s, that is the precision remains within 20% of the minimum in the large, blue egg-shaped area ($0.55<T_1∕T_1^{tune}<1.6,0.8<B_1∕B_1^{tune}<1.3$).

Fig. 2.

Color map of the normalized coefficient of variation, ε_T1, (Eq. 6) as a function of the true values of T₁ and B₁ for a protocol from Table 2 with $T=10T_1^{tune}$. The minimal error is ${\epsilon }_{T_1}^{min}=4.2$. Note that the precision remains within 20% of the minimum in the large, blue egg-shaped area ($0.55<T_1∕T_1^{tune}<1.6,0.8<B_1∕B_1^{tune}<1.3$).

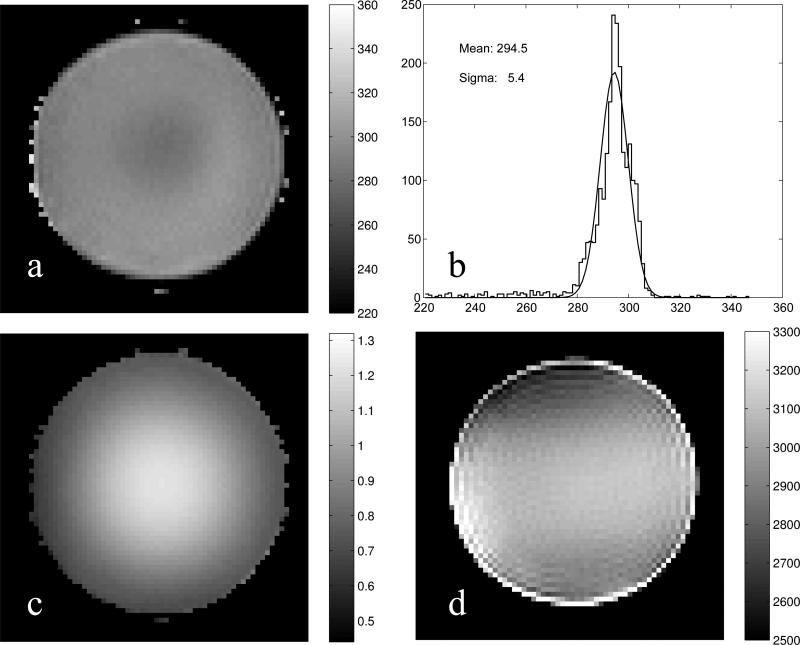
Experimentally, a uniform phantom is the ideal test bed to evaluate the sensitivity of a method to spatial B₁ inhomogeneity. Since the phantom is uniform, its T₁-map should be as well. A T₁ map at a slice near the center of the excited volume is depicted in Fig. 3a. A histogram of the T₁'s, the width of which can be used to gauge the precision, is shown in Fig. 3b. If we assume that the width is due to noise alone (ignoring contributions due to possible remaining B₁ inhomogeneity), the precision is rather remarkable, 1.8%. The B₁ map in Fig. 3c demonstrates a large flip angle non-uniformity that if left uncorrected would lead to considerable systematic errors in T₁ estimation [5] (see below). Since a receive-transmit coil was used, the reciprocity principle was utilized to correct for its receive profile and obtain a $T_2^{\ast }$-weighted spin density map (panel d). In analogy to the T₁ map, the $T_2^{\ast }$-weighted spin density of the phantom should also be uniform. However, unlike the T₁ map, $T_2^{\ast }$ is sensitive to the residual B₀ inhomogeneity that was not compensated by shimming, making it less uniform (Fig. 3d).

Fig. 3.

a: An axial T₁ map in a cylindrical phantom acquired at 3×3×3 mm³ resolution. b: Histogram of the T₁ values (jagged line) overlaid with a fitted Gaussian (solid line). Note that since the phantom is uniform the T₁ map should be as well. To this end, the histogram features a narrow peak at 294.5 ± 5.4 ms. c: Map of B₁ showing that at the center region the flip angle is higher while towards the rim it is lower than nominal by up to 20%. d: B₁-corrected $T_2^{\ast }$-weighted spin density (in arbitrary units) obtained using the reciprocity principle for the receive-transmit coil.

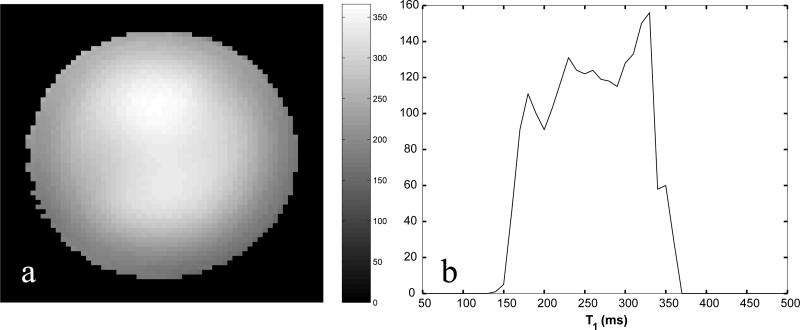
To appreciate the accuracy of the TRITONE method we present, in Fig. 4, a T₁ map acquired with the nearest equivalent optimal 2-point method (with the same tuning and acquisition time). It is evident from the map (panel a) and the histogram (panel b) that uncorrected B₁ inhomogeneity is responsible for very large variation of T₁'s that is absent in Fig. 3b.

Fig. 4.

a: An axial T₁ map in the same cylindrical phantom acquired using two-SPGR acquisition (without B₁ correction). b: Histogram of the T₁ values. Note that since the phantom is uniform the non-uniformity of the T₁ map and the width of the histogram are due to uncorrected B₁ inhomogeneity.

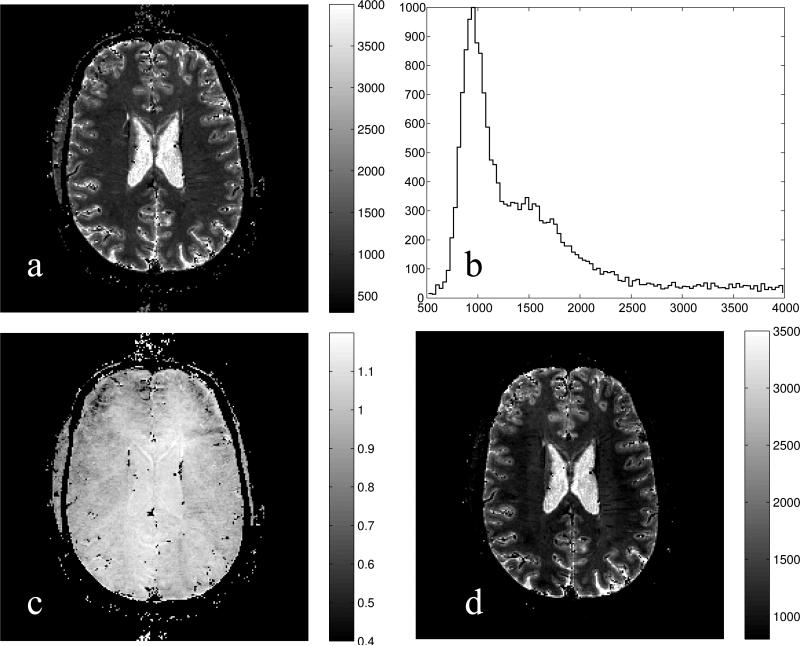
An in vivo 1×1×1 mm³ resolution map of T₁ is shown in Fig. 5a. The histogram of the T₁ values (panel b) exhibits a narrow peak at 950ms, a broad peak at about 1550ms and a tail at longer T₁'s. These features can be ascribed to the white matter, gray matter and CSF, respectively [13]. Although the in vivo B₁ map (Fig. 5c) demonstrates less non-uniformity compared to the phantom, it is still substantial. Left uncorrected, it would result in large systematic errors in the T₁ map. The receive-coil-profile corrected $T_2^{\ast }$-weighted spin density image is presented in Fig. 5d. Note that the effects of residual B₀ inhomogeneity that were not compensated by shimming are not apparent but can not be excluded.

Fig. 5.

a: An axial T₁ map in a human head at 1×1×1 mm³ resolution. b: Histogram of the T₁ values from the slice exhibits a narrow peak at 950 ms corresponding predominantly to the white matter. c: Map of B₁ shows that at the center region the flip angle is higher while towards the rim it is lower than nominal by about 15%. d: B₁-corrected $T_2^{\ast }$-weighted spin density (in arbitrary units) obtained using the reciprocity principle for the receive-transmit coil. In all panels, black speckles represent pixels where the signals could not be described by Eq. (1) presumably due to intravoxel variations of T₁ or motion.

Discussion

In vivo and in vitro studies demonstrated that despite substantial efforts in coil design and excitation pulse synthesis, the flip angles they produce still vary spatially at and above 3 T. This precludes the use of the current efficient two-SPGR method of T₁ estimation [1, 3] at these fields, because it requires precise flip angles [5, 7]. As a remedy we have proposed adding a third SPGR acquisition and showed how the unknown B₁ inhomogeneity can be excluded in post processing. We then presented a method for selecting the three sequence parameters to achieve the most efficient use of the available imaging time for T₁ mapping. We have demonstrated that the proposed TRITONE method of T₁ estimation is indeed insensitive to spatial variations and deviations of B₁ from its nominal value. All that remains is to compare the performances of TRITONE with the two-SPGR methods.

Since time is at a premium in in vivo MRI, performance comparisons of different methods have to be conducted assuming fixed total experiment duration including any time needed for the in situ B₁ calibration scan. The normalized coe cient of variation ε_T1 at $T_1^{tune}$ of the DESPOT1 method [1] can be as small as 4.5 [3] which, even without accounting for the calibration scan's duration, is worse than can be achieved with TRITONE (see Table 2). Combining the most efficient two-point method [3], characterized by ε_T1 = 3.6, with a calibration scan (which can claim more than 40% of the total time [5, 7]) rises its normalized coefficient of variation above that of TRITONE at intermediate and long experiment durations ($T>6T_1^{tune}$). Furthermore, B₁ measurement error from the calibration scan has to be incorporated into the error of the final T₁ estimate making exact comparisons of the efficiencies more difficult and dependent on the calibration procedure. Nevertheless, this contribution is not negligible because it is double the B₁ measurement error [5]: ±15% deviation in B₁ causes ±30% error in T₁ and thus even if the 2-point T₁ measurement were noise-free, the error in T₁ due to noise in the calibration scan alone would have been:

$$\frac{{\sigma }_{T_1}}{T_1}=2\frac{{\sigma }_{B_1}}{B_1}$$ (8)

Combining both sources of noise in quadrature (because noise in T₁ and B₁ measurements are independent) we can write for the precision of B₁-corrected 2-point method:

$${\left({\epsilon }_{T_1}^{B_1-corrected}\right)}^2=\frac{{\left({\epsilon }_{T_1}^{2-point}\right)}^2}{0.6}+4\frac{{\left({\epsilon }_{B_1}^{calib}\right)}^2}{0.4}$$ (9)

where we assumed 60%/40% split of the total experimental time for T₁ and B₁ measurements, as above. The normalized coefficient of variation for calibration scan, ${\epsilon }_{B_1}^{calib}$, depends on the protocol. For the sake of the argument let's assume that calibration is very precise, so that ${\epsilon }_{B_1}^{calib}=0.5{\epsilon }_{T_1}^{2-point}=1.8$. Then, ${\epsilon }_{T_1}^{B_1-corrected}=\sqrt{\frac{{3.6}^2}{0.6}+4\frac{{1.8}^2}{0.4}}=7.3$ making TRITONE the most efficient at about $T>(2-3)T_1^{tune}$ (see ${\stackrel{‒}{\epsilon }}_{T_1}$ in Table 2).

The two-point approach remains the method of choice for dynamic T₁ studies where acquisition time available must be short. In these studies the B₁ map acquired with a calibration scan may be assumed to be time invariant. To maintain high accuracy of B₁-corrected T₁'s the excitation pulse and slice selection should be identical in the calibration and T₁ mapping sequences, a feature automatically offered by the TRITONE method.

Similar to previous studies [1-3, 5, 7, 10], we assumed a single compartment model, i.e., that the signal from each pixel is characterized by unique values of T₁ and B₁. While this assumption can definitely be satisfied for T₁ in phantoms, uniqueness of B₁ is always an approximation. Unaccounted intravoxel flip angle variation, especially at the edges of the excited volume and intravoxel T₁ variation produce systematic errors in T₁ estimation. They may even lead to seemingly impossible signal behavior that can not be described by Eq. (1). In the previous and the presented methods such a situation can also arise due to sample motion through misregistration between images or disruption of the steady state. For the above reasons, 3D excitations (used here) which have more uniform excitation profiles than 2D ones are preferred.

In the numerical optimization leading to Table 2 all parameters were allowed to vary without any restrictions (within the search grid of Table 1). At higher fields, however, it may be necessary to exclude certain TR and flip angle combinations in order to satisfy SAR restrictions which are pulse shape and transmit coil dependent and thus need to be evaluated on a case by case basis. However, a protocol that passes SAR limits at high fields is likely to do so at low fields as well. Therefore, common protocol with identical look-up table can be utilized across all such fields.

Finally, we note that while we utilized the commercially available 3D EPI SPGR sequence, it would be simple to setup spiral, radial or any other type of SPGR sequence under the TRITONE umbrella to generate B₁-invariant T₁ maps. This is because the choice of k-space trajectory does not interfere with the spin excitation history and the only user-selectable parameters are the FOV, spatial resolution, and total examination time. The remaining SPGR sequence parameters are derived from these inputs through Table 2.

Conclusion

Fast efficient high resolution T₁ mapping techniques rely on precise knowledge of flip angles for accurate determination of the relaxation rate. Unfortunately, at higher magnetic fields the notion of flip angle is poorly defined due to non-uniform transmit coil profiles, wave effects, etc., degrading the accuracy of many quantitative techniques. The proposed TRITONE method addresses the issue of B₁ inhomogeneity by collecting three conventional 3D SPGR EPI images to produce both unbiased and precise T₁ maps. The post processing step, although computationally somewhat more involved than in the two-point methods, is still straightforward and can be incorporated into on-line reconstruction.

Appendix A

In the χ² fitting procedure, the variances of the estimated parameters are related to the variances ${\sigma }_m^2$ of the average images S_m through the diagonal elements of the covariance matrix C = (A^T A)⁻¹ where m-th row of matrix A is given by [16]

$$A_m.=\frac{1}{{\sigma }_m}\left(\frac{\partial S_m}{\partial {\rho }_0}\frac{\partial S_m}{\partial T_1}\frac{\partial S_m}{\partial B_1}\right)$$ (A.1)

Since in the problem considered the number of unknowns is equal to the number of images, the matrix A is square and therefore C = A⁻¹(A⁻¹)^T. Denoting $f_m=\frac{\partial S_m}{\partial {\rho }_0},g_m=\frac{\partial S_m}{\partial T_1}$ and $h_m=\frac{\partial S_m}{\partial B_1}$, the computation can be carried out to yield the diagonal element of C corresponding to the variance of T₁:

$${\sigma }_{T_1}^2=\frac{1}{{\rho }_0^2}\sum _{m=1}^3{q}_m^2{\sigma }_m^2$$ (A.2)

where

$$q_m=\frac{{\rho }_0}{\text{det}A}\text{det}\mid \begin{array}{ccc}\hfill f_1\hfill & \hfill {\delta }_{1,m}\hfill & \hfill h_1\hfill \\ \hfill f_2\hfill & \hfill {\delta }_{2,m}\hfill & \hfill h_2\hfill \\ \hfill f_3\hfill & \hfill {\delta }_{3,m}\hfill & \hfill h_3\hfill \end{array}\mid$$ (A.3)

and δ_i,j is the Kronecker symbol (δ_i=j = 1, δ_i≠j = 0). The explicit expressions of f_m, g_m and h_m for the SPGR sequence (Eq. 1) are:

$$\begin{array}{cc}\hfill f_m& \equiv \frac{\partial S_m}{\partial {\rho }_0}=\frac{1-e^{-T{R}_m∕T_1}}{1-e^{-T{R}_m∕T_1}\text{cos}\left(B_1{\alpha }_m\right)}\text{sin}\left(B_1{\alpha }_m\right)\hfill \\ \hfill g_m& \equiv \frac{\partial S_m}{\partial T_1}={\rho }_0\frac{T{R}_m}{T_1^2}\frac{f_m-\text{sin}\left(B_1{\alpha }_m\right)}{1-e^{-T{R}_m∕T_1}\text{cos}\left(B_1{\alpha }_m\right)}\hfill \\ \hfill h_m& \equiv \frac{\partial S_m}{\partial B_1}={\rho }_0\frac{{\alpha }_m{f}_m}{\text{sin}\left(B_1{\alpha }_m\right)}\frac{\text{cos}\left(B_1{\alpha }_m\right)-e^{-T{R}_m∕T_1}}{1-e^{-T{R}_m∕T_1}\text{cos}\left(B_1{\alpha }_m\right)}\hfill \end{array}$$ (A.4)

If the m-th scan is averaged N_m times, then ${\sigma }_m={\sigma }_0∕\sqrt{N_m}$, combining with Eq. (3) and using Eq. (4) the variance of T₁ becomes

$${\sigma }_{T_1}^2=\frac{1}{SN{R}_{max}^2}\cdot \frac{T_2^{\ast }}{T_{adc}}{e}^{\frac{T_{adc}}{T_2}-1}\cdot \frac{T}{2T_1}\sum _{m=1}^3\frac{q_m^2}{N_m}$$ (A.5)

Thus, given the set of three SPGR sequence settings (TR_m α_m, N_m, T_adc), the values of the partial derivatives f_m, g_m, h_m are computed using equation (A.4). The auxiliary quantities, q_m, are then evaluated using equation (A.3) and the error in T₁ estimate is computed via equation (A.5).