Abstract
Three atomistic, empirical models for phosphatidylglycerol (PG) lipids are tested against structural data in the crystal and liquid crystal states. Simulations of the anhydrous crystal of dimyristoyl-phosphatidylglycerol (DMPG) show that only the CHARMM force field describes the conformation and interactions of PG headgroups accurately. The other two models do not reproduce the native network of hydrogen bonds, suggesting the presence of biases in their conformational and nonbonded interaction properties. The CHARMM model is further validated in the biologically relevant liquid crystal phase by comparing experimental small-angle X-ray scattering spectra from DMPG unilamellar vesicles with data calculated from fluid bilayer simulations. The good agreement found in this model-free comparison implies that liquid crystal PG bilayers as described by CHARMM exhibit realistic bilayer thickness and lateral packing. Last, this model is used to simulate a fluid bilayer of palmitoyl-oleoyl-phosphatidylglycerol (POPG). The resulting view of POPG bilayer structure is at variance with that proposed previously based on simulations, in particular with respect to lateral packing of headgroups and the role of counterions.
Introduction
While molecular simulations of membranes can complement other measurements with details that are not resolved experimentally, they do rely on adequately calibrated empirical potentials. Such potentials, in turn, can best be validated against some form of well-resolved structural quantities. Although the liquid crystal and liquid-ordered phases are most relevant to biological membranes, much more precise structural data can be collected on solid-like phases, like the partly hydrated gel phase or anhydrous crystals, providing a precious basis for comparison with atomistic simulation models.1, 2 In general, zwitterionic lipids like phosphatidylcholine (PC) and phosphatidylethanolamine (PE) have been more widely studied than anionic lipids such as phosphatidylserine (PS) and phosphatidylglycerol (PG). PG lipids are, however, a ubiquitous component of biological membranes. They constitute as much as 20–25% of the lipid fraction of the plasma membrane in bacteria such as E. coli,3 and are involved in the photosynthetic process in the thylakoid membranes of chloroplasts.4 A significant amount of structural data on PG is available,5–10 despite limitations imposed by the complex phase behavior of PG/water systems.11 Moreover, a high-resolution crystallographic structure of dimyristoyl-phosphatidylglycerol (DMPG) has been determined by Pascher et al.12
Simulations of both pure palmitoyl-oleoyl-phosphatidylglycerol (POPG) bilayers13, 14 and POPG-containing mixtures15–18 have been reported. Kaznessis et al. and Pickholz et al. have performed simulation studies of DPPG monolayers.19, 20 Yet, only two of these publications include complete empirical force field parameters for PG, one by Elmore13 and one by Zhao et al.14 Both of these models are based on united-atom GROMOS/Berger lipids.21 In addition, a model for the PG headgroup can be constructed in a straightforward manner from elements of the CHARMM27 lipid force field,22, 23 yet its properties have not yet been fully documented. Simulations by Kaznessis et al.19 used the CHARMM26b2 force field, a close predecessor to CHARMM27; that work showed encouraging qualitative agreement with experimental surface/pressure isotherms. CHARMM lipids can be combined with united-atom acyl chains,24 which makes them as computationally affordable as the united-atom GROMOS-type models; this combination is used in the present work.
Here, we rely on the published crystal structure of DMPG12 to test and validate all three publicly available atomistic models for PG lipids: CHARMM, Elmore, and Zhao et al. The DMPG crystal is organized as a bilayer, hence providing a highly detailed view of a headgroup-headgroup interaction pattern comparable to that of a fluid bilayer. As a consequence, describing the DMPG crystal structure is a stringent test for both intramolecular and intermolecular terms of empirical potentials. In a second stage, accuracy of the CHARMM description of fluid-phase systems is tested based on a direct, model-free comparison with small-angle X-ray scattering (SAXS) spectra of DMPG vesicles.7, 10 Finally, we comment on the structure of a fluid POPG/water bilayer and compare it with previous reports.
Methods
Force fields for PG headgroups
Parameters for the models of Elmore13 and Zhao et al.14 were obtained from the websites of their respective authors. Topologies for D- and L-DMPG were constructed from the provided topologies for POPG. For simulations using these models, the GROMACS model for sodium ions was used, as in the respective original publications. For simplicity, we adopt the numbering convention used by Zhao et al. for oxygen atoms in the PG headgroups (Figure 1).
Figure 1.
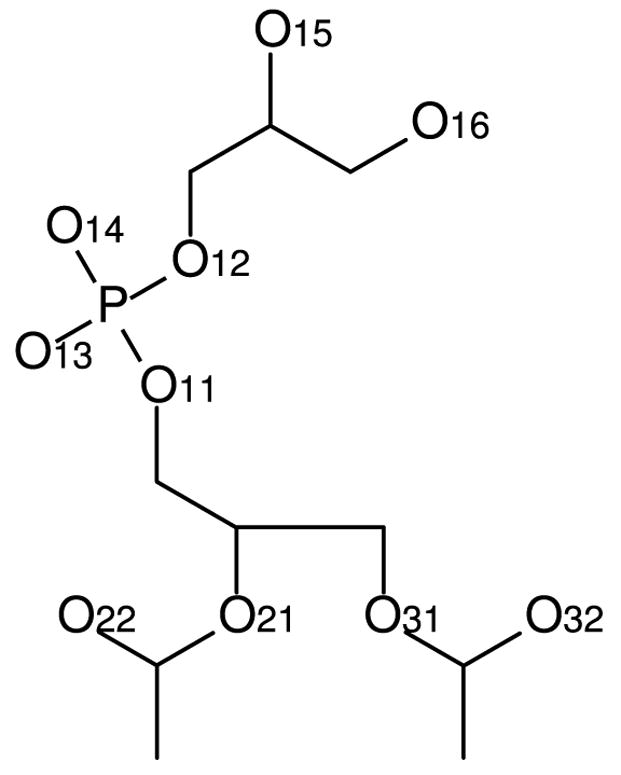
Numbering convention for oxygen atoms in the PG headgroup.
CHARMM simulations were based on the CHARMM27 set of parameters.23 Topology and parameters for the glycerol headgroup were taken from the phosphoglycerol residue that is used by CHARMM as a basis for parameterizing the phospholipid scaffold. Since the phosphoglycerol residue and phospholipids such as phosphatidylcholine share their phosphate group, they can be merged to yield a phosphatidylglycerol model without any additional parameterization. For convenience, the CHARMM-format topology file for DMPG and POPG is provided as supplementary information. In one simulation, acyl chains were represented by the united-atom model described previously;24 whereas a second simulation made use of the standard CHARMM27 force field. Sodium ions were represented by the model of Beglov and Roux.25
DMPG crystal simulations
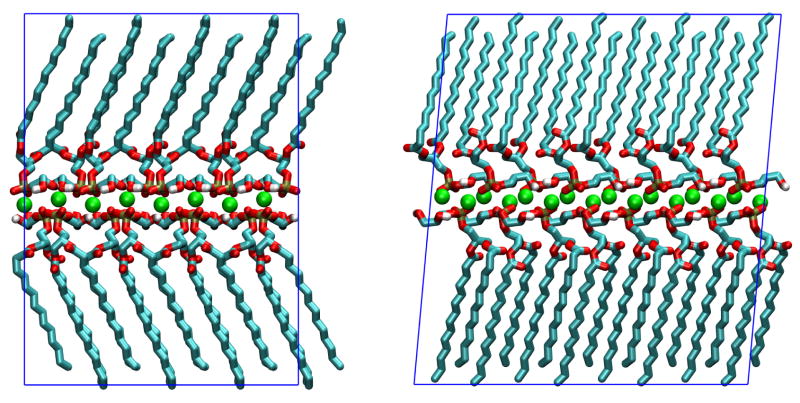
Pascher et al.12 provide atomic fractional coordinates for non-hydrogen atoms of the two DMPG molecules (with respective configurations D and L) and two sodium ions forming the asymmetric unit of the crystal. These coordinates were converted to Cartesian coordinates and replicated using symmetry operations of the P21 space group to form a supercell containing 64 DMPG molecules. The supercell had lattice parameters a = 41.48 Å, b = 33.93 Å, c = 45.52 Å and β = 95.22°. Hydrogen atoms were added as needed for simulations. The position of hydroxyl hydrogens was adjusted manually to be compatible with hydrogen bonds predicted by Pascher et al. based on the crystallographic structure. The supercell used for simulations is depicted in Figure 2.
Figure 2.
Periodic system used for DMPG crystal simulations: view along crystallographic directions a (upper panel) and b (lower panel). Atoms and ions are colored by element (Na is green, C is cyan, O is red, H is white and P is tan); the periodic supercell is represented by blue lines. Graphics rendered with VMD.41
Simulations of the Elmore and Zhao et al. models were performed using GROMACS version 3.3.26 Long range electrostatics were included through a particle-mesh Ewald scheme with a grid spacing of 1.2 Å. Lennard-Jones interactions were cut-off at 10 Å. The volume was kept constant; constant temperature was maintained at 200 K using Berendsen coupling with a coupling time of 0.2 ps. A short energy minimization was followed by a 100 ps dynamics simulation with a time step of 2 fs. Given the results of this relaxation stage, no further simulations were performed with these models (see results below).
Simulations of both CHARMM models were run using NAMD 2.6.27 The particle-mesh Ewald scheme was used for electrostatics with a grid spacing of 1.0 Å, while Lennard-Jones interactions were cut-off at 12 Å with a switching function acting between 10 and 12 Å. After an initial energy minimization, an NVT simulation was run for 100 ps with a target temperature of 200 K maintained using a weakly coupled Langevin thermostat (coupling constant of 0.2 ps−1). The system was then heated up to 298 K in a 1 ns NVT simulation. Finally, a 100 ns NPT simulation at 298 K and 1 bar was performed using the Nosé-Hoover Langevin piston algorithm28 with a fully flexible periodic cell. NAMD simulations used the r-RESPA integrator29 with a base time step of 2 fs and an extended time-step of 4 fs for soft, long-range force components.
Fluid phase DMPG and POPG bilayer simulations
Both DMPG and POPG simulations used the same CHARMM parameters as described above, with united-atom myristoyl, palmitoyl and oleoyl chains.24 The water model used was modified TIP3P.30 The hydrated, fluid bilayer model contained a periodic patch of 128 lipids and the same number of sodium counterions. The program NAMD 2.6 was used to run the simulations in the NPT ensemble at a temperature of 310 K and a pressure of 1 bar, the cell size being allowed to fluctuate independently in the z (membrane normal) and (x,y) directions. As a result, the surface tension in these bilayer simulations was zero. Other simulation parameters were identical to those of the crystal simulation.
Initial atomic coordinates for the POPG bilayer were taken from the simulations of Zhao et al.,14 obtained from the website of the authors. This system, containing 3527 water molecules (27.5 waters per lipid), was simulated for 140 ns. As the membrane area tended to expand, the interbilayer repeat distance decreased to approximately 64 Å. To ease the constraint of such an unnaturally small interbilayer distance (POPG does not experimentally form multilamellar phases), the thickness of the water layer was then increased by introducing 2048 additional water molecules: the resulting system was then simulated for 190 ns, monitoring for relaxation of the surface area and sodium counterion distribution. The fluid DMPG bilayer was constructed in several steps. First a DPPG bilayer was constructed by deleting atoms from the equilibrated POPG bilayer; after constant-pressure relaxation of this DPPG bilayer (data not shown), a configuration was taken and modified to obtain a DMPG/water system. This system was simulated for 300 ns in the conditions described above.
Headgroup reorientation time
The timescale on which headgroups reorient was estimated based on the dynamics of the vector u joining the phosphorus atom to the oxygen atom in the terminal hydroxyl of the glycerol headgroup. The following autocorrelation function C(t) was then computed:
| (1) |
where cos(θt0t) is equal to u(t0) · u(t0 + t), and the average in equation (1) is taken over all lipid headgroups and available values of t0. C(t) functions were well modeled by a combination of three exponentials, with respective decay times on the order of 100 ps, 1 ns and 10 ns.
Reconstruction of SAXS spectrum
We used a model-free approach that allows for reliable matching of simulations and experimental SAXS data. An electron density profile of the DMPG bilayer along its normal axis was first calculated from the simulated trajectory by binning with a space resolution of 1 Å at time intervals of 100 ps, over the last 100 ns of trajectory (well past the equilibration phase).
Intensities scattered at small angles by unilamellar vesicles were then reconstructed under the approximation of randomly oriented flat bilayers, which gives31
| (2) |
where I(q) is the scattered intensity, F(q) is the bilayer form factor and Δρ(z) is the relative electron density along the bilayer normal.
Results and discussion
DMPG crystal
The anhydrous sodium DMPG crystal is an interesting test case because the organization of the crystal is similar to that of the hydrated gel and fluid phases, as can be inferred by comparison with structural parameters of gel phase DPPG.12, 32
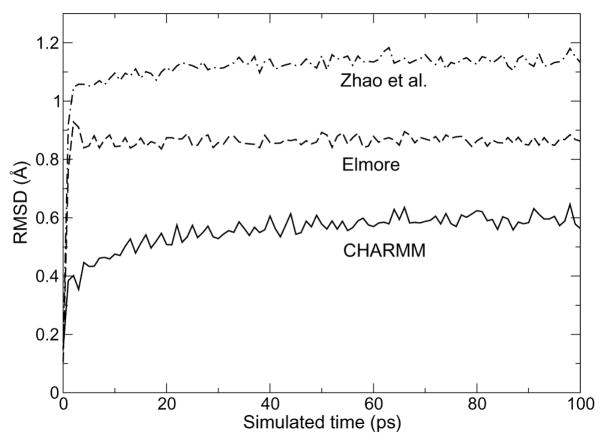
The root mean square deviation (RMSD) from the ideal crystal structure for each model of the 64-lipid supercell during a short, 100-ps relaxation at low temperature (200 K) is shown in Figure 3. All three curves show a rapid increase and reach a plateau, yet the initial increase is smoother for the CHARMM system, and the final value of 0.60 Å is significantly smaller than either of the GROMOS-based models (0.86 Å for Elmore and 1.14 Å for Zhao et al.). The origin of such different deviations from the crystal structure becomes clear when considering the evolution of hydrogen bond network between the headgroups, as illustrated in Figure 4.
Figure 3.
Root mean square deviation from the experimental structure of three DMPG crystal simulations using CHARMM (solid line), or the respective models of Elmore13 (dashed line) and Zhao et al.14 (dotted-dashed line)
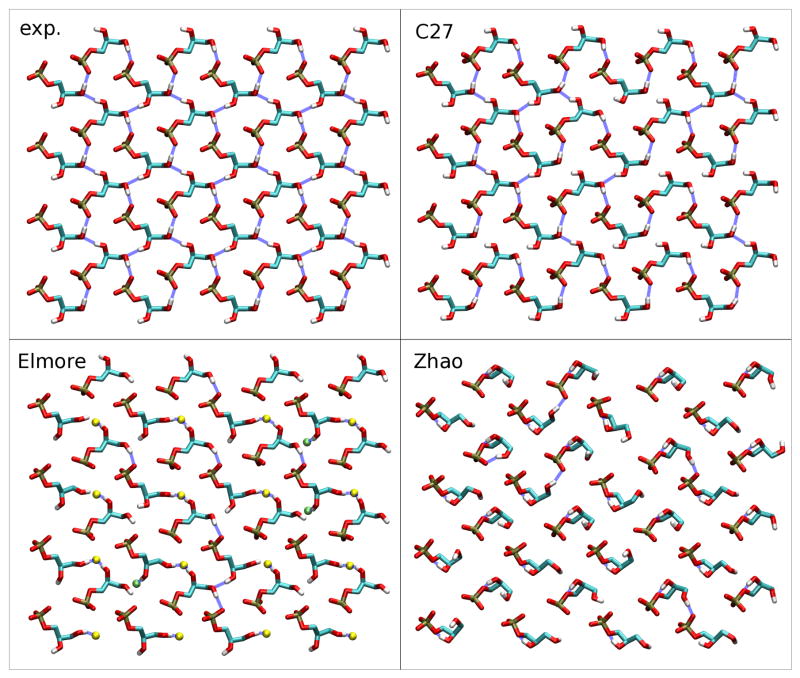
Figure 4.
Hydrogen-bonding network in the crystallographic structure (exp.) and after a short simulation with one of three models: CHARMM (C27), Elmore13 and Zhao et al.14 For clarity, only the phosphate and glycerol groups are represented, and non-polar hydrogens of C27 are omitted. For the Elmore model, some ester carbonyl oxygens are shown as pale green spheres (sn-1), resp. yellow spheres (sn-2). Blue dashed lines indicate hydrogen bonds.
In the crystallographic structure of Pascher at al.12 (Fig. 4), each headgroup is involved in four hydrogen bonds to its four nearest neighbors, each glycerol hydroxyl acting as a donor, and both the phosphate group and one glycerol hydroxyl acting as acceptors. In the CHARMM simulation, phosphate-glycerol bonding is robust, whereas thermal fluctuations result in transient breaking and reforming of glycerol-glycerol hydrogen bonds. The overall network remains intact. In contrast, upon relaxation with the Elmore model, a different bonding pattern emerges, where glycerol hydroxyl groups preferentially bind ester carbonyl oxygens. The original interaction network disappears almost completely early in the simulation and is replaced persistently with the new pattern. Deviation in hydrogen bonding is even more drastic in the Zhao et al. model, mostly due to the rapid and systematic formation of an intramolecular hydrogen bond between a glycerol hydroxyl (O15) and the glycerol oxygen (O12) participating in the phosphoester bond. This effectively results in the formation of a robust five-membered ring, correlated with a distortion of the headgroup conformation, and a loss of most hydrogen bonds present in the crystal structure. The authors of the model have reported systematic formation of this intramolecular hydrogen bond in the case of both pure POPG bilayers14 and mixtures with POPE,18 and have themselves noted14 the lack of experimental data backing this observation. This further suggests that conformational and bonding properties of the models are somewhat transferable between crystal and fluid-phase simulations.
The CHARMM models are further tested in a 100-ns room temperature simulation in the NPT ensemble with a fully flexible periodic cell. In the C27-UA simulation, lattice parameters level off very rapidly (on the order of 1 ns). At the end of the simulation, a is lower by 1%, b lower by 2%, c higher by 4% and β lower by 0.3% with respect to reported crystallographic parameters. The final RMSD is 1.7 Å, reflecting fluctuations in the supercell structure and to some extent the lattice parameters, but preservation of the crystal organization. Throughout that longer simulation, the structure of the hydrogen-bond network was unperturbed, as only reversible fluctuations of individual bonds occurred. One should note that the crystal packing of acyl chains can not be expected to be perfectly described by a united-atom model calibrated against fluid-phase properties.24, 33 The all-atom CHARMM27 model equilibrates on a somewhat longer timescale. After a slight initial drift, lattice parameters tend to get closer to their initial values and the RMSD from the ideal crystal decreases slightly. Final deviations are a: −0.3%, b: −2%, c: +1.6% and β: −0.1%, and a RMSD of 0.8 Å. Reproduction of the crystal structure by CHARMM27 is hence nearly-perfect.
These results lead us to conclude that both GROMOS-based models for the PG headgroup suffer from biases that likely affect the description of conformations and mutual interactions of PG lipids in bilayers. We find that the CHARMM models give good agreement with the crystallographic structure, thus fulfilling a necessary but perhaps not sufficient condition to provide an accurate description of less ordered phases of PG-containing systems.
Fluid phase DMPG bilayer
In order to validate the behavior of CHARMM PG in the hydrated, high-temperature fluid phase, we now turn to the liquid crystal-phase DMPG bilayer simulation. The slowest headgroup reorientation time in this system is 11 ns (see Methods), indicating that the structure of the headgroup region has ample time to equilibrate in the 300 ns simulation. As expected, the final bilayer area per headgroup, 58.5 Å2, is much expanded compared to that of the anhydrous crystal. A Langmuir-Blodgett deposition experiment by Marra34 found a deposition area of a DMPG monolayer on a DPPE layer to be 62 ± 2 Å2, and the author acknowledged a great uncertainty on the equilibrium value for a DMPG bilayer. For an equimolar mixture of egg PC and egg PG, Cowley et al.35 find an area of 67.5 Å2. Since egg lipids contain mostly acyl chains longer than myristoyl, a fraction of which is unsaturated, their area per headgroup is expected to be larger than that of DMPG. The lateral expansion of the membrane compared to the crystal coincides with the melting of the chains and disruption of the regular arrangement of PG headgroups, although some of its properties are conserved, as will be seen in the next section.
Structural data on this phase is available in the form of SAXS spectra of unilamellar vesicles. The weakly structured nature of such vesicles and the resulting absence of Bragg peaks from the spectra limit the amount of information that can be directly extracted from the data. Riske et al.7 use a stepwise model of the density to fit their SAXS data, but they mention that the 6 independent parameters in the model are far from being well-determined. Indeed, our numerical tests indicate that a number of unrealistic profiles give equally acceptable fits to the SAXS spectra (data not shown). Takahashi et al.10 use a three-Gaussian model for the electron density, which has only four free parameters. Although the fit quality and resulting electron density profiles are good for gel-phase data, fit quality deteriorates as temperature increases, and the modeled density profile for the liquid crystal-phase features unrealistically sharp peaks for the headgroup region (figure 2 in ref. 10). Both sets of results clearly indicate that purely diffuse X-ray scattering obtained from liquid crystal vesicles does not provide sufficient resolution to directly determine a transmembrane electron density profile. For this reason, we favored a model-free approach that relies on reconstructing SAXS scattered intensities directly from bilayer simulations according to equation 2 (see Methods).
Experimental and computed spectra are plotted in Figure 5. The excellent agreement indicates that the vertical structure of the bilayer is consistent with experiment on the nanometer scale. While not sensitive to atomic detail, this suggests that the bilayer thickness, and hence the area per lipid headgroup, is accurate. Based on this result, we conclude that the CHARMM description of PG headgroup interactions is realistic not only in the anhydrous crystal, but also in a hydrated, fluid environment. Interestingly, this also indicates that the CHARMM model of DMPG predicts a surface area compatible with experiment in tensionless simulations. In contrast, zwitterionic bilayers are known to shrink below their experimental area when simulated using CHARMM at zero surface tension.36, 37 We hypothesize that the net negative charge on PG headgroups modifies the balance between lateral pressure and lateral stress, reducing the sensitivity of the bilayer area to details of the force field that yield incorrect areas in zwitterionic bilayer simulations.
Figure 5.
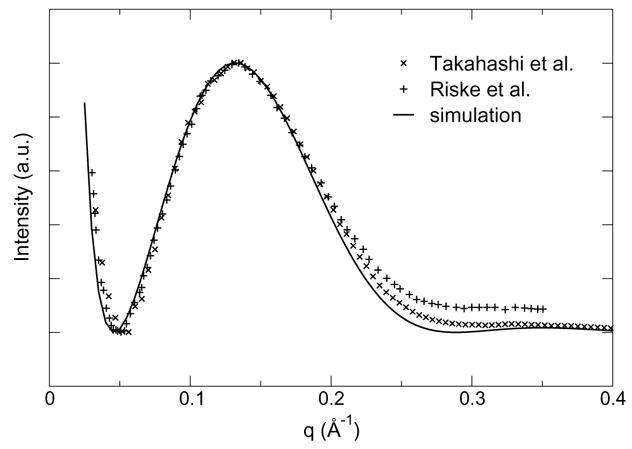
Model-free comparison of small-angle X-ray scattering intensity from DMPG vesicles7, 10 with data reconstructed from simulations using the CHARMM model.
Fluid phase POPG bilayer
The average area per headgroup in the Lα POPG bilayer is found to be 65 Å2, higher than that of DMPG by 6.5 Å2. This difference is reasonable given the longer chains and the disorder induced by the cis double bond in POPG. It is also consistent with the value of 67.5 Å2 measured by Cowley et al.35 for an equimolar mixture of egg PG and egg PC, whose acyl chain composition is well represented, on average, by POPG. This result contrasts with the smaller areas predicted by the GROMOS-based models of Elmore13 (56 Å2) and Zhao et al.14(53 Å2). The slowest headgroup reorientation timescale is found to be 15 ns.
The presence of multiple hydrogen donor and acceptor groups in the PG headgroup favors a complex network of H-bonds, as exemplified by the DMPG crystal structure. Furthermore, infrared spectroscopy results by Dicko et al.5 on liquid monolayers of DPPG suggests hydrogen bonding between hydroxyl in the glycerol headgroup and carbonyl moieties in the ester region. In the simulation, each PG headgroup forms an intermolecular H-bond with 40% probability, and an intramolecular one with 31% probability. Intermolecular H-bonds break up into 26% glycerol-phosphate, 7% glycerol-ester and 6% glycerol-glycerol. Intramolecular bonds occur mostly between the glycerol and phosphate groups (30%) and more rarely between glycerol and ester.
The most frequent intramolecular H-bond (20% probability) is formed between O16 and O12. This is analogous to the well-documented intramolecular H-bond formed by free glycerol (see ref. 38 and references within for gas and pure liquid phase properties; see ref. 39 for a discussion of structure in aqueous solution). In the Zhao et al. model,14 the probability of this bond forming is only 2%, probably due to the constraints imposed by the intramolecular H-bond between O15 and O12.
The formation of long-lived ions-lipid bridges described by Zhao et al.14 is also observed here. The quantitative distribution of ion-lipid interactions, however, is different. While Zhao et al. find most ion-lipid interactions (70%) to involve ester carbonyl and a minority (30%) the phosphate group, we find that interactions with the phosphate group are most likely (57%), followed by the glycerol (23%) and ester (20%) groups. In our simulations, lipid oxygen atoms account for 22% of Na+ coordination (1.23 of 5.63), compared to 39% (2.14 of 5.5) for Zhao et al. This correlates with a different vertical distribution of sodium ions (Figure 6). In particular, the bimodal distribution reported by Zhao et al. is not observed here.
Figure 6.
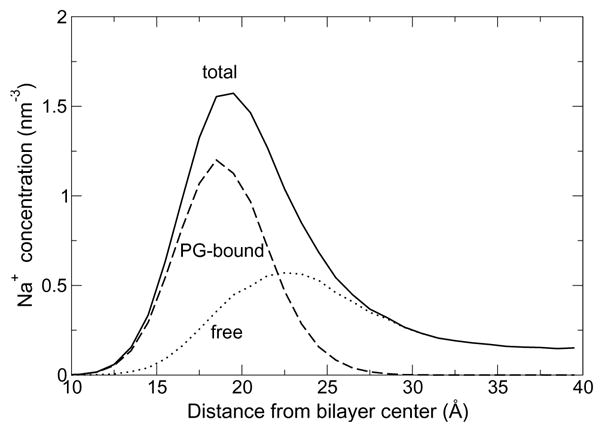
Vertical distribution of sodium counterions in the CHARMM POPG bilayer simulation (solid line). Sodium ions bound to PG oxygen atoms (dashed line) or free in solution (dotted line) are shown separately.
The stronger tendency to bind sodium ions may largely account for the smaller surface area of both the Elmore13 and Zhao models. Indeed, Zhao et al. suggest that strong sodium ion binding to carbonyl oxygens is the most important factor determining lateral packing density of the bilayer. In this context, it is interesting to note that CHARMM predicts both weaker ion/carbonyl binding and looser lateral arrangement of headgroups. Beyond the differences in lipid models, very different ion behavior among force fields have been reported,40 including a larger tendency towards condensation of the Na/Cl pair when using Gromos96 ions. This pinpoints the systematic need to cross-parametrize biological solutes and their solvent (water) and counterions to ensure consistency within a biomolecular force field (or a family thereof).
Membrane electrostatics are expected to be sensitive to both the conformation of headgroups and ion distribution around them. Vertical charge density profiles are plotted in Figure 7. The electrical multilayer structure is simpler than observed for the Zhao model, the total charge density exhibiting only one positive and one negative peak, and the amplitude of the peaks is smaller. The electrostatic potential profile, calculated from the Poisson equation, is smooth, close to error function-shaped (without oscillations). The relative potential of the bilayer core is measured to be +1.1 V.
Figure 7.
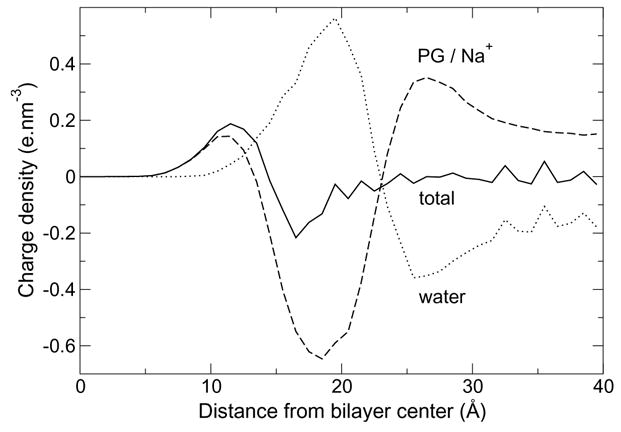
Charge density along the membrane normal in the CHARMM POPG bilayer simulation (solid line), with separate contributions from PG and counterions (dashed line) and water (dotted line).
It should be noted that the present simulations suffer from one limitation also present in previous work, namely, the absence of a thick layer of electrolyte solution allowing for polarization of the interface to fully decay. Simulating membranes from unilamellar vesicles remains challenging, all the more so in the presence of charged species. In this particular case, the use of periodic boundary conditions, ubiquitous in the field of membrane simulations, may well introduce as many artifacts as it avoids.
Conclusion
Simulating the structure of a crystal of DMPG is a stringent test for PG headgroup models. The present work demonstrates that a model based on CHARMM provides a robust and inexpensive description of the crystal structure. The standard, all-atom CHARMM model provides a more accurate description of the crystal packing of acyl chains, at a modest computational cost. Both GROMOS-based models that were tested show drastic deviations from the experimental structure, particularly in terms of interactions between neighboring PG headgroups. The pattern of hydrogen bonding deviates rapidly and irreversibly from that of the crystallographic structure. Inaccuracy in the conformational preferences of those models is likely to be a major cause of such deviation. This is expected to impact adversely the description of bilayer cohesion, hydration and surface area.
The CHARMM results are extended to hydrated, fluid-phase bilayer properties. Simulations of a DMPG bilayer compare favorably with experimental SAXS spectra, as shown using a model-free reconstruction approach. A POPG bilayer is simulated and compared with the results of GROMOS-based models. The surface area per headgroup is found to be significantly larger than previously predicted; this correlates with a tendency to bind sodium counter-ions less strongly and further away from the hydrophobic core of the membrane.
The structure of soft, self-assembled systems such as phospholipid bilayers results from a fine balance of conformational, intermolecular and hydration forces. Lipid bilayer simulations are extremely sensitive to model parameters describing such forces. As a result, a great gain in reliability could be obtained for new lipid models, as well as existing models that have not yet been validated, by thorough testing against all available structural data.
Supplementary Material
Acknowledgments
The authors gratefully acknowledge funding from the National Institutes of Health and the National Science Foundation.
Footnotes
Supporting information available
CHARMM-format topology file for residues DMPG, POPG, DMUG and POUG (with united-atom alkyl tails).
References
- 1.Tu K, Tobias DJ, Klein ML. J Phys Chem. 1995;99:10035–10042. [Google Scholar]
- 2.Tu K, Tobias DJ, Blasie JK, Klein ML. Biophys J. 1996;70(2):595–608. doi: 10.1016/S0006-3495(96)79623-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Dowhan W. Annu Rev Biochem. 1997;66:199–232. doi: 10.1146/annurev.biochem.66.1.199. [DOI] [PubMed] [Google Scholar]
- 4.Sato N, Hagio M, Wada H, Tsuzuki M. Proc Natl Acad Sci USA. 2000;97(19):10655–10660. doi: 10.1073/pnas.97.19.10655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Dicko A, Bourque H, Pézolet M. Chem Phys Lipids. 1998;96:125–139. [Google Scholar]
- 6.Degovics G, Latal A, Lohner K. J Appl Cryst. 2000;33:544–547. [Google Scholar]
- 7.Riske KA, Amaral LQ, Lamy-Freund MT. Biochim Biophys Acta. 2001;1511(2):297–308. doi: 10.1016/s0005-2736(01)00287-5. [DOI] [PubMed] [Google Scholar]
- 8.Miñones J, Dynarowicz-Łątka P, Seoane R, Iribarnegaray E, Casa M. Progr Colloid Polym Sci. 2004;123:160–163. [Google Scholar]
- 9.Pozo Navas B, Lohner K, Deutsch G, Sevcsik E, Riske KA, Dimova R, Garidel P, Pabst G. Biochim Biophys Acta. 2005;1716(1):40–48. doi: 10.1016/j.bbamem.2005.08.003. [DOI] [PubMed] [Google Scholar]
- 10.Takahashi H, Ito K. J Phys: Conf Ser. 2007;83:012022. [Google Scholar]
- 11.Lamy-Freund MT, Riske KA. Chem Phys Lipids. 2003;122(1–2):19–32. doi: 10.1016/s0009-3084(02)00175-5. [DOI] [PubMed] [Google Scholar]
- 12.Pascher I, Sundell S, Harlos K, Eibl H. Biochim Biophys Acta. 1987;896(1):77–88. doi: 10.1016/0005-2736(87)90358-0. [DOI] [PubMed] [Google Scholar]
- 13.Elmore DE. FEBS Lett. 2006;580(1):144–148. doi: 10.1016/j.febslet.2005.11.064. [DOI] [PubMed] [Google Scholar]
- 14.Zhao W, Róg T, Gurtovenko AA, Vattulainen I, Karttunen M. Biophys J. 2007;92(4):1114–1124. doi: 10.1529/biophysj.106.086272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Murzyn K, Pasekiewicz-Gierula M. Acta Biochimica Polonica. 1999;46(3):631–639. [PubMed] [Google Scholar]
- 16.Zaraiskaya T, Jeffrey KR. Biophys J. 2005;88(6):4017–4031. doi: 10.1529/biophysj.104.054601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Deol SS, Domene C, Bond PJ, Sansom MSP. Biophys J. 2006;90(3):822–830. doi: 10.1529/biophysj.105.071407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhao W, Róg T, Gurtovenko AA, Vattulainen I, Karttunen M. Biochimie. 2008;90(6):930–938. doi: 10.1016/j.biochi.2008.02.025. [DOI] [PubMed] [Google Scholar]
- 19.Kaznessis YN, Kim S, Larson RG. Biophys J. 2002;82(4):1731–1742. doi: 10.1016/S0006-3495(02)75525-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pickholz M, Oliveira ON, Skaf MS. Biophys Chem. 2007;125(2–3):425–434. doi: 10.1016/j.bpc.2006.10.010. [DOI] [PubMed] [Google Scholar]
- 21.Berger O, Edholm O, Jähnig F. Biophys J. 1997;72(5):2002–2013. doi: 10.1016/S0006-3495(97)78845-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Schlenkrich M, Brickmann J, MacKerell AD, Jr, Karplus M. Biological Membranes. In: Merz KM, Roux B, editors. A Molecular Perspective from Computation and Experiment. Birkhäuser; Boston: 1996. pp. 31–81. [Google Scholar]
- 23.Feller SE, MacKerell AD., Jr J Phys Chem B. 2000;104:7510–7515. [Google Scholar]
- 24.Hénin J, Shinoda W, Klein M. J Phys Chem B. 2008;112(23):7008–7015. doi: 10.1021/jp800687p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Beglov D, Roux B. J Chem Phys. 1994;100:9050–9063. [Google Scholar]
- 26.van der Spoel D, Lindahl E, Hess B, Groenhof G, Mark AE, Berendsen HJC. J Comput Chem. 2005;26(16):1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- 27.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel LRD, Kalé, Schulten K. J Comput Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bhandarkar M, Brunner R, Chipot C, Dalke A, Dixit S, Grayson P, Gullingsrud J, Gursoy A, Hardy D, Hénin J, Humphrey W, Hurwitz D, Krawetz N, Kumar S, Nelson M, Phillips J, Shinozaki A, Zheng G, Zhu F. NAMD user’s guide, version 2.6. Theoretical biophysics group, University of Illinois and Beckman Institute; Urbana, IL: Aug, 2006. [Google Scholar]
- 29.Tuckerman ME, Berne BJ, Martyna GJ. J Phys Chem B. 1992;97:1990–2001. [Google Scholar]
- 30.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 31.Glatter O, Kratky O, editors. Small-angle X-ray Scattering. Academic Press; London: 1982. [Google Scholar]
- 32.Watts A, Harlos K, Marsh D. Biochim Biophys Acta. 1981;645(1):91–96. doi: 10.1016/0005-2736(81)90515-0. [DOI] [PubMed] [Google Scholar]
- 33.Bareman JP, Klein ML. J Phys Chem. 1990;94(13):5202–5205. [Google Scholar]
- 34.Marra J. Biophys J. 1986;50(5):815–825. doi: 10.1016/S0006-3495(86)83522-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cowley AC, Fuller NL, Rand RP, Parsegian VA. Biochemistry. 1978;17(15):3163–3168. doi: 10.1021/bi00608a034. [DOI] [PubMed] [Google Scholar]
- 36.Benz RW, Castro-Román F, Tobias DJ, White SH. Biophys J. 2005;88(2):805–817. doi: 10.1529/biophysj.104.046821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Klauda JB, Kučerka N, Brooks BR, Pastor RW, Nagle JF. Biophys J. 2006;90(8):2796–2807. doi: 10.1529/biophysj.105.075697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chelli R, Procacci P, Cardini G, Califano S. Phys Chem Chem Phys. 1999;1(5):879–885. [Google Scholar]
- 39.Hénin J, Tajkhorshid E, Schulten K, Chipot C. Biophys J. 2008;94(3):832–839. doi: 10.1529/biophysj.107.115105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Patra M, Karttunen M. J Comput Chem. 2004;25(5):678–689. doi: 10.1002/jcc.10417. [DOI] [PubMed] [Google Scholar]
- 41.Humphrey W, Dalke A, Schulten K. J Mol Graph. 1996;14(1):33–8. 27–8. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.