Generalized concentration addition: A method for examining mixtures containing partial agonists

Abstract

Environmentally relevant toxic exposures often consist of simultaneous exposure to multiple agents. Methods to predict the expected outcome of such combinations are critical both to risk assessment and to an accurate judgment of whether combinations are synergistic or antagonistic. Concentration addition (CA) has commonly been used to assess the presence of synergy or antagonism in combinations of similarly-acting chemicals, and to predict effects of combinations of such agents. CA has the advantage of clear graphical interpretation: Curves of constant joint effect (isoboles) must be negatively-sloped straight lines if the mixture is concentration additive. However, CA cannot be directly used to assess combinations that include partial agonists, although such agents are of considerable interest. Here, we propose a natural extension of CA to a functional form that may be applied to mixtures including full agonists and partial agonists. This extended definition, for which we suggest the term “generalized concentration addition,” encompasses linear isoboles with slopes of any sign. We apply this approach to the simple example of agents with dose-response relationships described by Hill functions with slope parameter n=1. The resulting isoboles are in all cases linear, with negative, zero and positive slopes. Using simple mechanistic models of ligand-receptor systems, we show that the same isobole pattern and joint effects are generated by modeled combinations of full and partial agonists. Special cases include combinations of two full agonists and a full agonist plus a competitive antagonist.

Introduction

Three terms are used in toxicology and pharmacology to describe interactions between compounds: synergism indicates that the effect of a mixture exceeds that expected from the individual components; antagonism means that the combined effect is less than that expected; and additivity (non-interaction) means that the combined effect is equal to the expectation. These terms crucially depend on the definition of the expected, i.e., of non-interaction. When mechanistic details are known, a specific model may be constructed to represent the expected; such models may be complex and dependent on numerous physiological parameters (Krishnan et al. 2002). For most combinations, little mechanistic detail is available; in these situations, three broadly applicable definitions of non-interaction (“null models”) are generally employed.

The most common null model, although rarely explicitly stated, is effect summation. The expected effect is the sum of the individual effects:

$$f_{AB}([A],[B])=f_A([A])+f_B([B])$$ (1)

where f_A([A]) and f_B([B]) are the individual concentration-response curves for compounds A and B, and f_AB([A], [B]) is the joint concentration-response function of the mixture. Although intuitively appealing, this definition has unfortunate consequences. Consider a “sham combination” of two concentrations of the same compound A: Under (1), only compounds with linear concentration-response curves would be considered non-interactive (Berenbaum 1989). Because linear response is not common, effect summation is not generally considered a particularly useful definition of additivity.

The null model of independent action, originally called “independent joint action” by Bliss (1939) and “simple independent action” by Finney (1971), defines non-interaction as the sum of the effects minus their product:

$$f_{AB}([A],[B])=f_A([A])+f_B([B])-f_A([A])f_B([B])$$ (2)

For agents with concentration-response curves described by the probabilities of independent events, the probabilistic sum given by (2) is considered a valid non-interactive model. When individual effects are small, the product term can be ignored, reducing (2) to model (1). Independent action is used for modeling combinations with “dissimilar” mechanisms of action, including carcinogens (USEPA 2000).

The model of concentration addition (CA) is often used when compounds are judged to have “similar” mechanisms, a somewhat ambiguous concept (USEPA 2000). Also called dose addition, CA assumes that one compound can be substituted for another in proportion to their relative potencies. More precisely, concentration additivity of A and B is defined by

$$\frac{[A]}{[A_E]}+\frac{[B]}{[B_E]}=1$$ (3)

where [A_E] and [B_E] are the concentrations (or doses) of each compound alone (implicitly assumed to be positive) that cause response level E; if A and B are concentration additive, any dose combination ([A], [B]) satisfying equation (3) will then cause that same response (Berenbaum 1989). Equivalently, CA can be seen as the construction of a combination dose ([ A],[B]) with an effect equal to that of [B_E], where [A] is weighted by its relative potency at effect level E,

$$[B_E]=[B]+[A]\frac{[B_E]}{[A_E]}$$ (4)

Sham combinations clearly obey CA (Berenbaum 1989).

Equation (3) readily lends itself to graphical analysis. Plotting [A] on the x axis, [B] on the y axis, and response on the z axis yields a response surface (Figure 1a). Projecting the surface onto the xy plane yields isoboles, curves of equal effect, analogous to the contour lines on topographic maps (Figure 1b). The isobole for effect level E connects the concentrations [A_E] and [B_E] that, given individually, cause E; each combination dose ([A],[B]) that lies on the isobole also causes E (Figure 2). It is easily shown that isoboles obeying CA must be straight lines with negative slope by rewriting (3) as

$$[B]=[B_E]-\left(\frac{[B_E]}{[A_E]}\right)[A]$$ (5)

Isoboles that curve towards or away from the origin indicate synergism or antagonism, respectively, with respect to concentration addition (Figure 2). Examination of the shape of the isoboles—the method of isoboles—is the graphical equivalent of employing equation (3). Note that concentration-additive isoboles are linear only on the arithmetic scale, not the logarithmic scale often used by toxicologists when studying broad ranges of doses.

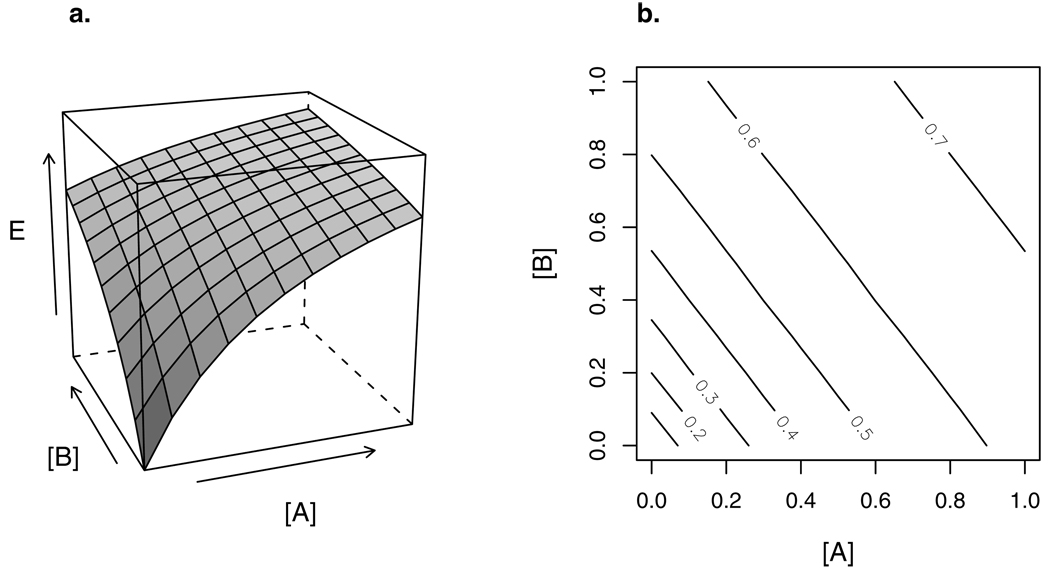
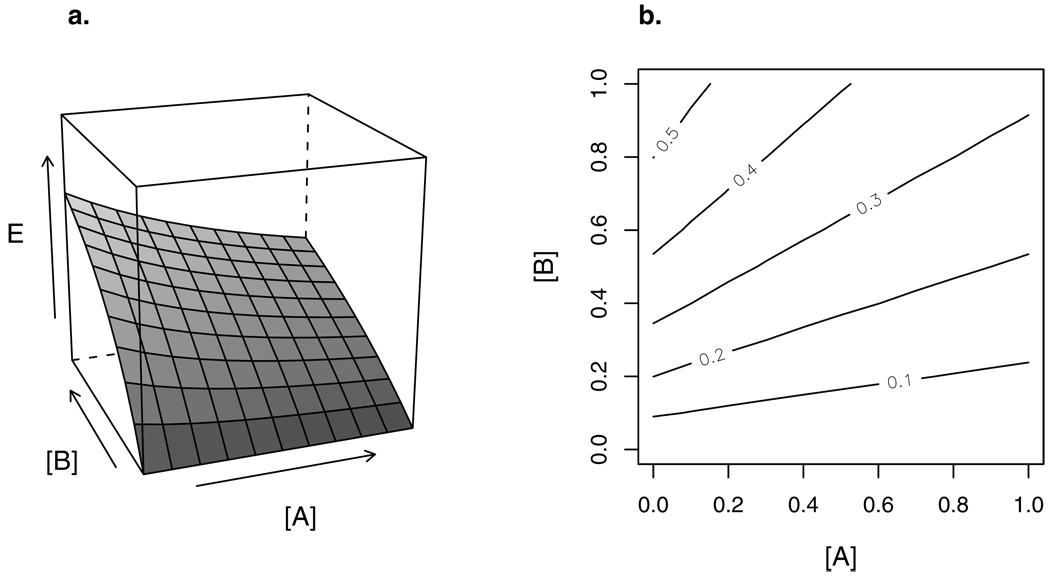
Figure 1.

(a) 3-D response surface of a combination of two agents: concentrations [A] and [B] are shown on the x and y axes, and concentration-additive response E on the z axis. The marginal concentration-response curves of A and B — the concentration-response curve for each compound individually — can be read on the xz and yz planes, respectively.

(b) Isoboles (contours) of the response surface in (a). These isoboles are straight, indicating concentration additivity. In this case they are also parallel, indicating that the two agents can be represented by a TEF, i.e., their dose-response curves differ only by a constant factor of potency.

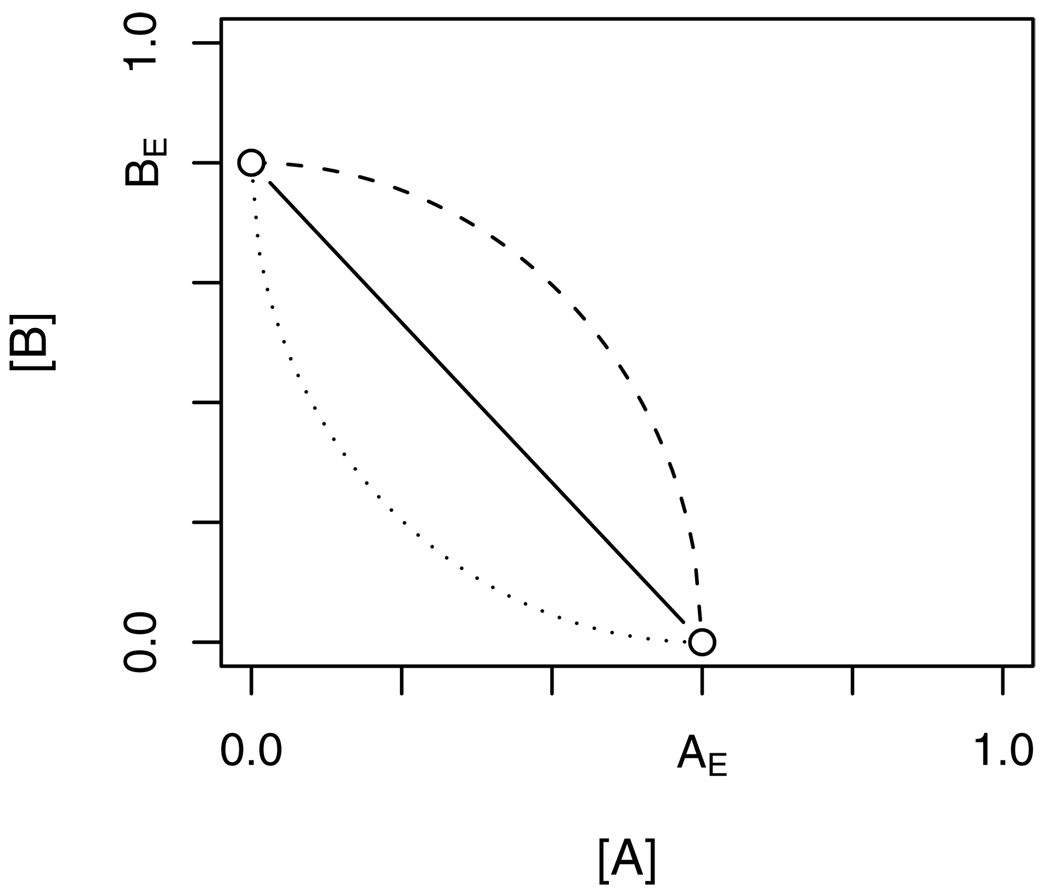
Figure 2.

Construction of isobole from individual agents. [A_E] and [B_E] are concentrations of A and B which, given alone, produce effect level E. The isobole of effect E connects all combination doses ([A],[B]) that also yield E. If A and B are concentration additive, the isobole is linear (solid line; see equation 5). Isoboles curving away from (dashed line) or towards the origin (dotted line) indicate “sub-additive” (antagonistic with respect to CA) or “supra-additive” (synergistic with respect to CA) departures, respectively, from the null model.

When the relative potencies of A and B are identical for every effect level—i.e., when dose-response curves are “parallel,” differing only by a constant factor of potency— [B_E]/[A_E] is a constant, the toxic equivalence factor or TEF (extending the idea beyond its usage for dioxin-like compounds; see Van den Berg et al. 2006). Using B as the reference compound, the joint effect is, from (4):

$$f_{AB}([A],[B])=f_B([B_E])=f_B([B]+\gamma [A]))$$ (6)

where γ=[B_E]/[A_E]. For γ<1, A acts as if it were a diluted form of B. Mathematically, TEFs are a special case of CA where the isoboles are parallel with slope (−γ) (as in Figure 1b). However, some authors define CA as always requiring this narrower assumption of constant relative potency (e.g., van der Hoeven 2004; USEPA 2000). This restriction greatly limits the practical utility of CA. More generally, equation (3) may describe combinations in which [B_E]/[A_E] varies with effect level, producing linear but non-parallel isoboles. Isobole slopes are still negative, since [A_E] and [B_E] are both positive.

In an eye-opening experiment, Silva et al. (2002) showed that a mixture of xenoestrogens evaluated with a reporter assay closely followed concentration addition, but not independent action or effect summation. They also pointed out an important limitation of the CA model: It cannot be applied to effect levels greater than that achieved by any single compound in the mixture. Suppose, for example, that A acts through the same receptor as B but has a smaller maximal effect, i.e., A is a partial agonist relative to B. Then for effect levels between the two maxima, there exists no positive value of [A_E] to use in equation (3). Unfortunately, many compounds of interest are partial agonists; notable examples include many ligands of the aryl hydrocarbon receptor (AhR) (Hestermann et al. 2000). Use of CA or TEF for such systems may not always be appropriate. For example, when using the TEF approach to estimate relative potency values for AhR agonists, an explicit assumption of full efficacy is made for even the lowest-efficacy partial agonist (Horii et al. 2009).

Here we propose an extension of concentration addition to a functional form that allows for the analysis of partial agonists. We examine isobole shapes of combinations of full and partial agonists by applying the new definition to a common dose-response function. Finally, we compare the joint effects and isobole shapes thus derived to those derived by using simple mechanistic models of receptor systems.

Results

A. Generalizing CA using inverse functions

As we have seen, CA cannot model combinations that include partial agonists (Silva 2002). This problem is most evident when considering isobolograms constructed from empirical data. In its usual interpretation, the CA equation (3) describes a line that connects the observed concentration of A that produces effect level E, [A_E], with the observed concentration of B yielding the same response, [B_E]. All combination doses ([A],[B]) lying on this line produce the same effect E, including the intercepts, the special combination doses ([A_E],0) and (0,[B_E]) (Figure 2). As [A_E] and [B_E] are empirical values, they are implicitly assumed to be positive; therefore, all isoboles obeying concentration addition must be negatively sloped. Conversely, if the combination doses ([A],[B]) yielding the same effect level are all observed to lie on a negatively-sloped line, one infers that the compounds are concentration additive.

However, suppose that a partial agonist A has (for example) 25% of the efficacy of full agonist B. Then there is no observed value of [A_E] for any effect level E>0.25, and, consequently, no way to draw the isobole. This is a problem if we rely on positive values of [A_E] based on observed data alone. However, toxicologists can often characterize the dose-response relationship as a mathematical function E = f_A([A]) with a great deal of confidence. In addition to a good empirical fit to a function, there may be strong theoretical reasons to expect a particular form of the dose-response relationship, as for example a dose-response curve derived from a mechanistic model of the system under study. Now suppose that the inverse function [A_E] = f_A⁻¹(E) exists for values of E between zero and the maximum value achieved by the full agonist B. (We might generalize this somewhat to require only piecewise invertibility to handle nonmonotonic functions). We obtain the functional form of concentration addition by substituting the inverse function for [A_E]:

$$\frac{[A]}{f_A^{-1}(E)}+\frac{[B]}{f_B^{-1}(E)}=1$$ (7)

To make the equation symmetrical, we’ve also assumed that the dose-response function for the B is invertible over the same range. While one can switch the role of A and B, here we will always assume that B is a full agonist.

Equation (7), which we’ll call generalized concentration addition (GCA), has a key conceptual difference from (3). Rather than relying on observed values of [A_E] and [B_E] to draw the expected isoboles assuming CA, we use empirical values to fit dose-response functions f_A([A]) and f_B([B]), and then predict the joint response using the inverse functions. How is this any different from CA, equation (3)? We’ve assumed that [A_E] = f_A⁻¹(E) exists for values of E between zero and the maximum value achieved by the full agonist B. The consequence is that [A_E] may now be negative. As we will see, this poses no conceptual difficulty: The denominators in (7) represent only the intercepts of the isoboles with the A and B axes; these values need not be observable to be calculated. Provided that the assumptions are met, the isoboles described by (7) can be drawn and must be linear; this is true even if an intercept is negative, as demonstrated by Figure 3. The actual concentrations [A] and [B] used in (7) must, of course, be non-negative. By relaxing the constraint on the sign of [A_E], we’ll see that we can generate linear isoboles with negative or positive slope, enabling us to model combinations of full and partial agonists.

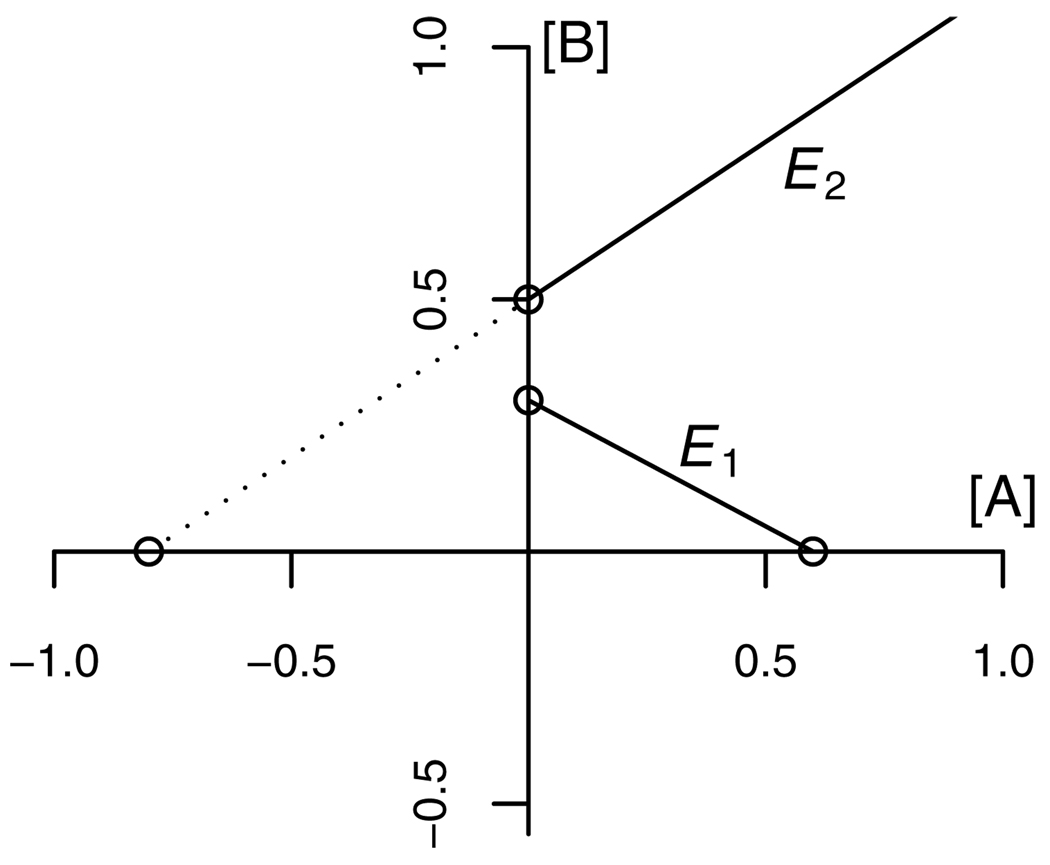
Figure 3.

Construction of the isobologram when A is a partial agonist relative to B. For a given effect level E, the GCA equation (7) describes an isobole which is linear with an intercept along the A-axis given by f_A⁻¹(E). Let α_A and α_B be the maximal effect levels of the two compounds. For effect levels E<α_A<α_Bf_A⁻¹(E) is a positive number ([A_E] in equation 3). Then the A-intercept of the isobole is positive and the isobole has a negative slope, as shown here for isobole E₁. Suppose that for effect levels α_A<E<α_Bf_A⁻¹(E) is negative. Then the A-intercept of the isobole is negative and the isobole has a positive slope, as shown here for isobole E₂.

B. Combinations of full and partial agonists

The generalized definition of concentration addition is not useful unless there exist dose-response functions that meet the assumptions regarding inverse functions. Here we present one such system.

One of the most common dose-response curves in toxicology and pharmacology is the Hill function with slope parameter 1:

$$E=f_A([A])=\frac{{\alpha }_A[A]}{[A]+K_A}$$ (8)

where K_A is the EC₅₀ and α_A is the maximal agonist effect, the largest response a ligand can produce in a tissue expressed as a fraction of that achievable by a full agonist of the same receptor; α thus varies between zero and one (Jenkinson et al. 1995). The Hill function is very commonly fit to empirical data. As we will discuss later, the same function can be derived from simple equilibrium models of receptor systems, providing a theoretical foundation for this choice of dose-response relationship.

Assume two agonists A and B have dose-response curves given by Equation (8). Without loss of generality, suppose that A has a smaller maximal agonist effect than B, i.e., 0<α_A<α_B. We may thus regard A as a partial agonist relative to B. We invert the dose-response functions:

$$\begin{array}{cc}[A_E]=f_A^{-1}(E)=\frac{K_{A}E}{{\alpha }_A-E}& [B_E]=f_B^{-1}(E)=\frac{K_{B}E}{{\alpha }_B-E}\end{array}$$ (9)

Importantly, the inverse functions exist for all E except for the asymptotes, where the agonist concentration becomes infinite. Substituting these expressions into the GCA equation (7), we obtain:

$$\frac{[A]({\alpha }_A-E)}{K_{A}E}+\frac{[B]({\alpha }_B-E)}{K_{B}E}=1$$ (10)

The equation for the isoboles is easily derived directly from (10):

$$[B]=\frac{E{K}_B}{{\alpha }_B-E}-\left(\frac{K_B}{K_A}\right)\left(\frac{{\alpha }_A-E}{{\alpha }_B-E}\right)[A]$$ (11)

We may also derive the joint effect function by solving (10) for E:

$$E=f_{AB}([A],[B])=\frac{{\alpha }_A\frac{[A]}{K_A}+{\alpha }_B\frac{[B]}{K_B}}{1+\frac{[A]}{K_A}+\frac{[B]}{K_B}}$$ (12)

The isobole equation (11) is the equation of a line (that is, one line for every value of E); isoboles of this concentration-additive combination must always be linear. For effect levels below the maximum of the partial agonist, 0<E<α_A, the isobole slopes are negative; this corresponds to the usual definition of concentration addition. However, these isoboles need not be parallel, i.e., this is not restricted to the TEF case. As E approaches the maximum of the partial agonist α_A, the isobole slopes approach the horizontal. For effect levels above the maximum effect of the partial agonist, α_A<E<α_B, the isobole slopes become positive (Figure 4). When α_A=α_B, we have two full agonists with parallel dose-response curves: all isoboles are linear with the same negative slope -K_B/K_A, i.e, the TEF case. In this situation, GCA and CA are equivalent.

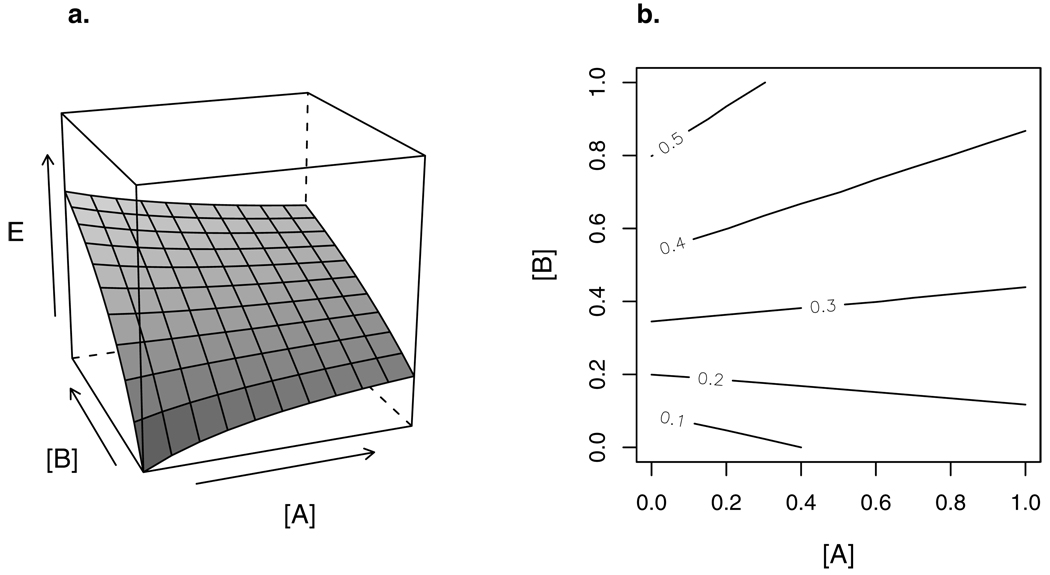
Figure 4.

(a) Response surface of a combination of full agonist B with partial agonist A. At low concentrations, A adds to the effect produced by B. At large concentrations, A competes with B for receptors, lowering the joint effect.

(b) Isoboles of the response surface in (a). The isoboles are always linear, but switch from negative to positive slope as the maximal effect of partial agonist A (here, α_A=0.25) is exceeded.

Our example shows that GCA may be used to make predictions regarding combinations of full and partial agonists, at least for Hill functions with slope factor n=1. In contrast to CA (equation 3), GCA (equation 7) allows isoboles of both negative and positive slopes.

C. Mechanistic models for combination experiments

One way to evaluate the usefulness of GCA is to examine plausible model systems where we know explicitly both the individual (marginal) dose-response curves and the effect of combination doses, i.e., the interior points on the response surface. We can then compare joint effects in the model system with those predicted by substituting the individual dose-response curves into the GCA equation. Models for the equilibrium kinetics of ligand-receptor systems provide a good starting point. Such models have wide application and are well developed for both partial and full agonists (Foreman and Johansen 2003; Kenakin 1997), allowing prediction of the binding and activation of the receptor population by multiple ligands. We will assume here that all effects of the ligands occur via the modeled receptors, that all receptors are identical, and that no other mechanisms exist to connect the exposures to the effect.

Full Agonists

We begin with a very simple kinetic model for two full agonists ligands A and B interacting with a receptor R that has a single binding site:

$$\begin{array}{cc}A+R\iff AR& B+R\end{array}\iff BR$$ (13)

where AR and BR are receptor-ligand complexes. At equilibrium, we have

$$\begin{array}{cc}{K}_A=\frac{[A][R]}{[AR]}& K_B=\frac{[B][R]}{[BR]}\end{array}$$ (14)

where K_A and K_B are the equilibrium dissociation constants. Assuming that the total concentration of receptors [R₀] is fixed, mass balance tells us

$$[R_0]=[R]+[AR]+[BR]$$ (15)

The simplest model of receptor action is occupancy theory: the effect E is directly proportional to the concentration of occupied receptors (Kenakin 1997). Assuming that AR and BR are equally effective, the total effect of A and B is simply [AR] + [BR], with maximal effect [R₀]. Here [R₀] acts as a biological parameter, the concentration of receptors in the tissue being modeled. We scale the effect to vary from zero to one by dividing by [R₀]. The joint effect of A and B is then given by

$$E=f_{AB}([A],[B])=\frac{[AR]+[BR]}{[R_0]}=\frac{\frac{[A]}{K_A}+\frac{[B]}{K_B}}{1+\frac{[A]}{K_A}+\frac{[B]}{K_B}}$$ (16)

An early derivation is given by Ariëns (1964). The marginal dose response curves can be derived from (16) by setting the concentration of one ligand to zero:

$$\begin{array}{c}{f}_A([A])=f_{AB}([A],0)=\frac{A/K_A}{1+A/K_A}=\frac{A}{K_A+A}\hfill \\ f_B([B])=f_{AB}(0,[B])=\frac{B/K_B}{1+B/K_B}=\frac{B}{K_B+B}\hfill \end{array}$$ (17)

This simple mechanistic model produces the same individual dose-response curves we used earlier (8) with the simplification that α_A=α_B=1. Similarly, the joint effects of the mechanistic model (16) are equivalent to those predicted by GCA (12). Solving (16) for [B], the isoboles of this system are

$$[B]=\frac{K_{B}E}{1-E}-\left(\frac{K_B}{K_A}\right)[A]$$ (18)

As the isoboles are all negatively sloped lines, the system obeys concentration addition (a special case of GCA). Indeed, it has a TEF equal to K_B/K_A, a consequence of the ligands differing only in their relative affinities. While no explicit assumption of CA was made in the derivation of (18), similarity of action may be implied by addition of liganded receptors in (16); this is consistent with the idea that CA is most appropriate for compounds that act via similar mechanisms. The equivalence of the joint effect function derived from the mechanistic model (16) with the GCA (or CA) approach for two full agonists (12) indicates the reasonableness of the latter approach. The occupancy theory model is limited, however, in that while the affinity of each ligand for the receptor can vary (via K_A and K_B), the ligands have equal maximal effects.

Competitive Antagonists

The kinetic model used above for full agonists is nearly identical to that commonly used in describing the action of a pure competitive antagonist, i.e., a compound that does not cause the effect but competes with agonists for receptor sites (Pratt and Taylor 1990). Consider compound A to be the antagonist. Since only the BR complex leads to effects, we simplify equation (16):

$$E=\frac{[BR]}{[R_0]}=\frac{\frac{[B]}{K_B}}{1+\frac{[A]}{K_A}+\frac{[B]}{K_B}}=\frac{[B]}{[B]+K_B(1+[A]/K_A)}$$ (19)

Compared with (16), only [B] remains in the numerator. This is the well-known Gaddum equation for a competitive antagonist (Kenakin 1997). The isoboles for this system are given by

$$[B]=\frac{K_{B}E}{1-E}+\left(\frac{E}{1-E}\right)\left(\frac{K_B}{K_A}\right)[A]$$ (20)

Isoboles described by (20) are linear; interestingly, since the A-intercept of (20) is always negative (−K_A), these isoboles always have positive slopes (Figure 5). The slopes vary, increasing as E approaches 1: that is, as more antagonist A is added, a larger dose of agonist B is required to maintain the same effect level. Competitive antagonists in this system thus share an important property with concentration-additive full agonists: both have linear isoboles. Although concentration addition is not ordinarily applied to competitive antagonists, Equation (19) can be derived from Equation (12) by setting the efficacy of the partial agonist α_A = 0, with α_B = 1.

Figure 5.

(a) Response surface of a combination of full agonist B with competitive antagonist A.

(b) Isoboles of the response surface in (a). Isoboles are linear with positive slope.

Partial agonists

Modeling of partial agonists requires more sophisticated assumptions than the occupancy model: in addition to setting the affinity of the ligand, we must also be able to set its maximal response. There is a clear separation in experimental data between affinity and efficacy, even though one might expect a relationship between the molecular forces governing ligand binding and those controlling the conformational changes of the receptor presumably required to cause an effect (Kenakin and Onaran 2002). One simple approach (Ariëns et al. 1956) begins with equations (14–15), but makes the assumption that the total effect is given by α_A[AR] + α_B[BR]:

$$E=f_{AB}([A]),[B])=\frac{{\alpha }_A[AR]+{\alpha }_B[BR]}{[R_0]}=\frac{{\alpha }_A\frac{[A]}{K_A}+{\alpha }_B\frac{[B]}{K_B}}{1+\frac{[A]}{K_A}+\frac{[B]}{K_B}}$$ (21)

This model, sometimes called “competitive agonism,” has been used to describe certain mixtures, for example, joint exposures of solvents on irritation of nasal passages in mice (Nielsen et al. 1988) and in rats (Cassee et al. 1996).

While allowing for partial agonism, (21) does not provide a mechanistic basis for the proportionality constants α_A and α_B. A number of mechanistic models are available to solve this problem. We will use the del Castillo–Katz model because of its mathematical simplicity; this model was originally developed to describe the behavior of nicotinic receptors where the liganded receptor switches between active and inactive states (Foreman and Johansen 2003). To our previous model for agonists we add an activation step that converts the ligand-receptor complex AR to its active form AR*. The kinetic scheme for a single ligand is

$$A+R\iff AR\iff {AR}^{*}$$ (22)

with mass balance equation and equilibrium constants

$$\begin{array}{c}[R_0]=[R]+[AR]+[{AR}^{*}]\hfill \\ K_A=\frac{[A][R]}{[AR]}{K}_{A^{*}}=\frac{[AR]}{[{AR}^{*}]}\hfill \end{array}$$ (23)

Assuming that the effect is proportional to the concentration of activated receptor [AR*], we obtain

$$\begin{array}{cc}E\hfill & =f_A([A])=\frac{[{AR}^{*}]}{[R_0]}=\frac{\frac{[A]}{K_A{K}_{A^{*}}}}{1+\frac{[A]}{K_A}\left(\frac{1+K_{A^{*}}}{K_{A^{*}}}\right)}\hfill \\ \hfill & =\frac{{\alpha }_A[A]/{K\prime }_A}{1+[A]/{K\prime }_A}=\frac{{\alpha }_A[A]}{{K\prime }_A+[A]}\hfill \end{array}$$ (24)

where we have defined the maximal agonist effect α_A and the macroscopic dissociation equilibrium constant K'_A as

$$\begin{array}{c}{\alpha }_A=\frac{1}{1+K_{A^{*}}}\hfill \\ {K\prime }_A=\frac{K_A{K}_{A^{*}}}{1+K_{A^{*}}}\hfill \end{array}$$ (25)

The individual dose-response described by equation (24) is also a Hill function with a slope parameter of one. The notable difference compared with (17) is the presence of the maximal effect α_A which, depending on K_A*, can range from zero to one (small values of K_A* favor the activation state and increase maximal effect). The del Castillo–Katz model thus provides a mechanistic model for partial agonism. The constant K'_A, interpretable as a macroscopic ligand-binding affinity, depends on both the microscopic dissociation constant K_A and the activation constant K_A*; the maximal effect α_A, or efficacy, is related only to the likelihood of the transition to the active state. The affinity and efficacy of a ligand are thus clearly separated in this model. Because the effect in (24) has been normalized to [R₀], the ligand-dependent maximal effect α_A is only the maximum possible in the specific tissue in question. Different tissues, with different values of [R₀], may have different absolute effects.

To find the joint effect of A and B under the del Castillo–Katz model, we broaden the scheme to two ligands, where each receptor-ligand complex requires an activation stage, and we extend the mass balance and equilibrium equation (23) to include B, obtaining

$$\begin{array}{cc}E\hfill & =f_{AB}([A],[B])=\frac{[{AR}^{*}]+[{BR}^{*}]}{[R_0]}=\frac{\frac{[A]}{K_A{K}_{A^{*}}}+\frac{[B]}{K_B{K}_{B^{*}}}}{1+\frac{[A]}{K_A}\left(\frac{1+K_{A^{*}}}{K_{A^{*}}}\right)+\frac{[B]}{K_B}\left(\frac{1+K_{B^{*}}}{K_{B^{*}}}\right)}\hfill \\ \hfill & =\frac{{\alpha }_A\frac{[A]}{{K\prime }_A}+{\alpha }_B\frac{[B]}{{K\prime }_B}}{1+\frac{[A]}{{K\prime }_A}+\frac{[B]}{{K\prime }_B}}\hfill \end{array}$$ (26)

where α_B and K'_B are defined in the same way as α_A and K'_A. Equation (26) is functionally equivalent to (21), differing only in the interpretation of the parameters. Most importantly, equation (21) and equation (26) are equivalent to the joint effect derived earlier by applying GCA to Hill functions with slope parameter of one (12). Hence, the isobole equation derived from (26) is equivalent to that derived earlier (11), with the reparameterization of the dissociation constants. This equivalence strongly suggests that GCA provides a useful approach to predicting the effects of mixtures of full and partial agonists acting by similar mechanisms.

As described earlier, the combination of a full and partial agonist has negatively sloped isoboles when E < α_A, an asymptote when E = α_A, and positively sloped isoboles for α_A ≤ E ≤ α_B (Figure 4). Equation (26) encompasses the full agonist model (16) and the competitive antagonist model (19) as special cases, via α_A=α_B and α_A=0, respectively. The patterns of isoboles produced by the various cases are described in Table 1.

Table 1.

Isoboles shapes for special cases of combinations of agents described by Hillfunctions with slope parameter of one

Case	Slopes of isoboles*
Concentration addition	Negative, not necessarily equal
TEFs	Negative and equal
Competitive antagonism	Positive
Partial agonist	Negative below maximal effect level of partial agonist; positive above

^*All isoboles are linear.

Discussion

We noted earlier two problems with the use of the CA model. First, some authors state that concentration addition holds only for parallel dose-response curves, i.e., the TEF case. However, when restricted to effect levels below the maximal effect of the partial agonist, isoboles of the partial agonism model (12, 26) are linear and negatively sloped but not parallel. This demonstrates that CA, in its usual form as defined by (3), can indeed apply to some non-TEF cases.

The second problem is the inability of concentration addition to model partial agonists. For effect levels above the maximum of the partial agonist A, no observed (positive) value of [A_E] exists. We have shown that this problem can be solved by generalizing CA using inverse functions (7). This approach requires confidence about the functional form of the dose-response curves and that these functions are invertible over the relevant range of effect. While CA produces linear isoboles of negative slope, GCA can produce linear isoboles with slopes of any sign. Conversely, since equation (7) is very general, it seems likely that any mixture possessing linear isoboles obeys GCA, regardless of the signs of the isobole slopes. Special cases of GCA include concentration addition as well as the TEF approach, itself a special case of CA.

We showed that GCA is not just a theoretical construct but can be applied to partial agonists modeled using a common dose response curve: Hill equations with slope parameter of one. This function is commonly applied to a wide number of diverse toxicants, notably including dioxin and other agonists of the AhR (Toyoshiba et al. 2004). Although often used empirically, the Hill equation with n=1 has a mechanistic basis in models of single-binding-site receptor systems like the AhR, as we have seen (equation 17, equation 24). In deriving these models, we have shown that the joint effects for these model systems were identical to those predicted by generalized concentration addition for the empirical Hill dose-response. These mechanistic models therefore provide strong support for the utility of the GCA model.

The mechanistic models also provide insight into the pattern of isobole slopes generated by combinations of full and partial agonists. In our kinetic models, mixtures of full agonists obeying concentration addition had negatively-sloped linear isoboles, while competitive antagonists had positively sloped linear isoboles (Table 1). It is therefore reasonable that mixtures of partial and full agonists have linear isoboles that are negatively sloped when the partial agonist contributes to the response, but positively sloped when the partial agonist cannot add to the effect but still competes with full agonists for receptors. Indeed, a competitive antagonist can be thought of as a special case of partial agonism where its maximal effect is zero. The idea that partial agonists competitively antagonize full agonists is not new. According to Goldstein, “The efficacy concept implies that partial agonists should have antagonist properties. Since they occupy receptor sites, yet produce only weak effects of their own, they should prevent access of strong agonists to these sites” (Goldstein et al. 1974). Ariëns referred to this property of partial agonists as “competitive dualism” (Ariëns 1964). For example, the effect of a full muscarinic agonist on isolated rat jejunum is competitively antagonized by the addition of a partial agonist (Figure 6). When transformed into a response surface and an isobologram, the data appear to match our model (Figure 7). Similarly, the competitive agonism model (equation 21), which we have shown can be derived via GCA (equation 26), has been used to describe respiratory irritation in rats exposed to a combination of full and partial agonist solvents (Cassee et al. 1996). Despite this longstanding knowledge of the dual nature of partial agonists, however, none of the existing null models for interaction—neither ES, IA, the TEF method, nor CA—can describe the competitive antagonistic effect of the partial agonist on the full agonist: In all of these models, the joint effect f_AB([A],[B]) can never be less than the effect due to the full agonist f_B([B]) alone.

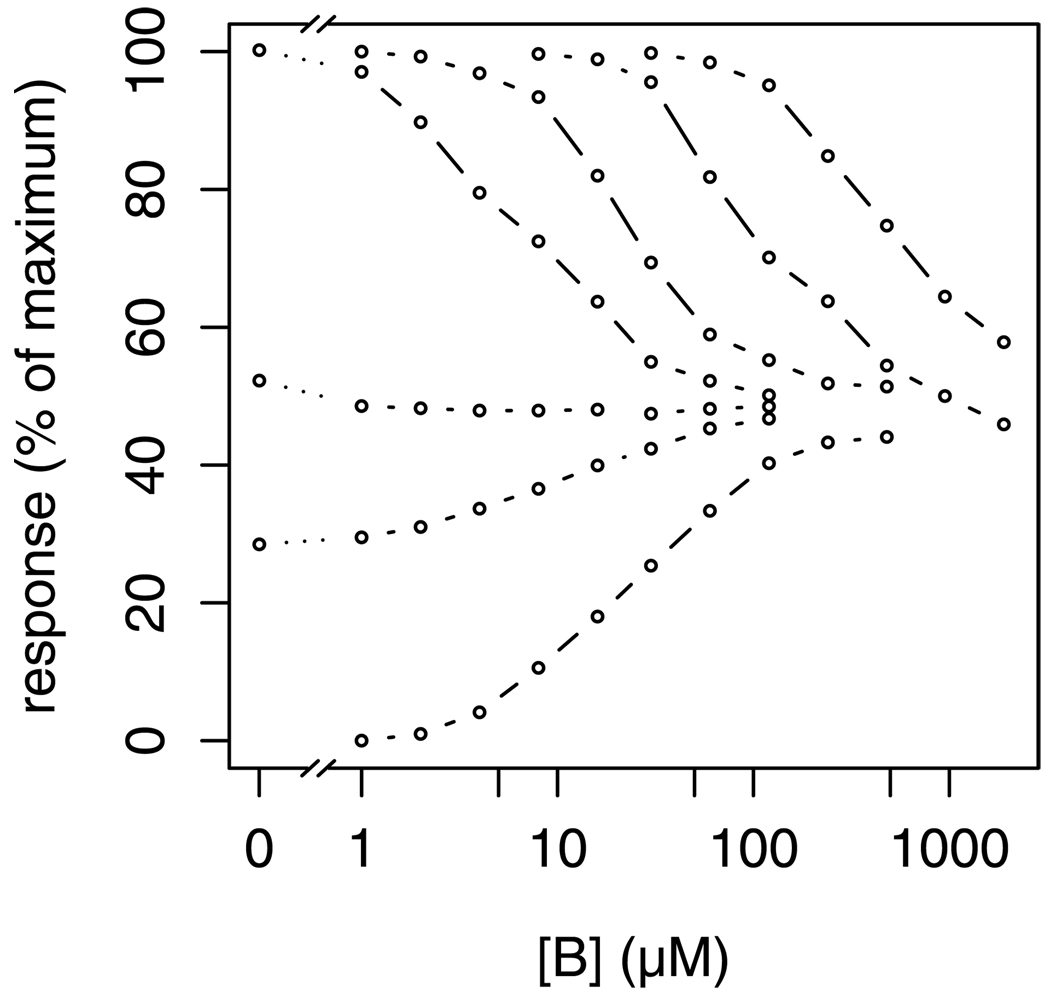
Figure 6.

Combination experiment of a partial agonist (B, on the x-axis) with a full agonist A. Curves indicate concentrations of A, from top, 2048, 512, 128, 32, 4, 2, and 0 µM. Response is percent of maximal contraction of isolated rat jejunum. Data are from Goldstein et al. 1974.

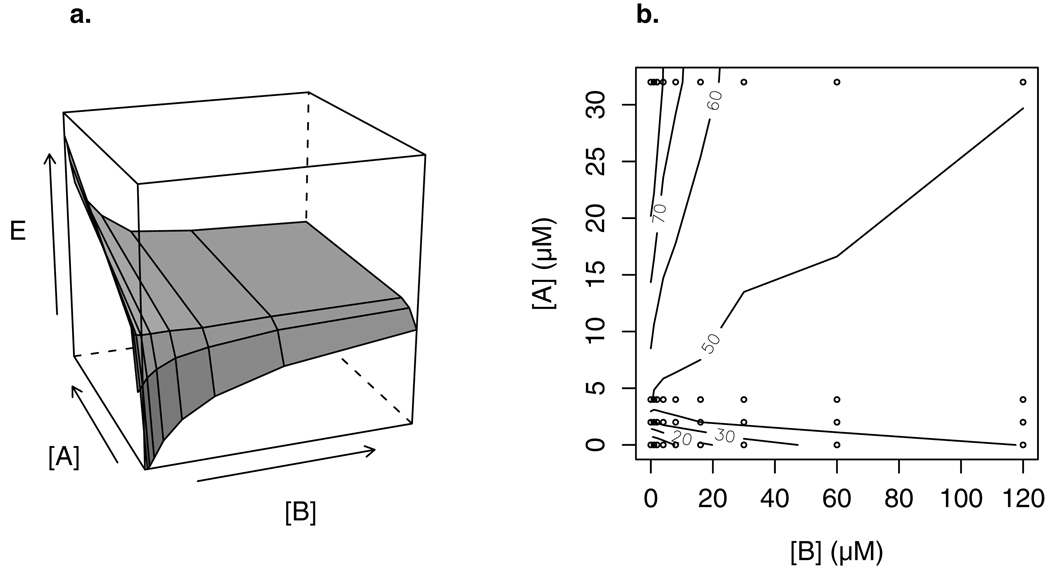
Figure 7.

(a) Response surface of the combination of two muscarinic agonists from the data in Figure 6: Full agonist A and partial agonist B.

(b) Isobologram of the response surface in (a), generated by plotting isoboles with the contour() function in R (www.r-project.org, version 2.4.1). The [A] and [B] ranges are the same as in (a); labels on isoboles are percent response. Isoboles switch from negatively to positively sloped as the effect level exceeds the maximal effect of the partial agonist B (about 44%, corresponding to a concentration of about 4 µM of full agonist A). Data points from Figure 6 are given by circles; isoboles are interpolated at all other points. Due to the large range of concentrations in the original data, only a part of the full combination space of Figure 6 is shown.

A prominent example of the problem of partial agonist mixtures lies in the TEF approach to dioxin-like agents. It has long been recognized that the TEF assumption of parallel dose-response curves may not be appropriate for some polychlorinated biphenyls (PCBs). At some doses, both individual PCB congeners and Aroclor mixtures have been shown to antagonize the AhR activity of full agonists like tetrachlorodibenzodioxin (TCDD) (Safe 1998; Aarts et al. 1995). Yet the TEF method assumes that all agonists have the same maximal effect as TCDD, even for partial agonists of very low efficacy (Horii et al. 2009). A GCA approach to mixtures of AhR ligands, by contrast, would provide for proper modeling of partial agonists, allowing the observed antagonism by low-efficacy AhR agonists.

The equivalence of the mechanistic models for partial agonists and the predictions of GCA sheds additional light on the meaning of GCA as a null model of interaction. If partial agonists are acting as antagonists above their maximal effect level—with competitive antagonists as an extreme version—then the ability of a null model like GCA to predict these outcomes indicates that competitive antagonism can be viewed as non-interactive. This suggests that “similarity of action” needs to be viewed more broadly than previously. The similarity of action in our mechanistic models may reside in the binding of ligands at a single site. Comparison of other, more complicated mechanistic models with the predictions of GCA appears to be a useful strategy.

For dose-response curves based on Hill equations with slope parameter of one, we found that mixtures of partial and full agonists had linear isoboles with varying slopes. Our conclusions differ from a recent paper by Grabovsky and Tallarida (2004) that found curved isoboles for mixtures of partial and full agonists obeying the same functions. We concur with a letter that questions that derivation (Lorenzo and Sanchez-Marin 2006), and provide here a counter-example. Equation (12) and Equation (26) provide a model for the combination of a partial and a full agonist that, as we have shown, has linear isoboles. The procedure of Grabovsky and Tallarida (2004) begins by assuming that a dose [B′] exists such that the combination dose ([A], [B]) is equivalent to the single-agent dose [B]+[B′]. From the marginal concentration-response curve (24), we find the dose [B′] that gives the same response as [A]:

$$\begin{array}{c}{f}_A([A])=\frac{{\alpha }_A[A]}{{K\prime }_A+[A]}=\frac{{\alpha }_B[B\prime ]}{{K\prime }_B+[B\prime ]}=f_B([B\prime ])\hfill \\ [B\prime ]=\frac{{\alpha }_A{K\prime }_B[A]}{{\alpha }_B{K\prime }_A+({\alpha }_B-{\alpha }_A)[A]}\hfill \end{array}$$ (27)

Again following Grabovsky and Tallarida, assume that the effect of the mixture of A and B is given by f_B([B]+[B′]):

$$f_{AB}([A],[B])=f_B([B]+[B\prime ])$$ (28)

Inserting (27) into the right-hand side of (28) yields

$$\begin{array}{cc}{f}_B([B]+[B\prime ])\hfill & =\frac{([B]+[B\prime ]){\alpha }_B}{{K\prime }_B+([B]+[B\prime ])}\hfill \\ \hfill & =\frac{{\alpha }_A{\alpha }_B{K\prime }_B[A]+{\alpha }_B^2{K\prime }_A[B]+{\alpha }_B({\alpha }_B-{\alpha }_A)[A][B]}{{\alpha }_B{K\prime }_B[A]+{\alpha }_B{K\prime }_A[B]+({\alpha }_B-{\alpha }_A)[A][B]+{\alpha }_B{K\prime }_A{K\prime }_B}\hfill \end{array}$$ (29)

Equation (29) generates curved isoboles. Under what conditions does this procedure yield the same result as (26), that is, does the assumption (28) hold? Substituting (26) into the left-hand side of (28), and for simplicity, setting K’_A=K’_B=1, we obtain:

$$[A][B]({\alpha }_A-{\alpha }_B)([A]({\alpha }_A-{\alpha }_B)-{\alpha }_B)=0$$ (30)

Solutions to (30) are limited: [A]=0 or [B]=0 (i.e., individual exposures given alone); α_A=α_B(i.e., A and B have the same maximum effect); and for combinations where [A] = α_B/(α_A − α_B). We conclude that the assumption f_AB([A], [B]) = f_B([B]+[B′]), cannot, in general, be used to derive the joint concentration-response surface and shapes of isoboles.

We believe that GCA may be useful in at least two ways: i) Providing a null model for predicting the effects of mixtures when there is strong confidence regarding the functional form of the marginal concentration-response curves; ii) Generating hypotheses regarding the mechanistic basis of mixtures by examining the linearity and slope pattern of the isoboles generated by empirical data. Numerous methods have been deployed in testing concentration additivity of mixtures, and most should apply equally well to GCA. The method of isoboles, illustrated in Figure 7, examines the shape of isoboles. This approach requires relatively few data points, making it appropriate for many existing datasets. Response surface analysis (Greco et al. 1995) is more data intensive, requiring careful spacing of a large number of repeated combination doses to construct a smooth surface. But comparison of observed and expected surfaces (generated using a null model such as GCA) is amenable to statistical hypothesis testing. Such data may often be generated with in vitro assays using automated experimental systems like plate readers. In either case, the straightness of the GCA isoboles applies only on arithmetic plots. Optimal experimental designs for testing GCA (or CA) models require dosing over a narrower range of arithmetically-spaced doses, rather than the more common logarithmic spacing. Numerous other designs for testing CA, like the ray design used by Silva et al. (2002), will also have direct application to GCA. Finally, although we have examined models for only two compounds, the equations for CA (3) and GCA (7) are easily extended to numerous compounds.

GCA, like CA, is a definition of non-interaction, not a mechanistic model. We examined the del Castillo–Katz mechanistic model of partial agonism because of its mathematical simplicity. The more widely used operational model assumes a hyperbolic transducer function linking receptor binding to activation (Black and Leff 1983). Isoboles of mixtures of full and partial agonists derived under the operational model follow the same general pattern as the results shown here: linear isoboles that switch from negative to positive slope as the joint effect exceeds the maximal effect of the partial agonist. Single-receptor systems like the del Castillo and Katz and operational models are plausible descriptions of diverse effects ranging from nasal irritation by solvents (Cassee et al. 1996) to the action of dioxin-like chemicals (Hestermann et al. 2000). For many systems like these, GCA should provide an accurate description.

Both models lend themselves to simple mechanistic interpretations of partial agonism. In the del Castillo-Katz model, efficacy is determined by the reversible transition of the liganded receptor to an active state. In the operational model, efficacy is determined by reversible binding of the liganded receptor to a third object: for example, the responsive element of a gene. While these are plausible ways of modeling partial agonists or competitive antagonists, there are other possibilities, for example, steady-state ternary complex models (Kenakin and Onaran 2002). In addition, non-reversible and non-competitive types of antagonism exist. Whether the GCA null model describes these other models is an open question, although we suggest that GCA might still provide an improved default model in situations where mechanism is unknown.

Both the del Castillo–Katz and the operational models result in dose-response curves that are Hill functions with slope parameter of one; research is needed on other dose-response functions and the details of their isobole patterns. The assumptions required for GCA may not always be met. For example, the inverse of a Hill function with slope parameter two does not generate real numbers for effects greater than the maximal effect level. We are currently addressing this issue using alternative mechanistically-based models. Where detailed mechanistic information is available, mechanistic models should provide a better-informed basis for predicting joint effects. GCA may, however, be a useful approach for similarly-acting compounds whose dose-response curves have been characterized but whose mechanisms are not well known, mixtures of which may include full agonists, partial agonists, and competitive antagonists. This flexibility can provide a simple tool for hazard assessment that is applicable in many situations in which traditional concentration addition (or a TEF model) is not appropriate.

The simple mechanistic models we derived ignore factors downstream of receptor activation, processes that are likely to be complex in any real system. We believe this problem to be less important then usually thought. Consider the isobole for effect level E caused by the joint action f_AB([A], [B]) of two ligands. Many further steps will likely follow before the ultimate effect E’ is realized. Suppose, however, that we can represent E’ as a function g(.), possibly unknown, of the initial effect E. The ultimate effect E′=g(E)=g(f_AB([A], [B])), depends only on the value of E. All points ([A], [B]) along the isobole—each causing effect level E—will then also lead to the ultimate effect E′, preserving the shape of the isobole. Although the response surface may be distorted vertically, the level sets of the surface are unchanged, and isoboles of E will also be isoboles of E′. This argument requires that all action by the ligands be mediated by the receptor system alone, potentially limiting applicability to certain dose ranges; in addition, we ignore events upstream from the receptor. Use of these ideas requires careful consideration of the mode of action of the compounds in the mixture.

In summary, we have shown that extension of the concentration addition definition to a functional form allows its use in assessing mixtures that include partial agonists. Generalized concentration addition encompasses combinations with linear isoboles of all slopes, and, like CA, should be broadly applicable for agents acting through similar mechanisms. GCA may prove useful in assessing mixtures of full and partial agonists. For example, GCA may be an improvement over the TEF model in more accurately assessing the toxicity of mixtures that include mono-ortho polychlorinated biphenyls and other partial agonist ligands of the aryl hydrocarbon receptor.