Abstract
In most solid-state NMR experiments, cross-polarization is an essential step to detect low-γ nuclei such as 13C and 15N. In this study, we present a new cross-polarization scheme using spin-locks composed of composite 0° pulses in the RF channels of high-γ and low-γ nuclei to establish the Hartmann-Hahn match. The composite 0° pulses with no net nutation angle {(2π)X −(2π)−X −(2π)Y −(2π)−Y−}n applied simultaneously to both high-γ(I) and low-γ(S) nuclei create an effective heteronuclear dipolar Hamiltonian , which 2 is capable of transferring the Z-component of the I spin magnetization to the Z-component of the S spin magnetization. It also retains a homonuclear dipolar coupling Hamiltonian that enables the flip-flop transfer among abundant spins. While our experimental results indicate that the new pulse sequence, called composite zero cross-polarization (COMPOZER-CP) performs well on adamantane, it is expected to be more valuable to study semi-solids like liquid crystalline materials and model lipid membranes. Theoretical analysis of COMPOZER-CP is presented along with experimental results. Our experimental results demonstrate that COMPOZER-CP overcomes the RF field inhomogeneity and Hartmann-Hahn mismatch for static solids. Experimental results comparing the performance of COMPOZER-CP with that of the traditional constant-amplitude CP and rampCP sequences are also presented in this paper.
Keywords: COMPOZER-CP, composite 0° pulse, liquid crystalline materials, lipid membranes
Introduction
Cross-polarization is a routinely used solid-state NMR technique to enhance the sensitivity of low-γ nuclei such as 13C and 15N under static and magic-angle spinning (MAS) experimental conditions. There are a number of studies that have well analyzed the theory underlying the CP phenomenon and the structure of spin Hamiltonians under double spin-lock in CP [1–4]. Several studies have shown that the efficiency of the originally reported CP pulse sequence using cw spin-locking RF irradiation is highly dependent on resonance offset and inhomogeneity of RF field. To overcome these problems, several different types of CP pulse sequences such as CPMOIST [5], VACP [6], rampCP [7], adiabatic-CP [8], and SADIS-CP [9] have been reported in the literatures. There are also other types of CP sequences such as LGCP [10], FFLG-CP [10], CP utilizing offset [11] or time-averaged precession frequency (TAPF) [12] for RF power reduction and WIM-CP [13] that have been demonstrated for additional specific applications. While most of the CP pulse sequences reported so far in the literature have been shown to be useful for studies on a variety of solids, they all have some limitations. By far, the rampCP is the most robust to overcome all of the above-mentioned experimental problems and therefore it is very commonly utilized in solid-state NMR applications. However, it has been noted that the rampCP requires a longer CP contact time, which is not desirable for samples with short T1ρ or samples that deteriorate under RF heating.
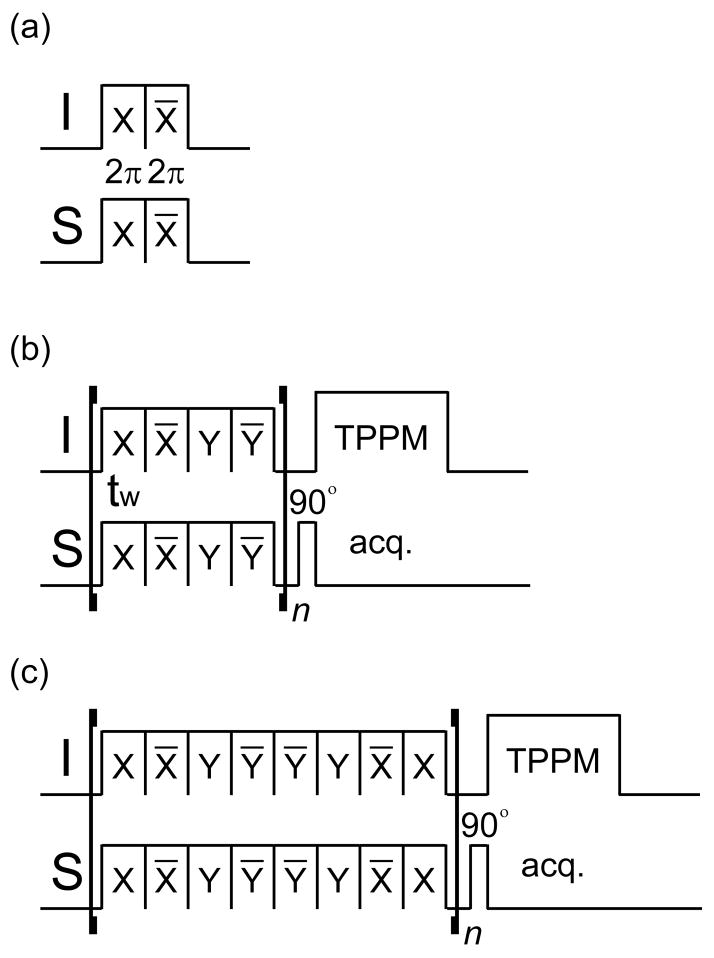
In this work, we have proposed a new cross-polarization pulse sequence using a 2π pulse as a building block. This choice is based on its built-in robustness for RF inhomogeneity as well as RF offset. To enhance these features, we may use a pair of 2π pulses with opposite phases X and −X, that we refer to as a composite 0° pulse (Figure 1a). The pair, however, does not provide the spin-locking field necessary for CP. In the conventional CP sequences mentioned above, transfer of transverse magnetization of heteronuclear spins occurs along the spin-locking RF fields at the X or Y axis in the rotating frame. On the other hand, CP along the Z-axis can be achieved either using WIM-24 spin-lock as in the HIMSELF sequence [14] or by the rotor-synchronized 12-rotor sequence under MAS [15]. In both these methods, an isotropic heteronuclear dipolar coupling Hamiltonian is realized by multiple pulses by suppressing the homonuclear dipolar interaction. While this feature has been well utilized in the line-narrowing studies, it is not useful for other experiments like CP to enhance the sensitivity of rare spins. In this work, we have proposed a new cross-polarization pulse sequence which makes it possible to create the enhanced Z-magnetization of rare spins. We have also explored the possibility of improving the efficiency of cross-polarization particularly for experimental conditions with poor RF field inhomogeneity and Hartmann-Hahn (HH) mismatch. We have designed a spin-lock sequence based on a composite 0° pulse and implemented in the CP pulse sequence for experiments under static experimental conditions (Figs. 1b and c). The cross-polarization efficiency of this new pulse sequence is demonstrated on adamantane. Theoretical treatment and experimental analyses to evaluate the efficiency of the new pulse sequence are reported in this paper.
Figure 1.
Radio frequency pulse sequences for COMPOZER-CP: (a) a pair of two 2 π pulse, (B) the basic COMPOZER-CP, and (C) the supercycled COMPOZER-CP.
Experimental
All experiments were performed on a 300 MHz Chemagnetics/Varian solid-state NMR spectrometer operating at 300.44 and 75.55 MHz for 1H and 13C nuclei respectively. A 5 mm double-resonance Doty MAS probe was used at room temperature. The rf-field intensity for both 1H 90° pulse, 13C 90° pulse and CP was 62.5 kHz, and both the nutation and the phase-modulation angles in the TPPM decoupling [16] were optimized for an RF intensity of ≈ 40 kHz to be 180° and ±7.5°, respectively. The ramping of the spin-lock in rampCP was ±5 kHz. Recycle delay was 2 s for all experiments. The 13C carrier frequency was chosen to be 33.6 ppm from TMS.
Theory
There are several studies that reported the spin Hamiltonians and spin dynamics under CP. Therefore, in this paper, we restrict our theoretical treatment to derive the effective Hamiltonians of hetero- and homonuclear dipolar couplings and the effect of offset under the double spin-lock of COMPOZER-CP sequence (Figure 1).
We consider a heteronuclear two spin system (I and S) under RF irradiation for a static sample. The dipolar interaction between these two spins is given by the Hamiltonian, Hd = dIZ SZ, where d is the dipole coupling constant. For simplicity, we neglect the chemical shift anisotropy interaction for both nuclei and assume the frequencies of the applied RF fields are on-resonance to the respective Larmor frequency of the I and S spins. The relevant Hamiltonian in a frame rotating at its respective Larmor frequency (i.e., the double rotating frame) is given by
| (1) |
where Hrf represents the double RF irradiation along the X axis and it is written as
| (2) |
where ω1I and ω1S are RF field strengths in the I and S nuclear channels, respectively. The evolution of the spin system during the double RF irradiation is defined by the propagator U(t) which is given by
| (3) |
where T is the Dyson time-ordering operator. It is possible to separate the evolution of the spin system under the heteronuclear dipolar interaction from that under the RF interaction as follows:
| (4) |
with
| (5) |
| (6) |
and
| (7) |
This equation signifies the time-dependence of the heteronuclear dipolar interaction due to the RF irradiations, and the time-dependent Hamiltonian can be derived as
| (8) |
Eq. (6) can be expressed by using the Magnus expansion [17] as follows:
| (9) |
| (10) |
| (11) |
The zeroth order average Hamiltonian (Eq. (10)) for an RF-irradiation period tW may be written as follows:
| (12) |
where Σ = ω1I +ω1S and Δ = ω1I − ω1S. For the conventional cross-polarization (CP) experiment at the exact Hartman-Hahn matching condition (Δ= 0), we may choose a cycle time tW to satisfy Σtw = 2nπ (U0 (tc) = U0 (t = 0) =1), where n is an integer. Then, the zeroth-order heteronuclear dipolar coupling Hamiltonian becomes
| (13) |
Since this form of the dipolar coupling Hamiltonian commutes with Hrf, the CP process is defined by to achieve a quasi-stationary spin-state, which is basically the eigen-state of the total Hamiltonian . A double spin-lock under the regular CP therefore transfers the X magnetization of I nuclei to S nuclei and the SX magnetization is detected by decoupling I nuclei.
In this study, we are interested in designing a CP sequence with the composite 0° pulses (2π)X−(2π)−X− as a building block, where (2π)φ denotes that the spin-lock pulse has a 360° flip angle with a phase φ. Since the (2π)X−(2π)−X− sequence does not provide the spin-locking field that can build-up the transverse magnetization, the Z axis for trapping the magnetization can be used. For this to happen, the effective Hamiltonian should have a flip-flop term ( I X SX + I Y SY ). The I X SX term in the Hamiltonian can be generated when the phase of the spin-lock is shifted from X to Y axis at t = tW. Therefore, the basic sequence can be (2π)X−(2π)Y− and the total zeroth order average Hamiltonian for a period t = 0 ~ 2tw becomes
| (14) |
This zeroth-order heteronuclear dipolar coupling Hamiltonian under the new double spin-lock sequence commutes with IZ+SZ but not with IZ−SZ. Therefore, this Hamiltonian brings a quasi-equilibrium longitudinal magnetizations among the I and S spin system. This suggests that it transfers the IZ magnetization to SZ. Furthermore, this double spin-lock sequence does not eliminate homonuclear dipolar interactions. In fact, the homonuclear dipolar Hamiltonian HD = D (3IZ1IZ2I − I12) under the double spin-lock sequence transforms to
| (15) |
at the zeroth order approximation.
Since RF pulses are not perfect, an offset typically deteriorates the efficiency of an RF pulse. Therefore, it is important to evaluate the role of offset during the new heteronuclear double spin-locks. When the RF irradiation is at off-resonance, we need to add the offset Hamiltonian, Hz = ωIIZ + ωS SZ, for both spins in Eq. (1). Then, evolution operator given in Eq. (6) becomes
| (16) |
with the time-dependent offset Hamiltonian as
| (17) |
To simplify the structure of this Hamiltonian, let us omit the offset terms of the S spin. Then the zeroth order average Hamiltonian of the time-dependent I spin offset Hamiltonian, HZ(t) in Eq. (17), for the irradiation period tW becomes:
| (18) |
By applying the above-mentioned cyclic condition of RF spin-lock irradiation ΣtW =2nπ and Δ = 0 to Eq. (18), we find that for even values of n. Therefore, offset effects can be suppressed during the spin-lock irradiation. Further, to reduce the effects of the RF field inhomogeneity, phases of the spin-lock pulses are inverted to generate a spin-lock sequence {(2π)X −(2π)−X −(2π)Y −(2π)−Y−}n. It can be shown that this spin-lock pulse sequence also eliminates the offset and RF field inhomogeneity effects in the S spin channel as well. As shown in Figure 1b, the new spin-lock pulse sequence is applied in both RF channels for the transfer of Z magnetization component from I to S nuclei without the need for a separate preparation pulse in the I spin channel. The net combination of pulses in the spin-lock has a 0° nutation angle and therefore it is named as COMPOZER-CP (composite zero cross-polarization). In Figure 1c, we show the COMPOZER-CP sequence which employs the basic COMPOZER-CP sequence (Figure 1b) as supercycles.
Lastly, we would like to point out that when we interchange the order of the Y and −Y pulses in one of the RF channel, the resulting zeroth order heteronuclear Hamiltonian contains a flop-flop term (IX SX − IY SY ), leading to the transfer of IZ to −SZ. This gives us a chance to examine the relative phases between the I and S channels of our spectrometer. In fact, we realized that the rotational directions of our 1H and 13C pulses, that is, the “naming” the Y and −Y are opposite in our spectrometer.
Results and Discussion
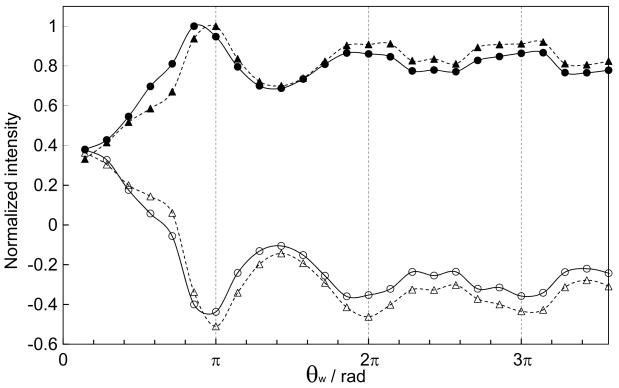
Figure 2 shows the nutation-angle (θw) dependence of the 13C signal intensity of adamantane (stational powder) at a contact time of 1.2 ms, where θw is given as ω1tw in the supercycled COMPOZER-CP (Figure 1c). Since we have not suppressed the 13C longitudinal magnetization before the application of the COMPOZER-CP sequence, the intensities at θw = 0 are not zero. It is shown that the application of the supercycled COMPOZER-CP sequence leads the −Z magnetization (the open circles and triangles), showing the definition of the pulse rotational axis of our 1H and 13C RF channels are opposite. Exchanging the Y and −Y pulses in the 13C channel, the transferred 13C magnetization becomes positive (the closed circles and triangles). These results show that the theoretical treatment presented above is appropriate and both of the flip-flop and flop-flop transitions can be used for CP. Figure 2 also shows that the CP efficiency becomes large, when θw is equal to nπ (n = integer), which is also in agreement with the theoretical prediction. In the experimental results presented below, we used θw = 2 π pulses.
Figure 2.
The nutation-angle (thetas;w) dependence of the 13C signal intensity of a static adamantane sample obtained by the supercycled COMPOZER-CP (Figure 1c). Both of the 1H and the 13C RF intensities were ca. 62.5 kHz, and the nutation-angle (thetas;w = ω1tw) was changed by keeping the total contact time to 1.2 ms. The circles and triangles represent the intensities of CH2 and CH peaks, respectively. The open symbols are the results for the flop-flop transfer, where the applied sequence in the pulse program was {(2π)X−(2π)−X−(2π)Y−(2π)−Y−} in both 1H and 13C rf channels. The filled ones show the flip-flop results, where the sequence was {(2π)X−(2π)−X−(2π)−Y−(2π)Y−} for 1H and {(2π)X−(2π)−X−(2π)Y−(2π)−Y−} for 13C. Apparently the rotational axis for both channels are opposite in the spectrometer used in this study. The signal intensities were normalized by the maximum intensity of the CH2 or CH peak obtained in a flip-flop experiment. The solid and dotted lines are for eye guidance.
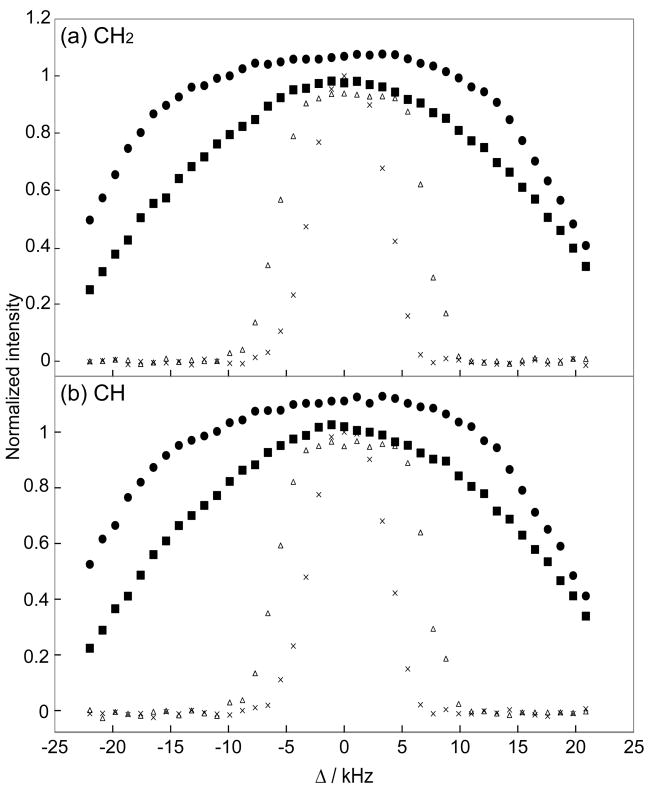
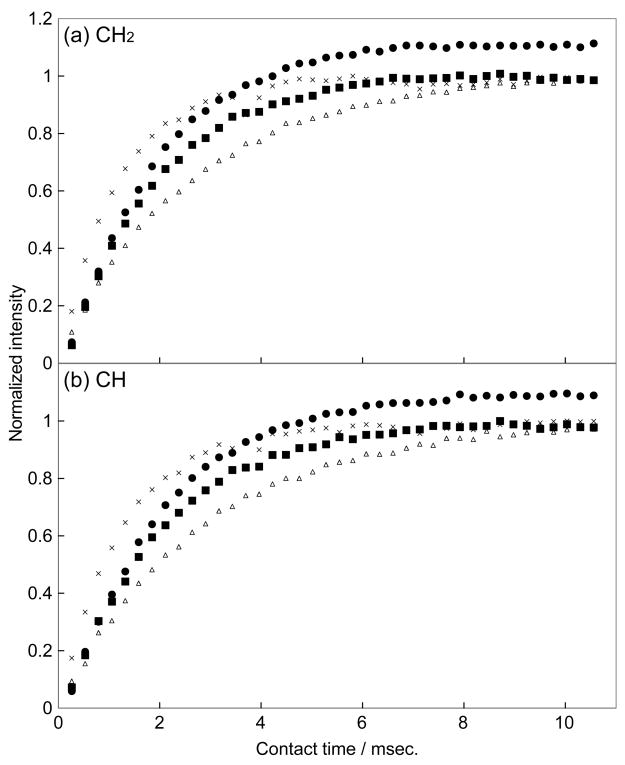
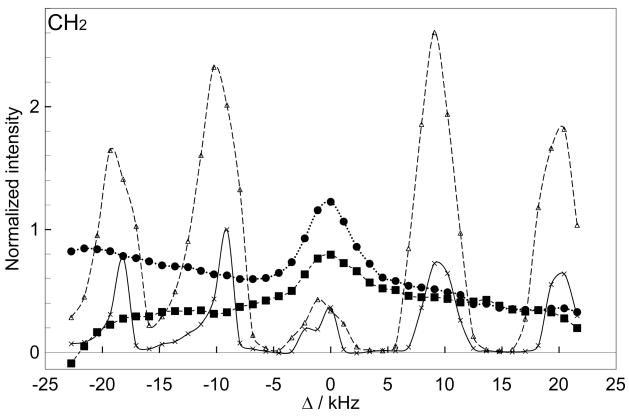
In Figure 3, we compared the effect of HH mismatch for the conventional CP, the rampCP, and the COMPOZER-CP. Figure 3a and 3b show the normalized intensities of the CH2 and CH peaks of adamantane, respectively, against the HH mismatch (Δ = ω1C − ω1H). In this experiment, we suppressed the 13C thermal-equilibrium magnetization before the application of the CP sequence. Clearly, the COMPOZER-CP sequences are superior to the CP and rampCP sequences in the compensation of the HH mismatch. Figure 3 shows that the COMPOZER-CP sequences are capable of suppressing HH mismatch over Δ/ω1C = ±20%. In Figure 4, we compared the contact-time dependence of the 13C magnetization for these sequences. Figures 4a and 4b show the normalized intensities of the CH2 and CH peaks, respectively. It is shown that the build-up rates for COMPOZER-CP sequences are faster than that of the rampCP sequence whereas they are slower than that of the CP sequence. The term “spin-lock” is used in this paper as the magnetization of both I and S nuclei are locked along the z-axis. This is strictly not the same as the “spin-lock” used in regular CP experiments where transverse magnetization is locked along the RF field axis. Figure 4, however, shows that the COMPOZER-CP does achieve spin-locking by retaining the magnetization of 1H and 13C nuclei along the z-axis, and that there is no significant difference between the spin-locking efficacies of rampCP and COMPOZER-CP.
Figure 3.
Performance of CP sequences against the HH mismatch (Δ= ω1C − ω1H) using a static adamantane sample: (a) CH2 peak and (b) CH peak. Crosses, open triangles, closed squares, and closed circles indicate the intensities obtained from CP, rampCP, COMPOZER-CP (Figure 1b), and the supercycled COMPOZER-CP (Figure 1c) experiments, respectively. The signal intensities were normalized by the maximum intensity of the CH2 or CH peak obtained in a CP. A contact time of 7.92 ms was used in all experiments.
Figure 4.
Cross-polarization build-up curves for a static adamantane sample: (a) CH2 peak and (b) CH peak. Crosses, open triangles, closed squares, and closed circles indicate the intensities obtained from CP, rampCP, COMPOZER-CP, and the supercycled COMPOZER-CP experiments, respectively. The signal intensities were normalized by the maximum intensity of the CH2 or CH peak obtained in a CP.
Effects of MAS on COMPOZER-CP have not been examined theoretically, however, our preliminary results indicate that its efficiency is deteriorated under MAS. For example, Figure 5 shows the effect of the HH mismatch under MAS (νr = 10 kHz) for the CH2 carbon of adamantane. For the rampCP and the conventional CP, the intensity becomes large at the modified HH condition of Δ = n ωR (ωR is the spinning frequency). On the other hand, the strong RF mismatch cancellation by COMPOZER-CP leads to an efficient CP at Δ = 0, however, the signal intensity is much smaller than the maximum signal achieved under rampCP. We also evaluated the efficiency of a ramped version of the COMPOZER-CP sequence (data not shown), however, our results suggest that ramping does not improve its efficiency. Nevertheless, the ramped version of the COMPOZER-CP sequence could be useful in situations where RF field inhomogeneity is very poor.
Figure 5.
Performance of COMPOZER-CP against the Hartmann-Hahn mismatch under MAS (νr = 10 kHz) for an adamantane sample: CH2 peak. Crosses, open triangles, closed squares, and closed circles indicate the intensities obtained from CP, rampCP, COMPOZER-CP, and the supercycled COMPOZER-CP experiments, respectively. The signal intensities were normalized by the maximum intensity of the CH2 peak obtained in a CP. A contact time of 7.92 ms was used in all experiments. The solid, long-dashed, dashed, and dotted lines are for eye guidance.
Conclusions
Our experimental results suggest that the new pulse sequence, COMPOZER-CP, is capable of transferring Z-magnetization via heteronuclear dipolar couplings from high-γ to low-γ nuclei. The structure of the homonuclear dipolar coupling Hamiltonian is such that it can assist the spin diffusion under the COMPOZER spin-locks, which further enhances the uniformity of CP. Experimental results for adamantane under a static experimental condition confirm that the COMPOZER-CP is better in overcoming the HH mismatch than the rampCP. Our experimental results also infer that the contact time required for cross-polarization in COMPOZER-CP sequence is shorter than that of the rampCP sequence. We believe that the COMPOZER-CP sequence and its ramped version will be useful to study static samples, particularly semi-solids like lipid bilayers and liquid crystalline materials. Such application is in progress and will be reported elsewhere.
Acknowledgments
M. Fukuchi was supported by research fellowship of Global COE program, International Center for Integrated Research and Advanced Education in Material Science, Kyoto-University, Japan. We thank the Chemistry exchange program between Japan and USA, and the NIH, for the funding support to A.R.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Schmidt-Rohr K, Spiess HW. Multidimensional Solid-State NMR and Polymers. Academic Press; New York: 1994. [Google Scholar]
- 2.Hartmann SR, Hahn EL. Nuclear double resonance in the rotating frame. Phys Rev. 1962;128:2042–2053. [Google Scholar]
- 3.Pines A, Gibby MG, Waugh JS. Proton-enhanced NMR of dilute spins in solids. J Chem Phys. 1973;59:569–590. [Google Scholar]
- 4.(a) Schaefer J, Stejskal EO. Carbon-13 nuclear magnetic resonance of polymers spinning at the magic angle. J Am Chem Soc. 1976;98:1031–1032. [Google Scholar]; (b) Stejskal EO, Schaefer J, Waugh JS. Magic-angle spinning and polarization transfer in proton-enhanced NMR. J Magn Reson. 1977;28:105–112. [Google Scholar]
- 5.Levitt MH, Suter D, Ernst RR. Spin dynamics and thermodynamics in solid-state NMR cross polarization. J Chem Phys. 1986;84:4243–4255. [Google Scholar]
- 6.(a) Peersen OB, Wu XL, Kustanovich I, Smith SO. Variable-amplitude cross-polarization MAS NMR. J Magn Reson. 1993;A104:334–339. [Google Scholar]; (b) Peersen OB, Wu XL, Smith SO. Enhancement of CP-MAS signal by variable-amplitude cross- polarization. Compensation for inhomogeneous B1 fields. J Magn Reson. 1994;A106:127–131. [Google Scholar]
- 7.Metz G, Xiaoling X, Smith S. Ramped-amplitude cross polarization in magic-angle-spinning NMR. J Magn Reson. 1994;A110:219–227. [Google Scholar]
- 8.(a) Hediger S, Meier BH, Kurur ND, Bodenhausen G, Ernst RR. NMR cross polarization by adiabatic passage through the Hartmann-Hahn condition (APHH) Chem Phys Lett. 1994;223:283–288. [Google Scholar]; (b) Hediger S, Meier BH, Ernst RR. Adiabatic passage Hartmann-Hahn cross polarization in NMR under magic angle sample spinning. Chem Phys Lett. 1995;240:449–456. [Google Scholar]; (c) Baldus M, Geurts DG, Hediger S, Meier BH. Efficient 15N-13C polarization transfer by adiabatic-passage Hartmann-Hahn cross polarization. J Magn Reson. 1996;A118:140–144. [Google Scholar]; (d) Hediger S, Signer P, Tomaselli M, Ernst RR, Meier BH. A combination of slow and fast RF field modulation for improved cross polarization in solid-state MAS NMR. J Magn Reson. 1997;125:291–301. [Google Scholar]
- 9.(a) Peng WK, Takeda K, Kitagawa M. A new technique for cross polarization in solid-state NMR compatible with high spinning frequencies and high magnetic fields. Chem Phys Lett. 2006;417:58–62. [Google Scholar]; (b) Peng WK, Takeda K. Efficient cross polarization with simultaneous adiabatic frequency sweep on the source and target channels. J Magn Reson. 2007;188:267–274. doi: 10.1016/j.jmr.2007.06.015. [DOI] [PubMed] [Google Scholar]; (c) Peng WK, Samoson A, Kitagawa M. Simultaneous adiabatic spin-locking cross polarization in solid-state NMR of paramagnetic complexes. Chem Phys Lett. 2008;460:531–535. [Google Scholar]
- 10.Ramamoorthy A, Wu CH, Opella SJ. Experimental aspects of multidimensional solid-state NMR correlation spectroscopy. J Magn Reson. 1999;140:131–140. doi: 10.1006/jmre.1999.1827. [DOI] [PubMed] [Google Scholar]
- 11.(a) Bax A, Hawkins BL, Maciel GE. Off-resonance cross-polarization: A technique to reduce rf power requirements for magnetization transfer experiments in solids. J Magn Reson. 1984;59:530–535. [Google Scholar]; (b) Shekar SC, Lee DK, Ramamoorthy A. Chemical shift anisotropy and offset effects in cross polarization solid-state NMR spectroscopy. J Magn Reson. 1996;157:223–234. doi: 10.1006/jmre.2002.2587. [DOI] [PubMed] [Google Scholar]; (c) Shekar SC, Lee DK, Ramamoorthy A. An experimental strategy to dramatically reduce the RF power used in cross polarization solid-state NMR spectroscopy. J Am Chem Soc. 2001;123:7467–7468. doi: 10.1021/ja016212t. [DOI] [PubMed] [Google Scholar]
- 12.Takegoshi K, McDowell CA. Cross polarization using a time averaged precession frequency. A simple technique to reduce radiofrequency power requirements for magnetization transfer experiments in solids. J Magn Reson. 1986;67:356–361. [Google Scholar]
- 13.Dvinskikh SV, Yamamoto K, Ramamoorthy A. Separated local field NMR spectroscopy by windowless isotropic mixing. Chem Phys Lett. 2006;419:168–173. doi: 10.1063/1.2212939. [DOI] [PubMed] [Google Scholar]
- 14.Yamamoto K, Dvinskikh SV, Ramamoorthy A. Measurement of heteronuclear dipolar couplings using a rotating frame solid-state NMR experiment. Chem Phys Lett. 2006;419:533–536. [Google Scholar]
- 15.Geen H, Titman JJ, Spiess HW. Heteronuclear magnetization transfer in rapidly spinning solids. Chem Phys Lett. 1993;213:145–152. [Google Scholar]
- 16.Bennett AE, Rienstra CM, Auger M, Lakshmi KV, Griffin RG. Heteronuclear decoupling in rotating solids. J Chem Phys. 1995;103:6951–6958. [Google Scholar]
- 17.(a) Haeberlen U, Waugh JS. Coherent averaging effects in magnetic resonance. Phys Rev. 1968;175:453–467. [Google Scholar]; (b) Mehring M. Principles of High Resolution NMR in Solids. 2. Springer-Verlag; Berlin: 1983. [Google Scholar]