Prehension synergies: A study of digit force adjustments to the continuously varied load force exerted on a partially constrained hand-held object

Abstract

We examined how the digit forces adjust when a load force acting on a hand-held object continuously varies. The subjects were required to hold the handle still while a linearly increasing and then decreasing force was applied to the handle. The handle was constrained, such that it could only move up and down, and rotate about a horizontal axis. In addition the moment arm of the thumb tangential force was 1.5 times the moment arm of the virtual finger (VF, an imagined finger with the mechanical action equal to that of the four fingers) force. Unlike the situation when there are equal moment arms, the experimental setup forced the subjects to choose between (a) sharing equally the increase in load force between the thumb and virtual finger but generating a moment of tangential force, which had to be compensated by negatively covarying the moment due to normal forces, or (b) sharing unequally the load force increase between the thumb and VF but preventing generation of a moment of tangential forces. We found that different subjects tended to use one of these two strategies. These findings suggest that the selection by the CNS of prehension synergies at the VF-thumb level with respect to the moment of force are non-obligatory and reflect individual subject preferences. This unequal sharing of the load by the tangential forces, in contrast to the previously observed equal sharing, suggests that the invariant feature of prehension may be a correlated increase in tangential forces rather than an equal increase.

Introduction

The forces when grasping an object need to be modulated when the weight of the object changes, for example, when holding a cup that is being filled with water. While the tangential, i.e. vertically oriented, force of the fingers must counter the increase in the load, the normal forces of the fingers increase also to prevent slipping. The changes in the normal and tangential digit forces must be coordinated in such a way that the total moment of force does not change.

Johansson et al. (1992) demonstrated that for two-digit (thumb and index finger) pinch grasping of an object, the grip force increases linearly with the load force, after a “catch-up” period. In Santello et al. (2000), the normal forces of the individual fingers were shown to co-vary linearly when the total grip and load force increased (while the subject lifted the object). This observation was made over different positions of the center of mass of the object. In Zatsiorsky et al. (2002), it was observed that for grasping a handle with different external torques, the total normal force increased with increasing torque magnitude, and a positive relation was seen between the mechanical advantage of a finger and the force applied by the finger.

The principle of superposition (Arimoto et al., 2001) states that commands for different task goals can be independently controlled, and their effects are summed. In terms of human prehension, it was observed that slip prevention and maintenance of rotational equilibrium could be achieved by controlling independently two subsets of central commands to the fingers (Zatsiorsky et al., 2004, Shim et al., 2005a).

In this work, we will consider how the grip (normal) and load (tangential) forces are modified in order to counter an external monotonically increasing and/or decreasing load force, under different external torque conditions. This task is novel for several reasons. First, it involves adjustment to a variable external force, while resisting constant external torques, using a five-digit grip rather than a two-finger grip used in previous studies (Johansson et al., 1992). Additionally, in this study, the handle translation is restricted to one direction, up and down, and a rotation is only allowed about a fixed axle perpendicular to the axes of normal and tangential force production. Finally, differently from the previous studies, the moment arms of the tangential forces for the thumb and virtual finger (VF, an imagined finger that produces the same wrench as the four fingers combined) were not equal; the moment arm of the thumb tangential force was 1.5 times the moment arm of the VF force. When the moment arm of the thumb and VF tangential forces are equal, an increase in load force may be shared equally by the thumb and VF, in which case, the moment due to the tangential forces will not change.

However, when the moment arms of the thumb and VF tangential forces are not equal, it is not possible to both share equally the increase in tangential forces and not introduce a change in the moment due to the tangential forces. If the change in load force is shared by an equal change in the thumb and VF tangential forces and hence the moment of the tangential forces changes, the normal forces must change their sharing pattern such that they compensate for the above mentioned change of the tangential moment with a change in the moment due to the normal forces.

We are interested in particular in describing the strategies the central nervous system (CNS) uses to resist the variable load force while preventing slipping and maintaining rotational equilibrium. We will describe these strategies in terms of the coordination of the grip (normal) and load (tangential) forces of the fingers at the virtual finger (VF) level

The following specific hypotheses have been addressed:

1. The tangential forces of the VF and the thumb increase with the load in constant proportion to the moment arms of the forces.

2. The normal forces change with the load independently of the load direction change, i.e. load increase or decrease. The normal forces of the VF and thumb are equal in magnitude at any external load values (the task mechanics do not require this equality; the force equality represents choice made by the central controller).

3. The principle of superposition is valid for the tested task. That is, the elemental variables can be divided into two independent subsets, one for slip prevention control (the normal forces of the thumb and VF), and one for tilt prevention control (the tangential forces, and the moments due to both the normal and tangential forces).

In previous studies on manipulation of hand-held objects, different subjects performed the tasks in a similar way with small inter-individual differences (Zatsiorsky et al., 2003). Because the objects used in the previous experiments closely resembled the objects used in everyday life we may surmise that similar coordination developed as a result of practice and learning. In the present study we wanted to expose the subjects to a task that is novel to them. The movement of the object was constrained in a way that is not typically encountered, and hence the subjects were not accustomed to manipulation of this type of object. We expected to find much larger differences in coordination among the subjects. If this assumption is confirmed, in the future we plan using the present task as a model for studying how the prehension coordination is being learned, and in particular to apply optimization methods in attempts to clarify what exactly is optimized (e.g. minimized) with practice and learning of multi-digit prehension.

Methods

Subjects

Eight right-hand dominant male subjects (mean age 28.6 ± 4.0 yr, weight 77.4 ± 14.2 kg, height 1.74 ± 0.06m, hand length from middle fingertip to distal crease of the wrist with the hand extended 18.5 ± 0.4cm, hand width at MCP level with the hand extended 9.0 ± 0.7cm) participated in this study. All subjects were healthy, with no known neurological or peripheral disorders. All of the subjects gave informed consent according to the policies of the Office for Research Protections at The Pennsylvania State University.

Apparatus

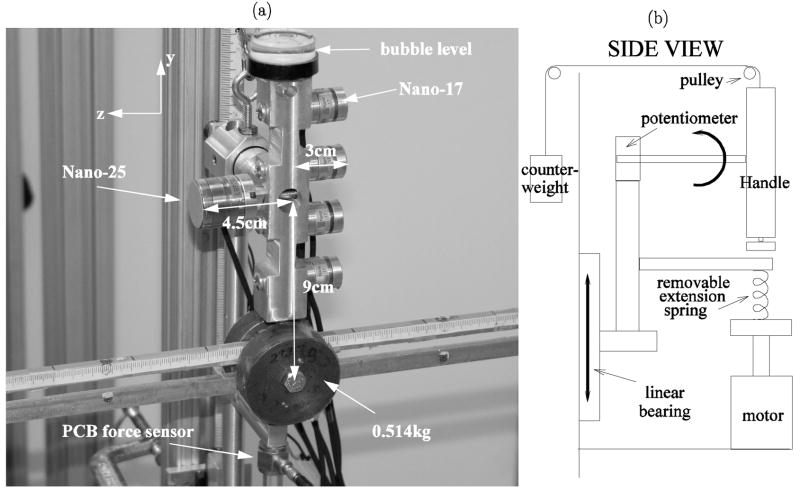
A novel apparatus, shown in Figure 1, was constructed for this study. Five 6-DOF force sensors (4 Nano-17, and one Nano-25 sensor for the thumb, ATI Industrial Automation, Garner, NC, USA) were attached to a handle in a comfortable grasping position. Sandpaper (320 grit) was attached to surface of the force sensors. A bar was attached to the bottom of the handle, allowing the application of different external torques by sliding a 0.514 kg weight, giving nine external torque levels of 0, ±0.2 Nm, ±0.4 Nm, ±0.6 Nm and ±0.8 Nm. The negative values of external torque correspond to supination efforts, and positive values to pronation efforts by the subject. The apparatus was designed such that it allowed movement in only two directions. Firstly, the entire handle could move up and down, in a nearly frictionless manner as the handle was attached to the base through a linear bearing. Additionally, the handle could rotate about a spindle going through the center of the handle (see Figure 1). Note that due to the different height of the Nano-25 and Nano-17 sensors the horizontal distance from the surface sensor to the axle of rotation was 4.5 cm for the thumb and only 3.0 cm for the finger sensors. Hence the moment arm of the thumb tangential force with respect to the axis of rotation was 1.5 times the moment arm of the finger forces.

Figure 1.

Experimental setup. (a) front view, (b) side view (schematic).

The handle was attached to a pneumatic actuator (Parker, Cleveland, OH, USA) through a unidimensional force sensor (model 208C02; PCB Piezotronics Inc, Depew, NY, USA) and an extension spring. The downward force on the handle could be controlled by extending the spring. A counter-weight attached to the handle through two low friction pulleys ensured that the initial vertical force on the handle was zero.

The coordinate system was fixed relative to the handle, with the y axis pointing up, and the z axis pointing to the left, such that the grip force of the thumb was in the negative z direction, and the grip forces of the other four fingers were in the positive z direction.

Experimental procedure

Before the experiment, the subjects were familiarized with the equipment and the procedure. They washed their hands with warm water and soap to normalize the skin condition. The subjects sat in a chair in front of the apparatus, with their right upper arm at approximately 45° flexion in the frontal plane, 45° flexion in the sagittal plane and with their elbow flexed such that the forearm was parallel to the horizontal plane. The forearm was pronated 90° to allow natural grasping of the handle, and together with the wrist was strapped to a stand, to prevent motion. The subjects were instructed to grasp the handle initially as lightly as possible, and then when the force was applied, to prevent the handle from translating or rotating. Visual feedback on the rotation of the handle was provided with a bubble level, and on the vertical position of the handle by a metal rod that moved along a marked scale. To prevent the handle from rotation the subjects should exert on the handle a moment of force that was opposite and equal to the external torque. In what follows we refer to the moment exerted by the subjects in pronation direction as positive and the moment in supination direction as negative. The designation is also accepted in the corresponding figures.

Each measurement had duration of 10 s. The trial began only after the subject had maintained the handle orientation vertical. A beep indicated the start of the trial. After 1 s, the force increased linearly over 3 s to a peak of 20 N, remained there for 2 s, then decreased linearly over 3 s to 0 N. The force generated by the actuator on the handle, as measured by the unidimensional force sensors, almost instantaneously reached the force rate of 6.67 N/s. To prevent fatigue, short rests (approximately 30 seconds) were given between repetitions, and longer rest periods (approximately 2 minutes) were provided between the different external torque levels.

Each of the nine external torque conditions was repeated 5 times, after two practice trials.

Data collection and analysis

The force/moment signals from the force sensors were digitized using a 16 bit A/D converter (PCI-6225, National Instruments, Austin, TX) at 500Hz. The data were collected using a custom program written in LabVIEW (National Instruments). The data analysis was performed using custom software written in Matlab (The MathWorks, Natick, MA). The raw force/moment signals were filtered using a 4^th order Butterworth low-pass filter at 5 Hz.

Trials where the handle translated more than 3 mm, or rotated more than 5° were not accepted. Due to the nature of the setup, translation of the handle caused extension or compression of the spring, and so changed the total amount of force applied by the actuator. To prevent different force changes across trials, only those with minimal translation were accepted. If the handle rotated a significant amount, then the normal forces would also contribute to preventing vertical translation of the handle. To ensure uniform analysis of the data, trials with excessive rotation were also not accepted. Unsatisfactory trials (less than 10% of total trials) were repeated during the experiment. For each external torque condition, the “best” trial was selected for further analysis, defined as the trial where the sum of the digit tangential forces was closest to the force applied by the motor, as measured by the PCB unidimensional force sensor. These trials were selected in order to reduce the amount of variance across conditions and subjects, so that all conditions would have a change of load force of approximately 20 N. All calculations were then performed only on these selected trials. In total 360 trials were recorded (8 subjects × 9 external torques ×5 trials), while 72 were used in the analysis (8 subjects × 9 external torques).

Previous studies have suggested that there is hierarchical control of prehension (Zatsiorsky et al, 2003), with an upper level where the task is shared between the thumb and VF, and a lower level where the action of the VF is shared among the individual fingers. As this paper seeks to describe the overall strategy used by the CNS to control prehension for this handle, we have chosen to analyze the forces only at the thumb-VF level.

In order to calculate the moment of force about the axis of rotation generated by the normal and tangential forces of the fingers, the point of wrench application needs to be known in order to determine the moment arms, as the fingers can roll on the sensors. This was calculated as follows (Zatsiorsky, 2002), where the y axis points upward, and the z axis points to the left, as shown in Figure 1:

$$Y_{\mathit{PWA}}=\frac{F_z{M}_x-F_x{M}_z}{F^2}-\frac{F_x{F}_y{M}_y-F_y^2{M}_x}{F^2{F}_z}$$ (1)

In the z direction, the moment arm is fixed by the position of the force sensor, and force production in the x direction was not studied.

The moment of force applied by the fingers, about the x axis was designated M, and was analyzed by dividing it into the component due to the tangential forces, M^t, and the component due to the normal forces, Mⁿ, and further subdivided into the components due to the VF and thumb tangential and normal forces, M^t_VF, M^t_th, Mⁿ_VF, Mⁿ_th, such that:

$$\begin{array}{c}M(t)=M^t(t)+M^n(t)\\ M^t(t)=M_{VF}^t(t)+M_{th}^t(t)=d_{VF}^t{F}_{VF}^t(t)-d_{th}^t{F}_{th}^t(t)\\ M^n(t)=M_{VF}^n(t)+M_{th}^n(t)=d_{VF}^n{F}_{VF}^n(t)+d_{th}^n{F}_{th}^n(t)\end{array}$$

where d are the moment arms for the relevant force.

For this task, maintenance of rotational equilibrium can be achieved in at least two different ways. In a task with equal moment arms of tangential forces, these two strategies can be achieved simultaneously, but this is not possible with unequal moment arms, as in this experiment.

The first is to maintain a constant moment due to the tangential forces (ΔM^t = 0), and a constant moment due to the normal forces (ΔMⁿ = 0), throughout the change in external load. For the tangential forces, this requires that:

$$0=\mathrm{\Delta }{M}^t(t)=d_{VF}^t\mathrm{\Delta }{F}_{VF}^t(t)-d_{th}^t\mathrm{\Delta }{F}_{th}^t(t)$$ (2)

ΔF^t_th and ΔF^t_VF are the change in tangential forces from the beginning of the trial. In general, the tangential forces of the thumb and VF at the start of the trial may not be zero, and correspond to a particular moment of tangential forces.

The changes in tangential forces are also required to sum to the load force change ΔL(t), where ΔL(0)=0.

$$\mathrm{\Delta }{F}_{th}^t(t)+\mathrm{\Delta }{F}_{VF}^t(t)=\mathrm{\Delta }L(t)$$ (3)

As the moment arm of the thumb is 1.5 times the length of the moment arm of the VF, to maintain the constant M^t the change of tangential forces of the thumb and VF needs to be:

$$\mathrm{\Delta }{F}_{VF}^t(t)=\frac{3}{5}L(t),\mathrm{\Delta }{F}_{th}^t(t)=\frac{2}{5}L(t)$$ (4)

If ΔM^t=0, in order for the overall moment to remain unchanged, ΔMⁿ=0. As the moment arm of the thumb normal force is approximately zero, this means that

$$M_{th}^n\approx 0$$

and hence

$$\mathrm{\Delta }{M}_{VF}^n\approx 0$$

As both Fⁿ_VF and dⁿ_VF can change throughout the movement, for the above condition to be true, then the normal force produced by the VF, and its moment arm must covary such that:

$$d_{VF}^n=\frac{M_{VF}^n(0)}{F_{VF}^n}$$ (5)

The VF moment arm is mainly altered by changing the sharing patterns of the normal force between the four fingers, and to a smaller degree by the displacements of the points of force application of the individual finger forces on the sensors (see equation 1).

An alternative strategy of tilt prevention would be to produce equal force increases with the thumb and VF (i.e. each finger increase by ΔL(t)/2). This has been observed in previous studies where the moment arms were equal for the thumb and the VF (Shim et al., 2005a). For the tangential forces, this would result in the generation of a moment throughout the trial:

$$\mathrm{\Delta }{M}^t(t)=d_{VF}^t\frac{\mathrm{\Delta }L(t)}{2}-d_{th}^t\frac{\mathrm{\Delta }L(t)}{2}=(d_{VF}^t-d_{th}^t)\frac{\mathrm{\Delta }L(t)}{2}=-0.0075\mathrm{\Delta }L(t)$$ (6)

This must be balanced by an increase in the moment due to the normal forces. As shown previously, the thumb does not contribute to Mⁿ and so the increase in moment must come from the VF:

$$\mathrm{\Delta }{M}_{VF}^n(t)=0.0075\mathrm{\Delta }L(t)=d_{VF}^n(t)F_{VF}^n(t)-M_{VF}^n(0)=d_{VF}^n(t)\mathrm{\Delta }{F}_{VF}^n(t)+\mathrm{\Delta }{d}_{VF}^n{F}_{VF}^n(0)$$ (7)

This can be achieved by a combination or individual changes of the VF normal force and the VF moment arm. Based on previous works, we expected that the thumb normal force will increase symmetrically with the VF normal force, although this is not required with the constrained apparatus, and does not significantly affect the moment of the normal forces due to its negligible moment arm (see Hypothesis 2 above).

Statistical Analysis

The statistical analysis was performed (a) within a trial, (b) across trials for individual subjects, and (c) for the entire group. In the individual trials the elemental variables (forces, moments and moment arms of the normal forces) could change as a function of the load change. The coefficients of correlations and linear regression equations (slopes and intercepts) we computed between these variables.

Several ANOVAs were performed to ascertain if different strategies were used across different conditions and subjects. A 2-way ANOVA was performed on the intercept of the thumb vs. VF normal force regression lines during the force increase, with factors Subject (8 levels) and External Torque (9 levels: 0, ±0.2 Nm, ±0.4 Nm, ±0.6 Nm and ±0.8 Nm). A 3-way ANOVA was performed on the gradient of this relationship with factors Subject (8 levels), External Torque (9 levels) and Force Direction (2 levels: ascending/descending direction). A 3-way ANOVA was performed on both the mean and standard deviation of the difference between the thumb and VF tangential forces, with factors Subject (8 levels), Force Direction (2 levels) and External Torque (9 levels). A repeated measures ANOVA was performed on M^t and Mⁿ with factors Subject (8 levels), External Torque (9 levels) and Load (9 levels: 0N, 2.5N, 5N, 7.5N, 10N, 12.5N, 15N, 17.5N, 20N). Post-hoc Tukey honestly significant difference tests were used to further analyze significant results. The p value for significance was set at 0.05.

Principal Component Analysis (PCA) was performed on the elemental variables within each trial, to determine if they can be divided into a number of independent sets, which suggests that the sets may be independently controlled. The correlation matrix of the elemental variables F^t_th, F^t_VF, Fⁿ_th, Fⁿ_VF, M^t_th, Mⁿ was constructed for each trial, by sampling the data at 100 points during the force increase, after detrending. Mⁿ was used rather than Mⁿ_VF and Mⁿ_th because Mⁿ_th was expected to be close to zero due to its approximately zero moment arm.

Detrending was achieved by performing linear regression, and subtracting the value of the regression line from the data. PCA was then performed on this matrix, with a variance maximizing rotation (varimax) applied to the eigenvectors, performed in Matlab. The loading coefficients for each variable in the principal component was calculated, and 0.35 was used as a minimum significant loading value.

As the comparison was performed within a trial, if detrending were not performed, the magnitude of correlations due to mechanical relationships would overwhelm any other correlations. The purpose of the PCA was to test for correlations that suggest independent control of different sets, hence correlated deviation in the detrended data would provide support of this hypothesis.

Results

Tangential forces

As was planned, the total tangential forces changed during the trials in the range between 0 N to 20 N in the ascending and descending directions. The tangential forces at the thumb-VF level showed a linear relation throughout the trials. Regression of these forces reveals a high R² value, with an average across conditions greater than 0.96 for all subjects.

The change in tangential forces throughout the trial can be characterized by the slope and intercept of the relation between thumb and VF tangential forces. The intercept indicates the initial sharing of the tangential forces between the fingers. A negative intercept means that the initial thumb tangential force was higher than the VF force, and vice-versa. These initial non-zero tangential forces are due to two causes – first the total tangential force at the start of the trial was not always zero. Due to friction in the apparatus, subjects were able to apply small tangential forces at the start of the trial. Additionally, by applying a positive tangential force with the thumb, and a negative (or smaller) tangential force with the VF, a supination (negative) moment could be applied without causing the handle to move in translation vertically. Pronation moments could be generated by the opposite pattern of the distribution of the tangential forces. Thus, the change in intercept with different external torques reflects different initial moments applied by the tangential forces, M^t. At the no external torque condition, the difference in tangential forces ranged from −6.6 N to 2.7 N (mean and standard deviation of −1.6 ± 3.4 N). For all subjects, at the −0.8 Nm condition, the intercept was negative. The value of the intercept became greater (i.e., it went from being negative to positive) as the external torque became greater, from negative to positive values. A 2-way ANOVA on the intercept (for the force ascending part) showed that it significantly depended on Subject (F_7,7=497.13, p<0.0001), and Torque (F_1,1=2614.1, p<0.0001). The interaction Subject × Torque was also significant (F_7,7=4.00, p<0.005), indicating that the dependence of the intercept on torque differed across subjects, although the differences were small. On average, the gradient of the increase in intercept with increase in external torque was 10.2 (±1.8) m⁻¹. The intercept magnitude varied across subjects, as follows from the above mentioned ANOVA results.

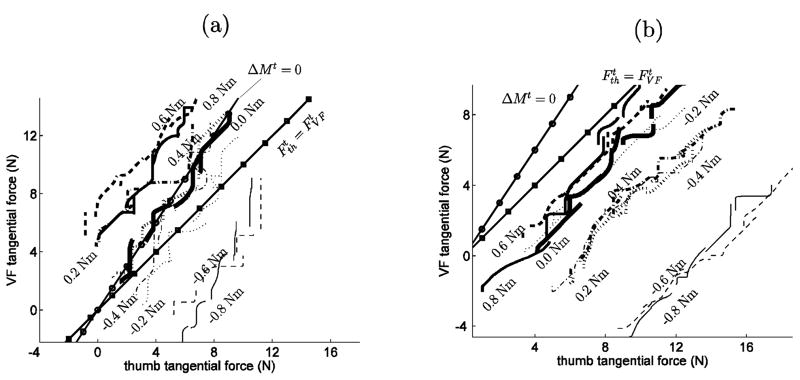
The slopes of the relation between thumb and VF tangential forces indicate the relative changes in tangential forces during the load increase or decrease. As described in the Introduction, if the slope is 1.5, due to the unequal moment arms, the imbalance in the tangential forces observed does not create a net moment, rather, the M^t stays at the same level as it was at the beginning of the trial. An example of this can be observed in Figure 2(a). In contrast, if the slope is 1, then the thumb and VF tangential forces increase at the same rate, and M^t changes throughout the trial. Figure 2(b) shows an example of this. The subjects generally used a technique somewhere between these two strategies, leading to the mean slope (average per subject) varying between 1.08 and 1.66. As subjects did not select solely one strategy or the other (slope of 1 or 1.5), we quantify on a per condition basis the selection of slope. Across all subjects and conditions, we divided the slopes into those less than 1.25, and those greater than 1.25. 62.5% of the conditions had a slope of greater than 1.25 (mean and standard deviation of 1.56 ± 0.26), whereas the remaining 37.5% has a slope with mean and standard deviation of 1.02 ± 0.14). A 3-way ANOVA showed that the slopes depended significantly on Subject (F_7,7 =9.54, p<0.0001) and External Torque (F_1,1=10.85, p<0.005) but not on the Force ascending/descending direction. As at the start of the trial the handle was at rotational equilibrium, any change in the moment due to the tangential force changes during the trial must be compensated by changes in the moment due to the normal forces in order to prevent the handle from tilting.

Figure 2.

VF-thumb tangential force relations during the trials for typical subjects, for all torque conditions. The line with the circle markers shows the slope of 1.5 (no changes in the net tangential moment), while the line with the square markers shows a slope of 1 (equal thumb and VF tangential forces changes). Note that the sign for external torque corresponds to the moments exerted by the subjects, such that negative values of external torque correspond to when the added weight is on the left side, and positive values to when the added weight is on the right side. (a) Example of subject where the slopes are approximately equal to 1.5 (b) Example of a subject where the slopes are approximately equal to 1.

Normal forces

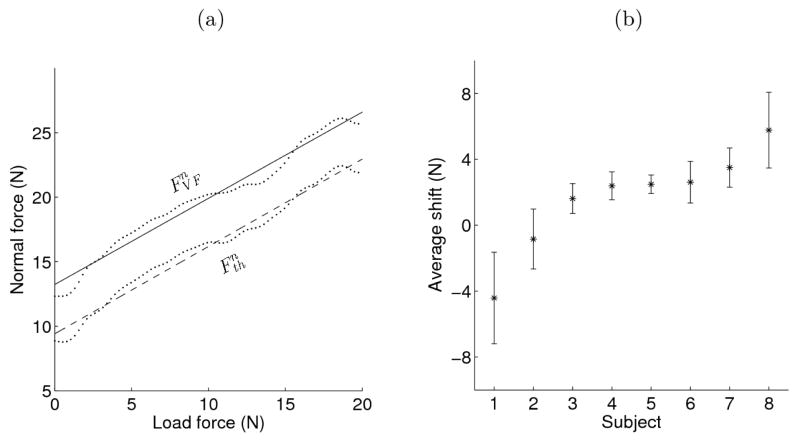
Due to the constrained nature of the apparatus (the handle could not move to the right or the left), the VF and thumb normal forces were not required to sum to zero, nor to be linearly related. The normal forces of both the thumb and VF always increased as the load force increased in a linear fashion. Figure 3(a) shows a typical example of how the normal forces increased during a trial.

Figure 3.

Thumb and VF normal forces during the increase of tangential force from 0 to 20 N. (a) Typical thumb and VF normal forces. Every 20th sample is plotted, along with the regression lines (Fⁿ_VF (t)=0.67 L(t)+13.2 N, Fⁿ_th=0.68 L(t) + 9.4 N). The correlation coefficient between the forces = 0.9991, regression between the forces: Fⁿ_th(t)=1.01 Fⁿ_VF(t) − 3.88N. Mean and standard deviation of the difference were 3.73 ± 0.17 N. (b) Mean and standard deviation of average difference (shift) between VF and thumb normal forces by subject (positive signifies the VF force greater than thumb force), sorted from minimum to maximum.

In order to study how the normal forces changed throughout the task performance, the mean and standard deviation of the difference between Fⁿ_VF and Fⁿ_th were computed for all conditions. The mean difference for individual trials across subjects ranged from −9.5 N to 10.9 N (positive indicates Fⁿ_VF is larger). For six of the eight subjects, on average, the VF normal force was of a greater magnitude than the thumb normal force. The two other subjects consistently showed the opposite pattern.

To determine whether the differences in normal forces were only due to subject preferences, or also due to changes in the external torque, a 3-way ANOVA was performed on the mean difference, with factors Subject, Force Direction and External Torque and all interactions. The results showed main effects for Subject (F_7,7=82.78, p<0.0001) and External torque (F_1,1 = 16.94, p<0.0001), but not for Force Direction.( F_1,1=2.31, p>0.1). While external torque had a significant effect, the change in the difference of normal forces across external torques was small, ranging from at 1.85±3.85 N at 0.8 Nm, to 2.87±3.27 N at 0.8 Nm. Furthermore, a post-hoc Tukey HSD, did not find any significant effect of external torque levels on the differences in normal forces. A significant interaction effect was found for Force Ascending/Descending direction±External Torque (F_1,1=12.47, p<0.001), and Subject × External Torque Moment (F7,7=10.61, p<0.0001), but in both cases, a post-hoc Tukey HSD did not find significant differences for any pair of conditions, indicating that the effects were small. Thus, it appears that the change in normal forces is mainly a matter of subject preference. While a main effect of External Torque on the difference in normal forces was observed, the effect was small. The means and standard deviations of the average differences between the VF and thumb normal forces for all the subjects are shown in Figure 3(b).

The standard deviation of the difference in normal forces within a trial was relatively small (maximally 1.8 N, over all subjects and conditions), indicating that the difference in normal forces did not change as the force increased and decreased. An ANOVA was performed for the standard deviation, with factors Subject, Force Direction, and External Torque. A main effect was observed only for Subject (F_7,7=6.23, p<0.0001). That is, the amount of fluctuation in the difference between thumb and VF normal forces during a trial is a matter of subject preference, and does not change systematically with different direction of the load change and external moment.

To investigate whether local conditions at the contact (i.e., the ΔF^t) affect the ΔF^n, the correlation coefficients between the mean values of ΔF^t and ΔFⁿ per trial were calculated for each subject (n =8). If local conditions are an important factor, then a high correlation would be expected. The correlation coefficient ranged from −0.52 to 0.74, however, it was only significant (at the p=0.05 level) for one subject. Based on these results, it seems that in general, local conditions do not determine the ΔFⁿ.

As the standard deviation of the difference between thumb and VF normal forces was generally small, this means that the slopes of the thumb and VF normal forces were approximately equal: the forces changed in parallel. Therefore, for the remainder of the analysis of the normal forces we will consider only the VF normal force.

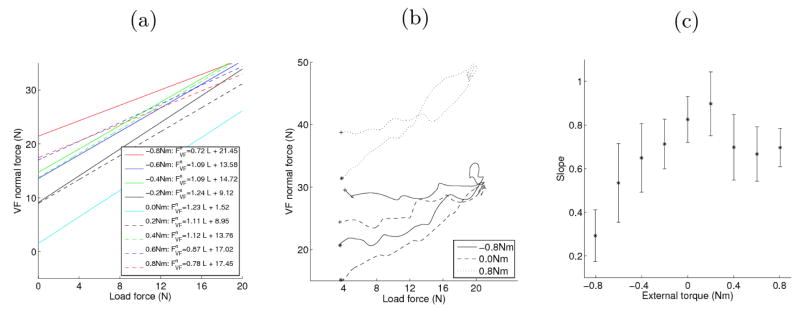
The VF normal force increased as the load increased in a linear fashion, but with different slopes depending on the external torque. This is apparent from Figure 4(a).

Figure 4.

The increase in VF normal force with an increase in the load. (a) Regression lines showing the increase in the VF normal force with an increase in the load, for a typical subject (b) Hysteresis loops for 3 external torque conditions for a typical subject. The (*) indicates the beginning of the trial, and the (+) the end of the trial. (c) The mean and standard error of the slope of the normal force vs. the load force, averaged across subjects, as a function of the torque for the force increase.

From Figure 4(b), hysteresis effects can be observed in the differences between the changes in normal force during load force increase (from 0 to 20 N), and during the force decrease (from 20 N to 0). During the hold period, the normal forces decreased slightly. During the force decrease, the normal forces did not return to their original levels before the force increase.

The slope of the VF normal force vs. the load force, as a function of the external torque is presented in Figure 4(c). It can be observed that at zero external moment, the normal forces increase in magnitude nearly equally to the increase in load force, while at non-zero torque magnitudes, the increase in the normal forces is much less. At the high external moment values, the initial normal force is higher than at other values (at −0.8 Nm: 25.1±3.6 N, at 0 Nm:13.1±5.0 N, at 0.8 Nm: 27.4±6.6 N, average and standard deviation across subjects) and so during the force increase, the normal force does not need to increase as much to prevent slipping. However, a large asymmetry is observed in the slopes with the direction of the external torque. When the external torque was negative, that is, the subjects were applying a supination moment, the slope was very low meaning that the normal force increased by only a small amount.

Tilt prevention

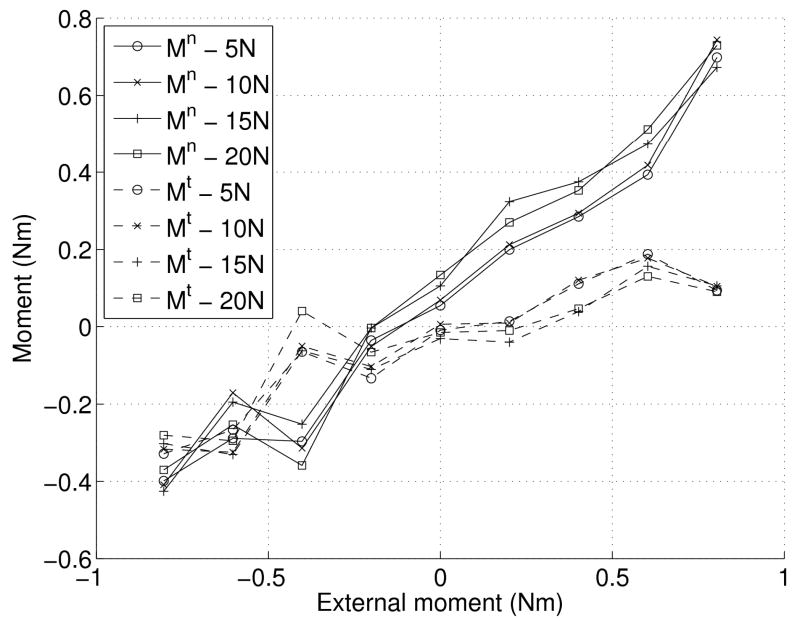
In order to maintain rotational equilibrium, the total moment generated by the digits must be equal and opposite of the external torque. In this task, the rotational equilibrium must be maintained while simultaneously increasing the tangential and grip forces. The contributions of the normal and tangential moments to the total moment for a typical subject are shown in Figure 5. As can be observed, there are large changes in the sharing pattern over different external torques, while there are relatively small changes as the load force increases. Similar patterns were observed across subjects. Only one subject showed an approximately equal contribution of Mⁿ and M^t at all external torques (i.e., Mⁿ ≈ M^t≈ τ_e/2, τ_e is the external torque) over all conditions. In all other subjects, at larger positive external torques (supination), the moment due to the normal force contributed a higher proportion of the total moment. For three of the subjects, the contribution of M^t due to the tangential forces was almost always negative.

Figure 5.

The moment due to the normal and tangential forces, plotted as a function of the external torque for a typical subject. The points plotted are the moments when the load force is at the given value (5N, 10N, 15N or 20N). This subject had a mean slope of the tangential thumb vs. VF force of 1.48±0.53, and the difference between the normal forces of the VF and thumb were on average of 2.55±1.18N (VF force higher). Note that the contribution of the M^t and Mⁿ into the total moment (M=M^t+Mⁿ) changes with the external torque.

A repeated measures ANOVA with the moment sampled at 9 equally spaced points during the force increase, with factors Subject, External Torque and Load (0, 2.5, 5, 7.5, 10, 12.5,15,17.5, and 20N) showed that both Mⁿ and M^t significantly depend on the External Torque, the Load and the Subject (Mⁿ :External Torque F_1,56 =1659.6, p<0.0001, Load F_4.3,240.8=20.31, p<0.0001, Subject F_7,56=28.42, p<0.0001; M^t: External Torque F_1,56=351.3, p<0.0001, Load F_2.4,134.5=12.24, p<0.0001, Subject F_7,56=28.67, p<0.0001 ). Furthermore, interaction effects were observed for Mⁿ: Load × Subject (F _30.1,240.8 = 4.34, p<0.0001), Load × Torque (F_4.3,240.8=5.60, p<0.0005) and Subject × Load × Torque (F_30.1,240.8, p<0.05), but not for Subject × External Torque (F_7,56=0.93, p=0.49), and for M^t: Load × Subject (F_16.8,134.5=6.13, p<0.0001), Load × External Torque (F_2.4,134.5, p < 0.005), Load × Subject × Torque (F_16.8,134.5=1.8, p < 0.05), but not for Subject × External Torque (F_7,56=1.61, p=0.15).

Although the load was found to be a significant factor, its effect on Mⁿ and M^t within a trial was small, as can be observed in Figure 5.

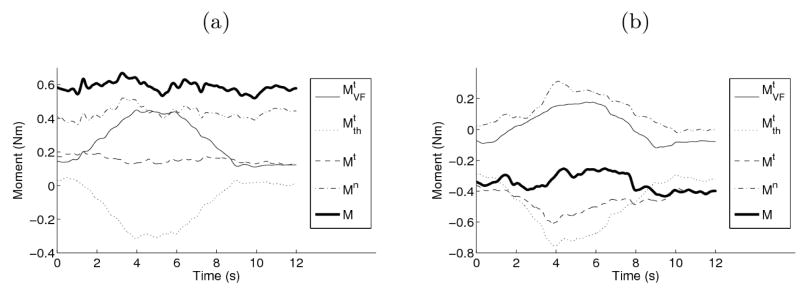
The contributions of the normal and tangential thumb and VF forces to the total moment during typical trials are shown in Figure 6. Figure 6(a) is for a subject where ΔM^t(t) ≈ 0, while Figure 6(b) is for a subject where there were significant changes to M^t(t) throughout the force increase.

Figure 6.

Contributions of M^t and Mⁿ to the total moment for a typical trial, where (a) the external moment is 0.6 Nm. In this example, both the Mⁿ and M^t remain constant. The regression coefficient between the thumb and VF tangential forces for this example is 1.68. The total moment applied by the fingers is slightly less than the external torque probably due to friction. In (b), a different subject, the external moment is −0.4 Nm, and in this example, in contrast, M^t changes significantly during the trial, requiring Mⁿ to also change to maintain a constant overall moment. For this example, the regression coefficient between the thumb and VF tangential forces is 0.95.

In both graphs, there are large changes in the M^t_VF (shown as the thin solid line). In Figure 6(a), this change is countered by M^t_th (shown as a dotted line). This is the representative of the subjects where the regression coefficient between F^t_th and F^t_VF was approximately 1.5. In Figure 6(b), the decrease in M^t_th is greater than the increase in M^t_VF, and hence to maintain rotational equilibrium, Mⁿ must also change. This graph is from one of the two subjects where approximately equal tangential forces were applied.

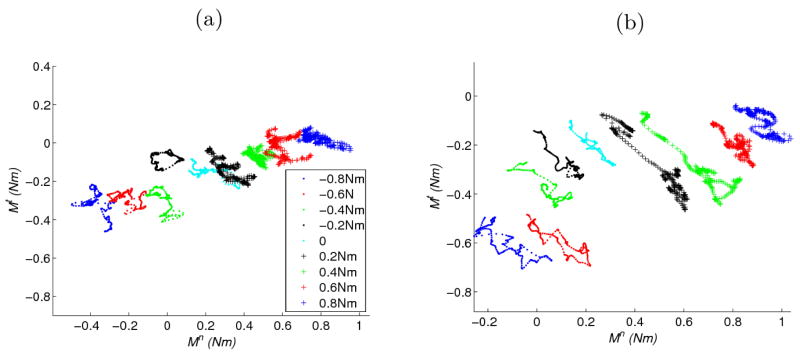
Two different patterns can be observed in the relation between Mⁿ and M^t depending on the subject and condition, which are shown in Figure 7. When the moment due to the tangential forces changes very little, the correlation between Mⁿ and M^t is relatively low (as is seen in Figure 7(a)). However, when there is a significant change in M^t, the correlation between Mⁿ and M^t is negative and of a higher magnitude (in Figure 7(b)). The negative correlation stabilizes the total moment. This appears to be evidence of two different strategies used by different subjects. The first is to allow M^t and Mⁿ to vary, and to inter-compensate using negative covariation, while the other is to stabilize both M^t and Mⁿ, in which case no inter-compensation is necessary.

Figure 7.

Relation between Mⁿ and M^t for two subjects showing different coordination patterns. (a) A typical subject where the moment due to tangential forces changes very little in the trial. The mean and standard deviation of the correlation coefficient between Mⁿ and M^t for this subject is −0.42 ±0.33. (b) A typical subject where there are significant changes in the tangential forces. The mean and standard deviation of the correlation coefficient between Mⁿ and M^t for this subject is −0.88 ± 0.08.

Superposition control

The principle of superposition was tested for the current experiment by using principal component analysis (PCA). If superposition control is used, then it should be possible to partition the elemental variables such that they can independently control different facets of the task.

PCA was performed on the elemental variables during the force increase, after detrending them, sampled at 100 points. A variance maximizing rotation (varimax) was applied to the eigenvectors. The analysis was performed for each of 72 trials (8 subjects × 9 external torques). Mⁿ was used rather than the components due to normal and tangential forces because the value of Mⁿ_th was approximately zero throughout the trials. The first three principal components (PCs) accounted for 96.1 ± 2.8% of the variance. Many of the PCs were similar across subjects and conditions. The first three principal components are presented in Table 1 for a typical subject. In the following description, PCs from different conditions were considered to be the same if the same elemental variables appeared significantly (i.e. had loadings greater than 0.35) and with the same signs.

Table 1.

Loadings of the first three principal components for a typical subject.

Variable	PC1	PC2	PC3
Ftth	0.00	0.00	−0.71
FtVF	−0.06	−0.58	0.03
Fnth	0.70	0.01	−0.01
FnVF	−0.69	0.00	−0.01
Mtth	0.00	0.00	0.71
MtVF	−0.06	−0.58	0.03
Mn	0.13	−0.57	−0.06

The covariance of the detrended variables was calculated at 100 time samples. The variables with large loadings are shown in bold.

The first PC in Table 1 consists of the normal forces, which change in a highly correlated way. This PC was observed in 47% of the cases, and explained on average 28.7±1.7% of the variance. The second PC consists of the tangential forces of the virtual finger, and the moment due to these forces, but also the moment due to the normal forces. This PC was observed in 15.3% of the cases, and explained on average 34.0 ± 4.14% of the variance. A similar PC, but without correlation of Mⁿ was observed in 59.7% of the cases, and explained on average 29.8 ± 1.8% of the variance.

The third PC consists of the tangential forces of the thumb, and the moment due to these forces. This PC was observed in 51.4% of the cases, and explained on average 29.8 ± 1.8% of the variance.

It should be noted that the normal forces were usually in a different PC to Mⁿ. In only 32% of the cases were the normal forces and Mⁿ in the same PC. In general the results agree with the predictions based on the principle of superposition: the moment of normal forces is in a different subset than the normal VF force.

Discussion

The task explored in the present research differs substantially from the previously studied tasks where either manipulation of (a) free objects (Shim et al., 2005, Gao et al., 2006) or (b) completely constrained objects (Shim et al., 2004) has been investigated. In the present study the object was partially constrained. It was allowed to move in the vertical direction but was not allowed to move horizontally. The rotation was allowed only about a single, fixed axis. Also, in contrast to other studies the moment arms of the tangential thumb and VF forces differed by factor 1.5. We will concentrate the discussion on the hypotheses formulated at the beginning of the paper:

1. The tangential forces of the VF and the thumb increase with the load in constant proportion to the moment arms of the forces.

2. The normal forces change with the load independently on the load direction change, i.e. load increase or decrease. The normal forces of the VF and thumb are equal at any external load values (the task mechanics do not require this equality; the force equality represents the choice made by the central controller).

3. The principle of superposition is valid for the tested task.

We also were interested in whether — similar to the previously studied tasks — all the subjects use similar coordination pattern to control the object or different subjects use diverse patterns. The results can be summarized as follows.

(1) The first hypothesis can be confirmed only for some subjects and rejected for others. The constant proportion to the moment arms of the forces mentioned in the hypothesis requires that the slope of the relation between thumb and VF tangential forces should be 1.5. In this case, due to the unequal moment arms, the M^t stays stays put throughout the trial. In experiments, the slopes varied among the subjects between 1.08 and 1.66 (average per subject). The differences in the slopes are indicative of the different strategies used. Although the slopes were not precisely 1 or 1.5, we discuss these two strategies, in order to compare these results with finding from previous prehension studies.

The tangential force changes with the slope 1.5 indicate that the moments of the tangential forces do not change during the trial. Hence the moments of the normal forces do not change either, and rotational equilibrium is achieved solely by the proper rate of the thumb and VF relative tangential force changes. If the slope is 1, then the thumb and VF tangential forces increase at the same rate, and M^t changes throughout the trial. Consequently, to maintain the total moment constant and prevent object tilting the moment of normal forces should change to compensate for the M^t variations.

In previous prehension studies, due to the equal moment arms for the tangential force of the thumb and the virtual finger, subjects were able to both equally share the increase in load force by tangential force changes of the thumb and virtual finger, and simultaneously maintain an approximately constant value of M^t. The unequal moment arms in this experiment required the subjects to make a choice between these two strategies. Although this task is different to previous prehension studies, in day-to-day life it is not uncommon to lift and manipulate objects with non-uniform densities, which would have different effective moment arms for the thumb and virtual finger.

The observed differences in the slopes indicate that in contrast to other studies rather than one strategy being used by all the subjects in all conditions, there appeared to be two different strategies used. In 62.5% of the conditions, the large changes in normal and tangential forces were shared in such a way that within a single trial, the moment due to the normal forces, and the moment due to the tangential forces did not change. This strategy is not required by the mechanics of the task. It results in the moment due to the tangential forces being almost constant throughout the changes in tangential forces. This is in contrast to the finding of Pataky et al. (2004), where approximately equal thumb and VF tangential forces changes were observed. This task is however different from that of Pataky et al. (2004) in that the moment arms are not equal.

The alternative strategy, used in the remainder of the conditions, was to counter the increase in load by increasing equally the tangential forces of both the thumb and virtual finger. As this in turn changes the moment (due to the unequal moment arms), the normal forces were required to covary such that the total moment was unchanged.

Across different external torque conditions, the sharing of the total moment between the moments due to normal and tangential forces differed considerably. This is in contrast to the Zatsiorsky et al. (2002), where the moments were shared equally between the moments due to normal and tangential forces regardless of the external torque or load. The difference between the results should be attributed to the differences in the task mechanics.

(2) The second hypothesis should be rejected: the force values were different for the ascending and descending parts of the load force changes and the thumb and VF normal forces were as a rule not equal. The second result was especially surprising: We expected the grasping synergy to be so robust that the normal forces of the thumb and VF would always be equal in magnitude even if this equality is not required by the task.

A possible reason for this difference is a lack of precision, as subjects were not provided with the usual feedback immediately available when grasping free objects, namely that the object would translate if the forces are not equal. A further explanation is that increasing the normal forces in the thumb or virtual finger would allow larger application of tangential forces for the appropriate side. This may help explain the observed differences in strategies for control of the tangential forces.

The normal forces showed different patterns, depending on the subject and the external torque condition. When the external moment was at its highest (0.8 Nm), the VF normal force increased very little with the increase in load force. This may be because the VF normal force begins already at a high level in order to maintain rotational equilibrium, so does not need to increase to prevent slipping. The normal force increased more at smaller external moment magnitudes, but not in a symmetrical way. These results can be contrasted to the findings in Zatsiorsky et al. (2002), where similarly the lowest normal forces were observed for zero external torque, and the increases of normal force for higher load forces were smaller with increased magnitude of the external torque. However, in Zatsiorsky et al. (2002), the force patterns were symmetrical. The differences observed may be due to the fact that here the moment arms for the thumb and virtual finger were different, and the task here is a dynamic one, whereas the aforementioned results were from a static case.

Despite the load force returning to zero at the end of the force decrease, the normal forces did not return to their initial levels. In two-finger grasping experiments with a similar pattern of externally applied force increase and decrease, hysteresis effects were not reported (Johansson et al., 1992), however in these experiments the direction of applied force was horizontal and not vertical as in the present experiment, and only two fingers were used. In a task where subjects were required to produce vertical forces on a fully constrained object, when the forces were produced always in the same direction (up), hysteresis was also not reported (De Freitas et al., 2007). However, this task involved two-finger self-produced forces rather than the external forces in this task. In many motor tasks, hysteresis of the muscles is observed (Kostyukov, 1998; van Groeningen et al. 1999), however, the large magnitude of hysteresis observed here is likely to have a neural basis. It appears that the subjects chose to maintain a relatively high level of normal force to allow them to resist future perturbations, although in this experimental setup there were none. Based on this reasoning, we would expect that if there was first a force decrease followed by a force increase, a similar increase of normal forces at the end would be observed.

In spite of different coordination patterns employed, the subjects quickly learned to successfully perform the task: the handle tilt was prevented and no slipping occurred. Hermsdorfer & Blankenfeld (2008) found that countering an external load is not as stable as self-performed movements, although after training the grip force and load force become better synchronized. As a very small amount of training was provided for this task (only two practice trials for each condition), it is possible that further training would have resulted in a single coordination pattern that all subjects will use (‘most efficient coordination pattern’). This pattern may differ from those observed or it may be one of them. This is an open question requiring further study.

(3) The third hypothesis was confirmed. This work seems to support the principle of superposition. A number of previous works looking at prehension have found that the elemental variables can be divided into two subsets, one for slip prevention control and one for tilt prevention control (Zatsiorsky et al., 2004, Shim et al, 2005a). In Shim et al (2005a), it was observed that the variables associated with moment production did not include the grip force, a finding replicated here. The lack of correlation of grip force and moment due to grip force is probably due to the observation here that for most of the subjects, the moment due to the normal forces is approximately constant, which requires covariation of the virtual finger moment arm (which is achieved by changing the sharing pattern), rather than changing the normal force magnitude. In contrast, the tangential forces and moment due to the tangential forces did covary. The separation observed here suggests that for this task as observed for other tasks, control may be divided into two subsets, one for load support, and one for tilt prevention.

One of the main differences between this study and other prehension studies was that in most previous studies, completely predictable unconstrained objects have been used, compared to the partially constrained object subject to external forces used in this experiment. Hence, we would not expect the findings from this study to be generalizable to all objects in day-to-day use. Based on the results of this study, we suggest that an invariant property when grasping an object subject to a changing external force is the correlated increase in tangential forces of the thumb and virtual finger, rather than the equal increases that have been observed previously. This appears to be due to the unequal moment arms. We propose that investigation of objects with non-uniform moment arms, as is the case with many common objects, is essential for gaining a greater understanding of prehension.

One of the least expected results of the study is the observation of two strategies of stabilizing the total moment of force displayed by different subjects. In a recent study (Gorniak et al., 2009), multi-digit synergies have been studied at both the upper level of the assumed hierarchy (VF level) and its lower level (individual finger, IF level). In that study, synergies have been defined as co-varied changes in elemental variables at the selected level of analysis stabilizing the output of that level. The study has shown, in particular, that the total moment of force (M) was stabilized at the VF level, while the moment produced by the tangential forces (M^t) was stabilized at the IF level, but not at the VF level. This finding makes sense if considered within the whole task of holding an object. The task may be viewed as involving three components: (1) The production of the required resultant tangential (load resisting) force; (2) The production of a zero resultant horizontal force (and sufficient normal forces at the interface between the digits and the object, given the friction); and (3) The production of a zero net moment of force. In the study of Gorniak et al. (2009), to satisfy the first requirement, all the subjects demonstrated, across trials, negative co-variation of the tangential forces produced by the thumb and the VF. This strategy effectively stabilized the resultant tangential force but it destabilized M^t by creating a force couple (the two forces are on the opposite sides of the axis of rotation).

This experiment examined the stabilization of total moment of force within a particular trial, with a constantly varying load force. The unequal moment arms for tangential forces of the thumb and the VF require that if the subject did not share the increase in tangential forces with the ratio between thumb and VF tangential forces of 2:3, they must negatively covary M^t and Mⁿ_, within a trial, to prevent rotation of the handle. While this negative covariation within a trial was observed for some subjects, others chose to increase the tangential forces in the ratio of 2:3, in effect, minimizing M^t variation, and allowing M to be stabilized without co-variation of M^t and Mⁿ. We suggest that this strategy may reflect the novelty of the task. Note that stereotypical motor patterns limiting the variance of elemental variables is typical of early stages of motor learning (Bernstein 1996; Latash et al. 2002; Kang et al. 2004). This may be viewed as a strategy of ensuring an acceptable level of accuracy in the absence of performance stabilizing synergies. One may expect this strategy to be substituted with synergic performance with sufficient practice: A prediction to be tested in future studies.