VASO-Based Calculations of CBV Change: Accounting for the Dynamic CSF Volume

Abstract

The goal of the vascular space occupancy (VASO) imaging technique is to use selective nulling of the blood signal to infer relative changes in cerebral blood volume (CBV). In accordance with recent work, we show that changes in the local CSF fraction (x_c) with activation can significantly impact the VASO signal, thereby limiting our ability to infer ΔCBV from ΔVASO alone. Here we calculate CBV change using a VASO-based method which ACcounts for the Dynamic Cerebrospinal (ACDC) fluid fraction. By combining data from two separate VASO acquisitions that eliminate either the blood signal (VASO_b) or the CSF signal (VASO_c), a nonlinear least-squares optimization may then be used to simultaneously solve for the relative changes in CBV and CSF with activation. The method is applied across the whole brain during a breath-holding task, offering insight into the relationship between changes in CBV and x_c associated with global vasodilatation. Calculations of mean changes in CBV in different volumes of interest obtained from the proposed method compare much better with previous (gold-standard) PET data than traditional VASO methods that do not account for a nonzero Δx_c with activation. This confirms the necessity of incorporating the dynamic CSF volume into VASO-based calculations of ΔCBV. Magn Reson Med 58:308–315, 2008.

While the noninvasiveness and high temporal resolution of blood oxygenation level-dependent (BOLD) imaging have led to its preferential status in functional MRI, the numerous contributors to the BOLD signal—cerebral blood flow (CBF), cerebral metabolic rate of oxygen (CMRO₂), and cerebral blood volume (CBV)—complicate its interpretation. Noninvasive acquisitions of CBF or CBV, using arterial spin labeling (ASL) (1) or vascular space occupancy-related methods (2,3), respectively, would not only lead to an improved understanding of BOLD, but also potentially offer superior stand-alone methods of fMRI. While quantitative ASL continues to suffer from issues such as transit time uncertainty and contamination from intravascular blood (4), interpretation of the VASO signal is also still under investigation (5–8). In particular, the impact of cerebrospinal fluid (CSF) on the VASO signal, both at rest (6,7,9) and during activation (6,8), has received recent attention. Partial volume effects within voxels containing CSF can significantly increase (or in some cases decrease) the magnitude of VASO signal changes (7). Furthermore, recent work (8) has suggested that a minor change in the CSF fraction with activation, such as the 5.6% decrease found by Donahue et al. (6) during visual stimulation, is sufficient to significantly impact the VASO signal.

While the concurrent nulling of blood and CSF via VASO-FLAIR offers an efficient method of measuring simultaneous changes in blood and CSF with activation, this can only be achieved in single slices (6,9). In contrast, the MAGIC (Multiple Acquisitions with Global Inversion Cycling) VASO technique first proposed by Lu et al. (10) has recently been extended to whole brain coverage, with demonstration of effective nulling of either blood or CSF in separate acquisitions depending on the choice of inversion time (8). MAGIC VASO employs a series of global inversion pulses between groups of slices in order to keep the longitudinal blood signal close to zero throughout the entire volume acquisition. The impact of incomplete blood nulling in particular slices has been investigated and shown to be significant (8), thereby prohibiting the simplifications used in CBV calculations performed in some previous VASO studies (2,5,6,11). In addition, examination of the sensitivity of the VASO signal to local resting CBV indicates that a 50% underestimation of CBV_rest would result in a 100% overestimation of the percent CBV change calculated from a simple VASO experiment (8). When assuming a uniform CBV_rest across the brain, as some studies have done (2,5,11), such errors are not improbable given that resting CBV has been shown to vary from 2.5 to 8.7 mL / 100 mL in different regions (12). Consequently, it becomes apparent that global CBV_rest maps must be used in calculations of percent CBV change from VASO. The present study is the first to use voxelspecific values obtained from a global CBV_rest map to calculate ΔCBV from VASO.

Our proposed technique uses separate acquisitions of blood-nulled and CSF-nulled VASO signals during rest and activation that allows for the calculation of relative changes in CBV while ACcounting for the Dynamic CSF volume (ACDC). To assess VASO ACDC, we employed a breath-holding paradigm to induce hypercapnia, which has been shown in numerous studies to cause widespread dilatation of the cerebral arterioles (13–19). To our knowledge, these are the first noninvasive whole-brain MRI measurements of CBV change that account for the change in local CSF fraction. These results are compared to VASO-based solutions that do not allow for CSF change and to previous literature on cerebral vascular reactivity. In addition, the relationship between relative changes in CSF and CBV is discussed with suggestions for further investigation.

MATERIALS AND METHODS

Theory

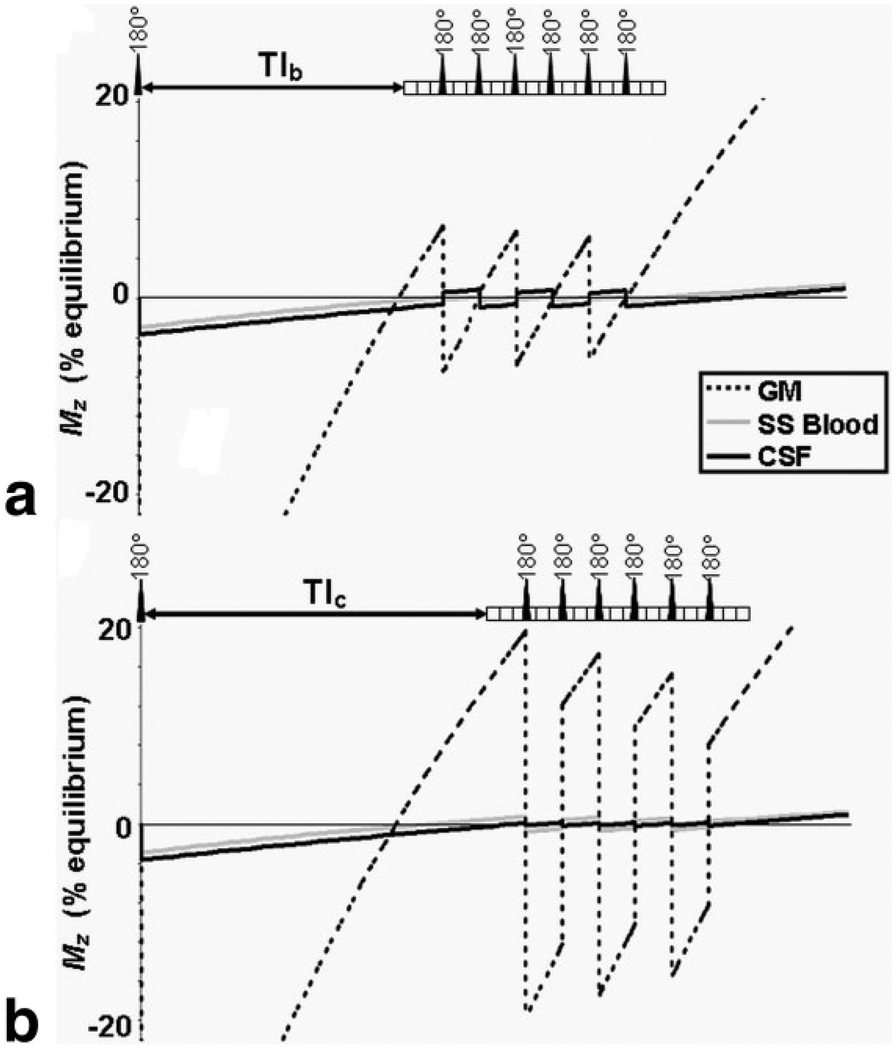
We have previously demonstrated the ability of MAGIC VASO to eliminate the signal from CSF instead of blood (8); this has the potential to provide additional information about local changes in x_c with activation. Let us define VASO_b and VASO_c, respectively, as the blood-nulled and CSF-nulled VASO signals. The longitudinal magnetizations of blood, gray matter (GM), and CSF as a function of time for VASO_b and VASO_c are shown in Fig. 1a,b for a 21-slice acquisition with three slices between global inversions. In all simulations the longitudinal relaxation times of white matter (WM), GM, blood, and CSF at 3.0 T are taken as 832 ms (20), 1331 ms (20), 1627 ms (21), and 3817 ms (9), respectively. With TR = 3 sec, the correct TIs to null the blood and CSF signals are TI_b = 752 ms and TI_c = 973 ms, respectively.

FIG. 1.

Longitudinal magnetizations of blood, CSF, and gray matter as function of time for (a) VASO_b and (b) VASO_c acquisitions (21 slices, 3 slices per global inversion, TR = 3 s, TI_b = 752 ms, TI_c = 973 ms). Each block in the pulse sequence represents the GE-EPI acquisition of an individual slice. This simulation assumes x_c = 0.1 and CBV = 5.5 mL / 100 mL.

Following previous work (8), ΔVASO_b,c depends on Δx_c, ΔCBV, x_c,rest, CBV_rest, and M_b,c(TI_b,c)/M_t(TI_b,c), where M_b,c is the longitudinal magnetization of blood or CSF relative to that of tissue (M_t) at the time of acquisition, TI_b or TI_c. In accordance with recent work by Donahue et al. (6), we note that M_b can be divided into fractions of steady-state (SS) and nonsteady-state (NS) blood such that ${\mathrm{M}}_{\mathrm{b}}={\mathrm{X}}^{\text{SS}}{\mathrm{M}}_{\mathrm{b}}^{\text{SS}}+{\mathrm{X}}^{\text{NS}}{\mathrm{M}}_{\mathrm{b}}^{\text{NS}}.$ For the TI range used in the present study (752–973 ms), it may be assumed that X^SS = CBV_venular/CBV and X^NS = CBV_arteriolar/CBV. In other words, at the time of acquisition, inflowing blood that has only experienced a single global inversion (NS) has reached the arteriolar compartment, while it is assumed that none of this NS blood has reached the venular compartment and consequently this fraction of the blood volume is in steady-state. According to previous literature, we assume that CBV_arteriolar = 0.3 · CBV (6,18), so it follows that X^NS = 0.3. Note that this assignment of steady-state and nonsteady- state blood fractions is somewhat speculative; however, the determination of these fractions on a voxel-wise basis is beyond the scope of this work. The expressions for the relative VASO_b and VASO_c signal changes are given in Eq. [1]. Note that when assuming 100% steady-state (X^NS = 0) and rearranging to solve for ΔCBV/CBV_rest, this equation simplifies to Eq. [2a] of our previous study (8), which did not account for the influence of nonsteady-state blood on VASO.

$$\begin{array}{ll}\frac{\mathrm{\Delta }{\mathit{\text{VASO}}}_{b,c}}{{\mathit{\text{VASO}}}_{b,c}}=\hfill & \frac{1}{\frac{(1-x_{c,\mathit{\text{rest}}})}{(1-x_{c,\mathit{\text{rest}}}-\mathrm{\text{Δ}}{x}_c)}\left[1-\frac{1-\left(\frac{1}{1-1/x_{c,\mathit{\text{rest}}}}\right)\left(\frac{C_{\mathit{\text{csf}}}}{C_{\mathit{\text{par}}}}\right)\frac{M_c(T{I}_{b,c})}{M_I(T{I}_{b,c})}}{1-\frac{M_b(T{I}_{b,c})}{M_I(T{I}_{b,c})}}\cdot \frac{C_{\mathit{\text{par}}}}{C_b{\mathit{\text{CBV}}}_{\mathit{\text{rest}}}}\right]}\hfill \\ \hfill & \times \{\left[1-X^{NS}\left(\frac{\frac{M_{b,c}}{M_t(T{I}_{b,c})}-\frac{M_b(T{I}_{b,c})}{M_t(T{I}_{b,c})}}{1-\frac{M_b(T{I}_{b,c})}{M_t(T{I}_{b.c})}}\right)\right]\frac{\mathrm{\Delta }\mathit{\text{CBV}}}{{\mathit{\text{CBV}}}_{\mathit{\text{rest}}}}-\frac{\mathrm{\text{Δ}}{x}_c}{(1-x_{c,\mathit{\text{rest}}}-\mathrm{\Delta }{x}_c)}\hfill \\ \hfill & \times \left[1-\frac{C_{\mathit{\text{par}}}}{C_b{\mathit{\text{CBV}}}_{\mathit{\text{rest}}}}\left(\frac{1-\left(\frac{C_{\mathit{\text{csf}}}}{C_{\mathit{\text{par}}}}\right)\frac{M_c(T{I}_{b,c})}{M_t(T{I}_{b,c})}}{1-\frac{M_b(T{I}_{b,c})}{M_t(T{I}_{b,c})}}\right)-X^{\mathit{\text{NS}}}\left(\frac{\frac{M_{b,c}}{M_t(T{I}_{b,c})}-\frac{M_b(T{I}_{b,c})}{M_t(T{I}_{b,c})}}{1-\frac{M_b(T{I}_{b,c})}{M_t(T{I}_{b,c})}}\right)\right]\}\hfill \end{array}$$ [1]

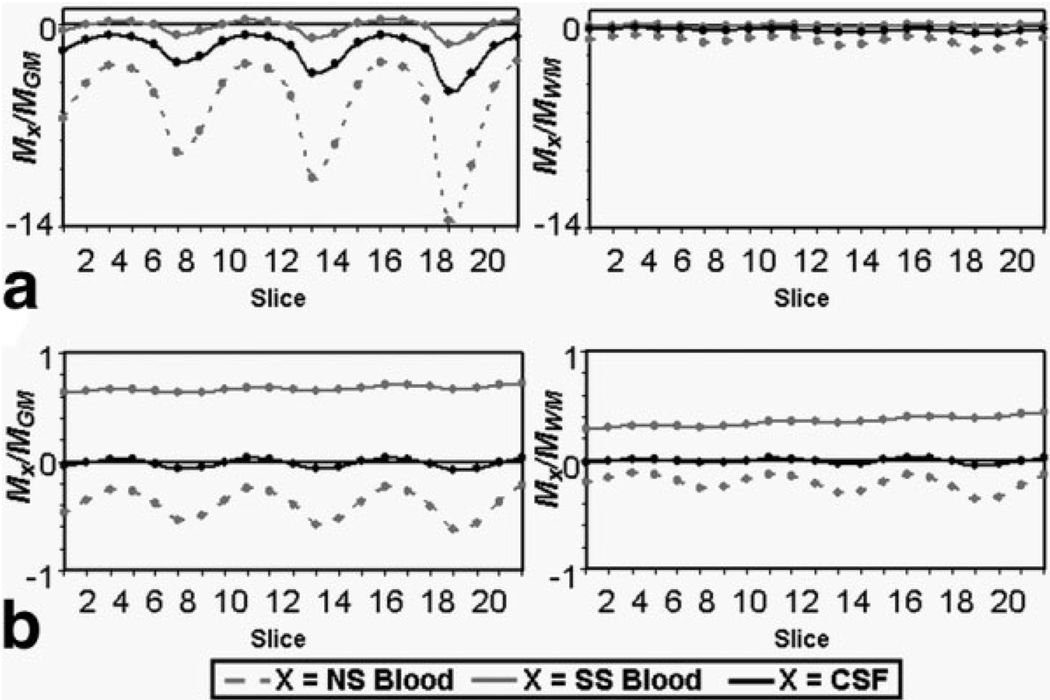
The water proton densities of parenchyma, blood, and CSF are taken as C_par = 0.89 mL water/mL parenchyma, C_b = 0.87 mL water/mL blood, and C_csf = 1.0 mL water/mL CSF, respectively (22). M_b,c/M_t ratios are determined for each slice using the simulated longitudinal magnetizations for the 21-slice MAGIC VASO_b and VASO_c sequences shown in Fig. 1, while the tissue type (t = GM or WM) for each voxel may be assigned by segmentation of a high-resolution anatomic image. The longitudinal magnetization ratios are shown for each slice of a VASO_b and VASO_c acquisition in Fig. 2. ${\mathrm{M}}_{\mathrm{b}}^{\text{NS}}$ has been modeled as having experienced only one repetition of the MAGIC VASO sequence, while simulations reveal that steady-state (i.e., ${\mathrm{M}}_{\mathrm{b}}^{\text{SS}}$ ) has been reached by the tenth repetition for both VASO_b and VASO_c acquisitions. The M_b,c/M_t ratios show significant variation between slices, but to a much higher degree in VASO_b (Fig. 2a) than VASO_c (Fig. 2b). This is a direct result of the shorter inversion time used in VASO_b. By commencing the series of global inversions on a steeper portion of the inversion-recovery curve, the various signals (blood, tissue, CSF) change more rapidly between successive inversions (see Fig. 1). A comparison of Fig. 1a and 1b also shows a clear advantage of the VASO_c acquisition over VASO_b in terms of signal-to-noise ratio (SNR). By using a longer inversion time, the tissue signal has regained much more of its equilibrium magnitude by the start of the slice acquisitions. This is confirmed by the raw VASO_b and VASO_c images in Fig. 3. This reveals the tradeoff between VASO_b and VASO_c: while the latter has less slice-dependent variation in magnetization ratios and superior SNR, it is almost completely insensitive to the redistribution of water between the tissue and blood compartments. This is because the longitudinal magnetizations of tissue and blood are both of the same sign in any given slice (see Fig. 1b), such that a water proton that changes compartments will only experience a small change in density (C_par vs. C_b). Conversely, VASO_b is sensitive to the redistribution of water from tissue to blood, but it is also sensitive to changes in the CSF fraction (8), which have the ability to confound calculations of ΔCBV/CBV_rest from VASO_b data alone. Therefore, acquisition of either VASO_b or VASO_c alone does not provide adequate information for determining changes in CBV. Instead, the combination of both datasets will produce two equations, one for VASO_b and one for VASO_c, easily allowing for the voxel-wise calculation of the two unknowns: Δx_c/x_c,rest and ΔCBV/CBV_rest (see Eq. [2]). Note that Eq. [1] stipulates that the values of x_c,rest and CBV_rest must also be known for each voxel prior to solving the system of equations. As discussed below, x_c,rest can be calculated from a normalized T₂-weighted TSE acquisition (23), while local CBV_rest values may be measured or taken from the literature. Thus, with voxel-wise values for x_c,rest and CBV_rest, and simulated values of all longitudinal magnetization ratios M_i/M_j in Eq. [1] (see Fig. 2) in conjunction with GM/WM segmentation, and with X^SS, X^NS, C_par, C_b, and C_csf taken from the literature, we arrive at the following system of equations:

$$\begin{array}{ll}\frac{\mathrm{\Delta }{\mathit{\text{VASO}}}_b}{{\mathit{\text{VASO}}}_b}=f_b\left(\frac{\mathrm{\Delta }\mathit{\text{CBV}}}{{\mathit{\text{CBV}}}_{\mathit{\text{rest}}}},\frac{\mathrm{\Delta }{x}_c}{x_{c,\mathit{\text{rest}}}}\right);\hfill & \frac{\mathrm{\Delta }{\mathit{\text{VASO}}}_c}{{\mathit{\text{VASO}}}_c}\hfill \\ \hfill & =f_c\left(\frac{\mathrm{\Delta }\mathit{\text{CBV}}}{{\mathit{\text{CBV}}}_{\mathit{\text{rest}}}},\frac{\mathrm{\Delta }{x}_c}{x_{c,\mathit{\text{rest}}}}\right)\hfill \end{array}$$ [2]

where the functions f_b and f_c correspond to Eq. [1] following substitution of the known VASO_b and/or VASO_c parameters listed above. Using the relative VASO_b and VASO_c signal changes, the system in Eq. [2] may be solved simultaneously on a voxel-by-voxel basis for Δx_c/x_c,rest and ΔCBV/CBV_rest.

FIG. 2.

Simulated longitudinal magnetization ratios of steady-state blood (M_b^SS), nonsteady-state blood (M_b^NS), and CSF (M_c) relative to gray matter (M_GM) or white matter (M_WM) for each slice of the (a) VASO_b and (b) VASO_c acquisitions.

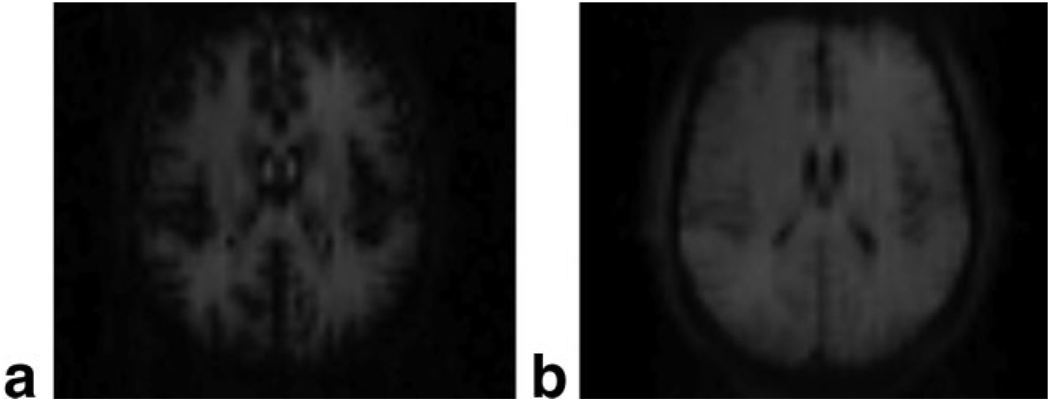
FIG. 3.

Raw images of slice 10 in a single subject for (a) VASO_b and (b) VASO_c.

MRI Experiments

Scans were performed on a Siemens (Erlangen, Germany) 3.0 T Trio Scanner. All 14 subjects (nine male, five female; mean age ± SD: 25 ± 4 years; range: 19–31 years) gave informed written consent prior to participating in the study, which was approved by the Yale Institutional Review Board.

A breath-holding paradigm was used to assess CBV changes stemming from global vasodilatation. The task consisted of 27-sec blocks of self-paced breathing, alternating with 21-sec blocks of breath-holding after inspiration, repeated five times with extra periods of normal breathing at the beginning and end for a total run time of 5 min. Subjects were prompted by visual cues projected to them from outside the scanner. The time remaining for the breath-hold period was communicated to subjects by a series of seven asterisks that disappeared individually every 3 sec until the 21-s block was over. Subjects were permitted to exhale slowly if desired during the breath-hold period, but not to inhale again until instructed to do so. Task performance was assessed by communication with subjects between scans and again at the end of the session.

The parameters for MAGIC VASO_b,c acquisitions used for ACDC were: 21 axial slices (3 per global inversion, for a total of 7 inversions) with a slice thickness of 4 mm and a 1 mm gap between slices, FOV = 224 × 196 mm², matrix = 64 × 56, bandwidth (BW) = 2004 Hz/Px, anterior to posterior phase-encode direction with a 5/8 partial Fourier acquisition, TE = 8.8 ms, TR = 3000 ms, TI_b = 752 ms, and TI_c = 973 ms. Spatially nonselective inversion was achieved with a sinc pulse transmitted by a body coil. Slices were acquired with single-shot gradient-echo echo planar imaging (GE-EPI) with a flip angle (FA) of 90°. To avoid stimulated echo formation, the multidirectional gradient cycling scheme proposed by Lu et al. (10) was used. A spectral-selective presaturation pulse (SPIR) was used prior to the first excitation pulse in each TR to suppress fat artifacts. All MAGIC VASO_b,c acquisitions were acquired in ascending and descending slice order (two runs of each) and averaged together for consistent SNR across slices. In addition, VASO_b runs were alternated with VASO_c runs to prevent run order effects. Each run was 5 min in duration, for a total of 40 min for all MAGIC VASO acquisitions.

For comparison, GE-EPI BOLD images with TE = 47 ms were acquired in a subset of eight subjects with identical slice positioning, resolution, and TR as MAGIC VASO (but with BW = 2442 Hz/Px). BOLD images were acquired as the second echo in a dual-echo CBF-BOLD sequence that only permitted half the coverage of MAGIC VASO (the CBF data are not presented in this article). Therefore, two partially overlapping sets of 12 axial slices comprising the upper and lower halves of the brain were combined to produce a single BOLD volume. For comparable contrast-to-noise for VASO and BOLD, three upper runs and three lower runs of CBF-BOLD were acquired in each subject, for a total of 30 min for all CBF-BOLD acquisitions.

High-resolution 3D-MPRAGE (1 × 1 × 1 mm³ resolution) acquisitions were performed for each subject to obtain GM/WM segmentation. To determine x_c,rest, T₂- weighted turbo spin echo images were acquired in each subject with the following parameters: slice thickness of 4 mm and a 1 mm gap between slices, FOV = 256 × 256 mm², matrix = 256 × 256, BW = 130 Hz/Px, anterior to posterior phase-encode direction with a 6/8 partial Fourier acquisition, TE = 116 ms, TR = 3000 ms, turbo factor = 15. Resting CBV data were obtained from a PET study involving dynamic 60-min 3D scans following intravenous injection of [11C]arachidonic acid (12); 35 simultaneous slices with 4.25-mm slice separation and in-plane resolutions of 6–7 mm were acquired in eight subjects.

Data Processing and Analysis

Theoretical modeling was performed using Maple 9.03 (Maplesoft, Waterloo Maple, Waterloo, Ontario). Image registration and analysis was performed using BioImage-Suite software (Yale University MRRC: www.bioimagesuite.org). The first four repetitions of VASO_b and the first eight repetitions of the VASO_c were discarded based on simulations indicating the time to reach steady-state. For the detection of activation the timecourses were correlated with box-car functions corresponding to the stimulus paradigm delayed by four repetitions. This 12-sec delay was used to account for the initial signal drop observed during inspiration breath-holding, which is the result of a transient decrease in PaCO₂ at onset (24,25). GLM normalized beta maps were acquired for MAGIC VASO data from each subject. All maps were smoothed using a 3D Gaussian function (σ = 3.0) prior to group analysis. The x_c,rest values for individual voxels were obtained on a subject-specific basis by normalizing the T₂-weighted TSE acquisition to the highest-intensity voxel (pure CSF) in the image (23). Given that resting CBV does not vary significantly across subjects, CBV_rest values for each voxel were taken from a single global CBV_rest map acquired from a previous PET study (12). The segmentation of each subject’s 3D MPRAGE into GM and WM was used to assign the slice-specific values of M_b,c/M_GM and M_b,c/M_WM. To determine the relative changes in CBV and CSF, the VASO_b and VASO_c equations (Eq. [2]) were solved simultaneously for ΔCBV and Δx_c on a voxel-by-voxel basis using a least-squares optimization in Matlab (MathWorks, Natick, MA) with the following constraints: −5% ≤ ΔCBV/CBV_rest ≤ 100%; −100% ≤ Δx_c/x_c,rest ≤ 50%. The norm of the residuals (i.e., sum of the squares) for each solution set was also calculated. To compare the VASO ACDC method to those that do not account for a change in CSF fraction with activation, the two equations were also solved simultaneously by least-squares optimization with the constraint Δx_c/x_c,rest = 0%. The initial values for all optimizations were ΔCBV/CBV_rest = 20% and Δx_c/x_c,rest = 0%. In addition to the two-equation methods, VASO_b data alone were also used to obtain a solution for ΔCBV/CBV_rest (with Δx_c/x_c,rest = 0) for comparison. All equation-solving and optimizations were performed at the 3.5 × 3.5 × 4 mm³ resolution of the MAGIC VASO acquisitions, with the GM/WM segmented maps and resting CSF/CBV maps resliced to the same resolution. Each subject’s functional data were registered to the corresponding 3D anatomic for that subject and all anatomic images were nonlinearly registered to a reference brain for comparison and group analysis. Nonlinear registration was used to reduce anatomic variability across subjects. The volumes of interest comprising GM and WM were defined from the mean of the GM and WM segmented MPRAGE images.

RESULTS

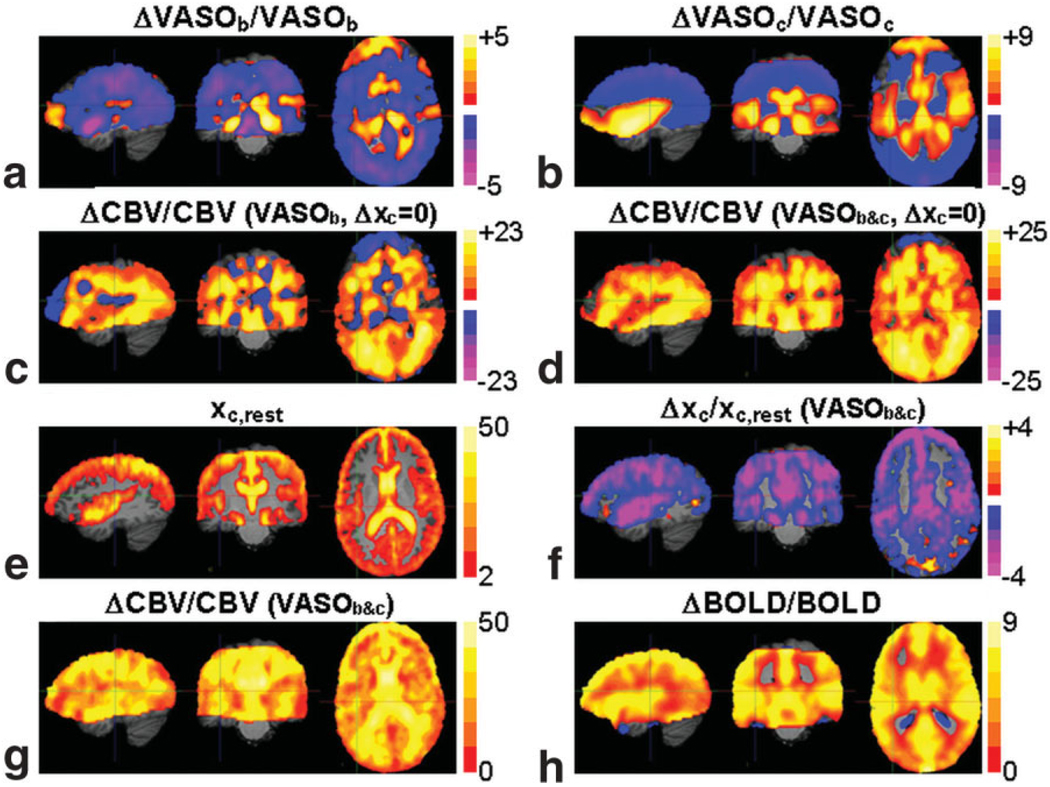
In Fig. 4 the mean percent signal change maps for VASO_b and VASO_c (n = 12) during the breath-holding task are presented along with the ΔCBV/CBV_rest maps calculated using three different methods: the VASO_b data alone (with Δx_c = 0) (Fig. 4c), the combined VASO_b and VASO_c data (with Δx_c = 0) (Fig. 4d), and the combined VASO_b and VASO_c data without a constraint on the dynamic CSF fraction (ACDC) (Fig. 4g). For both methods (d) and (g) that employ the least-squares optimization, the norms of the residuals were found to be identical within experimental error, with a mean of 0.0001% in GM and a maximum value of 0.003%. This error is negligible relative to the percent VASO_b and VASO_c signal changes typically observed (>0.1%). The two ΔCBV/CBV_rest maps obtained under the assumption of constant CSF fraction (Fig. 4c,d) exhibit several notable locations of zero CBV change and/or negative CBV change. These results are immediately called into question, as there is no physiological basis for vasoconstriction during hypercapnia. Moreover, these negative/absent signal changes are highly localized to regions of measurable CSF fraction, apparent from the mean x_c,rest map (n = 12) used in all three solutions (shown overlaid on the reference MPRAGE in Fig. 4e). Simultaneous solving of the VASO_b and VASO_c equations for ΔCBV/CBV_rest and Δx_c/x_c,rest by the least-squares method produces the mean percent signal change maps in Fig. 4f,g. There is a widespread decrease in the CSF fraction with hypercapnia, supporting the theory that blood vessel dilatation displaces CSF water in addition to tissue water. VASO ACDC results in a much more uniform ΔCBV/CBV_rest map (Fig. 4g), as compared to the results shown in Fig. 4c and Fig. 4d, which do not account for CSF volume change. As a standard for comparison, the mean BOLD percent signal change map (n = 8) in response to the breath-holding task is shown in Fig. 4h.

FIG. 4.

The mean percent signal change maps during hypercapnia for (a) VASO_b and (b) VASO_c. The composite ΔCBV/CBV_rest map calculated from VASO_b only, with Δx_c = 0 (c), and calculated from VASO_b and VASO_c, with Δx_c = 0 (d). The composite map of the resting CSF distribution overlaid on the MPRAGE (e). The mean percent change maps for Δx_c/x_c,rest (f) and ΔCBV/CBV_rest (g) calculated from VASO_b and VASO_c, with −100% < Δx_c/x_c,rest < 50% (VASO ACDC). Also shown for comparison is the mean percent BOLD signal change map during hypercapnia (h).

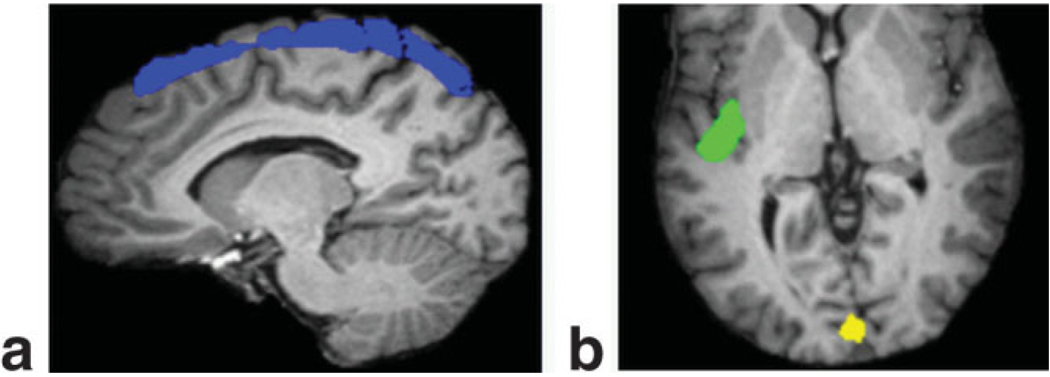
In Table 1 the mean relative percent changes in CBV and x_c within three distinct VOIs are presented for each of the three solutions, with the VOI definitions shown in Fig. 5. There is no significant difference between the mean ΔCBV/CBV_rest values for the two methods that constrain Δx_c to zero in the selected VOIs. However, a comparison of Fig. 4c and 4d indicates a slight discrepancy between the non-changing CSF solutions, where the former shows more voxels of negative ΔCBV, proximal to the auditory cortex, for instance. This disparity, discussed further in the following section, is eclipsed however by the major impact that incorporating the local change in CSF fraction has on our calculation of ΔCBV/CBV_rest. This is particularly evident in the superior cortex and auditory cortex VOIs. Without accounting for the 4.3% decrease in CSF fraction in the auditory cortex during hypercapnia and simply relying on the VASO_b data alone, the CBV increase would be estimated at 1.2%. Alternatively, by incorporating this seemingly small CSF change into our calculations using the ACDC method it is determined that the CBV increase is 8.4%. Similarly, by including the impact of the 2.7% decrease in CSF fraction in the superior cortical region, we obtain ΔCBV/CBV_rest = 10.4%, in contrast to the value of 0.7% calculated when assuming Δx_c = 0. This is nearly a 15-fold increase! Note that while the majority of the voxels in the brain experienced a decrease in CSF fraction during hypercapnia, there was a negligible change observed around the visual cortex. Consequently, the VOI measurements shown in Table 1 indicate that there is no appreciable difference between the method that incorporates changes in CSF volume and those methods which do not.

Table 1.

Mean Percent CBV (±SD) in VOIs During Hypercapnia

		ΔCBV/CBVrest (%)
Method		Superior cortex	Visual cortex	Auditory cortex
VASOb		0.7 ± 1.0	0.7 ± 1.4	1.2 ± 1.7
VASOb&c(Δxc = 0)		1.3 ± 1.0	2.2 ± 1.4	2.6 ± 1.4
VASOb&c(−100% <	Δxc/xc,rest < 50%)	10.4 ± 6.2	1.6 ± 1.4	8.4 ± 4.8
	Δxc/xc,rest (%) →	−2.7 ± 2.0	2.0 ± 2.4	−4.3 ± 3.5

CBV, cerebral blood volume; VOI, volume of interest; VASO, vascular space occupancy; SD, standard deviation. Solved for using three different methods, with corresponding percent x_c changes included for the final method.

FIG. 5.

Volumes of interest comprising the (a) superior cortex and (b) visual and auditory cortices.

When solving the equations for VASO_b and VASO_c simultaneously without constraining the change in CSF fraction, the mean values of ΔCBV/CBV_rest in response to the breath-holding task in GM and WM are 9.1 ± 5.7% and 9.8 ± 5.4%, respectively. Conversely, when the VASO_b and VASO_c equations are solved with the constraint Δx_c = 0, the mean ΔCBV/CBV_rest values are 3.0 ± 2.9% (GM) and 5.1 ± 3.5% (WM). Likewise, when solving the VASO_b equation alone (with Δx_c = 0) the mean ΔCBV/CBV_rest values are 1.7 ± 3.0% (GM) and 3.0 ± 4.0% (WM).

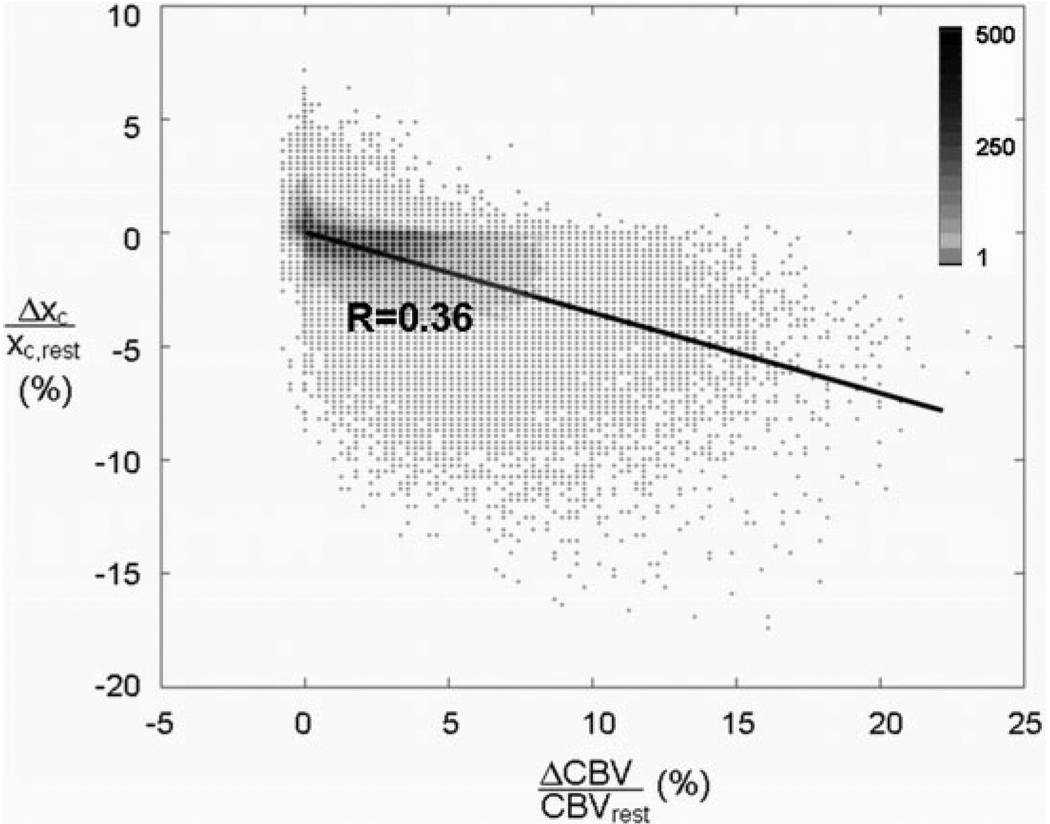
An examination of the relationship between Δx_c/x_c,rest and ΔCBV/CBV_rest across the whole brain during hypercapnia (Fig. 6) reveals some interesting aspects. The relative percent changes in CSF volume and CBV were calculated on a voxel-by-voxel basis and plotted for all subjects (n = 12). There is a significant inverse correlation between relative changes in CBV and the CSF fraction, which was fit using a linear regression (excluding data points for which Δx_c is identically zero). The relationship was also modeled using a natural logarithmic function; however, the difference in fit was statistically insignificant.

FIG. 6.

Percent CSF volume change as a function of percent CBV change in all voxels across all subjects as determined by VASO ACDC. The data are fit using a linear regression. The density of data points at each coordinate is indicated by the colorbar.

DISCUSSION

To demonstrate the new VASO-based technique of measuring CBV change the breath-holding task was selected for its ease of implementation and ability to induce global cerebral vasodilatation. The 21-sec periods of apnea were comfortably achievable by all subjects, while still of sufficient duration to elicit a significant hypercapnic response. Inspiration rather than the more challenging expiration breath-holding was used in an attempt to reduce potential task-correlated head motion associated with discomfort near the end of apneic periods (26).

When solving for relative CBV change using VASO ACDC, the mean values in GM and WM are in the range indicated by the literature on relative CBV changes resulting from hypercapnia in humans: 11.8% (17), 9.6 ± 5.7% (cortex) and 15.7 ± 15.0% (cerebellum) (19), and 8.0 ± 0.8% (GM) and 10.6 ± 1.1% (WM) (14) (for inspiration of 5% CO₂). Conversely, when using solution methods that employ the constraint Δx_c = 0, the mean ΔCBV/CBV_rest values are significantly lower than those for which the CSF fraction is permitted to change with activation and they do not compare as well to the previous literature.

Despite some minor differences, comparison of the two constant-x_c solutions (using either VASO_b,c or VASO_b) does serve to validate our two-equation method of determining ΔCBV/CBV_rest. The mean CBV changes in GM and WM VOIs for the two methods are identical within experimental error. It is probable that the discrepancies apparent in Fig. 4c,d could be the result of a lower SNR when using VASO_b data alone. In addition to the fact that the combination of VASO_b and VASO_c offers twice the volume of data, each VASO_c image inherently has a higher SNR due to the magnitude of the tissue signal (Fig. 2). This presents another benefit of using VASO_b and VASO_c data in combination. Comparing the relative variability of the results in Table 1 (measured as SD/mean), there is a 154% improvement in SNR for the VASO_{b,c (Δxc=0)} technique over using VASO_b alone, with a further 2% improvement when Δx_c is not constrained to zero. Since SNR is proportional to the square root of the number of acquisitions, the improvement from using VASO_c in combination with VASO_b far exceeds the gain in SNR that would be expected from purely doubling the number of VASO_b acquisitions (41% improvement). However, the additional time required for data analysis with this technique is clearly a disadvantage.

The intracranial space is comprised of 17% CSF by volume (27), with a complex distribution such that it is present not only in the ventricles but also in the cerebral fissures (23). The subarachnoid space, which is filled with CSF, is in direct contact with a thin layer known as the pia mater, which in turn adheres to every surface of the cortex (28). Beyond the ventricles the extent of the CSF distribution is apparent in Fig. 4e. Given the proximity of CSF to the cortical surface and its similar viscosity to water (29), it is highly likely that CSF will redistribute in response to local blood vessel dilatation. When allowing for a change in the local CSF fraction with cortical activation, the Δx_c/x_c,rest values in the current breath-holding task range from a minimum of −10% along the motor cortex to a maximum of +3% in the most distal regions of the brain. This can be explained by a redistribution of CSF in response to global vasodilatation: the CSF is expelled from central locations like the insular cistern by the increase in CBV, with some CSF relocating to the distal regions of the brain. This localized CSF increase likely reflects the fact that the overall volume of CSF in the intracranial space cannot change significantly (without ejecting CSF through the foramen magnum to expand the spinal dural sac), and therefore a widespread decrease in CSF fraction might be compensated by an increase elsewhere. Previous studies have shown that CSF pressure as measured in the cisterna magna rises significantly in response to hypercapnia, and it has been suggested that this is largely attributable to the mechanical effect of cerebral vasodilatation (30). Using VASO-FLAIR, a mean change in CSF fraction of −5.6% was found in the visual cortex during a visual stimulation task (6). Decreases in CSF volume have also been detected using spectroscopic water T₂ decay measurements during hypercapnia and visual stimulation (31). A significant VASO_b signal change was still detected in this study despite the influence of the CSF change. However, in another study involving auditory stimulation the auditory response observed with BOLD was completely undetected by VASO_b (8). Assuming the lack of VASO_b signal change in (8) is in fact due to a sufficient decrease in the local CSF fraction around the auditory cortex, the combined results (6,8) indicate that the degree to which the CSF fraction changes with activation is dependent on either the magnitude and/or location of the vasodilatation.

It would seem likely that the greater the increase in CBV, the greater the decrease in CSF fraction. This theory is supported by the results from the present breath-holding task, with Fig. 6 showing the relative CSF volume change plotted as a function of the relative CBV change on a voxel-by-voxel basis across all subjects. A significant negative correlation is observed between ΔCBV and Δx_c. However, it is important to note that the global nature of the hypercapnia task used in the present study prevents any analysis of the independent local responses to activation. It is not unlikely that the various compartments in question (blood, tissue, and CSF) will deform differently when the vasodilatation is localized (such as with auditory activation) and the surrounding region is relaxed and not subject to global activation. Depending on the proximity of CSF to the location of the hemodynamic response, it may be more preferable for one compartment to redistribute as opposed to another, thereby potentially altering the Δx_c–ΔCBV curve. VASO ACDC should be applied in further studies of localized activation to improve understanding of the local relationships between CBV change and CSF change.

The identical CBV sensitivities of GM and WM to hypercapnia are in agreement with previous PET studies (14,15). In contrast, our BOLD results indicate a lower sensitivity of WM to hypercapnia than GM (see Fig. 4h), in agreement with a number of other BOLD and CBF studies (16,24,25,32). Given that the resting microvascular blood volume of WM is significantly lower than that of GM, the absolute change in CBV anticipated with activation would also be lower. This has been suggested as a potential explanation for the reduced BOLD signal changes observed in WM (16). In view of the fact that the present VASO-based fMRI technique produces similar CBV changes in GM and WM, it is likely that the WM sensitivity of VASO is superior to that of BOLD. This could be associated with the different contrast mechanisms of VASO and BOLD: T₁ vs. T₂*, respectively. It is not surprising that BOLD sensitivity may be somewhat lower in WM than GM, given their average T₂ values: 79.6 ± 0.6 (WM) and 110 ± 2 (GM) (20). Note that the FAIR study that reported insignificant CBF changes in WM did not use a TE short enough to be insensitive to T₂*, and would consequently suffer from the same potential sensitivity limitations of BOLD. This points to another potential advantage of VASO functional imaging over BOLD.

CONCLUSIONS

In conclusion, we have presented a noninvasive VASO-based method for determining activation-induced CBV and x_c changes across the whole brain. We have shown that changes in the CSF fraction with activation can have a significant impact on the conventional blood-nulled VASO signal. By combining data from two separate VASO acquisitions that eliminate either the blood signal or the CSF signal, a nonlinear least-squares optimization may then be used to simultaneously solve for the relative changes in CBV and CSF with activation. Decreases in the CSF fraction were observed across most of the brain during hypercapnia, and shown to have a major impact on VASO-based CBV calculations. When accounting for all the local CSF changes with the VASO ACDC technique, the results compared very well with previous literature and no significant differences were found between the cerebral vascular reactivities of GM and WM. Further work will be required to characterize the relationship between CSF change and CBV change, but preliminary results indicate a strong correlation.