A Bayesian Meta-Analysis on Published Sample Mean and Variance Pharmacokinetic Data with Application to Drug-Drug Interaction Prediction

Summary

In drug-drug interaction (DDI) research, a two drug interaction is usually predicted by individual drug pharmacokinetics (PK). Although subject-specific drug concentration data from clinical PK studies on inhibitor or inducer and substrate's PK are not usually published, sample mean plasma drug concentrations and their standard deviations have been routinely reported. Hence there is a great need for meta-analysis and DDI prediction using such summarized PK data. In this paper, an innovative DDI prediction method based on a three-level hierarchical Bayesian meta-analysis model is developed. The three levels model sample means and variances, between-study variances, and prior distributions. Through a ketoconazle-midazolam example and simulations, we demonstrate that our meta-analysis model can not only estimate PK parameters with small bias, but also recover their between-study and between-subject variances well. More importantly, the posterior distributions of PK parameters and their variance components allow us to predict DDI at both population-average and study-specific levels. We are also able to predict the DDI between-subject/study variance. These statistical predictions have never been investigated in DDI research. Our simulation studies show that our meta-analysis approach has small bias in PK parameter estimates and DDI predictions. Sensitivity analysis was conducted to investigate the influences of interaction PK parameters, such as the inhibition constant Ki, on the DDI prediction.

1. Introduction

Pharmacokinetic approaches designed to characterize drug to absorption, distribution and elimination were well established (Rowland and Tozer 1995) and robust statistical methodologies were developed (Davidian and Giltinan 1995). Recently pharmacokinetic interactions among multiple drugs have received a great deal of attention because this phenomenon makes a significant contribution to adverse drug reaction profile of new drugs (Ito et al. 1998). The importance of drug-drug interactions (DDI) was exemplified by the interaction of ketoconazole (KETO) and terfenadine, which caused potentially life-threatening ventricular arrhythmias (Monahan et al. 1990), and the interaction between sorivudine and fluorouracil that resulted in fatal toxicity (Watabe et al. 1996; Okuda et al. 1997).

In the DDI research, one of the central questions is whether two individual drugs' pharmacokinetics (PK) models and their in-vitro DDI parameters can predict their in-vivo DDI (Ito et al. 1998). All the prior PK models and their parameters are summarized from multiple data sources (i.e. published PK studies in either literatures or public databases). Data for drug concentrations are usually published as sample mean profiles, together with standard deviations. Meta-analysis utilizing such summarized data is needed to obtain information from a vast existing resource.

Li et al. (2007) did some pioneer work in fitting PK models to sample mean data and evaluate the DDI prediction based on estimated PK parameters. They showed that it was feasible to draw inference for important PK parameters with summarized data, which were usually only available resource during the early phase DDI research. They proposed a mean model (see Section 2.5) for estimating PK parameters. This paper extends their work to estimation of both PK parameters and variance components. It also aims at predicting the both mean and variance of DDI, which are both interesting in practice. Understanding inter-individual variability is of great importance in PK studies. Large inter-individual variation usually means large environmental or genetic effects, which usually lead to pharmacogenetics studies. Readers can refer to Li et al. (2007) for a more detailed discussion of related issues and challenges for DDI prediction.

It is well known that the majority of DDIs depend on drug metabolizing enzymes and/or cell membrane drug transporters (www.Drug-Interactions.com). The single most important locus of DDIs is the cytochrome P450 (CYP) family of drug monooxygenases located in the gut-wall and liver (de Waziers et al. 1990). Among CYPs, CYP3A is the most abundant and accounts for approximately 30% and 90% of CYP protein in liver and intestine, respectively (Shimada et al. 1994). In addition, more than 60% of the drugs that are eliminated primarily by metabolism are metabolized by CYP3A. KETO is a potent and extensively characterized CYP3A inhibitor, and midazolam (MDZ) is a highly selective CYP3A substrate in vivo that does not depend on membrane transporters for intracellular access (Tsunoda et al. 1999). Therefore, the KETO-MDZ pair is employed as an inhibitor-substrate example to illustrate our model based approach to DDI prediction. This paper develops an innovative hierarchical Bayesian meta-analysis model for PK parameter and variance component estimation. In particular, we focus on performing DDI prediction based on meta-analysis. Actual computation is via a Monte Carlo Markov chain (MCMC) method.

2. Specification of Models for Meta-analysis

2.1 Pharmacokinetics Model Specification

KETO Pharmacokinetic Model

Table 1 and Figure 1 (a) summarize seven published KETO PK data sets that were used to establish the PK model of KETO. These data were obtained through digitalization from corresponding papers (Table 1). KETO was administered orally in all studies, although dosing forms and conditions could differ. Some studies (Figure 1a) with longer blood sample collection times demonstrated biphasic decline in plasma concentrations consistent with a two compartment PK model (Gascoigne et al. 1981; Huang et al. 1986; FDA 1999). Following the notation of Rowland and Tozer (1995), we have the following differential equation based models for drug quantities in two components, (A1_I,A2_I), after an oral dose,

Table 1. Published KETO and MDZ Data Sets.

Sources	dose (mg)	sample size per subject (time frame)	Size (M/F)	meal
KETO
(Gascoigne 1981)	200 capsule	5(1 – 24h)	3(N/A)	fasting
	200 solution	5(1 – 24h)	3(N/A)	fasting
	100,200,400 tablet	8(0.5-48h)	12(N/A)	meal
	200 solution	8(0.5-48h)	12(N/A)	meal
(Daneshmend 1981)	200, 400 tablet	14(0.5 – 48h)	28-44 6(6/0)	meal
(Daneshmend 1983)	200 tablet, 7(0-24h)	10(0.5-8h)	8(8/0)	fasting
(Daneshmend 1984)	200, 400, 600	13(0.5, 32h)	8(3/5)	meal
	800, tablet		(20-31)
(Huang 1986)	200 solution suspension, tablet	12(0.5-48h)	24(24/0)	fasting
	200, 400, 800 solution.	12(0.5-48h)	12(24/0)	fasting
(FDA 1999)	200 tablet	17(1/4-24h)	39(39/0)	fasting
	200 tablet	17(1/4-24)	23(24/0)	meal
(FDA 1999)	200 tablet	15(1/3-48)	24(24/0)	fasting
	200 tablet	15(1/3-48)	17(17/0)	meal
MDZ :
(Lee 2002)†	2 IV	27(1/2-6h)	12(6/6)	fasting
(Tsunoda 1999)	2 IV	12(1/4-8h)	9(6/3)	fasting

^†In the original paper, MDZ was through IV fusion in a very short period to 2mg, we used the portion of data after fusion and assume IV bolus administration.

Figure 1.

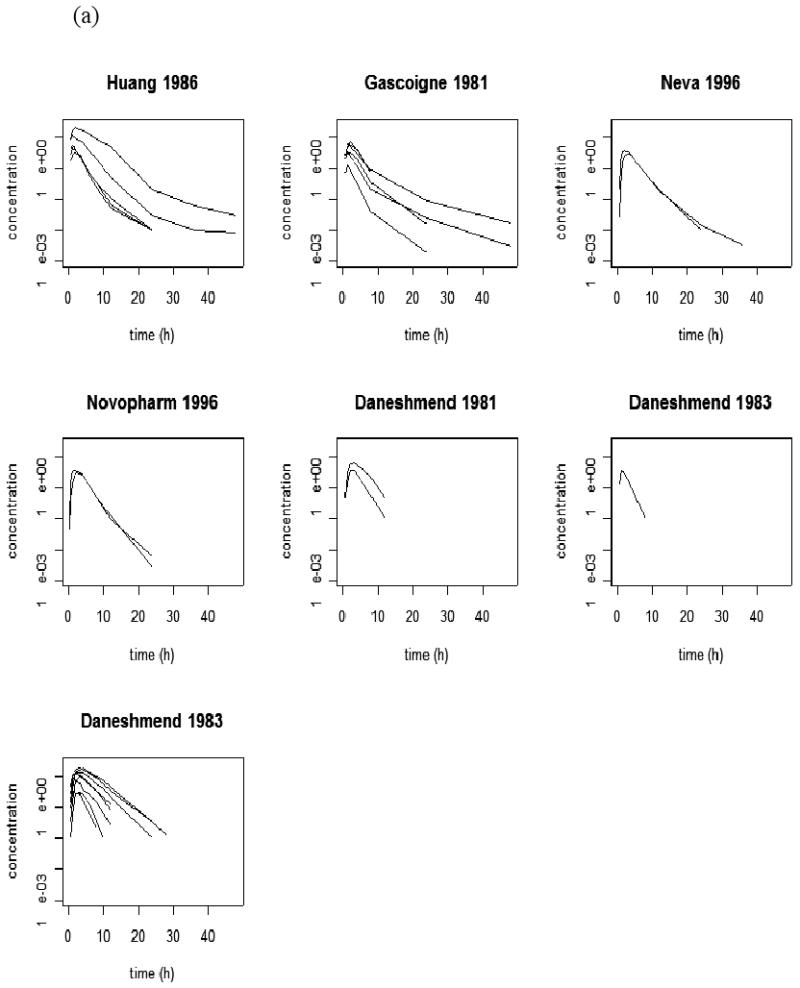
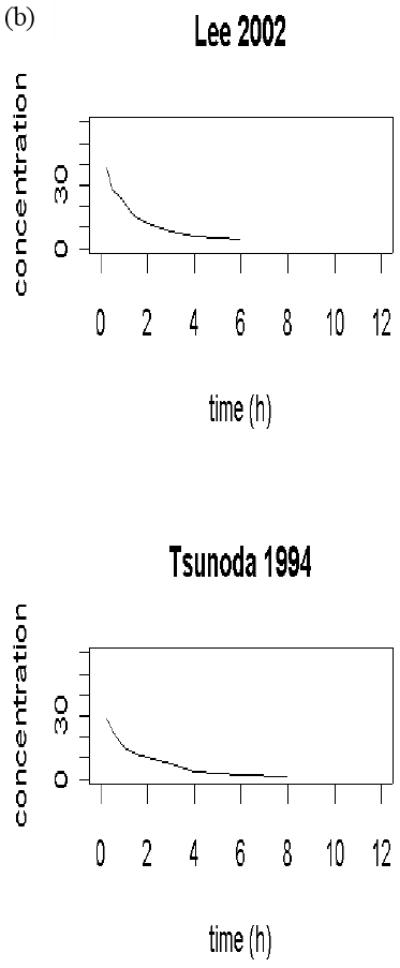
(a) published ketoconazole studies; (b) published midazolam studies. Every curve represents a sample mean drug concentration profile; multiple curves from one study represent multiple phases of a pharmacokinetics study.

$$\begin{array}{l}\frac{\text{dA}{1}_I}{\text{dt}}=F_I\times \text{Dose}\times k{a}_I\times e^{-k{a}_I\times t}-C{L}_I\times \frac{A{1}_I}{V{1}_I}+(-\frac{A{1}_I}{V{1}_I}+\frac{A{2}_I}{V{2}_I})\times \text{CL}{12}_I,\\ \frac{\text{dA}{2}_I}{\text{dt}}=(\frac{A{1}_I}{V{1}_I}-\frac{A{2}_I}{V{2}_I})\times \text{CL}{12}_I,(A{1}_I,A{2}_I){|}_{t=0}=(0,0)\cdot \end{array}$$ (1)

Here subscript I indicates the inhibitor, KETO; F_I is the bioavailability; ka_I is the absorption rate constant; (V1_I,V2_I) are the volumes of distribution in systemic and peripheral compartments; and CL12_I is the inter-compartment rate constant. CL_I is the clearance and it is modeled as CL_I = Q_h × CLint_I/(Q_h + CLint_I), where hepatic blood-flow, Q_h = 80 l/h (Price et al. 2003) is known, and the intrinsic hepatic clearance CLint_I =Vmax_I/(Km_I +A1_I /V1_I). As parameters F_I and Km_I are not readily identifiable from data, they were assumed to be known, F_I=0.7 (Cleary et al. 1992) and Km_I=0.5 (Li et al. 2007).

MDZ Pharmacokinetic Model

Table 1 and Figure 1 (b) summarize two published MDZ data sets obtained also through digitalization. They were used to establish the PK model of MDZ. It was assumed to follow a two-compartment model with an intravenous infusion.

$$\begin{array}{l}\frac{\text{dA}{1}_S}{\text{dt}}=-C{L}_S\times \frac{A{1}_S}{V{1}_S}+(-\frac{A{1}_S}{V{1}_S}+\frac{A{2}_S}{V{2}_S})\times \text{CL}{12}_S\\ \frac{\text{dA}{2}_S}{\text{dt}}=(\frac{A{1}_S}{V{1}_S}-\frac{A{2}_S}{V{2}_S})\times \text{CL}{12}_S,(A{1}_S,A{2}_S){|}_{t=0}=(\text{Dose},0)\cdot \end{array}$$ (2)

Here subscript S indicates the inhibitor, MDZ; (V1_S, V2_S) are the volumes of distribution in systemic and peripheral compartments; and CL12_S is the inter-compartment rate constant. CL_S is the clearance and modeled as CL_S = Q_h × CLint_S/(Q_h + CLint_S), and CLint_S = fu_S × Vmax_S /(Km_S + fu_S × A1_S/V1_S). As the parameter Km_S was not readily identifiable from data, it was assumed to be known as 2 (Li et al. 2007). The unbound fraction parameter fu_S is also fixed at 0.04 for MDZ.

KETO/MDZ Interaction Model

When KETO and MDZ are administrated separately, their corresponding PK data can be independently modeled by (1) and (2) respectively. However, when they are administrated simultaneously, models (1) and (2) need to be connected by (3) (Ito et al. 1998)

$$\text{CL}{int}_S=\frac{f{u}_S\times V{max}_S}{K{m}_S\times (1+\frac{f{u}_I\times A{1}_I}{M{W}_I\times \text{Ki}\times V{1}_I})+f{u}_S\times \frac{A{1}_S}{V{1}_S}}\cdot$$ (3)

As a result, (A1_I, A2_I, A1_S, A2_S) need to be jointly solved. In (3), fu_I=0.03 (Martinez-Jorda 1990) is the unbound fraction of KETO in plasma, MW_I=0.53 is the molecular weight of the inhibitor, and Ki is the inhibition constant. KETO is a potent inhibitor of CYP3A enzymes with a Ki value ranges from 0.0037 – 0.18 μM (Bourrie, et al. 1996; Gibbs, et al. 1999. von Moltke, et al. 1994, 1996; Wrighten and Ring, 1994). In these in-vitro experiments, K_i was obtained from incubations of KETO in human liver microsomes. Note that the equation (3) reduces to CLint_S = fu_S ×Vmax_S/(Km_S + fu_S × A1_S/V1_S) when there is no inhibitor (that is, when Ki = ∞).

Denote AUC_S,W as the substrate area under concentration curve (AUC) with inhibitor, and AUC_S,WO is the substrate AUC without inhibitor. For any given set of PK parameters for both inhibitor and substrate and their dose-combination, the substrate's concentration profiles (both with and without inhibitors) can be predicted, and their AUC_S,W and AUC_S,WO can be calculated via the trapezoidal rule (Rowland and Tozer 1995). A common criterion to evaluate the extent of interaction is the area under concentration ratio (AUCR) of substrate after and before inhibitor administration, AUCR=AUC_S,W /AUC_S,WO. Let (AŨC_S,W,AŨC_S,WO) be calculated AUCs based on PK parameter estimates from data, then AUCR can be calculated via AŨC_S,W/ AŨC_S,WO.

Model Based DDI Prediction

In the early drug development stage, a decision of continuing clinical trials for a candidate drug partially depends on its interaction with the other drugs (inducers or inhibitors). PK model based DDI prediction becomes critical, and precise prediction can guide drug development. Practically, inhibitor or inducer's PK models and parameters are estimated from their PK studies, while substrate's PK model and parameters are estimated from substrate's PK studies. Their interaction parameter, Ki, in (3) is measured from in-vitro studies. Then, DDI are predicted by the joint models from (1), (2), and (3).

This model based DDI prediction has been successfully implemented for simulating and predicting the effect of non-simultaneous substrate and inhibitor administration (Yang et al. 2003). However all PK parameters were treated as known without uncertainty in performing DDI prediction. From the statistical point of view, this deterministic approach is incomplete, because PK parameters of inhibitor (or inducer) and substrate estimated from published studies must have standard errors and these uncertainties need to be translated into their DDI prediction. On the other hand, some interaction parameters measured from in vitro studies, such as Ki, usually do not have reported standard error. That doesn't mean that these interaction parameters can be accurately estimated. The influence due to inaccurate estimates from these parameters on DDI prediction needs to be evaluated. For example, the range of KETO's Ki is cited as to be between 0.18 and 0.0037 μM from an FDA guideline document on DDI (FDA 2006) as well as in published literature (Bouurie et al. 1996, Gibbs et al. 1999, von Moltke et al. 1994, von Moltke et al. 1996, Wrighton and Ring 1994). It is therefore worthwhile to check how sensitive our model (in vivo) prediction is for different values of Ki.

2.2 Hierarchical Bayesian Meta-Analysis Model Specification

Notations

Before describing various models, we use the following notations throughout our paper. The subscript i will be used for subject, j for time point, k for study and h for (dosing) phase. We assume that there are n_kh subjects in the dosing phase h of study k; study k has H_k phases and there are total of K studies for a given drug. For ease of presentation, we assume all subjects within a dosing phase of a specific study are measured at the same time points for plasma concentration data. Therefore we have T_kh time points in the dosing phase h of study k. A parameter without subscript will be invariant across studies while a parameter with subscript varies according to the subscript. We also use bolded symbols for vectors and matrices. As examples, α will be a vector of parameters whose values are invariant across different studies, and β_ik is a vector of parameter for subject i from study k. The need for consider some parameters as invariant across different studies is to reduce the number of parameters. For example, in KETO, there are five different dosing routes: tablet with meal (TM), tablet fasting (TF), solution with meal (SLM), solution fasting (SLF), suspension fasting (SPF). The absorption rates corresponding to them satisfies the constraints ka_I,TM < ka_I,SLM < ka_I,SLF and ka_I,TM < ka_I,TF < ka_I,SPF < ka_I,SLF. So to reduce the number of parameters, we only make ka_I,TM,k to be study specific and introduce α =(Δka_I,TF, Δka_I,SLM, Δka_I,SPF, Δka_I,SLF), where the elements of α are restricted to be positive. In other words, we assume that the difference in absorption rates between different routes is study invariant.

Meta-Analysis Models for Individual Level Data

When individual level data are available for each study, summarizing PK parameters from multiple sources by meta-analysis has been addressed by applying Bayesian methods to construct a drug PK model from several clinical study data sets. (see e.g. Wakefield and Rahman 2000). In general, the following set of models are used

• subject-specific PK model:

$$[y_{\text{ijkh}}|\alpha ,{\beta }_{\text{ik}},z_{\text{jkh}}]\sim \text{MV}N[f(\alpha ,{\beta }_{\text{ik}},z_{\text{jkh}}),{\sigma }_0^2],$$ (4)

• subject-specific PK parameter model in study k:

$$[{\beta }_{\text{ik}}|{\beta }_k,\text{∑}]\sim \text{MVN}({\beta }_k,\text{∑}),$$ (5)

• study-specific PK parameter model:

$$[{\beta }_k|\beta ,\text{Ω}]\sim \text{MVN}(\beta ,\text{Ω})$$ (6)

In (4), y_ijkh represents log-transformed drug concentration at time t_jkh for subject i in phase h of study k. Here we use a generic notation z_jkh to denote available data and constants for a study subject at time t_jkh. It includes dosage, dosing route, and fixed constants such as Q_h, F_I, Km_I, fu_I, MW_I, Km_S, fu_S, and time point t_jkh at which plasma concentration is measured, The mean value f(α,β_ik,z_jkh) is the predicted log-transformed drug concentration for subject i at jth time point from phase h of study k. Basically, f(α,β_ik,z_jkh) corresponds to (part of) a numerical solution at given time points from (1) and (2) by input α, β_ik and z_jkh. So in the case that y_ijkh is the KETO concentration observed from the first compartment, then f(α,β_ik,z_jkh) =log(A1_I /V1_I) with A1_I solved from (1). The measurement error variation, ${\sigma }_0^2$, is assumed equal across studies. The variance components Σ and Ω are for subject-specific and study-specific PK parameters.

However, published data are often available in the form of sample average plasma concentration. In other words, only $({\overline{y}}_{•\text{jkh}},s_{\text{jkh}}^2)$, instead of y_ijkh are published. But model (4) obviously needs y_ijkh, and hence can not be directly implemented to perform meta-analysis with summarized data. Reconstructing a drug PK model from $({\overline{y}}_{•\text{jkh}},s_{\text{jkh}}^2)$ needs a new meta-analysis formulation and different Bayesian sampling algorithm.

Meta-Analysis Models with Sample Mean and Standard Deviation Data

As individual data are not available, it is an unrealistic goal to estimate subject level PK parameters. The sample mean data ȳ_•jkh at most provide information about study specific PK parameters β_k and study to study variation parameters Ω. The sample variance data $s_{\text{jkh}}^2$ at most provide information about between-subject heterogeneity parameter Σ. As a result, models based on (4) – (6) are only suitable when working on subject level data. When only sample mean and sample variance data are available, they need to be modified to make estimation feasible. In other words, the models should not involve β_ik. A natural approach is to base estimation methods on marginalized likelihood where β_ik is integrated out. However, as no analytic form is available for f(α, β_ik, z_jkh), direct integration is not feasible. The alternative we take is to first derive an approximation for f(α, β_ik,z_jkh) and then marginalize. Specifically, we adapt as follows.

By Taylor expansion at β_k, f(α,β_ik,z_jkh) can be approximated as

$$f(\alpha ,{\beta }_{\text{ik}},z_{\text{jkh}})\approx f\left(\alpha ,{\beta }_k,z_{\text{jkh}}\right)+{\left({\frac{\partial f}{\partial {\beta }_{\text{ik}}}|}_{{\beta }_{\text{ik}}={\beta }_k}\right)}^T({\beta }_{\text{ik}}-{\beta }_k).$$ (7)

Denote $F_{\text{jkh}}={\frac{\partial f}{\partial {\beta }_{\text{ik}}^T}|}_{{\beta }_{\text{ik}}={\beta }_k}$. Instead of individual level PK model (4), we assume the following approximated model $[y_{\text{ijkh}}|\alpha ,{\beta }_{\text{ik}},{\beta }_k,{\sigma }_0^2,z_{\text{jkh}}]\sim N(f(\alpha ,{\beta }_k,z_{\text{jkh}})+F_{\text{jkh}}^T({\beta }_{\text{ik}}-{\beta }_k),{\sigma }_0^2)$. Now by integrating out β_ik using the conditional distribution of β_ik given β_k,we have

$$[y_{\text{ijkh}}|\alpha ,{\beta }_k,z_{\text{jkh}},\sum ,{\sigma }_0^2]\sim N\left(f(\alpha ,{\beta }_k,z_{\text{jkh}}),F_{\text{jkh}}^T\sum F_{\text{jkh}}+{\sigma }_0^2\right).$$ (8)

As a result,

$$[{\overline{y}}_{•\text{jkh}}|\alpha ,{\beta }_k,z_{\text{jkh}},\sum ,{\sigma }_0^2]\sim N\left(f(\alpha ,{\beta }_k,z_{\text{jkh}}),\frac{F_{\text{jkh}}^T\sum F_{\text{jkh}}+{\sigma }_0^2}{n_{\text{kh}}}\right)$$ (9)

To obtain the approximate distribution for sample variance, $s_{\text{jkh}}^2=\text{∑}_{i=1}^{n_{\text{kh}}}{(y_{\text{ijkh}}-{\overline{y}}_{•\text{jkh}})}^2/(n_{\text{kh}}-1)$, we use the known fact the normalized sample variance of m i.i.d. normal variables has a chi-square distribution with degree of freedom m‒1. From the approximate model (8), we immediately obtain

$$\frac{\text{∑}_{i=1}^{n_{h_k}}{(y_{\text{ijkh}}-{\overline{y}}_{•\text{jkh}})}^2}{F_{\text{jkh}}^T\text{∑}{F}_{\text{jkh}}+{\sigma }_0^2}\sim {\chi }_{n_{\text{kh}}-1}^2,\text{or}\text{equivalently},\frac{(n_{\text{kh}}-1)}{F_{\text{jkh}}^T\text{∑}{F}_{\text{jkh}}+{\sigma }_0^2}{s}_{\text{jkh}}^2\sim {\chi }_{n_{\text{kh}}-1}^2$$ (10)

Notice that (9) and (10) depend only on β_k, Σ, and ${\sigma }_0^2$ Hence estimation of these parameters is feasible with mean and standard deviation data. Our estimation will be based on the following hierarchical models.

• Sample mean PK model

  $$[{\overline{y}}_{•\text{jkh}}|\alpha ,{\beta }_k,z_{\text{jkh}},\sum ,{\sigma }_0^2]\sim N\left(f(\alpha ,{\beta }_k,z_{\text{jkh}}),\frac{F_{\text{jkh}}^T\sum F_{\text{jkh}}+{\sigma }_0^2}{n_{\text{kh}}}\right)$$ (11)

• Sample variance PK model

  $$\frac{(n_{\text{kh}}-1)}{F_{\text{jkh}}^T\text{∑}{F}_{\text{jkh}}+{\sigma }_0^2}{s}_{\text{jkh}}^2\sim {\chi }_{n_{\text{kh}}-1}^2$$ (12)

• Study-specific PK parameter model:

  $$[{\beta }_k|\beta ,\text{Ω}]\sim \text{MVN}(\beta ,\text{Ω})$$ (13)

Many times, a main purpose of determining variability is to identify individuals at risk. However as our model is based on summarized data, no individual information is available. All we can do is to quantify variance for a given population. Of course if individual data are available, subject covariates can be used in explaining variability using individual level models.

Prior Specification and Posterior Distributions

Due to the nonlinear structure from PK models (1) - (2), no conjugate priors exists for all parameter except Ω. Vague priors are used for PK parameter population level PK parameters (α, β) and subject level heterogeneity parameter, (Σ, Ω, ${\sigma }_0^2$), where Σ = diag{ ${\sigma }_{\text{l}}^2$} and Ω = diag{ ${\omega }_{\text{l}}^2$}.

$$\begin{array}{l}p(\alpha ,\beta )=U(0,{10}^4);p({\sigma }_l^2)=U(a,b)\iff p({\sigma }_l^{-2})=\frac{{({\sigma }_{\iota }^{-2})}^{-2}}{(b-a)},l=0,1,\dots ,q;\\ p({\omega }_l^2)=U(a,b)\iff p({\omega }_l^{-2})=\frac{{({\omega }_l^{-2})}^{-2}}{(b-a)},l=1,\dots ,q.\end{array}$$ (14)

Variance components all follow a uniform prior because practically they rarely exceed the bound (a, b) = (0.01²,2²).

Let Ȳ_• = {ȳ_•jkh;j = 1,⋯,T_kh;k = 1, ⋯,K;h = 1, ⋯,H_k} be the sample mean data and $S=\left\{s_{\text{jkh}}^2;j=1,\cdots ,T_{\text{kh}};k=1,\cdots ,k;h=1,\cdots ,H_k\right\}$ the sample variance data. Then, the posterior probability distribution based on (11) - (13) and priors (14) is,

$$\begin{array}{l}p(\alpha ,{\beta }_1,\dots ,{\beta }_K,\text{∑},\Omega ,{\sigma }_0^2|{\overline{Y}}_{•},S,z)\\ \propto \left\{\prod _{k=1}^K\prod _{h=1}^{H_k}\prod _{j=1}^{T_{\text{kh}}}N\left({\overline{y}}_{•\text{jkh}}|f(\alpha ,{\beta }_k,t_{\text{jkh}}),\frac{F_{\text{jkh}}^T\text{∑}{F}_{\text{jkh}}+{\sigma }_0^2}{n_{\text{kh}}}\right)\right\}\\ \times \left\{\prod _{k=1}^K\prod _{h=1}^{H_k}\prod _{j=1}^{T_{\text{kh}}}{\chi }_{n_{h_k}-1}^2\left(\frac{(n_{\text{kh}}-1)s_{\text{jkh}}^2}{F_{\text{jkh}}^T\text{∑}{\text{F}}_{\text{jkh}}+{\sigma }_0^2}\right)\right\}\\ \times \left\{\prod _{k=1}^{K}p({\beta }_k|\beta ,\Omega )\right\}\times p(\alpha ,\beta )\times p(\sum )\times p(\Omega )\times p({\sigma }_0^2)\end{array}$$ (15)

The estimation procedure is implemented with a Monte Carlo Markov chain method. The posterior probability functions, p(β |•), p(α |•), p(β_k |•), p( ${\sigma }_0^{\mathrm{-2}}$ |•), p( ${\sigma }_{\text{l}}^{\mathrm{-2}}$|•), and p( ${\omega }_{\text{l}}^{-2}$|•) are derived in the Appendix. We defer the implementation details of our computation to the data analysis section.

An Alternative Bayesian Hierarchical Model for the Sample Mean PK Profile

In Li et al. (2007), instead of modeling both ȳ_•jkh and $s_{\text{jkh}}^2$ as in (10) and (11), only ȳ_•jkh is modeled. The variance of ȳ_•jkh is assumed to be $s_{\text{jkh}}^2/n_k$. So instead of (10), the following is used

$$[{\overline{y}}_{•\text{jkh}}|\alpha ,{\beta }_k,Z_{\text{jkh}},S_{\text{jkh}}^2]\sim N\left[f(\alpha ,{\beta }_k,Z_{\text{jkh}}),S_{\text{jkh}}^2/n_{\text{kh}}\right]$$ (16)

In the following context, (11)-(13) are referred as the mean-variance model and (13) and (16) are referred as the mean model. While both models are approximation models, there are two major differences between the mean-variance model (11)-(13) and the mean model, (13) and (16). Firstly, the mean model is not designed to recover the between-subject variance Σ, while the mean-variance can. Secondly, by using observed sample variance $s_{\text{jkh}}^2/n_k$ to represent the variance of ȳ_•jkh, model (16) should be more robust to model specification. It does not require Taylor expansion for approximation of f(α,β_ik,z_jkh). Of course the downside is observed sample variance can deviated from the true variance, depending on the number of subject in each study and the true variability of individual data. The MCMC algorithm for the mean model is described in the Appendix IV of Li et al. (2007).

DDI Prediction Based on Sample Mean and Standard Deviation Data

The key to estimate AUCR is to estimate AUC_S,W andAUC_S,WO. When estimates of these two AUCs are carried out by using population level parameters α and β, the ratio of AUC_S,W and AUC_S,WO leads to population level DDI which we denote by AUCR(α, β, Ki). When instead of β, study level parameters β_k are used, then we have study level DDI which we denote by AUCR (α, β_k, Ki). By the same token, we can use β_ik and obtain individual level DDI, AUCR(α, β_ik, Ki).

Based on posterior distributions of PK parameters from the mean-variance model, we are able to obtain a posterior distribution of AUCR at different levels. For example, a posterior sample of the distribution of population level DDI can be obtained by AUCR(α^(u), β^(u), Ki)., where {α^(u),β^(u)}_u=1,…,U are their posterior draws. Similarly, we can have posterior sample of study level DDI. However for subject-specific DDI, we can not proceed in the same way as no posterior draws of individual level β_ik are available (note that β_ik is not present in the mean-variance model). Instead we obtain samples of AUCR(α, β_ik,Ki) by first drawing β_ik from its prior distribution (4) with Σ replaced by its posterior draws. That is, given any specific draw of (α^(u), β_k^(u), Σ^(u)), we draw β_ik^(v), v=1,… V, from [β_ik | β_k^(u), Σ^(u)]. Corresponding to any draw of β_ik^(v), a sample of AUCR(α^(u),β_ik^(v), Ki) can be obtained. For any specific u, a total of V samples AUCR(α^(u),β_ik^(v), Ki) are obtained. Due to the study level nature of our data, this is a reasonable way for estimating subject-specific DDI. By estimating DDI distribution, our approach provides more information about DDI prediction, compared with the deterministic approach (Yang et al. 2003).

3. KETO/MDZ Example

The PK parameters of both KETO and MDZ are estimated from published studies using the proposed mean-variance model and mean-model from Section 2.2. The predicted log-transformed drug concentrations for KETO are calculated from the differential equation model (1) and the predicted log-transformed drug concentrations for MDZ are calculated from the differential equation model (2). Based on (known) DDI parameters, (Km_I, Km_S,fu_I, Ki,MW_I), the DDI outcome, AUCR, is then predicted by models (1) and (2) linked by (3).

From the appendix, only p( ${\omega }_{\text{l}}^{-2}$ |•) has an explicit form and hence can be simulated directly. Other posterior distributions, p(α |•), p(β_k |•), p( ${\sigma }_0^{\mathrm{-2}}$ |•), and p( ${\sigma }_{\text{l}}^{\mathrm{-2}}$ |•), are drawn through the Metropolis Hasting (MH) algorithm (Hastings et al. 1970). At each step, a random walk chain is used and the random pertubation is taken to mean normal with mean 0 and standard deviation of 10%. The mixing is well with such proposed density and the acceptance rate varies. For population parameter α, the acceptance rate is about 40% and for most of the study specific parameters β_k, the acceptance rates are close to 25%. Five independent chains were run simultaneously to determine the convergence with dispersed starting values on population parameters. It needed less than 4000 iterations for the estimated potential scale reduction criterion of Gelman and Rubin (1992) to be less than 1.2. By visual inspection of trace plots, almost all chains start to mix well after 500 iterations. The final results are based on a single chain of 50000 iterations after a burn-in of 10000. Every 10^th iteration after burn-in was extracted for summarizing results. The numerical strategies for solutions of the differential equations and the derivatives of differential equations were discussed in (Li et al. 2002; Li et al. 2004). Both MCMC algorithms and numerical solutions of differential equations are implemented in the statistical freeware R 2.2.1.

3.1 KETO Data Analysis

Table 1 and Figure 1 (a) summarize seven published KETO PK data sets that were used to establish the PK model of KETO. All studies employed oral (PO) dosing of the Nizoral (Janssen Pharmaceuticals) formulation. The participants in these seven studies were young and healthy. The model is defined as in (11)-(13) together with PK model (1). Here the study specific parameters are β_k=(V1_I,k, V2_I,k, CL12_I,k, Vmax_I,k, ka_I,TM,k) with corresponding population parameters β=(V1_I, V2_I, CL12_I,Vmax_I, ka_I,TM). We also take α = (Δka_I,TF, Δka_I,SLM, Δka_I,SPF, Δka_I,SLF) where elements of α are restricted to be positive. Both the variance matrix Σ of study specific parameters and Ω of subject specific parameters are taken to be diagonal. We use different diagonal elements $({\omega }_{V{1}_I}^2,{\omega }_{V{2}_I}^2,{\omega }_{V{\text{max}}_I}^2,{\omega }_{\text{CL}{12}_I}^2,{\omega }_{\text{ka}{1}_I}^2)$ for Ω and $({\sigma }_{V{1}_I}^2,{\sigma }_{V{2}_I}^2,{\sigma }_{V{\text{max}}_I}^2,{\sigma }_{\text{CL}{12}_I}^2,{\sigma }_{\text{ka}{1}_I}^2)$ for Σ. During the actual computation, we log-transform all PK parameters. The interpretation of the variance components is then the coefficient of variance (CV). The prior distributions follow the same formulations as those in (14).

Estimation results are reported in Table 2 and Figure 2. The 90% credit intervals of PK parameters are reported. Here are some highlights.

Table 2. Pharmacokinetics Parameter Estimates for KETO and MDZ.

Parameters		Methods
		Model 2*		Model 1**
		Estimate	90% CI***	Estimate	90% CI***
KETO:
V1I		20.6	(16.0, 24.6)	21.3	(17.5, 26.0)
V2I		24.4	(16.3, 37.0)	33.8	(17.9, 44.6)
V maxI		23.1	(20.1, 26.4)	22.2	(18.0, 26.9)
CL12I		3.22	(2.53, 4.04)	2.10	(1.10, 3.78)
kaI,TM		0.42	(0.37, 0.48)	0.45	(0.33, 0.65)
kaI,TF		0.61	(0.42, 1.10)	0.72	(0.53, 1.07)
kaI,SPF		2.03	(1.55, 2.35)	1.79	(0.95, 1.92)
kaI,SLM		0.70	(0.60, 0.98)	0.76	(0.58, 1.10)
kaI,SLF		2.72	(2.33, 3.14)	2.23	(1.65, 3.32)
ωV1I		0.22	(0.10, 0.42)	0.13	(0.06, 0.26)
ωV2I		0.44	(0.23, 0.81)	0.66	(0.33, 1.14)
ωVmaxI		0.17	(0.10, 0.29)	0.15	(0.08, 0.26)
ωCL12I		0.54	(0.35, 1.34)	0.77	(0.40, 1.37)
ωkaI		0.34	(0.17, 0.69)	0.40	(0.18, 0.71)
σV1I		0.067	(0.016, 0.13)	N/A
σV2I		0.316	(0.24, 0.40)	N/A
σV maxI		0.08	(0.04, 0.13)	N/A
σkaI		0.92	(0.86, 0.98)	N/A
σCL12I		0.32	(0.24, 0.40)	N/A
σI0		0.20	(0.06, 0.30)	N/A
MDZ :
V1S	78.8		(48.1, 120.7)	70.05	(51.1, 112.1)
V2S	53.3		(31.2, 89.7)	49.08	(29.9, 81.5)
V maxS	5125.4		(3035.2, 7936.4)	4488	(3051.8, 7001.3)
CL12S	42.1		(23.0, 68.2)	44.5	(24.5, 73.4)
ωS	0.31		(0.20, 0.51)	0.34	(0.21, 0.53)
σV1S	0.11		(0.03, 0.22)	N/A
σV2S	0.20		(0.05, 0.40)	N/A
σV maxS	0.15		(0.07, 0.23)	N/A
σCL12S	0.20		(0.05, 0.39)	N/A
σS0	0.10		(0.03, 0.17)	N/A

Model 2* : a Bayesian three-level hierarchical model for the sample mean and variance.

Model 1** : a Bayesian three-level hierarchical model for the sample mean.

90% CI*** : a 90% credit interval. It is represented by its relative scale to the mean.

Figure 2.

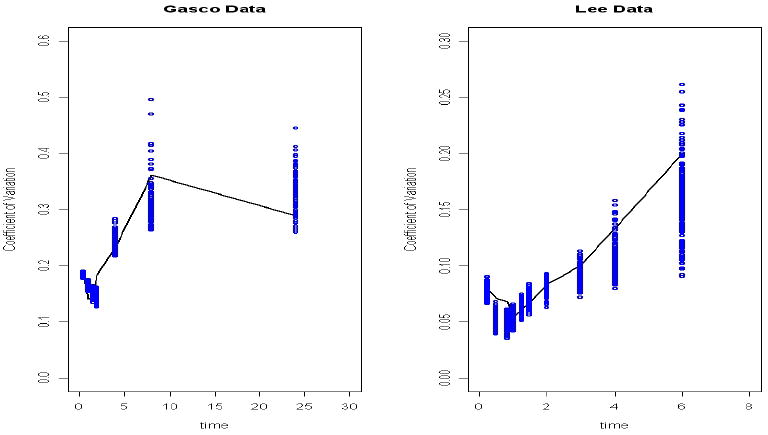
(a) The fitting of sample coefficient of variance from a ketoconazole study (Gascoigne et al. 1981). The solid line is the sample coefficient variance, and dots are the posterior draws of the predicted coefficient of variance. (b) The fitting of sample coefficient of variance from a midazolam study (Lee et al. 2002). The solid line is the sample coefficient variance, and dots are the posterior draws of the predicted coefficient of variance.

• Among the KETO PK parameter estimates, V2_I and CL12_I have wider 90% CI than the others, if the CIs are normalized by their means. This is because only three studies (Gascoigne et al. 1981; Huang et al. 1986; FDA 1999) had sampling time points late enough to detect the terminal phase of KETO elimination from plasma, while the other studies did not.

• V2_I and CL12_I's between-study CV estimates, 0.44 and 0.54 respectively, are larger than the other between-study CV estimates.

• ka_I, V2_I and CL12_I's between-subject CV estimates 0.92, 0.31 and 0.32 respectively, are larger than the other between-study CV estimates. One example of fitting to sample variances is illustrated by Figure 2(a) for a KETO study (Gascoigne et al. 1981). The within subject CV is estimated as 0.20.

• Both mean-variance model (model 2 in table 2) and mean-model (model 1 in table 2) have comparable performance in estimating PK parameters and their between-study CVs. All their 90% CIs are overlapped.

3.2 MDZ Data Analysis

Table 1 and Figure 1 (b) summarize two published MDZ data sets. They were used to establish MDZ's PK model and estimate its PK parameters. MDZ (administered as Versed®, Roche Pharmaceuticals) was administered in the fasting state in all studies. The participants in these two studies were young and healthy. Its mean-variance model is (11)-(13) together with the PK model (2). Here the study specific parameters are β_k= (V1_S,k, V2 _S,k, CL12_S,k, Vmax _S,k). As there are only two studies used in the analysis, the between study variances were assumed to be the same crossing different PK parameters, ω_s,1². The between subject variance, $\text{∑}=\text{diag}({\sigma }_{V{1}_s}^2,{\sigma }_{V{1}_s}^2,{\sigma }_{V{\text{max}}_s}^2,{\sigma }_{\text{CL}{12}_s}^2)$. We also log-transform the PK parameters and hence the interpretation of all the variance components is coefficient of variance (CV). The prior distributions follow the same formulations as those in (14). Estimation results are reported in Table 2. Here are some highlights.

• All of MDZ PK parameter estimates have comparable 90% CIs, if they are normalized by their means.

• The between-study CV is estimated as 0.32, within subject CV is estimated as 0.10. between-subject CV ranges from 0.11 to 0.20. The fitting of sample CV is displayed by an MDZ example (Lee et al. 2002) in Figure 2(b).

• Both mean-variance model (model 2 in table 2) and mean-model (model 1 in table 2) have comparable performance in estimating PK parameters and their between-study CVs. All their 90% CIs are overlapped.

3.3 KETO/MDZ Interaction Prediction

Assuming a simultaneous oral dose KETO and an IV dose for MDZ, the interaction PK models follow equations (1) and (2) connected by (3). The inhibition constant Ki is assumed to take value of (0.0037, 0.01, 0.18) μM to assess their influence on DDI prediction. In the simulation, the blood sampling time points are (0.25, 0.5, 1, 1.5, 2, 3, 4, 6, 12) hours after dose. MDZ is dosed at (2, 5, 10) mg levels, and KETO/MDZ is dosed at three combinations: 200/2mg, 400/5mg, 800/10mg. The predicted MDZ plasma concentrations are simulated both with and without KETO, and at three different Ki values. AUC and AUCR are calculated with the trapezoid rule (Rowland and Tozer 1995). Following our proposed DDI prediction procedures in section 2, population-average DDI, subject-specific DDI, and between-subject/study variance of DDI are predicted and displayed in Table 3. Here are some highlights.

Table 3. Population-Average and Subject-Specific AUCR Prediction.

Ki	Dose/Combination (KETO/MDZ)mg	Population-Average AUCR	Subject-Specific AUCR	Between-Subject/Study CV
0.0037	200/2	3.02 ×/÷ 1.112	2.94 ×/÷ 1.258	0.242×/÷ 1.090
0.01	200/2	2.43 ×/÷ 1.084	2.35 ×/÷ 1.222	0.217×/÷ 1.116
0.18	200/2	1.21 ×/÷ 1.014	1.19 ×/÷ 1.085	0.084×/÷ 1.078
0.0037	400/5	3.72 ×/÷ 1.130	3.50 ×/÷ 1.273	0.254×/÷ 1.116
0.01	400/5	3.17 ×/÷ 1.108	2.94 ×/÷ 1.255	0.234×/÷ 1.091
0.18	400/5	1.45 ×/÷ 1.020	1.39 ×/÷ 1.124	0.120×/÷ 1.066
0.0037	800/10	3.93 ×/÷ 1.139	3.61 ×/÷ 1.280	0.249×/÷ 1.155
0.01	800/10	3.56 ×/÷ 1.119	3.34 ×/÷ 1.260	0.224×/÷ 1.139
0.18	800/10	1.78 ×/÷ 1.028	1.69 ×/÷ 1.153	0.151×/÷ 1.058

Note: the results are presented as mean×/÷ (1+CV)*100%.

• The smaller the Ki, the larger the predicted AUCR. The larger the dose combination, the larger the predicted AUCR. These results fit well to previously published simulation studies (Yang et al. 2003).

• The smaller the Ki, the smaller between-subject/study CV. The larger the dose combination, the larger the CVs of population-average and subject-specific AUCRs.

• Subject-specific AUCR and population-average AUCR have very comparable mean estimates, but subject-specific AUCR has much higher CVs, which is due to the additional between-subject/study variations.

• The predicted mean between-subject/study CV is smaller than the CV of the subject-specific AUCR, because it doesn't contain the variability due to the uncertainties of PK parameter estimates.

4. Simulation Studies for PK Parameter Estimation and DDI Prediction

Based on our proposed hierarchical Bayesian model, sample mean drug concentration data and their sample variances were fitted to estimate PK parameters and variance components for KETO and MDZ. It is not clear whether the estimates are biased, and consequently whether the predicted AUCR and its variance are biased. To answer these questions, statistical simulations were conducted. We carry out simulation study based on the mean-variance model in this paper. For simulation under the mean model, readers are referred to Li et al. (2007).

In each simulated data set, eight studies for both KETO and MDZ were generated. KETO had 3 tablet dose levels (200mg, 400mg, 800mg) with meals and MDZ had IV bolus with 3 dosages (2mg, 5mg, 10mg). There were 24 subjects for each study. Individual data were simulated first and then summarized as mean and standard deviation data for analysis. The blood sampling time points were (0.25, 0.5, 1, 1.5, 2, 3, 4, 6, 12, 24, 36) hours after dose for KETO and (0.25, 0.5, 1, 1.5, 2, 3, 4, 6, 12) for MDZ. At each KETO dose, its subject specific plasma concentrations were simulated with a two-compartment model (1) and subject specific models (4) – (6). The population PK parameters are β = log(V1_I,V2_I, CL12_I,V max_I,ka_I,SLF). We utilized the similar PK parameters from prescribed data analysis as their true values (Table 2). The between subject variance matrix is taken as ${\sigma }_1^2{I}_{5\times 5}$ with ${\sigma }_1^2$ set to be 0.20². Study to study variance matrix is taken as ${\omega }_1^2{I}_{5\times 5}$ with ${\omega }_1^2$ set to be 0.30². The measurement error variance ${\sigma }_0^2$ is set as 0.10². Similar to the KETO, MDZ plasma concentrations were simulated with a two compartmental PK model (2) and subject specific models (4) – (6). The PK parameters are β = log(V1_S,V2_S,Vmax_S,CL12_S), and the true PK parameters are listed in Table 3 and are chosen to be close to their estimates in the prescribed MDZ data analysis. The between subject variance matrix is taken as ${\sigma }_1^2{I}_{4\times 4}$ with ${\sigma }_1^2$ set to be 0.20². Study to study variance matrix is taken as ${\omega }_1^2{I}_{4\times 4}$ with ${\omega }_1^2$ set to be 0.30². The measurement error variance ${\sigma }_0^2$ is set as 0.10². Totally, 100 simulated data sets were generated for both KETO and MDZ under each dose.

To fit the PK model in each simulation data set, an M-H algorithm was implemented as in the data example. To save computation time, initial values for PK parameters and variance components were chosen as their true values plus a random noise with a CV of approximately 10%. This increases the convergence rate of the algorithm, yet has minimum impact for the convergence itself. A total of 3000 iterations with 1000 burn-in were run to obtain PK parameter posterior distributions after the MCMC reached convergence. One in every five samples was picked to avoid autocorrelations. Both mean-variance model and mean-model were fitted to simulated data sets. Table 4 summarizes the PK parameters and variance components estimation biases for both approaches. Figure 3 summarizes the simulation results for AUCR prediction; and Figure 4 summarizes the AUCR's variation prediction. Here are the highlights for simulation results.

Table 4. Bias of PK Parameter Estimates.

Parameters	Methods
	Model 2*			Model 1**
	True	Est.	RB%	Est.	RB%
KETO:
V1I	24.0	23.3	-2.9%	23.4	-2.5%
V2I	35.0	33.4	-4.6%	33.3	-4.8%
V maxI	21.0	21.5	2.4%	21.6	2.9%
CL12I	2.0	2.15	7.5%	2.19	8.2%
kaI	0.5	0.49	-2.0%	0.49	-2.0%
ωV1I	0.30	0.31	3.0%	0.30	0.8%
ωV2I	0.30	0.30	0.9%	0.31	3.0%
ωV maxI	0.30	0.31	2.6%	0.30	0.9%
ωCL12I	0.30	0.30	0.5%	0.31	3.0%
ωkaI	0.30	0.29	-2.9%	0.30	0.3%
σI1	0.20	0.21	5.0%	N/A
MDZ:
V1S	78	80.0	2.6%	80.2	2.8%
V2S	53	55.0	3.8%	55.3	4.3%
V maxS	4878	4934	1.1%	4954	1.6%
CL12S	43	42.1	-2.09%	42.4	-1.4%
ωV1I	0.30	0.30	0.0%	0.32	6.7%
ωV2I	0.30	0.29	-3.2%	0.30	0.0%
ωV maxI	0.30	0.29	-3.2%	0.31	-2.9%
ωCL12I	0.30	0.29	-2.4%	0.30	-0.4%
σS1	0.20	0.21	5.0%	N/A

Model 2* : a Bayesian three-level hierarchical model for the sample mean and variance.

Model 1** : a Bayesian three-level hierarchical model for the sample mean.

Figure 3.

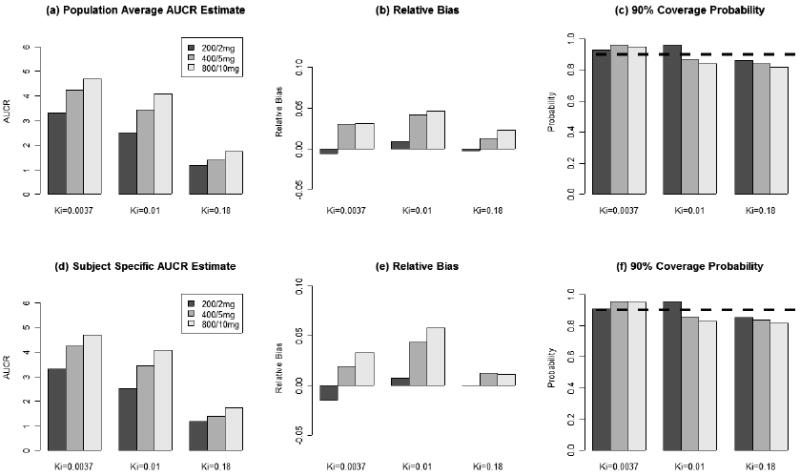
(a), (b), and (c) are population-average AUCR prediction estimates, relative bias, and 90% credit interval coverage probability respectively. (d), (e), and (f) are subject-specific AUCR prediction estimates, relative bias, and 90% credit interval coverage probability respectively. These results are based on 100 simulated data sets.

Figure 4.

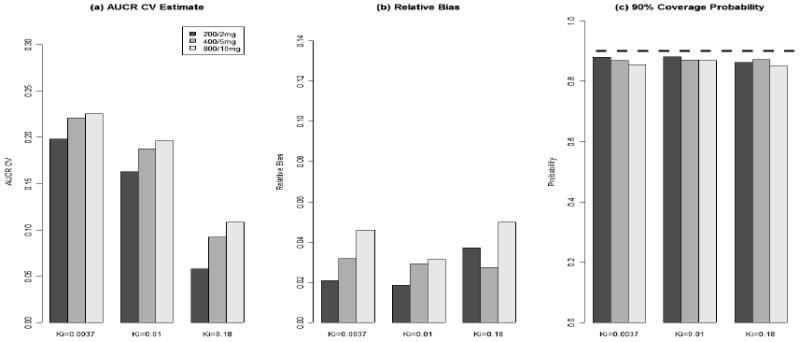
(a), (b), and (c) are between-subject/study AUCR coefficient of variance estimates, relative bias, and 90% credit interval coverage probability respectively. These results are based on 100 simulated data sets.

• In Table 4, except that CL12's relative bias is around 7.5%, all the other PK parameters have relative bias less than 5%. CL12 and V2's estimates have larger bias than the other PK parameters. It is true in both mean-variance model and mean-model.

• In Table 4, both the between-subject and between-study variances are estimated with less than 5% relative bias.

• In Figure 3, both subject-specific and population-average AUCR predictions have bias less than 5%. Their 90% CI coverage probabilities are close to their nominal levels.

• In Figure 4, AUCR's between-subject/study variation predictions have bias less than 5%, and their 90% CI coverage probabilities are close to their nominal levels.

5. Conclusions

In this paper, we have proposed a DDI prediction method based on an innovative three level hierarchical Bayesian model. It enables us to reconstruct a drug's PK model from multiple published PK studies. This approach can not only estimate PK parameters, but also can recover their between-study and between-subject variations. Most importantly, the posterior distributions of PK parameters and their variance components allow us to predict DDI at both population-average and study-specific levels. In addition, so we can also predict the DDI population and between-subject variance. These statistical predictions have never been investigated in a DDI research. Our simulation studies show that our meta-analysis approach has small bias in PK parameter estimates and DDI prediction, when using the published sample mean and variance data.

Both data analysis and simulation studies demonstrate that the mean-variance model proposed in this paper and the mean-model in Li et al. (2007) have comparable performances in PK parameter estimations. In (Li et al. 2007), it was shown that PK parameter estimation is robust to prior distribution selection. In addition, it was shown in the paper that a second-order Taylor expansion approximation in (10) did not reduce the bias much. This is consistent with that of the marginal quasi-likelihood (MQL) approach in generalized linear mixed model (Molenberghs and Verbeke 2005) (Chap. 14, p270-273). Other approximation method, such as penalized quasi-likelihood approach (PQL) was reported to have better performance (Breslow and Clayton 1993; Wolfinger and O'Connell 1993), which is a first order Taylor expansion around subject-specific parameters. However, as the subject-specific level PK parameter information is not available in the sample mean data, PQL approach is not applicable in our meta-analysis.

The competitive inhibition interaction model (3) between MDZ/KETO has been well established in both in-vitro studies (von Moltke et al. 1996 and Gibbs et al.1999) and in-vivo studies (Yang et al. 2003 and Chien, et al. 2006). There are multiple MDZ/KETO DDI studies (McCrea, et al. 1999; Lam, et al. 2003; lkkola, et al. 1994; Lee et al. 2002; and Tsunoda et al. 1999). Our proposed drug interaction models (1) ∼ (3) predict reasonably well in MDZ/KETO interaction, given a single dose 200mg IV MDZ and a single dose 2mg KETO PO and K_i = 0.0037 μM (Table 3). The predicted average AUCR = 3.02, and the reported average AUCR = 5.10 (Tsunoda et al. 1999). However, how to validate the model based DDI prediction is itself a highly challenging problem. Questions remain regarding how to determine the existence of DDI, how to test the equivalence between the predicted and the reported DDI, and how to expand the current two-compartmental interaction model to a physiological interaction model for possible improvement in DDI prediction. All these questions need significant joint efforts from statisticians and pharmacologists.

In this paper, we assume that the DDI PK model framework is known and correct. The unknown pieces are the pharmacokinetic parameters of the two drugs' two-compartment models. With a Bayesian approach, we are able to recover both the means and between-subject variances of the PK parameters from summarized data, which then leads to a valid DDI prediction. This paper establishes our Bayesian approach's feasibility and validity in recovering PK parameter means and variances from published summarized data. It serves as a fundamental building block for follow-up DDI model development and DDI prediction. The Bayesian models also provide a flexible framework to integrate prior knowledge into the estimation and prediction procedures.

Appendix Posterior Distributions

The following functions are conditional distributions to draw PK parameters and their variance components parameters in our three level hierarchical Bayesian model proposed in section 3.

Data analysis proposed in section 4 also utilized the following distributions. Assume the dimension of α is p, of β_ik, β_k, and β is q.

Population PK parameters (α, β=(β₁, ……, β_q)^T) and study level PK parameters β_k:

$$p(\alpha |•)\propto \left\{\prod _{h=1}^{H_k}\prod _{j=1}^{T_{\text{kh}}}N\left(f(\alpha ,{\beta }_k,z_{\text{jkh}}),\frac{F_{\text{jkh}}^T\text{∑}{F}_{\text{jkh}}+{\sigma }_0^2}{n_{\text{kh}}}\right)\right\}$$ (A1)

$$\begin{array}{l}p({\beta }_k|•)\propto \left\{\prod _{h=1}^{H_k}\prod _{j=1}^{T_{\text{kh}}}N\left(f(\alpha ,{\beta }_k,z_{\text{jkh}}),\frac{F_{\text{jkh}}^T\text{∑}{F}_{\text{jkh}}+{\sigma }_{0k}^2}{n_{\text{k}}}\right)\right\}\times \left\{\prod _{k=1}^{K}p({\beta }_k|\beta ,\Omega \right\}\\ p({\beta }_l|•)\propto N\left({\left\{\frac{1}{{\tau }_l^2}+\frac{K}{{\omega }_l^2}\right\}}^{-1}\left\{\frac{1}{{\tau }_l^2}{\mu }_l+\frac{K}{{\omega }_l^2}{\overline{\beta }}_{·l}\right\},{\left\{\frac{1}{{\tau }_l^2}+\frac{K}{{\omega }_l^2}\right\}}^{-1}\right)\end{array}$$ (A2)

$$\text{for}l=1,\mathrm{...},q;\text{where}{\overline{\beta }}_{·l}=\sum _{k=1}^K{\beta }_{\text{kl}}$$ (A3)

Variance components:

$$Pr({\omega }_{\mathrm{l}}^2|•)\sim \text{Inv}-\text{Gamma}\left[\left(\frac{K}{2}-1\right),\left(\frac{\text{∑}_{k=1}^K{({\beta }_{\text{kl}}-{\beta }_l)}^2}{2}\right)\right]\times 1_{{\omega }_l^2}(0.01{}^2,2{}^2)$$ (A4)

where $1_{{\omega }_l^2}$ (0.01²,2²) equals 1 when ${\omega }_l^2$ is inside (0.01², 2²) and 0 otherwise.

$$\begin{array}{l}p({\sigma }_l^2|•)\\ \propto \prod _{k=1}^K\prod _{h=1}^{H_k}\prod _{j=1}^{T_{\text{kh}}}{(F_{\text{jkh}}^T{F}_{\text{jkh}}{\sigma }_1^2+{\sigma }_0^2)}^{-\frac{n_{\text{kh}}}{2}+1}\\ \times exp\left\{-\frac{n_{\text{kh}}{\{{\overline{y}}_{•\text{jkh}}-f(\alpha ,{\beta }_k,z_{\text{jkh}})\}}^2+{\text{∑}_{i=1}^{n_{\text{kh}}}(y_{\text{ijkh}}-\overline{y}}_{•\text{jkh}}{)}^2}{2(F_{\text{jkh}}^T{\text{F}}_{\text{jkh}}{\sigma }_1^2+{\sigma }_0^2)}\right\}\times 1_{{\sigma }_1^2}({0.01}^2,2^2)\end{array}$$ (A5)

$$\begin{array}{l}p({\sigma }_0^2|•)\\ \propto \prod _{k=1}^K\prod _{h=1}^{H_k}\prod _{j=1}^{T_{\text{kh}}}{(F_{\text{jkh}}^T{F}_{\text{jkh}}{\sigma }_1^2+{\sigma }_0^2)}^{-\frac{n_{\text{kh}}}{2}+1}\\ \times exp\left\{-\frac{n_{\text{kh}}{\{{\overline{y}}_{•\text{jkh}}-f(\alpha ,{\beta }_k,z_{\text{jkh}})\}}^2+{\text{∑}_{i=1}^{n_{\text{kh}}}(y_{\text{ijkh}}-\overline{y}}_{•\text{jkh}}{)}^2}{2(F_{\text{jkh}}^T{\text{F}}_{\text{jkh}}{\sigma }_1^2+{\sigma }_0^2)}\right\}\times 1_{{\sigma }_0^2}({0.01}^2,2^2)\end{array}$$ (A6)

Here $1_{{\sigma }_1^2}$ (0 01²,2²) and $1_{{\sigma }_1^2}$ (0.01²,2²) are similarly defined as $1_{{\omega }_l^2}$ (0 01²,2²).