Summary
Purpose
A neural network simulation with realistic cortical architecture has been used to study synchronized bursting as a seizure representation. This model has the property that bursting epochs arise and cease spontaneously, and bursting epochs can be induced by external stimulation. We have used this simulation to study the time-frequency properties of the evolving bursting activity, as well as effects due to network stimulation.
Methods
The model represents a cortical region of 1.6 mm × 1.6 mm, and includes seven neuron classes organized by cortical layer, inhibitory or excitatory properties, and electrophysiological characteristics. There are a total of 65, 536 modeled single compartment neurons that operate according to a version of Hodgkin-Huxley dynamics. The intercellular wiring is based on histological studies and our previous modeling efforts.
Results
The bursting phase is characterized by a flat frequency spectrum. Stimulation pulses are applied to this modeled network, with an electric field provided by a 1 mm radius circular electrode represented mathematically in the simulation. A phase dependence to the post-stimulation quiescence is demonstrated, with local relative maxima in efficacy occurring before or during the network depolarization phase in the underlying activity. Brief periods of network insensitivity to stimulation are also demonstrated. The phase dependence was irregular and did not reach statistical significance when averaged over the full 2.5 seconds of simulated bursting investigated. This result provides comparison with previous in vivo studies which have also demonstrated increased efficacy of stimulation when pulses are applied at the peak of the local field potential during cortical afterdischarges. The network bursting is synchronous when comparing the different neuron classes represented up to an uncertainty of 10 msec. Studies performed with an excitatory chandelier cell component demonstrated increased synchronous bursting in the model, as predicted from experimental work.
Conclusions
This large scale multi-neuron neural network simulation reproduces many aspects of evolving cortical bursting behaviour as well as the timing-dependent effects of electrical stimulation on that bursting.
Keywords: Seizure simulation, neural network modeling, cortical stimulation, computer modeling
1. Introduction
It is unknown whether epilepsy originates from pathologic neurons or pathologic epileptic networks, or some combination of the two etiologies (Leussis and Heinrichs 2007; Kumar et al. 2007; Swann et al. 2007; Patrylo and Willingham 2007; Ang et al. 2006; Hirose 2006; Mantegazza et al. 2005; George 2004; Bernard et al. 2004; Mulley et al. 2003). Regardless of the initial pathophysiology, epilepsy is a network driven phenomenon. The abnormal electrical activity that is recognized as a seizure is the result of many neurons firing synchronously. It is known that the networks (e.g. hippocampal or neocortical) of epileptic foci have anatomical changes (e.g. sprouting or cellular loss) that may produce increased excitation (Sallin et al. 1995; Sutula 2002; Longo et al. 2003; Sutula et al. 1989; Arellano et al. 2004; Ribak 1985; Dinocourt et al. 2003; Wittner et al. 2005). Other authors have looked at the abnormal time-frequency characteristics of seizures in an effort to understand epilepsy further (Litt and Echauz 2002; Lopes da Silva et al. 2003; Jouny et al. 2005; Jouny et al. 2007).
Interest has also grown in ascertaining the characteristics of seizure onset, termination, and the possibility of using external stimulation pulses to stop seizures. One attractive hypothesis is that before the clearly visible ictal EEG changes or clinical seizure manifestations, there are changes that may be occurring minutes to hours beforehand that would allow one to predict seizure onset (Esteller et al. 2001; Litt and Echauz 2002; Sackellares et al. 2006; Haas et al. 2006). This has been the subject of considerable investigation and some preliminary reports suggest prediction can be performed effectively, in time to apply abortive stimulation pulses (Echauz et al. 2001; D'Alessandro et al. 2003). Furthermore Lesser et al. (Lesser et al. 1999) demonstrated, in a set of patients undergoing preresection evaluation, that the afterdischarges which occur during stimulation for localization could be aborted by a train of neighboring brief pulse stimulations. Of note, these authors demonstrated that the pulse used to abort the bursting activity was most effective during the depolarization phase of the recorded local field potential (by a factor of 1.9 in required applied current) (Motamedi et al. 2002). It is this phase dependence of electrical stimulation effects on bursting behaviour that we explore further in the context of a computational model.
Neuronal network modeling allows one to control and study the various influences on network behavior. In a recent paper, we presented the results of computational simulation studies examining geometric effects of external field stimulation on ongoing bursting activity in a neural network (Anderson et al. 2007). This effort applied a realistic electric field distribution from a small circular electrode represented mathematically as if it were mounted over an 800 μm × 800 μm region of modeled cortex. The cortical model consisted of discrete single compartment Hodgkin-Huxley type cells, and for the most part stimulation was assumed to take place at the position of the cell's axon initial segment, thereby sending synaptic effects to any cells connected to the cell being stimulated. These cells were spatially arranged in an architecturally realistic fashion incorporating a layered cortical structure as well as utilizing a columnar vertical organization for the neurons (Anderson et al. 2007). The medium was assumed to be electrically homogeneous, and effects due to the underlying white matter were ignored. Robust and active bursting activity was produced in the model using a small centrally located noise. These effects were similar to the one-compartment neural network bursting behaviour we have seen in previous architecturally nonspecific versions of the simulation (Kudela et al. 1997; Kudela et al. 2003a; Kudela et al. 2003b; Kudela et al. 2005; Franaszczuk et al. 2003). Other groups have also used architecturally realistic models to investigate transcranial magnetic stimulation (Esser et al. 2005).
This follow-up study reports on simulation data obtained from the architecturally realistic model to study the evolving bursting behaviour, as well as stimulation-induced effects on this spontaneous activity. The model demonstrates epileptic bursting triggered by low-level distributed cortical activity simulating baseline neighboring cortical input. This level of activity does not always trigger seizures, but can more easily do so depending on the level of network connectivity. The modeled surface area of our simulation represents 1.6 mm × 1.6 mm of cortex (65,536 neurons). We specifically explore effects due to the timing of the stimulation relative to the underlying network bursting phase, to search for any phase-dependent periods of stimulation efficacy or lack thereof.
2. Methods
2.1 Neural network model
In the present study we used the same spatial arrangement for our modeled cells as in the previous introductory study (Anderson et al. 2007; Anderson 2008), where it is described in detail. A brief description follows. The modeled cells were arranged in an architecturally realistic fashion incorporating a layered neocortical structure as well as utilizing a minicolumn-based vertical organization for the neurons (Anderson et al. 2007; Douglas and Martin 2004). The somatosensory and visual cortical model of Douglas and Martin was utilized because of its experimental support and ease of programming (Douglas and Martin 2004). The medium was assumed to be electrically homogenous, and effects due to the underlying white matter were ignored. In general, robust and active bursting activity was produced using a spatially distributed background activity described below. Sensitivity analyses of the various connectional possibilities were performed in (Anderson et al. 2007).
The cells used in this model are simulated one-compartment Hodgkin-Huxley neurons. There are four classes of excitatory cells including pyramidal cells in cortical layers II and III (treated as one layer), layer V, and layer VI, and stellate cells in layer IV. There are also three classes of inhibitory interneurons including basket cells, double-bouquet cells, and chandelier cells. The cells are organized into a minicolumnar arrangement consisting of 16 cells with wiring according to Figure 1. in (Anderson et al. 2007; Douglas and Martin 2004; Nieuwenhuys 1994). The total number of cells examined in this study was 65,536, representing a simulated cortical surface area of 1.6 mm × 1.6 mm, given a 25 μm center-to-center spacing for the minicolumns.
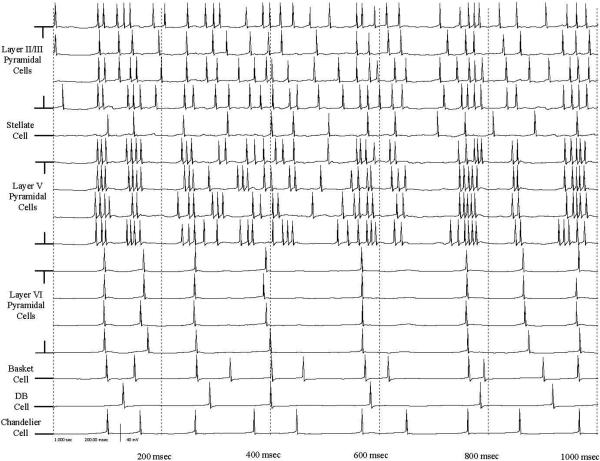
Figure 1.
Plot of cellular membrane potentials relative to the resting potential for all 16 cells contained within one minicolumn in the simulation during a period of active bursting for a one second recording. Rows 1−4 are the Layer II/III pyramidal cells, row 5 is the stellate cell, rows 6−9 are the Layer V pyramidal cells, row 10−13 are the Layer VI pyramidal cells, row 14 is the basket cell, row 15 is the double bouquet cell, and row 16 is the chandelier cell.
In general, the modeled layer II/III pyramidal cells make isotropic connections out to a radius of 300 μm, and are considered to be regular spiking cells as defined in (Anderson et al. 2007). Similarly, the modeled layer V pyramidal cells make isotropic connections to a radius of 300 μm, and are considered to be intrinsic bursting cells. The modeled layer IV stellate cells make no external connections outside of their minicolumn and are regular spiking cells. The modeled layer VI pyramidal cells make fewer connections than layer V pyramidal cells out to a radius of 300 μm, and are considered regular spiking cells.
The modeled inhibitory cell types (basket, double bouquet, and chandelier) make connections based on histological data (Peters and Sethares 1997; Kisvárday et al. 1986; Thomson and Deuchars 1997; Melchitzky et al. 2001; Douglas and Martin 2004; Lewis et al. 2002; Connors and Gutnick 1990; Budd and Kisvárday 2001; Kisvárday et al. 1993; Kisvárday et al. 2002; Lund and Wu 1997; DeFelipe et al. 1999; Kawaguchi and Kubota 1998). The modeled basket cells can make connections out to a radius of 1 mm, but the connection distribution function consists of a negative exponential after a distance of 50 μm from the cell body. The modeled basket cells are considered to be fast spiking cells. In the simulation, double bouquet cells make only sparse connections outside of their minicolumns and are considered fast spiking cells as well. The modeled chandelier cells make isotropic connections to 200 μm, and synapse with approximately 20% of pyramidal cells they encounter. These cells are implemented as regular spiking cells. Table 1 presents the baseline numbers of connections used in the simulations.
Table 1.
Numbers of connections formed between modeled neurons as a function of cell class, size range of connections is provided in (Anderson et al., 2007). These numbers are the connections between neurons external to their intrinsic minicolumn. Connections between neurons within their minicolumn are included in parentheses.
| Cell Type (Class Number) | Layer II/III Pyramidal(1) | Layer IV Stellate(2) | Layer V Pyramidal(3) | Layer VI Pyramidal(4) | Basket Cell(5) | Double Bouquet Cell(6) | Chandelier Cell (7) |
|---|---|---|---|---|---|---|---|
| Layer II/III Pyramidal(1) | 238 (3) | 58 (0) | 414 (4) | 0 (0) | 36 (1) | 0 (0) | 36 (1) |
| Layer IV Stellate (2) | 0 (4) | 0 (0) | 0 (0) | 0 (0) | 0 (1) | 0 (0) | 0 (1) |
| Layer V Pyramidal(3) | 46 (4) | 0 (0) | 110 (3) | 0 (4) | 16 (1) | 16 (1) | 16 (1) |
| Layer VI Pyramidal(4) | 20 (0) | 0 (1) | 0 (0) | 0 (4) | 4 (1) | 4 (1) | 4 (1) |
| Basket Cell(5) | 215 (4) | 54 (1) | 215 (4) | 215 (4) | 25 (0) | 10 (0) | 25 (1) |
| Double Bouquet Cell (6) | 8 (4) | 2 (1) | 8 (4) | 0 (0) | 19 (0) | 0 (0) | 19 (0) |
| Chandelier Cell (7) | 60 (4) | 15 (1) | 60 (4) | 0 (0) | 0 (0) | 0 (0) | 0 (0) |
The numerical simulation was based on the excitable membrane model of Hodgkin and Huxley (Hodgkin and Huxley 1952) as modified by Av-Ron et al. (Av-Ron 1994; Av-Ron et al. 1993), and is described in detail in (Anderson et al. 2007). The model parameters for the three different electrophysiology types simulated (regular spiking, intrinsic bursting, and fast spiking) are presented in tabular form in (Table 2, Anderson et al. 2007). The cells exhibit stable bursting or spiking activity with constant current injections of 5 μA/cm2, and the activity ceases when the input current is shut off.
Behavior among cells in a given class in the network is very similar, with the modeled layer V pyramidal cells exhibiting periodic bursting behaviour, and the other excitatory cells exhibiting regular spiking discharges.
The synaptic currents in the model on a given cell are represented as sums of currents taken over all the available synapses represented, with the individual synaptic conductances implemented as the difference of two exponentials with rise and fall time constants. This form allows for the representation of passive degradation effects within a dendritic arbor, or for the introduction of empirical size-reduction factors based on an active dendritic tree. In the current scheme, the weighting factors are chosen to provide realistic network bursting behaviour, and reflect empirical differences in PSP reduction as recorded at the soma for cells synapsing distally versus proximally using the recordings of (Williams 2005) and (Williams and Stuart 2003) for both EPSPs and IPSPs. In the current model, all double bouquet cells were assumed to synapse at greater than 500 μm from the soma, while all of the basket cells were assumed to take somal synaptic locations and their relative synaptic weights are adjusted accordingly. Inhibitory cell weights are less than zero, and chandelier cells, which synapse on the axon initial segment have large magnitude negative weightings (Williams 2005; Williams and Stuart 2003; Krimer and Goldman-Rakic 2001; Kalisman et al. 2003; Kisvárday et al. 2002; DeFelipe 1985; Paré et al. 1998). A few studies were also performed in which the chandelier cells had positive weightings (the same magnitude as pyramidal cell weights) to reproduce certain recent experimental findings (Szabadics et al. 2006).
2.2 Background activity
Synaptic current injections representing background activity from neighboring cortex are applied to 1% of the cells in the model. These cells are chosen randomly throughout the model space regardless of cell class with both 1% of inhibitory and excitatory cells affected. These synaptic current injections are implemented as a homogeneous Poisson noise process at an average rate of 1 Hz for each cell. There is no presynaptic cell in the model responsible for these current injections, but the rise and fall times of the current pulses follow the same dynamics as the other excitatory synapses represented. This was an effort to represent long-range input from regions of surrounding cortex, and to provide a base level of activity to the simulation. The background activity applied to separate neurons is uncorrelated. The kinetics of the charge injection is governed by the excitatory synaptic time scales per (Anderson et al. 2007), and are the same as other excitatory synapses used in the model. The synaptic conductance for this simulated activity is 0.7mS/ cm2 which is approximately a factor of ten higher than the typical excitatory synaptic connection used in the model, thereby giving these current injections a high probability of producing an action potential.
2.3 External field stimulation
The external field is simulated as the application of a current to a circular disk of radius 1 mm. The applied stimulation pulses take the form of a two-lobed square-wave train (anodal followed by cathodal), with each lobe lasting 0.1 sec. In the following studies, two consecutive pulses are applied during stimulation with each bipolar pulse separated by 5 msec. Ground is taken at infinity under the modeled medium, and the disk is represented mathematically as if it were centered over the modeled cortical surface. The determination of action potential production in the cells was based on an electric field gradient threshold oriented along the position of each axon initial segment. The choice of parameters used in this study was based on a sensitivity analysis of the various stimulation parameters performed in (Anderson et al. 2007).
2.4 Mean field potential derivation
An instantaneous mean field potential was derived from the model by first averaging the membrane potential over all of the cells represented (65,536 cells). The derivative of this average was then used as a representative of an average extracellular potential for the modeled cortical region in the spirit of (Henze et al. 2000). This signal was filtered (2−10 Hz, elliptical IIR filter) using the Matlab Signal Analysis toolbox (Mathworks, Natick, MA, USA) to produce the mean field potential (MFP) used for time-frequency analysis. The simulated size of our model (1.6 mm × 1.6 mm) is comparable to the size of a typical subdural recording electrode (2 mm diameter) so this derived MFP should provide a reasonable estimate of a locally recorded signal. The sign convention in this analysis is for positive MFP values to represent periods of depolarization in the modeled network.
The code for the simulation was written in C and developed in a Linux environment. The model runs on a cluster of sixteen 32-bit, 1 GHz, x86 architecture computers implemented as a distributed system. Each computer in the cluster performed the numerical integration calculations on a specific subnetwork, with data transfers between processors (representing neuronal connections crossing nodal boundaries) accomplished with Linux-based packet send and receive commands. Typical 10 second simulation runs on a 64 × 64 minicolumn model take 20 hours of wall-time to complete (2 hours/simulated second). CPU usage averaged 90% of this with the simulation representing the bulk of the load on the 16 node cluster, the remainder of the time was spent in input/output and packet transfer functions.
2.5 Time-frequency analysis
For time frequency evaluation of the numerical simulation studies the matching pursuit method of Mallat and Zhang was used to spectrally decompose the MFP (Mallat and Zhang 1993). This is an iterative procedure used to decompose a time-dependent signal into a linear combination of a restricted and specified dictionary of functions consisting of cosines, Gaussian modulated cosines (Gabor functions), and Dirac delta functions. The details of the application of the procedure to simulated signals are described elsewhere (Kudela et. al 2003b). The MP decomposition of the MFP is then displayed as a color-coded plot in the time-frequency domain.
3. Results
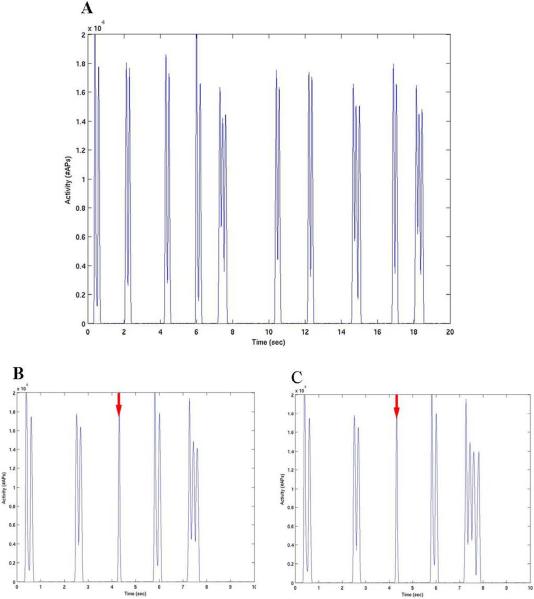
The connection pattern examined in these studies represented an alteration of one of the robustly bursting patterns examined in (Anderson et al. 2007; Pattern C), which in most computations and noise sources studied produced stable network bursting between 5 and 12.5 Hz for the dominant frequency modes exhibited. The numbers of extra-columnar connections formed by each cell is presented in Table 1. The numbers of connections formed along the periphery of the model were reduced to avoid boundary reflection effects. The connections were reduced starting at a distance of 300 μm from the edge by a multiplicative factor to express the reduction in numbers of connections more appropriate for an artificial boundary in an isotropic environment. The experiments incorporating these reduced boundary connections were better able to produce bursting phases with random onset and cessation times. A plot of the activity in row format for each of the 16 cells in one specific minicolumn over a one second period is shown in Figure 1. The network activity in the absence of any stimulation pulses demonstrates spontaneous onset and cessation of bursting periods shown in Figure 2 (A-C). A total of 131 10 second simulations were used to derive the phase-dependence data presented below.
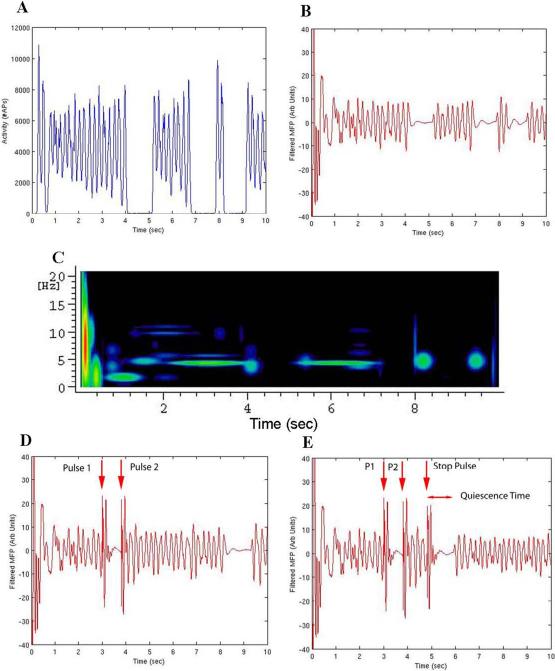
Figure 2.
(A-C) Model with no stimulation applied, same connection pattern as used in stimulation studies. (A) Summed Layer II/III pyramidal cell action potentials in 10 msec bins. (B) Filtered mean field potential. (C) MP analysis. (D) Filtered mean field potential of the same simulation with a stimulation pulse applied at 3.00 sec stopping the ongoing bursting activity. A second stimulation pulse at 3.8 sec is used to restart a stable long bursting period. Red arrows above the plot demonstrate the stimulation points. (E) Filtered mean field potential of the same pulse sequence, now with a further 3rd stimulation pulse (stop pulse) used to investigate the phase dependence of stimulation-induced activity alteration. Red arrows above the plot demonstrate the stimulation points.
3.1 Base activity
One measure of the efficacy of the stimulation in a network that has an underlying constant random background activity applied, is to look for the time it takes post-stimulation for the network to return to its intermittent bursting activity. An estimate of this is the time difference between the stimulation pulse used to alter the bursting activity and the time of the first returning network burst (“quiescence time”). In the set of experiments used to explore effects due to the relative phase of the applied stimulation pulse with respect to the underlying rhythmic activity, a two pulse stimulation paradigm was used to initiate a reproducible and stable pattern of activity on which a third (“stop”) pulse could be applied to investigate this phase dependence. The first stimulation pulse was applied at 3.0 seconds to stop the ongoing network activity previously demonstrated in Figure 2 (A-C), followed by a preparatory pulse at 3.80 seconds to start a long period of constant bursting activity demonstrated in Figure 2 (D). This method was used in part to produce reproducible behavior in the model to test the stop pulse on the same pattern of bursting over multiple trials, as well as to mimic the effects of stimulation-induced afterdischarges which have been altered by stop pulses in patients with implanted subdural grids implanted (Lesser et al. 1999; Motamedi et al. 2002).
3.2 Phase dependence
The stop pulse was then used to alter this constant bursting, and the timing between the 2nd and stop pulses was varied to investigate the phase dependence of the stimulation efficacy on stopping the ongoing bursting. The figure of merit used to gauge efficacy of the stimulation was the quiescence time in the Layer II/III pyramidal cells after the applied stop pulse. A representative plot of the activity alteration induced by the stop pulse is presented in Figure 2(E). A plot of the quiescence time is presented in Figure 3 (A) along with the underlying Layer II/III pyramidal cell activity that would be present if only the initiating stimulation pulse (the 2nd stimulation) were applied. As can be seen, there is an irregular phase dependence to the quiescence time, which grows more apparent after one second of continuous bursting activity (the “sawtooth” region demonstrated by the quiescence time peaks in red in Figure 3(A) between 1.0 and 3.0 seconds). The quiescence time was probed with the stop pulse from 0.02 to 2.49 seconds after the preparatory pulse, at a sampling interval of 0.02 seconds.
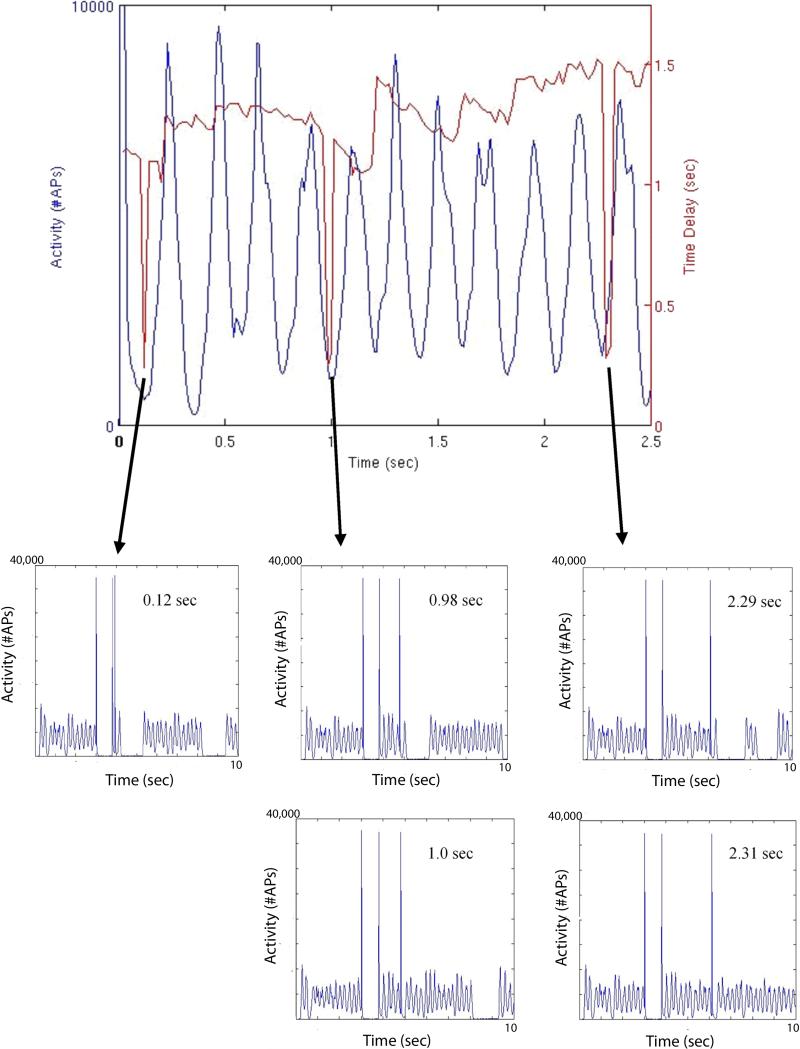
Figure 3.
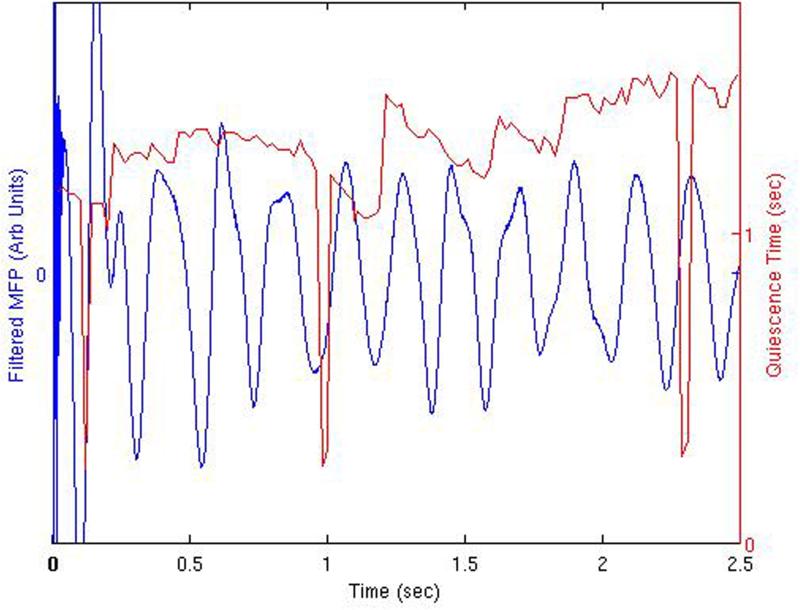
(A) Summed Layer II/III pyramidal cell action potentials in 10 msec bins, with superimposed stimulation-induced quiescent periods. The time interval between the second and third pulses of the three-pulse paradigm is demonstrated by the position of the quiescent period value. These quiescent periods induced by the stop pulse demonstrate a phase dependence with respect to the underlying activity. Also shown are the details of network activity occurring during the three periods of loss of stimulation efficacy at 0.12, 0.98−1.0, and 2.29−2.31 seconds into the constant bursting period (Layer II/III pyramidal cell activity). At 0.12 sec, 0.98 sec, and 2.29 sec, the activity does exhibit a period of quiescence, albeit delayed, with the presence of a single pulse of activity in the normally quiet post-stimulation window. The “sawtooth” region described in the text is demonstrated by the quiescence time peaks in red primarily between 1.0−3.0 seconds. (B) Similar plot demonstrating quiescent periods shown with the underlying network MFP.
This effect is further illustrated in the plot of the quiescence time displayed along with the underlying derived mean field potential in Figure 3(B). Demonstrated are regions of increased stimulation efficacy when the stimulation is applied during depolarization periods. This is more apparent after one second into the continuous bursting activity. Precipitous drops in quiescence time are demonstrated at 0.12 seconds, 0.98−1.0 seconds, and 2.29−2.31 seconds into the continuous activity. The MFP precedes the peak in cell activity since it represents the derivative of the average mean field potential. It also represents the physical observable that should be compared to a local field potential or electrocorticography recording in an experimental or clinical stimulation paradigm. Similar results are obtained when plotting the quiescence time associated just with the inhibitory cell component, or the quiescence time of the Layer V pyramidal cell component.
A plot of the quiescence time recorded for the five sampled points lying on either side of each MFP peak studied is presented in Figure 4(A), with the quiescence time normalized to its MFP peak value. The spread in values before the MFP peak is larger before the peak occurs, and the drops in efficacy can also be seen. The average peri-peak quiescence time is also presented in red in Figure 4(A). There was no statistical difference in average quiescence times taken between the pre- and post-peak values, however the standard errors of the mean are larger (ratio of sem before peak / after peak = 9.6, p=0.002, t-test) before the MFP peak.
Figure 4.
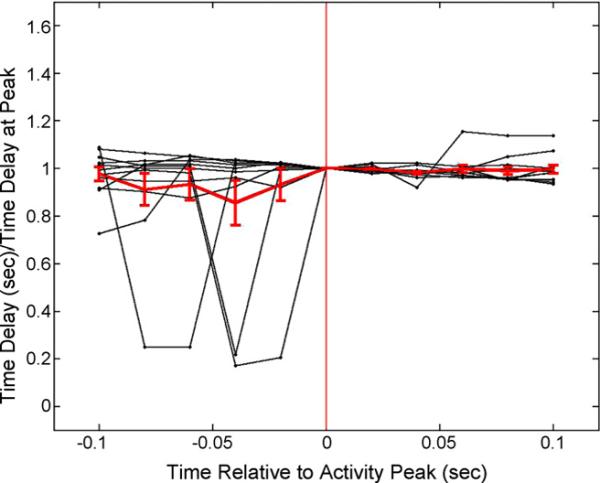
Plot of the five sampled quiescence times before and after each of the MFP peaks examined. Times are relative to the peak in the MFP. The vertical red line additionally indicates the peak location. The average of these 11 peri-peak measurements (± sem) is shown in red. There were no statistical differences in these values based on matched t-testing.
3.3 Insensitivity of Network to Stimulation
As shown in Figure 3(A), the brief periods of insensitivity to stimulation do not necessarily correspond to a quick return of constant bursting activity after the stop pulse. Rather for some of these time points (notably at 0.12 sec, 0.98 sec, and 2.29 sec) one activity peak appears in the quiescent window which is still represented at some level albeit delayed. At no other time points are these post-stimulation peaks present. The length of this delayed quiescent period is comparable to the delay times present at the troughs of the phase dependence in the remainder of the data in Figure 3(A). At the 1.0 sec and 2.31 sec stimulation points, the quiescence time is also very short but with continuous activity present for an extended period, and not just the single occurrence of one peak.
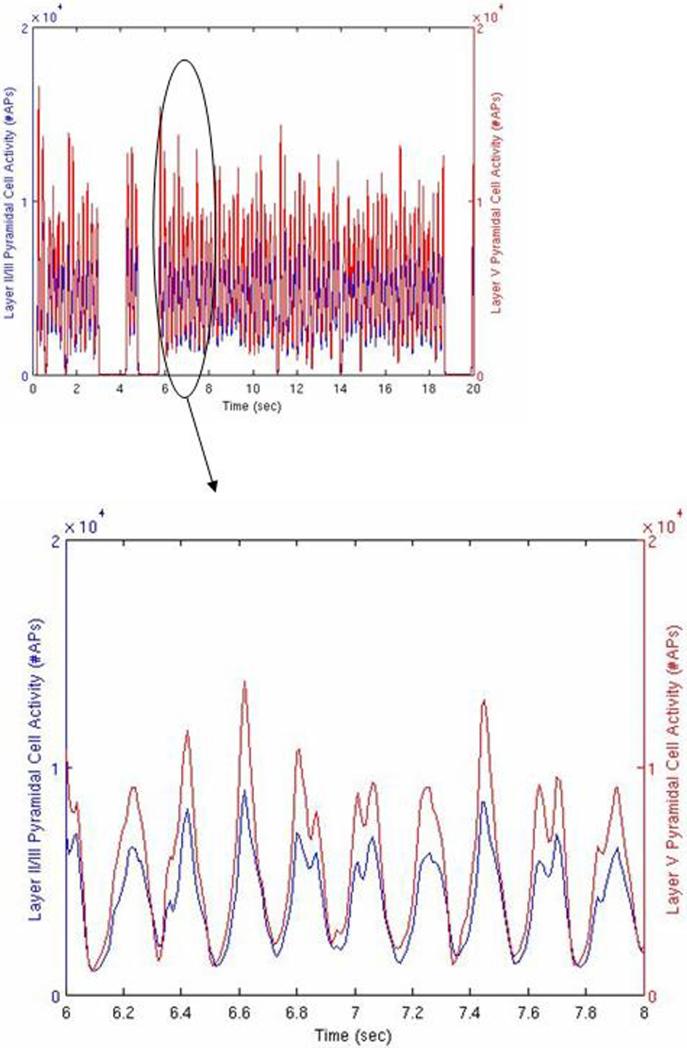
3.4 Synchronous bursting across cell types
The spread of the bursting activity remains fairly synchronous when comparing the two main excitatory laterally connecting cellular systems, namely the Layer II/III pyramidal cells and the Layer V pyramidal cells. This is demonstrated during a 20 second simulation with no stimulation applied in Figure 5. Similar synchrony is observed for the relative burst timing between the inhibitory cell component taken as a whole and the Layer II/III pyramidal cells. No statistical difference was found between the peak times in the expanded region of Figure 5, however the inhibitory cell component did demonstrate a lag behind the Layer II/III pyramidal cell component by 0.01 sec (p=0.002, matched t-test), which is at the sampling time resolution of the action potential binning.
Figure 5.
Network activity with no stimulation, 10 second simulation. Red line indicates summed action potentials in 10 msec bins for the Layer II/III pyramidal cells as a function of time. Blue line indicates the same for the Layer V pyramidal cells. Inset is the data presented in more detail from the 6.0 to 8.0 second region.
3.5 Effects due to excitatory chandelier cells
Additional simulations were run with flipped polarity for the chandelier cell component (from inhibitory to excitatory). This was an effort to include the state-dependent results of (Szabadics et al. 2006), in which the chandelier cell component in acute neocortical slice preparations can act as an excitatory influence on the axon initial segment of pyramidal cells. Interestingly, the underlying behavior becomes more synchronous with very little activity between the narrow bursting peaks, Figure 6(A). Variation in this activity can be induced by a single stimulation pulse which varies with the timing of the pulse as in Figure 6(B,C). The locations of the two stimulation pulses are marked with arrows, and as demonstrated they halt the ongoing bursting peak which occurs close to the 4 second mark. Additionally, the subsequent bursting activity is altered compared to Figure 6(A) but still highly synchronous. This more synchronous behavior is reminiscent of the onset of cortical ripples or synchronized hippocampal rhythms and was hypothesized by (Szabadics et al. 2006) as an effect of excitatory input from the chandelier cell component.
Figure 6.
(A) Network activity utilizing a model with excitatory chandelier cells. The synaptic weights used were the same as Layer II/III pyramidal cell excitatory connections. Note the more synchronous bursting pattern produced with a distributed background source, compared to the previous simulations. (B,C) Single stimulation pulses were applied at 4.308 sec (B) and 4.313 sec (C) on the underlying activity presented in (A). Stimulation times marked by the red arrow. Note the disruption of the bursting period between 4 and 5 seconds and the alteration of the subsequent bursting behavior compared to (A).
4. Discussion
4.1 Phase dependent stimulation effects
These modeling efforts, utilizing a neural network system of connected single compartment Hodgkin-Huxley based cells demonstrate many realistic properties of neocortical ictal activity. The network shows spontaneous onset and cessation of bursting activity, driven by a distributed background which has been implemented to represent neighboring random cortical input. In general, the major spectral components of the bursting activity stay constant during the bursting phase. Our results also show how this bursting activity can be affected by external stimulation using stimulation pulses from a single circular electrode represented in the model. Stimulation can induce bursting activity, stop it, or do very little to the underlying network activity. These effects appear to have a dependence on the phase of the bursting activity, with a stimulation cessation pulse being more effective if applied close to the peak in network activity for isolated windows during the bursting.
(Motamedi et al. 2002) describe the effects of stimulation pulses on stopping cortical afterdischarges within a population of patients undergoing implanted subdural electrode monitoring for seizure evaluation. This paper demonstrated a relative increase of efficacy at stopping cortical afterdischarges when stimulating during the negative peak (or depolarization phase under the electrode) of the recorded EEG. On average, for a stimulation pulse applied during the negative (depolarization) phase of the rhythm, the stimulation pulse was 1.9 times more likely to stop the afterdischarge than a pulse applied when the afterdischarge potential was positive in the experimental study of (Motamedi et al. 2002). Specifically, the authors reported a 69% rate of stopping afterdischarges with a brief stimulation pulse when the pulse was applied at the negative peak, compared to a 20% rate of stopping afterdischarges when the stimulation pulse was applied to the positive trough region of the waveform.
We similarly see increases in stimulation efficacy based on the quiescence time as a figure of merit which are correlated with the MFP peaks, and can be as large as a factor of 5 for the ratio of quiescence times. This additionally reproduces the results in Figure 10(A) from (Anderson et al. 2007), in which an increase in stimulation efficacy was also observed at the time of the peak in network activity, albeit in a smaller computational model measured over one single activity peak. These times are larger when the stop pulse in Figure 3(B) is applied during or just before the depolarization period of the derived mean field potential, and occurs in both the excitatory and inhibitory cellular components taken separately.
We find this to be an encouraging result derived from our network model that resembles experimental findings to date, and it can serve as a guide in the design of stimulation paradigms for clinical applications. This limited data set actually represents approximately 2620 hours of wall-time computer use, but clearly will need to be investigated further with other stimulation and background activity paradigms. A lot of effort has been placed on seizure detection in the development of closed loop responsive neurostimulation systems for seizure termination. But an equally important aspect of the stimulation technique might include the timing of the seizure pulse relative to the underlying electrocorticographic activity. This might also simplify the stimulation pulse sequence, and could offer a savings in battery life.
4.2 Periods of stimulation insensitivity
Another finding in the phase dependence results is that the periods of fluctuating stimulation efficacy are punctuated by brief periods of network insensitivity to the stimulation (notably at 0.12, 0.98−1.0, and 2.29−2.31 seconds of delay). Since (Motamedi et al. 2002) could not repeat the exact same pattern of underlying cortical activity over and over again to investigate the phase dependence on the same waveform, it would have been impossible for them to focus on specific regions of loss of activity in this manner. However, stimulation pulses were at times completely ineffective at stopping the afterdischarge activity as in our model. The presence of single peaks of activity in the post-stimulation windows at 0.12, 0.98, and 2.29 seconds stop pulse time is interesting, and might represent a transitional period leading into a region of complete loss of efficacy as at times 1.0 and 2.31 seconds for the stop pulse. No stimulation insensitivity is observed at 0.14 seconds for the stop pulse time, but this could be due to our choice of a 0.02 second sampling interval in that region which could have skipped the least effective stimulation time. The regions of stimulation insensitivity are very interesting and imply strong local time variations in the response to stimulation, furthermore they provide a signature that can be looked for in experimental data.
Additionally, when a stimulation pulse was effective in the work of Motamedi et al., the afterdischarge completely stopped, with no further resumption in epileptiform activity. Our simulation work was designed to produce several-second periods of stable bursting activity interspersed by random periods of network quiescence. Even after a “stop” stimulation pulse in this simulation, the network bursting will subsequently return because of the continuous background activity present, hence our need to use the quiescent time surrogate marker as a measure of stimulation efficacy. Earlier experimental paradigms in our modeling efforts also included stopping the background noise at 1 second into the simulation, with robust bursting activity continuing for a few seconds after that time point. Stimulation applied to these experiments after 1 second stops the bursting activity with no further return, since the underlying background has been halted.
4.3 Alternative studies
It is possible to alter this model so that it is more excitatory and easily produces continuous bursting activity (see Anderson et al. 2007 for examples). Our goal in this study was to examine a model that was more controllable through single pulse stimulation to more closely approximate the work of (Motamedi et al. 2002) and (Lesser et al. 1999), in which after discharges were produced and stopped by brief pulses of stimulation. It is true, however, that the more unstable continuous bursting connectivity patterns might be a better representation of a runaway epileptiform process.
Another future paradigm to explore might include calculating the probability of stopping the bursting with a stimulation pulse as a function of the level of background activity. As our efforts continue to become more realistic in representing underlying cortical activity, we should be able to reproduce the experimental paradigm more faithfully. Furthermore, since the current model readily supports bursting behaviour, it probably serves more as a representative of pathologic tissue and less as a surrogate of normal brain. Future efforts should include an interphase between pathologic and nonpathologic tissue to understand the spread of bursting into normal regions.
The actual phase dependence on the underlying bursting activity appears to grow stronger with time, specifically after one second into the continuous bursting examined in the “sawtooth” region of Figure 3. This increasing phase dependence might have a practical consequence regarding a stimulation system built to stop epileptic activity, implying that stop-pulses applied early after a seizure starts would be less dependent on their timing relative to the underlying MFP phase. Additional synaptic effects that are not included in this computational work but could also affect the phase dependence and its evolution over time include short-term synaptic plasticity and neurotransmitter depletion. Both of these effects have been investigated in computational models by our group and others (Kudela et al. 2004; Shouval et al. 2002; Swiercz et al. 2007), and need to be further explored in this paradigm since the size of these effects are unknown. Additionally, calcium concentration changes are known to affect the evolving bursting behavior of this class of computational model (Kudela et al. 2003b). The simulation described here maintained a constant level of calcium reuptake throughout each experiment, and the calcium fluctuations are strongly correlated with the underlying rhythmic activity. However, no association with peak to peak variations in the calcium concentration on stimulation efficacy were uncovered.
Clearly we have not explored delay times greater than 2.5 seconds for the application of the stop pulse, so it is unknown whether this region of phase dependence continues or only represents an island. We have shown that variation can occur however, which might represent a meaningful network property. For our purposes in this study, stopping a seizure within 2.5 seconds from the onset represents a clinically meaningful time-frame, and falls into the more effective experimental window of less than 4.5 seconds after initiation of the afterdischarges reported by (Motamedi et al. 2002). Interestingly, the recent studies of Lesser et al. (2008) point to short- term variations in the ability of cortical stimulation to produce afterdischarges. These authors point to alterations in the underlying cortical networks or the underlying preceding pattern of activity within those networks. This type of experimental effort is also amenable to our computational efforts, and the efficacy of bursting initiation should also be assessed as a function of timing of the stimulation pulse with respect to any underlying background activity.
In general, cellular bursting activity remains synchronous between the various inhibitory and excitatory cell classes as a function of time over the few seconds of studied activity, with only the inhibitory cellular component demonstrating a lag of 10 msec behind the Layer II/III pyramidal cell component. Timing differences by cortical layer can be seen in interictal spikes in human microelectrode recordings between these layers by current source density analysis, and these time differences are on the order of 10 msec which is at the currently recorded sampling resolution derived from the model (Ulbert et al. 2004). The synchrony we observe in our model is most likely due to rapid vertical intracolumnar spread based on the imposed cellular wiring, and will be most influenced by typical synaptic delay times, which are on the order of a few milliseconds in the simulation.
To further compare the laminar structure of the evolving bursting activity with experimental data, we will need to precisely define these delays to represent more realistic propagation times. Typical propagation velocities derived from our simulations for the wave-like bursting activity is on the order of 10 mm/sec, which is comparable to propagation speeds derived in epileptiform discharges in rat neocortex (8−150 mm/sec) (Wadman and Gutnick 1993). Our model does not include some of the saltatory aspects of this burst conduction, since the longer range cortical patch connectivity that exists at the 1 mm size-scale is not included in the extracolumnar wiring.
The main goal of this study was to investigate the phase dependence of the efficacy of external electrical stimulation to alter bursting activity. For this reason, the three pulse paradigm chosen in the experiment was used to set up a reproducible pattern of bursting activity and interrogate it. The pattern of activity after the second pulse was exactly the same in every trial up until the application of the stop pulse. Computational limits and limits on run-time of the code currently restrict efforts to examine a measure of interseizure intervals affected by stimulation as a benchmark, although this should be explored as the simulation infrastructure enlarges. The figure of merit chosen in this study (the time to return of bursting activity post-stimulation or quiescence time) was thought to be a good compromise for assessing the efficacy of the stimulation within short-time simulations. The phase dependence studies described here always used the same random connection pattern between cells, as well as the random order of background pulse application, again to ensure a reproducible activity pattern on which we could apply the stimulation paradigm. Altering the random number seeds used to produce the specific wiring patterns and Poisson background application do not alter the overall pattern of bursting activity observed, just the timing of burst initiation and cessation (in preparation).
Future studies should include modeling these same effects using a multicompartment representation for the neurons in which more accurate dendritic, somal, and axonal effects can be studied. One encouraging previous result from our laboratory demonstrated that single compartment models do reproduce the same features of bursting activity that more accurate multicompartment simulations show (Yang et al. 2003). One of the biggest gains that multicompartment modeling would provide is a more accurate estimate of electric field effects on the various excitable portions of the neurons as in (McIntyre and Grill 1999). Not only would this more accurately represent action potential production from an imposed field, but it would also allow a better estimate of the volume of stimulated tissue.
Additionally, the modeling results incorporating excitatory chandelier cell input (Figure 6), are extremely interesting and point toward a richer network behavior when some blend of chandelier polarity is included that is dependent on the network activity context. Axo-axonic cells can behave as excitatory influences because of the local relative depolarization of the axon initial segment relative to the soma. As noted by (Szabadics et al. 2006), this effect is probably dependent on the local network activity with the axo-axonic cells most likely acting in a bistable role depending on the underlying cortical state and relative depolarization of the soma. The simulations performed with the reversed synaptic polarity in the chandelier cell component produced a strong regularization of the bursting a result hypothesized by (Szabadics et al. 2006). A similar effect is observed from hyperpolarizing bitufted cells synapsing on pyramidal cell dendrites, where the timing of the synaptic input places the pyramidal cell network in a synchronized mode (Klausberger et al. 2004). This again points toward the need to perform these studies in a multicompartment format to address the possibility of this richer network behavior and more accurately predict stimulation effects.
4.4 Conclusions
Studies in preparation indicate that alterations in the random number seeds responsible for either generating the connection pattern (while holding the total connections constant), or the temporal order of background activity still produce spontaneous periods of bursting activity. A sensitivity analysis on the relative weights of total excitatory and inhibitory connections was also performed in (Anderson et al. 2007), demonstrating post-stimulation quiescence periods in all of the connection patterns studied. The underlying background activity remains constant between separate stimulation trials in the current study, only the state of the model changes depending on the timing of the stimulation. Our previous experience with single-compartment Hodgkin-Huxley based models (Franaszczuk et al. 2003; Anderson et al. 2007), ongoing studies in preparation, and experimental studies (Wagenaar et al. 2005; Madhavan et al. 2006; Vajda et al. 2008) indicate that longer post-stimulation quiescence periods translate to more disruptive stimulation.
In conclusion, we would like to emphasize the ability of this type of phenomenological modeling to provide data that is comparable to clinical data from epilepsy patients. The current simulation provides a mean field potential recorded from a small region of cortex comparable in size to the surface area under a typical subdural grid electrode. MP analysis or other types of time-frequency spectral analysis can be performed on this simulated data readily. This is analogous to clinical studies used to examine the time-frequency spectrum of epileptic bursting (Jouny et al. 2003; Jouny et al. 2005; Jouny et al. 2007), and makes comparisons between modeling efforts and clinical data easy to perform.
Acknowledgements
Supported in part by NIH NS51382 (PK), NIH NS38958 (PJF), and the Epilepsy Foundation (WSA).
Footnotes
Disclosures
None of the authors has any conflict of interest to disclose.
Contributor Information
William S. Anderson, Harvard Medical School Department of Neurosurgery Brigham and Women's Hospital 75 Francis Street CA 138F Boston, MA USA 02115 wsanderson@partners.org (o) +1(617)732−6838 (f) +1(617)713−3050.
Pawel Kudela, The Johns Hopkins Hospital Department of Neurology Meyer 2−147 600 North Wolfe Street Baltimore, MD USA 21287 pkudela@jhmi.edu (o) +1(443)287−8295 (f) +1(410)955−0751.
Seth Weinberg, The Johns Hopkins University Whiting School of Engineering Department of Biomedical Engineering 720 Rutland Avenue Baltimore, MD 21205 sweinbe9@jhmi.edu (o) +1(410)955−3131 (f) +1(410)502−9814.
Gregory K. Bergey, The Johns Hopkins Hospital Department of Neurology Meyer 2−147 600 North Wolfe Street Baltimore, MD USA 21287 gbergey@jhmi.edu (o) +1(410)955−7338 (f) +1(410)502−2507.
Piotr J. Franaszczuk, The Johns Hopkins Hospital Department of Neurology Meyer 2−147 600 North Wolfe Street Baltimore, MD USA 21287 pfranasz@jhmi.edu (o) +1(410)614−8770 (f) +1(410)955−0751.
5. References
- Anderson WS. 2008 http://senselab.med.yale.edu/senselab/modeldb.
- Anderson WS, Kudela P, Cho RJ, Bergey GK, Franaszczuk P. Studies of stimulus parameters for seizure disruption using neural network simulations. Biol. Cyber. 2007;97:173–194. doi: 10.1007/s00422-007-0166-0. PMID: 17619199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ang CW, Carlson GC, Coulter DA. Massive and specific dysregulation of direct cortical input to the hippocampus in temporal lobe epilepsy. J. Neurosci. 2006;26(46):11850–11856. doi: 10.1523/JNEUROSCI.2354-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arellano JI, Muñoz A, Ballesteros-Yáñez I, Sola RG, DeFelipe J. Histopathology and reorganization of chandelier cells in the human epileptic sclerotic hippocampus. Brain. 2004;127:45–64. doi: 10.1093/brain/awh004. [DOI] [PubMed] [Google Scholar]
- Av-Ron E. The role of a transient potassium current in a bursting neuron model. J Math. Biol. 1994;33:71–87. doi: 10.1007/BF00160174. [DOI] [PubMed] [Google Scholar]
- Av-Ron E, Parnas H, Segel LA. A basic biophysical model for bursting neurons. Biol. Cybern. 1993;69:87–95. doi: 10.1007/BF00201411. [DOI] [PubMed] [Google Scholar]
- Bernard C, Anderson A, Becker A, Poolos NP, Beck H, Johnston D. Acquired dendritic channelopathy in temporal lobe epilepsy. Science. 2004;305:532–535. doi: 10.1126/science.1097065. [DOI] [PubMed] [Google Scholar]
- Budd JM, Kisvárday ZF. Local lateral connectivity of inhibitory clutch cells in layer 4 of cat visual cortex (area 17). Exp. Brain. Res. 2001;140(2):245–250. doi: 10.1007/s002210100817. [DOI] [PubMed] [Google Scholar]
- Connors BW, Gutnick MJ. Intrinsic firing patterns of diverse neocortical neurons. TINS. 1990;13:99–104. doi: 10.1016/0166-2236(90)90185-d. [DOI] [PubMed] [Google Scholar]
- D'Alessandro M, Esteller R, Vachtsevanos G, Hinson A, Echauz J, Litt B. Epileptic seizure prediction using hybrid feature selection over multiple intracranial EEG electrode contacts: a report of four patients. IEEE Trans. Bio. Eng. 2003;50(5):603–615. doi: 10.1109/tbme.2003.810706. [DOI] [PubMed] [Google Scholar]
- DeFelipe J, Hendry SH, Jones EG, Schmechel D. Variability in the terminations of GABAergic chandelier cell axons on initial segments of pyramidal cell axons in the monkey sensory-motor cortex. J. Comp. Neurol. 1985;231:364–384. doi: 10.1002/cne.902310307. [DOI] [PubMed] [Google Scholar]
- DeFelipe J, González-Albo MC, Del Río MR, Elston GN. Distribution and patterns of connectivity of interneurons containing calbindin, calretinin, and parvalbumin in visual areas of the occipital and temporal lobes of the macaque monkey. J. Comp. Neurol. 1999;412(3):515–526. doi: 10.1002/(sici)1096-9861(19990927)412:3<515::aid-cne10>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
- Dinocourt C, Petanjek Z, Freund TF, Ben-Ari Y, Esclapez M. Loss of interneurons innervating pyramidal cell dendrites and axon initial segments in the CA1 region of the hippocampus following pilocarpine-induced seizures. J. Comp. Neuro. 2003;459:407–425. doi: 10.1002/cne.10622. PMID: 12687707. [DOI] [PubMed] [Google Scholar]
- Douglas RJ, Martin KAC. Neuronal circuits of the neocortex. Ann. Rev. Neurosci. 2004;27:419–451. doi: 10.1146/annurev.neuro.27.070203.144152. [DOI] [PubMed] [Google Scholar]
- Echauz J, Esteller R, Tcheng T, Pless B, Gibb B, Kishawi E, Litt B. Long-term validation of detection algorithms suitable for an implantable device. Epilepsia. 2001;42(suppl 7):35–36. [Google Scholar]
- Esser SK, Hill SL, Tononi G. Modeling the effects of transcranial magnetic stimulation on cortical circuits. J. Neurophysiol. 2005;94:622–639. doi: 10.1152/jn.01230.2004. [DOI] [PubMed] [Google Scholar]
- Estellar R, Echauz J, Tcheng T, Litt B, Pless B. Line length: an efficient feature of seizure onset detection.. Proc. 23rd Annu. Int. Conf. IEEE Eng. Med. Biol. Soc.; Istanbul. 2001. pp. 1707–1710. [Google Scholar]
- Franaszczuk PJ, Kudela P, Bergey GK. External excitatory stimuli can terminate bursting in neural network models. Epilepsy Res. 2003;53:65–80. doi: 10.1016/s0920-1211(02)00248-6. [DOI] [PubMed] [Google Scholar]
- George AL. Inherited channelopathies associated with epilepsy. Epilepsy Curr. 2004;4:65–70. doi: 10.1111/j.1535-7597.2004.42010.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haas SM, Frei MG, Osorio I. Strategies for adapting automated seizure detection algorithms. Med. Eng. Phys. 2007;29(8):895–909. doi: 10.1016/j.medengphy.2006.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henze DA, Borhegyi Z, Csicsvari J, Mamiya A, Harris KD, Buzsáki G. Intracellular features predicted by extracellular recordings in the hippocampus in vivo. J. Neurophysiol. 2000;84:390–400. doi: 10.1152/jn.2000.84.1.390. [DOI] [PubMed] [Google Scholar]
- Hirose S. A new paradigm of channelopathy in epilepsy syndromes: intracellular trafficking abnormality of channel molecules. Epilepsy Res. 2006;70(Suppl 1):S206–S217. doi: 10.1016/j.eplepsyres.2005.12.007. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. (London) 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. PMID: 12991237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jouny CC, Franaszczuk PJ, Bergey GK. Characterization of epileptic seizure dynamics using Gabor atom density. Clin. Neurophysiol. 2003;114:426–437. doi: 10.1016/s1388-2457(02)00344-9. [DOI] [PubMed] [Google Scholar]
- Jouny CC, Franaszczuk PJ, Bergey GK. Signal complexity and synchrony of epileptic seizures: is there an identifiable preictal period? Clin. Neurophysiol. 2005;116:552–558. doi: 10.1016/j.clinph.2004.08.024. [DOI] [PubMed] [Google Scholar]
- Jouny CC, Adamolekun B, Franaszczuk PJ, Bergey GK. Intrinsic ictal dynamics at the seizure focus: effects of secondary generalization revealed by complexity measures. Epilepsia. 2007;48:297–304. doi: 10.1111/j.1528-1167.2006.00963.x. [DOI] [PubMed] [Google Scholar]
- Kalisman N, Silberberg G, Markram H. Deriving physical connectivity from neuronal morphology. Biol. Cybern. 2003;88:210–218. doi: 10.1007/s00422-002-0377-3. [DOI] [PubMed] [Google Scholar]
- Kawaguchi Y, Kubota Y. Neurochemical features and synaptic connections of large physiologically-identified GABAergic cells in the rat frontal cortex. Neurosci. 1998;85(3):677–701. doi: 10.1016/s0306-4522(97)00685-4. PMID: 9639265. [DOI] [PubMed] [Google Scholar]
- Kisvárday ZF, Martin KA, Freund TF, Maglóczky Z, Whitteridge D, Somogyi P. Synaptic targets of HRP-filled layer III pyramidal cells in the cat striate cortex. Exp. Brain Res. 1986;64:541–552. doi: 10.1007/BF00340492. [DOI] [PubMed] [Google Scholar]
- Kisvárday ZF, Beaulieu C, Eysel UT. Network of GABAergic large basket cells in cat visual cortex (area 18): implication for lateral disinhibition. J. Comp. Neurol. 1993;327(3):398–415. doi: 10.1002/cne.903270307. [DOI] [PubMed] [Google Scholar]
- Kisvárday ZF, Ferecskó AS, Kovács K, Buzás P, Budd JML, Eysel UT. One axon-multiple functions: specificity of lateral inhibitory connections by large basket cells. J. Neurocytol. 2002;31(35):255–264. doi: 10.1023/a:1024122009448. [DOI] [PubMed] [Google Scholar]
- Klausberger T, Márton LF, Baude A, Roberts JDB, Magill PJ, Somogyi P. Spike timing of dendrite-targeting bistratified cells during hippocampal network oscillations in vivo. Nature Neurosci. 2004;7(1):41–47. doi: 10.1038/nn1159. [DOI] [PubMed] [Google Scholar]
- Krimer LS, Goldman-Rakic PS. Prefrontal microcircuits: membrane properties and excitatory input of local, medium, and wide arbor interneurons. J. Neurosci. 2001;21:3788–3796. doi: 10.1523/JNEUROSCI.21-11-03788.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kudela P, Franaszczuk PJ, Bergey GK. A simple computer model of excitable synaptically connected neurons. Biol. Cybern. 1997;77:71–77. doi: 10.1007/s004220050368. [DOI] [PubMed] [Google Scholar]
- Kudela P, Franaszczuk PJ, Bergey GK. Changing excitation and inhibition in simulated neural networks: effects on induced bursting behavior. Biol. Cybern. 2003a;88:276–285. doi: 10.1007/s00422-002-0381-7. PMID: 12690486. [DOI] [PubMed] [Google Scholar]
- Kudela P, Franaszczuk PJ, Bergey GK. Reduction of intracellular calcium removal rate can explain changes in seizure dynamics: studies in neuronal network models. Epilepsy Res. 2003b;57:95–109. doi: 10.1016/j.eplepsyres.2003.10.009. PMID: 15013051. [DOI] [PubMed] [Google Scholar]
- Kudela P, Franaszczuk PJ, Bergey GK. Synaptic plasticity in neuronal network models can explain patterns of bursting activity seen in temporal lobe epileptic seizures. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2004;1:715–717. doi: 10.1109/IEMBS.2004.1403258. PMID: 17271777. [DOI] [PubMed] [Google Scholar]
- Kudela P, Franaszczuk PJ, Bergey GK. Synaptic and cellular influences on the composite EEG signal during seizures.. Proc. 2nd Inter. IEEE EMBS Conf. Neural Eng.; Arlington, VA, IEEE. 2005. pp. 245–247. [Google Scholar]
- Kumar SS, Jin X, Buckmaster PS, Huguenard JR. Recurrent circuits in layer II of medial entorhinal cortex in a model of temporal lobe epilepsy. J. Neurosci. 2007;27:1239–1246. doi: 10.1523/JNEUROSCI.3182-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lesser RP, Lee HW, Webber WRS, Prince B, Crone NE, Miglioretti DL. Short-term variations in response distribution to cortical stimulation. Brain. 2008;131:1528–1539. doi: 10.1093/brain/awn044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lesser RP, Kim SH, Beyderman L, Miglioretti DL, Webber WR, Bare M, Cysyk B, Krauss G, Gordon B. Brief bursts of pulse stimulation terminate afterdischarges caused by cortical stimulation. Neurology. 1999;53(9):2073–2081. doi: 10.1212/wnl.53.9.2073. 1999. [DOI] [PubMed] [Google Scholar]
- Lewis DA, Melchitzky DS, Burgos GG. Specificity in the functional architecture of primate prefrontal cortex. J. Neurocytol. 2002;31(3−5):265–276. doi: 10.1023/a:1024174026286. [DOI] [PubMed] [Google Scholar]
- Leussis MP, Heinrichs SC. Temporal ontogeny of circuit activation prior to the onset of seizure susceptibility in EL/Suz mice. Neurosci. 2007;145:33–41. doi: 10.1016/j.neuroscience.2006.11.031. PMID: 17207935. [DOI] [PubMed] [Google Scholar]
- Litt B, Echauz J. Prediction of epileptic seizures. Lancet Neuro. 2002;1:22–30. doi: 10.1016/s1474-4422(02)00003-0. PMID: 12849542. [DOI] [PubMed] [Google Scholar]
- Longo B, Covolan L, Chadi G, Eugênio L, Mello AM. Sprouting of mossy fibers and the vacating of postsynaptic targets in the inner molecular layer of the dentate gyrus. Exp. Neuro. 2003;181:57–67. doi: 10.1016/s0014-4886(02)00046-8. PMID: 12710934. [DOI] [PubMed] [Google Scholar]
- Lopes da Silva F, Blanes W, Kalitzin SN, Parra J, Suffczynski P, Velis DN. Epilepsies as dynamical diseases of brain systems: basic models of the transition between normal and epileptic activity. Epilepsia. 2003;44(Suppl 12):72–83. doi: 10.1111/j.0013-9580.2003.12005.x. [DOI] [PubMed] [Google Scholar]
- Lund JS, Wu CQ. Local circuit neurons of macaque monkey striate cortex: IV. Neurons of laminae 1−3A. J. Comp. Neurol. 1997;384(1):109–126. doi: 10.1002/(sici)1096-9861(19970721)384:1<109::aid-cne7>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- Madhavan R, Chao ZC, Wagenaar DA, Bakkum DJ, Potter SM. Multi-site stimulation quiets network-wide spontaneous bursts and enhances functional plasticity in cultured cortical networks.. Proc 28th IEEE EMBS Ann Inter Conf; New York. Aug 30-Sep 3, 2006; 2006. pp. 1593–1596. [DOI] [PubMed] [Google Scholar]
- Mallat SG, Zhang ZF. Matching pursuits with time-frequency dictionaries. IEEE Trans. Sig. Proc. 1993;41:3397–3415. [Google Scholar]
- Mantegazza M, Gambardella A, Rusconi R, Schiavon E, Annesi F, Cassulini RR, Labate A, Carrideo S, Chifari R, Canevini MP, Canger R, Franceschetti S, Annesi G, Wanke E, Quattrone A. Identification of an Nav1.1 sodium channel (SCN1A) loss-of-function mutation associated with familial simple febrile seizures. Proc. Natl. Acad. Sci. USA. 2005;102:18177–18182. doi: 10.1073/pnas.0506818102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melchitzky DS, Gonzales-Burgos G, Barrionuevo G, Lewis DA. Synaptic targets of the intrinsic axon collaterals of supragranular pyramidal neurons in monkey prefrontal cortex. J. Comp. Neurol. 2001;430(2):209–221. doi: 10.1002/1096-9861(20010205)430:2<209::aid-cne1026>3.0.co;2-#. [DOI] [PubMed] [Google Scholar]
- Motamedi GK, Lesser RP, Miglioretti D, Mizuno-Matsumoto Y, Gordon B, Webber WRS, Jackson DC, Sepkuty JP, Crone NE. Optimizing parameters for terminating cortical afterdischarges with pulse stimulation. Epilepsia. 2002;43:836–846. doi: 10.1046/j.1528-1157.2002.24901.x. [DOI] [PubMed] [Google Scholar]
- Mulley JC, Scheffer IE, Petrou S, Berkovic SF. Channelopathies as a genetic cause of epilepsy. Curr. Opin. Neurol. 2003;16:171–176. doi: 10.1097/01.wco.0000063767.15877.c7. [DOI] [PubMed] [Google Scholar]
- Nieuwenhuys R. The neocortex: An overview of its evolutionary development, structural organization and synaptology. Anat. Embryol. 1994;190:307–337. doi: 10.1007/BF00187291. [DOI] [PubMed] [Google Scholar]
- Paré D, Lange EJ. Destexhe A. Inhibitory control of somatodendritic interactions underlying action potentials in neocortical pyramidal neurons in vivo: an intracellular and computational study. Neurosci. 1998;84:377–402. doi: 10.1016/s0306-4522(97)00530-7. PMID: 9539211. [DOI] [PubMed] [Google Scholar]
- Patrylo PR, Willingham A. Anatomic and electrophysiologic evidence for a proconvulsive circuit in the dentate gyrus of reeler mutant mice, an animal model of diffuse cortical malformation. Dev. Neurosci. 2007;29:73–83. doi: 10.1159/000096212. [DOI] [PubMed] [Google Scholar]
- Peters A, Sethares C. The organization of double bouquet cells in monkey striate cortex. J. Neurocytol. 1997;26(12):779–97. doi: 10.1023/a:1018518515982. PMID: 9482155. [DOI] [PubMed] [Google Scholar]
- Ribak CE. Axon terminals of GABAergic chandelier cells are lost at epileptic foci. Brain Res. 1985;326:251–260. doi: 10.1016/0006-8993(85)90034-4. [DOI] [PubMed] [Google Scholar]
- Sackellares JC, Shiau DS, Principe JC, Yang MC, Dance LK, Suharitdamrong W, Chaovalitwongse W, Pardalos PM, Iasemidis LD. Predictability analysis for an automated seizure prediction algorithm. J. Clin. Neurophysiol. 2006;23:509–520. doi: 10.1097/00004691-200612000-00003. [DOI] [PubMed] [Google Scholar]
- Sallin P, Tseng G-F, Hoffman S, Parada I, Prince DA. Axonal sprouting in layer V pyramidal neurons of chronically injured cerebral cortex. J. Neurosci. 1995;15(12):8234–8245. doi: 10.1523/JNEUROSCI.15-12-08234.1995. PMID: 8613757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shouval HZ, Castellani GC, Blais BS, Yeung LC, Cooper LN. Converging evidence for a simplified biophysical model of synaptic plasticity. Biol. Cyber. 2002;87(5−6):383–391. doi: 10.1007/s00422-002-0362-x. PMID: 12461628. [DOI] [PubMed] [Google Scholar]
- Sutula T, Cascino G, Cavazos J, Parada I, Ramirez L. Mossy fiber synaptic reorganization in the epileptic human temporal lobe. Ann. Neurol. 1989;26:321–330. doi: 10.1002/ana.410260303. [DOI] [PubMed] [Google Scholar]
- Sutula T. Seizure-induced axonal sprouting: assessing connections between injury, local circuits, and epileptogenesis. Epilepsy Curr. 2002;2(3):86–91. doi: 10.1046/j.1535-7597.2002.00032.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swann JW, Le JT, Lee CL. Recurrent seizures and the molecular maturation of hippocampal and neocortical glutamatergic synapses. Dev. Neurosci. 2007;29:168–178. doi: 10.1159/000096221. [DOI] [PubMed] [Google Scholar]
- Swiercz W, Cios K, Hellier J, Yee A, Staley K. Effects of synaptic depression and recovery on synchronous network activity. J. Clin. Neurophysiol. 2007;24:165–174. doi: 10.1097/WNP.0b013e318033756f. [DOI] [PubMed] [Google Scholar]
- Szabadics J, Varga C, Molnár G, Oláh S, Barzó P, Tamás G. Excitatory effect of GABAergic axo-axonic cells in cortical microcircuits. Science. 2006;311:233–235. doi: 10.1126/science.1121325. [DOI] [PubMed] [Google Scholar]
- Thomson AM, Deuchars J. Synaptic interactions in neocortical local circuits: dual intracellular recordings in vitro. J. Cereb. Cort. 1997;7:510–522. doi: 10.1093/cercor/7.6.510. PMID: 9276176. [DOI] [PubMed] [Google Scholar]
- Ulbert I, Heit G, Madsen J, Karmos G, Halgren E. Laminar analysis of human neocortical interictal spike generation and propagation: current source density and multiunit analysis in vivo. Epilepsia. 2004;45(Suppl 4):48–56. doi: 10.1111/j.0013-9580.2004.04011.x. [DOI] [PubMed] [Google Scholar]
- Vajda I, van Pelt J, Wolters P, Chiappalone M, Martinoia S, van Someren E, van Ooyen A. Low-frequency stimulation induces stable transitions in stereotypical activity in cortical networks. Biophys. J. 2008;94:5028–5039. doi: 10.1529/biophysj.107.112730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wadman WJ, Gutnick MJ. Non-uniform propagation of epileptiform discharge in brain slices of rat neocortex. Neurosci. 1993;52:255–262. doi: 10.1016/0306-4522(93)90154-8. PMID: 8450945. [DOI] [PubMed] [Google Scholar]
- Wagenaar DA, Madhavan R, Pine J, Potter SM. Controlling bursting in cortical cultures with closed-loop multi-electrode stimulation. J. Neurosci. 2005;25:680–688. doi: 10.1523/JNEUROSCI.4209-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams SR. Encoding and decoding of dendritic excitation during active states in pyramidal neurons. J. Neurosci. 2005;25:5894–5902. doi: 10.1523/JNEUROSCI.0502-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams SR, Stuart GJ. Voltage- and site-dependent control of the somatic impact of dendritic IPSPs. J. Neurosci. 2003;23:7358–7367. doi: 10.1523/JNEUROSCI.23-19-07358.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wittner L, Erőss L, Czirják S, Halász P, Freund TF, Maglóczky Z. Surviving CA1 pyramidal cells receive intact perisomatic inhibitory input in the human epileptic hippocampus. Brain. 2005;128:138–152. doi: 10.1093/brain/awh339. [DOI] [PubMed] [Google Scholar]
- Yang KH, Franaszczuk PJ, Bergey GK. The influences of somatic and dendritic inhibition on bursting patterns in a neuronal circuit model. Biol. Cybern. 2003;89:242–253. doi: 10.1007/s00422-003-0429-3. [DOI] [PubMed] [Google Scholar]