A comparison of HDR brachytherapy and IMRT techniques for dose escalation in prostate cancer: A radiobiological modeling study

Abstract

A course of one to three large fractions of high dose rate (HDR) interstitial brachytherapy is an attractive alternative to intensity modulated radiation therapy (IMRT) for delivering boost doses to the prostate in combination with additional external beam irradiation for intermediate risk disease. The purpose of this work is to quantitatively compare single-fraction HDR boosts to biologically equivalent fractionated IMRT boosts, assuming idealized image guided delivery (igIMRT) and conventional delivery (cIMRT). For nine prostate patients, both seven-field IMRT and HDR boosts were planned. The linear-quadratic model was used to compute biologically equivalent dose prescriptions. The cIMRT plan was evaluated as a static plan and with simulated random and setup errors. The authors conclude that HDR delivery produces a therapeutic ratio which is significantly better than the conventional IMRT and comparable to or better than the igIMRT delivery. For the HDR, the rectal gBEUD analysis is strongly influenced by high dose DVH tails. A saturation BED, beyond which no further injury can occur, must be assumed. Modeling of organ motion uncertainties yields mean outcomes similar to static plan outcomes.

INTRODUCTION

Recent clinical studies suggest that escalating dose from 68–70 to 74–80 Gy improves PSA control of locally advanced prostate cancer^{1, 2, 3, 4} but often results in grade-2 rectal and grade-2∕3 late bladder toxicities exceeding 10%.^{5, 6} Hence there is a significant clinical interest in devising new methods of treatment delivery that achieve such dose escalation without increasing or even reducing normal tissue toxicity.

Two delivery techniques are commonly used to achieve dose escalation to the prostate gland in the setting of intermediate or high risk disease: Intensity modulated radiation therapy (IMRT) and brachytherapy, both of which are used to deliver boost doses to the highest risk clinical target volume (CTV) (usually prostate gland±proximal seminal vesicles) preceded by 45–63 Gy to the pelvic lymph nodes and periprostatic tissues. These boost methods deliver substantially different physical dose distributions to the prostate and the surrounding structures and differ in their fractionation schedules. The IMRT boost is typically delivered with a 1.8–2.5 Gy∕fraction schedule, while the brachytherapy boost can be delivered as one to three large high dose rate (HDR) fractions^{7, 8} or a single low dose rate (LDR) permanent implant.⁹ HDR interstitial brachytherapy techniques are of increasing interest as dose-escalation boosts delivered in conjunction with an external beam.^{7, 8} HDR advantages relative to LDR permanent implants include freedom from geometric uncertainties arising from edema resolution and seed migration and potentially very accurate dose delivery if dwell times are optimized with intraoperative imaging. Compared with IMRT, minimal, if any planning target volume (PTV) margins are thought to be required, which offers a possibility of greater sparing of organs at risk (OARs). Finally, the presumed low α∕β ratio of prostate tumor in relation to late-responding tissues in organs at risk¹⁰ should favor the large fraction sizes typical of HDR, which may confer more favorable therapeutic ratios. HDR doses as large as 2×11.5 Gy have been safely combined with whole pelvic doses of 40–50Gy.^{7, 8}

Despite the potential for HDR to improve clinical outcomes, very few realistic dosimetric comparisons of HDR and IMRT boosts have been published¹¹ for prostate cancer and other sites (see Ref. 12 for an exception). To better understand the interplay between physical coverage and fractionation differences between IMRT and HDR prostate boosts, we have utilized radiobiological models to compare three treatment modalities on a series of patient planning CT image sets: Fractionated IMRT optimized on the CTV, simulating idealized image guidance techniques; a margin-free single-fraction HDR boost; and fractionated IMRT boosts with conventional PTV margins and setup techniques.

The present work is not the first effort directed toward comparing different methods of delivery of radiation therapy in the treatment of prostate cancer. Most prior studies^{13, 14} comparing external beam and HDR treatments have been limited, however, to the tumor control end points and were based on idealized dose volume histograms (DVHs). Like the study of Pieters et al.,¹² our study is based upon clinically realistic prostate and normal tissue DVHs obtained from nine consecutively treated patients and considers both tumor control and normal tissue complication end points. In contrast to the study of Pieters et al., which was limited to DVH coverage metrics derived from cumulative isoeffective dose distributions for fixed combinations of external beam and brachytherapy, our analysis uses mathematical outcome models as surrogates for tumor control probability (TCP) and normal tissue complication probability (NTCP). Because of the large differences between IMRT and HDR fraction size and relative dose distributions, DVH metrics alone may not provide an unambiguous ranking of different treatment techniques as HDR advantages, such as better OAR sparing, often come at the cost of substantially greater dose heterogeneity. Radiobiologically based outcome surrogates could provide physicians a framework for better understanding these trade-offs, developing hypotheses for testing via clinical studies, and in choosing the optimum dose-escalation methodology. Our paper uses established radiobiological modeling tools to compare the potential effectiveness of the three boost techniques

MATERIALS AND METHODS

In this paper, we compare single-fraction HDR boost to a traditional IMRT fractionated regimen [conventional IMRT (cIMRT) boost] and to an idealized image guided adaptive radiation therapy regimen [image guided IMRT (igIMRT) boost]. The igIMRT boost assumes that the PTV margin can be reduced to zero by image guided adaptive techniques. The first two boost techniques (HDR and cIMRT) are currently used clinically at our institution, while the igIMRT technique is one of the subjects of a multiyear research effort that has been recently initiated at our institution. In this work we chose to compare the boost modalities directly, making minimum assumptions about the extended CTV external beam treatment that precedes or follows (in our institution HDR boost precedes IMRT whole-pelvis therapy) the boost regimen. The boosts were designed to deliver the same biologically equivalent dose (BED) of 36 Gy to the periphery of the prostate gland. The biological equivalence was derived using the linear-quadratic model, assuming that α∕β=3 Gy for the prostate gland.^{10, 15, 16} This compromise α∕β value was selected to be within the upper bound of the uncertainties associated with the unusually low values (as small as 1.2 Gy) favored by the current radiobiological literature.

Patient selection

Nine intermediate risk prostate patients who were treated either with external beam irradiation alone or with an in-house Internal Review Board approved protocol (6–9 Gy single fraction of HDR followed by a conformal IMRT plan delivering 63 Gy in 28 fractions to a CTV expanded to include prostate and seminal vesicles plus a 5 mm margin and 50.4 Gy to the electively treated pelvic lymph node volume) were selected for this study. All patients who were chosen for this study would have been eligible for an HDR boost, although some of them were treated with external beam alone. Otherwise, the selected patients were treated consecutively in our department. The mean and range of prostate volumes were 33 and 25.2–48.9 cm³, respectively.

Treatment planning

Along with HDR boosts, two forms of IMRT boosts were investigated: (1) cIMRT boost was planned using PTV as its target; (2) simulated igIMRT was planned using CTV as its target. The linear-quadratic model was used to derive the following biologically equivalent dose prescriptions: A single fraction of 9 Gy for HDR and nine fractions of 2.25 Gy for igIMRT and cIMRT. For all three modalities, the planning goal was to deliver the prescribed dose to 98% of the target.

In our clinical practice, HDR is planned intraoperatively using target volumes and OAR anatomy derived from transrectal ultrasound (TRUS) images acquired immediately after needle insertion, while IMRT is planned in simulator∕CT images. To ensure that our conclusions were not affected by systematic differences between TRUS and x-ray CT imaging, HDR and IMRT treatments were planned on the same set of contours derived from the IMRT planning CT image set. For each patient the prostate gland without margin was defined as the CTV. The PTV for cIMRT was formed by expanding CTV by 10 mm (6 mm posteriorly). For HDR and idealized igIMRT no margin was used so that the PTV was identical to the CTV. Rectum, bladder, and urethra were manually segmented on the planning CT as OARs. The sigmoid colon was excluded from the rectal volume. The urethra was approximated by a surrogate structure^{17, 18} consisting of 5 mm circular contours placed at the center of each transverse prostate contour.

HDR treatment planning

For each CT data set, an HDR boost was planned using the Varian BrachyVision treatment planning system (version 8.1, Varian Medical Systems, Palo Alto, CA). A total of 12–16 needles were used in each plan. Three planes with a mostly peripheral placement of needles ensured a good urethral dose sparing. The active dwell positions were placed on the whole length of each of the needles contained within the prostate. Geometric-based optimization was used to obtain an initial plan and dose. This type of optimization does not take into account any dose constraints on the volume of planning structures but instead uses the needles’ relative position. As a consequence, a peripheral dose point and the relative geometry of applicators are the only driving factors in the optimization process. The next step was a dose volume based optimization. The typical constraints were as follows: For prostate coverage a D₉₈≥D_prescr (for a D_prescr=9 Gy) and V₁₅₀<5–6 cc and V₂₀₀<1.5 cc, for urethra a D₉₀<80%D_prescr, D₃₀<(110%–115%)D_prescr, and D₁₀<(120%–125%)D_prescr, and for rectum a D₃₀<(50%–60%)D_prescr. A special effort was made in the HDR planning to enclose 98% of the prostate volume within the prescription dose of 9 Gy. For some patients for which both prostate coverage and urethral sparing at the abovementioned values proved very difficult, a reduced coverage was allowed (at least 93% of the prostate volume is covered by the prescription dose for all patients) in order to limit urethral dose. In select cases a manual adjustment of dwell times using BrachyVision’s dose shaping utilities was employed to reduce dose to structures not used for optimization (bladder, seminal vesicles, etc.). The urethra dose sparing constraints were somewhat relaxed relative to clinical planning, as CT-drawn urethra surrogates were used for this study.

IMRT treatment planning

For each patient, the planning CT data set was used to plan seven-field igIMRT and cIMRT boosts. All IMRT plans were generated using equally spaced 18 MV coplanar beams with step-and-shoot delivery with the Varian 21EX accelerator equipped with 120 leaf Millenium MLC. IMRT optimization was performed using the inverse planning software available in the Pinnacle version 7.9 system (Philips Medical Systems, Milpitas, CA), with the following constraints on organs at risk: For the bladder, D₁₀≤0.75⋅D_prescr and D₃₀≤0.5⋅D_prescr, and for the rectum, D₅≤0.75⋅D_prescr and D₅₀≤0.25⋅D_prescr, where D_prescr≈D₉₈ is the prescribed dose. The adaptive superposition∕convolution algorithm was utilized to calculate the dose distribution. In IMRT plans the 98% coverage of the CTV by the prescription dose of 9∗2.25 Gy=20.25 Gy was routinely achieved.

Simulation of setup and tissue motion errors

The analysis of cIMRT delivery was performed in two ways: Static (cIMRT-S) without correction for geometric uncertainty and cIMRT-U, which simulated the impact of setup and tissue motion errors on the delivered dose distribution. Random and systematic errors were assumed to be normally distributed 3D rigid translations of prostate and organs at risk with standard deviations of 3 mm. These values are a simplification of Van Herk’s¹⁹ geometric error distributions recommended for prostate treatment without image guidance.¹⁹ Random errors were simulated by convolving the incident photon beam fluence with a Gaussian kernel.²⁰ Systematic error was simulated by recomputing the dose distribution for each of 50 offsets randomly selected from the Gaussian error distribution. This resulted in an ensemble of dose volume histograms, coverage metrics, and simulated clinical outcome metrics.

Evaluation of clinical outcome surrogates

Conversion of physical dose to biologically equivalent dose

For the purpose of plan evaluation, physical doses were converted to the BED using the linear-quadratic formula

$$\text{BED}\left(\mathbf{r}\right)=D\left(\mathbf{r}\right)\left(1+\frac{D\left(\mathbf{r}\right)}{n\cdot \left(\alpha ∕\beta \right)}\right),$$ (1)

where D(r) is the total physical dose delivered at position r and n is the number of fractions.

Tumor control

The evaluation end point for tumor control is a variation of equivalent uniform dose which was introduced by Jones and Hoban²¹ under the name of equivalent uniform biologically equivalent dose (EUBED). We renamed this index to equivalent survival dose (ESD) to avoid confusion with other forms of equivalent uniform dose used in the present paper:

$$\text{ESD}=-\frac{1}{\alpha }\text{ln}\left(\frac{1}{N}\sum _{i=1}^N{e}^{-\alpha \cdot {\text{BED}}_i}\right),$$ (2)

where α is given by the linear-quadratic model, BED_i is the total BED in the ith CTV voxel, and N denotes the number of CTV voxels. Assuming a uniform density of clonogenic cells in the CTV, ESD denotes the BED which, if uniformly delivered to the CTV, would give the same fraction of surviving cells as a given nonuniform BED distribution. The ESD index can be used to rank partial treatments (boosts), for which a direct calculation of TCP would be meaningless. Furthermore, ESD can be used to estimate the difference in TCP between different boost regimens used in conjunction with a common extended field external beam (EFEB) treatment regimen, which delivers uniform dose to the prostate and the surrounding volumes. Our analysis of TCP gains and∕or losses relative to cIMRT-S assumes that EFEB therapy delivers the same uniform BED distribution to the CTV for all choices of boost treatment. Under these assumptions, the Appendix0 shows that TCPs for two full treatment courses employing different boost modalities (IMRT and HDR) are given by

$${\text{TCP}}_{\text{EFEB}+\text{HDR}}={\left({\text{TCP}}_{\text{EFEB}+\text{IMRT}}\right)}^C,$$ (3)

$$C=e^{-\alpha \left({\text{ESD}}_{\text{HDR}}-{\text{ESD}}_{\text{IMRT}}\right)},$$

where ESD_HDR and ESD_IMRT are ESD indices computed for boosts only.

Clinical complications in organs at risk

Generalized equivalent uniform BED (gBEUD), an extension of the concept of general equivalent uniform dose (gEUD),²² was used as comparative surrogate for normal tissue toxicity,

$$\text{gBEUD}={\left(\sum _{i=1}^N{\nu }_i{\left({\text{BED}}_i\right)}^a\right)}^{1∕a},$$ (4)

where BED_i denotes the isoeffective dose in the ith voxel or DVH bin of the OAR, ν_i is the fraction of the OAR volume receiving BED_i, N is the number of voxels or bins, and a is an organ- and end-point-dependent fitting parameter. This modified gEUD was adopted because of a need to compare toxicity from regimens with very different fractionation schedules. Since our aim is to rank boosts, not complete courses of treatment, we cannot use NTCP models directly. The gBEUD model is equivalent to using the widely used Kutcher–Burman (KB) (Ref. ²³) effective volume DVH reduction method, which assumes complications having a power-law dependence on OAR volume, with an exponent equal to the inverse, 1∕a, of the gEUD-gBEUD parameter. Thus our choice of toxicity surrogate is consistent with the most widely used NTCP model, the Lyman-Kutcher-Burman (LKB) NTCP model²⁴ used in conjunction with the KB DVH reduction method. Published studies,^{25, 26, 27} proposing LKB model fits to clinical data, can be used directly to determine the parameter a in Eq. 4. A recently published comparative analysis of six different NTCP models²⁸ suggests that the gEUD, when combined with several specific NTCP models, provides a good fit to clinical data obtained in external beam treatments of prostate patients. A salient feature of these models is a monotonic rise in NTCP as gEUD increases. Hence the gEUD can be used as a surrogate for NTCP models, ranking plans by likelihood of complications without explicitly computing the NTCP. Because the published a parameters used by our study are based upon correlations between clinical outcomes and physical doses, substituting BED for physical dose in Eq. 4 may introduce additional uncertainty. One deals with this uncertainty by examining the robustness of one’s conclusions in the widest range of parameter a that can be found in the literature.^{26, 29}

BED saturation analysis in organs at risk

In applying the gBEUD model to brachytherapy dose distributions, we discovered a previously unreported problem: The sensitivity of gBEUD to high doses in the tail of the HDR cumulative DVH. Even volumes containing only a few voxels can cause dramatic gBEUD elevations when exposed to doses significantly in excess of the prescribed dose. Recognizing that such small focal hotspots may not be predictive of complications, an additional gBEUD parameter, the BED saturation threshold, ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$, was introduced. As 3D HDR dose distributions are characterized by very small volumes irradiated to very high doses, it seems reasonable to assume the existence of an isoeffective dose threshold beyond which tissue in such small OAR subvolumes is damaged beyond the possibility of repair and further dose increases to these subvolumes are of no clinical significance. Under this assumption, the 3D BED distribution in the HDR boost is modified so that in all voxels in which the actual BED is higher than ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$, isoeffective dose is replaced by the assignment $\text{BED}={\text{BED}}_{\text{sat}}^{\text{gBEUD}}$:

$$\text{gBEUD}\left({\left\{{\nu }_i,{\text{BED}}_i\right\}}_{i=1}^N:a,{\text{BED}}_{\text{sat}}^{\text{gBEUD}}\right)={\left[\sum _{{\text{BED}}_i\le {\text{BED}}_{\text{sat}}^{\text{gBEUD}}}{\nu }_i{\left(BE{D}_i\right)}^a+\left(\sum _{{\text{BED}}_i>{\text{BED}}_{\text{sat}}^{\text{gBEUD}}}{\nu }_i\right)\cdot {\left({\text{BED}}_{\text{sat}}^{\text{gBEUD}}\right)}^a\right]}^{1∕a}.$$ (5)

In the absence of published data, we assumed that ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$ is equal to the prescription BED and have assessed the sensitivity of our findings to the choice of this parameter. A similar analysis was performed for ESD index, in which case the saturation threshold was denoted by ${\text{BED}}_{\text{sat}}^{\text{ESD}}$. The summary of radiobiological parameters used in this work is presented in Table 2.

Table 2.

Summary of gBEUD values for bladder and rectum. The bottom row shows values of the exponent a used in the calculation. A BED saturation threshold of 36 Gy was used to calculate gBEUD for HDR boost. Errors represent standard error over patients, except for cIMRT-U where two errors are shown. The first error is average end point change for one std dev envelope of DVHs, and the second error, in parantheses, is the standard error over patients for unmodified DVHs. Estimates of parameter a are based on Refs. ²⁶, ²⁹.

Modality	Generalized equivalent uniform BED for late effects				ESD(Gy)
	Bladder: ≥g3 toxicity	Rectum: ≥g2 bleeding	Rectum: ≥g3 toxicity	Rectum: ≥g3 bleeding	CTV(prostate)
HDR	16.1±3.0	15.3±2.3	21.9±2.0	27.6±1.5	45.1±3.4
igIMRT	21.9±1.6	17.5±1.7	22.2±1.5	26.8±1.2	38.4±0.4
cIMRT-S	30.1±1.4	22.2±1.7	27.5±1.5	31.6±1.4	38.4±0.8
cIMRT-U	28.1±1.0±(2.1)	21.6±1.1±(1.7)	26.3±1.0±(1.7)	30.5±1.0±(1.5)	38.3±0.1±(0.7)
a	7.7	4.4	8.3	16.7	–
α (Gy−1)	–	–	–	–	0.16
α∕β (Gy)	3	3	3	3	3

RESULTS

Organ coverage

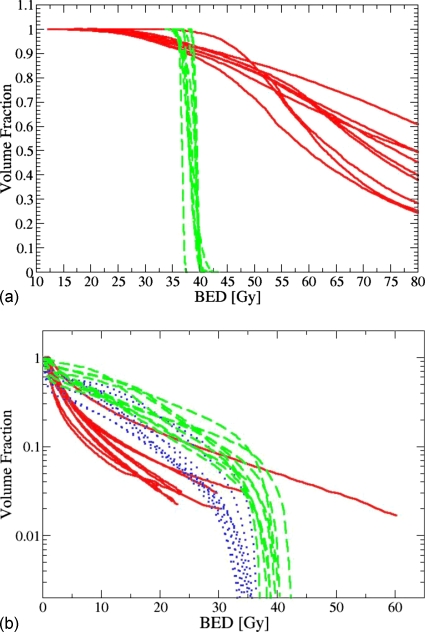
Table 1 and Fig. 1 illustrate the CTV and OAR coverage achieved by the three boost modalities, computed on the basis of DVHs in which physical dose was substituted by the BED. HDR achieves similar CTV coverage by the prescribed BED as IMRT but with substantially increased dose heterogeneity. On the other hand, for all organs except urethra, HDR has OAR sparing capability comparable to (if not slightly better than) idealized igIMRT at the 30% and 3% volume coverage levels. However, IMRT gives significantly smaller absolute maximum doses to bladder and rectum than HDR due to the long high dose tails of the latter. These results are qualitatively similar to those recently published by Pieters et al.¹²

Table 1.

Cumulative DVH indices, normalized to the prescription BED. BED₃₀ and BED₃ corresponds to normalized BED at 30% and 3%, respectively, of the organ volume. VOL_X is a fraction of prostate volume that is covered by a BED isoline of X% of the prescription BED. Errors represent standard error over patients, except for cIMRT-U, where two errors are shown. The first error is average end point change for one sigma envelope of DVHs, and the second error, in parenthesis, is standard error over patients for unmodified DVHs.

Organ	Volume (cm3)	Index	Modality
			HDR	igIMRT	cIMRT-S	cIMRT-U
Rectum	96±41	BED30	0.16±0.08	0.34±0.08	0.46±0.09	0.45±0.05±(0.07)
		BED3	0.66±0.04	0.73±0.27	0.9±0.2	0.88±0.1±(0.3)
Bladder	117±78	BED30	0.11±0.03	0.17±0.07	0.4±0.2	0.4±0.1±(0.2)
		BED3	0.37±0.15	0.74±0.27	1.0±0.2	0.95±0.1±(0.2)
Urethra	4.5±1.9	BED30	1.67±0.14	1.03±0.03	1.08±0.02	1.08±0.01±(0.02)
		BED3	2.0±0.1	1.05±0.03	1.1±0.03	1.1±0.01±(0.03)
CTV (prostate)	33±7	VOL98	0.94±0.03	0.99±0.02	1.0±0.0	1.0±0.0±(0.0)
		VOL110	0.9±0.04	0.07±0.08	0.42±0.29	0.42±0.1±(0.30)
		VOL125	0.83±0.04	0.0	0.0	0.0
		VOL150	0.74±0.06	0.0	0.0	0.0

Figure 1.

(a) BED prostate (CTV) dose volume histograms for HDR and IMRT boost plans. Each solid line corresponds to a patient receiving HDR boost, and each dashed line corresponds to a patient receiving a cIMRT boost. (b) BED rectum dose volume histograms for HDR and IMRT boost plans. Each solid line corresponds to a patient receiving HDR boost, each dotted line corresponds to a patient receiving an igIMRT boost, and each dashed line corresponds to a patient receiving a cIMRT boost. Note that HDR DVHs are truncated at approximately 2% of organ volume due to binning. The maximum physical dose in HDR boost falls in the 11.1–35.5Gy range with an average of 21.8 Gy, which corresponds to BED range of 52.2–461.7 Gy, with an average of 211 Gy

Evaluation end points

The effectiveness of different modalities in controlling tumor and avoiding normal tissue toxicity is ranked by comparing ESD and gBEUD values averaged over all patients. These averages are summarized in Table 2, with errors representing the standard error over patients for all modalities, with the exception of cIMRT-U. For cIMRT-U two errors are cited. The first error represents an average error due to motion. For each patient, one standard deviation envelope was computed for all DVHs. Evaluation end points were computed for two simulated DVHs, each corresponding to the upper∕lower boundary of the envelope. The differences between the two end point values were recorded as motion errors for a given patient. These motion errors were subsequently averaged over nine patients and cited as the first error in Table 2. The second error is the standard error over the population of nine patients using evaluation end points computed on unmodified (average) cIMRT-U DVHs. Regarding tumor control, we find that, on average, HDR boost delivers an approximately 16% larger ESD (22% higher than the prescribed BED) than does igIMRT or cIMRT for the same prescribed BED. This implies that HDR boost should offer better local tumor control of the tumor than an IMRT treatment for the same prescribed minimum dose. The impact of enhanced ESD in HDR boosts is evaluated in Table 3 using the uniform extended field treatment model of Eq. 3. If EFEB with IMRT boosting is assumed to realize very low TCP levels, simply replacing the IMRT boost with the HDR boost having the same nominal BED₉₈ prescribed dose can improve TCP three- to fivefold. When high levels of local control can be achieved by using external beam alone, more modest 7%–13% gains in TCP are predicted for brachytherapy boosting. The predictions of large therapeutic gains, shown in Table 3, are subject to modeling uncertainties which include uncertainties in the choice of values of model parameters and uncertainties in the distribution of clonogenic cells in the delineated target volumes.

Table 3.

Estimated TCP achieved (second row) when an IMRT boost is replaced with HDR in a full treatment as a function of assumed TCP (first row) achieved by the EFEB+IMRT combination.

Assumed TCP achieved by ESDEFEB+ESDIMRT	0.10	0.20	0.40	0.60	0.80	0.90
Predicted TCP when IMRT boosting is replaced by HDR giving the same prescribed BED	0.47	0.59	0.74	0.84	0.93	0.97

BED saturation analysis

Tumor control

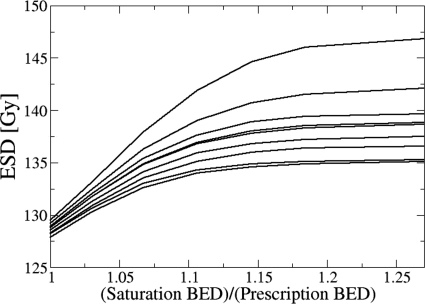
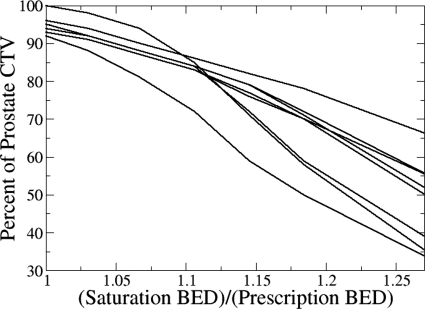
The impact of ${\text{BED}}_{\text{sat}}^{\text{ESD}}$ choice on HDR boost ESD is summarized in Figs. 23. Both plots were constructed assuming a uniform EFEB dose of 59 Gy in 2 Gy fractions. Figure 2 shows that ESD approaches saturation at nearly the same ${\text{BED}}_{\text{sat}}^{\text{ESD}}$ for all patients, which is approximately equal to 115% of the full prescription BED of 134 Gy. For ${\text{BED}}_{\text{sat}}^{\text{ESD}}=1.15\cdot {\text{BED}}_{\text{prescr}}$, Fig. 3 shows that 50%–80% of the prostate volume receives a total $\text{BED}>{\text{BED}}_{\text{sat}}^{\text{ESD}}$. The saturation of the ESD index occurs when the cell survival fraction in voxels receiving a total $\text{BED}>{\text{BED}}_{\text{sat}}^{\text{ESD}}$ is negligibly small when compared to the survival fraction in voxels receiving lower BED. Hence, the result shown in Fig. 3 strongly suggests that a large percentage of prostate volume (>50%) receives BED which is high enough to fully control the tumor or even cause ablation of prostate tissue.

Figure 2.

ESD for a combination of EFEB (59 Gy in 2 Gy fractions) and HDR (9 Gy) plotted as a function of saturation BED, ${\text{BED}}_{\text{sat}}^{\text{ESD}}$, normalized to the total prescribed BED. Each curve denotes one of the nine patients. Note that the shape of this plot does not depend on the dose delivered by the prior treatment, as long as the prior dose distribution is uniform. Any uniform distribution of the prior dose adds a constant to the ESD.

Figure 3.

The percentage of prostate volume with cumulative BED exceeding the threshold, ${\text{BED}}_{\text{sat}}^{\text{ESD}}$, as a function of total ${\text{BED}}_{\text{sat}}^{\text{ESD}}$ (BED from HDR interstitial boost and EFEB treatment of 59 Gy in 2 Gy fractions) relative to total prescribed BED. Each curve represents one of the nine patients.

Clinical complications in organs at risk

The summary of gBEUD values obtained with the BED saturation threshold set to the prescription BED, ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}={\text{BED}}_{\text{prescr}}$, is shown in Table 2. The expected complication rates, as measured by the gBEUD, are highest for the conventional IMRT boost. For complications having relatively low volume power-law exponents (low grade rectal bleeding and bladder toxicity), HDR boost yields lower complication rates than even theoretically error-free igIMRT. For higher values of a, the expected complication rates from HDR and igIMRT boosts are similar. For all end points, igIMRT and HDR are superior to cIMRT.

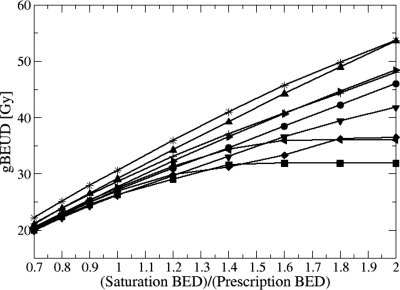
The influence of ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$ choice on the gBEUD for severe rectal bleeding from HDR boosts is summarized in Fig. 4. In contrast to the ESD metric, for most patients there is no “natural” saturation threshold choice for which gBEUD asymptotically approaches a saturation value with increasing ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$. Thus ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$ constitutes an additional adjustable biological model parameter which can significantly affect the ranking of competing plans. One way to cope with a newly introduced parameter, for which little data exist to specify its value, is to assess the sensitivity of modality ranking to the choice of its value and to accept only conclusions that remain valid for a relatively wide range of ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$ choices. The results of such an analysis are shown in Table 4. The range of ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$ values over which ranking is preserved is largest for end points with smaller volume-dependence exponents, a. Increased sensitivity to focal hotspots with increasing a is expected since gBEUD approaches maximum BED under these conditions. Ranking reversal for bladder complications occurs only for large ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}∕{\text{BED}}_{\text{prescr}}>2$, while for rectum ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}∕{\text{BED}}_{\text{prescr}}\approx 1$ can produce ranking reversal. Table 1 shows that HDR BED₃ for bladder is 2.5- to threefold smaller than IMRT, while for rectum, HDR BED₃ is similar to that of igIMRT and only 27% smaller than for cIMRT. Except for severe rectal bleeding (a=16.7), the relative ranking between the HDR boost and the conventional IMRT boost is unchanged over a wide range of ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$ values, while the relative ranking of the HDR boost and the simulated igIMRT boost is very sensitive to small variations around the selected value of ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}∕{\text{BED}}_{\text{prescr}}=1$. Thus, we conclude that for a fixed BED prescription dose, HDR boost offers more freedom from late toxicity than cIMRT while HDR and igIMRT are, at best, equivalent.

Figure 4.

Rectal gBEUD for HDR interstitial brachytherapy boosts as a function of gBEUD threshold, ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$, relative to prescribed BED. The choice of a=16.7 corresponds to ≥g3 rectal bleeding. No additional EFEB dose is assumed for this analysis. Each line corresponds to a patient.

Table 4.

The normalized BED saturation threshold at which gBEUD, averaged over the nine HDR boost plans, equals the corresponding mean IMRT gBEUD (“mean” column). The “One std dev” column gives the ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$ value at which the HDR mean gBEUD exceeds IMRT gBEUD by one standard deviation (gBEUD_HDR=gBEUD_IMRT+σ_IMRT).

Organ	igIMRT		cIMRT-S
	Mean	One std dev	Mean	One std dev
Rectum a=4.4	1.4	>2.0	>2.0	>2.0
Rectum a=8.3	1.05	1.3	1.55	>2.0
Rectum a=16.7	0.95	1.0	1.2	1.4
Bladder a=7.7	>2.0	>2.0	>2.0	>2.0

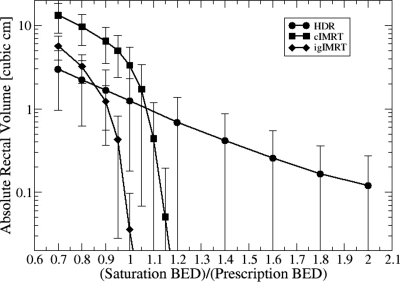
Additional insight into the modality ranking reversal phenomenon is illustrated by Fig. 5, which plots rectal BED saturation volume (absolute volume of the rectum receiving ${\text{BED}>\text{BED}}_{\text{sat}}^{\text{gBEUD}}$) against ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}∕{\text{BED}}_{\text{prescr}}$. HDR boost irradiates significantly less rectal volume than the conventional IMRT boost for isoeffective doses between 90% (igIMRT) and 110% (cIMRT) of BED_prescr. For larger doses, HDR rectal coverage is larger than that of IMRT, slowly falling from volumes of 1–2 to 0.2 cm³ for relative saturation thresholds of 2. Hence, the stability of ranking with respect to rectal gBEUD will depend on the magnitude of a with high values (severe rectal bleeding) showing great sensitivity to the choice of threshold and penalizing modalities such as HDR which have the possibility of focal hotspots in organs adjacent to the treatment volume. End points with relatively low a values (moderate rectal bleeding, a=4.4) will exhibit less sensitivity to threshold choice and to focal hotspots and will tend to penalize modalities, e.g., cIMRT and even igIMRT, which treat large volumes of rectal wall to more moderate doses.

Figure 5.

Absolute rectal volume receiving a prostate boost BED exceeding the threshold ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$ plotted vs ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$ in multiples of prescribed BED. No EFEB dose was included this plot.

Simulated motion errors

The effect of simulated setup and tissue motion errors on the coverage of the prostate (CTV) is negligible for all patients. The probability that 98% of the CTV volume is covered by the prescription BED is greater than 99.8% for all patients when the simulated organ motion is considered. This result indicates that the PTV planning margin adequately compensates for the simulated organ motion. The effects of simulated motion errors on the gBEUD measure are noticeable but still relatively small. The average value of gBEUD tends to decrease by about 5% when simulated motion is included (Table 2), and this trend is similar for all patients. Since the average gBEUD decreases due to motion, the probability of an increase in gBEUD due to motion effects is quite low. As an example, for rectum g2 toxicity (a=4.4), the probability that the effects of motion errors increase the gBEUD by 10% with respect to the static estimate is in the range of 0.4%–17%, with an 8% average over all patients. Conversely, the simulation predicts much higher probability that gBEUD decreases due to motion. As an example, for rectum g2 toxicity (a=4.4), the probability that the effects of motion errors decrease the gBEUD by 10% with respect to the static estimate is in the range of 22%–50%, with a 37% average over all patients. The probability that the effects of motion errors decrease the gBEUD by 20% with respect to the static estimate is in the range of 0.4%–17%, with an 8% average over all patients. Even a 20% decrease in gBEUD would not substantially alter rankings between an HDR boost and an IMRT boost, except perhaps for the highest values of gBEUD exponent. Given the uncertainties which are inherent in the motion simulation itself, one can say that static gBEUD estimates are a reasonable approximation for actual gBEUD values, and that effects of organ motion by themselves are not likely to alter the conclusions of this paper. One does note, however, that a systematic decrease in gBEUD due to organ motion may be an effect which is worthy of further study, a study which would use clinical imaging data in lieu of a simplified simulation.

DISCUSSION

Modeling uncertainties

The results presented in Sec. 3 indicate that substituting an HDR boost for an IMRT boost should increase local control of the tumor provided that the peripheral BED is the same in both boosts (Tables 2, 3). These results are affected by biological effect modeling uncertainties, including knowledge of the α∕β ratio, the value of α, and the validity of the simple BED formalism for high fraction sizes that characterize the HDR delivery.

Uncertainty in the value of α∕β

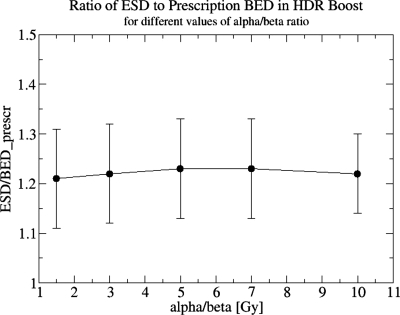
If the actual value of α∕β is smaller than the assumed value, the actual impact of an HDR boost, in terms of tumor control, will be greater than the estimates shown in Table 3. On the other hand, if the true α∕β value is higher than that assumed, our ESD computations will overestimate the tumor control achievable by HDR boost for a given physical dose level. One may even reach a point when an HDR boost will be less effective than a nearly homogeneous dose distribution in an IMRT boost. Figure 6 shows that the ESD gain due to HDR boost dose heterogeneity, expressed as a fraction of BED_prescr, is a constant 1.22 and essentially independent of the α∕β ratio. Based on this result, it is easy to show that, for HDR and IMRT boosts physical dose prescriptions that are equivalent at the assumed α∕β=3 Gy, the “true” value of α∕β can be as high as 4.9 Gy before ESD_HDR=ESD_IMRT, i.e., a 9 Gy dose of HDR is more effective at promoting tumor control than nine IMRT fractions of 2.25 Gy for all α∕β<4.9 Gy. This line of reasoning suggests that it is clinically prudent to use conservative assumptions about the α∕β ratio in developing hypofractionated dose-delivery schedules. A recent review³⁰ indicated that most recent α∕β estimates, based upon comparison of control rates in various patient cohorts treated with different time-dose-fractionation schemes, were confined to the range of 0.97–4.96 Gy. Hence a choice of α∕β=3 Gy seems reasonable.

Figure 6.

ESD normalized to the prescription BED in an HDR boost, averaged over nine patients, and plotted against the value of α∕β ratio. For each α∕β ratio the physical dose prescription was recomputed to match BED=36 Gy, and the ESD was recomputed using the modified dose prescription. Error bars correspond to standard error over nine patients.

Uncertainty in the value of α

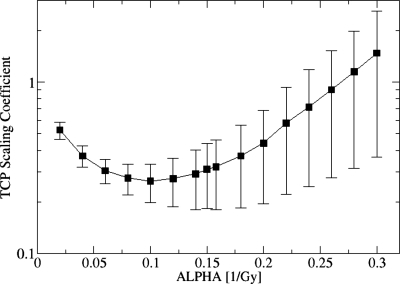
The relative effectiveness of an HDR boost depends on the value of parameter α. This dependence is illustrated in Fig. 7 and shows that the advantage an HDR boost has in tumor control diminishes as α increases and may even reverse (C>1) for very large values of α. The reduction in HDR boost effectiveness for larger values of α is caused by an increasing sensitivity of the ESD index to cold spots in the inhomogeneous BED distribution. Mathematically, ESD index converges to the minimum BED in the BED distribution, as α goes to infinity. This dependence, while noteworthy, is of limited clinical significance. One notes that a patient with a tumor which is characterized by an unusually large value of α (relative to the general population) would be expected to achieve good local control with either boost method as a high value of α implies enhanced sensitivity of tumor cells to damage by radiation. The value of α used in the present work (α=0.16 Gy⁻¹) is based on the work by Levegrun et al.,³¹ who presented comprehensive fits of biopsy confirmed tumor control data to the Webb-Nahum³² and Niemierko-Goitein³³ models. These fits place the value of α in the 0.09–0.16 range. Since the advantage of HDR boost in tumor control diminishes as the value of α increases (Fig. 7), it is prudent to choose a value of α which is at the upper end of the range. The work by Levegrun et al. also shows that the best fits to the Webb-Nahum models are obtained when the effects of α population averaging are negligibly small. Hence, no effects of population averaging were considered in this paper. One can estimate the effects of population averaging on tumor control fairly easily by using Fig. 7.

Figure 7.

Dependence of the factor C in Eq. 3 on the choice of value for the parameter α in the linear-quadratic model. If C<1, the TCP predicted for the treatment with HDR boost is greater than the TCP for the treatment with an IMRT boost. Errors represent a standard error over the population of nine patients.

Uncertainty in the dose-to-BED conversion

It has been suggested by some authors that the linear-quadratic model does not adequately describe cell kill in hypofractionated treatments.^{34, 35, 36} The failure of the model is usually expressed as a modification to the functional relationship between the physical dose and the BED [Eq. 1]. At present there appears to be no consensus opinion whether the linear-quadratic model overestimates³⁴ or underestimates³⁵ the biological effectiveness of high doses per fraction. Regardless of the direction of the deviation, its impact on major conclusions of the present paper should be fairly limited. Considering tumor control first, in Fig. 6 one observes that the enhancement of the ESD index in an HDR boost is nearly independent of the value of α∕β. This somewhat counterintuitive observation is explained by a rapid saturation of cell survival fraction in subvolumes of high dose, which is shown by the BED saturation analysis in Figs. 23. Thus, even if one significantly changes the dose-to-BED relation in Eq. 1, the enhancement of the ESD index in an HDR boost should be mostly preserved. Considering organs at risk, the impact of changes in dose-to-BED relation would be most strongly felt in the estimates of gBEUD in an HDR boost, as it would either enhance or reduce the influence of small focal hotspots. The importance of small hotspots is suppressed by the BED saturation hypothesis, however [Eq. 5], which would most likely preserve the ranking of HDR and IMRT boosts. A more detailed discussion of uncertainties created by dose-to-BED conversion requires quantitative modeling of possible deviations from linear-quadratic cell kill model. Such quantitative modeling will be a subject of future work.

TCP advantage in treatments with HDR boost

The better tumor control achieved by HDR boost is due to the highly nonuniform dose distribution which is associated with HDR delivery. That hotspots relative to the peripheral dose can enhance cell kill and compensate for peripheral underdoses was first demonstrated by Ling et al.³⁷ for permanent seed implants. The present analysis shows that similar effects can be achieved with an HDR boost, even if the dose delivered by the boost is a relatively small fraction of the overall dose prescription. One can further hypothesize that similar gains in tumor control could be obtained in an IMRT treatment if an IMRT boost purposely delivers a nonuniform dose distribution to the CTV. Results of the present analysis (Table 3) suggest that the ongoing clinical use of treatments with HDR and IMRT boosts provide a unique opportunity to test this hypothesis. Moreover, a comparison of the two boost methods may provide a new opportunity for clinical tests of the Poisson TCP model and the linear-quadratic cell kill model. Equation 3 shows that a comparison of TCP in two treatment techniques, when these techniques are applied to similar patient populations, effectively eliminates the density of clonogenic cells as an adjustable parameter of the Poisson TCP model (though one continues to rely on an assumption that clonogenic cells are uniformly distributed throughout the target). Hence, a comparison of clinical local control in treatments with both boost methods can lead to better constraints on the parameters of the linear-quadratic cell kill model. A relatively recent publication by Galalae et al.⁷ compares clinical disease control rates for similar cohorts of patients treated with IMRT alone or IMRT with an HDR boost. This comparison strongly suggests that significant gains in clinical control of prostate cancer can be achieved when IMRT treatments are augmented by an HDR boost, and the reported gains in clinical control are largest for patients in the highest risk groups, who have a high risk of failure when treated with IMRT alone. The work by Galalae et al. shows that clinical data needed to compare the outcomes of two boost methods may already exist, and that the reported data exhibit qualitative similarity to the results of our modeling study.

Application of gEUD∕gBEUD based models to strongly inhomogeneous dose distributions in organs at risk

Our analysis of normal tissue complication surrogates suggests that the gBEUD or gEUD based NTCP models are problematic for comparing brachytherapy and external beam treatments. The gEUD is a one-parameter data-fitting tool for describing the correlation between observed adverse events and the associated OAR DVH characteristics of the delivered dose distribution in an evaluated population of patients. The validity of extrapolating gBEUD or gEUD predictions to other populations depends upon the similarity of the two populations and the treatment techniques used. The published clinical results,^{25, 26, 27, 38, 39} upon which our gEUD parameter estimates rest, are all external beam treatment experiences. Such gEUD or gBEUD fits cannot be applied to very different relative dose distributions characteristic of HDR brachytherapy, as either measure is very sensitive to small focal hotspots that do characterize the HDR delivery but are entirely absent in the external beam delivery. The excessive sensitivity of gEUD to very small hotspots is built into the mathematical definition of this index, as gEUD has no mechanism that would reflect the saturation of the biological effectiveness of high doses. In a mathematical limit, the gEUD can be dominated by a single voxel being exposed to a very high dose, which cannot properly reflect clinical effects of a dose distribution. One can cope with this problem by postulating a clinically and biologically plausible concept of a “saturation” BED level, which causes near complete depletion of cells in the local region so irradiated. Thus the marginal impact of higher isoeffective dose to these regions is minimal. However, in contrast to the ESD model (Fig. 2), there is no “natural” value for the saturation threshold, ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$ (Fig. 4), which means that the BED saturation threshold becomes a new, adjustable parameter of the model which can influence plan rankings and hence the conclusions of a study such as ours. The present study made a plausible estimate of ${\text{BED}}_{\text{sat}}^{\text{gBEUD}}$ based upon saturation of the surviving fraction of clonogenic cells and examined the robustness of the plan rankings with respect to this choice (Table 4). Based on such analysis one observes that it may be feasible to use gBEUD to rank plans with very different dose distributions but only if one of the plans is clearly inferior. For example, one can see in Fig. 5 that HDR boost irradiates much smaller volumes of the rectum than the cIMRT boost, up to the prescription BED. One would intuitively expect that HDR causes fewer complications than cIMRT, unless small focal hotspots are critically important to the complication rate. In contrast, volumes irradiated by igIMRT are comparable to or smaller than volumes irradiated by HDR in the same BED range. One would expect, just by inspection of Fig. 5, that the relative ranking of two modalities should be similar. The relative rankings in Table 4 agree with these estimates which means that the rankings based on the gBEUD measure offer no meaningful distinction between plans with similar though not identical DVHs. One approach to this problem is to develop a new gEUD-like measure which reflects the expected saturation of a biological effect of high doses. Such new measure would perform the same function as gEUD or gBEUD and be used as a data fitting tool which would accommodate simultaneous fitting to external beam and brachytherapy clinical data sets. Another approach is to abandon the gBEUD∕gEUD model altogether in favor of a more mechanistically grounded model such as the cluster model⁴⁰ or binomial statistics∕critical subunit NTCP model.^{41, 42} Both of these models would be expected to exhibit plausible damage saturation in the face of focal hotspots, as they are based upon a common Poisson model of functional subunit survival vs dose. However, these models suffer from the disadvantages of a larger number of adjustable parameters (five to eight), applicable only to full treatment courses, and the need to perform extensive fitting to both external beam and brachytherapy data sets.

The OAR complication rankings which were presented in this paper were applied to boosts only rather than a full treatment course. Such a comparison is somewhat disadvantageous to the HDR method, as it amplifies the relative importance of small focal hotspots which would become less pronounced, in relative terms, when combined with a more homogeneous BED distribution from the external beam treatment. We chose not to quantify this disadvantage, as too many assumptions would have to be made about the prior treatment. Since accounting for the prior treatment would improve HDR rankings, the conclusions of the present paper would largely remain unchanged, even if the prior treatment was fully accounted for.

CONCLUSIONS

Our study strongly suggests that high dose-rate interstitial brachytherapy prostate boost implants support both superior rectal and bladder dose avoidance and better local control of the tumor when compared to conventional non-image-guided IMRT, as long as a reasonably accurate value of α∕β is used to calculate the HDR dose prescription. The gain in local tumor control is particularly pronounced for these patients for whom the IMRT dose prescription is suboptimal and would result in a relatively low TCP. The gain in rectal and bladder protection is strongest for normal tissue toxicity end points that exhibit large volume effects (small EUD parameter a). The HDR rectal and bladder dose avoidance end points are very similar to those of igIMRT, although strictly speaking we have shown only that the normal tissue end point employed by this study, gBEUD, is too uncertain to rank these two modalities. Finally, we conclude that using gEUD to compare complication rates in brachytherapy and external beam treatments is not suitable since gEUD, especially when combined with the linear-quadratic model, exhibits an exaggerated response to intense focal hotspots. Because gEUD validation data sets are based upon the relatively homogeneous dose distributions characteristic of external beam radiotherapy, the responses of current gEUD model fits to high dose DVH tails are not constrained by clinical data. New and more robust approaches to modeling of normal tissue complications are needed to support more clinically precise and relevant comparisons of brachytherapy and external beam techniques. Despite these reservations, HDR interstitial brachytherapy deserves more study as a technologically less challenging but potentially more effective alternative to image guided radiation therapy of localized, surgically accessible tumors.

APPENDIX: DERIVATION OF EQ. 3

ESD represents a BED which, if applied uniformly, generates the same surviving fraction of the clonogenic cells as an inhomogeneous BED distribution. Hence,

$$\rho V{e}^{-\alpha \text{ESD}}=\rho \frac{V}{N}\sum _{i=1}^{i=N}{e}^{-\alpha {\text{BED}}_i},$$ (A1)

where ρ is the density of clonogenic cells and V is the CTV volume.

Assuming that the probability of tumor control is the Poisson probability that no clonogens survive, the TCP for uniform ρ is given by

$$\text{TCP}=\text{exp}\left(-\rho V{e}^{-\alpha \text{ESD}}\right)$$ (A2)

The TCP value corresponding to partial treatment courses are not clinically relevant, but one can use the ESD of a boost to estimate the TCP for the full treatment regimens if one assumes that the extended field (EFEB) treatment delivers a uniform dose, BED_EFEB. If one substitutes BED_full=BED_boost,i+BED_EFEB for BED_i in Eq. A1, one can conclude that ESD_full=BED_EFEB+ESD_boost and

$${\text{TCP}}_{\text{full}}=\text{exp}\left(-\rho V{e}^{-\alpha \left({\text{BED}}_{\text{EFEB}}+{\text{ESD}}_{\text{boost}}\right)}\right).$$ (A3)

Equation A3 allows one to compare TCP in different treatment regimens, each delivering the same BED_EFEB but a different boost modality:

$$\frac{\text{ln}\left({\text{TCP}}_{\text{EFEB}+\text{IMRT}}\right)}{\text{ln}\left({\text{TCP}}_{\text{EFEB}+\text{HDR}}\right)}=e^{-\alpha \left({\text{ESD}}_{\text{HDR}}-{\text{ESD}}_{\text{IMRT}}\right)},$$ (A4)

where ESD_HDR and ESD_IMRT denote the ESDs for the HDR and IMRT boosts, respectively. This implies

$${\text{TCP}}_{\text{EFEB}+\text{HDR}}={\left({\text{TCP}}_{\text{EFEB}+\text{IMRT}}\right)}^C,$$ (A5)

$$C=e^{-\alpha \left({\text{ESD}}_{\text{HDR}}-{\text{ESD}}_{\text{IMRT}}\right)}.$$

The exponent C depends only on the difference between ESD values for the two boosts and does not depend on the BED_EFEB. As shown in the main text, on average, ΔESD=ESD_HDR−ESD_IMRT≃7 Gy. Assuming that α=0.16 Gy⁻¹, TCP improvements obtained when IMRT boosts are replaced with radiobiologically matched HDR boosts are summarized in Table 3. The TCP gains shown in Table 3 are nearly independent of the value of α∕β, as long as the peripheral dose prescriptions for both boosts are radiobiologically equivalent.