Multiscale registration of planning CT and daily cone beam CT images for adaptive radiation therapy

Abstract

Adaptive radiation therapy (ART) is the incorporation of daily images in the radiotherapy treatment process so that the treatment plan can be evaluated and modified to maximize the amount of radiation dose to the tumor while minimizing the amount of radiation delivered to healthy tissue. Registration of planning images with daily images is thus an important component of ART. In this article, the authors report their research on multiscale registration of planning computed tomography (CT) images with daily cone beam CT (CBCT) images. The multiscale algorithm is based on the hierarchical multiscale image decomposition of E. Tadmor, S. Nezzar, and L. Vese [Multiscale Model. Simul. 2(4), pp. 554–579 (2004)]. Registration is achieved by decomposing the images to be registered into a series of scales using the (BV, L²) decomposition and initially registering the coarsest scales of the image using a landmark-based registration algorithm. The resulting transformation is then used as a starting point to deformably register the next coarse scales with one another. This procedure is iterated at each stage using the transformation computed by the previous scale registration as the starting point for the current registration. The authors present the results of studies of rectum, head-neck, and prostate CT-CBCT registration, and validate their registration method quantitatively using synthetic results in which the exact transformations our known, and qualitatively using clinical deformations in which the exact results are not known.

INTRODUCTION

Image registration is the process of determining the optimal spatial transformation that brings two images into alignment with one another. More precisely, given two images A(x) and B(x), image registration is the process of determining the optimal spatial transformation ϕ such that A(x) and B[ϕ(x)] are similar. Image registration is necessary, for example, for images taken at different times, from different perspectives, or from different imaging devices. Applications of image registration include image-guided radiation therapy (IGRT), intensity-modulated radiation therapy (IMRT), image-guided surgery, functional MRI analysis, and tumor detection, as well as many nonmedical applications, such as computer vision, pattern recognition, and remotely sensed data processing. See Refs. ^{1, 2, 3, 4} for an overview of image registration. Our focus in this article is registration of computed tomography (CT) and cone beam computed tomography (CBCT) images for image-guided radiation therapy.

IGRT is the use of patient imaging before and during treatment to increase the accuracy and efficacy of radiation treatment. The goals of IGRT are to increase the radiation dose to the tumor, while minimizing the amount of healthy tissue exposed to radiation. As imaging techniques and external beam radiation delivery methods have advanced, IGRT (used in conjunction with IMRT) has become increasingly important in treating cancer patients. Numerous clinical studies and simulations have demonstrated that such treatments can decrease both the spread of cancer in the patient and reduce healthy tissue complications.^{5, 6, 7}

IGRT is typically implemented in the following way. CT images are obtained several days or weeks prior to treatment and are used for planning dose distributions, patient alignment, and radiation beam optimization. Immediately prior to treatment, CBCT images are obtained in the treatment room and are used to adjust the treatment parameters to maximize the radiation dose delivered to the tumor. This enables the practitioner to adjust the treatment plan to account for patient movement, tumor growth or movement, and deformation of the surrounding organs. To adjust the patient position and radiation beam angles and intensities based on the information provided by the CBCT images, the CBCT images must first be registered with the planning CT images. Ideally, an adaptive radiotherapy treatment (ART) will eventually be implemented in which the patient alignment and∕or radiation beam angles are continuously updated in the treatment room to maximize radiation dose to the tumor and minimize radiation to healthy tissue. Such a treatment program would require real-time multimodality registration of images obtained during treatment with planning images obtained prior to treatment. Thus, accurate registration of images acquired from different machines at different times is an important step in the adaptive treatment process.

In a conventional CT imaging system, a motorized table moves the patient through a circular opening in the imaging device. As the patient passes through the CT system, a source of x rays rotates around the inside of the circular opening. The x-ray source produces a narrow, fan-shaped beam of x rays used to irradiate a section of the body. As x rays pass through the body, they are absorbed or attenuated at different levels, and image slices are reconstructed based on the attenuation process. Three-dimensional images are constructed using a series of two-dimensional slices taken around a single axis of rotation.

In a CBCT imaging system, on the other hand, a cone-shaped beam is rotated around the patient, acquiring images incrementally at various angles around the patient. The reconstructed data set is a three-dimensional image without slice artifacts, which can then be sliced on any plane for two-dimensional visualization. CBCT images contain low frequency components that are not present in CT images (similar to inhomogeneity related components in magnetic resonance images). One of the challenges in CT-CBCT image registration is thus to account for artifacts and other components that appear in one of the modalities but not in the other. See Refs. ^{8, 9} for a discussion of registration of CT and CBCT images.

In Refs. ^{10, 11, 12}, we presented a series of multiscale registration algorithms that were shown to be particularly effective for registration of noisy images. In this article, we extend our previous work to multiscale registration of CT-CBCT images. The motivation for applying our multiscale registration algorithm to CT-CBCT registration is that artifacts that appear, for example, in CBCT images but not in CT images can be treated in a similar way as noise. Moreover, different anatomical structures in the images to be registered undergo different types of transformations, and thus mapping of the different regions should be approached differently. Our multiscale registration algorithm first registers the coarse scales (such as main shapes, bones, and essential features) of each image, and then uses finer details (such as artifacts and noise) to iteratively refine the resulting transformation.

The structure of this article is as follows. In Sec. 2, we briefly discuss ordinary deformable and landmark-based registration algorithms and present the details of our multiscale registration algorithm. In Sec. 3, we present several examples to illustrate the accuracy of the multiscale registration technique. Section 4 concludes.

METHODS

B-splines deformable registration

Splines-based deformable registration algorithms use a mesh of control points in the images to be registered and a spline function to interpolate transformations away from these points. The basis spline (B-spline) deformation model has the property that the interpolation is locally controlled. Perturbing the position of one control point affects the transformation only in a neighborhood of that point, making the B-splines model particularly useful for describing local deformations. The control points act as parameters of the B-splines deformation model and the degree of nonrigid deformation, which can be modeled depends on the resolution of the mesh of control points. See Refs. ^{13, 14} for a detailed description of B-splines transformation models. In this article, we will use a B-splines deformable registration algorithm, in conjunction with the multiscale decomposition and landmark-based registration, with a uniform eight by eight grid of control points chosen automatically.

Landmark-based registration

Landmark-based registration is an image registration technique which is based on physically matching a finite set of image features. See Refs. ^{4, 15} for a detailed description of landmark-based registration models. The problem is to determine the transformation such that for a finite set of control points, any control point of the moving image is mapped onto the corresponding control point of the fixed image. More precisely, if A and B are two images to be registered, let F(A,j) and F(B,j), j=1,…,m be given control points of the images. The solution ϕ of the registration problem is then a map ϕ:R²→R² such that

$$F(A,j)=\varphi \left[F(B,j)\right],j=1,\dots ,m.$$

More generally, the solution ϕ:R²→R² of the registration problem can be defined to be the transformation ϕ that minimizes the distance

$$D^{\mathrm{LM}}\left(\varphi \right)≔\sum _{j=1}^m{\Vert F(A,j)-\varphi [F\left(B\right),j]\Vert }^2$$

between the control points.

For the examples presented in this article, we use an implementation of landmark-based registration in which the transformation ϕ is restricted to translation, rotation, scaling, and shear (i.e., ϕ is an affine transformation). We use four pairs of control points for each example. The control points used in the landmark-based registration are chosen manually, and we are currently working on incorporating automatically detected control points in the algorithm. In Ref. 12, we demonstrated that the multiscale registration algorithm is robust with respect to the location of the landmarks. In particular, the accuracy of the multiscale algorithm is not dependent on exact matching of the landmarks; due to the iterative nature of the registration method, we achieve accurate registration results even if the landmark locations are perturbed approximately 10 mm from their exact locations.

Multiscale deformable registration

Hierarchical multiscale image decomposition

The multiscale registration techniques that we developed in Refs. ^{10, 11, 12} are based on the hierarchical (BV, L²) multiscale image representation of Ref. 16. This multiscale decomposition will provide a hierarchical expansion of an image that separates the essential features of the image (such as large shapes and edges) from the fine scales of the image (such as details and noise). The decomposition is hierarchical in the sense that it will produce a series of expansions of the image that resolve increasingly finer scales, and hence, include increasing levels of detail. The mathematical spaces L², the space of square-integrable functions, and BV, the space of functions of bounded variation, will be used in the decomposition

$$L^2=\{f\mid {\Vert f\Vert }_{L^2}≔\int f^2<\infty \},$$

$$\mathrm{BV}=\{f\mid {\Vert f\Vert }_{\mathrm{BV}}≔\underset{h\ne 0}{\sup }{\mid h\mid }^{-1}{\Vert f(\cdot +h)-f(\cdot )\Vert }_{L^1}<\infty \}.$$

Generally, images can be thought of as being elements of the space L²(R²), while the main features of an image (such as edges) are in the subspace BV (R²). The multiscale image decomposition of Ref. 16 interpolates between these spaces, providing a decomposition in which the coarsest scales are elements of BV and the finest scales are elements of L². More precisely, the decomposition is given by the following. Define the J-functional J(f,λ) as follows:

$$J(f,\lambda )≔\underset{u+v=f}{\inf }(\lambda {\Vert v\Vert }_{L^2}^2+{\Vert u\Vert }_{\mathrm{BV}}),$$ (1)

where λ>0 is a scaling parameter that separates the L² and BV terms. Let [u_λ,v_λ] denote the minimizer of J(f,λ). The BV component, u_λ, captures the coarse features of the image f, while the L² component, v_λ (referred to as the residual), captures the finer features of f such as noise. The minimization of J(f,λ) is interpreted as a decomposition f=u_λ+v_λ, where u_λ extracts the edges of f and v_λ extracts the textures of f. This interpretation depends on the scale λ, since texture at scale λ consists of edges when viewed under a refined scale (e.g., 2λ). Upon decomposing f=u_λ+v_λ, we proceed to decompose v_λ as follows:

$$v_{\lambda }=u_{2\lambda }+v_{2\lambda },$$

where

$$[u_{2\lambda },v_{2\lambda }]=\underset{v+v=v_{\lambda }}{\arg \inf }J(v_{\lambda },2\lambda ).$$

Thus, we obtain a two-scale representation of f given by f≅u_λ+u_2λ. Repeating this process results in the following hierarchical multiscale decomposition of f. Starting with an initial scale λ=λ₀, we obtain an initial decomposition of the image f,

$$f=u_0+v_0,$$

$$[u_0,v_0]=\underset{u+v=f}{\arg \inf }J(f,{\lambda }_0).$$

We then refine this decomposition to obtain

$$v_j=u_{j+1}+v_{j+1},$$

$$[u_{j+1},v_{j+1}]=\underset{u+v=v_j}{\arg \inf }J(v_j,{\lambda }_0{2}^{j+1}),j=0,1,\dots .$$

After k steps of this process, we have

$$f=\sum _{j=0}^k{u}_j+v_k,$$ (2)

which gives the multiscale image decomposition

$$f\sim u_0+u_1+\dots +u_k,$$ (3)

with a residual v_k. As described in Ref. 16, the initial scale λ₀ should capture the smallest oscillatory scale in f, though in practice λ₀ is typically determined experimentally. The starting scale λ₀ should be chosen in such a way that only large shapes and main features of the image f are observed in u₀. For the medical images that we have worked with, we have found that λ₀=0.01 works well.

Multiscale registration algorithm

For the general setup, suppose that we want to register two images A and B with one another. The iterated multiscale registration algorithm is implemented as follows.

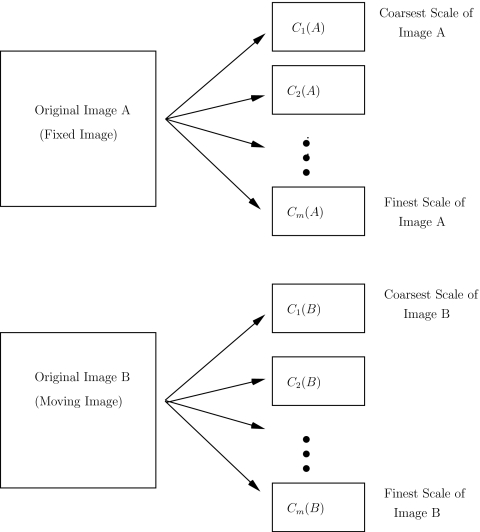
• (1)
  Apply the multiscale (BV, L²) decomposition to both images. Let m denote the number of hierarchical scales used in the decomposition. For the registration problems considered here and in our previous work, we use m=8 hierarchical scales in the image decompositions. Let

  $$C_k\left(A\right)≔\sum _{j=0}^k{u}_j$$

  denote the kth scale of the image A. See Fig. 1.
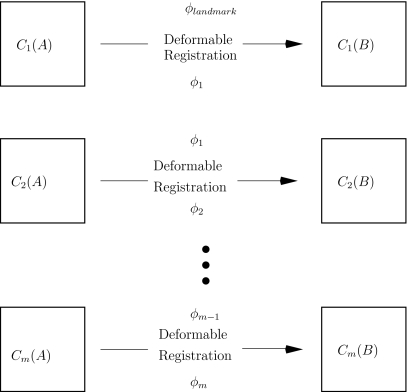
• (2)Register the coarse scales C₁(A) and C₁(B) with one another using a landmark-based registration algorithm. This step allows the practitioner to incorporate known anatomical information about the images to be registered (such as correspondence of bony structures) into the registration process. Let ϕ_landmark denote the resulting transformation. See Fig. 2.
• (3)Use ϕ_landmark as the starting point to deformably register C₁(A) and C₁(B) with one another. This step allows the practitioner to refine the coarse-scale landmark-based transformation obtained in the previous step, while at the same time guaranteeing that the large-scale features (such as bony structures) are still matched with one another. Let ϕ₁ denote the resulting transformation. Next, use ϕ₁ as a starting point to deformably register the next scales C₂(A) and C₂(B) with one another. Let ϕ₂ denote the transformation obtained upon registering C₂(A) with C₂(B). Iterate this method, at each stage using the transformation computed by the previous scale registration algorithm as the starting point for the current registration. Note that the landmark-based registration is only used for registering the coarsest scales of the images; the iterative deformable registration component of the algorithm fine tunes the registration result obtained with the coarse-scale landmark-based registration. See Fig. 3.

Figure 1.

Step 1 of the multiscale registration algorithm: decompose each of the images to be registered into m hierarchical scales.

Figure 2.

Step 2 of the multiscale registration algorithm: register the coarse scales using a landmark-based registration algorithm.

Figure 3.

Step 3 of the multiscale registration algorithm: iteratively register the scales with one another, at each stage using the previous scale transformation as the starting point for the new registration procedure.

See Sec. 3C for a discussion of the computational costs of the multiscale algorithm.

RESULTS AND DISCUSSION

In this section, we demonstrate the accuracy of the multiscale registration algorithm with image registration experiments using both synthetic and clinical deformations. All of the images used in this section were acquired at the Stanford University Medical Center.

Quantitative evaluation of synthetic results

To quantitatively evaluate the multiscale registration algorithm, we consider several registration problems in which the transformation between the fixed and moving images is known. We consider both rigid and nonrigid deformations.

Rigid deformations

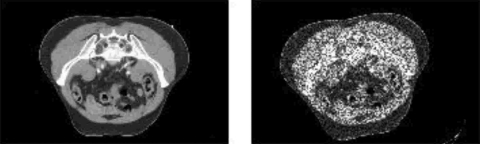
We begin with a CT image of the rectum, and deform the image using a known transformation. To simulate a rigid transformation, we translate the original CT image 13 mm in the horizontal (X) direction, 17 mm in the vertical (Y) direction, and rotate the image 10 deg about its center. Finally, to simulate the noise components that appear in CBCT images, we add synthetic multiplicative (speckle) noise to the deformed image. The original CT image and the noisy, deformed image are illustrated in Fig. 4.

Figure 4.

The original and noisy deformed CT images of the rectum.

We repeat this procedure for 50 different CT images of the rectum and use the multiscale registration algorithm (restricted to rigid transformations) to register the noisy deformed images with the original CT images. The results (X translation, Y translation, and rotation angle) of the multiscale registration algorithm are presented graphically in Fig. 5; recall that the known deformation parameters are 13 mm in X, 17 mm in Y, and 10 deg rotation. The results presented in Fig. 5 demonstrate that the multiscale registration algorithm accurately recovers the actual deformation parameters.

Figure 5.

The X translation, Y translation, and rotation angle deformation parameters obtained upon registering the noisy deformed rectum images with the CT images using the multiscale registration algorithm.

Nonrigid deformations

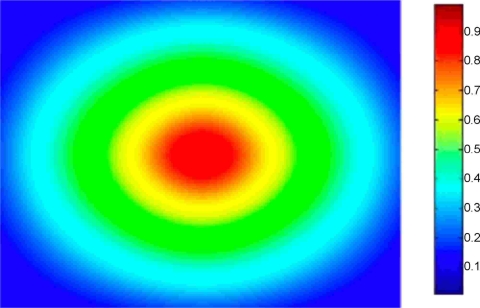
Next, we present a quantitative evaluation of the multiscale algorithm for nonrigid deformations. We begin with a CT image of the rectum, and deform the image using a known nonrigid transformation. To simulate a nonrigid transformation, we deform (warp) the CT image using a known splines vector field deformation by assigning random transformation parameters at each B-spline node of the image. Finally, to simulate the noise components that appear in CBCT images, we add synthetic multiplicative (speckle) noise to the deformed image. We add the same level of noise as that illustrated in Fig. 4. In Fig. 6, we illustrate the vector deformation field that graphically represents the known deformation between the images. The deformation field represents graphically the magnitude of the deformation at each pixel in the image. Each vector in the deformation field represents the geometric distance between a pixel in the original CT image and the corresponding pixel in the deformed image. The magnitude of the vector deformation ranges from 0 to 20 mm.

Figure 6.

The deformation field illustrating the known vector deformation between the original rectum CT image and the noisy deformed image. The magnitude of the vector deformation ranges from 0 to 20 mm.

We repeat this procedure for 50 different CT images of the rectum, and use the multiscale registration algorithm to register the noisy deformed images with the original CT images. To quantitatively evaluate the results, we compute the pixelwise sum of mean absolute differences (MADs) between the vector deformation field computed by the multiscale algorithm and the known exact vector deformation field for each pair of images

$$\mathrm{MAD}(C,K)=\frac{1}{N}\sum _{i=1}^N\mid C_i-K_i\mid ,$$

where N is the total number of pixels, C_i is the magnitude of the ith vector in the deformation field computed by the multiscale registration algorithm, and K_i is the magnitude of the ith vector in the known exact deformation field. If the computed deformation field C and the known deformation field E are exactly the same (i.e., if the multiscale algorithm recovers the exact deformation between the images), then MAD(C,K)=0. Poor matches result in larger values of MAD(C,K). In Table 1, we present the mean, median, minimum, and maximum MADs obtained upon registering the 50 CT images with the noisy deformed images using the multiscale algorithm. For reference, we also include in Table 1 the mean, median, minimum, and maximum MADs obtained upon registering the 50 CT images with the non-noisy deformed images using a standard B-splines deformable registration algorithm. Since the B-splines technique has been validated to accurately recover deformations,^{3, 8, 14} we can use the MADs obtained with the B-splines algorithm for non-noisy registration as benchmark values for comparison with the multiscale algorithm for both non-noisy and noisy registration. We observe that the MADs obtained using the multiscale registration algorithm are similar to or better than those obtained using a standard B-splines registration algorithm. Thus, we conclude that the multiscale registration algorithm accurately registers the CT images with both the non-noisy and noisy deformed images. See Refs. ^{10, 11, 12} for additional data on multiscale registration of noisy images.

Table 1.

The mean, median, minimum, and maximum MADs between the computed and known vector deformation fields. The first column contains the MADs obtained upon using the multiscale registration algorithm to register the CT images with the non-noisy deformed images; the second column contains the MADs obtained upon using the multiscale registration algorithm to register the CT images with the noisy deformed images; the third column contains the MADs obtained upon using a standard B-splines deformable registration algorithm to register the CT images with the non-noisy deformed images.

	Multiscale MAD: non-noisy	Multiscale MAD: noisy	B-splines MAD: non-noisy
Mean	0.0224	0.0257	0.0236
Median	0.0213	0.0251	0.0229
Minimum	0.0095	0.0104	0.0110
Maximum	0.0340	0.0415	0.0352

Clinical results

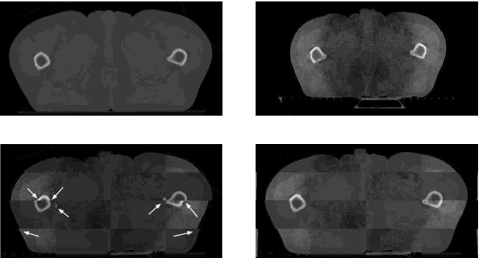
Next, we present the results obtained with the multiscale registration algorithm for clinical CT-CBCT rectum, head-neck, and prostate registration (Figs. 789). In each example, we illustrate a two-dimensional slice of the CT image (upper left), the corresponding slice of the CBCT image (upper right), a checkerboard comparison of the images after ordinary (i.e., nonmultiscale) B-splines deformable registration (lower left), and a checkerboard comparison of the images after multiscale registration (lower right). We have highlighted areas of misregistration in the checkerboard images after ordinary B-splines registration with arrows. In particular, we notice that misalignment occurs in bony structure regions after ordinary registration, and that we are able to recover this misalignment using the multiscale registration algorithm. The accurate registration of bony structures obtained with multiscale registration is due to the fact that we approach mapping of bony structures differently than mapping of other regions (such as tissue). We first register bony structures with one another using a coarse-scale landmark-based registration, and then use an iterative splines-based registration to refine the result.

Figure 7.

Rectum example. Planning CT image (upper left), daily CBCT image (upper right), checkerboard comparison after ordinary B-splines deformable registration (lower left), checkerboard comparison after multiscale registration (lower right). The arrows indicate examples of areas of misalignment between the images after ordinary registration.

Figure 8.

Head and neck example. Planning CT image (upper left), daily CBCT image (upper right), checkerboard comparison after ordinary B-splines deformable registration (lower left), checkerboard comparison after multiscale registration (lower right). The arrows indicate examples of areas of misalignment between the images after ordinary registration.

Figure 9.

Prostate example. Planning CT image (upper left), daily CBCT image (upper right), checkerboard comparison after ordinary B-splines deformable registration (lower left), checkerboard comparison after multiscale registration (lower right). The arrows indicate examples of areas of misalignment between the images after ordinary registration.

To demonstrate the accuracy and applicability of our method, we have illustrated example slices which contain different anatomical features. We performed a total of 50 two-dimensional rectum CT-CBCT registration examples, 50 two-dimensional head-neck CT-CBCT registration examples, and 50 two-dimensional prostate CT-CBCT registration examples. Here, we present the visual registration results for one rectum example, one head-neck example, and one prostate example, and note that the results obtained with all other slices are similar to those presented here. All of the registrations presented in this section were performed slice-by-slice (i.e., no three-dimensional motion was considered). In Sec. 3B2, we consider three-dimensional registration.

Mutual information similarity measures

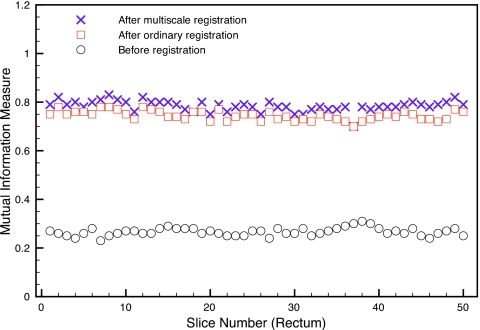
In Fig. 10, we present the mutual information similarity measures between the planning CTs and daily CBCTs before registration (circles), after ordinary B-splines deformable registration (squares), and after multiscale registration (crosses) for all 50 slices considered for the rectum registration example. The mutual information similarity measures for the head-neck and prostate examples are similar to those presented in Fig. 10 for the rectum example, so we do not include them here. In Table 2, we present the mean mutual information measure (taken over all 50 slices) before registration, after ordinary B-splines registration, and after multiscale registration. For all examples, and for all image slices, the similarity measures increased after multiscale registration and were slightly higher than the similarity measures after B-splines registration. However, we note that the increased mutual information similarity values do not completely represent the improved accuracy obtained with multiscale registration that we have observed visually in Figs. 789. Nevertheless, they do capture the qualitative trend of a better matching using our multiscale registration algorithm. See, Refs. ^{2, 17} for an overview of the use of mutual information in multimodality image registration.

Figure 10.

The mutual information similarity measures between the rectum planning CTs and daily CBCTs before registration, after B-splines deformable registration, and after multiscale registration.

Table 2.

The mean mutual information between the planning CTs and daily CBCTs before registration, after B-splines deformable registration, and after multiscale registration.

Mutual information	Rectum	Prostate	Head-neck
Before registration	0.34	0.21	0.20
After B-splines registration	0.75	0.64	0.74
After multiscale registration	0.79	0.65	0.76

Finally, we note that, although the visual results and mutual information similarity measures indicate that the multiscale registration algorithm accurately registers the planning CT and daily CBCT images, there is some mismatch observed in the registration results. For example, in Fig. 7, there is mismatch observed in the checkerboard comparison after multiscale registration in skin on the left and right sides, and in bone on the right side. We are currently working on techniques for further improving the accuracy of the multiscale registration algorithm.

Three-dimensional multiscale registration

In Ref. 12, we extended the multiscale hierarchical (BV,L²) image decomposition of Ref. 16 to three-dimensional images and presented the details of the computational implementation of multiscale registration for three-dimensional images. In clinical practice, three-dimensional registration of CT and CBCT volumes is an important component of adaptive radiation therapy, as two-dimensional registration of image slices cannot account for all possible deformations between the planning and daily images.

We used the three-dimensional multiscale registration algorithm described in Ref. 12 to register three-dimensional rectum, head-neck, and prostate planning CT and daily CBCT volumes with one another. To evaluate the accuracy of the registration algorithm, we computed the mutual information similarity measure between the planning CT volumes and daily CBCT volumes before registration, after B-splines deformable registration, and after multiscale registration. The results are presented in Table 3. As in the two-dimensional cases, we observe that the multiscale registration algorithm accurately registers the three-dimensional volumes with one another.

Table 3.

The mutual information similarity measures between the three-dimensional planning CT volumes and daily CBCT volumes before registration, after B-splines deformable registration, and after multiscale registration.

Mutual information	Rectum	Prostate	Head-neck
Before registration	0.33	0.29	0.32
After B-splines registration	0.78	0.71	0.82
After multiscale registration	0.86	0.81	0.89

Computation

For all of the examples presented in this article, computations were performed on a Dell Dimension 8400 Intel Pentium 4 CPU (3.40 GHz, 2.00 GB of RAM). The total time required per slice for the multiscale registration algorithm (including decomposition of the images to be registered) is approximately 30–50 s. For the types of medical images considered here, decomposition of the images (illustrated schematically in Fig. 1) into hierarchical scales requires approximately 5 s per image. Landmark-based registration of the coarse scales (illustrated schematically in Fig. 2) requires approximately 15–20 s per image, and iterative deformable registration of all of the remaining scales (illustrated schematically in Fig. 3) requires approximately 15–20 s. In an ideal implementation of ART, real-time registration of the CT and CBCT images will be performed in the treatment room so that treatment can be continuously updated and optimized; thus, we are currently working on improving the computational efficiency of the multiscale registration algorithm. Parallel computing techniques can be used to increase the speed of the algorithm.

The Insight Toolkit (ITK), an open-source software toolkit sponsored by the National Library of Medicine and the National Institutes of Health, was used for the iterative B-splines deformable registration portion of the multiscale registration algorithm. MATLAB was used for the multiscale decomposition and for the landmark-based registration.

CONCLUSIONS

In this article, we have presented the results of a multiscale registration algorithm for registration of planning CT and daily CBCT medical images. The multiscale algorithm is based on combining the hierarchical multiscale image decomposition of Ref. 16 with standard landmark-based and free-form deformable registration techniques. Our hybrid technique allows the practitioner to incorporate a priori knowledge of corresponding bony or other anatomical structures into the registration process by using a landmark registration algorithm to register the coarse scales of the fixed and moving images with one another. The transformation produced by this coarse scale landmark registration is then used as the starting point for a multiscale deformable registration in which the remaining scales are iteratively registered with one another, at each stage using the transformation computed by the previous scale registration as the starting point for the current scale registration.

We have demonstrated with several synthetic and clinical image registration experiments that the multiscale registration algorithm is applicable to CT-CBCT registration, which is an important component of ART and IGRT. One of the main features of our multiscale registration algorithm is that it can be used in conjunction with any standard registration technique(s). Thus, the multiscale algorithm can be easily customized to various image registration problems.