Optimization of an adaptive neural network to predict breathing

Abstract

Purpose: To determine the optimal configuration and performance of an adaptive feed forward neural network filter to predict breathing in respiratory motion compensation systems for external beam radiation therapy. Method and Materials: A two-layer feed forward neural network was trained to predict future breathing amplitudes for 27 recorded breathing histories. The prediction intervals ranged from 100 to 500 ms. The optimal sampling frequency, number of input samples, training rate, and number of training epochs were determined for each breathing history and prediction interval. The overall optimal filter configuration was determined from this parameter survey, and its accuracy for each breathing example was compared to the individually optimal filter setups. Prediction accuracy was also compared to breathing stability as measured by the autocorrelation of the breathing signal. Results: The survey of filter configurations converged on a standard setup for all examples of breathing. For 24 of the 27 breathing histories the accuracy of the standard filter for a 300 ms prediction interval was within a few percent of the individually optimized filter setups; for the remaining three histories the standard filter was 5%–15% less accurate. Conclusions: A standard adaptive neural network filter setup can provide approximately optimal breathing prediction for a wide range of breathing patterns. The filter accuracy has a clear correlation with the stability of breathing.

INTRODUCTION

Respiratory motion compensation during external beam radiation therapy is a topic of continuing interest and research.^{1, 2} The movement of lung tumors during free breathing has become a paradigmatic example of this problem. Compensation strategies currently being employed or under development include temporal gating of the beam,^{3, 4} repositioning of the linear accelerator,^{5, 6} adjustment of the collimating aperture,^{7, 8} electromagnetic steering of a charged particle beam,⁹ and compensatory shift of the treatment couch.^{10, 11} Because no system response can occur instantaneously, all methods must make a future prediction of the tumor position to cover for the lag time between the detection of the tumor position and the compensatory system response. Lag times can range from 50 to several hundred milliseconds, during which a lung tumor can move several millimeters or more.

This study addresses the problem of predicting breathing motion to compensate lag time. From among various possible strategies, the authors have adopted an adaptive neural network filter algorithm. Such a filter is trained on examples of a specific patient’s breathing so that it can “learn” the characteristic pattern and mimic the behavior. If the breathing pattern is nonstationary (i.e., if it changes amplitude and∕or period over time) the filter can be continuously retrained to adjust to the changing pattern.

Stationary and adaptive neural networks to predict breathing have been investigated by a number of researchers.^{12, 13, 14, 15, 16, 17, 18} In previous work it has been demonstrated that breathing prediction can be done more accurately with an adaptive linear filter than a stationary linear filter, and that an adaptive neural network can perform better than an adaptive linear filter.^{12, 17} In this study we continue the development of the adaptive neural network algorithm by addressing three issues: (1) can a single standard filter configuration make an approximately optimal prediction for a wide variety of breathing patterns? (2) How much accuracy is likely to be lost if a standard filter is used instead of one optimized to each particular patient? And (3) how is the prediction accuracy related to characteristics of the breathing signal? For this analysis we have optimized and evaluated an adaptive neural network predictor using 27 examples of breathing movement that display a wide range of properties.

A neural network signal predictor is a heuristic type of learning algorithm that uses past samples of a signal in a weighted nonlinear combination to predict its future amplitude. There are a variety of basic architectures including feed-forward and recurrent networks, different training methodologies such as backpropagation, and a variety of algorithms to adjust the weights. A network can have two or more layers of neurons, each with multiple neurons and connected by one of several types of nonlinear transfer functions. This variety of configurations presents an enormous space in which to search for the best possible predictor. We have not attempted to make an exhaustive search of all these configurations for the globally optimal predictor. Rather, we have proceeded in stages to identify an effective basic architecture and then optimize it.

Earlier studies¹² showed that a feed-forward network trained via backpropagation could predict breathing with reasonable accuracy over time intervals up to 1 s, and that a two-neuron input layer coupled via a sigmoid transfer function to a single output neuron did about as well as larger networks with more neurons and more layers. This simple architecture still has several free parameters that must be set when configuring the filter. These include the sampling rate for the breathing signal, the number of sequential samples that are used as filter input, the learning rate of the network, and the number of training cycles (epochs) used to initialize the filter. In the present study we have made a comprehensive survey of these parameters to see if there is a basic configuration that works well for most representative examples of breathing, or if different sets of parameters are clearly optimal for different basic characteristics of the breathing pattern.

The accuracy of the prediction will depend not only on the intrinsic accuracy of the filter itself but also on the character of the breathing signal. Clearly, a more complex and unstable breathing pattern will be harder to predict than a simple, stable pattern. This makes it difficult to assess and compare the performance of predictive filters that have been tested on different sets of breathing data. Stability and∕or complexity can be revealed by the behavior of the autocorrelation function of a breathing time series S(t). The autocorrelation of S(t) shows how much the signal at a future time τ resembles the signal at the present time. A purely sinusoidal S(t) will have an average autocorrelation coefficient that is constant in time, while a nonstationary S(t) will have an autocorrelation coefficient that decays over time. The faster the breathing pattern changes, the faster the autocorrelation decays, and the harder it is for the filter to keep up with the changes. Therefore, we have made an assessment of prediction accuracy as it relates to the stability of each patient’s breathing.

METHOD AND MATERIALS

The neural network analyzed in this study was a two-layer feed-forward network with two input (hidden-layer) neurons and one output neuron connected by a sigmoid transfer function. The inputs to the filter consisted of N sequential samples of the breathing amplitude distributed to each of the two input neurons. Each input-layer neuron also had a weighted offset. The filter output was a prediction of the future breathing amplitude τ seconds in advance. The basic schematic of this process is illustrated in Fig. 1. The network was trained and updated via backpropagation using least mean squares (LMS) to adjust the weights according to Eq. 1

$$w_i(t+1)=w_i\left(t\right)+2\mu ϵ\left(t\right)D(t-i);0<i<N,$$ (1)

where ϵ(t)=P(t)−D(t) is the error in the current estimated signal sample P(t) and the parameter μ determines the speed of convergence. The development of this filter architecture has been described in detail in earlier publications.^{12, 15, 17} The results using LMS updating compare favorably with earlier results using the Levenberg-Marquardt algorithm (cf. Refs. ^{15, 17}).

Figure 1.

A schematic of an adaptive neural network to predict a signal amplitude τ seconds in the future, showing the use of a tapped delay line to provide n data inputs D(t-i) and the error correction via backpropagation to minimize the difference between the prediction P(t) and the actual signal D(t). The ring buffer saves the predictions until the corresponding data sample is available for comparison.

Breathing data

We used three independent sets of patient breathing data to evaluate the filter performance. Each set of data consisted of chest displacements recorded continuously in three dimensions at a sampling frequency of 30 Hz using optical tracking devices. The recordings lasted anywhere from 5 min to 1 h. Fourteen of the patient data sets were recorded at the Georgetown University CyberKnife treatment facility. (Nine of these records have been analyzed in a prior study.¹⁷) These records were arbitrarily selected to represent a wide variety of breathing patterns, including highly unstable and irregular examples. Seven more breathing time series were recorded at Virginia Commonwealth University (VCU) for free-breathing patients. A final group of six patients at VCU were recorded while they were coached to regularize their breathing. Each patient’s breathing record was used to independently train and test the predictive accuracy of the filter.

For the purposes of testing, the 1D anterior∕posterior component of motion of 167 s (5000 samples at 30 Hz) was extracted from each 3D patient data set. To suppress baseline drifts and large amplitude fluctuations, each patient’s breathing time series was centered on its mean and normalized to unity variance. This preprocessing step emulated the operation of the filter in real time by calculating a running mean and variance using a weighted sliding window that spanned approximately two breathing cycles of data history.

Network training

The first 40 s segment of each patient’s breathing record was used to train the filter. The latency (prediction interval) was designated τ and each sampled time step was designated t_i. A sliding window containing N sequential amplitude samples from t_i−t_i−N−1−τ up to t_i−τ (known as a tapped delay line) was advanced one step at a time through the recorded data to produce 40−N−τ sequential training examples. For the ith training example the target data consisted of the breathing amplitude at t_i. The N tapped samples were applied to the filter inputs as in Fig. 1 to calculate a predicted signal. Each time the sliding window was advanced one sample, the difference between the filter output and the actual amplitude at t_i was passed backwards via LMS backpropagation to update the filter weights. This pattern mode of training¹⁹ is the logical basis for backpropagation, realistically simulates the function of a predictive filter as it is presented with real-time data, and generalizes in a natural way to later adaptation once the filter has been initially trained.

To get the two input neurons functioning independently we followed the usual practice of randomizing the starting weights before starting to train the filter. The training process then cycled M times through the training set (i.e., went through M training epochs) while updating the weights.

The random starting weights sometimes produce good filters, but sometimes produce poor filters. To get the best starting configuration of the filter the training process was repeated ten times, each time with different random initial weights. For each training trial the filter was tested on a verification data set consisting of the second 40 s long sample of data. The training pass that produced the best prediction of the validation data was then used as the starting configuration for the test data.

Network adaptation and testing

Once trained, the filter was presented with 86 s of test data in a simulated real-time prediction mode. Each time a new amplitude sample was made available, the filter made a prediction of the future amplitude τ seconds in advance. When the future amplitude sample became available for comparison to the predicted value, it was used to update the weights via backpropagation. This continuous training mode is a natural extension of backpropagation in a real-time adaptive filter application. Each adaptive backpropagation step took 13 microseconds on a 300 MHz processor, which is fast compared to the input data sampling rate; consequently, the filter can easily operate in real time.

A real-time adaptive filter uses the tapped delay line approach described above to sample the signal and update the weights. However, when testing predictive filters on prerecorded retrospective data one must be careful to correctly simulate prospective real-time prediction and adaptation. In particular, one must ensure that the weights do not learn about the future breathing amplitude before it would become known in real time. If one simply takes the window of N samples delayed by τ as inputs, computes the filter output and the error at t_i and then updates the weights, as in the training process described above, then the weight adjustments never lag more than one sample behind the true signal, even when the latency time τ is greater than one sample. This will give better predictions than one would get in real life. To properly simulate real-time adaptive prediction by more than one sample in advance, one must save the predicted amplitudes (in a ring buffer, for example) and then use the appropriately delayed prediction sample in the buffer to compute the error with respect to the current data sample and update the weights. This is illustrated in Fig. 1.

The metric for prediction accuracy was the (dimensionless) normalized root-mean-square error (nRMSE) between the predicted and actual amplitudes for all samples in each test data set. The use of a dimensionless error metric allows an unbiased comparison of filter performance for signals of different amplitude. If the standard deviation of the signal amplitude is σ then the (dimensioned) RMSE=σnRMSE. For example, a sine wave with 1.0 cm peak-to-peak amplitude has a standard deviation σ=0.354 cm; if the nRMSE prediction error is 0.10 this would translate to a root-mean-square error of 0.0354 cm. An nRMSE accuracy of 0.50 translates to an uncertainty of 0.18 cm. When nRMSE=1.00 the prediction error equals the signal’s sigma and the filter has no predictive power—i.e., one might just as well use the average.

We evaluated the filter’s accuracy as a function of its parameters by making a four-dimensional parameter survey, varying the number of input samples from 5 to 30 in increments of 5, varying the number of training epochs from 10 to 400 in increments of 50, downsampling the data by factors of 2 and 3, and varying the training rate μ from 0.25∕trace(R) to 0.0125∕trace(R), where [R] is an estimate of the covariance matrix of the input samples. The matrix R was computed as a running covariance via a sliding window whose width was equal to the number of input samples and which added to the cumulative estimate of trace(R) with each new time step. Thus, trace(R) was updated with each new data sample after preprocessing. By this process μ was automatically adapted to each individual breathing pattern according to a rule that had only one free parameter—namely the scaling factor with respect to 1∕trace(R).

Quantifying the stability of the breathing time series

For a finite length of continuous patient breathing signal S(t), the autocorrelation coefficient C(τ) is defined as the cross-correlation integral of S(t) with itself, at delay time τ :

$$C\left(\tau \right)=\int S\left(t\right)S(t-\tau )dt.$$ (2)

For a stationary periodic signal the average value of C(τ) vs τ will be approximately constant, while for a nonstationary signal the average of C(τ) will become smaller with increasing τ. We can characterize the stability of the signal by the inverse of the rate at which the average correlation coefficient decays with τ. We call this the correlation decay time. To compute the decay time, we set a 60 s window at a point in the breathing time series and computed C(τ) for 0< <60 s. The peak values of the positive half cycle of the autocorrelation coefficient were plotted in a semilog scale as a function of τ. The inverse slope of the graph gave the decay time for that particular position of the breathing signal window. A rapidly changing signal will have a short decay time; a slowly changing signal will have a long decay time; a perfectly stationary signal will have an infinite decay time.

RESULTS

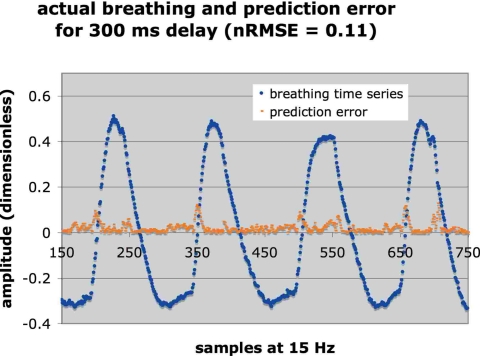
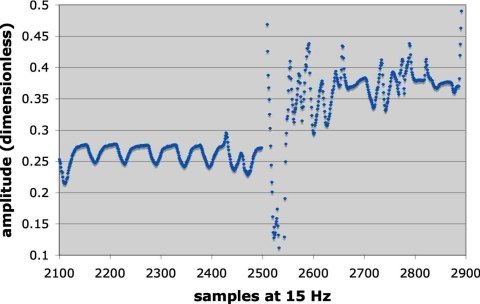
Figures 2 and 3 illustrate two examples of breathing to show the wide range of behavior represented in the 27 samples. Figure 2 also includes the prediction error for 300 ms latency (nRMSE=0.11) so as to provide a visual interpretation of the nRMSE. For Fig. 2 the log of the correlation decay time was 3.34 while for Fig. 3 it was 1.94, indicating that the pattern in Fig. 3 was more unstable than Fig. 2. For the signal illustrated in Fig. 3 the patient began breathing in a fairly regular pattern, which provided the initial training data. A few minutes later the patient began breathing very erratically, which underscored the advantage of adapting the filter weights via continuous retraining to accommodate such changes.

Figure 2.

An example of breathing coached to regularize its period and amplitude (log of autocorrelation decay 3.34), together with the prediction error at 300 ms latency. The nRMSE was 0.11.

Figure 3.

An example of a highly irregular breathing pattern (log of the autocorrelation decay 1.94). The filter was trained on the earlier, more regular part of the signal and tested on the later, more erratic signal. The nRMSE was 0.56 for the test data.

Our first objective was to find the set of four filter parameters that provided the best overall prediction accuracy for the 27 examples of breathing. These optimal parameters would then be used to set up a standard prediction filter. We used the accuracy of the predictions for a 300 ms delay time to determine the optimal training rate, number of training epochs, sampling frequency (i.e., downsampling from 30 Hz), and number of sequential signal samples (after downsampling) to use as inputs.

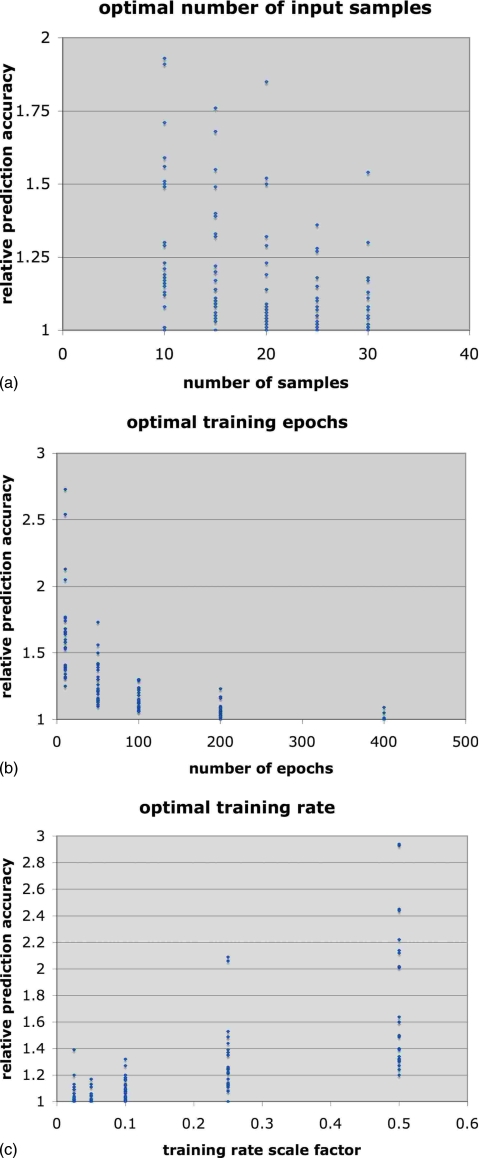
Downsampling by a factor of 2 from 30 to 15 Hz gave the best prediction accuracy for all but one breathing series, so we have set the optimal downsampling factor to 2. To determine the optimum for each of the other three parameters, we plotted the variation in prediction accuracy for each breathing example as a function of each parameter, with the other parameters simultaneously set at the values that gave the best prediction for that particular example. We then normalized the prediction errors for each example to the minimum error for that example so that we could combine all the results into a single scatterplot. These plots are shown in Figs. 4a, 4b, 4c. We found that when only five samples were provided to the filter inputs the filter frequently failed to converge during training. Therefore, we limited the optimal search to the range of 10–30 inputs. The optimal number of samples was between 20 and 25 signal taps [Fig. 2a]. Using 20 samples gave the best overall accuracy on average, compared to 25 samples, but there were more outliers (i.e., larger errors for some breathing series) compared to 25 samples. We have therefore identified 25 samples as the generally optimal number. We note that this is consistent with results observed in an earlier analysis of predictive neural networks for a much smaller number of test cases.¹⁵ The two parameters that had the greatest influence on the prediction accuracy were the training rate and number of epochs. The optimal number of training epochs was reached asymptotically at 400 epochs [Fig. 2b], but there was in fact very little improvement after 200 epochs. The accuracy improved with decreasing training rate, reaching its optimal value at μ≅0.025∕tr(R) [Fig. 2c]. There was a general trend that favored more training epochs as the training rate decreased.

Figure 4.

The optimization graphs, showing the variation of prediction accuracy as a function of: (a) the number of input samples (at 15 Hz); (b) the number of training epochs; (c) the training rate scaled from 0.5∕tr(R), where [R] is an estimate of the signal covariance matrix.

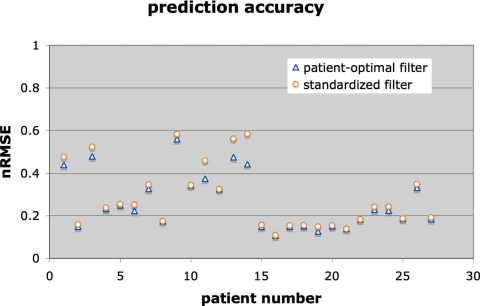
Our second concern was to see if a standard filter configuration based on the optimal parameters could make reasonably accurate predictions for all of the breathing examples. In other words, we looked at how much accuracy was sacrificed by using the standard filter setup instead of the absolute best filter setup for each individual example. This result is shown in Fig. 5, where we compare the absolute best prediction at 300 latency for each breathing series to the accuracy of the standard filter set up with 25 taps at 15 Hz and trained with μ≅0.025∕tr(R) for 400 epochs.

Figure 5.

The nRMSE for a standard filter applied to all breathing examples (circles), compared to the nRMSE for a filter optimized separately for each breathing example (triangles).

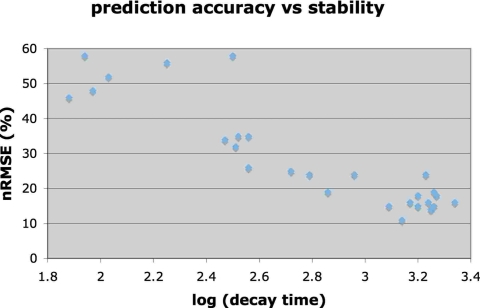
Figure 6 shows the relationship between the prediction accuracy of the standard filter and the stability of each breathing pattern, where the breathing stability was charac-terized by the decay over time of its autocorrelation function. We also looked for general trends between the optimal filter parameters and the breathing characteristics. All cases were best predicted with the standard training rate and number of epochs, but there was a slight trend for the more regular breathing (coached data) to have optimal filters that downsampled by 3 (to 10 Hz) and had 25–30 taps.

Figure 6.

The nRMSE of the standard filter at a latency of 300 ms for each breathing example, compared to the stability of that breathing signal (as measured by the decay constant of the signal’s autocorrelation).

Finally, for prediction latencies of 0 to 500 ms we summarize in Table 1 the nRMSE of the filter optimized for each patient and in Table 2 the nRMSE for the standard filter applied to each patient.

Table 1.

Best nRMSE for the filter optimized to each patient.

Patient	Delay
	0	100	200	300	400	500 ms
1	0.001	0.124	0.339	0.439	0.613	0.690
2	0.001	0.054	0.109	0.149	0.210	0.237
3	0.001	0.119	0.347	0.479	0.728	0.815
4	0.001	0.093	0.184	0.233	0.326	0.363
5	0.001	0.075	0.189	0.250	0.358	0.413
6	0.001	0.089	0.185	0.223	0.328	0.372
7	0.002	0.079	0.238	0.326	0.501	0.583
8	0.001	0.066	0.137	0.175	0.236	0.272
9	0.008	0.178	0.435	0.560	0.790	0.889
10	0.001	0.090	0.265	0.343	0.435	0.474
11	0.005	0.109	0.299	0.375	0.527	0.570
12	0.001	0.088	0.237	0.325	0.464	0.538
13	0.002	0.100	0.355	0.475	0.646	0.713
14	0.002	0.080	0.305	0.443	0.629	0.658
15	0.001	0.058	0.125	0.149	0.199	0.215
16	0.001	0.035	0.082	0.108	0.159	0.201
17	0.001	0.058	0.127	0.149	0.200	0.221
18	0.001	0.052	0.116	0.152	0.194	0.207
19	0.001	0.042	0.105	0.127	0.157	0.182
20	0.001	0.053	0.115	0.151	0.193	0.211
21	0.001	0.049	0.105	0.139	0.192	0.221
22	0.001	0.059	0.129	0.183	0.257	0.311
23	0.001	0.079	0.163	0.229	0.290	0.349
24	0.001	0.107	0.186	0.224	0.304	0.336
25	0.001	0.089	0.149	0.187	0.241	0.283
26	0.001	0.139	0.271	0.331	0.442	0.501
27	0.001	0.059	0.129	0.184	0.277	0.351

Table 2.

Best nRMSE per patient for the standard filter.

Patient	Delay
	0	100	200	300	400	500 ms
1	0.026	0.138	0.355	0.476	0.699	0.819
2	0.024	0.060	0.126	0.165	0.217	0.267
3	0.043	0.134	0.364	0.524	0.790	0.954
4	0.016	0.094	0.184	0.233	0.330	0.382
5	0.085	0.084	0.191	0.255	0.382	0.437
6	0.031	0.095	0.204	0.252	0.354	0.402
7	0.039	0.079	0.248	0.346	0.544	0.657
8	0.022	0.071	0.137	0.175	0.246	0.273
9	0.105	0.188	0.452	0.583	0.827	0.925
10	0.024	0.097	0.278	0.346	0.458	0.474
11	0.117	0.133	0.343	0.460	0.704	0.749
12	0.020	0.097	0.237	0.325	0.519	0.583
13	0.046	0.127	0.355	0.562	0.777	0.774
14	0.060	0.130	0.398	0.585	0.971	1.007
15	0.028	0.063	0.127	0.157	0.205	0.226
16	0.012	0.039	0.082	0.108	0.176	0.213
17	0.032	0.063	0.128	0.154	0.208	0.233
18	0.015	0.055	0.124	0.155	0.206	0.225
19	0.035	0.055	0.114	0.149	0.219	0.264
20	0.014	0.055	0.124	0.154	0.208	0.224
21	0.019	0.053	0.105	0.139	0.205	0.234
22	0.027	0.060	0.133	0.183	0.307	0.334
23	0.034	0.085	0.178	0.241	0.371	0.430
24	0.024	0.109	0.204	0.243	0.344	0.389
25	0.027	0.093	0.151	0.187	0.257	0.285
26	0.025	0.139	0.289	0.348	0.478	0.511
27	0.037	0.063	0.142	0.192	0.316	0.399

CONCLUSIONS

Table 1 shows that the adaptive neural network can exactly reproduce each breathing trace when there is no lag time. As one would expect, the accuracy decreases with lag time. Table 2 shows that the standard filter becomes less optimal as the predicted lag time increases beyond about 200 ms but remains effective even for 500 ms delay.

As Fig. 5 shows, for all but three breathing examples the standard filter prediction for 300 ms latency was only slightly less accurate (i.e., the nRMSE increased by less than 5%) than the filters optimized for each patient separately. For three examples the error of the standard filter increased by 5%–15% above the optimal accuracy. We conclude that a standard filter can provide effective prediction for a wide range of breathing patterns. (We note that the learning parameter μ automatically adapts to each breathing pattern via the covariance R and so our standard configuration refers to the scaling parameter that relates μ to R).

It is to be expected that the temporal stability of a patient’s breathing will influence its predictability in tumor tracking control loops. The autocorrelation decay rate describes breathing stability. If the breathing signal changes period and∕or mean amplitude over time then the average autocorrelation will diminish with time. Under those circumstances a stationary prediction filter trained on a short sample of breathing will perform well initially, but will lose accuracy as the breathing pattern slowly changes. To deal with this, the filter must be made to adapt as the input signal changes, by continuously retraining on the new data. However, retraining takes time; one would expect that if the signal’s autocorrelation changes very rapidly, the filter might not be able to keep up with it and its prediction accuracy will diminish.

Figure 6 shows a clear linear correlation between the log of the autocorrelation decay time and the nRMSE of the standard adaptive neural network prediction filter. Because the accuracy of the standard filter closely matched the accuracy of customized filter configurations, this correlation is equally clear for the individually optimized filter results.

We detected a slight tendency in the optimization survey to favor more input samples for the most stable breathing patterns; otherwise, there was no noticeable relationship between signal stability and the optimal filter configuration.

If two different predictive filter designs have been tested on two different sets of breathing data, the differences in performance can be due as much to the intrinsic difficulties presented by the test data as to the relative merits of the two filters. This makes it difficult to compare in an unbiased way the accuracy of control loop algorithms that have been tested in different environments. This study suggests that the stability of the breathing pattern offers a good indication of a breathing pattern’s inherent predictability. We propose that the decay time of the autocorrelation function can provide a means to categorize different breathing examples according to their intrinsic predictability, thus enabling a less biased comparison of different breathing prediction studies.

SUMMARY

All of the respiratory compensation methods being investigated for radiation therapy require predictive filters to compensate intrinsic system latencies. We have been studying heuristic predictive filters starting with stationary linear tapped delay lines and culminating with adaptive nonlinear neural networks. A stationary linear tapped delay line is a special case of a stationary network and a stationary neural network is a special case of an adaptive network. Although in many cases a stationary and∕or linear filter can make accurate predictions of simple, stable breathing patterns, the adaptive network can always be expected to perform as well or better than the simpler predictive filters, with the added advantage of being able to respond to transient changes or inherently unstable breathing patterns. The adaptive filter is more robust than the linear filter,¹⁷ and adaptation via continuous retraining adds little or no computational burden to the filter. Thus, although its full capabilities might not always be needed, nothing is lost and much can be gained by using an adaptive neural network in a respiration-compensating control loop. We have furthermore shown in this study that a standard configuration of such a filter can provide satisfactory accuracy for a wide range of breathing patterns, thus avoiding the extra complication of customizing the filter setup on a case-by-case basis. Finally, we provide a basis for comparing different methods of breathing prediction that have been tested using different data sets that can vary in their inherent predictability.