Front Instabilities and Invasiveness of Simulated Avascular Tumors

Abstract

We study the interface morphology of a 2D simulation of an avascular tumor composed of identical cells growing in an homogeneous healthy tissue matrix (TM), in order to understand the origin of the morphological changes often observed during real tumor growth. We use the GlazierGraner-Hogeweg model, which treats tumor cells as extended, deformable objects, to study the effects of two parameters: a dimensionless diffusion-limitation parameter defined as the ratio of the tumor consumption rate to the substrate transport rate, and the tumor-TM surface tension. We model TM as a nondiffusing field, neglecting the TM pressure and haptotactic repulsion acting on a real growing tumor; thus our model is appropriate for studying tumors with highly motile cells, e.g., gliomas. We show that the diffusion-limitation parameter determines whether the growing tumor develops a smooth (noninvasive) or fingered (invasive) interface, and that the sensitivity of tumor morphology to tumor-TM surface tension increases with the size of the dimensionless diffusion-limitation parameter. For large diffusion-limitation parameters we find a transition (missed in previous work) between dendritic structures, produced when tumor-TM surface tension is high, and seaweed-like structures, produced when tumor-TM surface tension is low. This observation leads to a direct analogy between the mathematics and dynamics of tumors and those observed in nonbiological directional solidification. Our results are also consistent with biological observation that hypoxia promotes invasive growth of tumor cells by inducing higher levels of receptors for scatter factors that weaken cell-cell adhesion and increase cell motility. These findings suggest that tumor morphology may have value in predicting the efficiency of antiangiogenic therapy in individual patients.

1 Introduction

This paper presents simulations of a simplified model of tumor invasion using the Glazier-Graner-Hogeweg (GGH) model (Graner and Glazier, 1992; Glazier and Graner, 1993; Glazier et al., 2007),¹ as implemented in the CompuCell3D (Chaturvedi et al., 2003; Izaguirre et al., 2004; Cickovski et al., 2005) (CC3D) modeling environment.² Our model includes growing, spatially-extended tumor cells, surrounding tissue matrix (TM) represented as a nondiffusing field secreting nutrients, a diffusing field representing matrix-degrading enzymes (MDEs) that degrade TM, and a diffusing nutrient field (substrate) which governs the rate of tumor-cell growth. By modeling TM as a nondiffusing field, we neglect TM pressure and haptotactic repulsion which act on a real growing tumor, so our model is most appropriate for studying tumors with highly motile cells, e.g., gliomas. We show that even this highly simplified model reproduces and extends existing simulation results obtained using other methods, providing a platform for exploring new phenomenology due to explicit cell shape, TM properties and vascular-tumor interactions. Unlike previous cell-oriented studies of tumor morphologies as a function of individual parameters, we study the simultaneous effects of two parameters: a dimensionless diffusion-limitation parameter which we define below, and the tumor-TM surface tension.

The development of a primary solid tumor begins when mutations in certain key genes transform a single normal cell into a cell which does not obey the body's homeostatic mechanisms, leading to inappropriate proliferation (Weinberg, 2006). An individual tumor cell has the potential to divide repeatedly to form a cluster of tumor cells. Further growth and proliferation leads to an avascular tumor that contains up to 10⁶ cells (Anderson, 2005). While much current cancer literature focuses on sub-populations of stem-like tumor cells and the variable mitotic potential of individual cells (see (Trédan et al., 2007) and references therein), we assume here that all cells are identical in their capacities and responses. Introducing cell variability in our simulations would be straightforward, but would complicate interpretation in this preliminary study. Initially, adhesion between the cells and the pressure of surrounding tissue tends to keep such tumors compact and roughly spherical. Surgical removal at this stage can usually eliminate such tumors completely. Growth of such tumor spheroids depends on diffusion of nutrients and waste products, usually limiting the spheroid's maximum size. The decreasing concentration of nutrients and increasing concentration of waste products, and the increasing hydrostatic pressure towards the center of the spheroid, cause the tumor to organize into a dynamic but constant-volume concentric structure, with proliferating cells at the tumor surface, quiescent (live, but nonproliferating) cells below them, and a core of necrotic (dying) cells. To grow larger, the tumor must recruit blood vessels from the pre-existing vascular network via neoangiogenesis (Folkman, 1995), to supply nutrients and remove waste.

Tumors can be benign or malignant (cancerous). A benign tumor is usually self-limited in growth and contains cells which do not invade surrounding tissues and do not spread to other parts of the body (Weinberg, 2006). A malignant tumor, in contrast, is not self-limited in growth and contains cells which can invade surrounding tissues (through the secretion of MDEs or by entering the circulatory system) and moving to distant sites in the body, resulting in secondary tumors (metastases) (Weinberg, 2006). Metastasizing tumors are generally difficult or impossible to treat and are the main cause of cancer deaths. Most tumors are initially benign. Whether the transition to malignancy requires additional mutations, and if so, the nature of these mutations, continues to be the subject of enormous research effort (Anderson, 2005). While tumors are often genetically heterogeneous, we will show that even genetically homogeneous tumors can be invasive.

Some researchers have suggested that a growing tumor that maintains a uniform (i.e. compact and smooth) interface with the surrounding tissue tends to be non-invasive, while one that produces a rough or fingered interface, or breaks up into multiple separate subtumors, tends to be invasive (Weinberg, 2006; Friedel et al., 2004). This possible association between tumor-margin morphology and malignancy has inspired a considerable body of work on interface-instabilities of simplified models of growing tumors. In this case, malignancy would not necessarily require additional mutations, since a number of mechanisms can cause fingering of an initially smooth, growing tumor spheroid: irregularities in the distribution or availability of nutrients (Anderson et al., 2006; Gerlee and Anderson, 2007a,b; Anderson et al., 2007; Rejniak, 2005) decreasing the average adhesion among tumor cells or increasing their adhesion to the stroma (TM) (Christofori, 2006; Guiot et al., 2007); mutations decreasing surface tension at the tumor-tissue interface (Cristini et al., 2005); vascular or elastic anisotropies in the tumor environment (Cristini et al., 2003); locally increased rates of cell proliferation (possibly due to mutations) (Anderson, 2005; Frieboes et al., 2006); and inhomogeneities in the distributions of TM components (Anderson, 2005; Anderson et al., 2006; Frieboes et al., 2006).

A number of factors contribute to the degree of proliferation and invasiveness of cancer cells. Cell-adhesion receptors (e.g., cadherins and integrins) bind cells to other cells and to the extracellular matrix (ECM), a complex mixture of nondiffusing macromolecules (MM), some predominantly structural (e.g., collagens) and others important for cell adhesion, spreading and motility (e.g., laminin, fibronectin and vitronectin) (Burridge and Chrzanowska-Wodnicka, 1996). Secondary mutations or epigenetic effects reduce some tumor cells' cell-cell adhesiveness and increase their cell-ECM adhesiveness by changing the relative numbers of the corresponding receptors (Huang and Ingber, 1999). Mutated tumor cells may also modify the distribution in the ECM of molecules to which cells adhere, e.g., fibronectin, increasing cell motility (Carter, 1965; Quigley et al., 1983; Lacovara et al., 1984; McCarthy and Furcht, 1984; Klominek et al., 1993; Lawrence and Steeg, 1996; Debruyne et al., 2002). Changes in cell-adhesion-receptor binding state and spatial distribution can, in turn, affect signal-transduction pathways that regulate many aspects of cell function (Burridge and Chrzanowska-Wodnicka, 1996; Hynes, 1992), including DNA transcription, cell proliferation, cell differentiation, cytoskeletal organisation, cell motility and levels of receptor activation (Clark and Brugge, 1995).

Tumor cells can secrete MDEs, such as the plasminogen activator system and the large family of matrix metalloproteinases, that degrade the ECM which maintains the integrity of normal tissues (Lawrence and Steeg, 1996; Liotta et al., 1983; Stetler-Stevenson et al., 1993), weakening the normally compact and impermeable cell-sheets known as epithelia and destroying the structural integrity of mesenchyme, thus permitting both tumor expansion and cancer-cell migration into the surrounding tissue (Matrisian, 1992; Mignatti and Rifkin, 1993; Thorgeirsson et al., 1994; Hotary et al., 2003). Such secretion is a crucial part of invasion and metastasis. In addition to opening physical migratory pathways, MDEs can interfere with the normal functioning of several classes of cell-surface receptors, including cadherins, CD-44, integrins and receptors for fibronectin, laminin and vitronectin, all of which normally negatively regulate cell motility and growth (Stetler-Stevenson et al., 1993; Radotra et al., 1994; Koochekpour et al., 1995).

The difficulty of observing and controlling the multiple factors influencing the growth of real tumors experimentally makes computer simulations an attractive way to investigate the roles of different biological and physical mechanisms in determining tumor properties. Mathematical models of tumor growth (Chaplain, 1996) range from simple fitting of experimental data on the growth kinetics of tumor spheroids using various growth laws (Gompertzian, logistic and exponential (Wheldon, 1986; Retsky et al., 1990; Marusic et al., 1994)) to sophisticated simulations of tumor-induced neoangiogenesis and capillary-network formation (Chaplain, 1996; Anderson and Chaplain, 1998), tumor spreading at early (Sherratt and Nowak, 1992; Ward and King, 1999) and later invasive stages (Orme and Chaplain, 1996; Gatenby and Gawlinski, 1996; Perumpanani et al., 1996; Anderson et al., 2000) and invading travelling waves of cancer cells (Orme and Chaplain, 1996; Gatenby and Gawlinski, 1996; Perumpanani et al., 1996; Byrne et al., 1999). Tumor simulations usually employ one or more of a few major classes of model. Continuum and solid-mechanics models (Chaplain and Sleeman, 1993; Tracqui, 1995; Khain and Sander, 2006; Macklin and Lowengrub, 2007; Frieboes et al., 2007; Li et al., 2007; Swanson et al., 2003) consider physical pressures and forces among cells and TM, capturing tumor structure at the tissue level, but do not describe a tumor's cellular and subcellular properties, making mechanisms such as cell-cell adhesion difficult to include. Point-cell models (cellular automata) allow more realistic stochastic descriptions at cellular (Kimmel and Axelrod, 1991; Smolle and Stettner, 1993; Qi et al., 1993; Kansal et al., 2000; Dormann and Deutsch, 2002) and subcellular levels (Düchting, 1990; Düchting et al., 1996) but neglect the shapes of cells. Hybrid multi-cell models combine discrete representations of individual tumor cells with continuum representations of diffusible chemicals (Anderson, 2005; Rejniak, 2005) and either discrete, continuum or hybrid models of the surrounding tissue. In hybrid models, coupled, nonlinear partial-differential equations (PDEs) model the dynamics of the chemical fields and continuum TM (if used), a cell-level model describes specific cell properties (cell adhesion, chemotaxis, haptotaxis,³ cell motility and force generation and cell division), while a subcellular model for each cell regulates cell proliferation, consumption of nutrients and secretion of enzymes, death, mutation and differentiation (Anderson, 2005).

Anderson's hybrid discrete-continuum (HDC) model (Anderson, 2005) employs one such hybrid approach, modeling a tumor as a collection of distinct cells, each with a set of phenotypic traits that define the cell's behavior: a proliferation rate (the time a cell requires to produce two daughter cells), a cell-cell adhesion value (the number of neighbors to which a cell preferentially adheres), a nutrient consumption rate (how much substrate a cell consumes at its current grid location), an MDE production rate (how much enzyme a cell produces at its current grid location) and a haptotactic rate (how quickly a cell moves in response to gradients within the ECM). The model also describes how each cell interacts with other cells and its microenvironment. The other variables that represent the tumor's microenvironment are continuous concentrations of substrate, MDE and TM which evolve via a set of reaction-diffusion equations. Individual cells are grid points on a 2D lattice with a grid spacing equal to a cell diameter of 25 μm. During its life cycle a cell applies its phenotype as it follows a set of rules for survival (determined by substrate availability), proliferation, shift to quiescence (due to lack of space) and mutation. The cells of a given phenotype proliferate at a constant rate if the local substrate concentration is above a threshold, otherwise they become necrotic (die). At each cell division, cells have a small probability of mutating from one phenotype to another. Cell migration via haptotaxis plays an important role in the simulated tumor's development. Cell migration is constrained by a cell's phenotype and available space on the lattice. Interactions between cells and their microenvironment produce different tumor morphologies and patterns of mutation: homogeneous TM promotes spherical, uniform tumors while heterogeneous TM favors fingered, irregular, invasive tumors. Cell phenotypes with lower cell-cell adhesion tend to be more aggressive than those with higher cell-cell adhesion.

Rejniak's hybrid model of avascular tumor growth (Rejniak, 2005) represents individual cells and their properties. It represents tumor tissue as a conglomerate of elastic cells satisfying Hooke's law and TM as an incompressible viscous fluid obeying the Navier-Stokes equation. The cells proliferate depending on the local concentration of substrate, which in turn evolves according to a reaction-diffusion equation. The morphology of the developing tumor depends on the local dynamics of growing cells that compete for space and substrate with their neighbors (Rejniak, 2005).

Several groups have developed GGH models of tumor growth, both of benign spherical morphologies (Stott et al., 1999; Drasdo and Höhme, 2003; Jiang et al., 2005) and of malignant fingered tumors (Turner and Sherratt, 2002; Turner et al., 2004b). The GGH simulations of fingered malignant tumors, with a population of adhesive tumor cells experiencing a haptotactic gradient due to secreted MDEs, demonstrated that cell adhesivity could influence the morphology of the invading front and that stronger haptotaxis promoted invasiveness (Turner and Sherratt, 2002; Turner et al., 2004b). In this paper we combine aspects of these previous models with specific extensions to study tumor-interface instabilities (Rejniak, 2005). For simplicity, we assume that the growth rate of tumor cells increases linearly with the local concentration of a single limiting substrate, with no concentration threshold for tumor cells to grow. In this case, the diffusion-limitation parameter, a dimensionless ratio of the tumor consumption rate to the substrate transport rate determines whether the tumor has a uniform or fingered margin, while the tumor-TM surface tension (see section 3.1) affects the detailed tumor morphology. We construct a 2D phase diagram showing the effects of these parameters on tumor morphology. Khain and Sander (Khain and Sander, 2006), and Macklin and Lowengrub (Macklin and Lowengrub, 2007), constructed a 2D phase diagram for different parameters for a continuum model of tumor growth. However, as far as we know, no phase diagram exists for a discrete cell model.

2 Mathematical Structure of the Tumor Model

Because of the complexity of tumor growth, all tumor simulations must make multiple simplifying assumptions and select a limited number of biological mechanisms to investigate. By treating cells phenomenologically we reduce the interactions of roughly 10⁵–10⁶ gene products to few behaviors (Merks and Glazier, 2005). Our cells are spatially extended and deformable (section 3.1), move (section 3.2), adhere to each other (section 3.1), consume substrate, grow at a rate proportional to the local substrate concentration, divide when their volume doubles (section 3.3), and secrete MDE (section 3.4).

Our choice of biological mechanisms generally follows that made in Anderson's HDC model (Anderson, 2005), with the important difference that our cells are extended, elastic and use a more natural representation of cell adhesion. We follow the HDC model because it translates easily into a GGH simulation, is well understood mathematically, provides a useful set of typical parameter values, produces simple and biologically-reasonable growth kinetics, and has resulted in numerous published papers which we can use as benchmarks. As in (Anderson, 2005), we model solid tumors before vascularization, i.e. without an established blood supply. Since we focus on the role of cell-cell adhesion and competition for nutrients at the tumor-TM interface where the tumor cells are alive and proliferating, we simplify Anderson's model (Anderson, 2005) by simulating single-cell-type tumors, omitting necrotic and quiescent cells which are essentially absent at the tumor-TM interface during early stages of fingering and thus not directly relevant to instability mechanisms. We may, if we wish, interpret nongrowing or very slow-growing cells as quiescent.

We use the GGH model (Graner and Glazier, 1992; Glazier and Graner, 1993; Glazier et al., 2007) (see section 3) to represent spatially-extended tumor cells rather than the HDC model's point cells (Anderson, 2005). As in (Anderson, 2005), we include three distinct fields: a TM field representing a homogenized version of the cells and ECM of the normal tissue surrounding the tumor, an MDE field produced by tumor cells, which degrades the TM field, and a substrate field representing the concentration of a substrate limiting tumor-cell growth. A set of coupled nonlinear PDEs models the tumor's interaction with fields (Anderson, 2005). In general, all interactions follow the law of mass-action, decay is first-order and diffusion constants are spatially uniform. MDE (denoted by m) degrades TM (denoted by f) according to (Stetler-Stevenson et al., 1996; Chambers and Matrisian, 1997) (equation (2) in (Anderson, 2005)):

$$\frac{\partial f}{\partial t}=-{\delta }_f\mathit{mf},$$ (1)

where δ_f is a positive constant. Degradation does not consume MDE. Tumor cells produce MDE at a constant rate S_m > 0 (the rate of MDE production per tumor cell); MDE then diffuses uniformly (equation (3) in (Anderson, 2005)):

$$\frac{\partial m}{\partial t}=D_m{\nabla }^{2}m+S_{m}N\left(\mathrm{x}\right),$$ (2)

where D_m > 0 is the diffusion constant of MDE. N(x) equals 1 inside tumor cells, otherwise it is 0. To model the transport of nutrients (glucose, oxygen, etc.) by the vasculature in surrounding normal tissue, TM produces substrate (denoted c̃) at a constant rate per unit density. The substrate diffuses and is consumed by the tumor cells at a constant rate per cell:

$$\frac{\partial \tilde{c}}{\partial t}=D_c{\nabla }^2\tilde{c}+S_{c}f-C_{c}N\left(\mathrm{x}\right),$$ (3)

where D_c, S_c and C_c are positive constants representing respectively the substrate-diffusion constant, the substrate-production rate per unit TM and the substrate-consumption rate per tumor cell. Our substrate-consumption rate C_c combines the uptake and decay rates of substrate, but is formally identical to equation (4) in (Anderson, 2005).

Since the production of substrate by TM occurs at a constant rate, we must keep the substrate concentration c̃ everywhere below a biological saturation value (or maximum solubility) in tissue c₀. The substrate concentration also cannot become negative, so to this equation we add the additional condition: 0 ≤ c̃. Dividing equation (3) by c₀ gives:

$$\frac{\partial c}{\partial t}=D_c{\nabla }^{2}c+ϴ(1-c)\frac{S_c}{c_0}f-ϴ\left(c\right)\frac{C_c}{c_0}N\left(\mathrm{x}\right),$$ (4)

where:

$$c=\frac{\tilde{c}}{c_0},$$ (5)

is the normalized substrate concentration and Θ is the Heaviside step function. The substrate-consumption rate for the normalized substrate field is:

$$k=\frac{C_c}{c_0}.$$ (6)

We now must keep c everywhere below 1. Anderson's model (Anderson, 2005) used the same constraint, although it did not state so explicilty. Otherwise equation (4) in (Anderson, 2005) would have yielded an exponential growth of the substrate concentration c, which did not occur. We also normalize and impose non-negativity conditions on m and f (Anderson, 2005). The initial conditions for our normalized fields are: c = 1, m = 0, and f = 1 everywhere.

In our recent GGH model of biofilm growth (Popławski et al., 2008) we showed that biofilm morphology depended mainly on a single parameter, the nondimensional ratio of the maximum biomass-growth rate to the maximum substrate-transport rate: the growth-group parameter G (Picioreanu et al., 1998a,b). This parameter is closely related to the growth number in (Dockery and Klapper, 2002). For our tumor growth simulations, we can rewrite G (equation (9) in (Popławski et al., 2008)), as a Diffusion-Limitation Parameter:

$$G=\frac{L^{2}g}{D_c{c}_0},$$ (7)

where L is the size of the simulation domain and g is the maximum specific growth rate (amount of new tumor produced per unit time per unit tumor). Substituting equation (6) into (7) gives:

$$G=\frac{L^2\mathit{gk}}{D_c{C}_c}.$$ (8)

In our simulations, we vary G by varying the normalized substrate-consumption rate k (which corresponds to varying the background substrate concentration c₀ for an unnormalized substrate field). We simulate growth of cells by increasing their volume V at a rate proportional to the local limiting-substrate concentration:

$$\frac{1}{V}\frac{\mathit{dV}}{\mathit{dt}}=\mathit{gc}.$$ (9)

So when c = 1, the specific growth rate $\frac{1}{V}\frac{\mathit{dV}}{\mathit{dt}}$ is maximal and equals g. Anderson's (Anderson, 2005) and Rejniak's (Rejniak, 2005) models used a substrate-concentration threshold, below which tumor cells became necrotic and stopped growing. Since we do not model necrosis (or quiescence), we do not need to introduce a threshold for tumor growth.

Equations (1), (2) and (4) govern the dynamics of the three fields that control the tumor's growth in our model. If we simplify our model by eliminating the fields f and m and requiring that the medium produce substrate, equation (3) reduces to the heat-conduction equation in directional solidification (Davis, 2001; Langer, 1980; Bechhoefer and Liebchaber, 1987; Saito et al., 1989):

$$\frac{\partial T}{\partial t}=D_T{\nabla }^{2}T+K\frac{\partial ∊}{\partial t},$$ (10)

in which the temperature T is replaced by the substrate concentration c̃ (with the opposite sign), the thermal conductivity D_T by the substrate diffusion constant D_c, the latent heat K by the consumption rate C_c (corresponding to G), and the time gradient of the volume fraction of the solid phase $∊,\frac{\partial ∊}{\partial t}$, is well approximated by N(x) if the consumption of substrate is significant only near the tumor-TM interface (which is valid in the transport-limited regime, see subsection 5.2) (Langer, 1980; Kobayashi, 1993). In directional solidification, the ability of diffusion to remove latent heat from the liquid-solid interface limits the growth of the solid. Analogously, as we will see later, the ability of diffusion to supply substrate limits the growth of the tumor. Crystalline boundary energy anisotropy in solidification (Davis, 2001) is equivalent to tumor-cell-TM surface tension in our simulations, γ.

3 GGH Methodology

Now that we have defined our mathematical model of tumor growth, we must translate it into a GGH simulation (Glazier et al., 2007). As in (Rejniak, 2005), and unlike many other hybrid models, we represent tumor cells as spatially-extended objects with variable shapes. Unlike Rejniak's force-based model (Rejniak, 2005), the GGH model uses an effective-energy formalism. Treating cells as extended, deformable objects allows us to investigate the role in tumor invasion of tumor-cell-tumor-cell and tumor-cell-TM adhesion, which are both significant in many types of biological pattern formation (Steinberg, 1963). As in these other models, we treat substrate, MDE and TM as continuous fields obeying appropriate PDEs.

All GGH models include Objects, Interaction Descriptions, Dynamics and Initial Conditions. Objects in a GGH model can be Generalized Cells or Fields. Generalized Cells are spatially-extended domains, which reside on a single Cell Lattice and in the current model represent either tumor cells or non-tumor tissue (Glazier et al., 2007; Balter et al., 2007). Generalized Cells carry a set of state descriptors, e.g., cells' target volumes and volumes at which mitosis occurs.

Fields are continuously-variable concentrations, each of which resides on its own lattice. Our model uses Fields to represent diffusing MDE and substrate, and nondiffusing TM, evolving according to equations (1), (2) and (3) (see also section 3.4). Interaction Descriptions and Dynamics define how the various Objects behave both biologically and physically. For Generalized Cells, these behaviors and interactions are embodied primarily in the Effective Energy, which determines a Generalized Cell's shape, motility, adhesion and response to extracellular signals (Glazier et al., 2007). The Effective Energy creates forces which drive most pattern dynamics (Steinberg, 1963; Graner and Glazier, 1992; Glazier and Graner, 1993; Glazier et al., 2007).

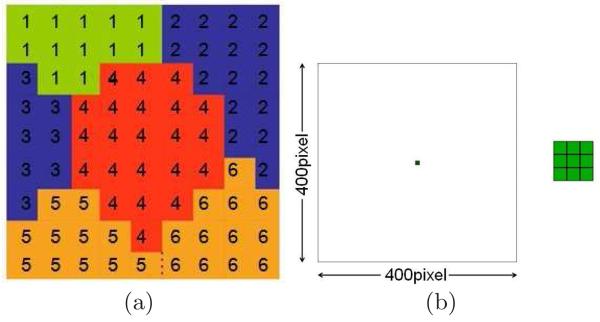
Mathematically, N spatially-extended Generalized Cells indexed by σ lie on a 2D, fourth-neighbor square Cell Lattice; the value at a Cell-Lattice site (pixel) i is σ if this site lies in Generalized Cell σ. A collection of Cell-Lattice sites with the same index represents a Generalized Cell, as shown in Figure 1, subfigure (a). Each Generalized Cell has an associated Generalized-Cell type τ in our model, TM for tissue medium and t for tumor cell. Auxiliary Equations describe how each Generalized Cell's absorption and secretion of diffusing chemicals change the Generalized Cells' internal states and how Generalized Cells divide (Glazier et al., 2007). The Initial Condition specifies the initial configurations of Generalized Cells and Fields, and Generalized Cells' internal states.

Fig. 1.

(a) Detail of a typical GGH Cell-Lattice configuration in 2D showing portions of six Generalized Cells. Each Generalized Cell is a collection of Cell-Lattice sites (squares) with the same index value. The colors indicate Generalized-Cell types. The number of Cell-Lattice sites in a Generalized Cell is its volume and the number of links along its boundary (interfaces with sites containing other indices) is its surface area. (b) The initial 2D configuration for all our simulations: nine tumor cells situated at the center of the simulation domain. The space outside the cells represents normal tissue with an initially homogeneous density and concentration of substrate (see subsection 3.4). The size of the Cell Lattice corresponds to 16 mm. The inset shows an enlargement of the tumor cells.

3.1 Effective Energy

The Effective Energy ε in our tumor simulations includes three terms (Graner and Glazier, 1992; Glazier and Graner, 1993; Glazier et al., 2007):

$$\begin{array}{cc}\hfill & ℰ=\underset{\mathbf{i},\mathbf{j}\text{neighbors}}{\Sigma }J(\tau \left(\sigma \left(\mathbf{i}\right)\right),\tau \left(\sigma \left(\mathbf{j}\right)\right))(1-\delta (\sigma \left(\mathbf{i}\right),\sigma \left(\mathbf{j}\right)))\hfill \\ \hfill & +\underset{\sigma }{\Sigma }{\lambda }_{\mathrm{V}}\left(\tau \left(\sigma \right)\right){(V\left(\sigma \right)-V_{\mathrm{t}}\left(\tau \left(\sigma \right)\right))}^2+\underset{\sigma }{\Sigma }{\lambda }_{\mathrm{S}}\left(\tau \right){(S\left(\sigma \right)-S_{\mathrm{t}}\left(\tau \left(\sigma \right)\right))}^2.\hfill \end{array}$$ (11)

The first term describes the surface adhesion between Generalized Cells (i.e. between tumor cells and tumor cells, and between tumor cells and TM) in terms of symmetric Contact Energies J(τ,τ′) = J(τ,τ′) (Graner and Glazier, 1992; Glazier and Graner, 1993; Glazier et al., 2007). For adhesive interactions J < 0 and for repulsive J > 0. Smaller J corresponds to greater adhesivity. We use a fourth-neighbor interaction range to calculate the Contact Energy, which reduces Cell-Lattice anisotropy effects (Holm et al., 1991). The units of J are energy/unit boundary length in 2D. The use of fourth-order neighbors means that each unit of nearest-neighbor boundary contributes multiple times to the contact energy. Since this rescaling is the same for both tumor-cell-tumor-cell and tumor-cell-TM contact, changing the range does not change the sign of the surface tension, but it does affect the relative sizes of the three Effective Energy terms and we need to rescale T, λ_V and λ_S appropriately to produce an equivalent simulation.

We know that filopodium or pseudopodium extension is a major component of cell migration. Because filopodia are much smaller than 1 Cell-Lattice site in our simulations (see subsection 3.3), we cannot model them explicitly. The GGH model, however, includes filopodia implicitly via the interaction range of the Contact Energies J. The length of filopodia in our simulations using fourth-neighbor interaction equals 4 pixels or 160 μm. We also implicitly include pseudopodia' exploration of the microenvironment via the fluctuation amplitude T (see subsection 3.2).

The second term models the Generalized Cells as ideal gas ‘balloons’ of constant mass and prevents Generalized-Cell disappearance; V (σ) is the volume in Cell-Lattice sites of Generalized Cell σ, V_t its Target Volume, and λ_V(τ) its inverse compressibility. Comparing this Volume-Constraint term to the elastic energy of an isotropic medium (Landau and Lifshitz, 1986) allows us to associate λ_V with the modulus of hydrostatic compressibility $K:{\lambda }_V=\frac{K}{2V_t}$; similarly for λ_S. The third term represents the elasticity of a cell membrane; S(σ) is the surface area of Generalized Cell σ, S_t its Target Surface Area, and λ_S(τ) its inverse membrane elasticity (Chaturvedi et al., 2003; Izaguirre et al., 2004). We model TM as one unconstrained Generalized Cell: λ_V(TM) = λ_S(TM) = 0. The first two terms in equation (11) play competing roles: the Contact-Energy term shrinks Generalized Cells, while the Volume Constraint imposes the condition V ∼ V_t. As a result, the equilibrium volume of Generalized Cells is somewhat smaller than V_t; the larger λ_V, the smaller the difference between the average V and V_t.

We can define the surface tension γ(t, TM) in terms of the Contact Energies J (Graner and Glazier, 1992; Glazier and Graner, 1993):

$$\gamma (t,\mathit{TM})\equiv J(t,\mathit{TM})-\frac{J(t,t)}{2}.$$ (12)

The surface tension controls the tendency of tumor cells to disperse or cluster. If γ(t, TM) ≥ γc, where $\gamma c=\frac{T}{20}$ is of the order of the approximate critical surface tension below which cell dissociation occurs (the factor of 20 is the number of neighbors in the 2D fourth-order neighborhood) and T is a parameter characterizing the intrinsic cell motility (Mombach et al., 1995) (see subsection 3.2), tumor cells will tend to cluster together; otherwise, they will tend to separate and migrate through the surrounding tissue (Glazier and Graner, 1993). The surface tension depends only on the difference between J(t, t) and J(t, TM); thus we can have a negative surface tension for strongly cohesive tumor cells, if tumor-cell-TM adhesivity is very strong, or positive surface tension for tumor cells for small tumor-cell-tumor-cell cohesion, if tumor-cell-TM adhesion is even smaller. For notational convenience, we write γ in place of γ(t, TM).

3.2 Dynamics and cell motility

To model cytoskeletally-driven cell motility, the Cell Lattice evolves through attempts by Generalized Cells to extend their boundaries into neighboring Cell-Lattice sites, slightly displacing the Generalized Cells which currently occupy those sites. These attempted extensions change the Effective Energy, and we accept each one with a probability that depends on the change according to a Boltzmann Acceptance Function (Glazier et al., 2007). Thus, the Cell Lattice evolves with displacement velocities proportional to the gradient of the total Effective Energy (Graner and Glazier, 1992; Glazier and Graner, 1993) as defined in equation (11) (e.g., variations in Contact Energy are the driving mechanism of biological cell sorting (Steinberg, 1963; Beysens et al., 2000)). Our rearrangement dynamics is relaxational Monte-Carlo-Boltzmann-Metropolis dynamics (Graner and Glazier, 1992; Glazier and Graner, 1993; Glazier et al., 2007; Metropolis et al., 1953). At each step we randomly select a Cell-Lattice site i and attempt to change its index from σ(i) to the index σ′ = σ(i′) of a Cell-Lattice site i′ randomly chosen in its fourth-order neighborhood. We accept the change with a probability P:

$$P(\sigma \left(\mathbf{i}\right)\to {\sigma }^{\prime }\left(\mathbf{i}\right))=\theta \left(\Delta ℰ\right)e^{-\Delta ℰ∕\mathit{kT}}+\theta (-\Delta ℰ),$$ (13)

where Δε is the difference in Effective Energy produced by the change and T represents the cell's intrinsic cytoskelletally-driven motility. One Monte Carlo Step (MCS) corresponds to n index-change attempts, where n is the total number of Cell-Lattice sites.

Since we do not model explicitly haptotactic repulsion and pressure on the tumor cells from the surrounding normal tissue, tumor cells move freely, which is realistic only for tumors developing in environments that do not constrain tumor-cell motility, e.g., gliomas (Frieboes et al., 2007; Mariani et al., 2001). However, the tumor-TM surface tension creates an effective hydrostatic pressure on the tumor. While not perfectly identical to a tumor growing in an elastic or viscoelastic tissue, increasing the surface tension reproduces many of the effects of increasing the rigidity of an explicitly-modeled external tissue. We could thus create a rough simulation of tumors growing in environments that constrain tumor-cell motility, if we increased the tumor-TM surface tension to produce a similar hydrostatic pressure on the growing tumor. We emphasize that the Cell Lattice evolves to minimize the total Effective Energy locally and on average at each displacement attempt, but not globally (over the time of simulation). As a tumor grows, its Effective Energy increases because the Contact Energies for tumor cells are positive. Our average dynamics is equivalent to solving the equations for the forces and resulting displacements at each MCS, and produces the same patterns.

3.3 Cell size and growth

Figure 1, subfigure (b) shows the initial 2D configuration of our simulations. The dimension of the domain in pixels is 400 × 400. We are free to assign the length scale, which, with the diffusion constant of the tumor cells, fixes the time scale in the simulation.⁴ In our simulations, each simulated tumor cell (Generalized Cell of type t) initially occupies a 3 × 3 (in pixels) square. We set the size of 1 pixel to 40 μm, so the size of the simulation domain corresponds to 16 mm. Therefore the size of 1 simulated tumor cell is 120 μm, which is about 5 times greater than the size of real tumor cells (Anderson, 2005; Melicow, 1982; Folkman and Hochberg, 1973), so 1 simulated tumor cell represents 25 real tumor cells. Since the size of tumor cells is much smaller than the penetration and capillary lengths (see section 5.3), the cell size is not critical in our simulations. However, coarse-graining the cells in this way greatly speeds the simulation. Note that since G is dimensionless, its value is independent of our choice of length scale.

We simulate growth of tumor cells by increasing their V_t at a rate proportional to the local limiting-substrate concentration c (Popławski et al., 2007):

$$\frac{1}{V_{\mathrm{t}}}\frac{{\mathit{dV}}_{\mathrm{t}}}{\mathit{dt}}=\mathit{gc},$$ (14)

where g is a growth rate, effectively implementing equation (9) because V ≈ V_t. We measure the concentration c at the cell's center of mass, which is equivalent, because of the fast diffusion of limiting substrate, to the average c over the cell's surface. The initial Target Volume for tumor cells ${V_t}^0=9$. When a tumor cell reaches the doubling volume $V_d=2{V_t}^0=18$, it divides and splits along a random axis into two tumor cells with Target Volumes ${V_t}^0$ (Balter et al., 2007).⁵ To prevent growing cells from changing shape, we adjust S_t so that the nondimensional ratio $S_t{V_t}^{-1∕2}$ remains constant, i.e. $S_t=\sqrt{\frac{V_t}{{V_t}^0}}{S}_t^0$. We set $S_t^0=3$, which produces roughly spherical cells.

3.4 Fields

We define three Fields: 1) a diffusible substrate whose concentration c locally determines the rate of potential cell growth, 2) a diffusing MDE whose concentration m represents all of the material-degrading components the tumor cells secrete, 3) a nondiffusing TM whose concentration f represents the normal tissue surrounding the tumor. These fields are nonexclusive, i.e. they can have nonzero values at each point simultaneously and co-occupy space with cells. The rate of cell growth within a tumor depends on many factors, but in almost all cases, the rate of cell growth depends on the availability of a few key limiting factors or substrates, whose identity depends on tumor type. The HDC model of Anderson assumes oxygen to be the single limiting factor. However, the limiting factor is more frequently glucose in anaerobic tumors.

Tumor cells produce MDE at a constant rate at the cell's center of mass. Tumor cells absorb substrate at their respective centers of mass. Substrate and MDE diffuse uniformly on their Field lattices using a forward-Euler algorithm run N′ times per MCS (one run of the diffusion solver defines a Monte-Carlo substep), where N′ depends on the time and distance scales we have chosen, and the diffusion constants. If 1 pixel corresponds to a meters and 1 MCS to b seconds then, for example, D_c (in pixel²/MCS) relates to the physical diffusion constant of substrate D (in m²/s) via: $D_c=\frac{b}{a^2}D$. In the GGH model we can use either no-flux or periodic boundary conditions at each edge of the simulation domain. The GGH model also allows us to impose a no-flux condition at the boundaries of particular Generalized Cells. In our simulations we use no-flux boundary conditions at all Field edges.

4 Parameter Values

Choosing parameter values for biological simulations is always somewhat problematic, since we lack experimental measurements for many of them. Fortunately, the properties of our tumor model are quite robust to substantial variations in many parameters, which we then choose in a range which exhibits the general class of behavior we observe experimentally. The motility T rescales the Effective Energy, i.e. the Contact-Energy coefficients J(τ, τ′) and the constraint coefficients λ_V and λ_S. In the GGH model, the dynamics and patterns therefore depend not on the absolute values of Contact Energies and constraint strengths, but on these values divided by T. To the best of our knowledge, no one has measured the adhesion parameters for a tumor cell line, although measurement would be possible in a parallel-plate compression experiment (Beysens et al., 2000; Foty et al., 1994, 1996; Forgacs et al., 1998).

Because the Contact Energy between two Cell-Lattice sites that belong to the same Generalized Cell is defined to be zero, we set all J(τ, τ′) positive to prevent Generalized Cells from dissociating. Since MDE diffusion is very slow and TM degradation by MDE is strong, f ∼ 0 at all pixels occupied by tumor cells and f ∼ 1 at all pixels occupied by TM. We set T = 25 (Glazier et al., 2007). We require γ ≥ 0 to keep the tumor cells from floating off into the TM spontaneously. We choose the range of Cell-Adhesion coefficients (as related to T which sets the Effective-Energy scale) following previous papers that used the GGH model (Glazier et al., 2007). Our simulations use J(TM, TM) = 0 and J(t, TM) = 8. We vary J(t, t) from 4, for which γ = 6, to 16, for which γ = 0. For γ > 6, the simulated morphologies do not differ much from those for γ = 6. We set λ_V = 20 and λ_S = 2, which prevents Generalized Cells from nonbiological disappearing or freezing.

The experimental diffusion constant D_t for tumor cells in human breast tumors (Kumar et al., 2006) and brain tumors, such as glioblastomas (Bray, 1992; Burgess et al., 1997; Sander and Deisboeck, 2002), is on the order of 10⁻13 m²s⁻1. We take D_t = 1.7 × 10⁻¹³ m²s⁻1 (Burgess et al., 1997). The diffusion constant for our simulated tumor cells is about 0.01 pixel²MCS⁻¹, so 1000 MCS approximately corresponds to 1 day. We take D = 2.5 × 10⁻11 m²s⁻1, which is on the order of the diffusion constant for glucose in normal connective tissue (Chapman and Pardy, 1972; Jain, 1987; Casciari et al., 1988). Therefore D_c = 1.5 pixel²MCS⁻¹.⁶

Anderson estimated his model parameters (Anderson, 2005)) (equations (1), (2) and (3)) from the available experimental data (Anderson et al., 2000; Calabresi and Schein, 1993; Bray, 1992; Terranova et al., 1985; Casciari et al., 1992; Johansson et al., 2000; Sherwood, 2001; Freyer et al., 1984). We adopt these parameters, translating them into GGH units. The background substrate concentration within the tissue is about 6.7×10⁻¹² M m⁻³ (Sherwood, 2001), and we take this value as the default c₀ that we use in the normalization of the substrate Field. Tumor cells consume substrate at a rate C_c of 6.25 × 10⁻¹⁷ M cell⁻¹s⁻¹ (Casciari et al., 1992). Thus the normalized consumption-rate k (per pixel²) in equation (6) equals 0.054 MCS⁻¹. We denote this default value k₀. From (Anderson, 2005) we also set: δ_f = 0.45 MCS⁻¹, D_m = 0.00015 pixel²MCS⁻¹, S_m = 0.09 MCS⁻¹ and S_c = 0.045 MCS⁻¹. The cell-cycle period for the fastest-growing human tumor cells is about 8 h (Calabresi and Schein, 1993) so we use this rate for cells experiencing the maximum substrate concentration c₀; integrating equation (14) over one cell-cycle period using the normalized c₀ = 1 gives g = 0.002 MCS⁻¹. Equation (7) gives, for k = k₀, G = G₀≅210.

In this paper, we examine the impact of changing the cell metabolism which changes the diffusion-limitation parameter G and the tumor-TM surface tension γ on tumor morphology. As we will see in the next section, G determines whether the growing tumor has a smooth or fingered interface, i.e. whether its morphology is uniform or invasive. We vary k from 0.01 to 0.06, corresponding approximately to G from 40 to 240, which covers the complete range of possible morphologies. Smaller values of G produce the same patterns as G = 40 and values of G > 240 prevent tumor-cell proliferation. Table 1 lists our model parameters.

Table 1.

List of model parameters in our simulations of tumor growth.

Diffusion-limitation parameter G	40–240
Tumor-TM surface tension γ	0–6
Tumor-TM Contact Energy	8
Tumor-cell motility T	25
Tumor-cell doubling volume Vd	18
Tumor inverse compressibility λV	20
Tumor inverse membrane elasticity λS	2
Tumor-cell shape parameter $S_t^0$	3
Substrate diffusion constant Dc	1.5 pixel2 MCS−1
TM degradation rate δf	0.45 MCS−1
MDE diffusion constant Dm	0.00015 pixel2 MCS−1
MDE production rate Sm	0.09 MCS−1
Substrate production rate Sc	0.045 MCS−1
Tumor-cell growth rate g	0.002 MCS−1

5 Results

In this section we consider the impact of varying G and γ (γ(t, TM) in equation (12)). To describe tumor morphologies quantitatively, we use the circularity P, defined in 2D as:

$$P=4\pi \frac{\text{surface area}}{{\text{perimeter}}^2},$$ (15)

and the fractal dimension D_f of the boundary, determined by box counting (Dubuc et al., 1989). P = 1 for a perfect circle, while P approaching 0 indicates an increasingly elongated polygon. In our simulations, Cell-Lattice anisotropy keeps P <̃0.7. In 2D, D_f = 1 for a perfectly smooth boundary and D_f ∼ 2 for an infinitely rough boundary.

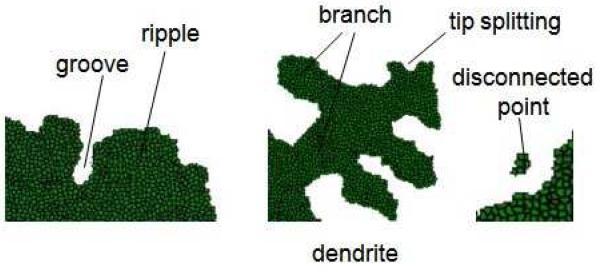
Since our initial tumor is compact, we look to see how P changes in time. If P decreases by more than 10%, we define the structure as branched, otherwise it is unbranched (U). Following Refs. (Brener et al., 1992; Stalder and Bilgram, 2001) we classify branched morphologies as either compact (C) or fractal (F), and either dendritic (D) or seaweed-like (S). We use the fractal dimension D_f (D_f < 2 in 2D) to discriminate between fractal and compact structures, setting a cutoff D_f = 1.6 between fractal and compact structures. We call structures with pronounced orientational order dendritic, and structures without apparent orientational order seaweed-like. The fractal seaweed-like morphology (FS) is DLA-like (equivalent to a structure produced by diffusion-limited aggregation) (Witten and Sander, 1983). For unbranched tumors, the distinction between dendrites and seaweeds loses its meaning. Figure 2 shows the terminology we use in this paper to describe the morphology of simulated tumors.

Fig. 2.

Terminology describing the morphology of simulated tumors.

5.1 Growth-limited regime

Small G corresponds to a growth-limited regime (Popławski et al., 2008). The substrate penetrates most of the tumor and reaches most cells. We begin with G = 40. In this case, the simulated tumors are dense, fast-growing and spherical (U). Figure 3 shows the time evolution of a simulated tumor for a high tumor-TM surface tension γ = 6. For high γ we expect simulated tumors to be compact. Figure 4 shows tumor morphology for G = 40 for a low surface tension γ = 0. The simulated tumor remains spherical (U).

Fig. 3.

Tumor growth in a 2D simulation with G = 40 and γ = 6. See text for other parameter values. The surface of the developing spherical tumor is smooth - U.

Fig. 4.

Tumor growth in a 2D simulation with G = 40 and γ = 0. See text for other parameter values. The surface of the developing spherical tumor is smooth, as in Figure 3 - U.

Larger G slows the growth of the tumor (since the local substrate concentration decreases in the presence of tumor cells) and produces a more irregular (grooved) tumor-TM interface. Figure 5 shows the time evolution of a simulated tumor with G = 80 for a high surface tension γ = 6 (CS). Figure 6 shows the corresponding tumor morphology with G = 80 for a low surface tension γ = 0. The surface of the developing tumor is rougher than for γ = 6 (CS).

Fig. 5.

Tumor growth in a 2D simulation with G = 80 and γ = 6. See text for other parameter values. The surface of the developing compact tumor is grooved - CS.

Fig. 6.

Tumor growth in a 2D simulation with G = 80 and γ = 0. See text for other parameter values. The surface of the developing tumor is grooved and slightly more irregular than that in Figure 5 - CS.

As we increase G, diffusing substrate penetrates fewer cell diameters past the surface layer of the tumor. Initially, substrate is present throughout the tumor, which grows in all directions. As the tumor grows, its cells consume substrate and the substrate concentration develops a gradient, increasing in the radial direction away from the tumor centroid. Locally, cells near the tumor surface in protruding regions experience higher concentrations of substrate and hence grow faster than others. These cells proliferate more quickly, while the cells in the narrow valleys, where the interface between the tumor and TM lags significantly behind the furthest local radial position of the tumor, experience low concentrations of substrate and slow their growth. Figure 7 shows the time evolution of a simulated tumor with G = 120 for a high surface tension γ = 6 (CD). Figure 8 shows tumor morphology for G = 120 for a low surface tension γ = 0. The structure is highly branched (CS). Figures 3-8 show that while the tumor-TM surface tension does not affect the overall morphology significantly for low G, the morphology becomes more sensitive to surface tension for higher G.

Fig. 7.

Tumor growth in a 2D simulation with G = 120 and γ = 6. See text for other parameter values. The surface of the developing tumor produces thick fingers with narrow valleys - CD.

Fig. 8.

Tumor growth in a 2D simulation with G = 120 and γ = 0. See text for other parameter values. The surface of the developing tumor is much more branched than that in Figure 7 - CS.

5.2 Transport-limited regime

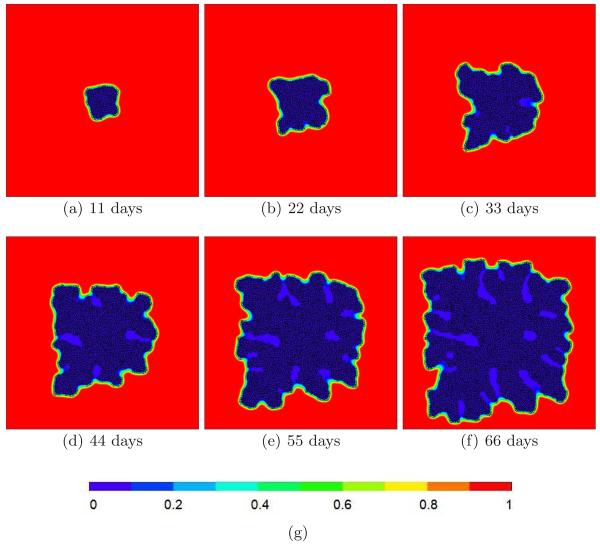
Large G corresponds to a transport-limited regime (Popłlawski et al., 2008). The substrate penetrates only a short distance into the tumor so the tumor grows more slowly than for smaller values of G. Figure 9 shows the time evolution of a simulated tumor with G = 160 for a high surface tension γ = 6. The grooves are wider and deeper than for lower values of G and the structure of the tumor becomes compact and dendritic (CD). Figure 10 shows the corresponding substrate concentrations, indicating the role of the substrate in the fingering instability. Figure 11 shows tumor morphology with G = 160 for a low surface tension, γ = 0. For low surface tensions we expect less compact structures with more branches. Instead of the dendritic pattern that forms at high surface tensions, the simulated tumor seaweed is DLA-like (FS). The effect of surface tension on morphology is dramatic for large G.

Fig. 9.

Tumor growth in a 2D simulation with G = 160 and γ = 6. See text for other parameter values. The developing tumor produces thinner fingers with deep valleys, approaching a dendritic morphology - CD.

Fig. 10.

(a)–(f) Substrate concentrations in a 2D simulation with G = 160 and γ = 6. See text for other parameter values. The substrate only penetrates a thin layer of the tumor, producing a fingering instability. (g) Color code for substrate concentration.

Fig. 11.

Tumor growth in a 2D simulation with G = 160 and γ = 0. See text for other parameter values. The developing seaweed-like or DLA-like tumor produces numerous thin branches - FS.

At G = 200 (which is near the value used by Anderson in (Anderson, 2005)) for a high surface tension, γ = 6, the availability of nutrients is so limited that cell proliferation nearly stops, and the simulated tumor forms a squared-off dendrite (Figure 12) (CD). The width of the dendritic spines does not increase much as we increase G. Figure 13 shows tumor morphology at G = 200 for a low surface tension, γ = 0. The simulated tumor is DLA-like (FS). Some branches detach from the core of the tumor, thus becoming potential new centers of growth. Such a mechanism can enhance tumor invasion and lead to metastatis. Some single cells also disperse into the TM.

Fig. 12.

Tumor growth in a 2D simulation with G = 200 and γ = 6. See text for other parameter values. The developing tumor has a square dendritic structure - CD.

Fig. 13.

Tumor growth in a 2D simulation with G = 200 and γ = 0. See text for other parameter values. The developing seaweed-like or DLA-like tumor produces thin branches that detach from the backbone of the tumor - FS.

At G = 240 for a high surface tension, γ = 6, so many cells stop dividing that some branches of the dendritic tumor stop growing, as in Figure 14 (CD). Figure 15 shows tumor morphology at G = 240 for a low surface tension, γ = 0. Again, a DLA-like tumor forms (FS). The smaller the tumor-TM surface tension, γ, the faster the growth of the tumor, because for large G, tumor cells must diffuse to find substrate to maintain their growth rather than having substrate diffuse to reach them. The smaller γ, the larger the diffusion coefficient for the tumor cells (Turner et al., 2004a).

Fig. 14.

Tumor growth in a 2D simulation with G = 240 and γ = 6. See text for other parameter values. The developing tumor has a truncated square dendritic structure - CD.

Fig. 15.

Tumor growth in a 2D simulation with G = 240 and γ = 0. See text for other parameter values. The developing seaweed-like or DLA-like tumor produces thin branches that detach from the backbone of the tumor - FS.

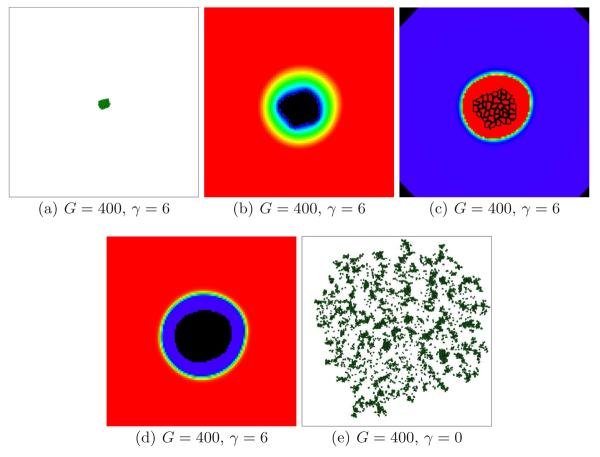
Figure 16, subfigure (a) shows a simulated tumor with G = 400 and γ = 6. Subfigure (b) shows that the substrate concentration even near the tumor-TM interface is close to zero, so the tumor effectively stops growing (tumor cells become quiescent). Subfigures (c) and (d) show the corresponding MDE and TM Fields. The tumor occupies a region with a high concentration of MDE that has degraded all the TM Field. TM far from the tumor still produces substrate, but the substrate is essentially exhausted at the tumor surface. Subfigure (e) shows a simulated tumor with G = 400 and γ = 0. The lack of surface tension enhances spreading of the tumor cells, so the tumor grows continuously. This result agrees with experiments showing that less adhesive tumors are more invasive (Christofori, 2006).

Fig. 16.

(a) Under-developed tumor in a 2D simulation with G = 400 and γ = 6 after 150 days. See text for other parameter values. (b) The enlarged tumor from subfigure (a) and the substrate concentration c near the tumor-TM interface. Black - c = 0, red - c = 1. (c) The MDE concentration m. (d) The TM concentration f. (e) Dispersing tumor in a 2D simulation with G = 400 and γ = 0 after 120 days. See text for other parameter values.

5.3 Phase diagram for simulated morphologies

In Figure 17 we summarize the tumor morphologies for different values of G and γ at the moment when the tumor reaches the size of the simulation domain ( 16 ∼mm). For small G the substrate reaches most cells, which grow in all directions, no valleys form and the tumor-TM interface remains smooth. As we increase G, the substrate penetrates less deeply into the tumor. Cells near the tumor surface experience higher concentrations of substrate and proliferate more quickly, producing fingers, while the space between fingers fills slowly or not at all with new cells. Thus the competition for substrate between tumor cells results in a fingering instability (Cristini et al., 2003; Moore et al., 2002; Miura and Shiota, 2002; Hartmann and Miura, 2006) which generates a fingered tumor morphology.

Fig. 17.

Tumor morphologies as a function of γ and G (see text for other parameter values), observed when the simulated tumor reaches the size of the simulation domain (∼16 mm). First row - γ = 6, second - γ = 4, third - γ = 2, fourth - γ = 0. First column - G = 40, second - G = 80, third - G = 120, fourth - G = 160, fifth - G = 200, sixth - G = 240.

We find that the tumor-TM surface tension does not affect tumor morphologies significantly for low G. In this regime, simulated tumors are unbranched and spherical (G = 40, Figure 17, subfigures: (a), (g), (m), and (s)), or rippled with no tip splitting, i.e. compact and seaweed-like (CS) (G = 80, Figure 17, subfigures: (b), (h), (n), and (t)). The morphology becomes more sensitive to γ at higher G (G = 120, 160, 200, and 240), when the simulated tumors are branched. At high surface tensions (γ = 4 and γ = 6), the branched tumor becomes compact and dendritic (CD) (Figure 17, subfigures: (c), (d), (e), (f), (i), (j), (k), and (l)). At intermediate surface tensions (γ = 2), the branched tumor is CS (Figure 17, subfigure (o)), or becomes fractal and dendritic (FD) (Figure 17, subfigures: (p), (q), and (r)). Finally, at low surface tensions (γ = 0), the tumor is CS (Figure 17, subfigure (u)), or fractal and seaweed-like (FS or DLA-like) (Figure 17, subfigures: (v), (w), and (x)). We produce DLA-like structures, observed in gliomas, because our model lacks excluded-volume haptorepulsion.

The tumors in Figure 17 are connected, except for subfigures (w) and (x), where they divide into many disconnected parts. The detachment of these parts results from the lack of tumor-TM surface tension and a lower spatial density of tumor cells, so the disconnected cells do not reconnect. Figure 17, subfigure (l) has one disconnected branch. This branch grew from a single cell that had detached from the rest of the tumor and reached higher concentrations of substrate.

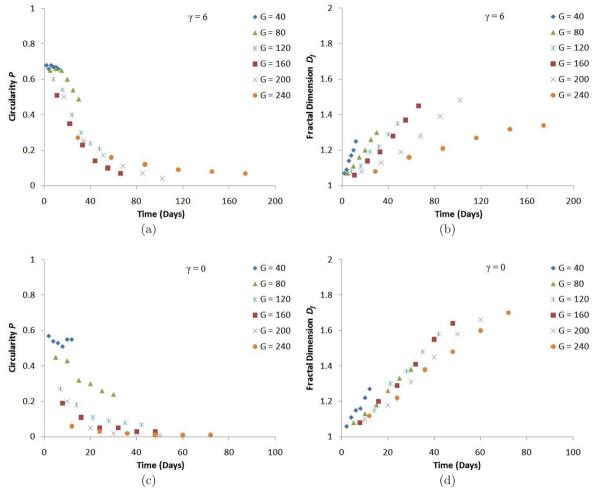
For our simulated tumor morphologies in Figure 17, the circularity P increases with surface tension γ, and decreases with increasing G. Fractal dimension D_f decreases as γ increases, and increases with G (subfigures (f) and (l) deviate from the general behavior because the growth of the structures is truncated). Figure 18 shows that P decreases in time (except for G = 40 where it remains roughly constant) while D_f increases. These dependencies of P and D_f are consistent with our observation that competition for substrate favors branching instabilities while surface tension stabilizes the tumor-TM interface. We also observe that D_f increases in time in a nearly linear fashion, while the decrease of P saturates. Thus the slope $\frac{{\mathit{dD}}_f}{\mathit{dt}}$ is approximately constant for each simulation and depends on G and γ, and thus is a satisfactory way to characterize tumor morphology dynamics. Table 2 shows this dependence for γ = 6 and γ = 0.

Fig. 18.

(a) Circularity P as a function of time for 2D simulations of tumor growth with γ = 6. (b) Fractal dimension D_f as a function of time for 2D simulations of tumor growth with γ = 6. (c) Circularity P as a function of time for 2D simulations of tumor growth with γ = 0. (d) Fractal dimension D_f as a function of time for 2D simulations of tumor growth with γ = 0.

Table 2.

The dependence of the slope $\frac{{\mathit{dD}}_f}{\mathit{dt}}$ (in MCS⁻¹) on G and γ.

G	40	80	120	160	200	240
γ = 6	0.018	0.009	0.007	0.007	0.005	0.002
γ = 0	0.020	0.013	0.015	0.014	0.012	0.010

We mentioned in section 2 that our model is similar to that for directional solidification (Davis, 2001; Langer, 1980; Bechhoefer and Liebchaber, 1987; Saito et al., 1989; Kobayashi, 1993). Thus we expect that the mechanism of the dendrite-to-seaweed transition in directional solidification (Ludwig, 1999; Pocheau and Georgelin, 2006) will apply to our model of tumor growth. A necesssary condition for the formation of dendrites in directional solidification (Glicksman et al., 2007) is a sufficiently large anisotropy of the surface free energy (surface tension) of the solid-liquid interface (Stalder and Bilgram, 2001; Langer, 1987; Müller-Krumbhaar et al., 1991). The simulated structures are dendritic because of destabilization of the lateral surfaces of the principal branch near its tip. The condition for solidification is a low undercooling, which for a constant temperature of the liquid far from the solid (corresponding to a constant substrate concentration far from the growing tumor) is equivalent to a large latent heat K (Kobayashi, 1993). For large K, tip splitting occurs and branches compete with each other to remove heat, because faster-growing branches suppress the growth of slower branches by thickening or sprouting side branches (Kobayashi, 1993).

In our simulations, dendrites form for high tumor-TM surface tensions and high G. We already know that G in our model corresponds to the latent heat in directional solidification (see section 2). Since the GGH Cell Lattice is weakly anisotropic, surface-tension anisotropy is proportional to γ. Therefore surface-tension anisotropy plus competition for substrate generates dendritic structures in the GGH model. For low tumor-TM surface tensions, the surface-tension anisotropy is also low, so the simulated patterns are seaweed-like (Kobayashi, 1993).

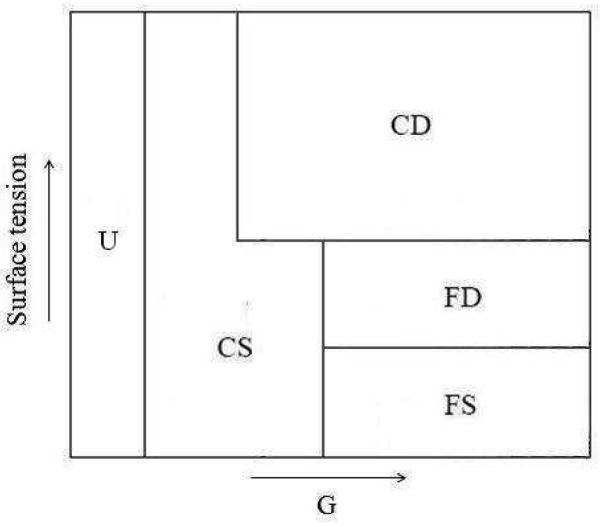
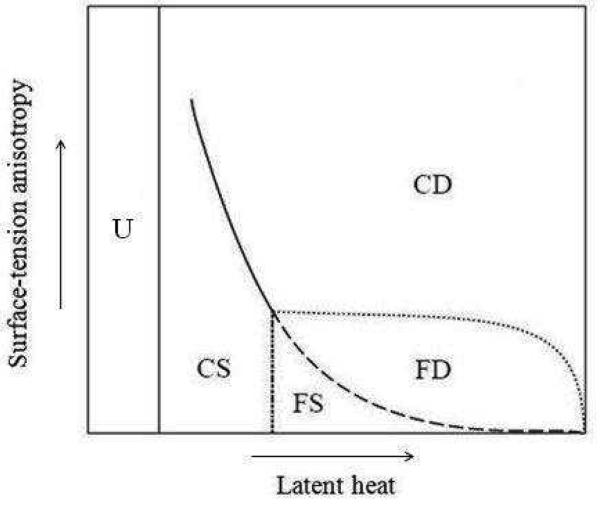
Overall, that structures in directional solidification are more sensitive to surface-energy anisotropy for large latent heats, corresponds to our observation that simulated tumor morphologies are more sensitive to surface tension for larger G. Therefore Figure 17 agrees with the results in (Kobayashi, 1993) and suggests that the mechanism responsible for the observed tumor morphologies is the same as the mechanism responsible for directional solidification morphologies. To show this agreement, we sketch in Figure 19 a phase diagram displaying how the four branched morphological combinations, CS, CD, FD and FS, and the unbranched region U relate to G and γ. Comparing our diagram to the phase diagram for directional solidification, adapted from (Brener et al., 1992; Stalder and Bilgram, 2001) (Figure 20), makes clear that the latent heat and the surface-tension anisotropy in directional solidification correspond to G and γ, respectively, in our simulated tumor growth.

Fig. 19.

Schematic phase diagram for GGH simulations of tumor growth showing five regions: unbranched structures (U), compact seaweeds (CS), compact dendrites (CD), fractal dendrites (FD), and fractal seaweeds (FS), as a function of G and γ.

Fig. 20.

Schematic phase diagram for directional solidification showing five regions: unbranched structures (U), compact seaweeds (CS), compact dendrites (CD), fractal dendrites (FD), and fractal seaweeds (FS), as a function of latent heat and surface-tension anisotropy. Adapted from (Brener et al., 1992; Stalder and Bilgram, 2001).

5.4 Effects of other parameters

In the previous sections we showed that the nondimensional diffusion-limitation parameter G and the tumor-TM surface tension γ greatly affected simulated tumor morphologies. We must also check how other parameters affect patterning of growing tumors. For example, different combinations of J can give the same value of γ. Figure 21 shows tumor morphologies, circularity and fractal dimension at the moment when the tumor reaches the size of the simulation domain, for: λ_V = 40 (b), λ_V = 10 (c), λ_S = 1 (d), all for γ = 6 and G = 160, achieved using a different combination of contact energies: J(m, t) = J(t, t) = 12 (e); all other parameters as in Figure 9. Panel (a) shows the morphology for the parameter values in Figure 9. While increasing/decreasing constraint strengths by a factor of two changes the number and width of branches, the structures remain compact and dendritic. On the other hand, increasing G by a factor of two truncates the dendrites, and decreasing G by a factor of two produces a compact tumor with P = 0.47 and D_f = 1.30 with ripples rather than branches and without tip splitting. Decreasing γ by a factor of two decreases P to 0.05, and increases D_f to 1.58. Therefore changing other parameters has less effect on tumor morphology than changing G or γ by the same factor.

Fig. 21.

Tumor morphologies with G = 160 and γ = 6 for different constraints, contact energies, and interaction ranges. (a) Figure 9(f). (b) λ_V = 40. (c) λ_V = 10. (d) λ_S = 1. (e) J(m, t) = J(t, t) = 12. (f) Eighth-neighbor interaction range. All other parameters as in Figure 9. The standard deviation for D_f is ∼ 0.01, and for P is less than 0.01.

We mentioned in subsection 3.1 that changing the interaction range affects the relative sizes of the three Effective Energy terms and that we need to scale T, λ_V, and λ_S appropriately to produce an equivalent simulation. Since the interaction range also affects surface-tension anisotropy (larger ranges give smaller anisotropies), we expect that increasing the range should change morphologies near the dendrite-seaweed boundary from dendrites to seaweeds. Figure 21, subfigure (f) shows how an eighth-neighbor interaction range for a tumor simulated with G = 160 and γ = 6, with T, λ_V, and λ_S multiplied by the appropriate rescaling factor of 2.2,⁷ reduces the anisotropy of the simulated pattern, i.e. it is seaweed-like. The simulated tumor remains compact, and has fewer, thicker branches than for its fourth-neighbor realization.

6 Discussion

Our simulations show that whether a simulated growing tumor develops a smooth or fingered interface depends primarily on G, while the detailed morphology of the fingered tumor depends on the surface tension γ(t, T M). The transition from a smooth to fingered interface for GGH-simulated avascular tumors occurs around G = 100, while for GGH-simulated biofilms it occurs around G = 10 (Popławski et al., 2008), perhaps, because in tumor simulations the substrate diffuses in 2D, while in biofilm simulations it diffuses effectively in 1D.

In our GGH simulations of biofilm growth we showed that changing the vertical dimension of the simulation domain, l_z, greatly affects biofilm morphology, because G is proportional to $l_z^2$ (Popławski et al., 2008). Since the interaction between the growing tumor and the substrate does not depend on the boundaries of the simulation domain, G, which is proportional to L, is scale dependent and thus may not be the most accurate description of our tumor-morphology regimes. In our simulations, we do not vary the size of the square simulation domain L, so G is an accurate, relative measure of how the tumor cells compete for substrate. In order to compare our simulated biofilm and tumor patterns, we must use equivalent scale factors L in equation (7) for G. Replacing L = 400 pixel in equation (7) with L = 100 pixel (Popławski et al., 2008) translates the transition value of G ∼ 100 for tumors into G ∼ 6, much closer to the observed transition value of G ∼ 10 for biofilms.

To explain why the tumor-TM surface tension γ is crucial only for high values of G we note that G sets a typical diffusion or penetration length, $l_p=\sqrt{\frac{D_c}{k}}=\sqrt{\frac{D_c{G}_0}{k_{0}G}}$, while γ sets the capillary length, $l_c=\frac{\gamma }{\nu }$ where ν is the kinematic viscosity.⁸ The capillary length is the critical length below which small structures are suppressed. Perturbations smaller than the capillary length are damped. If l_p >> l_c, surface tension does not affect the overall tumor morphology. In the opposite limit, l_p << l_c, the simulated structures have typical widths of order l_c rather than l_p. We also have a length cutoff of one cell diameter. If either l_c or l_p << 1 cell diameter, the cell diameter replaces it in calculations concerning the instability.

If γ = 6, the condition l_p < l_c is satisfied only for larger G (G = 200 and 240). The corresponding dendritic structures have widths of order l_c rather than l_p so these widths do not decrease much as G increases, as Figure 17 shows. As G decreases, the difference l_p – l_c increases and tumor morphologies become less sensitive to surface tension, as Figure 17 shows. Since, for our values of G, the tumor cell size is smaller than l_p (l_p = 12.1 pixel for G = 40 and l_p = 4.9 pixel for G = 240), the cell size is not critical in our simulations. The tumor cell size is larger than l_c only for γ = 0.

For low G, the tumor cells near the tumor-TM interface grow fast enough to find more substrate. For larger G, they grow more slowly, and in order to maintain their growth, they must diffuse to reach substrate. In this case, the substrate-diffusion/cell-diffusion ratio δ becomes a significant factor controlling tumor morphology (Khain and Sander, 2006), as does the tumor-TM surface tension, which in the GGH model relates to the cell diffusion coefficient via the Effective Energy (Turner et al., 2004a).

The volume and surface-area constraints, and the interaction range, also affect the tumor-cell diffusion coefficient in the GGH model via the Effective Energy (Turner et al., 2004a). In future work we will study GGH-simulated tumor morphologies as a function of δ, and examine whether δ suffices to characterize the effects of surface tension, constraints and interaction ranges on the simulated patterns.

Figures 3-15 show that our simulated avascular tumors grow linearly with time to a good approximation. This observation is consistent with the results of Brú et al. (Brú et al., 2003) who compared the functional forms characterizing tumor growth and molecular beam epitaxy (MBE) growth (Brú et al., 1998). Their study of several solid tumors developing in vitro as well as in vivo showed that tumor dynamics is compatible with MBE growth, characterized by: 1) a linear growth rate, 2) growth only at the outer border of the cell colony, and 3) cell diffusion at the colony surface. The first two conditions are consistent with the constancy of the substrate penetration length in our model, while the third condition is significant only for tumors with low surface tensions.

Because TM provides substrate to the tumor only at the tumor-TM interface, we can regard our 2D simulations of tumor growth as nearly equivalent to 2D cross sections of 3D growing tumors. We simulated avascular tumor growth in 2D following Ref. (Anderson, 2005), because it was more efficient computationally. However, we have repeated a limited number of our simulations in 3D and found that the same competition-for-substrate mechanism drives fingering instability in 3D. Figure 22, subfigures (a) and (b) show 2D cross-sections of 3D tumors corresponding to those shown in Figures 3 and 9, when the tumor-TM interface reaches the boundary of a cubical volume of ∼ 4 mm³. Although some parts of the tumor appear disconnected in the 2D sections, the tumor is completely connected in 3D.

Fig. 22.

(a) 2D cross section of a 3D tumor with G = 40 and γ = 6. (b) 2D cross section of a 3D tumor with G = 120 and γ = 6. (c) Preliminary simulation of an unbranched avascular multi-cell-type tumor with G = 40 and γ = 2. Green - normal tumor cells, blue - quiescent tumor cells, black - necrotic tumor cells, red - mutated (less adhesive and more invasive) tumor cells. (d) Preliminary simulation of a branched multi-cell-type tumor with G = 160 and γ = 2. Blue - normal and quiescent tumor cells, black - necrotic tumor cells, red - mutated tumor cells.

While we recognize that most tumors are much more complex than our simple simulations, our goal was to understand the physics of the fingering instability as a function of the tumor-cell adhesivity and substrate consumption rate. Therefore, in this paper, we simulated only growth of simple avascular tumors with a single cell phenotype (a homogeneous population), leaving tumors with several phenotypes to future papers. We already have preliminary simulations of 2D avascular tumors with four cell types: proliferating, quiescent (no proliferation), necrotic, and mutated (less adhesive and faster growing), following Ref. (Anderson, 2005). Figure 22, subfigures (c) and (d), shows a sample unbranched tumor (small G) and a sample branched tumor (large G) for these four cell-type simulations. These preliminary simulations show that multi-phenotype tumors exhibit morphological dependence on G similar to that of single-phenotype tumors.

Anderson (Anderson, 2005) found that the overall tumor morphology in his simulations depended on variations in the TM: homogeneous TM promoted spherical, uniform tumors while heterogeneous TM distributions favored fingering instabilities and irregular, invasive tumors. While real TM is certainly heterogeneous, our goal was to check under what conditions tumors branch even if the matrix is homogeneous, a more stringent test of our proposed branching mechanism. We found that, even with uniform TM, low nutrient availability produced invasive morphologies with aggresive tumor-cell phenotypes, with lower cell-cell adhesion and higher cell-TM adhesion. Our results confirm the significance of cell-cell adhesion in the early development of tumors.

We also assumed that TM supplies substrate at a constant rate (homeostasis) and we defined an upper limit on the substrate concentration that corresponds to the maximum solubility of the substrate in TM. These assumptions are equivalent to the constant-concentration boundary condition at the surface of blood vessels and are valid if the TM contains a high density of capillaries, i.e. if the spacing between capillaries is small compared to the tumor diameter, as in gliomas. In real tumors the supply of substrate by capillaries is more complex. In future work we will simulate growth of tumors surrounded by an explicitly heterogeneous vascular network that supplies substrate.

TM exerts pressure on most growing tumors, reducing tumor-cell motility. GGH simulations of such tumors could represent the TM using Generalized Gells rather than Fields (we will report simulations of such systems in future papers). We could also use higher tumor-TM surface tensions to partially represent such pressure. The results of this paper, which made the assumptions and simplifications discussed in the preceeding paragraphs, should therefore be compared with 2D cross sections of 3D spheroids of highly motile tumor cells in vivo, embedded in a TM with a high density of capillaries (effectively equivalent to a homogeneous matrix), e.g., glioma spheroids. We could also compare our results to experiments on 2D tumors grown in vitro in a homogeneous gel.

Pennacchietti et al. (Pennacchietti et al., 2003) showed that hypoxia (a shortage of oxygen) promotes invasive growth of tumor cells by activating transcription of the met proto-oncogene, which increases levels of the Met tyrosine kinase, a high affinity receptor for hepatocyte growth factor (HGF) (Nakamura et al., 1986, 1989; Rubin et al., 1993). HGF is a scatter factor (Trusolino and Comoglio, 2002) that coordinates specific cytokines (Liotta and Kohn, 2001) to weaken cell-cell contacts and increase cell motility (Stoker et al., 1987; Gherardi et al., 1989). Thus hypoxia, although does not stimulate basal-cell migration, significantly sensitizes tumor cells to HGF stimulation, enhancing HGF-induced cell motility (Pennacchietti et al., 2003; Condeelis et al., 2005). Because smaller tumor-TM surface tension speeds diffusion of tumor cells, we observe that our results that show (Figure 17) larger sensitivity of simulated tumor morphologies to variations in γ for substrate-deprived tumors (larger G) agree with the dynamics of real tumors. Our study suggests an experimentally-testable hypothesis: that HGF decreases tumor-TM surface tension. We could measure the surface tension of a particular type of tumor using the parallel-plate apparatus of Foty et al. (Beysens et al., 2000; Foty et al., 1994, 1996; Forgacs et al., 1998). If these experiments validated our hypothesis, we could then compare an image of a real tumor with the phase diagram in Figure 17 to infer whether the tumor was hypoxic or not and whether the concentration of HGF was high or low. This information would then indicate whether antiangiogenic agents would be likely to suppress the tumor, or, paradoxically, increase its invasiveness.

Our simulations also suggest that, for large G, tumor cells must diffuse to find substrate to maintain their growth, which is easier for low γ. To test this hypothesis, we suggest an experiment to check how the morphology of a 2D tumor grown in vitro in a gel depends on the gel's viscosity η. We expect high η would promote dendrites, while low η would promote seaweeds.

Our results also support the idea, suggested in Ref. (Pennacchietti et al., 2003), that we need to therapeutically suppress cell motility when targeting tumor angiogenesis, in order to prevent the spread of tumor cells because of oxygen deprivation. Antiangiogenic polypeptides used as chemotherapies to contain tumor growth by suppressing neoangiogenesis also induce tumor hypoxia (Blagosklonny, 2001), sometimes resulting in increased tumor malignancy. Also because hypoxia can induce an epithelial-mesenchymal transition (EMT) (Christofori, 2006) through Notch signaling (Sahlgren et al., 2008), depriving the tumor of key substrates can have a therapeutic effect opposite from that desired or expected. EMT is one of the initial steps in metastasis, transforming cells from a nonmotile, epithelial morphology to one more migratory and invasive, e.g. through down-regulation of E-cadherin (Huber et al., 2005; Lee et al., 2006). Our model of avascular tumors, which explains biological pattern formation in terms of physical parameters, substrate competition and surface tension, could help determine the conditions under which the net effect of antiangiogenic factors on a developing tumor is therapeutically beneficial. It suggests the counterintuitive result that, in some cases, we might be able to use proangiogenic factors to reduce metastasis by decreasing hypoxia.

7 Summary

Our simple 2D tumor model with a single tumor-cell phenotype represents tumor cells as spatially-extended objects with variable shapes, allowing us to explicitly include tumor-cell-tumor-cell and tumor-TM adhesion. Our GGH simulations used the kinetics of the HDC model (Anderson, 2005) with some simplifications (no pressure or haptorepulsion from TM, no quiescence, necrosis, or substrate-concentration threshold for tumor-cell growth) and modifications (tumor-cell growth depends on the local concentration of a single substrate). We coarse-grained to a cell size approximately five times the real value. Instead of modeling TM explicitly, we treated it as a nondiffusing field and a single, unconstrained Generalized Cell, and used the tumor-TM adhesion coefficients to represent the interactions between tumor cells and surrounding normal tissue.

We showed that the selection of smooth-interface (non-invasive) vs. fingered (invasive) growth depends on the tumor's substrate consumption rate per unit substrate transport rate, the diffusion-limitation parameter G, while the detailed morphology also depends on the tumor-TM surface tension. Lack of competition for nutrients promotes spherical, benign tumors. Large G, due to either low concentrations of nutrients in the environment causing tumor-cell competition, or to cells with a very high substrate consumption rate, generates a fingering instability and irregular, invasive tumors. Our results agree with experiments showing that tumors branch into the surrounding tissues if the nutrient supply is too small (or nutrient uptake is too large) (Cristini et al., 2005, 2003; Frieboes et al., 2006), but differ from those in Ref. (Anderson, 2005) where fingering occurs without such competition. They also agree with Rejniak's simulations of avascular-tumor growth where cells compete for oxygen (Rejniak, 2005), with nutrient-dependent morphology changes seen using both the HDC model (Anderson et al., 2006) and an evolutionary hybrid cellular-automaton model (Gerlee and Anderson, 2007a,b), and with a recent hybrid cellular-automaton model of cell-colony growth by Gerlee and Anderson (Gerlee and Anderson, 2007c), in which the tumor cells grow at a constant rate above a threshold concentration of a nutrient and stay inactive below this concentration (Gerlee and Anderson, 2007c). The experimental behaviors of tumors (Cristini et al., 2005; Frieboes et al., 2006) and developing alveoli in lungs (Miura and Shiota, 2002; Hartmann and Miura, 2006), and simulations of growing biofilms (Popławski et al., 2008; Picioreanu et al., 1998a), agree with the results of our simulations, suggesting that the ratio of the substrate consumption (or growth) rate to the substrate diffusion rate may be a universal factor that affects morphology in many biological situations.

The simulated morphologies result from the competition between proliferation, which destabilizes the surface of the tumor, and adhesion, which stabilizes this surface (Frieboes et al., 2006). The sensitivity of tumor morphology to tumor-TM surface tension increases with nutrient consumption, causing a directional-solidification-like transition at high G between dendritic structures, produced when the tumor-TM surface tension γ is high, and seaweed-like or DLA-like structures, produced when γ is low. The seaweed-like tumors may arise because we did not model the pressure the surrounding normal tissue exerts on the tumor. In future work, we will include the surrounding tissue explicitly, permitting study of pressure-induced glycolytic tumor phenotypes (Gerlee and Anderson, 2007a,b), the effects of tissue heterogeneity and tumor-cell chemotaxis and haptotaxis.

In our simulations, the tumor-TM surface tension is constant in time and the same for all cells. Real tumor cell adhesivity varies from cell to cell and changes in time as cells mutate. Our preliminary simulations of tumor-cell mutations (Figure 22, subfigures (c) and (d)) indicate that the effects of cell adhesivity are particularly important for tumors growing in environments where the cells compete for resources.

Our results might conceivably explain part of the reason for the paradoxical effect of antiangiogenic agents in increasing cancer metastasis and may suggest non-obvious therapeutic strategies.

Appendix: Implementing the Tumor Simulation

A: CC3DML code for tumor simulations

Our simulations use CompuCell3D (Chaturvedi et al., 2003; Izaguirre et al., 2004; Cickovski et al., 2005; Chaturvedi et al., 2004, 2005), an open-source environment for simulating the development of multicellular organisms.⁹ The CompuCell3D implementation of the GGH uses CompuCell3D Markup Language (CC3DML) and Python to specify models, facilitating model sharing and validation (Balter et al., 2007).

To illustrate the translation of our model into CC3DML code, we describe the structure and meaning of the relevant parts of the simulation, corresponding to our simulations with G = 10 (the complete CC3DML code, the Python Plugins and Steppables, and the PIF and TXT files used in our simulations are available for download from http://www.compucell3d.org/Models/tumor).

The first section of a CC3DML Configuration File (enclosed between 〈Potts〉 and 〈/Potts〉 tags) defines the global parameters of the Cell Lattice and the simulation:

〈CompuCell3D〉

〈Potts〉

〈Dimensions x=“400” y=“400” z=“1”/〉

〈Steps〉100000〈/Steps〉

〈Temperature〉25〈/Temperature〉

〈Flip2DimRatio〉0.1〈/Flip2DimRatio〉

〈Boundary_x〉NoFlux〈/Boundary_x〉

〈Boundary_y〉NoFlux〈/Boundary_y〉

〈FlipNeighborMaxDistance〉2.1〈/FlipNeighborMaxDistance〉

〈/Potts〉

.The line:

〈Dimensions x=“400” y=“400” z=“1”/〉

sets the size of the Cell Lattice to 400 × 400 × 1, i.e. the Cell Lattice is 2D and extends in the xy plane. The basis of the Cell Lattice is 0 in each direction, so the Cell-Lattice sites in the x and y directions have indices ranging from 0 to 399.

The lines:

〈Steps〉100000〈/Steps〉

〈Temperature〉25〈/Temperature〉

tell CompuCell3D that the simulation should last 100000 MCS, with the intrinsic cell motility in equation (13), T = 25. The line:

〈Flip2DimRatio〉0.1〈/Flip2DimRatio〉

,tells CompuCell3D that one MCS contains N′ = 1/0.1 = 10 diffusion substeps. The next line:

〈FlipNeighborMaxDistance〉2.1〈/FlipNeighborMaxDistance〉

,specifies the range for the source pixel to copy to the target pixel in an update attempt (in pixels) to be at most fourth neighbor. 1 would correspond to nearest-neighbor interactions (Glazier et al., 2007; Balter et al., 2007). The longer the search range, the more isotropic and computationally intensive the simulation. The CC3DML tags 〈Boundary_x〉 and 〈Boundary_y〉 impose boundary conditions on the Cell Lattice; in our case, no-flux boundary conditions.

The second section of the CC3DML file defines Plugins, which CompuCell3D refers to every time it calculates the Effective Energy in equation (11). The Plugins define the types, behaviors and interactions of Objects in the simulation. The ability to specify Plugins (and Steppables, see below) dynamically gives CompuCell3D its flexibility.

The CellType plugin informs CompuCell3D what Generalized-Cell Types we are using in the simulation:

〈Plugin Name=“CellType”〉

〈CellType TypeName=“TM” TypeId=“0”/〉

〈CellType TypeName=“Tumor” TypeId=“1”/〉

〈/Plugin〉

.Each line contains the name of a Generalized-Cell Type that the simulation uses and assigns it to an integer-valued TypeId. Background normal tissue, denoted TM, is assigned a TypeId=0 (since the Generalized Cell with TypeId=0 does not have a volume or surface-area constraint by default). We also define the Tumor Cell Type.

The Contact plugin defines the contact energies J(τ, τ′) between Generalized Cells and the interaction range (Depth) of the neighborhood used in the Contact-Energy summation in equation (11):

〈Plugin Name=“Contact”〉

〈Energy Type1=“TM” Type2=“Tumor”〉8〈/Energy〉

〈Energy Type1=“Tumor” Type2=“Tumor”〉4 〈/Energy〉

〈Depth〉2.1〈/Depth〉

〈/Plugin〉

.The VolumeLocal plugin defines the Volume-Constraint term, with a separate V_t for each cell, as in equation (11):

〈Plugin Name=“VolumeLocal”〉

〈LambdaVolume〉20〈/LambdaVolume〉

〈/Plugin〉

.The SurfaceLocal plugin defines the Surface-Area-Constraint term, with a separate S_t for each cell, as in equation (11):

〈Plugin Name=“SurfaceLocal”〉

〈LambdaSurface〉2〈/LambdaSurface〉

〈/Plugin〉

.The CenterOfMass plugin enables CompuCell3D to track the center of mass of each cell, e.g., to control cell growth (see below):

〈Plugin Name=“CenterOfMass”/〉

.The Mitosis plugin defines the doubling volume at which a Tumor cell divides into two Tumor cells with equal volumes:

〈Plugin Name=“Mitosis”〉

〈DoublingVolume〉18〈/DoublingVolume〉

〈/Plugin〉

.By default, the orientation of the cleavage plane is random.

The third section of the CC3DML file contains Steppables. The PIFInitializer Steppable, executed only once at the beginning of a simulation, reads the initial condition for the Cell Lattice from the file Tumor.PIF:

〈Steppable Type=“PIFInitializer”〉

〈PIFName〉Tumor.PIF〈/PIFName〉

〈/Steppable〉

.The PIF file for n Generalized Cells contains at least n lines, each of which consists of: the Index of a Generalized Cell, its Type and the range (in pixels) of a parallelipiped this cell occupies on the Cell Lattice (x_min, x_max, y_min, y_max, z_min, z_max). Using multiple lines/cell allows specification of arbitrary geometries. By default, all Cell-Lattice points that are not included in the PIF file are occupied by the Generalized Cell of TypeId=0.

CompuCell3D executes the remaining Steppables once at the conclusion of every MCS substep. The FlexibleDiffusionSolverFE Steppable introduces Fields and defines their secretion, consumption, diffusion, decay and interactions. Here we show the Steppable that implements equation (3) for the Substrate Field:

〈Steppable Type=“FlexibleDiffusionSolverFE”〉

〈DiffusionField〉

〈DiffusionData〉

〈FieldName〉Substrate〈/FieldName〉

〈DiffusionConstant〉0.15〈/DiffusionConstant〉

〈Concentration Thresholds MinConcentration=“0.000001” MaxConcentration=1”/〉

〈CouplingTerm InteractingFieldName=“TM” CouplingCoefficient=“0.0045”/〉

〈ConcentrationFileName〉Substrate.TXT〈/ConcentrationFileName〉

〈/DiffusionData〉

〈SecretionData〉

〈Secretion Type=“Tumor”〉−0.0054〈/Secretion〉

〈/SecretionData〉

〈/DiffusionField〉

〈/Steppable〉

.The DiffusionConstant line corresponds (after multiplying by N′) to D_c in equation (3), the Coupling-Coefficient to S_c and the constant in the SecretionData to C_c. The ConcentrationThresholds line sets the maximum and minimum allowed substrate concentrations. The Substrate.TXT file sets the initial distribution c(x, y, z) of the substrate, with the format: x, y, z, c(x, y, z). In our simulations the initial Substrate Field is 1 everywhere. The CC3DML file ends with the line:

〈/CompuCell3D〉

.

B: PIF file

Our simulations begin with nine Tumor Generalized Cells in a square located at the center of the simulation domain (see Figure 1):

0 Tumor 196 198 196 198 0 0

1 Tumor 196 198 199 201 0 0

2 Tumor 196 198 202 204 0 0

3 Tumor 199 201 196 198 0 0

4 Tumor 199 201 199 201 0 0

5 Tumor 199 201 202 204 0 0

6 Tumor 202 204 196 198 0 0

7 Tumor 202 204 199 201 0 0

8 Tumor 202 204 202 204 0 0

C: Python Steppable file

CompuCell3D reads the parameters describing secretion, consumption and diffusion of the Substrate Field from the CC3DML code. We define the growth of Tumor cells in response to the Substrate Field in a Python Steppable file. The part of this file that implements proliferation of Tumor cells in response to substrate consumption is:

def setField1Name(self,fieldName):

self.field1Name=fieldName

self.field1=field=CompuCell.getConcentrationField(self.simulator,fieldName)

…

xCM=cell.xCM/float(cell.volume)

pt.x=int(xCM)

if xCM-pt.x>0.5:

pt.x+=1

…

conc1=self.field1.get(pt)

GrowthRate=0.0027

if cell.type==1:

cell.targetVolume+=GrowthRate*conc1

cell.targetSurface=3*sqrt(cell.targetVolume)

The first three lines read the current values of the Substrate Field at all Cell-Lattice sites and associate them with the matrix self.field1Name. The next four lines calculate the coordinates rounded to the nearest integer of the centers of mass of each Tumor Generalized Cell. The last five lines: read the value conc1 of the self.field1Name matrix (the Substrate Field) at the center of mass of each Generalized Cell, increase the Generalized Cell's target volume V_t (implementing growth) by the product GrowthRate*conc1 (which corresponds to gc in equation (14)), and increase the Generalized Cell's target surface area S_t so that the nondimensional ratio $S_t{V_t}^{-1∕2}$, which controls the average shape of cells, remains constant and equal to 3.