Abstract
Mathematical modeling and computer simulation have become crucial to biological fields from genomics to ecology. However, multi-cell, tissue-level simulations of development and disease have lagged behind other areas because they are mathematically more complex and lack easy-to-use software tools that allow building and running in-silico experiments without requiring in-depth knowledge of programming. This tutorial introduces Glazier-Graner-Hogeweg (GGH) multi-cell simulations and CompuCell3D, a simulation framework that allows users to build, test and run GGH simulations.
Keywords: Glazier-Graner-Hogeweg model, GGH, CompuCell3D, Python, C++, mitosis, cell growth, cell sorting, chemotaxis, CPM, multi-cell modeling, tissue-level modeling, developmental biology, computational biology
I. Introduction
Most contemporary life scientists, whether theoretical or experimental, have relatively narrow disciplinary training. This specialization is partly a consequence of the speed of current progress in the life sciences and concomitant growth in the number of active researchers.
While the success of contemporary biology might lead naïve observers to conclude that our understanding is a simple superposition of achievements in the subfields composing life sciences, only rarely can we understand how a biological phenomenon operates by analyzing and understanding how its isolated components operate.
Just as knowing how transistors work is not sufficient to design and build a modern microprocessor, knowing the “function” of an enzyme does not suffice to design cells' biochemical networks or even to predict the phenotypic effect of knocking out specific genes.
Systems biology is a scientific discipline that studies complex interactions in biology, relying more on knowledge integration than on detailed studies of individual biological subsystems. Systems biologists often build mathematical models and computer simulations of living cells, tissues, organs or even entire organisms to embody their understanding of this integration.
The last decade has seen fairly realistic simulations of single cells that can confirm or predict experimental findings. Because they are computationally expensive, they can simulate at most several cells at once. Even more detailed subcellular simulations can replicate some of the processes taking place inside individual cells. E.g., Virtual Cell (http://www.nrcam.uchc.edu) supports microscopic simulations of intracellular dynamics to produce detailed replicas of individual cells, but can only simulate single cells or small cell clusters.
Simulations of tissues, organs and organisms present a somewhat different challenge: how to simplify and adapt single cell simulations to apply them efficiently to study, in-silico, ensembles of several million cells. To be useful, these simplified simulations should capture key cell-level behaviors, providing a phenomenological description of cell interactions without requiring prohibitively detailed molecular-level simulations of the internal state of each cell. While an understanding of cell biology, biochemistry, genetics, etc. is essential for building useful, predictive simulations, the hardest part of simulation building is identifying and quantitatively describing appropriate subsets of this knowledge. In the excitement of discovery, scientists often forget that modeling and simulation, by definition, require simplification of reality.
One choice is to ignore cells completely, e.g., Physiome (1) models tissues as continua with bulk mechanical properties and detailed molecular reaction networks, which is computationally efficient for describing dense tissues and non-cellular materials like bone, extracellular matrix (ECM), fluids, and diffusing chemicals (2, 3), but not for situations where cells reorganize or migrate.
Multi-cell simulations are useful to interpolate between single-cell and continuum-tissue extremes because cells provide a natural level of abstraction for simulation of tissues, organs and organisms (4). Treating cells phenomenologically reduces the millions of interactions of gene products to several behaviors: most cells can move, divide, die, differentiate, change shape, exert forces, secrete and absorb chemicals and electrical charges, and change their distribution of surface properties. The Glazier-Graner-Hogeweg (GGH) approach facilitates multiscale simulations by defining spatially-extended generalized cells, which can represent clusters of cells, single cells, sub-compartments of single cells or small subdomains of non-cellular materials. This flexible definition allows tuning of the level of detail in a simulation from intracellular to continuum without switching simulation framework to examine the effect of changing the level of detail on a macroscopic outcome, e.g., by switching from a coupled ordinary-differential-equation (ODE) Reaction-Kinetics (RK) model of gene regulation to a Boolean description or from a simulation that includes subcellular structures to one that neglects them.
II. GGH Applications
Because it uses a regular cell lattice and regular field lattices, GGH simulations are often faster than equivalent Finite Element (FE) simulations operating at the same spatial granularity and level of modeling detail, permitting simulation of tens to hundreds of thousands of cells on lattices of up to 10243 pixels on a single processor. This speed, combined with the ability to add biological mechanisms via terms in the effective energy, permit GGH modeling of a wide variety of situations, including: tumor growth (5-9), gastrulation (10-12), skin pigmentation (13-16), neurospheres (17), angiogenesis (18-23), the immune system (24, 25), yeast colony growth (26, 27), myxobacteria (28-31), stem-cell differentiation (32, 33), Dictyostelium discoideum (34-37), simulated evolution (38-43), general developmental patterning (14, 44), convergent extension (45, 46), epidermal formation (47), hydra regeneration (48, 49), plant growth, retinal patterning (50, 51), wound healing (47, 52, 53), biofilms (54-57), and limb-bud development (58, 59).
III. GGH Simulation Overview
All GGH simulations include a list of objects, a description of their interactions and dynamics and appropriate initial conditions.
Objects in a GGH simulation are either generalized cells or fields in two dimensions (2D) or three dimensions (3D). Generalized cells are spatially-extended objects (Figure 1), which reside on a single cell lattice and may correspond to biological cells, sub-compartments of biological cells, or to portions of non-cellular materials, e.g. ECM, fluids, solids, etc. (8, 48, 60-72). We denote a lattice site or pixel by a vector of integers, , the cell index of the generalized cell occupying pixel by and the type of the generalized cell by . Each generalized cell has a unique cell index and contains many pixels. Many generalized cells may share the same cell type. Generalized cells permit coarsening or refinement of simulations, by increasing or decreasing the number of lattice sites per cell, grouping multiple cells into clusters or subdividing cells into variable numbers of subcells (subcellular compartments). Compartmental simulation permits detailed representation of phenomena like cell shape and polarity, force transduction, intracellular membranes and organelles and cell-shape changes. For details on the use of subcells, which we do not discuss in this chapter see (27, 31, 73, 74). Each generalized cell has an associated list of attributes, e.g., cell type, surface area and volume, as well as more complex attributes describing a cell's state, biochemical interaction networks, etc.. Fields are continuously-variable concentrations, each of which resides on its own lattice. Fields can represent chemical diffusants, non-diffusing ECM, etc.. Multiple fields can be combined to represent materials with textures, e.g., fibers.
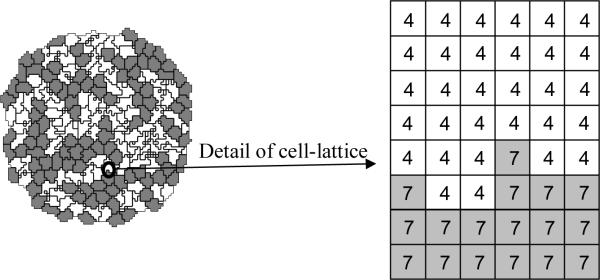
Figure 1.
Detail of a typical two-dimensional GGH cell-lattice configuration. Each colored domain represents a single spatially-extended cell. The detail shows that each generalized cell is a set of cell-lattice sites (or pixel), , with a unique index, σ , here 4 or 7. The color denotes the cell type, .
Interaction descriptions and dynamics define how GGH objects behave both biologically and physically. Generalized-cell behaviors and interactions are embodied primarily in the effective energy, which determines a generalized cell's shape, motility, adhesion and response to extracellular signals. The effective energy mixes true energies, such as cell-cell adhesion with terms that mimic energies, e.g., the response of a cell to a chemotactic gradient of a field (75). Adding constraints to the effective energy allows description of many other cell properties, including osmotic pressure, membrane area, etc. (76-83).
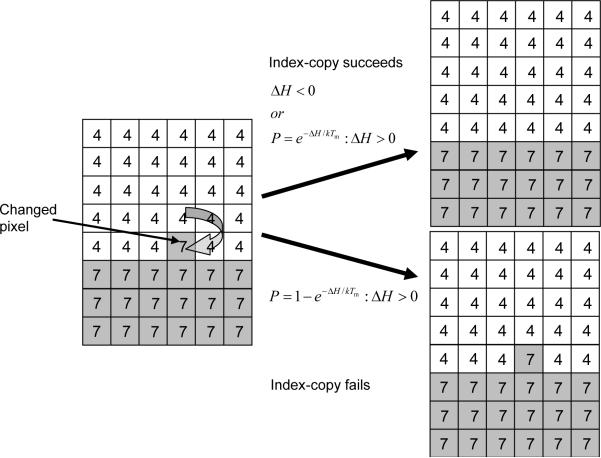
The cell lattice evolves through attempts by generalized cells to move their boundaries in a caricature of cytoskeletally-driven cell motility. These movements, called index-copy attempts, change the effective energy, and we accept or reject each attempt with a probability that depends on the resulting change of the effective energy, ΔH, according to an acceptance function. Nonequilibrium statistical physics then shows that the cell lattice evolves to locally minimize the total effective energy. The classical GGH implements a modified version of a classical stochastic Monte-Carlo pattern-evolution dynamics, called Metropolis dynamics with Boltzmann acceptance (84, 85). A Monte Carlo Step (MCS) consists of one index-copy attempt for each pixel in the cell lattice.
Auxiliary equations describe cells' absorption and secretion of chemical diffusants and extracellular materials (i.e., their interactions with fields), state changes within cells, mitosis, and cell death. These auxiliary equations can be complex, e.g., detailed RK descriptions of complex regulatory pathways. Usually, state changes affect generalized-cell behaviors by changing parameters in the terms in the effective energy (e.g., cell target volume or type or the surface density of particular cell-adhesion molecules).
Fields also evolve due to secretion, absorption, diffusion, reaction and decay according to partial differential equations (PDEs). While complex coupled-PDE models are possible, most simulations require only secretion, absorption, diffusion and decay, with all reactions described by ODEs running inside individual generalized cells. The movement of cells and variations in local diffusion constants (or diffusion tensors in anisotropic ECM) mean that diffusion occurs in an environment with moving boundary conditions and often with advection. These constraints rule out most sophisticated PDE solvers and have led to a general use of simple forward-Euler methods, which can tolerate them.
The initial condition specifies the initial configurations of the cell lattice, fields, a list of cells and their internal states related to auxiliary equations and any other information required to completely describe the simulation.
III.A. Effective Energy
The core of GGH simulations is the effective energy, which describes cell behaviors and interactions.
One of the most important effective-energy terms describes cell adhesion. If cells did not stick to each other and to extracellular materials, complex life would not exist (86). Adhesion provides a mechanism for building complex structures, as well as for holding them together once they have formed. The many families of adhesion molecules (CAMs, cadherins, etc.) allow embryos to control the relative adhesivities of their various cell types to each other and to the noncellular ECM surrounding them, and thus to define complex architectures in terms of the cell configurations which minimize the adhesion energy.
To represent variations in energy due to adhesion between cells of different types, we define a boundary energy that depends on J(τ(σ), τ (σ′)), the boundary energy per unit area between two cells (σ, σ′) of given types (τ (σ) τ, (σ′)) at a link (the interface between two neighboring pixels):
| (1) |
where the sum is over all neighboring pairs of lattice sites and (note that the neighbor range may be greater than one), and the boundary-energy coefficients are symmetric,
| (2) |
In addition to boundary energy, most simulations include multiple constraints on cell behavior. The use of constraints to describe behaviors comes from the physics of classical mechanics. In the GGH context we write constraint energies in a general elastic form:
| (3) |
The constraint energy is zero if value=target_value (the constraint is satisfied) and grows as value diverges fromtarget_value. The constraint is elastic because the exponent of 2 effectively creates an ideal spring pushing on the cells and driving them to satisfy the constraint. λ is the spring constant (a positive real number), which determines the constraint strength. Smaller values of λ allow the pattern to deviate more from the equilibrium condition (i.e., the condition satisfying the constraint). Because the constraint energy decreases smoothly to a minimum when the constraint is satisfied, the energy-minimizing dynamics used in the GGH automatically drives any configuration towards one that satisfies the constraint. However, because of the stochastic simulation method, the cell lattice need not satisfy the constraint exactly at any given time, resulting in random fluctuations. In addition, multiple constraints may conflict, leading to configurations which only partially satisfy some constraints.
Because biological cells have a given volume at any time, most GGH simulations employ a volume constraint, which restricts volume variations of generalized cells from their target volumes:
| (4) |
where for cell σ, λvol (σ) denotes the inverse compressibility of the cell, ν (σ) is the number of pixels in the cell (its volume), and Vt (σ) is the cell's target volume. This constraint defines P ≡ -2λ (ν(σ)-Vt(σ)) as the pressure inside the cell. A cell with ν < Vt has a positive internal pressure, while a cell with ν > Vt has a negative internal pressure.
Since many cells have nearly fixed amounts of cell membrane, we often use a surface-area constraint of form:
| (5) |
where s (σ) is the surface area of cell (σ), St is its target surface area, and λsurf (σ) is its inverse membrane compressibility.1
Adding the boundary energy and volume constraint terms together (equations (1) and (4)), we obtain the basic GGH effective energy:
| (6) |
III.B. Dynamics
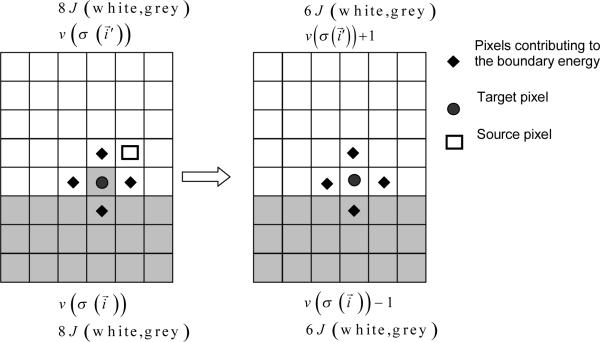
A GGH simulation consists of many attempts to copy cell indices between neighboring pixels. In CompuCell3D the default dynamical algorithm is modified Metropolis dynamics. During each index-copy attempt, we select a target pixel, , randomly from the cell lattice, and then randomly select one of its neighboring pixels, , as a source pixel. If they belong to the same generalized cell (i.e., if ) we do not need copy index. Otherwise the cell containing the source pixel attempts to occupy the target pixel. Consequently, a successful index copy increases the volume of the source cell and decreases the volume of the target cell by one pixel.
In the modified Metropolis algorithm we evaluate the change in the total effective energy due to the attempted index copy and accept the index-copy attempt with probability:
| (7) |
where Tm is a parameter representing the effective cell motility (we can think of Tm as the amplitude of cell-membrane fluctuations). Equation (7) is the Boltzmann acceptance function. Users can define other acceptance functions in CompuCell3D. The conversion between MCS and experimental time depends on the average values of ΔH / Tm. MCS and experimental time are proportional in biologically-meaningful situations (87-90).
III.C. Algorithmic Implementation of Effective-Energy Calculations
Consider an effective energy consisting of boundary-energy and volume-constraint terms as in equation (6). After choosing the source and destination pixels (the cell index of the source will overwrite the target pixel if the index copy is accepted), we calculate the change in the effective energy that would result from the copy. We evaluate the change in the boundary energy and volume constraint as follows. First we visit the target pixel's neighbors . If the neighbor pixel belongs to a different generalized cell from the target pixel, i.e., when (see equation (1)), we decrease ΔH by . If the neighbor belongs to a cell different from the source pixel we increase ΔH by .
The change in volume-constraint energy is evaluated according to:
| (8) |
, where and denote the volumes of the generalized cells containing the source and target pixels, respectively.
In this example, we could calculate the change in the effective energy locally, i.e., by visiting the neighbors of the target of the index copy. Most effective energies are quasi-local, allowing calculations of ΔH similar to those presented above. The locality of the effective energy is crucial to the utility of the GGH approach. If we had to calculate the effective energy for the entire cell lattice for each index-copy attempt, the algorithm would be prohibitively slow.
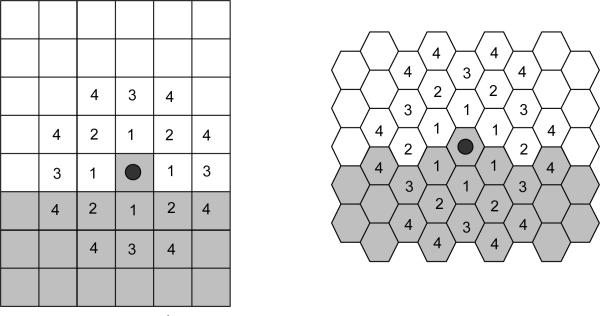
For longer-range interactions we use the appropriate list of neighbors, as shown in Figure 4 and Table 1. Longer-range interactions are less anisotropic but result in slower simulations.
Figure 4.
Locations of nth-nearest neighbors on a 2D square lattice and a 2D hexagonal lattice.
Table 1.
Multiplicity and Euclidian distances of nth-nearest neighbors for 2D square and hexagonal lattices. The number of nth neighbors and their distances from the central pixel differ in a 3D lattice. CompuCell3D calculates distance between neighbors by setting the volume of a single pixel (whether in 2D or 3D) to 1.
| Neighbor Order | Number of Neighbors | Euclidian Distance | Number of Neighbors | Euclidian Distance |
|---|---|---|---|---|
| 1 | 4 | 1 | 6 | |
| 2 | 4 | 6 | ||
| 3 | 4 | 2 | 6 | |
| 4 | 8 | 12 |
IV. CompuCell3D
One advantage of the GGH model over alternative techniques is its mathematical simplicity. We can implement fairly easily a computer program that initializes the cell lattice and fields, performs index copies and displays the results. In the 15 years since the GGH model was developed, researchers have written numerous programs to run GGH simulations. Because all GGH implementations share the same logical structure and perform similar tasks, much of this coding effort has gone into rewriting code already developed by someone else. This redundancy leads to significant research overhead and unnecessary duplication of effort and makes model reproduction, sharing and validation needlessly cumbersome.
To overcome these problems, we developed CompuCell3D as a framework for GGH simulations (91, 92). Unlike specialized research code, CompuCell3D is a simulation environment that allows researchers to rapidly build and run shareable GGH-based simulations. It greatly reduces the need to develop custom code and its adherence to open-source standards ensures that any such code is shareable.
CompuCell3D supports non-programmers by providing visualization tools, an eXtensible Markup Language (XML) interface for defining simulations, and the ability to extend the framework through specialized modules. The C++ computational kernel of CompuCell3D is also accessible using the open-source scripting language Python, allowing users to create complex simulations without programming in lower-level languages such as C or C++. Unlike typical research code, changing a simulation does not require recompiling CompuCell3D.
Users define simulations using CompuCell3D XML (CC3DML) configuration files and/or Python scripts. CompuCell3D reads and parses the CC3DML configuration file and uses it to define the basic simulation structure, then initializes appropriate Python services (if they are specified) and finally executes the underlying simulation algorithm.
CompuCell3D is modular: each module carries out a defined task. CompuCell3D terminology calls modules associated with index copies or index-copy attempts plugins. Some plugins calculate changes in effective energy, while others (lattice monitors) react to accepted index copies, e.g., by updating generalized cells' surface areas, volumes or lists of neighbors. Plugins may depend on other plugins. For example, the Volume plugin (which calculates the volume-energy constraint in equation (4)) depends on VolumeTracker (a lattice monitor), which, as its name suggests, tracks changes in generalized cells' volumes. When implicit plugin dependencies exist, CompuCell3D automatically loads and initializes dependent plugins. In addition to plugins, CompuCell3D defines modules called steppables which run either repeatedly after a defined intervals of Monte Carlo Steps or once at the beginning or end of the simulation. Steppables typically define initial conditions, alter cell states, update fields or output intermediate results.
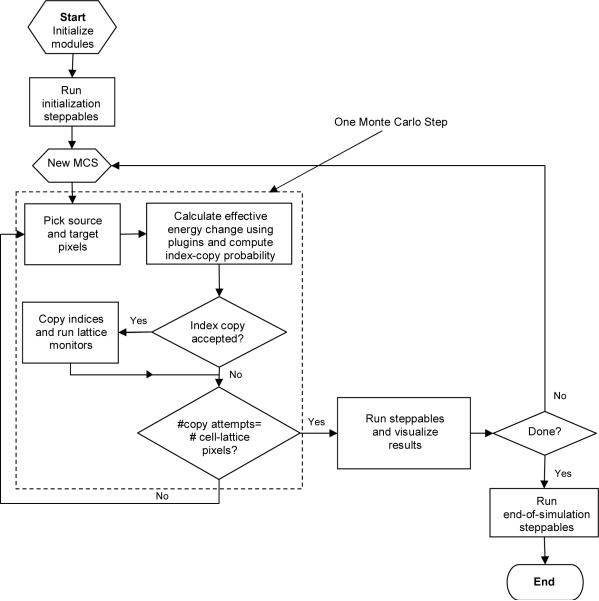
Figure 5 shows the relations among index-copy attempts, Monte Carlo Steps, steppables and plugins.
Figure 5.
Flow chart of the GGH algorithm as implemented in CompuCell3D.
CompuCell3D includes a Graphical User Interface (GUI) and visualization tool, CompuCell Player (also referred to as Player). From Player the user opens a CC3DML configuration file and/or Python file and hits the “Play” button to run the simulation. Player allows users to define multiple 2D or 3D visualizations of generalized cells, fields or various vector plots while the simulation is running and save them automatically for post-processing.
V. Building CC3DML-Based Simulations Using CompuCell3D
To show how to build simulations in CompuCell3D, the reminder of this chapter provides a series of examples of gradually increasing complexity. For each example we provide a brief explanation of the physical and/or biological background of the simulation and listings of the CC3DML configuration file and Python scripts, followed by a detailed explanation of their syntax and algorithms. We can specify many simulations using only a simple CC3DML configuration file. We begin with three examples using only CC3DML to define simulations.
V.A A Short Introduction to XML
XML is a text-based data-description language, which allows standardized representations of data. XML syntax consists of lists of elements, each either contained between opening (<Tag>) and closing (</Tag>) tags:2
<Tag Attribute1=“text1”>ElementText</Tag>
or of form:
<Tag Attribute1=“attribute_text1” Attribute2=“attribute_text2”>
We will denote the <Tag>…</Tag> syntax as a <Tag> tag pair. The opening tag of an XML element may contain additional attributes characterizing the element. The content of the XML element (ElementText in the above example) and the values of its attributes (text1, attribute_text1, attribute_text2) are strings of characters. Computer programs that read XML may interpret these strings as other data types such as integers, Booleans or floating point numbers. XML elements may be nested. The simple example below defines an element Cell with subelements (represented as nested XML elements) Nucleus and Membrane assigning the element Nucleus an attribute Size set to “10” and the element Membrane an attribute Area set to “20.5”, and setting the value of the Membrane element to Expanding:
<Cell><Nucleus Size=“10”/><Membrane Area=“20.5”>Expanding</Membrane></Cell>
Although XML parsers ignore indentation, all the listings presented in this chapter are block-indented for better readability.
V.B Grain-Growth Simulation
One of the simplest CompuCell3D simulations mimics crystalline grain growth or annealing. Most simple metals are composed of microcrystals, or grains, each of which has a particular crystalline-lattice orientation. The atoms at the surfaces of these grains have a higher energy than those in the bulk because of their missing neighbors. We can characterize this excess energy as a boundary energy. Atoms in convex regions of a grain's surface have a higher energy than those in concave regions, in particular than those in the concave face of an adjoining grain, because they have more missing neighbors. For this reason, an atom at a convex curved boundary can reduce its energy by “hopping” across the grain boundary to the concave side (62). The movement of atoms moves the grain boundaries, lowering the net configuration energy through annealing or coarsening, with the net size of grains growing because of grain disappearance. Boundary motion may require thermal activation because atoms in the space between grains may have higher energy than atoms in grains. The effective energy driving grain growth is simply the boundary energy in equation (1).
In CompuCell3D, we can represent grains as generalized cells. CC3DML Listing 1 defines our grain-growth simulation.
Each CC3DML configuration file begins with the <CompuCell3D> tag and ends with the </CompuCell3D> tag. A CC3DML configuration file contains three sections in the following sequence: the lattice section (contained within the <Potts> tag pair), the plugins section, and the steppables section. The lattice section defines global parameters for the simulation: cell-lattice and field-lattice dimensions (specified using the syntax <Dimensions x=“x_dim” y=“y_dim” z=“z_dim”/>), the number of Monte Carlo Steps to run (defined within the <Steps> tag pair) the effective cell motility (defined within the <Temperature> tag pair) and boundary conditions. The default boundary conditions are no-flux. However, in this simulation, we have changed them to be periodic along the x and y axes by assigning the value Periodic to the <Boundary_x> and <Boundary_y> tag pairs. The value set by the <NeighborOrder> tag pair defines the range over which source pixels are selected for index-copy attempts (see Figure 4 and Table 1).
The plugins section lists the plugins the simulation will use. The syntax for all plugins which require parameter specification is:
<Plugin Name=“PluginName”><ParameterSpecification/></Plugin>
The CellType plugin uses the parameter syntax
<CellType TypeName=“Name” TypeId=“IntegerNumber”/>
to map verbose generalized-cell-type names to numeric cell TypeIds for all generalized-cell types. It does not participate directly in index copies, but is used by other plugins for cell-type-to-cell-index mapping. Even though the grain-growth simulation fills the entire cell lattice with cells of type Grain, the current implementation of CompuCell3D requires that all simulations define the Medium cell type with TypeId 0. Medium is a special cell type with unconstrained volume and surface area that fills all cell-lattice pixels unoccupied by cells of other types.3
The Contact plugin calculates changes in the boundary energy defined in equation (1) for each index-copy attempt. The parameter syntax for the Contact plugin is:
<Energy Type1=“TypeName1” Type2=“TypeName1”>EnergyValue</Energy>
where TypeName1 and TypeName2 are the names of the cell types and EnergyValue is the boundary-energy coefficient,J(TypeName1,TypeName2, between cells of TypeName1 and TypeName2 (see equation (1)). The <NeighborOrder> tag pair specifies the interaction range of the boundary energy. The default value of this parameter is 1.
The steppables section includes only the UniformInitializer steppable. All steppables have the following syntax:
<Steppable Type=“SteppableName” Frequency=“FrequencyMCS”><ParameterSpecification/></Steppable>
The Frequency attribute is optional and by default is 1 MCS.
CompuCell3D simulations require specification of initial condition. The simplest way to define the initial cell lattice is to use the built-in initializer steppables, which construct simple regions filled with generalized cells.
The UniformInitializer steppable in the grain-growth simulation defines one or more rectangular (parallelepiped in 3D) regions filled with generalized cells of user selectable types and sizes. We enclose each region definition within a <Region> tag pair. We use the <BoxMin> and <BoxMax> tags to describe the boundaries of the region, The <Width> tag pair defines the size of the square (cubical in 3D) generalized cells and the <Gap> tag pair creates space between neighboring cells. The <Types> tag pair lists the types of generalized cells. The grain-growth simulation uses only one cell type, Grain, but we can also initialize cells using types randomly chosen from the list, as in Listing 2.
<Steppable Type=“UniformInitializer”><Region><BoxMin x=“10” y=“10” z=“0”/><BoxMax x=“90” y=“90” z=“1”/><Gap>0</Gap><Width>5</Width><Types>Condensing,NonCondensing</Types></Region></Steppable>
Listing 2. CC3DML code excerpt using the UniformInitializer steppable to initialize a rectangular region filled with 5 × 5 pixel generalized cells with randomly-assigned cell types (either Condensing or NonCondensing).
The coordinate values in BoxMax element must be one more than the coordinates of the corresponding corner of the region to be filled. So to fill a square of side 10 beginning with pixel location (5,5) we use the following region-boundary specification:
<BoxMin x=“5” y=“5” z=“0”/><BoxMax x=“16” y=“16” z=“1”/>
Listing the same type multiple times results in a proportionally higher fraction of generalized cells of that type. For example,
<Types>Condensing,Condensing,NonCondensing</Types>
will allocate approximately 2/3 of the generalized cells to type Condensing and 1/3 to type NonCondensing. UniformInitializer allows specification of multiple regions. Each region is independent and can have its own cell sizes, types and cell spacing. If the regions overlap, later-specified regions overwrite earlier-specified ones. If region specification does not cover the entire lattice, uninitialized pixels have type Medium.
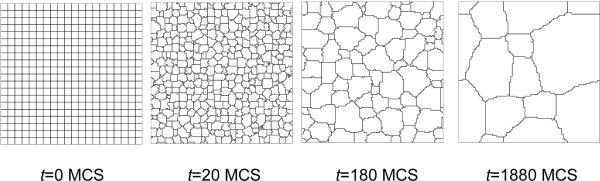
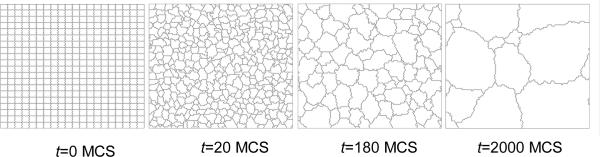
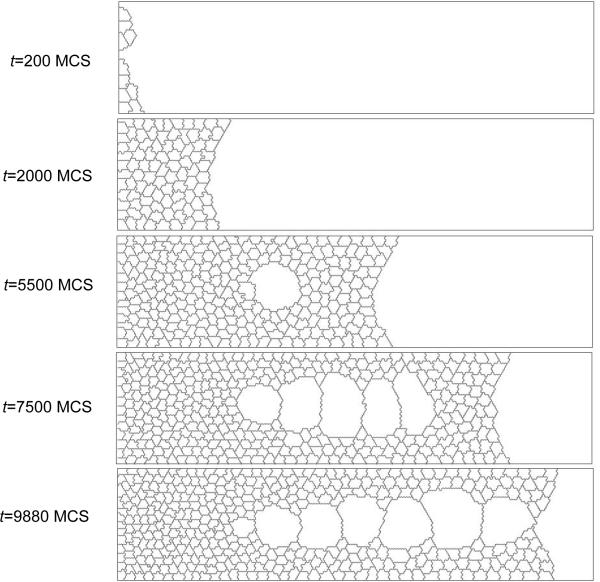
Figure 6 shows sample output generated by the grain-growth simulation.
Figure 6.
Snapshots of the cell-lattice configuration for the grain-growth simulation on a 100 × 100 pixel 3rd-neighbor square lattice, as specified in Listing 1. Boundary conditions are periodic in both directions.
One advantage of GGH simulations compared to FE simulations is that going from 2D to 3D is easy. To run a 3D grain-growth simulation on a 100 × 100 × 100 lattice we only need to make the following replacements in Listing 1:
<Dimensions x=“100” y=“100” z=“1”/> →<Dimensions x=“100” y=“100” z=“100”/>
and,
<BoxMax x=“100” y=“100” z=“1”/> → <BoxMax x=“100” y=“100” z=“100”/>
Grain growth simulations are particularly sensitive to lattice anisotropy, so running them on lower-anisotropy lattices is desirable. Longer-range lattices are less anisotropic but cause simulations to run slower. Fortunately a hexagonal lattice of a given range is less anisotropic than a square lattice of the same range. To run the grain-growth simulation on a hexagonal lattice, we add <LatticeType>Hexagonal</LatticeType> to the lattice section in Listing 1 and change the two occurrences of:
<NeighborOrder>3</NeighborOrder> → <NeighborOrder>1</NeighborOrder>
Figure 7 shows snapshots for this simulation.
Figure 7.
Snapshots of the cell-lattice configuration for the grain-growth simulation on a 100 × 100 pixel 1st -neighbor hexagonal lattice as specified in Listing 1 with substitutions described in the text. The x and y length units in an hexagonal lattice differ, resulting in differing x and y dimensions for a cell lattice with an equal number of pixels in the x and y directions.
One inconvenience of the current implementation of CompuCell3D is that it does not automatically rescale parameter values when interaction range, lattice dimensionality or lattice type change. When changing these attributes, users must recalculate parameters to keep the underlying physics of the simulation the same.
CompuCell3D dramatically reduces the amount of code necessary to build and run a simulation. The grain-growth simulation took about 25 lines of CC3DML instead of 1000 lines of C, C++ or Fortran.
V.C Cell-Sorting Simulation
Cell sorting is an experimentally-observed phenomenon in which cells with different adhesivities are randomly mixed and reaggregated. They can spontaneously sort to reestablish coherent homogenous domains (93, 94). Sorting is a key mechanism in embryonic development.
The grain-growth simulation used only one type of generalized cell. Simulating sorting of two types of biological cell in an aggregate floating in solution is slightly more complex. Listing 3 shows a simple cell-sorting simulation. It is similar to Listing 1 with a few additional modules (shown in bold). The effective energy is that in equation (6).
<CompuCell3D><Potts><Dimensions x=“100” y=“100” z=“1”/><Steps>10000</Steps><Temperature>10</Temperature><NeighborOrder>2</NeighborOrder></Potts><Plugin Name=“Volume”><TargetVolume>25</TargetVolume><LambdaVolume>2.0</LambdaVolume></Plugin><Plugin Name=“CellType”><CellType TypeName=“Medium” TypeId=“0”/><CellType TypeName=“Condensing” TypeId=“1”/><CellType TypeName=“NonCondensing” TypeId=“2”/></Plugin><Plugin Name=“Contact”><Energy Type1=“Medium” Type2=“Medium”>0</Energy><Energy Type1=“NonCondensing” Type2=“NonCondensing”>16</Energy><Energy Type1=“Condensing” Type2=“Condensing”>2</Energy><Energy Type1=“NonCondensing” Type2=“Condensing”>11</Energy><Energy Type1=“NonCondensing” Type2=“Medium”>16</Energy><Energy Type1=“Condensing” Type2=“Medium”>16</Energy><NeighborOrder>2</NeighborOrder></Plugin><Steppable Type=“BlobInitializer”><Region><Gap>0</Gap><Width>5</Width><Radius>40</Radius><Center x=“50” y=“50” z=“0”/><Types>Condensing,NonCondensing</Types></Region></Steppable></CompuCell3D>
Listing 3. CC3DML configuration file simulating cell sorting between Condensing and NonCondensing cell types. Highlighted text indicates modules absent in Listing 1. Notice how little modification of the grain-growth CC3DML configuration file this simulation requires.
The main change from Listing 1 to the lattice section is that we omit the boundary condition specification and use default no-flux boundary conditions.
In the CellType plugin we introduce the two cell types, Condensing and NonCondensing, in place of Grain. In addition we do not the fill lattice completely with Condensing and NonCondensing cells so the interactions with Medium become important. The boundary-energy matrix in the Contact plugin thus requires entries for the additional cell-type pairs. The hierarchy of boundary energies listed results in cell sorting.
We also add the Volume plugin, which calculates the volume-constraint energy as given in equation (4). In this plugin the <TargetVolume> tag pair sets target volume Vt = 25 for both Condensing cells and NonCondensing and the <LambdaVolume> tag pair sets the constraint strength λvol = 2.0 for both cell types. We will see later how to define volume-constraint parameters for each cell type or each cell individually.
In the cell-sorting simulation we initialize the cell lattice using the BlobInitializer steppable which specifies circular (or spherical in 3D) regions filled with square (or cubical in 3D) cells of user-defined size and types. The syntax is very similar to that for UniformInitializer.
Looking in detail at the syntax of BlobInitializer in Listing 3, the <Radius> tag pair defines the radius of a circular (or spherical) domain of cells in pixels. The <Center> tag, with syntax <Center x=“x_position” y=“y_position” z=“z_position”/>, defines the coordinates of the center of the domain. The remaining tags are the same as for UniformInitializer. As with UniformInitializer, we can define multiple regions. We can use both UniformInitializer and BlobInitializer in the same simulation. In the case of overlap, later-specified regions overwrite earlier ones.
We show snapshots of the cell-sorting simulation in Figure 8. The less cohesive NonCondensing cells engulf the more cohesive Condensing cells, which cluster and form a single central domain. By changing the boundary energies we can produce other cell-sorting patterns (95, 96).
Figure 8.
Snapshots of the cell-lattice configurations for the cell-sorting simulation in Listing 3. The boundary-energy hierarchy drives NonCondensing (light grey) cells to surround Condensing (dark grey) cells. The white background denotes surrounding Medium.
V.D Bacterium-and-Macrophage Simulation
In the two simulations we have presented so far, the cellular pattern develops without fields. Often, however, biological patterning mechanisms require us to introduce and evolve chemical fields and to have cells' behaviors depend on the fields. To illustrate the use of fields, we model the in vitro behavior of bacteria and macrophages in blood. In the famous experimental movie taken in the 1950s by David Rogers at Vanderbilt University, the macrophage appears to chase the bacterium, which seems to run away from the macrophage. We can model both behaviors using cell secretion of diffusible chemical signals and movement of the cells in response to the chemical (chemotaxis): the bacterium secretes a signal (a chemoattractant) that attracts the macrophage and the macrophage secretes a signal (a chemorepellant) which repels the bacterium (97).
Listing 4 shows the CC3DML configuration file for the bacterium-and-macrophage simulation.
<CompuCell3D><Potts><Dimensions x=“100” y=“100” z=“1”/><Steps>100000</Steps><Temperature>20</Temperature><LatticeType>Hexagonal</LatticeType></Potts><Plugin Name=“CellType”><CellType TypeName=“Medium” TypeId=“0”/><CellType TypeName=“Bacterium” TypeId=“1” /><CellType TypeName=“Macrophage” TypeId=“2”/><CellType TypeName=“Red” TypeId=“3”/><CellType TypeName=“Wall” TypeId=“4” Freeze=“”/></Plugin><Plugin Name=“VolumeFlex”><VolumeEnergyParameters CellType=“Macrophage” TargetVolume=“150” LambdaVolume=“15”/><VolumeEnergyParameters CellType=“Bacterium” TargetVolume=“10” LambdaVolume=“60”/><VolumeEnergyParameters CellType=“Red” TargetVolume=“100” LambdaVolume=“30”/></Plugin><Plugin Name=“SurfaceFlex”><SurfaceEnergyParameters CellType=“Macrophage” TargetSurface=“50” LambdaSurface=“30”/><SurfaceEnergyParameters CellType=“Bacterium” TargetSurface=“10” LambdaSurface=“4”/><SurfaceEnergyParameters CellType=“Red” TargetSurface=“40” LambdaSurface=“0”/></Plugin><Plugin Name=“Contact”><Energy Type1=“Medium” Type2=“Medium”>0</Energy><Energy Type1=“Macrophage” Type2=“Macrophage”>150</Energy><Energy Type1=“Macrophage” Type2=“Medium”>8</Energy><Energy Type1=“Bacterium” Type2=“Bacterium”>150</Energy><Energy Type1=“Bacterium” Type2=“Macrophage”>15</Energy><Energy Type1=“Bacterium” Type2=“Medium”>8</Energy><Energy Type1=“Wall” Type2=“Wall”>0</Energy><Energy Type1=“Wall” Type2=“Medium”>0</Energy><Energy Type1=“Wall” Type2=“Bacterium”>150</Energy><Energy Type1=“Wall” Type2=“Macrophage”>150</Energy><Energy Type1=“Wall” Type2=“Red”>150</Energy><Energy Type1=“Red” Type2=“Red”>150</Energy><Energy Type1=“Red” Type2=“Medium”>30</Energy><Energy Type1=“Red” Type2=“Bacterium”>150</Energy><Energy Type1=“Red” Type2=“Macrophage”>150</Energy><NeighborOrder>2</NeighborOrder> </Plugin><Plugin Name=“Chemotaxis”><ChemicalField Source=“FlexibleDiffusionSolverFE” Name=“ATTR”><ChemotaxisByType Type=“Macrophage” Lambda=“1”/></ChemicalField><ChemicalField Source=“FlexibleDiffusionSolverFE” Name=“REP”><ChemotaxisByType Type=“Bacterium” Lambda=“-0.1”/></ChemicalField> </Plugin><Steppable Type=“FlexibleDiffusionSolverFE”><DiffusionField><DiffusionData><FieldName>ATTR</FieldName><DiffusionConstant>0.10</DiffusionConstant><DecayConstant>0.00005</DecayConstant><DoNotDiffuseTo>Wall</DoNotDiffuseTo><DoNotDiffuseTo>Red</DoNotDiffuseTo></DiffusionData><SecretionData><Secretion Type=“Bacterium”>200</Secretion></SecretionData></DiffusionField><DiffusionField><DiffusionData><FieldName>REP</FieldName><DiffusionConstant>0.10</DiffusionConstant><DecayConstant>0.001</DecayConstant><DoNotDiffuseTo>Wall</DoNotDiffuseTo><DoNotDiffuseTo>Red</DoNotDiffuseTo></DiffusionData><SecretionData><Secretion Type=“Macrophage”>200</Secretion></SecretionData></DiffusionField></Steppable><Steppable Type=“PIFInitializer”><PIFName>bacterium_macrophage_2D_wall_v3.pif</PIFName></Steppable></CompuCell3D>
Listing 4. CC3DML configuration file for the bacterium-and-macrophage simulation.
The simulation has five generalized-cell types: Medium, Bacterium, Macrophage, Red blood cells and a surrounding Wall. It also has two diffusible fields, representing a chemoattractant, ATTR, and a chemorepellent, REP. Because the default boundary-energy between any generalized-cell type and the edge of the cell lattice is zero, we define a surrounding wall to prevent cells from sticking to the cell-lattice boundary. As in our previous simulations, we assign cell types using the CellType plugin. Note the new syntax in the line specifying the cell type making up the walls:
<CellType TypeName=“Wall” TypeId=“4” Freeze=“”/>
The Freeze=“” attribute excludes generalized cells of type Wall from participating in index copies, which makes the walls immobile.
We replace the Volume plugin with VolumeFlex and add the plugin SurfaceFlex. These plugins allow independent assignment of target values and constraint strengths in the volume-constraint and surface-constraint energies (equations (4) and (5)). These plugins require a line for each generalized-cell type, specifying the type name and the target volume (or target surface area), and λvol (or λsurf ) for that generalized-cell type, e.g.:
<VolumeEnergyParameters CellType=“Name” TargetVolume=“Value” LambdaVolume=“Value ”/>
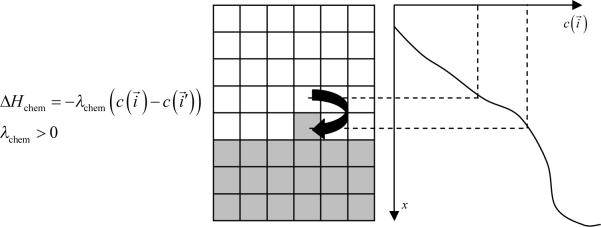
We implement the actual bacterium-macrophage “chasing” mechanism using the Chemotaxis plugin, which specifies how a generalized cell of a given type responds to a field. The Chemotaxis plugin biases a cell's motion up or down a field gradient by changing the calculated effective-energy change used in the acceptance function, equation (7). For a field :
| (9) |
where is the chemical field at the index-copy target pixel, the field at the index-copy source pixel, and λchem the strength and direction of chemotaxis. If λchem > 0 and , then ΔHchem is negative, increasing the probability of accepting the index copy in equation (7). The net effect is that the cell moves up the field gradient with a velocity . If λ < 0 is negative, the opposite occurs, and the cell will move down the field gradient. Plugins with more sophisticated ΔHchem calculations (e.g., including response saturation) are available within CompuCell3D (see the CompuCell3D User Guide).
In the Chemotaxis plugin we must identify the names of the fields, where the field information is stored, the list of the generalized-cell types that will respond to the fields, and the strength and direction of the response (Lambda =λchem). The information for each field is specified using the syntax:
<ChemicalField Source=“where field is stored” Name=“field name”><ChemotaxisByType Type=“cell_type1” Lambda=“lambda1”/><ChemotaxisByType Type=“cell_type2” Lambda=“lambda1”/></ChemicalField>
In our current example, the first field, named ATTR, is stored in FlexibleDiffusionSolverFE. Macrophage cells are attracted to ATTR with λchem = 1. None of the other cell types responds to ATTR. Similarly, Bacterium cells are repelled by REP with λchem = -0.1.
Keep in mind that fields are not created within the Chemotaxis plugin, which only specifies how different cell types respond to the fields. We define and store the fields elsewhere. Here, we use the FlexibeDiffusionSolverFE steppable as the source of our fields. The FlexibleDiffusionSolverFE steppable is the main CompuCell3D tool for defining diffusing fields, which evolve according to the diffusion equation:
| (10) |
where is the field concentration and , and denote the diffusion constant (in m2/s), decay constant (in s-1) and secretion rates (in concentration/s) of the field, respectively. , , and may vary with position and cell-lattice configuration.
As in the Chemotaxis plugin, we may define the behaviors of multiple fields, enclosing each one within <DiffusionField> tag pairs. For each field defined within a <DiffusionData> tag pair, users provide values for the name of the field (using the <FieldName> tag pair), the diffusion constant (using the <DiffusionConstant> tag pair), and the decay constant (using the <DiffusionConstant> tag pair). Forward-Euler methods are numerically unstable for large diffusion constants, limiting the maximum nominal diffusion constant allowed in CompuCell3D simulations. However, by increasing the PDE-solver calling frequency, which reduces the effective time step, CompuCell3D can simulate arbitrarily large diffusion constants. For more information, see the CompuCell3D User Guide.
Each optional <DoNotDiffuseTo> tag pair, with syntax:
<DoNotDiffuseTo>cell_type</DoNotDiffuseTo>
prevents the field from diffusing into field-lattice pixels where the corresponding cell-lattice pixel, , is occupied by a cell, , of the specified type. In our case, chemical fields do not diffuse into the pixels occupied by Wall or Red cells. The optional <SecretionData> tag pair defines a subsection which identifies cells types that secrete or absorb the field and the rates of secretion:
<SecretionData><Secretion Type=“cell_type1”>real_rate1</Secretion><Secretion Type=“cell_type2”>real_rate2</Secretion><SecretionData>
A negative rate simulates absorption. In the bacterium and macrophage simulation, Bacterium cells secrete ATTR and Macrophage cells secrete REP.
We load the initial configuration for the bacterium-and-macrophage simulation using the PIFInitializer steppable. Many simulations require initial generalized-cell configurations that we cannot easily construct from primitive regions filled with cells using BlobInitializer and UniformInitializer. To allow maximum flexibility, CompuCell3D can read the initial cell-lattice configuration from Pixel Initialization Files (PIFs). A PIF is a text file that allows users to assign multiple rectangular (parallelepiped in 3D) pixel regions or single pixels to particular cells.
Each line in a PIF has the syntax:
Cell_id Cell_type x_low x_high y_low y_high z_low z_high
where Cell_id is a unique cell index. A PIF may have multiple, possibly non-adjacent, lines starting with the same Cell_id; all lines with the same Cell_id define pixels of the same generalized cell. The values x_low, x_high, y_low, y_high, z_low and z_high define rectangles (parallelepipeds in 3D) of pixels belonging to the cell. In the case of overlapping pixels, a later line overwrites pixels defined by earlier lines. The following line describes a 6 × 6-pixel square cell with cell index 0 and type Amoeba:
0 Amoeba 10 15 10 15 0 0
If we save this line to the file 'amoebae.pif', we can load it into a simulation using the following syntax:
<Steppable Type=“PIFInitializer”><PIFName>amoebae.pif</PIFName></Steppable>
Listing 5 illustrates how to construct arbitrary shapes using a PIF. Here we define two cells with indices 0 and 1, and cell types Amoeba and Bacterium, respectively. The main body of each cell is a 6 × 6 square to which we attach additional pixels.
0 Amoeba 10 15 10 15 0 01 Bacterium 25 30 25 30 0 00 Amoeba 16 16 15 15 0 01 Bacterium 25 27 31 35 0 0
Listing 5. Simple PIF initializing two cells, one each of type Bacterium and Amoeba.
All lines with the same cell index (first column) define a single cell.
Figure 10 shows the initial cell-lattice configuration specified in Listing 5:
Figure 10.
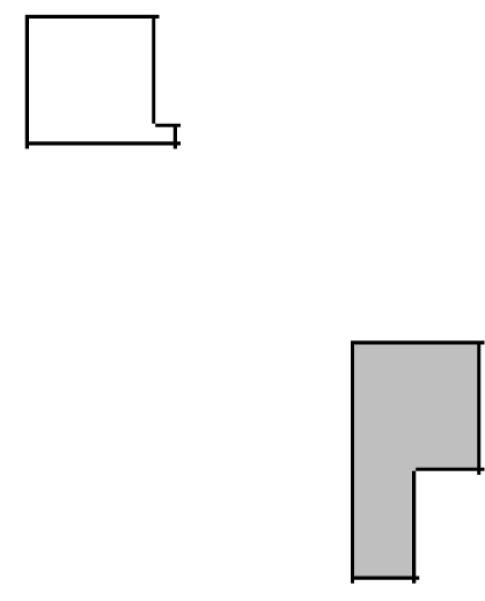
Initial configuration of the cell lattice based on the PIF in Listing 5.
In practice, because constructing complex PIFs by hand is cumbersome, we generally use custom-written scripts to generate the file directly, or convert images stored in graphical formats (e.g., gif, jpeg, png) from experiments or other programs.
Listing 6 shows the PIF for the bacterium-and-macrophage simulation.
0 Red 10 20 10 20 0 01 Red 10 20 40 50 0 02 Red 10 20 70 80 0 03 Red 40 50 0 10 0 04 Red 40 50 30 40 0 05 Red 40 50 60 70 0 06 Red 40 50 90 95 0 07 Red 70 80 10 20 0 08 Red 70 80 40 50 0 09 Red 70 80 70 80 0 010 Wall 0 99 0 1 0 010 Wall 98 99 0 99 0 010 Wall 0 99 98 99 0 010 Wall 0 1 0 99 0 011 Bacterium 5 5 5 5 0 012 Macrophage 35 35 35 35 0 013 Bacterium 65 65 65 65 0 014 Bacterium 65 65 5 5 0 015 Bacterium 5 5 65 65 0 016 Macrophage 75 75 95 95 0 017 Red 24 28 10 20 0 018 Red 24 28 40 50 0 019 Red 24 28 70 80 0 020 Red 40 50 14 20 0 021 Red 40 50 44 50 0 022 Red 40 50 74 80 0 023 Red 54 59 90 95 0 024 Red 70 80 24 28 0 025 Red 70 80 54 59 0 026 Red 70 80 84 90 0 027 Macrophage 10 10 95 95 0 0
Listing 6. PIF defining the initial cell-lattice configuration for the bacterium-and-macrophage simulation. The file is stored as `bacterium_macrophage_2D_wall_v3.pif'.
In Listing 4 we read the cell lattice configuration from the file 'bacterium_macrophage_2D_wall_v3.pif' using the lines:
<Steppable Type=“PIFInitializer”><PIFName>bacterium_macrophage_2D_wall_v3.pif</PIFName></Steppable>
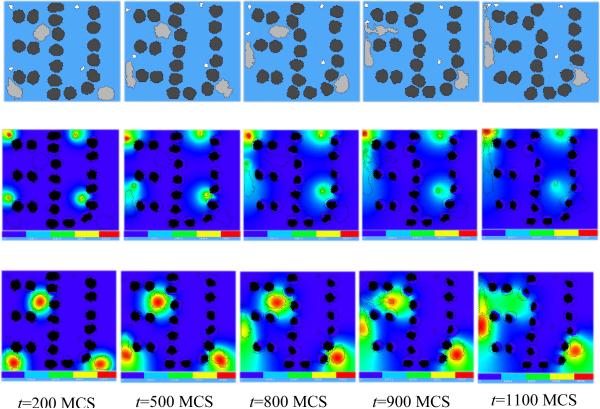
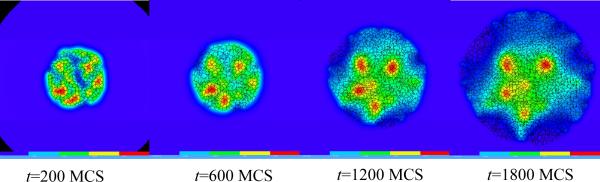
Figure 11 shows snapshots of the bacterium-and-macrophage simulation. By adjusting the properties and number of bacteria, macrophages and red blood cells and the diffusion properties of the chemical fields, we can build a surprisingly good reproduction of the experiment.
Figure 11.
Snapshots of the bacterium-and-macrophage simulation from Listing 4 and the PIF in Listing 6 saved in the file `bacterium_macrophage_2D_wall_v3.pif'. The upper row shows the cell-lattice configuration with the Macrophages in grey, Bacteria in white, red blood cells in dark grey and Medium in blue. Middle row shows the concentration of the chemoattractant ATTR secreted by the Bacteria. The bottom row shows the concentration of the chemorepellant REPL secreted by the Macrophages. The bars at the bottom of the field images show the concentration scales (blue, low concentration, red, high concentration).
VI. Python Scripting
CC3DML is convenient for building simple simulations such as those we presented above. To describe more complex simulations, CompuCell3D allows users to write specialized, shareable modules in C/C++ (through the CompuCell3D Application Programming Interface, or CC3D API) or Python (through a Python-scripting interface). C and C++ modules have the advantage that they run at native speed. However, developing them requires knowledge of both C/C++ and the CC3D API, and their integration with CompuCell3D requires recompilation of the source code. Python module development is less complicated, since Python has simpler syntax than C/C++ and users can modify and extend a library of Python-module templates included with CompuCell3D. Moreover, Python modules do not require recompilation.
Tasks performed by CompuCell3D modules either relate to index-copy attempts (plugins) or run either once, at the beginning or end of a simulation, or once every several MCS (steppables). Tasks run every index-copy attempt, like effective-energy-term calculations, are the most frequently-called tasks in a GGH simulation and writing them in Python may slow simulations. However, steppables and lattice monitors are good candidates for Python implementation and cause negligible performance degradation. Python implementations are suitable for most cell-parameter adjustments that depend on the state of the simulation, e.g., simulating cell growth in response to a chemical, cell-type differentiation and changes in cell-cell adhesion.
VI.A A Short Introduction to Python
Python is an object-oriented scripting language with all the syntactic constructs present in any modern programming language. Python supports popular flow-control statements such as if-elif-else conditional instructions and for and while loops. Unlike C/C++, Python does not use ';' to end lines or '{' and '}' to define code blocks. Instead, Python relies on indentation to define blocks of code. if statements, for or while loops and their subsections are created by a ':' and increasing the level of indentation. The end of a block is indicated by a decrease in the level of indentation. Python uses the '=' operator for assignments and '==' for checking equality between objects. For example, in the following code:
b=2if b==2:a=10for c in range(0,a):b=a+cprint b
we indent the body of the if statement and the body of the inner for loop. The for loop is executed inside the if statement. a=0 assigns the variable a a value of 10, while b==2 is true if b has a value of 2. The for loop assigns the variable c values 0 through a-1 and executes instructions inside the loop body.
As an object-oriented language, Python supports classes, inheritance and polymorphism. Accessing members of objects uses the '.' operator. For example, to access the real part of a complex number, we use the following code:
a=complex(2,3)a=1.5+0.5jprint a.real
Here, real is a member of the Python class complex, which represents complex numbers. If the object has composite subobjects, we use the '.' operator recursively:
object.subobject.member_of_subobject
Users may define Python objects without declaring their type. A single data structure such as a list or dictionary can store objects of multiple types. Python provides automatic memory management, which frees users from remembering to deallocate memory for objects that are no longer used.
Long source code lines can be carried over to the following line using the '\' character:
very_long_variable_name = \very_long_variable_name * very_important_constant
Note that double underscore '__' has a reserved meaning in Python and should not be confused with a single underscore '_'.
We will present additional Python features in the subsequent sections and explain step-by-step some basic concepts of Python programming (for more on Python, see Learning Python, by Mark Lutz (98)). For more information on Python scripting in CompuCell3D, see our Python Tutorials and CompuCell3D User Guide (available from the CompuCell3D website, www.compucell3d.org).
VI.B Building Python-Based CompuCell3D Simulations
Python scripting allows users to augment their CC3DML configuration files with Python scripts or to code their entire simulations in Python (in which case the Python script looks very similar to the CC3DML script it replaces). Listing 7 shows the standard block of template code for running a Python script in conjunction with a CC3DML configuration file.
import sysfrom os import environfrom os import getcwdimport stringsys.path.append(environ[“PYTHON_MODULE_PATH”])import CompuCellSetupsim,simthread = CompuCellSetup.getCoreSimulationObjects()#Create extra player fields here or add attributesCompuCellSetup.initializeSimulationObjects(sim,simthread)#Add Python steppables heresteppableRegistry=CompuCellSetup.getSteppableRegistry()CompuCellSetup.mainLoop(sim,simthread,steppableRegistry)
Listing 7. Basic Python template to run a CompuCell3D simulation through a Python interpreter. Later examples will be based on this script.
The import sys line provides access to standard functions and variables needed to manipulate the Python runtime environment. The next two lines,
from os import environfrom os import getcwd
import environ and getcwd housekeeping functions into the current namespace (i.e., current script) and are included in all our Python programs. In the next three lines,
import stringsys.path.append(environ[“PYTHON_MODULE_PATH”])import CompuCellSetup
we import the string module, which contains convenience functions for performing operations on strings of characters, set the search path for Python modules and import the CompuCellSetup module, which provides a set of convenience functions that simplify initialization of CompuCell3D simulations.
Next, we create and initialize the core CompuCell3D modules:
sim,simthread = CompuCellSetup.getCoreSimulationObjects()CompuCellSetup.initializeSimulationObjects(sim,simthread)
We then create a steppable registry (a Python container that stores steppables, i.e., a list of all steppables that the Python code can access) and pass it to the function that runs the simulation:
steppableRegistry=CompuCellSetup.getSteppableRegistry()CompuCellSetup.mainLoop(sim,simthread,steppableRegistry)
In the next section, we extend this template to build a simple simulation.
VI.C Cell-Type-Oscillator Simulation
Suppose that we would like to add a caricature of oscillatory gene expression to our cell-sorting simulation (Listing 3) so that cells exchange types every 100 MCS. We will implement the changes of cell types using a Python steppable, since it occurs at intervals of 100 MCS.
Listing 8 shows the changes to the Python template in Listing 7 that are necessary to create the desired type switching (changes are shown in bold).
import sysfrom os import environfrom os import getcwdimport stringsys.path.append(environ[”PYTHON_MODULE_PATH”])import CompuCellSetupsim,simthread = CompuCellSetup.getCoreSimulationObjects()from PySteppables import *class TypeSwitcherSteppable(SteppablePy):def __init__(self,_simulator,_frequency=100):SteppablePy.__init__(self,_frequency)self.simulator=_simulatorself.inventory=self.simulator.getPotts().getCellInventory()self.cellList=CellList(self.inventory)def step(self,mcs):for cell in self.cellList:if cell.type==1:cell.type=2elif (cell.type==2):cell.type=1else:print ”Unknown type. In cellsort simulation there should\ only be two types 1 and 2”#Create extra player fields here or add attributesCompuCellSetup.initializeSimulationObjects(sim,simthread)#Add Python steppables heresteppableRegistry=CompuCellSetup.getSteppableRegistry()typeSwitcherSteppable=TypeSwitcherSteppable(sim,100);steppableRegistry.registerSteppable(typeSwitcherSteppable)CompuCellSetup.mainLoop(sim,simthread,steppableRegistry)
Listing 8. Python script expanding the template code in Listing 7 into a simple TypeSwitcherSteppable steppable. The code illustrates dynamic modification of cell parameters using a Python script. Lines added to Listing 7 are shown in bold.
A CompuCell3D steppable is a class (a type of object) that holds the parameters and functions necessary for carrying out a task. Every steppable defines at least 4 functions:__init__(self, _simulator, _frequency), start(self), step(self, mcs) and finish(self).
CompuCell3D calls the start(self) function once at the beginning of the simulation before any index-copy attempts. It calls the step(self, mcs) function periodically after every _frequency MCS. It calls the finish(self) function once at the end of the simulation. Listing 8 does not have explicit start(self) or finish(self) functions. Instead, the class definition:
class TypeSwitcherSteppable(SteppablePy):
causes the TypeSwitcherSteppable to inherit components of the SteppablePy class. SteppablePy contains default definitions of the start(self), step(self,mcs) and finish(self) functions. Inheritance reduces the length of the user-written Python code and ensures that the TypeSwitcherSteppable object has all needed components. The line:
from PySteppables import *
makes the content of `PySteppables.py' file (or module) available in the current namespace. The PySteppables module includes the SteppablePy base class.
The __init__ function is a constructor that accepts user-defined parameters and initializes a steppable object. Consider the __init__ function of the TypeSwitcherSteppable:
def __init__(self,_simulator,_frequency=100):SteppablePy.__init__(self,_frequency)self.simulator=_simulatorself.inventory=self.simulator.getPotts().getCellInventory()self.cellList=CellList(self.inventory)
In the def line, we pass the necessary parameters: self (which is used in Python to access class variables from within the class), _simulator (the main CompuCell3D kernel object which runs the simulation), and _frequency (which tells steppableRegistry how often to run the steppable, here, every 100 MCS). Next we call the constructor for the inheritance class, SteppablePy, as required by Python. The following statement:
self.simulator=_simulator
assigns to the class variable self.simulator a reference to _simulator object, passed from the main script. We can think about Python reference as a pointer variable that stores the address of the object but not a copy of the object itself. The last two lines construct a list of all generalized cells in the simulation, a cell inventory, which allows us to visit all the cells with a simple for loop to perform various tasks. The cell inventory is a dynamic structure, i.e., it updates automatically when cells are created or destroyed during a simulation.
The section of the TypeSwitcherSteppable steppable which implements the cell-type switching is found in the step(self, mcs) function:
def step(self,mcs):for cell in self.cellList:if cell.type==1:cell.type=2elif (cell.type==2):cell.type=1else:print ”Unknown type”
Here we use the cell inventory to iterate over all cells in the simulation and reassign their cell types between cell.type 1 and cell.type 2. If we encounter a cell.type that is neither 1 nor 2 (which we should not), we print an error message.
Once we have created a steppable (i.e., created an object of class TypeSwitcherSteppable) we must register it using registerSteppable function from steppableRegistry object:
typeSwitcherSteppable=TypeSwitcherSteppable(sim,100);steppableRegistry.registerSteppable(typeSwitcherSteppable)
CompuCell3D will not run unregistered steppables. As we will see, much of the script is not specific to this example. We will recycle it with slight changes in later examples.
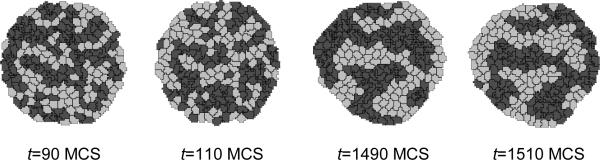
Figure 12 shows snapshots of the cell-type-oscillator simulation.
Figure 12.
Results of the Python cell-type-oscillator simulation using the TypeSwitcherSteppable steppable implemented in Listing 8 in conjunction with the CC3DML cell-sorting simulation in Listing 3. Cells exchange types and corresponding adhesivities and colors every 100 MCS; i.e., between t=90 MCS and t=110 MCS and between t=1490 MCS and t=1510 MCS.
We mentioned earlier that users can run simulations without a CC3DML configuration file. Listing 9 shows the cell-type-oscillator simulation written entirely in Python, with changes to Listing 8 shown in bold.
def configureSimulation(sim):import CompuCellimport CompuCellSetupppd=CompuCell.PottsParseData()ppd.Steps(20000)ppd.Temperature(5)ppd.NeighborOrder(2)ppd.Dimensions(CompuCell.Dim3D(100,100,1))ctpd=CompuCell.CellTypeParseData()ctpd.CellType(“Medium”,0)ctpd.CellType(“Condensing”,1)ctpd.CellType(“NonCondensing”,2)cpd=CompuCell.ContactParseData()cpd.Energy(“Medium”,“Medium”,0)cpd.Energy(“NonCondensing”,“NonCondensing”,16)cpd.Energy(“Condensing”,“Condensing”,2)cpd.Energy(“NonCondensing”,“Condensing”,11)cpd.Energy(“NonCondensing”,“Medium”,16)cpd.Energy(“Condensing”,“Medium”,16)vpd=CompuCell.VolumeParseData()vpd.LambdaVolume(1.0)vpd.TargetVolume(25.0)bipd=CompuCell.BlobInitializerParseData()region=bipd.Region()region.Center(CompuCell.Point3D(50,50,0))region.Radius(40)region.Types(“Condensing”)region.Types(“NonCondensing”)region.Width(5)CompuCellSetup.registerPotts(sim,ppd)CompuCellSetup.registerPlugin(sim,ctpd)CompuCellSetup.registerPlugin(sim,cpd)CompuCellSetup.registerPlugin(sim,vpd)CompuCellSetup.registerSteppable(sim,bipd)import sysfrom os import environfrom os import getcwdimport stringsys.path.append(environ[“PYTHON_MODULE_PATH”])import CompuCellSetupsim,simthread = CompuCellSetup.getCoreSimulationObjects()configureSimulation(sim)from PySteppables import *class TypeSwitcherSteppable(SteppablePy):def __init__(self,_simulator,_frequency=100):SteppablePy.__init__(self,_frequency)self.simulator=_simulatorself.inventory=self.simulator.getPotts().getCellInventory()self.cellList=CellList(self.inventory)def step(self,mcs):for cell in self.cellList:if cell.type==1:cell.type=2elif (cell.type==2):cell.type=1else:print “Unknown type. In cellsort simulation there should only be two types 1 and 2”#Create extra player fields here or add attributes CompuCellSetup.initializeSimulationObjects(sim,simthread)#Add Python steppables here steppableRegistry=CompuCellSetup.getSteppableRegistry()typeSwitcherSteppable=TypeSwitcherSteppable(sim,100); steppableRegistry.registerSteppable(typeSwitcherSteppable)CompuCellSetup.mainLoop(sim,simthread,steppableRegistry)CompuCellSetup.mainLoop(sim,simthread,steppableRegistry)
Listing 9. Stand-alone Python cell-type-oscillator script containing an initial section that replaces the CC3DML configuration file from Listing 3. Lines added to Listing 8 are shown in bold.
The configureSimulation function replaces the CC3DML file from Listing 3. After importing CompuCell and CompuCellSetup, we have access to functions and modules that provide all the functionality necessary to code a simulation in Python. The general syntax for the opening lines of each block is:
snpd=CompuCell.SectionNameParseData()
where SectionName refers to the name of the section in a CC3DML configuration file and snpd is the name of the object of type SectionNameParseData. The rest of the block usually follows the syntax:
snpd.TagName(values)
where TagName corresponds to the name of the tag pair used to assign a value to a parameter in a CC3DML file. For values within subsections, the syntax is:
snpd.SubsectionName().TagName(values)
To input dimensions, we use the syntax:
snpd.TagName(CompuCell.Dim3D(x_dim,y_dim,z_dim))
where x_dim, y_dim, and z_dim are the x, y and z dimensions. To input a set of (x,y,z) coordinates, we use the syntax:
snpd.TagName(CompuCell.Point3D(x_coord,y_coord,z_coord))
where x_coord, y_coord, and z_coord are the x, y, and z coordinates.
In the first block (PottsParseData), we input the cell-lattice parameter values using the syntax:
ppd.ParameterName(value)
where ParameterName matches a parameter name used in the CC3DML lattice section.
Next we define the cell types using the syntax:
ctpd.CellType(“cell_type”,cell_id)
The next section assigns boundary energies between the cell types:
cpd.Energy(“cell_type_1”,“cell_type_2”,contact_energy)
We specify the rest of the parameter values in a similar fashion, following the general syntax described above.
The examples in Listing 8 and Listing 9 define the TypeSwitcherSteppable class within the main Python script. However, separating extension modules from the main script and using an import statement to refer to modules stored in external files is more practical. Using separate files ensures that each module can be used in multiple simulations without duplicating source code, and makes scripts more readable and editable. We will follow this convention in our remaining examples.
VI.D Two-Dimensional Foam-Flow Simulation
CompuCell3D can simulate simple physical experiments with foams. Indeed, GGH techniques grew out of foam-simulation techniques (73). Our next example shows how to use CC3DML and Python scripts to simulate quasi-two-dimensional foam flow.
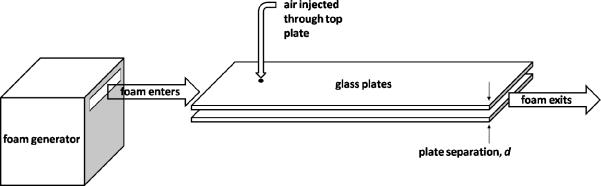
The experimental apparatus (Figure 13) consists of a channel created by two parallel rectangular glass plates separated by 5 mm, with the gap between their long sides sealed and that between their short sides open. A foam generator injects small, uniform size bubbles at one short end, pushing older bubbles towards the open end of the channel, creating a foam flow. The top glass plate has a hole through which we inject air. Bubbles passing under this point grow because of the air injected into them, forming characteristic patterns (Figure 14) (99).
Figure 13.
Schematic of experiment for studying quasi-2D foam flow.
Figure 14.
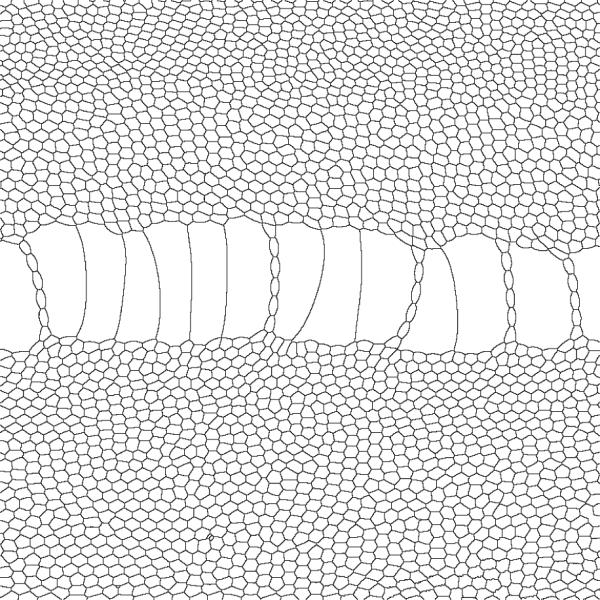
Detail of processed experimental image of flowing quasi-2D bubbles. Image size is 15 cm × 15 cm.
Generalized cells will represent bubbles in this simulation. To simulate this experiment in CompuCell3D we need to write Python steppables that 1) create bubbles at one end of the channel, 2) inject air into the bubble which includes a given location (the identity of this bubble will change in time due to the flow), 3) remove bubbles at the open end of the channel. We will store the source code in a file called `foamairSteppables.py'. We will also need a main Python script to call these steppables appropriately.
We simulate bubble injection by creating generalized cells (bubbles) along the lattice edge corresponding to the left end of the channel (small-x values of the cell lattice). We simulate air injection into a bubble at the injection point, by identifying the bubble currently at the injection point and increasing its target volume at a fixed rate. Removing a bubble from the simulation simply requires assigning it a target volume of zero once it comes close to the right end of the channel (large-x values of the cell lattice).
We first define a CC3DML configuration file for the foam-flow simulation (Listing 10).
<CompuCell3D><Potts><Dimensions x=“200” y=“50” z=“1”/><Steps>10000</Steps><Temperature>5</Temperature><LatticeType>Hexagonal</LatticeType></Potts><Plugin Name=“VolumeLocalFlex”/><Plugin Name=“CellType”><CellType TypeName=“Medium” TypeId=“0”/><CellType TypeName=“Foam” TypeId=“1”/></Plugin><Plugin Name=“Contact”><Energy Type1=“Medium” Type2=“Medium”>5</Energy><Energy Type1=“Foam” Type2=“Foam”>5</Energy><Energy Type1=“Foam” Type2=“Medium”>5</Energy><NeighborOrder>3</NeighborOrder></Plugin><Plugin Name=“CenterOfMass”/></CompuCell3D>
Listing 10. CC3DML configuration file for the foam-flow simulation. This file initializes needed plugins but all of the interesting work is done in Python.
The CC3DML configuration file is simple: it initializes the VolumeLocalFlex, CellType, Contact and CenterOfMass plugins. We do not use a cell-lattice-initializer steppable, because all bubbles are created as the simulation runs. We use VolumeLocalFlex because individual bubbles will change their target volumes during the simulation. We also include the CenterOfMass plugin to track the changing centroids of each bubble. The CenterOfMass plugin in CompuCell3D actually calculates , the centroid of the generalized cell multiplied by volume of the cell:
| (11) |
so the actual centroid of the bubble is:
| (12) |
The ability to track a generalized-cell's centroid is useful if we need to pick a single reference point in the cell. In this example we will remove bubbles whose centroids have x-coordinate greater than a cutoff value.
We will implement the Python script in four sections: 1) a main script (Listing 11), which runs every MCS and calls the steppables to (2) create bubbles at the left end of the cell lattice (BubbleNucleator, Listing 12), (3) enlarge the target volume of the bubble at the injector site (AirInjector, Listing 13), and (4) set the target volume of bubbles at the right end of the cell lattice to zero (BubbleCellRemover, Listing 14). We store classes (2-4) in a separate file called `foamairSteppables.py'.
import sysfrom os import environimport stringsys.path.append(environ[“PYTHON_MODULE_PATH”])import CompuCellSetupsim,simthread = CompuCellSetup.getCoreSimulationObjects()#Create extra player fields hereCompuCellSetup.initializeSimulationObjects(sim,simthread)#Add Python steppables heresteppableRegistry=CompuCellSetup.getSteppableRegistry()from foamairSteppables import BubbleNucleatorbubbleNucleator=BubbleNucleator(sim,20)bubbleNucleator.setNumberOfNewBubbles(1)bubbleNucleator.setInitialTargetVolume(25)bubbleNucleator.setInitialLambdaVolume(2.0)bubbleNucleator.setInitialCellType(1)steppableRegistry.registerSteppable(bubbleNucleator)from foamairSteppables import AirInjectorairInjector=AirInjector(sim,40)airInjector.setVolumeIncrement(25)airInjector.setInjectionPoint(50,25,0)steppableRegistry.registerSteppable(airInjector)from foamairSteppables import BubbleCellRemoverbubbleCellRemover=BubbleCellRemover(sim)bubbleCellRemover.setCutoffValue(170)steppableRegistry.registerSteppable(bubbleCellRemover)CompuCellSetup.mainLoop(sim,simthread,steppableRegistry)
Listing 11. Main Python Script for foam-flow simulation. Changes to the template (Listing 7) are shown in bold.
The main script in Listing 11 builds on the template Python code in Listing 7; we show changes in bold. The line:
from foamairSteppables import BubbleNucleator
tells Python to look for the BubbleNucleator class in the file named `foamairSteppables.py'.
bubbleNucleator=BubbleNucleator(sim, 20)
creates the steppable BubbleNucleator that will run every 20 MCS. The next few lines in this section pass the number of bubbles to create, which in our case is one:
bubbleNucleator.setNumberOfNewBubbles(1)
the initial Vt for the new bubble, which is 25 pixels:
bubbleNucleator.setInitialTargetVolume(25)
the initial λvolfor the bubble:
bubbleNucleator.setInitialLambdaVolume(2.0)
and the bubble's type.id:
bubbleNucleator.setInitialCellType(1)
Finally, we register the steppable:
steppableRegistry.registerSteppable(bubbleNucleator)
The next group of lines repeats the process for the AirInjector steppable, reading it from the file `foamairSteppables.py':
from foamairSteppables import AirInjector
AirInjector is run every 40 MCS:
airInjector=AirInjector(sim, 40)
and increases Vt by 25:
airInjector.setVolumeIncrement(25)
for the bubble occupying the pixel at the point (50, 25, 0) on the cell lattice:
airInjector.setInjectionPoint(50,25,0)
As before, the final line registers the steppable:
steppableRegistry.registerSteppable(airInjector)
The final new section reads the BubbleCellRemover steppable from the file `foamairSteppables.py':
from foamairSteppables import BubbleCellRemover
and invokes the steppable, telling it to run every MCS; note that we have omitted the number after sim:
bubbleCellRemover=BubbleCellRemover(sim)
Next we set 170 as the x-coordinate at which we will destroy bubbles:
bubbleCellRemover.setCutoffValue(170)
and, finally, register BubbleCellRemover
steppableRegistry.registerSteppable(bubbleCellRemover)
We must also write Python code to define the three steppables BubbleNucleator, AirInjector, and BubbleCellRemover and save them in the file `foamairSteppables.py'.
Listing 12 shows the code for the BubbleNucleator steppable.
from CompuCell import Point3Dfrom random import randintclass BubbleNucleator(SteppablePy):def __init__(self,_simulator,_frequency=1):SteppablePy.__init__(self,_frequency)self.simulator=_simulatordef start(self):self.Potts=self.simulator.getPotts()self.dim=self.Potts.getCellFieldG().getDim()def setNumberOfNewBubbles(self,_numNewBubbles):self.numNewBubbles=int(_numNewBubbles)def setInitialTargetVolume(self,_initTargetVolume):self.initTargetVolume=_initTargetVolumedef setInitialLambdaVolume(self,_initLambdaVolume):self.initLambdaVolume=_initLambdaVolumedef setInitialCellType(self,_initCellType):self.initCellType=_initCellTypedef createNewCell(self,pt):print “Nucleated bubble at ”,ptcell=self.Potts.createCellG(pt)cell.targetVolume=self.initTargetVolumecell.type=self.initCellTypecell.lambdaVolume=self.initLambdaVolumedef nucleateBubble(self):pt=Point3D(0,0,0)pt.y=randint(0,self.dim.y-1)pt.x=3self.createNewCell(pt)def step(self,mcs):for i in xrange(self.numNewBubbles):self.nucleateBubble()
Listing 12. Python code for the BubbleNucleator steppable, saved in the file `foamairSteppables.py'. This module creates bubbles at points with random y coordinates and x coordinate of 3.
The first two lines import necessary modules, where the line:
from CompuCell import Point3D
allows us to access points on the simulation cell lattice, and the line:
from random import randint
allows us to generate random integers.
In the constructor of the BubbleNucleator steppable class we assign to the variable self.simulator a reference to the simulator object from the CompuCell3D kernel. In the start(self) function, we assign a reference to the Potts object from the CompuCell3D kernel to the variable self.Potts:
self.Potts=self.simulator.getPotts()
and assign the dimensions of the cell lattice to self.dim:
self.dim=self.Potts.getCellFieldG().getDim()
In addition to the four essential steppable member functions (__init__(self, _simulator, _frequency), start(self), step(self, mcs) and finish(self)), BubbleNucleator includes several functions, some of which set parameters and some of which perform necessary tasks. The functions setNumberOfNewBubbles, setInitialTargetVolume and setInitialLambdaVolume accept the values passed from the main Python script in Listing 11.
The CreateNewCell function requires that we pass the coordinates of the point, pt, at which to create a new bubble:
def CreateNewCell (self,pt):
Then we use a built-in CompuCell3D function to add a new bubble at that location:
cell=self.Potts.createCellG(pt)
assigning the new cell a target volume Vt = targetVolume:
cell.targetVolume=self.initTargetVolume
type, τ = type:
cell.type=self.initCellType
and compressibility λvol = lambdaVolume:
cell.lambdaVolume=initLambdaVolume
based on the values passed to the BubbleNucleator steppable from the main script. The first three lines of the nucleateBubble function create a reference to a point on the cell lattice (pt=Point3D(0,0,0)), assign it a random y-coordinate between 0 and y_dim-1:
pt.y=randint(0,self.dim.y-1)
and an x-coordinate of 3:
pt.x=3
The line calls the createNewCell function and passes it the point (pt) at which to create the new bubble:
self.createNewCell(pt)
Finally, the step(self,mcs) function calls the nucleateBubble function self.numNewBubbles times per MCS.
Listing 13 shows the code for the AirInjector steppable.
class AirInjector(SteppablePy):def __init__(self,_simulator,_frequency=1):SteppablePy.__init__(self,_frequency)self.simulator=_simulatorself.Potts=self.simulator.getPotts()self.cellField=self.Potts.getCellFieldG()def start(self): passdef setInjectionPoint(self,_x,_y,_z):self.injectionPoint=CompuCell.Point3D(int(_x),int(_y),int(_z))def setVolumeIncrement(self,_increment):self.volumeIncrement=_incrementdef step(self,mcs):if mcs <5000:returncell=self.cellField.get(self.injectionPoint)if cell:cell.targetVolume+=self.volumeIncrement
Listing 13. Python code for the AirInjector steppable which simulates air injection into the bubble currently occupying the cell-lattice pixel at location (x,y,z). Air injection begins after 5000 MCS to allow the channel to partially fill with bubbles. The steppable is saved in file `foamairSteppables.py'.
The first three lines of the __init__(self,_simulator,_frequency) function are identical to the same lines in the BubbleNucleator steppable (Listing 12). The final line of the function:
self.cellField=self.Potts.getCellFieldG()
loads the cell-lattice parameters. The start(self) function in this steppable does not do anything:
def start(self): pass
The next two functions read the injectionPoint and volumeIncrement passed to the AirInjector steppable by the main Python script (Listing 11). The step function uses these values to identify the bubble at the injection site, self.injectionPoint:
and then increment that bubble's target volume Vt by self.volumeIncrement:
cell=self.cellField.get(self.injectionPoint)
Note the syntax:
if cell:
which we use to test whether a cell is Medium or not. Medium in CompuCell3D is assigned a NULL pointer, which, in Python, becomes a None object. Python evaluates the None object as False and other objects (in our case, bubbles) as True, so the task is only carried out on bubbles, not Medium.
In the first two lines of the step(self,mcs) function, we tell the function not to perform its task until 5000 MCS have elapsed:
if mcs <5000: return
The 5000 MCS delay allows the simulation to establish a uniform flow of small bubbles throughout a large portion of the cell lattice.
Finally, we define the BubbleCellRemover steppable (Listing 14).
class BubbleCellRemover(SteppablePy):def __init__(self,_simulator,_frequency=1):SteppablePy.__init__(self,_frequency)self.simulator=_simulatorself.inventory=self.simulator.getPotts().getCellInventory()self.cellList=CellList(self.inventory)def start(self):self.Potts=self.simulator.getPotts()self.dim=self.Potts.getCellFieldG().getDim()def setCutoffValue(self,_cutoffValue):self.cutoffValue=_cutoffValuedef step(self,mcs):for cell in self.cellList:if cell:if int(cell.xCM/float(cell.volume))>self.cutoffValue:cell.targetVolume=0cell.lambdaVolume=10000
Listing 14. Python code for the BubbleCellRemover steppable. This module removes cells once the x-coordinates of their centroids > cutoffValue by setting their target volumes to zero and increasing their λvol to 10000. Like the other steppables in the foam-flow simulation, we save it in the file `foamairSteppables.py'.
At each MCS we scan the cell inventory looking for cells whose centroid has an x-coordinate close to the right end of the lattice and remove these cells from the simulation by setting their target volumes to zero and increasing λvol to 10000.
The first two lines of the __init__ (self,_simulator,_frequency) function are identical to the corresponding lines in the BubbleNucleator and AirInjector steppables (Listing 12 and Listing 13). In the third line of the function, we gain access to the generalized-cell inventory:
self.inventory=self.simulator.getPotts().getCellInventory()
and in the fourth line we make a list containing all of the generalized cells in the simulation:
self.cellList=CellList(self.inventory)
The start(self) function is identical to that of the BubbleNucleator steppable (Listing 12), and performs the same function.
The next function:
setCutoffValue(self,_cutoffValue)
reads the cutoffValue for the x-coordinate that we passed to BubbleCellRemover from the main Python script (Listing 11). Finally, the step(self, mcs) function iterates through the cell inventory. We first check to make sure that the cell is not Medium:
if cell:
For each non-Medium cell we test whether the x-coordinate of the cell's centroid is greater than the cutoffValue:
if int(cell.xCM/float(cell.volume))>self.cutoffValue:
and, if it is, set that cell's targetVolume, Vt, to zero:
cell.targetVolume=0
and its λvol 10000:
cell.lambdaVolume=10000
Running the CC3DML file from Listing 10 and the main Python script from Listing 11 (which loads the steppables in Listing 12, Listing 13 and Listing 14 from the file `foamairSteppables.py') produces the snapshots shown in Figure 15.
Figure 15.
Results of the foam-flow simulation on a 2D 3rd-neighbor hexagonal lattice. Simulation code is given in Listing 10,Listing 11, Listing 12, Listing 13 and Listing 14.
VI.E. Diffusing-Field-Based Cell-Growth Simulation
One of the most frequent uses of Python scripting in CompuCell3D simulations is to modify cell behavior based on local field concentrations. To demonstrate this use, we incorporate stem-cell-like behavior into the cell-sorting simulation from Listing 1. This extension requires including relatively sophisticated interactions between cells and diffusing chemical, FGF (100).
We simulate a situation where NonCondensing cells secrete FGF, which diffuses freely through the cell lattice and obeys:
| (13) |
where [FGF] denotes the FGF concentration and Condensing cells respond to the field by growing at a constant rate proportional to the FGF concentration at their centroids;
| (14) |
When they reach a threshold volume, the Condensing cells undergo mitosis. One of the resulting daughter cells remains a Condensing cell, while the other daughter cell has an equal probability of becoming either another Condensing cell or a DifferentiatedCondensing cell. DifferentiatedCondensing cells do not divide.
Each generalized cell in CompuCell3D has a default list of attributes, e.g. type, volume, surface (area), target volume, etc.. However, CompuCell3D allows users to add cell attributes during execution of simulations. E.g., in the current simulation, we will record data on each cell division in a list attached to each cell. Generalized cell attributes can be added using either C++ or Python. However, attributes added using Python are not accessible from C++ modules.
As in the foam-flow simulation, we divide the necessary simulation tasks among different Python modules (or classes) which we save in a file 'cellsort_2D_field_modules.py' and call from the main Python script. We reuse elements of the CC3DML files we presented earlier to construct the CC3DML configuration file, presented in Listing 15.
<CompuCell3D><Potts><Dimensions x=“200” y=“200” z=“1”/><Steps>10000</Steps><Temperature>10</Temperature><NeighborOrder>2</NeighborOrder></Potts><Plugin Name=“VolumeLocalFlex”/><Plugin Name=“CellType”><CellType TypeName=“Medium” TypeId=“0”/><CellType TypeName=“Condensing” TypeId=“1”/><CellType TypeName=“NonCondensing” TypeId=“2”/><CellType TypeName=“CondensingDifferentiated” TypeId=“3”/></Plugin><Plugin Name=“Contact”><Energy Type1=“Medium” Type2=“Medium”>0</Energy><Energy Type1=“NonCondensing” Type2=“NonCondensing”>16</Energy><Energy Type1=“Condensing” Type2=“Condensing”>2</Energy><Energy Type1=“NonCondensing” Type2=“Condensing”>11</Energy><Energy Type1=“NonCondensing” Type2=“Medium”>16</Energy><Energy Type1=“Condensing” Type2=“Medium”>16</Energy><Energy Type1=“CondensingDifferentiated”Type2=“CondensingDifferentiated”>2</Energy><Energy Type1=“CondensingDifferentiated”Type2=“Condensing”>2</Energy><Energy Type1=“CondensingDifferentiated”Type2=“NonCondensing”>11</Energy><Energy Type1=“CondensingDifferentiated” Type2=“Medium”>16</Energy><NeighborOrder>2</NeighborOrder></Plugin><Plugin Name=“CenterOfMass”/><Steppable Type=“FlexibleDiffusionSolverFE”><DiffusionField><DiffusionData><FieldName>FGF</FieldName><DiffusionConstant>0.10</DiffusionConstant><DecayConstant>0.00005</DecayConstant></DiffusionData><SecretionData><Secretion Type=“NonCondensing”>0.05</Secretion></SecretionData></DiffusionField></Steppable><Steppable Type=“BlobInitializer”><Region><Gap>0</Gap><Width>5</Width><Radius>40</Radius><Center x=“100” y=“100” z=“0”/><Types>Condensing,NonCondensing</Types></Region></Steppable></CompuCell3D>
Listing 15. CC3DML code for the diffusing-field-based cell-growth simulation.
The CC3DML code is a slightly extended version of the cell-sorting code in Listing 3 plus the FlexibleDiffusionSolverFE discussed in the bacterium-and-macrophage simulation (see Listing 4). The initial cell-lattice does not contain any CondensingDifferentiated cells. These cells appear only as the result of mitosis. We use the VolumeLocalFlex plugin to allow the target volume to vary individually for each cell, allowing cell growth as discussed in the foam-flow simulation. We manage the volume-constraint parameters using a Python script. The CenterOfMass plugin provides a reference point in each cell at which we measure the FGF concentration. We then adjust the cell's target volume accordingly.
To build this simulation in CompuCell3D we need to write several Python routines. We need: 1) A steppable, VolumeConstraintSteppable to initialize the volume-constraint parameters for each cell and to simulate cell growth by periodically increasing Condensing cells' target volumes in proportion to the FGF concentration at their centroids. 2) A plugin, CellsortMitosis, that runs the CompuCell3D mitosis algorithm when any cell reaches a threshold volume and then adjusts the parameters of the resulting parent and daughter cells. This plugin also appends information about the time and type of cell division to a list attached to each cell. 3) A steppable, MitosisDataPrinterSteppable, that prints the cell-division information from the lists attached to each cell. 4) A class, MitosisData, which MitosisDataPrinterSteppable uses to extract and format the data it prints. 5) A main Python script to call the steppables and the CellsortMitosis plugin appropriately. We store the source code for routines 1)-4) in a separate file called `cellsort_2D_field_modules.py'.
Listing 16 shows the main Python script for the diffusing-field-based cell-growth simulation, with changes to the template (Listing 7) shown in bold.
import sysfrom os import environfrom os import getcwdimport stringsys.path.append(environ[“PYTHON_MODULE_PATH”])import CompuCellSetupsim,simthread = CompuCellSetup.getCoreSimulationObjects()#add additional attributespyAttributeAdder,listAdder=CompuCellSetup.attachListToCells(sim)CompuCellSetup.initializeSimulationObjects(sim,simthread)#notice importing CompuCell to main script has to be#done after call to getCoreSimulationObjects()import CompuCellchangeWatcherRegistry=CompuCellSetup.getChangeWatcherRegistry(sim)stepperRegistry=CompuCellSetup.getStepperRegistry(sim)from cellsort_2D_field_modules import CellsortMitosiscellsortMitosis=CellsortMitosis(sim,changeWatcherRegistry,\ stepperRegistry)cellsortMitosis.setDoublingVolume(50)#Add Python steppables heresteppableRegistry=CompuCellSetup.getSteppableRegistry()from cellsort_2D_field_modules import VolumeConstraintSteppablevolumeConstraint=VolumeConstraintSteppable(sim)steppableRegistry.registerSteppable(volumeConstraint)from cellsort_2D_field_modules import MitosisDataPrinterSteppablemitosisDataPrinterSteppable=MitosisDataPrinterSteppable(sim)steppableRegistry.registerSteppable(mitosisDataPrinterSteppable)CompuCellSetup.mainLoop(sim,simthread,steppableRegistry)
Listing 16. Main Python script for the diffusing-field-based cell-growth simulation. Changes to the template code (Listing 7) shown in bold.
The first change to the template code (Listing 7) is:
pyAttributeAdder,listAdder=CompuCellSetup.attachListToCells(sim)
which instructs the CompuCell3D kernel to attach a Python-defined list to each cell when it creates it. This list serves as a generic container which can store any set of Python objects and hence any set of generalized-cell properties. In the current simulation, we use the list to store objects of the class MitosisData, which records the Monte Carlo Step at which each cell division involving the current cell or its parent, happened, as well as, the cell index and cell type of the parent and daughter cells.
Because one of our Python modules is a lattice monitor, rather than a steppable, we need to create stepperRegistry and changeWatcherRegistry objects, which store the two types of lattice monitors:
changeWatcherRegistry=CompuCellSetup.getChangeWatcherRegistry(sim)stepperRegistry=CompuCellSetup.getStepperRegistry(sim)
The CellsortMitosis plugin is a lattice monitor because it acts in response to certain index-copy events; it is invoked whenever a cell's volume reaches the threshold volume for mitosis. The following lines create the CellsortMitosis lattice monitor and register it with the stepperRegistry and changeWatcherRegistry:
Because the base class inherited by CellsortMitosis, unlike our steppables, handles registration internally, we do not have to register CellsortMitosis explicitly. We can now set the threshold volume at which Condensing cells divide:
from cellsort_2D_field_modules import CellsortMitosis cellsortMitosis = CellsortMitosis(sim,changeWatcherRegistry,\ stepperRegistry)
Next we import the VolumeConstraintSteppable steppable, which initializes cells' target volumes and compressibilities at the beginning of the simulation and also implements chemical-dependent cell growth for Condensing cells, and register it:
cellsortMitosis.setDoublingVolume(50)
Finally, we import, create and register the MitosisDataPrinterSteppable steppable, which prints the content of MitosisData objects for cells that have divided:
from cellsort_2D_field_modules import VolumeConstraintSteppablevolumeConstraint=VolumeConstraintSteppable(sim)steppableRegistry.registerSteppable(volumeConstraint)
The number of MitosisData objects stored in each cell at any given Monte Carlo Step depends on cell type (NonCondensing cells do not divide, whereas Condensing cells can divide multiple times), and how often a given cell has divided.
Moving on to the Python modules, we consider the VolumeConstraintSteppable steppable shown in Listing 17.
class VolumeConstraintSteppable(SteppablePy):def __init__(self,_simulator,_frequency=1):SteppablePy.__init__(self,_frequency)self.simulator=_simulatorself.inventory=self.simulator.getPotts().getCellInventory(self.cellList=CellList(self.inventory)def start(self):for cell in self.cellList:cell.targetVolume=25cell.lambdaVolume=2.0def step(self,mcs):field=CompuCell.getConcentrationField(self.simulator,“FGF”)comPt=CompuCell.Point3D()for cell in self.cellList:if cell.type==1: #Condensing cellcomPt.x=int(round(cell.xCM/float(cell.volume)))comPt.y=int(round(cell.yCM/float(cell.volume)))comPt.z=int(round(cell.zCM/float(cell.volume)))concentration=field.get(comPt)# get concentration at comPt# and increase cell's target volumecell.targetVolume+=0.1*concentration
Listing 17. Python code for the VolumeConstraintSteppable, saved in the file `cellsort_2D_field_modules.py', for the diffusing-field-based cell-growth simulation. The VolumeConstraintSteppable provides dynamic volume constraint parameters for each cell, which depend on the cell type and the chemical field concentration at the cell's centroid.
The __init__ constructor looks very similar to the one in Listing 14, with the difference that we pass _frequency=1 to update the cell volumes once per MCS. We also request the field-lattice dimensions and values from CompuCell3D:
self.dim=self.simulator.getPotts().getCellFieldG().getDim()
and specify that we will work with a field named FGF:
self.fieldName=“FGF”
The script contains two functions: one that initializes the cells' volume-constraint parameters (start(self)) and one that updates them (step(self, mcs)).
The start(self) function executes only once, at the beginning of the simulation. It iterates over each cell (for cell in self.cellList:) and assigns the initial cells' targetVolume (Vt (σ) = 25 pixels) and lambdaVolume (λvol(σ) = 2.0 ) parameters as the VolumeLocalFlex plugin requires.
The first line of the step(self, mcs) function extracts a reference to the FGF concentration field defined using the FlexibleDiffusionSolverFE steppable in the CC3DML file (each field created in a CompuCell3D simulation is registered and accessible by both C++ and Python). The function then iterates over every cell in the simulation. If a cell is of cell.type 1 (Condensing - see the CC3DML configuration file, Listing 15), we calculate its centroid:
centerOfMassPoint.x=int(round(cell.xCM/float(cell.volume))) centerOfMassPoint.y=int(round(cell.yCM/float(cell.volume))) centerOfMassPoint.z=int(round(cell.zCM/float(cell.volume)))
and retrieve the FGF concentration at that point:
concentration=field.get(centerOfMassPoint)
We then increase the target volume of the cell by 0.01 times that concentration:
cell.targetVolume+=0.01*concentration
We must include the CenterOfMass plugin in the CC3DML code. Otherwise the centroid (cell.xCM, cell.yCM, cell.zCM) will have the default value (0,0,0).
Listing 18 shows the code for the CellsortMitosis plugin. The plugin divides the mitotic cell into two cells and adjusts both cells' attributes. It also initializes and appends MitosisData objects to the original cell's (self.parentCell) and daughter cell's (self.childCell) attribute lists.
from random import randomfrom PyPluginsExamples import MitosisPyPluginBaseclass CellsortMitosis(MitosisPyPluginBase):def __init__(self,_simulator,_changeWatcherRegistry,\_stepperRegistry):MitosisPyPluginBase.__init__(self,_simulator,\_changeWatcherRegistry,_stepperRegistry)def updateAttributes(self):self.parentCell.targetVolume=self.parentCell.volume/2.0self.childCell.targetVolume=self.parentCell.targetVolumeself.childCell.lambdaVolume=self.parentCell.lambdaVolumeif (random()<0.5): self.childCell.type=self.parentCell.typeelse:self.childCell.type=3##record mitosis data in parent and daughter cellsmcs=self.simulator.getStep()mitData=MitosisData(mcs,self.parentCell.id,self.parentCell.type,\self.childCell.id,self.childCell.type)#get a reference to lists storing Mitosis dataparentCellList=CompuCell.getPyAttrib(self.parentCell)childCellList=CompuCell.getPyAttrib(self.childCell)parentCellList.append(mitData)childCellList.append(mitData)
Listing 18. Python code for the CellsortMitosis plugin for the diffusing-field-based cell-growth simulation, saved in the file `cellsort_2D_field_modules.py'. The plugin handles division of cells when they reach a threshold volume.
The second line of Listing 18:
from PyPluginsExamples import MitosisPyPluginBase
lets us access the CompuCell3D base class MitosisPyPluginBase.
CellsortMitosis inherits the content of the MitosisPyPluginBase class.
MitosisPyPluginBase internally accesses the CompuCell3D-provided Mitosis plugin, which is written in C++, and handles all the technicalities of plugin initialization behind the scenes. The MitosisPyPluginBase class provides a simple-to-use interface to this plugin. To create a customized version of MitosisPyPluginBase, CellsortMitosis, we must call the constructor of MitosisPyPluginBase from the CellsortMitosis constructor:
MitosisPyPluginBase.__init__(self,_simulator,\ _changeWatcherRegistry,_stepperRegistry)
We also need to reimplement the function updateAttributes(self), which is called by MitosisPyPluginBase after mitosis takes place, to define the post-division cells' parameters. The objects self.childCell and self.parentCell that appear in the function are initialized and managed by MitosisPyPluginBase. In the current simulation, after division we set Vt for the parent and daughter cells to half of the Vt of the parent just prior to cell division. λvol. is left unchanged for the parent cell and the same value is assigned to the daughter cell:
self.parentCell.targetVolume=self.parentCell.volume/2.0self.childCell.targetVolume=self.parentCell.targetVolumeself.childCell.lambdaVolume=self.parentCell.lambdaVolume
The cell type of one of the two daughter cells (childCell) is randomly chosen to be either Condensing (i.e., the same as the parent type) or CondensingDifferentiated, which we have defined to be cell.type 3 (Listing 15):
if (random()<0.5):self.childCell.type=self.parentCell.typeelse: self.childCell.type=3
The parent cell remains Condensing. We now add a description of this cell division to the lists attached to each cell. First we collect the data in a list called mitData:
mcs=self.simulator.getStep()mitData=MitosisData(mcs,self.parentCell.id,self.parentCell.type,\self.childCell.id,self.childCell.type)
then we access the lists attached to the two cells:
parentCellList=CompuCell.getPyAttrib(self.parentCell)childCellList=CompuCell.getPyAttrib(self.childCell)
and append the new mitosis data to these lists:
parentCellList.append(mitData)childCellList.append(mitData)
Listing 19 shows the Python code for the MitosisData class, which stores the data on the cell division that we append to the cells' attribute lists after each cell division.
class MitosisData:def __init__(self,_MCS,_parentId,_parentType,_offspringId,\_offspringType):self.MCS=_MCSself.parentId=_parentIdself.parentType=_parentTypeself.offspringId=_offspringIdself.offspringType=_offspringTypedef __str__(self):return “Mitosis time=”+str(self.MCS)+”\parentId=“+str(self.parentId)+”\offspringId=“+str(self.offspringId)
Listing 19. Python code for the MitosisData class for the diffusing-field-based cell-growth simulation, saved in the file `cellsort_2D_field_modules.py'. MitosisData objects store information about cell divisions involving the parent and daughter cells.
In the constructor of MitosisData, we read in the time (in MCS) of the division, along with the parent and daughter cell indices and types. The __str__(self) convenience function returns an ASCII string representation of the time and cell indices only, to allow the Python print command to print out this information.
Listing 20 shows the Python code for the MitosisDataPrinterSteppable steppable, which prints the mitosis data to the user's screen.
class MitosisDataPrinterSteppable(SteppablePy):def __init__(self,_simulator,_frequency=100):SteppablePy.__init__(self,_frequency)self.simulator=_simulatorself.inventory=self.simulator.getPotts().getCellInventory()self.cellList=CellList(self.inventory)def step(self,mcs):for cell in self.cellList:mitDataList=CompuCell.getPyAttrib(cell)if len(mitDataList) > 0:print “MITOSIS DATA FOR CELL ID”,cell.id for mitData in mitDataList:print mitData
Listing 20. The Python code for the MitosisDataPrinter steppable for the diffusing-field-based cell-growth simulation, saved in the file `cellsort_2D_field_modules.py'. The steppable prints the cell-division history for dividing cells (see Figure 18).
Figure 18.
Sample output from the MitosisDataPrinterSteppable steppable in Listing 20.
The constructor is identical to that for the VolumeConstraintSteppable steppable (Listing 17). Within the step(self,mcs) function, we iterate over each cell (for cell in self.cellList:) and access the Python list attached to the cell (mitDataList=CompuCell.getPyAttrib(cell)). If a given cell has undergone mitosis, then the list will have entries, and thus a nonzero length. If so, we print the MitosisData objects stored in the list:
if len(mitDataList) > 0:print “MITOSIS DATA FOR CELL ID”,cell.idfor mitData in mitDataList:print mitData
Figure 16 and Figure 17 show snapshots of the diffusing-field-based cell-growth simulation. Figure 18 shows a sample screen output of the cell-division history.
Figure 16.
Snapshots of the diffusing-field-based cell-growth simulation obtained by running the CC3DML file in Listing 15 in conjunction with the Python file in Listing 16. As the simulation progresses, NonCondensing cells (light gray) secrete diffusing chemical, FGF, which causes Condensing (dark gray) cells to proliferate. Some Condensing cells differentiate to CondensingDifferentiated (white) cells.
Figure 17.
Snapshots of FGF concentration in the diffusing-field-based cell-growth simulation obtained by running the CC3DML file in Listing 15 in conjunction with the Python files in Listing 16, Listing 17, Listing 18, Listing 19, Listing 20. The bars at the bottom of the field images show the concentration scales (blue, low concentration; red, high concentration).
VII. Conclusion
In most cases, building a complex CompuCell3D simulation requires writing Python modules, a main Python script and a CC3DML configuration file. While the effort to write this code can be substantial, it is much less than that required to develop custom simulations in lower-level languages. Working from the substantial base of Python templates provided by CompuCell3D further streamlines simulation development. Python programs are fairly short, so simulations can be published in journal articles, greatly facilitating simulation validation, reuse and adaptation. Finally, CompuCell3D's modular structure allows new Python modules to be reused from simulation to simulation. The CompuCell3D website, www.compucell3d.org, allows users to archive their modules and make them accessible to other users.
We hope the examples we have shown will convince readers to evaluate the suitability of GGH simulations using CompuCell3D for their research.
All the code examples presented in this chapter are available from www.compucell3d.org. They will be curated to ensure their correctness and compatibility with future versions of CompuCell3D.
Figure 2.
GGH representation of an index-copy attempt for two cells on a 2D square lattice - The “white” pixel (source) attempts to replace the “grey” pixel (target). The probability of accepting the index copy is given by equation (7).
Figure 3.
Calculating changes in the boundary energy and the volume-constraint energy on a nearest-neighbor square lattice.
Figure 9.
Connecting a field to GGH dynamics using a chemotaxis-energy term. The difference in the value of the field c at the source, , and target, , pixels changes the ΔH of the index-copy attempt. Here and λ > 0, so ΔHchem < 0, increasing the probability of accepting the index-copy attempt in equation (7).
VIII. Acknowledgements
We gratefully acknowledge support from the National Institutes of Health, National Institute of General Medical Sciences, grants 1R01 GM077138-01A1 and 1R01 GM076692-01, and the Office of Vice President for Research, the College of Arts and Sciences, the Pervasive Technologies Laboratories and the Biocomplexity Institute at Indiana University. Indiana University's University Information Technology Services provided time on their BigRed clusters for simulation execution. Early versions of CompuCell and CompuCell3D were developed at the University of Notre Dame by J.A.G., Dr. Mark Alber and Dr. Jesus Izaguirre and collaborators with the support of National Science Foundation, Division of Integrative Biology, grant IBN-00836563. Since the primary home of CompuCell3D moved to Indiana University in 2004, the Notre Dame team have continued to provide important support for its development.
Footnotes
Because of lattice discretization and the option of defining long range neighborhoods, the surface area of a cell scales in a non-Euclidian, lattice-dependent manner with cell volume, i.e., s (v ≠ (4π1/3(3ψ2/3 see (61) on bubble growth.
In the text, we denote XML, CC3DML and Python code using the Courier font. In listings presenting syntax, user-supplied variables are given in italics. Broken-out listings are  . Punctuation at the end of boxes is implicit.
. Punctuation at the end of boxes is implicit.
We highlight in yellow sections or text describing CompuCell3D behaviors which may be confusing or lead to hard-to-track errors.
IX. References
- 1.Bassingthwaighte JB. Strategies for the Physiome project. Annals of Biomedical Engineering. 2000;28:1043–1058. doi: 10.1114/1.1313771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Merks RMH, Newman SA, Glazier JA. Cell-oriented modeling of in vitro capillary development. Lecture Notes in Computer Science. 2004;3305:425–434. [Google Scholar]
- 3.Turing AM. The Chemical Basis of Morphogenesis. Philosophical Transactions of the Royal Society B. 1953;237:37–72. [Google Scholar]
- 4.Merks RMH, Glazier JA. A cell-centered approach to developmental biology. Physica A. 2005;352:113–130. [Google Scholar]
- 5.Dormann S, Deutsch A. Modeling of self-organized avascular tumor growth with a hybrid cellular automaton. In Silico Biology. 2002;2:1–14. [PubMed] [Google Scholar]
- 6.dos Reis AN, Mombach JCM, Walter M, de Avila LF. The interplay between cell adhesion and environment rigidity in the morphology of tumors. Physica A. 2003;322:546–554. [Google Scholar]
- 7.Drasdo D, Hohme S. Individual-based approaches to birth and death in avascular tumors. Mathematical and Computer Modelling. 2003;37:1163–1175. [Google Scholar]
- 8.Holm EA, Glazier JA, Srolovitz DJ, Grest GS. Effects of Lattice Anisotropy and Temperature on Domain Growth in the Two-Dimensional Potts Model. Physical Review A. 1991;43:2662–2669. doi: 10.1103/physreva.43.2662. [DOI] [PubMed] [Google Scholar]
- 9.Turner S, Sherratt JA. Intercellular adhesion and cancer invasion: A discrete simulation using the extended Potts model. Journal of Theoretical Biology. 2002;216:85–100. doi: 10.1006/jtbi.2001.2522. [DOI] [PubMed] [Google Scholar]
- 10.Drasdo D, Forgacs G. Modeling the interplay of generic and genetic mechanisms in cleavage, blastulation, and gastrulation. Developmental Dynamics. 2000;219:182–191. doi: 10.1002/1097-0177(200010)219:2<182::aid-dvdy1040>3.3.co;2-1. [DOI] [PubMed] [Google Scholar]
- 11.Drasdo D, Kree R, McCaskill JS. Monte-Carlo approach to tissue-cell populations. Physical Review E. 1995;52:6635–6657. doi: 10.1103/physreve.52.6635. [DOI] [PubMed] [Google Scholar]
- 12.Longo D, Peirce SM, Skalak TC, Davidson L, Marsden M, Dzamba B. Multicellular computer simulation of morphogenesis: blastocoel roof thinning and matrix assembly in Xenopus laevis. Developmental Biology. 2004;271:210–222. doi: 10.1016/j.ydbio.2004.03.021. [DOI] [PubMed] [Google Scholar]
- 13.Collier JR, Monk NAM, Maini PK, Lewis JH. Pattern formation by lateral inhibition with feedback: A mathematical model of Delta-Notch intercellular signaling. Journal of Theoretical Biology. 1996;183:429–446. doi: 10.1006/jtbi.1996.0233. [DOI] [PubMed] [Google Scholar]
- 14.Honda H, Mochizuki A. Formation and maintenance of distinctive cell patterns by coexpression of membrane-bound ligands and their receptors. Developmental Dynamics. 2002;223:180–192. doi: 10.1002/dvdy.10042. [DOI] [PubMed] [Google Scholar]
- 15.Moreira J, Deutsch A. Pigment pattern formation in zebrafish during late larval stages: A model based on local interactions. Developmental Dynamics. 2005;232:33–42. doi: 10.1002/dvdy.20199. [DOI] [PubMed] [Google Scholar]
- 16.Wearing HJ, Owen MR, Sherratt JA. Mathematical modelling of juxtacrine patterning. Bulletin of Mathematical Biology. 2000;62:293–320. doi: 10.1006/bulm.1999.0152. [DOI] [PubMed] [Google Scholar]
- 17.Zhdanov VP, Kasemo B. Simulation of the growth of neurospheres. Europhysics Letters. 2004;68:134–140. [Google Scholar]
- 18.Ambrosi D, Gamba A, Serini G. Cell directional persistence and chemotaxis in vascular morphogenesis. Bulletin of Mathematical Biology. 2005;67:195–195. doi: 10.1016/j.bulm.2004.04.004. [DOI] [PubMed] [Google Scholar]
- 19.Gamba A, Ambrosi D, Coniglio A, de Candia A, di Talia S, Giraudo E, Serini G, Preziosi L, Bussolino F. Percolation, morphogenesis, and Burgers dynamics in blood vessels formation. Physical Review Letters. 2003;90:118101. doi: 10.1103/PhysRevLett.90.118101. [DOI] [PubMed] [Google Scholar]
- 20.Novak B, Toth A, Csikasz-Nagy A, Gyorffy B, Tyson JA, Nasmyth K. Finishing the cell cycle. Journal of Theoretical Biology. 1999;199:223–233. doi: 10.1006/jtbi.1999.0956. [DOI] [PubMed] [Google Scholar]
- 21.Peirce SM, van Gieson EJ, Skalak TC. Multicellular simulation predicts microvascular patterning and in silico tissue assembly. FASEB Journal. 2004;18:731–733. doi: 10.1096/fj.03-0933fje. [DOI] [PubMed] [Google Scholar]
- 22.Merks RMH, Brodsky SV, Goligorksy MS, Newman SA, Glazier JA. Cell elongation is key to in silico replication of in vitro vasculogenesis and subsequent remodeling. Developmental Biology. 2006;289:44–54. doi: 10.1016/j.ydbio.2005.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Merks RMH, Glazier JA. q-bio/0505033. 2005. Contact-inhibited chemotactic motility can drive both vasculogenesis and sprouting angiogenesis. [Google Scholar]
- 24.Kesmir C, de Boer. RJ. A spatial model of germinal center reactions: cellular adhesion based sorting of B cells results in efficient affinity maturation. Journal of Theoretical Biology. 2003;222:9–22. doi: 10.1016/s0022-5193(03)00010-9. [DOI] [PubMed] [Google Scholar]
- 25.Meyer-Hermann M, Deutsch A, Or-Guil M. Recycling probability and dynamical properties of germinal center reactions. Journal of Theoretical Biology. 2001;210:265–285. doi: 10.1006/jtbi.2001.2297. [DOI] [PubMed] [Google Scholar]
- 26.Nguyen B, Upadhyaya A, van Oudenaarden A, Brenner MP. Elastic instability in growing yeast colonies. Biophysical Journal. 2004;86:2740–2747. doi: 10.1016/S0006-3495(04)74327-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Walther T, Reinsch H, Grosse A, Ostermann K, Deutsch A, Bley T. Mathematical modeling of regulatory mechanisms in yeast colony development. Journal of Theoretical Biology. 2004;229:327–338. doi: 10.1016/j.jtbi.2004.04.004. [DOI] [PubMed] [Google Scholar]
- 28.Borner U, Deutsch A, Reichenbach H, Bar M. Rippling patterns in aggregates of myxobacteria arise from cell-cell collisions. Physical Review Letters. 2002;89:078101. doi: 10.1103/PhysRevLett.89.078101. [DOI] [PubMed] [Google Scholar]
- 29.Bussemaker HJ, Deutsch A, Geigant E. Mean-field analysis of a dynamical phase transition in a cellular automaton model for collective motion. Physical Review Letters. 1997;78:5018–5021. [Google Scholar]
- 30.Dormann S, Deutsch A, Lawniczak AT. Fourier analysis of Turing-like pattern formation in cellular automaton models. Future Generation Computer Systems. 2001;17:901–909. [Google Scholar]
- 31.Börner U, Deutsch A, Reichenbach H, Bär M. Rippling patterns in aggregates of myxobacteria arise from cell-cell collisions. Physical Review Letters. 2002;89:078101. doi: 10.1103/PhysRevLett.89.078101. [DOI] [PubMed] [Google Scholar]
- 32.Zhdanov VP, Kasemo B. Simulation of the growth and differentiation of stem cells on a heterogeneous scaffold. Physical Chemistry Chemical Physics. 2004;6:4347–4350. [Google Scholar]
- 33.Knewitz MA, Mombach JC. Computer simulation of the influence of cellular adhesion on the morphology of the interface between tissues of proliferating and quiescent cells. Computers in Biology and Medicine. 2006;36:59–69. doi: 10.1016/j.compbiomed.2004.08.002. [DOI] [PubMed] [Google Scholar]
- 34.Marée AFM, Hogeweg P. How amoeboids self-organize into a fruiting body: Multicellular coordination in Dictyostelium discoideum. Proceedings of the National Academy of Sciences of the USA. 2001;98:3879–3883. doi: 10.1073/pnas.061535198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Marée AFM, Hogeweg P. Modelling Dictyostelium discoideum morphogenesis: the culmination. Bulletin of Mathematical Biology. 2002;64:327–353. doi: 10.1006/bulm.2001.0277. [DOI] [PubMed] [Google Scholar]
- 36.Marée AFM, Panfilov AV, Hogeweg P. Migration and thermotaxis of Dictyostelium discoideum slugs, a model study. Journal of Theoretical Biology. 1999;199:297–309. doi: 10.1006/jtbi.1999.0958. [DOI] [PubMed] [Google Scholar]
- 37.Savill NJ, Hogeweg P. Modelling morphogenesis: From single cells to crawling slugs. Journal of Theoretical Biology. 1997;184:229–235. doi: 10.1006/jtbi.1996.0237. [DOI] [PubMed] [Google Scholar]
- 38.Hogeweg P. Evolving mechanisms of morphogenesis: on the interplay between differential adhesion and cell differentiation. Journal of Theoretical Biology. 2000;203:317–333. doi: 10.1006/jtbi.2000.1087. [DOI] [PubMed] [Google Scholar]
- 39.Johnston DA. Thin animals. Journal of Physics A. 1998;31:9405–9417. [Google Scholar]
- 40.Groenenboom MA, Hogeweg P. Space and the persistence of male-killing endosymbionts in insect populations. Proceedings in Biological Sciences. 2002;269:2509–2518. doi: 10.1098/rspb.2002.2197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Groenenboom MA, Maree AF, Hogeweg P. The RNA silencing pathway: the bits and pieces that matter. PLoS Computational Biology. 2005;1:155–165. doi: 10.1371/journal.pcbi.0010021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kesmir C, van Noort V, de Boer RJ, Hogeweg P. Bioinformatic analysis of functional differences between the immunoproteasome and the constitutive proteasome. Immunogenetics. 2003;55:437–449. doi: 10.1007/s00251-003-0585-6. [DOI] [PubMed] [Google Scholar]
- 43.Pagie L, Hogeweg P. Individual- and population-based diversity in restriction-modification systems. Bulletin of Mathematical Biology. 2000;62:759–774. doi: 10.1006/bulm.2000.0177. [DOI] [PubMed] [Google Scholar]
- 44.Silva HS, Martins ML. A cellular automata model for cell differentiation. Physica A. 2003;322:555–566. [Google Scholar]
- 45.Zajac M, Jones GL, Glazier JA. Model of convergent extension in animal morphogenesis. Physical Review Letters. 2000;85:2022–2025. doi: 10.1103/PhysRevLett.85.2022. [DOI] [PubMed] [Google Scholar]
- 46.Zajac M, Jones GL, Glazier JA. Simulating convergent extension by way of anisotropic differential adhesion. Journal of Theoretical Biology. 2003;222:247–259. doi: 10.1016/s0022-5193(03)00033-x. [DOI] [PubMed] [Google Scholar]
- 47.Savill NJ, Sherratt JA. Control of epidermal stem cell clusters by Notch-mediated lateral induction. Developmental Biology. 2003;258:141–153. doi: 10.1016/s0012-1606(03)00107-6. [DOI] [PubMed] [Google Scholar]
- 48.Mombach JCM, de Almeida RMC, Thomas GL, Upadhyaya A, Glazier JA. Bursts and cavity formation in Hydra cells aggregates: experiments and simulations. Physica A. 2001;297:495–508. [Google Scholar]
- 49.Rieu JP, Upadhyaya A, Glazier JA, Ouchi NB, Sawada Y. Diffusion and deformations of single hydra cells in cellular aggregates. Biophysical Journal. 2000;79:1903–1914. doi: 10.1016/S0006-3495(00)76440-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Mochizuki A. Pattern formation of the cone mosaic in the zebrafish retina: A cell rearrangement model. Journal of Theoretical Biology. 2002;215:345–361. doi: 10.1006/jtbi.2001.2508. [DOI] [PubMed] [Google Scholar]
- 51.Takesue A, Mochizuki A, Iwasa Y. Cell-differentiation rules that generate regular mosaic patterns: Modelling motivated by cone mosaic formation in fish retina. Journal of Theoretical Biology. 1998;194:575–586. doi: 10.1006/jtbi.1998.0777. [DOI] [PubMed] [Google Scholar]
- 52.Dallon J, Sherratt J, Maini PK, Ferguson M. Biological implications of a discrete mathematical model for collagen deposition and alignment in dermal wound repair. IMA Journal of Mathematics Applied in Medicine and Biology. 2000;17:379–393. [PubMed] [Google Scholar]
- 53.Maini PK, Olsen L, Sherratt JA. Mathematical models for cell-matrix interactions during dermal wound healing. International Journal of Bifurcations and Chaos. 2002;12:2021–2029. [Google Scholar]
- 54.Kreft JU, Picioreanu C, Wimpenny JWT, van Loosdrecht MCM. Individual-based modelling of biofilms. Microbiology. 2001;147:2897–2912. doi: 10.1099/00221287-147-11-2897. [DOI] [PubMed] [Google Scholar]
- 55.Picioreanu C, van Loosdrecht MCM, Heijnen JJ. Two-dimensional model of biofilm detachment caused by internal stress from liquid flow. Biotechnology and Bioengineering. 2001;72:205–218. [PubMed] [Google Scholar]
- 56.van Loosdrecht MCM, Heijnen JJ, Eberl H, Kreft J, Picioreanu C. Mathematical modelling of biofilm structures. Antonie Van Leeuwenhoek International Journal of General and Molecular Microbiology. 2002;81:245–256. doi: 10.1023/a:1020527020464. [DOI] [PubMed] [Google Scholar]
- 57.Popławski NJ, Shirinifard A, Swat M, Glazier JA. Simulations of single-species bacterial-biofilm growth using the Glazier-Graner-Hogeweg model and the CompuCell3D modeling environment. Mathematical Biosciences and Engineering. 2008;5:355–388. doi: 10.3934/mbe.2008.5.355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Chaturvedi R, Huang C, Izaguirre JA, Newman SA, Glazier JA, Alber MS. A hybrid discrete-continuum model for 3-D skeletogenesis of the vertebrate limb. Lecture Notes in Computer Science. 2004;3305:543–552. [Google Scholar]
- 59.Popławski NJ, Swat M, Gens JS, Glazier JA. Adhesion between cells, diffusion of growth factors, and elasticity of the AER produce the paddle shape of the chick limb. Physica A. 2007;373:521–532. doi: 10.1016/j.physa.2006.05.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Glazier JA, Weaire D. The Kinetics of Cellular Patterns. Journal of Physics: Condensed Matter. 1992;4:1867–1896. [Google Scholar]
- 61.Glazier JA. Grain Growth in Three Dimensions Depends on Grain Topology. Physical Review Letters. 1993;70:2170–2173. doi: 10.1103/PhysRevLett.70.2170. [DOI] [PubMed] [Google Scholar]
- 62.Glazier JA, Grest GS, Anderson MP. Ideal Two-Dimensional Grain Growth. In: Anderson MP, Rollett AD, editors. Simulation and Theory of Evolving Microstructures. The Minerals, Metals and Materials Society; Warrendale, PA: 1990. pp. 41–54. [Google Scholar]
- 63.Glazier JA, Anderson MP, Grest GS. Coarsening in the Two-Dimensional Soap Froth and the Large-Q Potts Model: A Detailed Comparison. Philosophical Magazine B. 1990;62:615–637. [Google Scholar]
- 64.Grest GS, Glazier JA, Anderson MP, Holm EA, Srolovitz DJ. Coarsening in Two-Dimensional Soap Froths and the Large-Q Potts Model. Materials Research Society Symposium. 1992;237:101–112. [Google Scholar]
- 65.Jiang Y, Glazier JA. Extended Large-Q Potts Model Simulation of Foam Drainage. Philosophical Magazine Letters. 1996;74:119–128. [Google Scholar]
- 66.Jiang Y, Levine H, Glazier JA. Possible Cooperation of Differential Adhesion and Chemotaxis in Mound Formation of Dictyostelium. Biophysical Journal. 1998;75:2615–2625. doi: 10.1016/S0006-3495(98)77707-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Jiang Y, Mombach JCM, Glazier JA. Grain Growth from Homogeneous Initial Conditions: Anomalous Grain Growth and Special Scaling States. Physical Review E. 1995;52:3333–3336. doi: 10.1103/physreve.52.r3333. [DOI] [PubMed] [Google Scholar]
- 68.Jiang Y, Swart PJ, Saxena A, Asipauskas M, Glazier JA. Hysteresis and Avalanches in Two-Dimensional Foam Rheology Simulations. Physical Review E. 1999;59:5819–5832. doi: 10.1103/physreve.59.5819. [DOI] [PubMed] [Google Scholar]
- 69.Ling S, Anderson MP, Grest GS, Glazier JA. Comparison of Soap Froth and Simulation of Large-Q Potts Model. Materials Science Forum. 1992;94-96:39–47. [Google Scholar]
- 70.Mombach JCM. Universality of the threshold in the dynamics of biological cell sorting. Physica A. 2000;276:391–400. [Google Scholar]
- 71.Weaire D, Glazier JA. Modelling Grain Growth and Soap Froth Coarsening: Past, Present and Future. Materials Science Forum. 1992;94-96:27–39. [Google Scholar]
- 72.Weaire D, Bolton F, Molho P, Glazier JA. Investigation of an Elementary Model for Magnetic Froth. Journal of Physics: Condensed Matter. 1991;3:2101–2113. [Google Scholar]
- 73.Glazer JA, Balter A, Popławski N. Magnetization to Morphogenesis: A Brief History of the Glazier-Graner-Hogeweg Model. In: Anderson ARA, Chaplain MAJ, Rejniak KA, editors. Single-Cell-Based Models in Biology and Medicine. Birkhauser Verlag Basel; Switzerland: 2007. pp. 79–106. [Google Scholar]
- 74.Walther T, Reinsch H, Ostermann K, Deutsch A, Bley T. Coordinated growth of yeast colonies: experimental and mathematical analysis of possible regulatory mechanisms. Engineering Life Sciences. 2005;5:115–133. [Google Scholar]
- 75.Keller EF, Segel LA. Model for chemotaxis. Journal of Theoretical Biology. 1971;30:225–234. doi: 10.1016/0022-5193(71)90050-6. [DOI] [PubMed] [Google Scholar]
- 76.Glazier JA, Upadhyaya A. First Steps Towards a Comprehensive Model of Tissues, or: A Physicist Looks at Development. In: Beysens D, Forgacs G, editors. Dynamical Networks in Physics and Biology: At the Frontier of Physics and Biology. EDP Sciences/Springer Verlag; Berlin: 1998. pp. 149–160. [Google Scholar]
- 77.Glazier JA, Graner F. Simulation of the differential adhesion driven rearrangement of biological cells. Physical Review E. 1993;47:2128–2154. doi: 10.1103/physreve.47.2128. [DOI] [PubMed] [Google Scholar]
- 78.Glazier JA. Cellular Patterns. Bussei Kenkyu. 1993;58:608–612. [Google Scholar]
- 79.Glazier JA. Thermodynamics of Cell Sorting. Bussei Kenkyu. 1996;65:691–700. [Google Scholar]
- 80.Glazier JA, Raphael RC, Graner F, Sawada Y. The Energetics of Cell Sorting in Three Dimensions. In: Beysens D, Forgacs G, Gaill F, editors. Interplay of Genetic and Physical Processes in the Development of Biological Form. World Scientific Publishing Company; Singapore: 1995. pp. 54–66. [Google Scholar]
- 81.Graner F, Glazier JA. Simulation of biological cell sorting using a 2-dimensional extended Potts model. Physical Review Letters. 1992;69:2013–2016. doi: 10.1103/PhysRevLett.69.2013. [DOI] [PubMed] [Google Scholar]
- 82.Mombach JCM, Glazier JA. Single Cell Motion in Aggregates of Embryonic Cells. Physical Review Letters. 1996;76:3032–3035. doi: 10.1103/PhysRevLett.76.3032. [DOI] [PubMed] [Google Scholar]
- 83.Mombach JCM, Glazier JA, Raphael RC, Zajac M. Quantitative comparison between differential adhesion models and cell sorting in the presence and absence of fluctuations. Physical Review Letters. 1995;75:2244–2247. doi: 10.1103/PhysRevLett.75.2244. [DOI] [PubMed] [Google Scholar]
- 84.Cipra BA. An Introduction to the Ising-Model. American Mathematical Monthly. 1987;94:937–959. [Google Scholar]
- 85.Metropolis N, Rosenbluth A, Rosenbluth MN, Teller AH, Teller E. Equation of state calculations by fast computing machines. Journal of Chemical Physics. 1953;21:1087–1092. [Google Scholar]
- 86.Forgacs G, Newman SA. Biological Physics of the Developing Embryo. Cambridge Univ. Press; Cambridge: 2005. [Google Scholar]
- 87.Alber MS, Kiskowski MA, Glazier JA, Jiang Y. On cellular automation approaches to modeling biological cells. In: Rosenthal J, Gilliam DS, editors. Mathematical Systems Theory in Biology, Communication and Finance. Springer-Verlag; New York: pp. 1–40. [Google Scholar]
- 88.Alber MS, Jiang Y, Kiskowski MA. Lattice gas cellular automation model for rippling and aggregation in myxobacteria. Physica D. 2004;191:343–358. [Google Scholar]
- 89.Novak B, Toth A, Csikasz-Nagy A, Gyorffy B, Tyson JA, Nasmyth K. Finishing the cell cycle. Journal of Theoretical Biology. 1999;199:223–233. doi: 10.1006/jtbi.1999.0956. [DOI] [PubMed] [Google Scholar]
- 90.Upadhyaya A, Rieu JP, Glazier JA, Sawada Y. Anomalous Diffusion in Two-Dimensional Hydra Cell Aggregates. Physica A. 2001;293:549–558. [Google Scholar]
- 91.Cickovski T, Aras K, Alber MS, Izaguirre JA, Swat M, Glazier JA, Merks RMH, Glimm T, Hentschel HGE, Newman SA. From genes to organisms via the cell: a problem-solving environment for multicellular development. Computers in Science and Engineering. 2007;9:50–60. doi: 10.1109/MCSE.2007.74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Izaguirre JA, Chaturvedi R, Huang C, Cickovski T, Coffland J, Thomas G, Forgacs G, Alber M, Hentschel G, Newman SA, Glazier JA. CompuCell, a multi-model framework for simulation of morphogenesis. Bioinformatics. 2004;20:1129–1137. doi: 10.1093/bioinformatics/bth050. [DOI] [PubMed] [Google Scholar]
- 93.Armstrong PB, Armstrong MT. A role for fibronectin in cell sorting out. Journal of Cell Science. 1984;69:179–197. doi: 10.1242/jcs.69.1.179. [DOI] [PubMed] [Google Scholar]
- 94.Armstrong PB, Parenti D. Cell sorting in the presence of cytochalasin B. Journal of Cell Science. 1972;55:542–553. doi: 10.1083/jcb.55.3.542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Glazier JA, Graner F. Simulation of the differential adhesion driven rearrangement of biological cells. Physical Review E. 1993;47:2128–2154. doi: 10.1103/physreve.47.2128. [DOI] [PubMed] [Google Scholar]
- 96.Glazier JA, Graner F. Simulation of biological cell sorting using a two-dimensional extended Potts model. Physical Review Letters. 1992;69:2013–2016. doi: 10.1103/PhysRevLett.69.2013. [DOI] [PubMed] [Google Scholar]
- 97.Ward PA, Lepow IH, Newman LJ. Bacterial factors chemotactic for polymorphonuclear leukocytes. American Journal of Pathology. 1968;52:725–736. [PMC free article] [PubMed] [Google Scholar]
- 98.Lutz M. Learning Python. O'Reilly & Associates, Inc.; Sebastopol, CA: 1999. [Google Scholar]
- 99.Balter AI, Glazier JA, Perry R. Probing soap-film friction with two-phase foam flow. Philosophical Magazine. 2008 submitted. [Google Scholar]
- 100.Dvorak P, Dvorakova D, Hampl A. Fibroblast growth factor signaling in embryonic and cancer stem cells. FEBS Letters. 2006;580:2869–2287. doi: 10.1016/j.febslet.2006.01.095. [DOI] [PubMed] [Google Scholar]