Passive Ventricular Mechanics Modelling Using MRI of Structure and Function

Abstract

Patients suffering from dilated cardiomyopathy or myocardial infarction can develop left ventricular (LV) diastolic impairment. The LV remodels its structure and function to adapt to pathophysiological changes in geometry and loading conditions and this remodeling process can alter the passive ventricular mechanics. In order to better understand passive ventricular mechanics, a LV finite element model was developed to incorporate physiological and mechanical information derived from in vivo magnetic resonance imaging (MRI) tissue tagging, in vivo LV cavity pressure recording and ex vivo diffusion tensor MRI (DTMRI) of a canine heart. MRI tissue tagging enables quantitative evaluation of cardiac mechanical function with high spatial and temporal resolution, whilst the direction of maximum water diffusion (the primary eigenvector) in each voxel of a DTMRI directly correlates with the myocardial fibre orientation. This model was customized to the geometry of the canine LV during diastasis by fitting the segmented epicardial and endocardial surface data from tagged MRI using nonlinear finite element fitting techniques. Myofibre orientations, extracted from DTMRI of the same heart, were incorporated into this geometric model using a free form deformation methodology. Pressure recordings, temporally synchronized to the tissue tagging MRI data, were used to simulate the LV deformation during diastole. Simulation of the diastolic LV mechanics allowed us to estimate the stiffness of the passive LV myocardium based on kinematic data obtained from tagged MRI. This integrated physiological model will allow more insight into the regional passive diastolic mechanics of the LV on an individualized basis, thereby improving our understanding of the underlying structural basis of mechanical dysfunction in pathological conditions.

1 Introduction

Cardiac cells adapt to physiological, geometric and loading changes leading to regional thickening or thinning of the ventricular wall, and enhancement or degradation of regional muscle function. Studying regional function can therefore lead to an improved understanding of the underlying structural basis of ventricular mechanics. In particular, insight can be gained into pathological conditions such as myocardial ischemia and infarction, where there can be significant localized mechanical changes in the myocardium with only minor changes in global function [1].

MRI tissue tagging enables quantitative evaluation of cardiac mechanical function with high spatial and temporal resolution. Reconstruction of the 3D motion of the heart from the tag positions during the cardiac cycle requires specialized image processing and mathematical techniques [2].

Diffusion tensor magnetic resonance imaging (DTMRI) measures the preferred orientations of the local self-diffusion of water molecules in biological tissues. Studies have shown that the direction of maximum diffusion (the primary eigenvector) correlates with the observed myofibre orientation from histological studies [3]. The primary eigenvector, therefore can be used for mapping the 3D orientation of the myocardial fibres throughout the heart muscle [4]. Myocardial fibre orientation is an important determinant of myocardial wall stress [5] and exhibits a large regional and transmural variation.

It was hypothesized that integrating experimental information obtained from in vivo tagged MRI and ex vivo DTMRI would add insight to normal and abnormal regional cardiac function and passive diastolic mechanics. In this study, we developed a method to combine in vivo tagging and pressure recordings with ex vivo DTMRI in dog, using data acquired at the National Institutes of Health in collaboration with Johns Hopkins University [6]. A host mesh fitting approach was used to transform the fibre orientation data from the DTMR images to the LV model. Using this integrated model, a finite deformation elasticity problem was then solved for early diastolic filling to simulate the mechanics of the LV. In this study, we extend the approach in [7] to non-invasively characterize material properties of LV using in vivo tagged MRI, in vivo cavity pressure recordings and ex vivo DTMRI. Minimizing the difference between the measured and modeled LV cavity volume allowed us to estimate a stiffness constitutive parameter of the ventricular myocardium. Simulation results were compared against the observed motions of a set of material points tracked using MR tissue tagging.

2 Imaging, Segmentation and Model Creation

All studies were approved by the local Institutional Review Boards, and conformed to the “Guide for the Care and Use of Laboratory Animals” published by the National Institutes of Health (NIH publication No. 85-23, revised 1985).

Tagged MR Imaging was performed using a General Electric 1.5T CV/i scanner and a 4 element phased array knee coil. Short axis stripe tagged images (Fig. 1a & 1b) were acquired using the 3D fast gradient echo pulse sequence with the following parameters: 180mm × 180mm × 128-160 mm field of view, 384 × 128 × 32 acquisition matrix, 12° imaging flip angle, ±62.5 kHz bandwidth, TE/TR=3.4/8.0 ms, 5 pixel tag spacing, and 5 mm slice thickness.

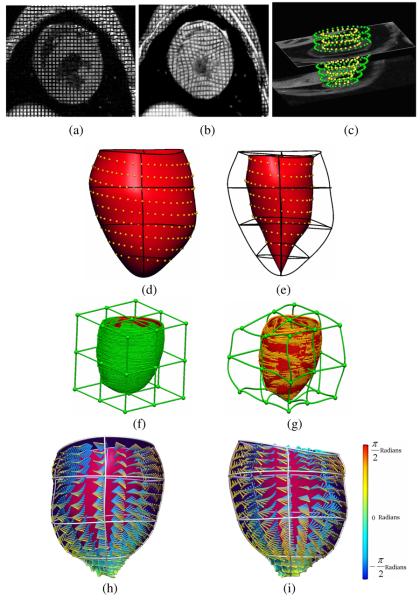
Fig. 1.

(a) Short-axis tagged MR image at end-diastole and (b) end-systole. (c) Zinc Digitizer screenshot showing segmented contours from short-axis images. (d) Posterior view of the epicardial surface fitted to the segmented epicardial surface contours; RMS error = 0.3 mm and (e) endocardial surface; RMS error = 0.3 mm. (f) Undeformed host mesh with landmark points (green) and target points (red); RMS error = 2.67 mm and (g) deformed host mesh with updated landmark points (gold) and target points (red); RMS error = 0.47 mm. (h) Anterior and (i) posterior view of the LV showing fitted fibre vectors.

Tissue tag detection was performed on 11 evenly-spaced short axis MR tagged images spanning from the base to apex, using the Findtags program by Guttman et al [8]. The LV motion obtained from the tagged images was analyzed using four-dimensional b-spline based motion analysis [9], where the positions and strains of regularly-spaced material points within the myocardium were tracked in 3D space and in time. Concurrent LV pressure was also measured and temporally synchronized throughout the cardiac cycle during the tagged MRI using a MR compatible Millar pressure transducer.

Diffusion Tensor MR imaging was performed following the MR tagging study. The heart was excised and fixed in the end diastolic configuration for collecting DTMRI data. The procedures are described in [6]. Diffusion tensor data were reconstructed from the diffusion weighted images and the maximum diffusion eigenvector of each voxel was calculated in each DTMR image. Each image had 160 × 160 in-plane measurements (zero pad interpolated to 256 × 256) and there were 116 slices. The resolution of the DTMRI data was 313μm × 313μm × 800μm.

Surface contour segmentation of tagged MRIs and DTMRIs were performed using the Zinc Digitizer [10]. Prior to surface contour segmentation, the short-axis images were aligned with cardiac coordinate system for finite element geometric fitting (Fig. 1c). For this study, the surface contours were defined to exclude the papillary muscles.

Myofibre orientation data were obtained by extracting the maximum diffusion eigenvector within the LV myocardium using the segmented surface contours as a mask to exclude any voxels outside of the LV myocardium. The masks for the DTMR images were each eroded by one pixel to eliminate noisy data at the edge of the myocardium.

A LV finite element model was created in the cardiac coordinate system (with x orientated along the long axis of the LV, y directed from the left ventricle to right ventricle, and z directed from anterior to posterior) based on nonlinear finite element fitting of the model geometry to the segmented contours of the tagged MR images. The nonlinear optimization was based on sequential quadratic programming. The model consisted of 16 finite elements, which included 4 circumferential elements, 4 longitudinal elements and 1 transmural element (Fig. 1d & 1e). Three-dimensional tri-cubic Hermite interpolation functions were used to provide spatial gradient continuity across element boundaries.

3 Embedding Myocardial Fibre Orientation

A host mesh transformation was used to resolve the differences in heart shape due to the different imaging conditions, i.e., in vivo tagged MRI versus ex vivo DTMRI. The slice thicknesses for the two data sets were significantly different, (tagged MRI 5 mm and DTMRI 0.8 mm) making it difficult to use standard image based non-rigid registration methods because of the comparatively low through-plane resolution of the tagged MRI.

In order to ensure consistent geometry for the two techniques before embedding the myofibre orientation, a variant of free form deformation (FFD) referred to as host mesh fitting was used. This technique is used to customize generic models to specific cases using a set of landmark points and target points. In this study, it was used to transform the DTMRI fibre vectors into the in vivo geometric model from the tagged MRI data. The landmark points were the surface contours segmented from DTMRI using the Zinc digitizer [10], and the corresponding target points were the projections of these surface contours onto the LV model. Both data sets were embedded into an 8-element tri-cubic Hermite host mesh cube.

The RMS (root mean squared error) Euclidean distance between the landmark points and target points was minimized by varying the nodal parameters of the host mesh. After minimization, a transformation matrix was calculated for each embedded landmark point based on their interpolated coordinates before and after deforming the host mesh (Fig. 1f & 1g). The transformation obtained through host mesh fitting was applied to all myofibre origins to approximately align them into the geometric model. This host mesh transformation involved a translation and rotation of each DTMRI derived myofibre vector.

Myofibre orientation fitting was completed after mapping all myofibre vectors into the geometric model. The fibre angle (defined as the elevation angle above the circumferential short-axis plane) was calculated for each vector prior to fitting. The imbrication angle and sheet angle were not considered for this study. Myofibre orientations were incorporated into the geometric model as a fibre angle field (interpolated using tri-cubic Hermite basis functions), which was fitted using nonlinear optimization. Fig. 1h & 1i illustrate the LV model with the fitted fibre orientation and demonstrates the variation throughout the LV wall.

4 Passive Left Ventricular Mechanics

Passive LV mechanics was simulated using the finite element method (FEM) to solve the stress equilibrium equations that govern finite deformation elasticity. Tri-cubic Hermite interpolation functions were used to describe the deformed geometry and trilinear Lagrange interpolation was chosen for the hydrostatic pressure resulting in spatially continuous predicted strain and stress distributions. Using the temporally synchronized LV cavity pressure recording as the loading condition, a system of nonlinear equations was assembled and solved using FEM and Newton's method [11].

The nodal positions and in-plane spatial derivatives of the basal plane were fixed to mimic the stiff atrio-ventricular valve plane. The passive diastolic filling phase was simulated by inflating the reference LV model to a pressure of 0.5 kPa to match the pressure recordings at the end-diastolic state. The pressure loading was applied to the endocardial surface of the model as a pressure boundary constraint in incremental steps of 0.1 kPa.

The stress-strain behaviour of the ventricular myocardium was modelled using the transversely-isotropic constitutive relation in Eq. 1 [12].

$$\begin{array}{cc}\hfill & W=C_1{e}^Q\hfill \\ \hfill & \text{where}Q=C_2{E}_{\mathit{ff}}^2+C_3(E_{\mathit{cc}}^2+E_{\mathit{rr}}^2+2E_{\mathit{cr}}^2)+2C_4(E_{\mathit{fc}}{E}_{\mathit{cf}}+E_{\mathit{fr}}{E}_{\mathit{rf}})\hfill \end{array}$$ (1)

where E_αβ are the components of Green's (Lagrange) strain tensor referred to fibre (f), cross-fibre (c) and radial (r) material coordinates. C₁ - C₄ are the myocardial constitutive parameters (table 1) adapted from [13] and tuned to our kinematic data using the following approach. Given the predicted deformation provided by the FE simulation, and actual deformation from the end-diastolic tagged MR images, the value of the in vivo stiffness parameter C₁ (initially 1.2 kPa [13]) was tuned by minimizing the difference between predicted and measured LV cavity volume at the end-diastolic frame. The optimal value of C₁ was 2.2 kPa, corresponding to a predicted end-diastolic LV cavity volume of 23 ml, which matched the experimental estimate.

Table 1.

Constitutive parameters of the canine LV midwall

C1 (kPa)	C2	C3	C4
2.2	26.7	2.0	14.7

The displacement of a set of regularly spaced material points was used to assess the accuracy of the passive mechanics model prediction. These material points, located at the sub-epicardial surface, midwall, and the sub-endocardial surface, were tracked using four-dimensional b-spline based motion analysis [8]. The tracked points were firstly embedded into the reference LV model, and the local finite element coordinates were determined for each point. Based on the nodal position of the inflated model, the global coordinates of the points were updated and compared against their tracked coordinates. The overall RMS error between the predicted and tracked coordinates was 0.41mm. Fig. 2a & 2b show a 3D color map of the individual errors for all material points.

Fig. 2.

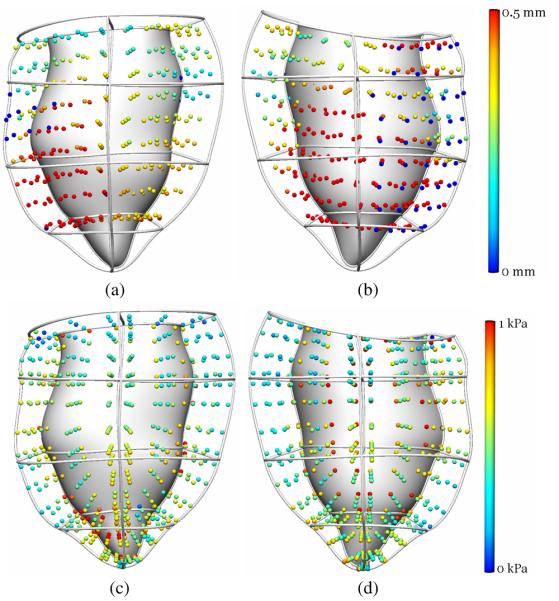
(a) Anterior and (b) posterior views of the individual errors between predicted and tracked material points coordinates. (c) Anterior and (d) posterior view of the maximum principal stress distribution at each Gauss point of the predicted end-diastolic model.

The stress tensor was evaluated based on the local strain and constitutive parameters listed above. The maximum principal stress calculated at each Gauss point is illustrated in Fig. 2c & 2d. Stress was maximal at the endocardial surface where pressure loading was applied.

5 Conclusions

We have developed finite element based modelling methods to integrate cardiac structural and functional observations derived from in vivo tagged canine MRI and LV cavity pressure data, and ex vivo microstructural information. Simulation of the diastolic LV mechanics using this model and subsequent comparison against observed deformation of the LV from cine tagged MR images allowed us to estimate the LV muscle stiffness constitutive parameter. This type of modelling may be used to provide us with insight into regional distributions of myocardial stress and functional measures such as local energy consumption. Models between healthy and diseased states will also allow us to investigate the underlying mechanisms for LV dysfunction.