Evaluation of Peak Overlap in Migration-Time Distributions Determined by Organelle Capillary Electrophoresis: Type-II Error Analogy Based on Statistical-Overlap Theory

Abstract

Organelles commonly are separated by capillary electrophoresis (CE) with laser-induced fluorescence detection. Usually, it is assumed that peaks observed in the CE originate from single organelles, with negligible occurrence of peak overlap. Under this assumption, migration-time and mobility distributions are obtained by partitioning the CE into different regions and counting the number of observed peaks in each region. In this paper, criteria based on statistical-overlap theory are developed to test the assumption of negligible peak overlap and to predict conditions for its validity. For regions of the CE having constant peak density, the numbers of peaks (i.e., intensity profiles of single organelles) and observed peaks (i.e., maxima) are modeled by probability distributions. For minor peak overlap, the distributions partially merge, and their mergence is described by an analogy to the Type-II error of hypothesis testing. Criteria are developed for the amount of peak overlap, at which the number of observed peaks has an 85% or 90% probability of lying within the 95% confidence interval of the number of peaks of single organelles. For this or smaller amounts of peak overlap, the number of observed peaks is a good approximation to the number of peaks. A simple procedure is developed for evaluating peak overlap, requiring determination of only the peak standard deviation, the duration of the region occupied by peaks, and the number of observed peaks in the region. The procedure can be applied independently to each region of the partitioned CE. The procedure is applied to a mitochondrial CE.

Introduction

Biological particles including microorganisms, viruses, intact cells, and organelles migrate in the presence of an electric field. All these particles types have a net negative electrical charge on their surface at biological pH thereby presenting a negative electrophoretic mobility. This property has made it possible to develop methodologies to analyze and characterize biological particles using capillary electrophoresis (CE) [1,2]. One of these methodologies is the CE analysis of organelles (e.g., mitochondria) using biological pH under isotonic conditions [3]. When fluorescently-labeled organelles are analyzed by CE coupled to laser-induced-fluorescence detection (LIF), the electropherograms consist of a collection of narrow resolved peaks that migrate out in a migration time window that is dependent on the separation conditions and, most importantly, on the range of electrophoretic mobility distributions of the organelles in the biological sample. Thus, in previous reports it has been postulated that electrophoretic mobility distributions of individual organelles can be determined from these experimental data [4]. These reports have mostly assumed that each observed peak represents an individual organelle and only recently considered the possibility that some observed peaks may be comprised of more than one organelle peak [5]. This report describes the development and use of models based on the statistical-overlap theory to establish the conditions under which the observed peaks can be used to obtain electrophoretic mobility distributions of individual organelles.

Fig. 1a is a simulated organelle CE containing 1000 peaks and 812 observed peaks. Here, a “peak” is a fluorescence intensity profile of a single organelle as it travels through the LIF detector, whereas an “observed peak” is a detected maximum that is comprised of one or more organelle peaks. The numbers of peaks and observed peaks differ because of peak overlap. It is clear that the peak density (or number of peaks per unit time) varies in the CE, with most peaks eluting near the CE’s center and only a few eluting near its beginning and end. This variation is caused by a nonuniform distribution of migration times that is characteristic of the organelle sample and its analysis.

Figure 1.

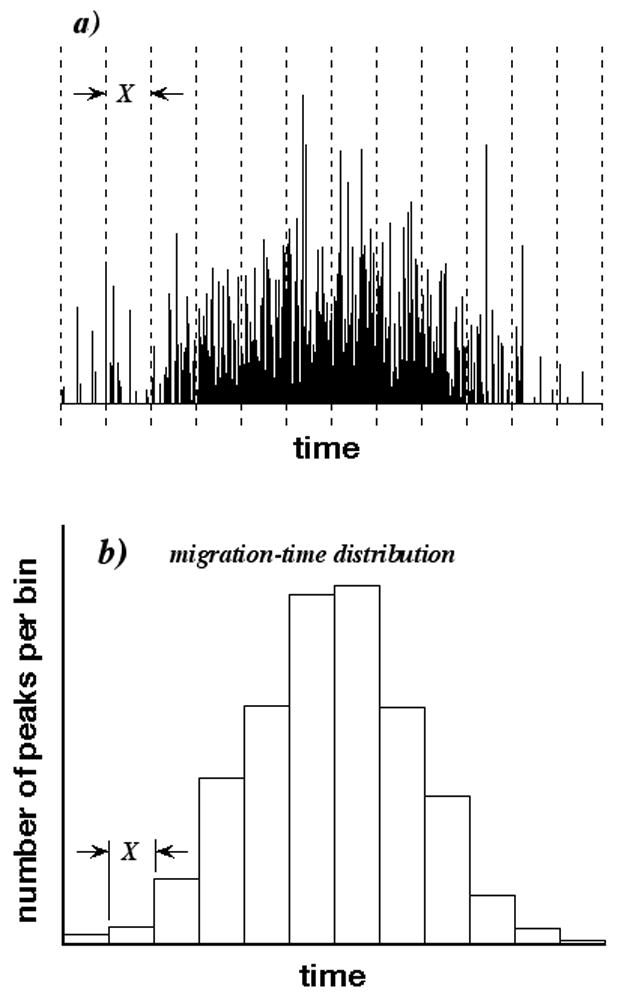
a) Simulated organelle CE containing 1000 peaks and 812 observed peaks (maxima). CE is partitioned into 12 bins having duration X and represented by dashed lines. b) Migration-time distribution of CE determined by counting peak numbers in different bins.

In principle, we can measure the migration-time distribution by partitioning the CE into bins (represented by the dashed lines in Fig. 1a), in which the peak density is almost constant, and counting the number of peaks in each bin. The mobility distribution can be calculated from the migration-time distribution by a simple transformation. The histogram in Fig. 1b is the desired migration-time distribution, with each class interval having a height equaling the peak number in the corresponding bin. Unfortunately, peak numbers typically are unknown, because of peak overlap; only observed-peak numbers can be determined easily by counting maxima. All migration-time distributions based on observed-peak numbers are biased, because some peaks are not counted. If peak overlap is low, however, we are willing to accept a small bias in identifying the number of observed peaks with the number of peaks.

Statistical fluctuations among the number of injected particles (from hundreds to thousands) in organelle CE affect the numbers of peaks and observed peaks in individual CEs. These fluctuations suggest the bias due to peak overlap might be investigated using statistical-overlap theory (SOT). In SOT, we assume that an experimental separation is a member of a large ensemble of separations, in which the number, migration times, and heights of peaks and observed peaks are governed by probability distributions [6–10]. Examples of ensemble members resembling a separation are shown elsewhere [11]. We also assume that attributes of the experimental separation can be calculated from the ensemble. Both the numbers of peaks m and observed peaks p vary in different separations of the ensemble (e.g., replicate injections in organelle CE), and the variations can be expressed by probability distributions. Figs. 2a and 2b show discrete probability distributions of p and m, as determined by numerical methods mimicking the ensemble and described in the Procedures section. In Fig. 2a, peak overlap is high, the p and m distributions are well separated, and p is always much less than m. If peak overlap is reduced, however, the two distributions partially merge as shown in Fig. 2b. Some highly probable p values are the same as highly probable m values. This is the case of interest to us, in which equal values of p and m occur with high likelihood. However, by approximating m by p, we make an error in identifying a member of the p distribution with a member of the m distribution. This is very similar to the Type-II error of hypothesis testing, in which one accepts a member of an actual distribution as a member of a postulated but incorrect distribution. In our problem, the m distribution is postulated, because the peak number is wanted, but it is incorrect, because the peak number is obscured by peak overlap. In contrast, the p distribution is correct, because the observed-peak number is the countable attribute. In this paper, we model conditions under which m can be approximated by p with an analogy to the Type-II error. Our modeling assures us that the number of observed peaks p corresponds to a plausible number of peaks m. The model is general and can be applied to separations other than CE.

Figure 2.

a) Graph of probability vs. p and m for discrete p distribution (normal-weight histogram) and discrete m distribution (bold histogram), when peak overlap is high. b) As in a) but when peak overlap is low.

Theory

Basics of SOT

In SOT, an infinite ensemble determines the probability distributions of both p and m. The m distribution is typically characteristic of the mixture; for complex multi-component mixtures, m usually is assumed to be Poisson distributed for empirical [12–14] and theoretical [15–17] reasons. We make that assumption here, although its validity in organelle CE may be only approximate. The distribution of m, coupled with specific sequences of migration times and peak heights, determines the p distribution [13,18]. Several theoretical approaches exist in SOT, among them Fourier analysis [19], pulse-point statistics [20], and the point-process statistics [15,21] used here.

Analogy between peak counting and Type-II error

The bold curve in Fig. 3 is a postulated probability distribution of a generic continuous random variable. We generally accept the probability α that data drawn from this distribution are rejected as distribution members, with α equal to the producer’s risk (or the significance level, if expressed as a percentage). This is the Type I error, associated with one or both tails of the postulated distribution. It establishes a confidence interval spanning the acceptance region (i.e., the central abscissa of the distribution) bounded by the lower and upper confidence limits L₁ and L₂ shown in the figure. For a two-tailed application, two rejection (or critical) regions having areas α/2 lie beyond the confidence limits, as shown by the heavily shaded regions. For the common 95% confidence interval, α= 0.05.

Figure 3.

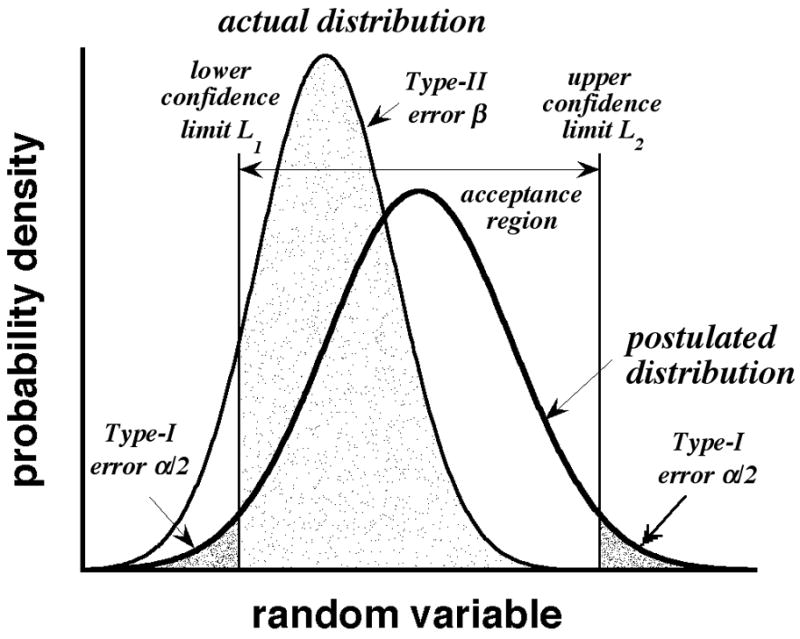
Illustration of Type-I and Type-II errors. Bold and normal-weight curves are postulated and actual distributions, respectively.

We now consider the consequences of the postulated distribution being incorrect. The curve of normal weight lying to its left in Fig. 3 describes the actual (i.e., correct) distribution. The area β of this distribution lies in the acceptance region of the postulated (but incorrect) distribution, as shown by the lightly shaded region. β is the Type-II error (or consumer’s risk), equal to the probability that data drawn from the actual distribution are accepted as members of the postulated distribution. More detail on Type-I and Type-II errors can be found in statistics textbooks (e.g., ref 22).

The similarity of Figs. 2b and 3 is not coincidental. We propose that p is a “good” approximation to m, if there is a high probability β that p falls in the acceptance region of the m distribution. If β is large, we can approximate migration-time distributions in CE simply by counting the numbers of observed peaks in different bins (see Fig. 1a).

The analogy between counting peaks and the Type-II error is not exact, however. In a true Type-II error, the random variable has the same meaning (e.g., mass, volume, etc.) in both the postulated and actual distributions. In contrast, p and m are observed peaks and peaks, respectively, and have different meanings unless all observed peaks are resolved. In most ensemble members, fewer observed peaks are found than peaks because of peak overlap. Inevitably, p is a biased representation of m, unless all peaks are resolved. Our modeling by a Type-II error merely controls the bias in a quantifiable and familiar manner and, as previously stated, assures us that p is a plausible (if not actual) m value.

Given this model, we need to find the amount of peak overlap that makes the p and m distributions partially merge for a large, pre-specified β. It makes no sense to set β equal to 1 − α. This corresponds to exact mergence of the p and m distributions, and occurs only if all peaks are resolved. We must tolerate a small amount of peak overlap and thus choose β to be slightly smaller than 1 − α. Specifically, we consider α= 0.05 and two Type-II-error thresholds, 0.85 and 0.90, which we call β_t. In other words, the acceptance region of the m distribution spans the 95% confidence interval, and 85% or 90% of the p distribution falls in this interval. Our methods, however, are general and apply to all appropriate α and β.

Equations for the mean and variance of p and m

Because we assume peak density in the CE bins is constant within a given bin (see Fig. 1a), only constant-density p and m distributions need to be considered, with the results applying independently to each bin. Equations for the Poisson distribution of peak number m [23] and the distribution of observed-peak number p for Poisson distributed m [18] are known. The latter, however, is given by a finite series containing terms of alternating sign, and extensive significant figures can be required for accurate evaluation. As shown in Figs. 2a and 2b, the envelopes of the p and m distributions are Gaussian-like. For simplicity, we model the distributions by Gaussians and subsequently justify the modeling. Let m̄ and ${\sigma }_m^2$ equal the mean and variance of the number of peaks in the separation ensemble, with p̄ and ${\sigma }_p^2$ equaling the mean and variance of the number of observed peaks. Although both p and m are integral, p̄ and m̄ do not have to be integers. In SOT, the means p̄ and m̄ are related by the saturation A

$$A=4\overline{m}\sigma R_s^{\ast }/X$$ (1)

which is a metric of peak crowding [15]. (The usual symbol in SOT for saturation is α but this also is the usual symbol for the Type-I error.) In Eq. (1), σ is the standard deviation of peaks in the relevant bin, X is the bin duration (see Figs. 1a and 1b), and $R_s^{\ast }$ is the average minimum resolution that separates two adjacent peaks into different observed peaks. As is well known, the Gaussian approximation to the Poisson distribution of m has mean m̄ and variance ${\sigma }_m^2=\overline{m}$. For Poisson distributed m, the Gaussian approximation to the p distribution has mean [15]

$$\overline{p}=\overline{m}exp(-A)$$ (2)

and variance [18]

$${\sigma }_p^2=\overline{m}exp(-A)[1-2Aexp(-A)]$$ (3)

which is less than or equal to ${\sigma }_m^2$.

In SOT, the value of $R_s^{\ast }$ depends on the definition of an observed peak. For observed peaks that are defined as maxima, $R_s^{\ast }$ is not an arbitrary value but a specific function that depends on the distribution of peak heights [24] and the amount of peak overlap [25] in a manner that is nonintuitive to most practitioners. For empirical [9,12,26–28] and theoretical [9,29] reasons, peaks usually are assumed to have an exponential distribution of heights. Here, our results will implicitly incorporate this $R_s^{\ast }$ function to simplify interpretation. Recently this function was adsorbed into a new variable, the effective saturation [30].

In typical applications of SOT, σ measures the dispersion of an extremely large number of molecules of a single compound. In the CE of organelles, it measures the dispersion of a single organelle, as determined by its transit time through an on-line detection cell. Despite this difference, SOT still can be applied as long as the peak profiles are Gaussian or Gaussian-like.

Relation between m̄, σ, and X for β_t

For any m̄, we must find the saturation that satisfies the equation

$${(2\pi {\sigma }_p^2)}^{-1/2}\underset{\overline{m}-z{\sigma }_m}{\overset{\overline{m}+z{\sigma }_m}{\int }}exp[-{(p-\overline{p})}^2/(2{\sigma }_p^2)]dp={\beta }_t$$ (4)

with p̄ and ${\sigma }_p^2$ defined by Eqs. (2) and (3), respectively. The integrand on the left-hand side of Eq. (4) is the Gaussian approximation to the p distribution (henceforth, the Gaussian p distribution). The integration limits coincide with the confidence limits of the Gaussian approximation to the m distribution (henceforth, the Gaussian m distribution), with ${\sigma }_m=\sqrt{\overline{m}}$ and z=1.9599 (α= 0.05). Eq. (4) determines the threshold saturation A_t, for which the area β_t of the Gaussian p distribution lies in the acceptance region of the Gaussian m distribution. For saturations less than A_t, this area exceeds β_t; for saturations exceeding A_t, this area is less than β_t.

The relation between m̄ and A_t determined by Eq. (4) is subject to two errors. First, the actual p and m distributions are discrete, not Gaussian. Second, the confidence limits of the discrete m distribution are integers, but those of the Gaussian m distribution typically are not integers. The consequence of these errors is discussed below.

Using Eq. (1) and the dependence of $R_s^{\ast }$ on saturation for exponentially distributed peak heights [25], we can convert the relation between m̄ and A_t into one between m̄ and the threshold reduced peak standard deviation (σ/X)_t, which is the dimensionless ratio σ/X at the threshold saturation. Both σ and X can be measured experimentally, allowing us to relate σ/X and p to A_t and β_t.

Procedures

Calculation of threshold saturation and reduced standard deviation

Eq. (4) was solved by bisection for β_t = 0.85 and 0.90 (α= 0.05), and for integral values of m̄ between 10 and 1000, inclusive. The solution was the threshold saturation, A_t, which determines Eq. (4) via Eqs. (2) and (3). In each bisection step, the left-hand side of Eq. (4) was evaluated from numerical values of the error function, with linear interpolation between tabulated arguments spaced by 0.001. The relationship between m̄ and A_t was converted into one between m̄ and (σ/X)_t using Eq. (1) and the relation between $R_s^{\ast }$ and saturation for exponentially distributed peak heights [25].

Monte-Carlo simulation of discrete m and p distributions

The Poisson distribution of peaks along the migration-time axis was modeled by a Poisson distribution of points at the peak centers. For each point distribution, the number of intervals between adjacent points sufficient for separation was counted. By repeating this process many times, the peak and observed-peak distributions were constructed. Specifically, Poisson distributed points were simulated along the migration-time axis x with the iterative expression, x_n+1=x_n−X ln(1−R)/m̄ [31], where R is a random number between 0 and 1, m̄ is the average number of coordinates in interval X, and n is the coordinate index (x_n+1≥x_n since ln(1−R) is negative). In each simulation, the Poisson process was initiated far away (x₁ = −3) from the arbitrary region of interest between x = 0 and x = 1 (X = 1), and the m coordinates in this region were collected. For select m̄ and A_t, the critical interval $4\sigma R_s^{\ast }=A_t/\overline{m}$ that separates adjacent peaks into observed peaks was calculated with Eq. (1) and compared to intervals between adjacent points along the axis. A pair of adjacent points with an interval smaller than A_t/m̄ belonged to the same observed peak. The number of observed peaks p was counted. The simulation was repeated 5 × 10⁵ times, and discrete distributions were built from the p and m values.

Application to experimental CE

The migration-time distribution of a mitochondrial CE described elsewhere [32] was estimated using the Type-II error analogy. The CE was acquired at 100 Hz. Maxima produced by baseline noise were removed by clipping. The standard deviations of six segments of baseline having durations of 8 to 50 s were pooled to estimate the average baseline noise. The lower bound of the baseline was estimated at 34 points spanning the CE and linearly interpolated. Six standard deviations of average noise then were added to the interpolated lower noise bound, and all signal below this sum was clipped. The peak standard deviation σ was calculated by moments analysis of 13 isolated observed peaks spanning the clipped CE. The total number of observed peaks p_tot in the clipped CE was identified with the number of signals having greater height than their immediately adjacent neighbors. The migration times of observed peaks were partitioned among N equally spaced bins, with N equal to the integral truncation of

$$N={(2p_{\mathit{tot}})}^{1/3}+1$$ (5)

which is one bin larger than the minimum bin number predicted by a common statistics formula [33]. The number p of observed peaks in each bin was counted and interpreted.

Results and Discussion

Comparison of discrete and Gaussian p and m distributions at threshold saturation

Graphs of probability (for discrete distributions) and probability density (for continuous distributions) vs. p and m are shown in Fig. 4 for m̄ = 10, 50, and 250. The probability is given by symbols associated with discrete p and m values determined by Monte-Carlo simulation. The probability density is given by curves associated with the Gaussian p and m distributions. Both were computed at the threshold saturations A_t determined from Eq. (4) for β_t = 0.85 or 0.90 (α= 0.05). Values of A_t are reported in the panels. The vertical bars represent the confidence limits of the Gaussian m distribution. The p distributions have less breadth than the m distributions (σ_p≤σ_m) and maximize at greater probability (or probability density), since both distributions are normalized. In general, the Gaussian envelopes agree well with the discrete probabilities. This is not surprising for the Gaussian m distribution. However, the Gaussian and discrete p distributions are slightly shifted, indicating the agreement is not exact.

Figure 4.

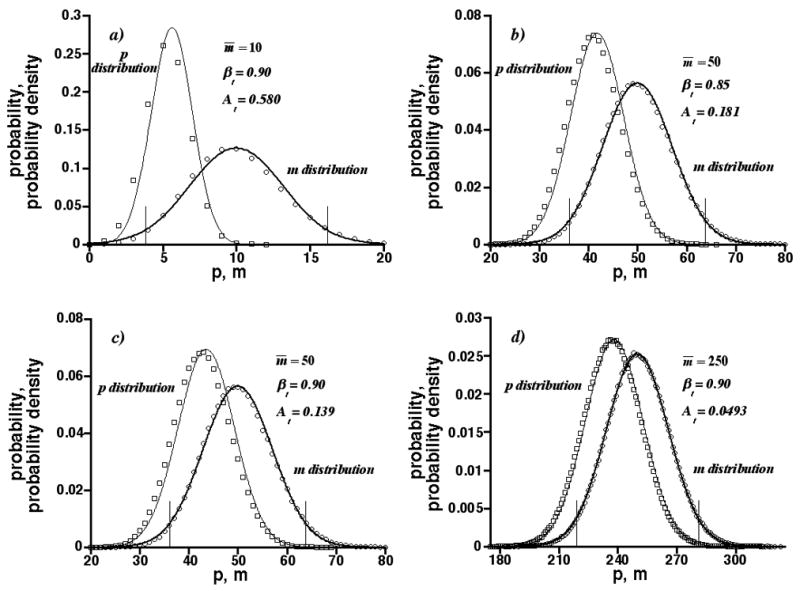
Graphs of probability and probability density vs. p and m at threshold saturations A_t calculated from Eq. (4). Circles and squares are simulation results for discrete m and p distributions, respectively; bold and normal-weight curves are Gaussian m and Gaussian p distributions, respectively; vertical lines are confidence limits of Gaussian m distributions. m̄ = 10, 50, and 250; β_t = 0.85 and 0.90 (α= 0.05).

Figs. 4a, 4c, and 4d show the threshold saturation A_t decreases with increasing m̄ at constant β_t. This happens, because the relative breadths of the Gaussian p and m distributions, as measured by their relative standard deviations σ_p/p̄ and σ_m/m̄, decrease with m̄^−1/2 (e.g., see Eq. (3)). However, the relative difference between the distribution means, (m̄ − p̄)/m̄ = [1 − exp(− A)], is independent of m̄. Therefore, as m̄ increases the interval between the p and m distributions becomes smaller to maintain β_t, causing A_t to decrease. Less peak overlap can be tolerated as m̄ increases. In addition, Figs. 4b and 4c show the threshold saturation decreases as β_t increases at constant m̄. This happens, because the interval between the p and m distributions becomes smaller to increase β_t, causing A_t to decrease. Less peak overlap can be tolerated as β_t increases.

Relation between m̄ and threshold saturation

Fig. 5a is a graph of m̄ vs. the threshold saturation A_t for β_t = 0.85 and 0.90 (α= 0.05), as determined from Eq. (4). The inset shows results for m̄ as small as 10. The Gaussian m and p distributions become poor approximations as m̄ drops below 10 but we are not unduly concerned, as separation bins containing fewer than 10 peaks will have only minor effects on most migration-time distributions. As reported, the threshold saturation decreases with increasing m̄. However, it can be surprisingly large for small m̄. Also as reported, it is larger for the smaller β_t. The resolution between the Gaussian p and m distributions at the threshold saturation is discussed in Part One of Supplementary Material to this paper.

Figure 5.

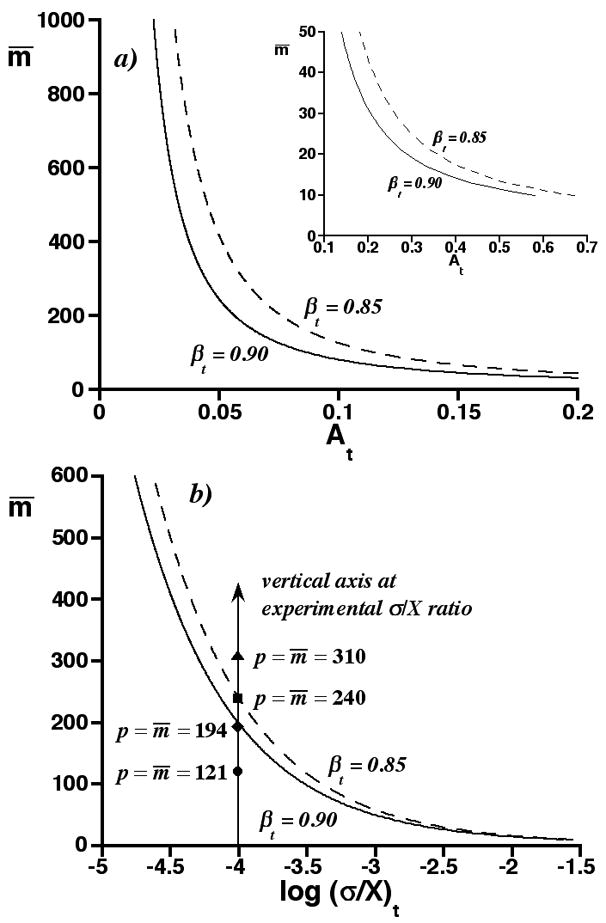
a) Graph of m̄ vs. threshold saturation A_t for β_t = 0.85 and 0.90 (α= 0.05). Inset shows results for small m̄. b) Graph of m̄ vs. log (σ/X)_t for β_t = 0.85 and 0.90 (α= 0.05), as calculated from a) for exponentially distributed peak heights. Symbols on vertical axis represent four conditional assignments, p = m̄, at experimental σ/X ratio.

As noted earlier, Eq. (4) is subject to error, because it is based on continuous distributions instead of discrete ones. In Part Two of Supplementary Material to this paper, we report results of Monte Carlo simulations of discrete p and m distributions for some (m̄, A_t) coordinates in Fig. 5a. The average Type-II error of these discrete distributions agrees within 0.5% of β_t, if the lower confidence limit of the Gaussian m distribution is rounded to the nearest integer and this integer is included in the acceptance region of the discrete m distribution. Therefore, the curves in Fig. 5a are sufficient for further interpretation.

Relation between m̄, σ, and X at threshold saturation: graphical procedure for Type-II error analogy

Fig. 5b is a graph of m̄ vs. the common logarithm of the threshold reduced peak standard deviation, (σ/X)_t, derived from the curves in Fig. 5a, Eq. (1), and the relation between saturation and $R_s^{\ast }$ for exponentially distributed peak heights [25]. The m̄ range is reduced relative to Fig. 5a for clarity. The curves represent m̄ and (σ/X)_t values, at which the acceptance region of the Gaussian m distribution contains area β_t of the Gaussian p distribution. For convenience, we call them threshold curves. The general shape of the threshold curves is similar to the curves in Fig. 5a, since the saturation and σ/X are proportional (see Eq. (1)).

To use the threshold curves, we first partition a CE (or other separation) into bins, measure the peak standard deviation σ in, and duration X of, a bin, and count the number of observed peaks p in the bin. (If we are concerned that σ is biased by peak overlap in organelle CE, we must dilute the sample to obtain some peaks of single organelles and determine σ from them.) Next, we draw a vertical axis through the (σ/X)_t value equaling the experimental σ/X ratio, as shown in Fig. 5b. Finally, we make the conditional assignment, p = m̄, and graph p on the vertical axis. The symbols on the vertical axis in Fig. 5b are four such graphs. On doing so, one of three conditions is met:

1. If p lies well below the intersection of the vertical axis and threshold curve, then β is much larger than β_t. Here, p is a good estimate of m.

2. If p lies near or on this intersection, then β is close to β_t. However, it may be smaller, and we should be cautious in accepting p as an estimate of m.

3. If p lies well above the intersection, then β is much smaller than β_t. Here, p is a poor estimate of m and should be rejected.

This procedure then is repeated for each bin and its associated values of p and σ/X.

Justification of procedure

The ordinate of the vertical axis in Fig. 5b is m̄ and therefore proportional to saturation (see Eq. (1)). For any m̄, the saturation depends on the specific (σ/X)_t ratio at which the axis is drawn. In all cases, however, m̄ values on the axis and below the threshold curve are paired with saturations less than A_t, for which β > β_t. In contrast, m̄ values on the axis and above the threshold curve are paired with saturations greater than A_t, for which β < β_t. For the m̄ on both the axis and the threshold curve, the saturation equals A_t and β = β_t.

The conditional assignment, p = m̄, is probably confusing. We are not asserting that p actually equals m̄, anymore than we previously asserted that p equals m. Rather, the experimental value of p is a plausible outcome only for a small m̄ range, and the conditional assignment p = m̄ helps us gauge that range. This is important, because the threshold curves in Fig. 5b depend on m̄, which we do not know. In fact, of p, m, m̄, and saturation A, we only know p with certainty. Without gauging the range of m̄ by the conditional assignment, the threshold curves can be overinterpreted, leading to β’s that can be smaller than expected and the acceptance of biased p values.

The limitations of the threshold curves are discussed in conjunction with Fig. 6. The ordinate in all panels of Fig. 6 is the vertical axis in Fig. 5b, located at log(σ/X)_t=−4.01 (this value is arbitrary for this discussion, but was chosen to correspond to the organelle CE interpreted below). The different panels in Fig. 6 address the four different p = m̄ assignments in Fig. 5b. Fig. 6a shows three possible Gaussian p distributions (normal-weight curves) and m distributions (bold curves) for p = 121. These distributions are graphed against implicit axes of p and m (as in Fig. 4), which are not shown. The left-most distribution pair is based on the conditional assignment, p = m̄ = 121. As expected, the Gaussian m distribution maximizes at p. Two other distribution pairs lie to its right. One corresponds to a smaller m̄ (111); the other, to a larger m̄ (141). All three distribution pairs are plausible, since p = 121 has a reasonable probability of occurence in each (this p value is indicated on all three Gaussian p distributions by circles connected with a horizontal line). Any of these distribution pairs could be the correct one. Given only p, we cannot know m̄, the saturation, or β exactly.

Figure 6.

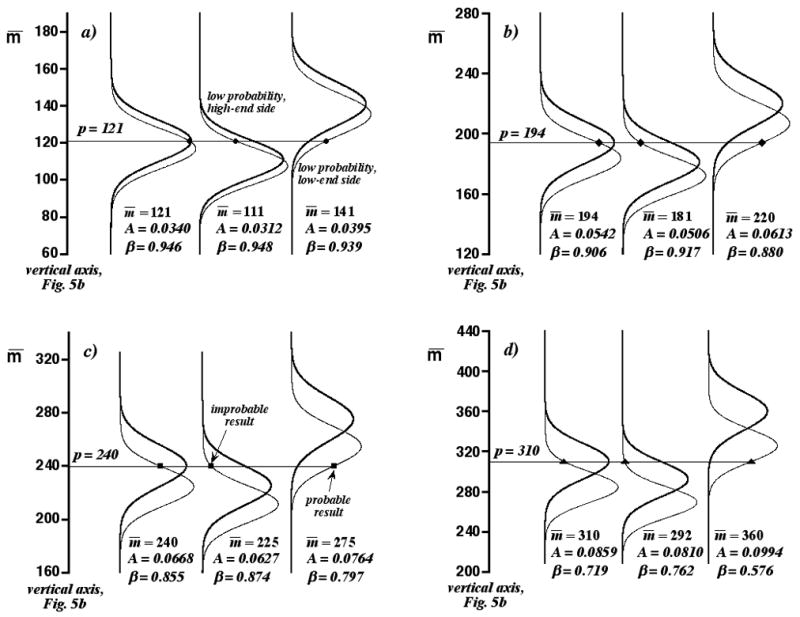
Panels of Gaussian p distributions (normal-weight curves) and Gaussian m distributions (bold curves) for different m̄ along vertical axis in Fig. 5b. Three distribution pairs are shown in each panel. Left-most distribution pairs correspond to the four conditional assignments, p = m̄, in Fig. 5b. Symbols are p values connected by horizontal lines (the symbols are the same as in Fig. 5b). Saturations A and Type-II errors β are reported. a) p = m̄ = 121. b) p = m̄ = 194. c) p = m̄ = 240. d) p = m̄ = 310.

This discouraging fact is mitigated, however, by our previous assertion that p = m̄ is a likely outcome only for a small m̄ range. For example, m̄ cannot be much less than 111. If it were, then the central distribution pair in Fig. 6a would have to “slide down” the vertical axis, but without changing p. In this case, p = 121 would become an improbable result sampled from the low-probability, high-end side of the Gaussian p distribution. This side of the distribution is identified in Fig. 6a. However, this is inconsistent with the determination of p = 121 by the separation; while it could be improbable, it is not likely so. Similarly, m̄ cannot be much larger than 141. If it were, the right-most distribution pair in Fig. 6a would have to “slide up” the vertical axis, and p = 121 would become an improbable result sampled from the low-probability, low-end side of the Gaussian p distribution. This side also is identified in Fig. 6a. The value of p restricts the range of plausible m̄ values, saturations, and β’s, and these restrictions are the basis of the conditional assignment, p = m̄. The actual saturations and β’s of the three distribution pairs in Fig. 6a are reported in the panel. In all cases, β > β_t and p is a good approximation to m. This is consistent with our earlier assertion that conditional assignments (in this case, p = m̄ = 121) lying well below the intersection of the threshold curves and the vertical axis in Fig. 5b correspond to acceptable p values.

Similar arguments can be made for the distribution pairs in Figs. 6b–6d, which are related to the remaining conditional assignments in Fig. 5b. However, as we “slide up” the vertical axis, we are increasingly likely to encounter plausible but undesirably large saturations (and small β’s), even in the vicinity of the threshold curves. The left-most distribution pair in Fig. 6b corresponds to the conditional assignment, p = m̄ = 194, which lies on the vertical axis in Fig. 5b just below the threshold curve for β_t = 0.90. Because the saturation is greater than in Fig. 6a, this distribution pair is more separated, with p lying more than before on the high-end side of the Gaussian p distribution. However, the range of β’s for the three distribution pairs in Fig. 5b is close to β_t (0.880 ≤ β ≤0.917). The left-most distribution pair in Fig. 6c corresponds to p = m̄ = 240, which lies on the vertical axis in Fig. 5b just below the threshold curve for β_t = 0.85. Here, the saturation is even greater than in Fig. 6b and p lies even more on the high-end side of the Gaussian p distribution. There are two consequences to this. First, m̄ cannot be much smaller than the conditional assignment, because p becomes an improbable result sampled from the low-probability, high-end side of the Gaussian p distribution (see the middle distribution pair in Fig. 6c). In contrast, m̄ can be much larger than the conditional assignment, with β considerably smaller than β_t (see the right-most distribution pair in Fig. 6c, for which β = 0.797). This large m̄ is plausible, because p = 240 has a high likelihood of occurrence. These behaviors are even more pronounced in Fig. 6d for p = m̄ = 310, which lies well above the threshold curves in Fig. 5b. Therefore, we think it is best to error on the side of caution and accept p as an approximation to m, only if p lies well below the threshold curves.

These criteria probably can be refined. However, the objective of this paper is to provide simple guidelines for the acceptance or rejection of the number of observed peaks p as an approximation to the number of peaks m.

Computational procedure for Type-II error analogy

We actually do not advocate graphing p on a vertical axis in graphs of m̄ vs. log(σ/X)_t. The graph in Fig. 5b was used only to explain our procedure in a simple manner. For 10 ≤ m̄ ≤600, the threshold curves in Fig. 5b are described by the empirical fits

$$\overline{m}=-645.74-1277.8s-985.84s^2-377.68s^3-72.008s^4-5.6743s^5;{\beta }_t=0.85$$ (7a)

and

$$\overline{m}=-751.38-1429.1s-1061.4s^2-391.14s^3-71.756s^4-5.4210s^5;{\beta }_t=0.90$$ (7b)

where s=log(σ/X)_t. These fits describe the m̄ value determined by the intersection of the threshold curves and any vertical axis drawn in Fig 5b. The absolute value of the maximum difference between these curves and fits is less than 2.5. In practice, one can take the common logarithm of the experimental ratio σ/X for a CE bin, interpret it as s, and evaluate Eq. (7). If the number of observed peaks p in the bin is much less than the m̄ so evaluated, then condition 1) of our graphical procedure applies, in which p lies well below the threshold curves. In contrast, if p almost equals the evaluated m̄, then condition 2) applies, in which p almost lies on the threshold curves. Finally, if p is much greater than the evaluated m̄, then condition 3) applies, in which p lies well above the threshold curves.

Application of procedure to mitochondrial CE

Fig. 7a is a mitochondrial CE first discussed in ref 32. The tops of the four observed peaks of greatest height are clipped to show the smaller observed peaks. The baseline noise was analyzed in the six intervals bracketed by arrows. The inset shows the noise level at the electropherogram end prior to clipping. The clipped CE contains p_tot = 527 observed peaks, which determined N = 11 bins of duration X = 90.4 s in accordance with Eq. (5). The asterisks identify the 13 observed peaks used to determine the peak standard deviation σ. Although we are not sure these are peaks of single mitochondria, they are well isolated from other signals. The average σ so determined is 8.84 ms, with an RSD of 12.4. The small RSD is consistent with both the determination of σ from single mitochondria and the independence of σ of migration time. Because σ is constant throughout the CE, the σ/X ratio for all bins is 9.78 × 10⁻⁵. This ratio is the same as that for the vertical axis shown in Fig. 5b (log [9.78 × 10⁻⁵] = −4.01). All bins contained 121 or fewer observed peaks. As established previously, p values of 121 or less satisfy condition 1) of our graphical procedure (see Figs. 5b and 6a). Similarly, our computational procedure gives m̄ estimates from Eqs. (7a) and (7b) of 243.2 and 200.0, respectively, both of which are much larger than p = 121. Consequently, the p values in all 11 bins are good approximations to the numbers of peaks and can be used to construct an acceptably unbiased migration-time distribution. Fig. 7b is the distribution so determined. The heights of the 11 class intervals equal the numbers of observed peaks (or numbers of peaks, within the approximation). The distribution is similar to that in Fig. 1b, in which most peaks are found in the central region of the CE. Interestingly, most peaks in the largest bin have small heights.

Figure 7.

a) Experimental mitochondrial CE. Baseline noise was analyzed in the six intervals bracketed by arrows. Asterisks identify observed peaks used to calculate peak standard deviation σ. Inset shows electropherogram end prior to noise clipping. b) Migration-time distribution determined from CE and Type-II error analogy.

Selection of bin number

Statisticians have proposed several formulas for the estimation of bin number [34–36], of which Eq. (5) is an example. The general principles are clear. The bin number should not be too small; otherwise, real variations in the distribution are lost. But it also should not be too large; otherwise, the binning too closely mirrors the sampled data and not the underlying distribution. This merits reflection, because it may be tempting to partition CEs into more bins than the formulas suggest. By increasing the number of bins, one decreases the number of peaks per bin, increases the threshold saturation (see Fig. 5a), and increases the amount of peak overlap permitted in the bin. However, in doing so, one also gets a distorted migration-time distribution. Rather than do this, we think it is better to improve the separation and decrease peak overlap.

Conclusion

In this paper, we used an analogy to the Type-II error of hypothesis testing to predict from SOT the conditions for which the number of observed peaks in organelle CE is a good approximation to the number of peaks. The theory and the procedure based on it confirm that the mitochondrial CE in Fig. 7a has negligible peak overlap. This CE is similar to many organelle CEs previously reported in the literature in duration, peak width, and peak density [37–39]. Based on this similarity, it is reasonable to conclude that most of these published CEs are also free of significant peak overlap, and that mobility distributions calculated from them are basically valid. While this has been commonly assumed, our work justifies the validity of the assumption. However, we should not assume that peak overlap always will be negligible in organelle CE, particularly in CEs developed with chip technology producing relatively wide peaks [40] or CEs having high peak densities due to insufficient sample dilution or injection-volume overload [41]. Our simple procedure can be used to rapidly screen such CEs for peak overlap. Unlike some applications of SOT, it does not require a specialized base of knowledge or detailed understanding of probability. We encourage such screenings in future work.