TREEQA: QUANTITATIVE GENOME WIDE ASSOCIATION MAPPING USING LOCAL PERFECT PHYLOGENY TREES

Abstract

The goal of genome wide association (GWA) mapping in modern genetics is to identify genes or narrow regions in the genome that contribute to genetically complex phenotypes such as morphology or disease. Among the existing methods, tree-based association mapping methods show obvious advantages over single marker-based and haplotype-based methods because they incorporate information about the evolutionary history of the genome into the analysis. However, existing tree-based methods are designed primarily for binary phenotypes derived from case/control studies or fail to scale genome-wide.

In this paper, we introduce TreeQA, a quantitative GWA mapping algorithm. TreeQA utilizes local perfect phylogenies constructed in genomic regions exhibiting no evidence of historical recombination. By efficient algorithm design and implementation, TreeQA can efficiently conduct quantitative genom-wide association analysis and is more effective than the previous methods. We conducted extensive experiments on both simulated datasets and mouse inbred lines to demonstrate the efficiency and effectiveness of TreeQA.

1. Introduction

Genome wide association (GWA) mapping locates genes or narrows regions in the genome that have significant statistical connections to phenotypes of interest. The discovery of these genes and regions offers the potential to increase understanding of biological processes controlling manifestation of phenotypes.

The most frequent genetic variants are single nucleotide polymorphisms (SNPs), in which a single nucleotide in the genome differs between individuals within a species. With the development of low-cost genotyping technologies, extensive SNP data can be cheaply and efficiently produced, which further increases the computational complexity of GWA mapping. Thus, there is an evident need for fast and effective GWA mapping methods.

Existing methods of association mapping look for similarities among samples (chromosomes, haplotypes, etc.) that are correlated with the phenotypes. If strong associations are present, the variance of the phenotype within groups of similar samples is substantially smaller than the variance over all samples.

For example, in single marker-based^17,5 and haplotype-based association mapping^10,4,12, samples are grouped according to their genetic variation at a single marker or a set of markers. For case/control phenotypes, markers that can divide samples into (almost) pure classes are reported. Though these methods employ different strategies for grouping samples, the derived groups are evaluated without further consideration of the intergroup similarities or alternate groupings.

In observation of this, tree-based association methods^14,18,13 utilize phylogenies constructed over the samples. The phylogeny tree is a rich yet compact representation of genetic similarities of the samples. It provides sensible groupings of samples at multiple resolutions. However, the existing methods either handle only case/control phenotypes^14,18 or do not scale to GWA mapping¹³.

In this paper, we introduce TreeQA, a tree-based quantitative GWA mapping algorithm. TreeQA utilizes local perfect phylogeny trees constructed in genomic regions exhibiting no evidence of historical recombination by the 4-gamete test². Given a perfect phylogeny, TreeQA evaluates all implied groupings and finds the strongest associations to the phenotype. Furthermore, TreeQA can identify and remove outliers during association analysis.

A brute-force implementation consists of a double loop: for every phylogeny tree, and for every grouping represented by the tree, we conduct a separate ANOVA test to measure its association to the phenotype, and keep track of the best groupings and trees. This approach is inefficient and prone to multiple test errors¹. Both the number of trees and number of groupings per tree can be very large^a. This large number of possible groupings requires many ANOVA tests, which is not only expensive computationally, but also gives rise to spurious associations^b. Thus, permutation tests are necessary to ensure the statistical significance of the discovered associations, which will further increase the computational burden.

TreeQA exploits the following properties: (1) Groupings generated from the same tree obey a partial order, thus allowing reuse of intermediate computations; (2) A grouping may be derived from different trees, but only need to be evaluated once; and (3) Different phenotype permutations may share a substantial number of common computations that need to be computed only once. Thus, TreeQA employs two prefix-tree structures²¹ to organize all observed sample subsets and groupings to facilitate the caching and retrieval of reusable computations and guide the enumeration and evaluation of groupings. As a result, TreeQA is able to handle quantitative GWA mapping very efficiently and is more effective and robust in association mapping than previous methods.

2. Related Work

Single-feature association mapping^17,5 considers the sample groupings induced independently by each single marker. Statistical tests such as χ² and F-tests are used to measure the association between the phenotype and each grouping. These methods are computationally efficient, however, they do not utilize the additional information content carried by haplotypes over single markers.

To address this shortcoming, haplotype-based methods have been developed. HAM¹⁵ considers combinations of three consecutive SNPs along the genome. QHPM⁸ uses frequent pattern mining methods to find haplotype patterns in the data, upon which sample groupings are created and evaluated. HapMiner¹⁰ clusters samples using consecutive subsets of markers, and then assess the phenotype’s association strength.

The utility of local phylogenies in association mapping has been recently explored in TreeLD¹³, Blossoc¹⁴, and TreeDT¹⁸. These methods use trees to represent sample similarities. Their approach is to exhaustively examine all possible groupings implied by the given phylogenies without explicitly excluding any outliers. Both Blossoc and TreeDT assume simple categorical (binary) phenotypes. TreeLD handles quantitative phenotypes but is not scalable to GWA analysis.

Some other work^6,7,16 uses a global phylogeny structure, e.g., ancestral recombination graph, over all markers in association mapping. However, because of the high computational cost of global phylogeny construction, these methods are not scalable to genome-wide analysis.

3. Preliminaries

We use a binary matrix H = S × M to represent a SNP dataset, where S = {s₁, s₂, …, s_n} is the set of samples, and M = {m₁, m₂, …, m_z} is the SNP marker set. Each sample is represented by a binary vector, in which ’0’ represents the majority alleles and ’1’ represents the minority alleles. We use f(s_i) to denote the phenotype value of a sample s_i and F(S′) to denote the phenotype values of samples in a subset S′. An example matrix H containing 10 samples and 10 SNP markers with phenotype is shown in Fig. 1(a).

Figure 1.

Example: a SNP dataset and a perfect phylogeny tree

Compatible region

A consecutive region of the genome is called a compatible region iff any pair of markers in that region are compatible by the 4-gamete test². That is, among the 4 possible haplotypes formed by the two markers, at most three of them occur.

A compatible region is a genomic region exhibiting no evidence of historical recombination. In Fig. 1(a), the region from markers m₁ to m₈ is a compatible region. We use C_u,v to denote a compatible region from markers m_u to m_v.

Maximal Compatible region

A compatible region is a maximal compatible region iff it can not be extended on either side to include more SNPs and remains compatible.

Perfect Phylogeny Tree

A phylogeny tree for a set of samples is perfect if the phylogeny avoids homoplasy. Every SNP is introduced by a mutation and is represented by an edge of the tree. Given a genomic region, a perfect phylogeny exists iff the region is a compatible region.

We use T_u,v to denote the perfect phylogeny tree of compatible region C_u,v. Given C_1,8 in Fig. 1(a), its tree T_1,8 is shown in Fig. 1(b). All samples are at the leaf nodes. Samples having identical haplotypes in the region share the same leaf node in the tree, e.g., s₁ and s₅. Each internal node represents a hypothetical common ancestor of a subset of samples. Each edge uniquely corresponds to a SNP (or a historical mutation). Interested readers may refer to paper³ for inferring perfect phylogenies from a set of SNPs.

Let E(T_u,v) = {e₁, e₂, …, e_p} denote the set of edges in T_u,v. The removal of each edge partitions the samples into two subsets denoted by S⁽⁰⁾(e_i) and S⁽¹⁾(e_i). Given a tree T_u,v, we can generate 2|E(T_u,v)| sample subsets by removing each edge separately. We denote this set of sample subsets by S^(E)(T_u,v), S^(E)(T_u,v) = {S^(j)(e_i)|j = {0, 1}, e_i ∈ E(T_u,v)}.

Definition 3.1

A grouping of a sample subset S′, G(S′), is formed by a set of disjoint subsets of S′, $G(S\prime )=\{S_1^{\prime },S_2^{\prime },\dots ,S_k^{\prime }\},S_i^{\prime }\subset S\prime ,S_i^{\prime }\cap S_j^{\prime }=\varnothing ,{\displaystyle {\cup }_{i=1}^k{S}_i^{\prime }=S\prime }$. Given a tree T_u,v, we say a grouping G(S′) follows $T_{u,v}\mathit{\text{iff}}\forall S_i^{\prime }\in G(S\prime ),S_i^{\prime }\in S^{(E)}(T_{u,v})$.

For example, grouping G(S′) = {{s₁, s₅, s₂, s₃}, {s₈, s₉, s₇, s₁₀}} follows the tree in Fig. 1(b), while grouping G(S′) = {{s₁, s₂}, {s₈, s₄}} does not.

Definition 3.2

Given a sample subset S′, G₁(S′) is called a parent-grouping of G₂(S′) (G₂(S′) called a child-grouping of G₁(S′)) $\mathit{\text{iff}}\forall S_i^{\prime }\in G_1(S\prime )$

$$\exists S_j^{\prime }\in G_2(S\prime ),s.t.S_i^{\prime }=S_j^{\prime }.\mathit{\text{OR}}\exists \{S_{j_q}^{\prime }|S_{j_q}^{\prime }\in G_2(S\prime ),q=1,\dots ,u\},s.t.S_i^{\prime }={\displaystyle \underset{q=1}{\overset{u}{\cup }}{S}_{j_q}^{\prime }}$$

A child-grouping represents a finer partition of its parent-grouping on the same set of samples. For example, grouping {{s₁, s₅, s₂, s₃}, {s₄, s₆}} is the parent-grouping of {{s₁, s₅}, {s₂, s₃}, {s₄, s₆}}. We summarize the notations in Table 1.

Table 1.

Summary of Notations

S, si, $S_i^{\prime }$	the sample set, a sample, a subset of samples
M, mi	the marker set, a marker
H	a binary matrix representing the data
Cu,v	a compatible interval of H
f(si)	phenotype value of sample si
$F(S_i^{\prime })$	the set of phenotype values of the samples in $S_i^{\prime }$
Gi(S′)	a grouping of a sample subsets S’
Tu,v	the perfect phylogeny tree of Cu,v
E(Tu,v)	the edge set of Tu,v
S(E)(Tu,v)	the set of sample subsets implied in tree Tu,v (leaf-sets)

Association between a Compatible Region and a Phenotype

We use the one-way ANOVA test with permutations to measure the association between a grouping of samples and a quantitative phenotype. To accelerate the execution, we re-derive the formula of the ANOVA test.

Given a grouping $G(S\prime )=\{S_1^{\prime },\dots ,S_k^{\prime }\},\text{for every}{S}_i^{\prime }\in G(S\prime )$, we calculate

$$SQ(S_i^{\prime })={\displaystyle \sum _{s_j\in S_i^{\prime }}}f{(s_j)}^2,SM(S_i^{\prime })={\displaystyle \sum _{s_j\in S_i^{\prime }}}f(s_j)$$ (1)

$${\mathit{\text{SSE}}}_i=\mathit{\text{SQ}}(S_i^{\prime })-\mathit{\text{SM}}{(S_i^{\prime })}^2/|S_i^{\prime }|,{\mathit{\text{SSB}}}_i=\mathit{\text{SM}}{(S_i^{\prime })}^2/|S_i^{\prime }|$$ (2)

Combining all subsets together, we have $MM=\frac{1}{|S\prime |}{\displaystyle {\sum }_{i=1}^k}SM(S_i^{\prime })$ and

$$MSE=\frac{1}{|S\prime |-k}{\displaystyle \sum _{i=1}^k}SS{E}_i,MSB=\frac{1}{k-1}({\displaystyle \sum _{i=1}^k}SS{B}_i-|S\prime |·M{M}^2)$$ (3)

We obtain a base score for grouping G(S′)

$$F_0(G(S\prime ))=\frac{\mathit{\text{MSB}}}{\mathit{\text{MSE}}}$$ (4)

A higher score indicates a stronger association between the grouping and the phenotype. Given the tree and the data in Fig. 1 and the following two groupings: $G(S_1^{\prime })=\{\{s_2,s_3\},\{s_4,s_6\},\{s_8,s_9\}\},G(S_2^{\prime })=\{\{s_2,s_3\},\{s_8,s_9\}\}$, the scores are $F_0(G(S_1^{\prime }))=0.44,F_0(G(S_2^{\prime }))=4.16$. Thus, grouping $G(S_2^{\prime })$ has a stronger association with the phenotype than grouping $G(S_1^{\prime })$.

To correct the multiple test errors, we apply a permutation test on G(S′) to calculate a significance score. To permute the phenotype, the phenotype values in F(S′) are randomly re-assigned to samples in S′. Then we calculate an F-score using the permuted phenotype following Eqs.1 to 4.

Assume that we conduct nPerm random permutations in total, for each permutation, we get score F_j(j = 1…nPerm). Among the nPerm F-scores, let p be the number of scores which are greater than or equal to the base score F₀(G(S′)), i.e., p = |{ F_j| F_j ≥ F₀(G(S′)), j ∈ 1…nPerm}|. Then the significant score (P score) of G(S′) is

$$P(G(S\prime ))={\text{log}}_{10}\left(\frac{\mathit{\text{nPerm}}}{p}\right)$$ (5)

A higher P score indicates that the association between grouping G(S′) and the phenotype is more significant.

Definition 3.3. The association between a compatible region and a phenotype

For a compatible region C_u,v, the highest P score achieved by any grouping following T_u,v is regarded as the P score of C_u,v. The P score represents the association between the compatible region and the phenotype,

$$P(C_{u,v})=\mathit{\text{max}}\{P(G_j(S\prime ))|\forall G_j(S\prime )\mathit{\text{follows}}{T}_{u,v},S\prime \subseteq S\}.$$ (6)

Problem Definition

Given a SNP data and a quantitative phenotype, calculate the P-score of every maximal compatible region and report the most significant ones.

4. TreeQA Algorithm

TreeQA takes two major steps: 1) identify maximal compatible regions in the genome and construct the perfect phylogenies of the regions; 2) compute the association between each compatible region and the phenotype.

4.1. Maximal Compatible Region and Phylogeny Construction

TreeQA scans the markers in a left to right order. In order to find the maximal compatible regions, it continuously extends the current region by adding the next marker until the new marker is incompatible with some markers in the region. And it maximizes the overlap between two consecutive regions. Assume that the current compatible region is C_u,v, and marker m_v+1 is incompatible with markers m_i1, …, m_ik, u ≤ i₁ < … < i_k ≤ v, then TreeQA starts the next compatible region at marker m_ik+1. For each maximal compatible region, TreeQA utilizes the inferring algorithm³ to construct the local perfect phylogeny.

4.2. Association Computing

In the second step, TreeQA takes as input a quantitative phenotype and a set of local perfect phylogenies. It considers all possible groupings following the phylogenies and systematically explores the search space of these groupings in a carefully designed order such that intermediate computations can be maximally reused.

According to Definition 3.1, any grouping of a sample subset^c that follows a tree T_u,v can be created from non-overlapping subsets in S^(E)(T_u,v). By utilizing the lexicographical order^d of subsets in S^(E)(T_u,v), TreeQA can enumerate and evaluate all combinations of non-overlapping subsets systematically.

TreeQA enumerates all groupings via a depth-first recursive procedure. TreeQA extends the current grouping by including a new sample subset which does not overlap with any subsets in the current grouping. The association of each new grouping to the phenotype via a permutation test is computed. The P score of the corresponding maximal compatible region is updated accordingly. The enumeration continues recursively for each newly extended grouping.

Consider the tree in Figure 1. There are 14 sample subsets in S^(E)(T_1,8). Assume that the subsets have the following order,

$$\begin{array}{l}s{e}_1=\{s_1,s_5\},s{e}_2=S-s{e}_1,s{e}_3=\{s_2,s_3\},s{e}_4=S-s{e}_3,s{e}_5=\{s_4,s_6\}\\ s{e}_6=S-s{e}_5,s{e}_7=\{s_8,s_9\},s{e}_8=S-s{e}_7,s{e}_9=\{s_7,s_{10}\},s{e}_{10}=S-s{e}_9\\ s{e}_{11}=\{s_1,s_5,s_2,s_3\},s{e}_{12}=S-s{e}_{11},s{e}_{13}=\{s_8,s_9,s_7,s_{10}\},s{e}_{14}=S-s{e}_{13}\end{array}$$

TreeQA first generates a grouping containing se₁ only. Among the remaining sample subsets, {se₂, se₃, se₅, se₇, se₉, se₁₂, se₁₃} do not overlap with se₁. In the next step, a grouping {se₁, se₂} is formed by adding se₂ into the current grouping and its P score is calculated. P(C_1,8) is updated accordingly. Since all other sample subsets overlap with se₁ or se₂. Thus, no new grouping can be extended from {se₁, se₂}. Then, TreeQA examines the next grouping extended from {se₁}, {se₁, se₃}, and all groupings extended from it. After examining all groupings containing se₁, TreeQA will start from the grouping {se₂} and extend it recursively to generate all groupings containing se₂ but not se₁. This process continues until all distinct groupings are enumerated.

4.3. Effective Permutation

We found that more than 90% of the execution time of TreeQA is spent in permutation tests. Given a grouping G(S′), a permutation test is conducted in two steps: 1) randomly re-assigning the phenotype values in F(S′) to samples in S′; 2) calculating the corresponding F score by Eq. 4.

Given a subset S′, both steps take O(|S′|) time. TreeQA exploits maximal reusability of intermediate computation shared by permutation through the following two optimizations:

1. in Tree: Common computation units shared by permutation tests of parent/child-groupings in a tree.

2. amg Tree: Common computation units shared by permutation tests on groupings following multiple trees.

We use two global prefix-tree structures²¹, Tree_grouping and Tree_subset to organize groupings and sample subsets examined thus far respectively to enable effective permutation tests.

4.3.1. inTree: Effective permutation tests within a tree

A pair of parent/child-groupings always involve the same set of samples. Let S′ denote a set of samples. For the permutation tests of the parent/child groupings of S′, instead of re-assigning the phenotype values in F(S′) independently for each grouping, they can share the same set of random permutations of F(S′).

For example, given the example in Fig. 1 and a pair of parent/child-groupings, G₁(S′) = {{s₁, s₅, s₂, s₃}, {s₈, s₉, s₇, s₁₀}} and G₂(S′) = {{s₁, s₅}, {s₂, s₃}, {s₈, s₉, s₇, s₁₀}}, their F₀ scores are: F₀(G₁(S′)) = 9.79 and F₀(G₂(S′)) = 4.32. Assume that after a random permutation, the new phenotype values for the samples are: f(s₁) = 85, f(s₂) = 79, f(s₃) = 109, f(s₅) = 61, f(s₇) = 86, f(s₈) = 97, f(s₉) = 78, f(s₁₀) = 54. Using this new assignment, we can calculate the new F scores for both groupings: F (G₁(S′)) = 0.12 and F (G₂(S′)) = 0.7. By reusing the phenotype permutation between G₁(S′) and G₂(S′), we save O(|S′|) runtime in each permutation.

A child-grouping represents a finer partition of sample subsets in its parent-grouping. We say a grouping is at the finest level if it does not have any child-groupings. We use a global prefix-tree Tree_grouping to index all groupings and maintain the parent/child relationship through auxiliary links (from a child-grouping to its parent-groupings). For each permutation of the phenotype, the F scores of a finest grouping and all of its parent-groupings are calculated together. We examine the finest grouping immediately followed by the examination of its parent groupings for maximum computation reuse. If a finest child-grouping has n parent-groupings, we save O(n|S′|) time in each permutation.

4.3.2. amgTree: Effective permutation among trees

The same grouping occurs repeatedly in different trees. We only need to compute its P score at its first occurrence. We use Tree_grouping to store and retrieve the P score of all examined groupings. If the grouping formed by TreeQA can be found in Tree_grouping, its P score is directly used. Otherwise, its P score is calculated and stored in Tree_grouping.

4.4. Reuse of Intermediate Computation of Statistical Tests

For any sample subset S′, SQ(S′) and SM(S′) calculated using the original phenotype values (with no permutation) may be reused in any grouping containing S′ and all its parent-groupings. We denote them by SQ₀(S′) and SM₀(S′) respectively in the following discussion.

We employ a global prefix-tree Tree_subset to keep track of all sample subsets in any groupings examined thus far. Three values are stored at the leaf node corresponding to the subset S′: (subset ID, SQ₀(S′), SM₀(S′)).

For example, given the 10 samples and their phenotype values in Fig. 1(a), we calculate the base score F₀ of grouping G₁(S′) = {{s₁, s₅}, {s₂, s₃}, {s₇, s₁₀}}.

$$\begin{array}{l}S{Q}_0(S_{1_1}^{\prime })=19106,S{Q}_0(S_{1_2}^{\prime })=16805,S{Q}_0(S_{1_3}^{\prime })=9000.\\ S{M}_0(S_{1_1}^{\prime })=194,S{M}_0(S_{1_2}^{\prime })=183,S{M}_0(S_{1_3}^{\prime })=132.\\ F_0(G_1(S\prime ))=547.17/212.17=2.58.\end{array}$$

The SQ₀ and SM₀ values of the three subsets are then stored in Tree_subset. Given a parent-grouping of G₁(S′), G₂(S′) = {{s₁, s₅, s₂, s₃}, {s₇, s₁₀}}, we can retrieve the values of SQ₀ and SM₀ and use them to calculate F₀(G₂(S′)),

$$\begin{array}{l}S{Q}_0(S_{2_1}^{\prime })=S{Q}_0(S_{1_1}^{\prime })+S{Q}_0(S_{1_2}^{\prime })=35911,S{Q}_0(S_{2_2}^{\prime })=S{Q}_0(S_{1_3}^{\prime }).\\ S{M}_0(S_{2_1}^{\prime })=S{M}_0(S_{1_1}^{\prime })+S{M}_0(S_{1_2}^{\prime })=377,S{M}_0(S_{2_2}^{\prime })=S{M}_0(S_{1_3}^{\prime }).\\ F_0(G_2(S\prime ))=1064.08/166.69=6.38.\end{array}$$

The reuse of SQ₀(S′) and SM₀(S′) between parent/child groupings may work in conjunction with the inTree effective permutation. Besides, SQ₀(S′) and SM₀(S′) can also be reused by any groupings that contain the subset S′.

5. Results

We compare TreeQA with the following algorithms: 1) SMA, our implementation of the Single Marker Association algorithm^17,5; 2) HAM, our implementation of the Haplotype Association Mapping algorithm¹⁵ that slides a 3-SNP window through the genome; 3) HapMiner¹⁰, downloaded from the website^e; and 4) TreeLD¹³, downloaded from the website^f. Both SMA and HAM use the oneway ANOVA test for fair comparison.

QHPM⁸ is not used for comparison because it is not scalable to large data sets. Blossoc¹⁴ and TreeDT¹⁸ are not used because they require categorical phenotypes.

5.1. Experiments on Simulated Data

We use Coasim¹¹ to simulate 1000 sequences with scaled recombination rate ρ = 400 that corresponds roughly to 10 cM. 10,000 SNP markers are placed uniformly at random over the sequences.

SNP markers on the sequences are randomly selected as causative loci with one, two and three causative mutations. The first SNP is always selected randomly from all SNPs. In the cases of two and three mutations, the second and third causative SNPs are selected from compatible SNPs that are located less than 10 SNPs away from the first SNP. Phenotype values are sampled from four Gaussian distributions: N₁(140, 35), N₂(90, 35), N₃(50, 40), and N₄(10, 35). The one-mutation case uses N₁ and N₃. The two-mutation case uses N₁, N₂ and N₃. The three-mutation case uses all four Gaussian distributions. After assigning the phenotype values, all causative SNPs are removed from the data and we randomly select 100 sequences for our experiments.

SMA, HAM and HapMiner output the top one scoring locus as a point estimation of the causative locus, while TreeQA outputs the top one compatible region. We compare the effectiveness of the algorithms by measuring the distance (in cM) from the top one scoring locus or the center of the top one region to the causative SNP (or the average distance to every causative SNP). We call the distance the Prediction error.

Since HapMiner can not finish processing 10,000 SNP markers in a reasonable time, we only use the first 1,000 markers of each sequence when applying HapMiner on the simulated data.

The comparison of SMA, HAM, HapMiner and TreeQA is shown in Figure 2. The x-axis represents the prediction error (distance) to the causative locus and the y-axis represents the percentage of causative loci which are found in distance less than x. In all three cases, the estimated loci by TreeQA are closer to the causative loci than those by SMA, HAM and HapMiner.

Figure 2.

Comparison of SMA, HAM, HapMiner and TreeQA on the simulated data

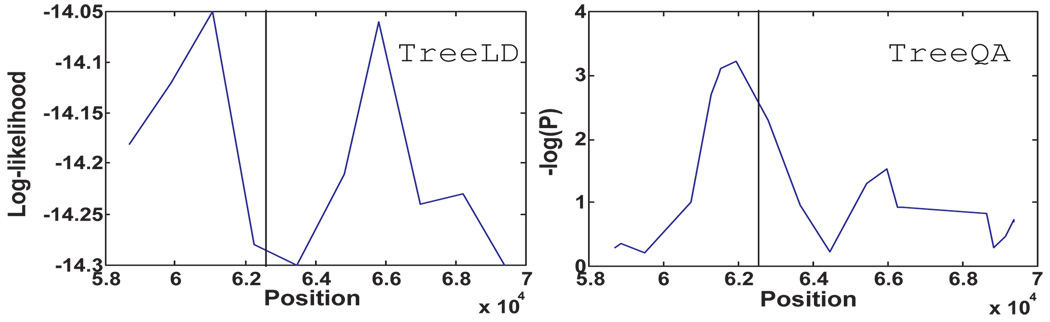
The TreeLD algorithm uses local phylogenies and analyzes quantitative phenotypes. However, TreeLD can only process a very small amount of data in reasonable time. Therefore, we select 36 samples and 20 SNP markers from the simulated data for performance comparison. A one-mutation causative locus is selected from the 20 SNPs. For TreeQA, instead of generating maximal compatible regions as discussed in Sec. 4, a compatible region is generated around each SNP and contains up to five SNPs. TreeLD takes about two hours to analyze this small data while TreeQA finishes in seconds. Figure 3 plots the results from TreeLD and TreeQA. The x-axis represents the simulated positions in the genome and the y-axis represents the scores of the SNPs. The vertical line demonstrates the causative locus. TreeQA detects a peak near the causative locus while TreeLD identifies two spurious peaks.

Figure 3.

Comparison of TreeLD and TreeQA on the simulated data

5.2. Experiments on Mouse Genotype Data

We used a set of mouse genotypes that combines experimental and imputed data^g20 from the Jackson Laboratory, consisting of 74 samples. The dataset contains over 7 million SNP markers distributed over all 20 chromosomes. We removed wild derived mouse inbred strains since they are quantitatively and qualitatively different than other laboratory inbred strains and we only used in our experiments the remaining 55 samples that have a share set of common ancestral relationships¹⁹.

We used high density lipoprotein cholesterol (HDL-C) levels in blood as the test phenotype, downloaded from the Mouse Phenome Database^h. Several HDL-C datasets are available, each of which was collected under different conditions, and are thus treated as separate phenotypes. Some candidate genes that may play a role in regulating HDL-C levels are reported in⁹.

We apply SMA, HAM and TreeQA on the data and examine how close they can identify the top peak near the locus of those candidate genes.

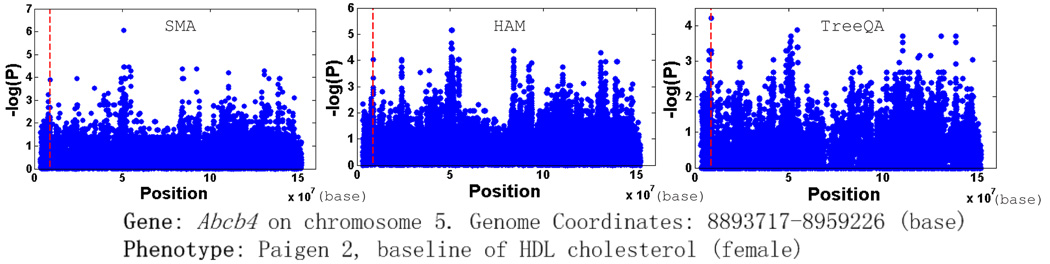
TreeQA detects top peaks near the locations for over 10 of the candidate genes⁹, including Ppara, Abcb4 and Rxrb. The top peaks reported by SMA and HAM are often far from the locations of these genes. Due to space limitation, we only show the results for one of them, Abcb4, in Figure 4.

Figure 4.

Compare SMA, HAM and TreeQA on the mouse genotype data

The perfect phylogeny corresponding to the peak point (compatible region from 8799298 to 8801558 (base)) found by TreeQA is plotted in Fig. 5. The phenotype values of the samples are in parentheses. Samples with unknown phenotype values are omitted from the tree. The subtree on the right contains samples having high phenotype values while the subtree at the bottom contains samples having low values. Other subtrees are considered as outliers and are excluded from the grouping. SMA and HAM fail to identify the locus because they only examine sample groupings that can be generated from single SNPs or 3-SNP windows, which are a small subset of the groupings examined by TreeQA.

Figure 5.

The perfect phylogeny at the peak point found by TreeQA in Figure 4

TreeQA takes about 10 minutes to analyze each chromosome which contains around 40000 SNPs on average. SMA and HAM take slightly less time than TreeQA. Both HapMiner and TreeLD are unable to finish in reasonable time.

6. Conclusion

In this paper, we present a tree-based quantitative GWA mapping algorithm, TreeQA. TreeQA utilizes local perfect phylogenies in detecting associations. Perfect phylogenies provide sensible groupings of samples at multiple resolutions. TreeQA explores the space of all possible groupings implied by the perfect phylogenies in a carefully designed order so that intermediate computations can be maximally reused. Our experimental results on both simulated and real data show that TreeQA can efficiently conduct quantitative GWA analysis and is more effective than the previous methods.