A Method for the Alignment of Heterogeneous Macromolecules from Electron Microscopy

Abstract

We propose a feature-based image alignment method for single-particle electron microscopy that is able to accommodate various similarity scoring functions while efficiently sampling the two-dimensional transformational space. We use this image alignment method to evaluate the performance of a scoring function that is based on the Mutual Information (MI) of two images rather than one that is based on the cross-correlation function. We show that alignment using MI for the scoring function has far less model-dependent bias than is found with cross-correlation based alignment. We also demonstrate that MI improves the alignment of some types of heterogeneous data, provided that the signal to noise ratio is relatively high. These results indicate, therefore, that use of MI as the scoring function is well suited for the alignment of class-averages computed from single particle images. Our method is tested on data from three model structures and one real dataset.

Introduction

Single-particle electron microscopy (EM) is used to resolve the three-dimensional (3D) structure of large macromolecular complexes (Frank, 2002a; van Heel et al., 2000). The reconstruction of a 3D structure from randomly orientated two-dimensional (2D) projections requires the assignment of both 2D translational alignment parameters and relative 3D Euler angles. Image alignment is used to assign translational parameters to raw images so that they can be classified and averaged in 2D, and to compare projections with an initial model so that Euler angles can be assigned (projection matching) (Penczek et al., 1994). Due to the large number of raw images and model templates used in a reconstruction, computationally efficient alignment methods based on the Fast Fourier Transform are widely used (Joyeux and Penczek, 2002). This use of the Fast Fourier Transform enables the processing of very large datasets, but limits the scoring function to cross-correlation or one of its variants.

The refinement of a 3D structure relies on the availability of an initial 3D model. This initial 3D model can be from a closely related structure generated by EM or X-ray crystallography, an ab initio reconstruction obtained using Random Conical Tilt (RCT) (Radermacher et al., 1987), or a reconstruction obtained using a common line based method (Penczek et al., 1996; van Heel, 1987). The initial 3D model is used as a template for the assignment of translational parameters and Euler angles. The raw data can then be used to calculate a new structure which again is used to assign translation and Euler-angle parameters to the raw images. This process (projection matching) is used iteratively to improve the accuracy of parameter assignment, resulting in progressively higher resolution structures.

This basic projection matching approach relies heavily on the structural homogeneity of the macromolecule being studied. Problems arise when the macromolecule exhibits structural flexibility or alternative assemblies (Brink et al., 2004; Leschziner and Nogales, 2007; Orlova et al., 1999; Roseman et al., 2001; Saibil et al., 2001; Staley and Guthrie, 1998; Yang et al., 2002). Currently, the most successful approach for studying such samples is to biochemically isolate, or fix the structure in a single conformational state before microscopy (Frank, 2003); however, this is not always feasible. Several computational methods have been developed to study heterogeneous data, either by classifying the data into homogeneous subsets (Burgess et al., 2004; Fu et al., 2007; Hall et al., 2007; White et al., 2004), or by quantifying variability in the final reconstruction (3D variance) (Penczek et al., 2006b). One approach for dealing with heterogeneous data uses maximum likelihood-based classification (Scheres et al., 2007) whereby the Expectation Maximization steps reassign the raw images into several structurally distinct models. However, this approach is extremely computationally expensive and requires a large quantity of experimental data. 3D variance can be used as a tool to analyze heterogeneity in a reconstruction, enabling regions of high variability to be further investigated using other tools (Penczek et al., 2006a). Another approach uses cross-correlation of common lines (CCCL) (Hall et al., 2007) to segregate the 2D averages of raw particles (class-averages) into homogeneous 3D structures. This approach essentially clusters class-averages into groups that represent distinct conformational states. The methods of 3D-variance and CCCL rely on the accurate assignment of in plane translation and Euler angle parameters, generally found by projection matching. However heterogeneity within the data has a detrimental effect on projection matching by reducing the accuracy of parameter assignment, and therefore lowering the quality of the final reconstruction and the ability of these methods to work.

The cross-correlation function is widely used to optimize alignment between two images. It has been shown to be very successful in aligning highly noisy images to model templates. It is of most use when the particles are structurally homogeneous. Heterogeneous data are problematic, as templates from a single model cannot be fully representative of the data being studied; thus, multiple models can be used in the processing of heterogeneous data (Brink et al., 2004; Falke et al., 2005; Valle et al., 2002). In this approach, translation, relative Euler angles, and conformational state are assigned to particle projection images according to the template for which they have the highest cross-correlation. This approach was successful on multiple occasions when processing EM data of the ribosome (Frank, 2003), but relies on the availability of multiple starting models that account for the heterogeneity within the sample.

Here we present a computationally efficient alignment method that is not limited in the scoring function which is used. The method identifies basic image features that are used to define local directions that are subsequently used to superimpose two images. The identified image features allow a more efficient sampling of transformational space than an exhaustive search approach. Our data indicate that the application of a scoring function based on the Mutual Information (MI) improves the alignment of heterogeneous particles when aligning to a single model, given that the signal to noise ratio of the images being aligned approaches that which is expected for class-averages. Mutual information measures the amount of shared information between two images. It has been extensively used in medical imaging for image registration (alignment) (Maes et al., 1996; Pluim et al., 2003; Viola and Wells, 1995). For example, two images of roughly the same brain area obtained using two different techniques, such as PET, which captures functional processes, and CT, which captures structural information, can be aligned based on their shared information rather than on a linear relationship between gray level distributions. In the field of electron microscopy mutual information has been previously used for the alignment of 3D volumes that differ in resolution (Telenczuk et al., 2006).

We demonstrate the performance of MI as a scoring function using three model structures and one real dataset. As model structures we use the 50s and 70s subunits of the E. coli ribosome (Gabashvili et al., 2000; Matadeen et al., 1999), the multiprotein splicing factor SF3b (Golas et al., 2005), and the Kelnow fragment of DNA polymerase I (Beese et al., 1993). The ribosome structure was used in the development of the method and demonstrates the ability of Mutual Information to utilize a single model for the alignment of heterogeneous data that show alternative molecular assemblies. SF3b is used to demonstrate the model independent nature of our alignment method, while the Klenow fragment of DNA polymerase I is used as a test for the type of heterogeneity observed in the real cryo-EM data of eIF3-IRES complex (Siridechadilok et al., 2005), i.e., a constant structure with a protruding flexible domain. Cryo-EM data from human translation initiation factor eIF3 bound to the flexible internal ribosome entry site (IRES) from the hepatitis C virus (HCV) (Siridechadilok et al., 2005) are used to show that our new method is successful for use with experimental images of biological macromolecules.

Our results indicate that Mutual Information leads to a better alignment than cross-correlation when the signal-to-noise ratio (SNR) is at the level usually found in class-averages, e.g., SNR of 1:1. Therefore, the best use of the MI based alignment is in the reconstruction approaches that first compute class-averages from raw data and then align class-averages to a model (Elad et al., 2008; Hall et al., 2007). Thus, we expect that our approach will improve the alignment step of such methods and consequently will lead to a better reconstruction of multiple models from heterogeneous data.

Methods

Given a set of template images, {m_i}, consisting of evenly spaced 2D projections of an initial 3D model, and a set of raw images, {r_i}, boxed from an electron micrograph, projection matching is the problem of finding, for each raw image r_i, the template image m_i to which it is most similar. The raw images, {r_i}, have unknown in-plane translation and rotation parameters relative to the model projections {m_i}. It is therefore necessary to first solve the alignment problem; i.e., given two images m_i and r_j find a superposition such that the similarity between two images is maximized.

A similarity measure based on the dot product of image pixels is widely used in image processing. To integrate the dot product with the image alignment problem, the cross-correlation function (CCF) is used to describe the dot product optimization. In case of translations, the CCF is defined as:

$$\text{CCF}(m_i,r_j,t)=\sum _k{m}_i(k)r_j(k+t),$$

where t is a translation applied to image r_j and k runs over the image pixels. For simplicity we omit discussion of the dot product optimization that involves rotations. A CCF variant, the normalized cross-correlation function (NCCF), is usually more appropriate for image comparison since image brightness may vary among the samples. NCCF is defined as:

$$\text{NCCF}(m_i,r_j,t)=\sum _k\frac{(m_i(k)-\overline{m})(r_j(k+t)-\overline{r})}{{\sigma }_m{\sigma }_r},$$

where m̄ and r̄ are image mean values, and σ_m and σ_r are standard deviations. Mean and standard deviation values can be computed either based on all image pixels or only within the area where the dot product is being applied. In the later case the NCCF is called locally normalized cross-correlation function (LNCCF). One reason for the widespread use of the CCF and its variants is their computationally efficiency. Using the Fast Fourier Transform (FFT), the translation that maximizes the CCF can be found in O(nlog(n)), where n is the image size. The CCF and NCCF measure similarity between two images based on their pixel dot product. However, if we wish to apply a different scoring function, like Mutual Information used below, a naïve approach would be to perform an exhaustive search over all possible rotations and translations, which is computationally expensive.

We propose an alignment technique based on feature extraction that avoids an exhaustive search and is able to efficiently find a high scoring superposition between two images. Feature based alignment approaches are extensively used in computer vision (Forsyth and Ponce, 2002). Using features that can range from simple forms such as corners and edges to more complex structures such as lines, curves, object boundaries and areas, a superposition between two images is computed by alignment of the defined features. Since the number of features is usually significantly smaller than the number of image pixels, a feature-based alignment can be potentially more efficient than an exhaustive search. The high levels of noise associated with electron microscopy images, and the visible lack of features, makes the application of such methods difficult. In our approach we therefore utilize basic features that are likely to be preserved between noisy images, such as local extreme values. Our method is composed of five major stages:

1. Preprocessing and feature detection

This stage is done separately for each image. Due to different contrast conditions, each image is normalized; i.e., value(p)=|value(p)-μ| / σ, where value(p) is the gray level at pixel p, μ and σ are the mean and standard deviation of the gray levels within the image. Next, we detect local extreme (maximum and minimum) values: E = {e_i}. A pixel is a local maximal extreme value if all of its eight neighbors have lower or equal gray value. A pixel is a local minimal extreme value if all of its eight neighbors have greater or equal gray level. Notice that some extreme value pixels can be direct neighbors. An example of a set E is demonstrated in Figure 1, second column.

Figure 1.

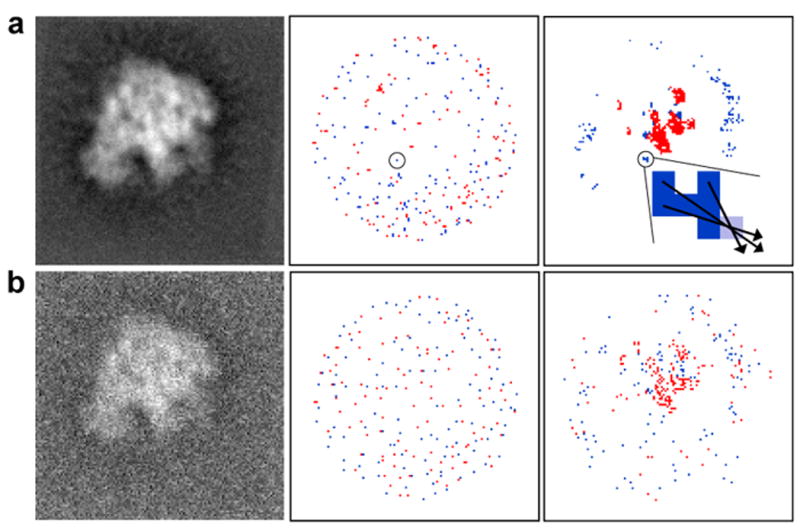
Example demonstrating the feature extraction approach applied to a 50S ribosome projection. The first column shows simulated images that were computed (a) at SNR 5:1, and (b) at SNR 1:1. The second column shows the set, E, of local extreme values, where maximum values are colored red and minimum values are colored blue. The third column shows the set, S, of significant values (red for high densities and blue for low densities). Even with the increased level of noise shown in (b), the members of the two sets, S, (top rightmost and bottom rightmost images) are distributed at similar locations. The zoomed region in the top right panel shows six pixels from the set S, colored in dark blue, and the nearest pixel from the set E, colored in light blue. Three arrows are shown as examples of the directions that are defined by the vectors, F, from elements in S to elements in E.

We then define the set of pixels at which there is a significant gray value in the image, S = {p : |value(p)-μ′| > ασ′}, where μ ′ and σ′ are the mean and standard deviation after normalization (equal to zero and one respectively), while α is a dynamic parameter that has initial value of two and is then iteratively decreased by 10% if the size of S is too small. Operationally, we require the size of S to be at least 50. An example of a set S is demonstrated in Figure 1, third column. A set of vectors based on S and E are defined as:

$$\text{F}=\{\text{f}=(\text{s},\text{e}):\text{s}\in \text{S}\text{and}\text{e}=\underset{\text{e}\in \text{E},\text{e}\ne \text{s}}{argmin}|\text{s }-\text{ e}|\},$$

i.e., each point from S selects the closest point from E to make a vector in F.

2. Construction of transformations

To define a 2D transformation that superimposes image B onto A we align two vectors, one from A and one from B. For each image the vector set is defined by F (Figure 1, top rightmost image). Therefore a set of 2D transformations is defined as the product of all possible vector pairs: F(A) × F(B). Specifically, given a vector pair f_A=(s_A, e_A) and f_B=(s_B, e_B) a transformation T[f_A,f_B] is constructed such that, after applying the transformation on B, the starting point of f_A and f_B coincide and the vector directions are equal, i.e., T[f_A,f_B](s_B)= s_A and three points (s_A, e_A, T[f_A,f_B](e_B)) are collinear. We only match vector pairs of equal local extreme value type; i.e., e_A and e_B should be either both local maximum or both local minimum.

3. Pose-clustering

The number of transformations computed at Stage 2 can be relatively high, and applying a scoring function for each of the transformations can be expensive. However, high scoring alignments usually have a large number of features with similar transformations. Therefore, the number of transformations can be significantly reduced by a pose-clustering technique (Olson, 1993; Stockman, 1987). Similar transformations are grouped together into clusters, and only transformations representing large enough clusters are used for scoring image similarity. In order to test whether two transformations are similar enough they are applied to the same set of pixels. If the corresponding pixels are transformed into nearby locations then the transformations are considered similar. Applying a transformation on the whole set of image pixels is time consuming. Usually, the image corners will show the largest deviation between any two transformations. Therefore, we define two transformations, T_i and T_j, to be similar if the maximal distance between T_i(p_t) and T_j(p_t), t=1,2, is less than one pixel, where points {p_t} are selected as two diagonally opposite corner pixels, (0,0) and (N-1,N-1), of an N×N image. We apply an heuristic greedy clustering procedure (in general, finding an optimal solution to a clustering problem is computationally intractable). First, we map transformations into four-dimensional bins based on the transformed points {p_t}. Each transformation gets a vote equal to the number of similar transformations located in nearby bins. The binning strategy allows to reduce computational time over all pairwise comparisons of transformations. Next, we select a transformation (a cluster representative) that has the largest vote. Transformations that contributed to a cluster are marked and cannot be selected as cluster representatives at later iterations, however they are allowed to contribute to other clusters (therefore, this is a fuzzy clustering approach). We continue iteratively selecting a transformation with the next largest vote until we collect two thousand transformations (cluster representatives). Eventually, the two thousand transformations are evaluated with the scoring function to determine image similarity.

For example, in the case of 128×128 images and translations limited to 10 pixels from the image center, the number of transformations computed in the previous stage can be about 120,000. The total number of possible clusters in the pose clustering step is about 25,000, given the above defined similarity of transformations. Consequently, we pick only 2,000 high scoring transformations.

4. Scoring Function

Let p_A(a) define the fraction of pixels with gray value a in image A (the marginal probability). Given two aligned images A and B let p_AB(a, b) define the fraction of aligned (superimposed) pixels with gray value a in A and b in image B (the joint probability). Then, the mutual information of two aligned images is given by:

$$\text{Mutual}\text{Information}(A,B)=\sum _{a,b}{p}_{AB}(a,b)log\frac{p_{AB}(a,b)}{p_A(a)p_B(b)}.$$

We use mutual information to measure similarity between two images for each superposition from the previous stage. For the scoring we rescale the original non-normalized images to the smaller gray level range of [1:t], where t is the number of gray levels. With the presence of noise, the original 256 gray levels, usually used in EM images, do not produce the best result in the alignment and projection matching. We found that for the parameter t the value of 20-50 gives the best results in our experiments (t=20 is used as the default parameter). Such a down-scaling of gray levels can be seen as a noise suppression mechanism. Selecting an appropriate number of gray levels is a known problem for effective use of the mutual information function, especially for noisy images (Zhu and Cochoff, 2002).

5. Iterative Projection Matching

Due to different gray level distributions, some images tend to receive high scores even when aligned to an incorrect template. This phenomenon can happen for any scoring function. Consider the following example. There are three model projections, m1, m2 and m3, and three images, i1, i2 and i3. Consider the following scores from an alignment procedure (higher value corresponds to a better fit):

	m1	m2	m3
i1	10	6	5
i2	11	5	7
i3	12	8	9

The standard, direct, approach to the projection matching problem is to select the best fitting template for each image i. In our example all images i1, i2 and i3 would be matched to m1. However, high alignment scores of m1 can be due to a particular pattern that gives a high score with any image. Therefore, to prevent such spurious matches we add a step to check the significance of the matching. We define a matching of i to m to be K-th significant if i is ranked K-th among all image scores with template m. We start to look for the first significant solutions. Only i3 satisfies this criterion. Therefore we match i3 to m1 and remove its scores with other templates.

	m1	m2	m3
i1	10	6	5
i2	11	5	7
i3	12	-	-

After we remove the scores of i3 with m2 and m3, the second highest scores of i1 and i2 are first significant matches. Therefore, we match i1 to m2 and i2 to m3. When no first significant matching is found we look for the second significant matching and so on. Setting K too large may also result in spurious matches with low scores. When K reaches its maximal allowed value and there are no K-th significant matches we apply the standard matching procedure which selects the highest scoring template image for any unmatched raw image. The pseudo-code for our iterative projection matching is given below:

1. K=1.

2. While K< Threshold. (Our default is #images/#templates.)

3. For each image I.

4. Find the highest scored template for which I is at most K-th significant.

5. If found, then match I to that template.

6. End For each.

7. Remove the scores of matched images, besides the scores with correspondingly matched templates, from the future considerations.

8. If no K-th significant matching is found then K=K+1.

9. End While.

10. Match any unmatched raw image to its highest scored template.

The improvement obtained by using our iterative matching procedure rather than the standard, direct matching is demonstrated by results that are included in Table 2.

Table 2.

Success of alignment and matching for the case of synthetic, heterogeneous data in which noisy 50S ribosome projections are aligned with noise-free templates for the 70S ribosome. The columns show the percentage of correctly aligned and matched 50S noisy images. The notation (NCCF, FE+MI, IMatch) is the same as in Table 1.

SNR	NCCF	IMatch(NCCF)	FE+MI	IMatch(FE+MI)
no noise	15%	40%	19%	67%
5:1	14%	36%	18%	71%
2:1	14%	35%	19%	74%
1:1	15%	35%	17%	54%
1:2	11%	20%	10%	11%
1:3	7%	10%	7%	7%
1:5	3%	2%	0%	0%

Results

The results obtained with the alignment technique that applies feature extraction (FE) and the MI scoring function were compared with the results we obtained when we used NCCF-based alignment as it is implemented in the commonly used software packages Spider (Frank, 2002b) and Imagic (van Heel et al., 2001), as well as our own implementation. We refer to our feature extraction based alignment that applies mutual information scoring function as FE+MI. Specific program parameters were consistent with those used in the routine use of such programs. In our own implementation we applied the locally normalized cross-correlation function (LNCC), where the dot product, means, and standard deviations are computed within the circular mask of a noisy image and within the corresponding circular area of a template image. The image filtering step can be an ad hoc procedure depending on image data. To avoid a possible bias, in all our experiments the images where filtered in the same manner. Differences in the algorithms implemented in Spider and Imagic can lead to discrepancies between the alignment results. Therefore, we report only the best results obtained either by Spider, Imagic or by our own implementation, and thus, for simplicity, we identify the “best” results with the notation “NCCF” without mentioning a particular implementation.

Synthetic data generated for the 70S ribosome and its 50S sub-complex

We selected the well studied structure of the 70S ribosome (EBI EMDB (Tagari et al., 2002), entry EMD-1003, resolution 11.5A (Gabashvili et al., 2000)) and its 50S sub-complex (EBI Database EMDB, entry EMD-1019, resolution 7.5A (Matadeen et al., 1999)) from E. coli. Our goal was to simulate an experimental case with heterogeneous data in which EM images may contain a mixture of 70S and 50S ribosome projections, while using a single model of the 70S ribosome as a template for the angular assignment. Therefore, we performed two experiments. First, the 70S ribosome was used as a template for the alignment of 70S projections, as an example of aligning images for a homogeneous structure. Second, the 70S ribosome was used as a template for the alignment of 50S projections, as an example of aligning images of heterogeneous structures. Since the difference in volume between 70S and 50S is more than 40%, there are many ways in which the 50S subunit could be misaligned to the 70S template. As a result, we consider this case to be a very challenging test for the image alignment and projection matching problem.

212 template images were generated from equally spaced projections of the 70S ribosome. We first compare the NCCF based method with our alignment approach, based on MI, for the case of homogeneous data. We applied various levels of Gaussian noise to the 212 projections of the 70S ribosome. These noisy images are aligned with the noise-free 70S templates. The projection matching accuracy is measured as a percent of images which are, first, correctly matched to its corresponding templates and, second, the alignment between these pairs (image superposition) deviates at most 1 pixel and 5 degrees from the optimal alignment. As shown in Table 1, NCCF and FE+MI perform comparably at the signal to noise ratios (SNR) of 1:5 or higher. For noisier images, NCCF is more accurate than FE+MI. We discuss below how such accuracy relates to model dependency.

Table 1.

Success of alignment for the case of synthetic, homogeneous data in which noisy projections are matched to noise-free templates. The columns show the percentage of noisy images that are correctly aligned and matched to template images. The notation NCCF and FE+MI, respectively, refer to the results for alignment in which images at the specified levels of noise are matched based on the highest scoring template. The notation “IMatch(FE+MI)” refers to the results obtained when iterative projection matching is used to match noisy images (see Methods). (a) Results for 212 noisy images and 212 templates of the 70S ribosome. (b) Results for 300 noisy images and 300 templates of the multiprotein splicing factor SF3b.

(a) 70S ribosome
SNR	NCCF	FE+MI	IMatch(FE+MI)
1:2	100%	100%	100%
1:5	100%	94%	94%
1:7	97%	39%	46%
1:10	83%	0%	0%
(b) Multiprotein splicing factor SF3b
SNR	NCCF	FE+MI	IMatch(FE+MI)
1:2	100%	100%	100%
1:5	100%	100%	100%
1:7	99%	94%	94%
1:10	99%	41%	41%
1:15	94%	0%	0%
1:20	73%	0%	0%

Despite its high accuracy for the alignment of homogeneous data, NCCF based methods gave 85% errors in aligning and matching 50S projections to the 70S templates even in the case of noise-free projections. FE+MI, on the other hand, correctly aligned and matched using the proposed above iterative matching at least 54% of the projections with the SNR greater than one. The results are summarized in Table 2.

Alignment by mutual information is less model biased than alignment by cross-correlation

We investigate how FE+MI and NCCF based alignments behave for a case in which the model structure is not related to the experimental data. Model dependence occurs when a template-based alignment results in class-averages that resemble more the model projections (templates) than the projections of the experimental structure. It has been widely shown that NCCF based alignment can result in model dependence (Grigorieff, 2000). Here, we show that MI is far less model biased than NCCF. If not enough information is shared between the model and raw data, then the MI based alignment fails completely.

We first demonstrated that if pure noise is given as an input, then mutual information reconstructs noise, while cross-correlation reconstructs a model-dependent image from the noise. As an illustration of the model-independence of FE+MI, we employed the frequently used image of Einstein as a template. Alignment and averaging was performed for 1000 images of Gaussian noise with the same average and variance as the template (the images contain only the noise, not the template). Figure 2 shows the sum (average) of aligned images that were obtained by cross-correlation and by FE+MI, respectively.

Figure 2.

Model-dependency test. A familiar photograph of Einstein is used as a model, and 1000 images of pure white noise are aligned to the model. (a) The reconstruction that is based on the use of the NCCF for alignment shows model dependency. (b) The reconstruction that is based on the use of mutual information is close to random.

We next considered what happens when one attempts to align two unrelated structures, splicing factor SF3b and 70S ribosome, both of which are non-symmetrical. For the purpose of these experiments, SF3b is scaled (x1.25) in relation to the ribosome in order to model two similarly sized globular structures. For both structures we produced 736 equally spaced projections for use as templates. For SF3b we then generated 2000 randomly oriented projections and added noise to the level of SNR = 1:3.

In the first experiment we used both FE+MI and standard NCCF-based alignment to align noisy SF3b images to the template projections of the 70S ribosome. Figure 3 (a) shows the Fourier Shell Correlation (FSC) (Harauz and van Heel, 1986) between reconstructions from halves of the SF3b noisy images, and (B) shows FSC between reconstructions of the SF3b data and the ribosome model. Clearly, cross-correlation based reconstruction of SF3b shows non-random low frequency similarity with the ribosome model, while mutual information based reconstruction lacks any significant information. From visual inspection, cross-correlation based reconstruction has some structural features that are similar to the ribosome template, while FE+MI based reconstruction looks like an average of randomly oriented images of SF3b (Figure 4 (a,b)).

Figure 3.

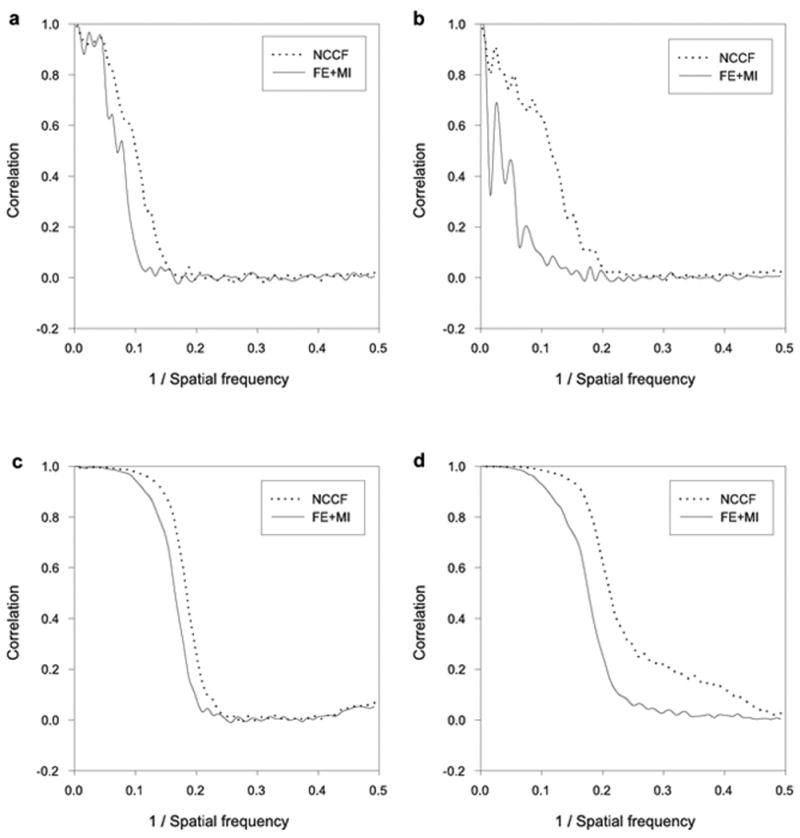
Model dependency test on synthetic data sets. Comparison of reconstructed structure resolution for NCCF and FE+MI. (a) FSC between reconstructions obtained from halves of the SF3b data when a ribosome template structure is used to align and assign Euler angles to the SF3b data. (b) FSC between reconstructions of the SF3b data and the ribosome data when a ribosome template structure is used to align and assign Euler angles to the two respective data sets. (c) FSC between reconstructions obtained from halves of the SF3b data when a SF3b template structure is used to align and assign Euler angles to the SF3b data. (d) FSC between (1) a reconstruction of the SF3b data obtained after alignment with the NCCF and FE+MI method and (2) a reconstruction of the SF3b data with no alignment error and no error in the assignment of Euler angles. A SF3b template was used to align and assign Euler angles to the SF3b data.

Figure 4.

Model dependency test on synthetic data sets. (a) An example of noisy images of SF3b used for the reconstruction. (b) Reconstruction of SF3b images using the 70S ribosome as a template. First row are ribosome templates. Second row are reprojections from the cross-correlation-based reconstruction. Third row are reprojections from the mutual information-based reconstruction. Columns correspond to the same projection angle relative to the ribosome model. (c) Same as (b), with SF3b as the template model.

Next, we verify that both methods are able to reconstruct the original SF3b structure from its noisy images using the correct template images from SF3b itself. Figure 3 (c) shows the FSC between reconstructions from halves of the SF3b data. Using the 0.5 criteria (Penczek, 1998) estimated resolutions were 11Å and 12Å for the NCCF and FE+MI reconstructions respectively. We computed the “best” possible reconstruction of SF3b with no alignment/matching error by back-projecting the noisy images with the known parameters from the initial forward projection. Figure 3 (d) shows FSC between the “best” reconstruction and two reconstructions based on NCCF and FE+MI alignments. While the NCCF based reconstruction is closer to the SF3b model, our reconstruction is almost comparable in terms of FSC resolution. From visual inspection both reconstructions look similar (Figure 4 (c)).

Synthetic data generated for Klenow fragment of DNA polymerase I

Three different synthetic conformations of the Klenow fragment of DNA polymerase I, previously generated by Hall et al., 2007, were filtered to 20Å resolution. The three conformations are not meant to represent known conformational states of the molecule, but they nevertheless serve as a reasonable model for a protein complex with a small flexible domain extending from the main body of the structure. For each conformation we produced 400 projections at random orientations and added noise to give a final SNR of 1:1. To simulate a reconstruction in which heterogeneity has not been taken into account we back-projected all 1200 (3×400) noisy images to create a 3D model that is an average of all conformations. From this averaged model we produced 212 template projections.

To test how FE+MI compares with NCCF when a model does not fully represent the data we aligned and assigned Euler angels to all the noisy images, using the template projections produced from the averaged model. We then calculated a reconstruction from each homogeneous set of 400 aligned images. To measure the quality of the alignment and projection matching we calculated the Fourier shell correlation (FSC) between the homogeneous reconstructions and reconstructions of the same data with no alignment or Euler angle assignment error, Figure 5. The FSC curves show slight variability between conformations, but in all cases the curve from the FE+MI reconstructions has correlation to higher spatial frequency than NCCF. It is clear from the FSC plots that the reconstructions from the images aligned using FE+MI more closely match the reconstructions with no alignment error. Therefore FE+MI has performed better at alignment and Euler angle assignment than NCCF. Note that each reconstruction contains only particles of one conformation; therefore any difference between the reconstruction and the error free reconstruction is due to inaccuracy in the alignment.

Figure 5.

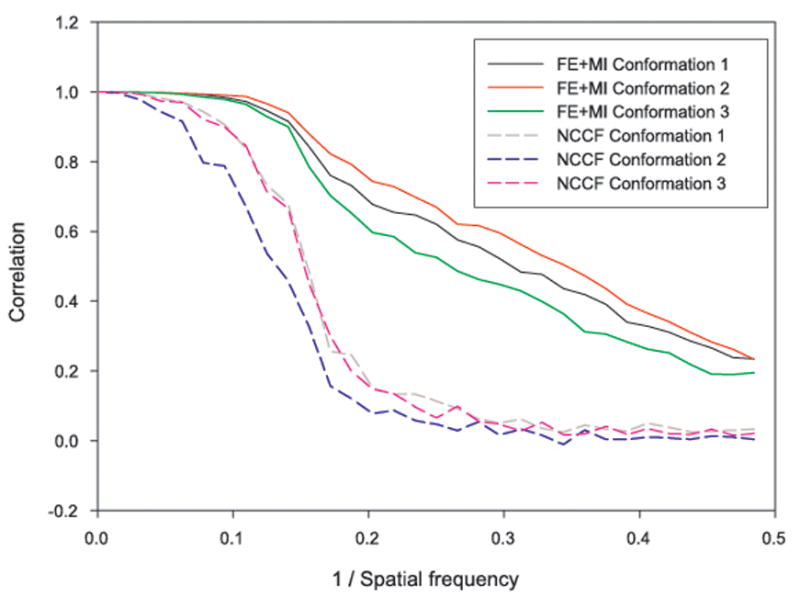
Fourier shell correlation (FSC) plots of reconstructions that were obtained after aligning the images by FE+MI and by the use of NCCF for three model conformations of the Klenow fragment of DNA polymerase I. The FSC was calculated between reconstructions in which the translational and Euler angle parameters where re-assigned using either FE+MI or NCCF and reconstructions without translational or Euler angle error. It can be seen that the FSC plots for the FE+MI reconstructions are consistently better than for the NCCF, showing that the FE+MI reconstructions more closely resemble those without errors.

Experimental data of eIF3-IRES complex

To test the FE+MI method on real cryo-EM images we used data from a eIF3-IRES structure. The structure has been previously published (Siridechadilok et al., 2005), and it has also been used in the development of other methodologies (Hall et al., 2007). The eIF3-IRES structure was found to have a stable central domain, connected to a flexible protrusion, shown to be IRES RNA. It was possible to calculate homogeneous class-averages using focused classification (Hall et al., 2007). For focused classification the variance is used to define a specific area within the image on which to base classification. A method based on the cross-correlation of common lines (CCCL) was developed so that these class-averages could be related in 3D space in order that reconstructions could then be made that reflect flexibility within the structure (Hall et al., 2007). Critical to this method is the assignment of relative Euler angles to the 2D class-averages by aligning them to references from an average structure. The usefulness of our method in cases such as this was demonstrated using the Klenow model data. To make a comparison between NCCF and FE+MI, the alignment and assignment of Euler angels was carried out followed by the CCCL approach. The resulting reconstructions were used as references for multi reference projection matching where all raw images are realigned to the best matching model. The final reconstructions after multi reference projection matching are compared in Figure 6.

Figure 6.

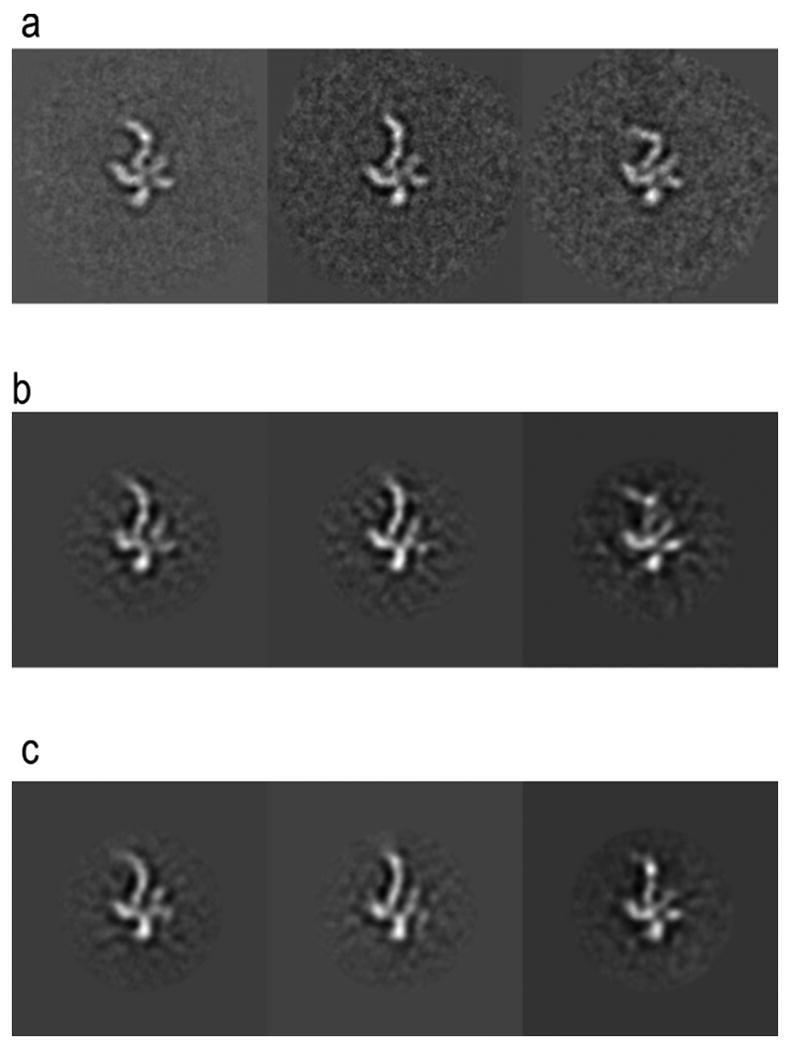
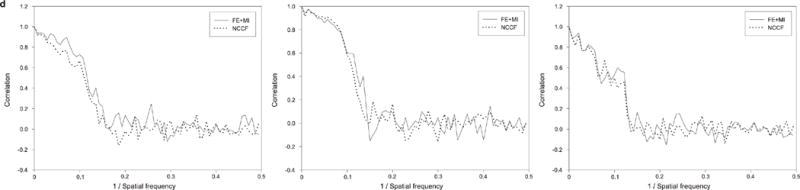
Results from using FE+MI and NCCF for aligning experimental heterogeneous eIF3-IRES data. All images are from the same projection direction. (a) Initial class-averages resulting from focused classification, showing three distinct conformations of the IRES particle. (b) Projections at the same Euler angle as (a) for the structures resulting from FE+MI alignment. (c) Projections from the structures resulting from using NCCF for alignment. (d) Fourier ring correlation plots comparing original class-averages (a)_to results from FE+MI (b) and CCF (c). The three plots correspond to the conformations shown in columns 1, 2 and 3.

Figure 6 shows the results from using both NCCF and FE+MI in such an approach, shown are the initial 2D class-averages, compared with equivalent projections of the resulting final 3D reconstructions. It can be seen from the results that in the reconstructions for which FE+MI was used the definition of the flexible region in the final reconstruction more closely matches the initial 2D class-averages from focused classification.

Method Efficiency

An exhaustive search in three parameters of transformation (two translational and one rotational parameter) can be used to evaluate any possible scoring function. However, an exhaustive search is computationally expensive. Here we compare the running time and accuracy of our version of feature-based alignment with an exhaustive search.

Our method detects pixels that represent local extreme values and pixels with above-average significance and uses them to define a transformation. Unlike an exhaustive search, not every possible transformation is going to be evaluated. Increasing the number of transformations analyzed will increase the accuracy, but also the run time, therefore a tradeoff must be made.

There are many parameters in our alignment algorithm that influence the running time and the alignment accuracy. One of the most influential parameters is the number of transformations reported after the pose-clustering procedure. Since computing a scoring function for each transformation is time consuming (it takes time proportional to the size of the images), it is preferable to consider the smallest number of transformations. Ideally, the largest transformation cluster after the pose-clustering procedure should correspond to the correct alignment; however, in practice, many more of the larger clusters should be evaluated with a scoring function. Figure 7 (a) shows the alignment accuracy and the running time of aligning two images as a function of the number of reported pose-clustering transformations. The graph shows the accuracy of aligning 50S ribosome images at SNR 1:2 and 1:7 with 70S ribosome templates. The images have 128×128 pixels. We define an alignment to be nearly correct if it deviates not more than 5 degrees from the correct rotation and no more than (1,1) pixel shift from the correct translation. We chose 2,000 transformations as a default parameter in all reported experiments, as it has sufficient accuracy and running time of only 2.2 seconds. In comparison, under the same conditions, the exhaustive procedure is able to perform an angular sampling of only 35 degrees at the same running time of 2.2 seconds.

Figure 7.

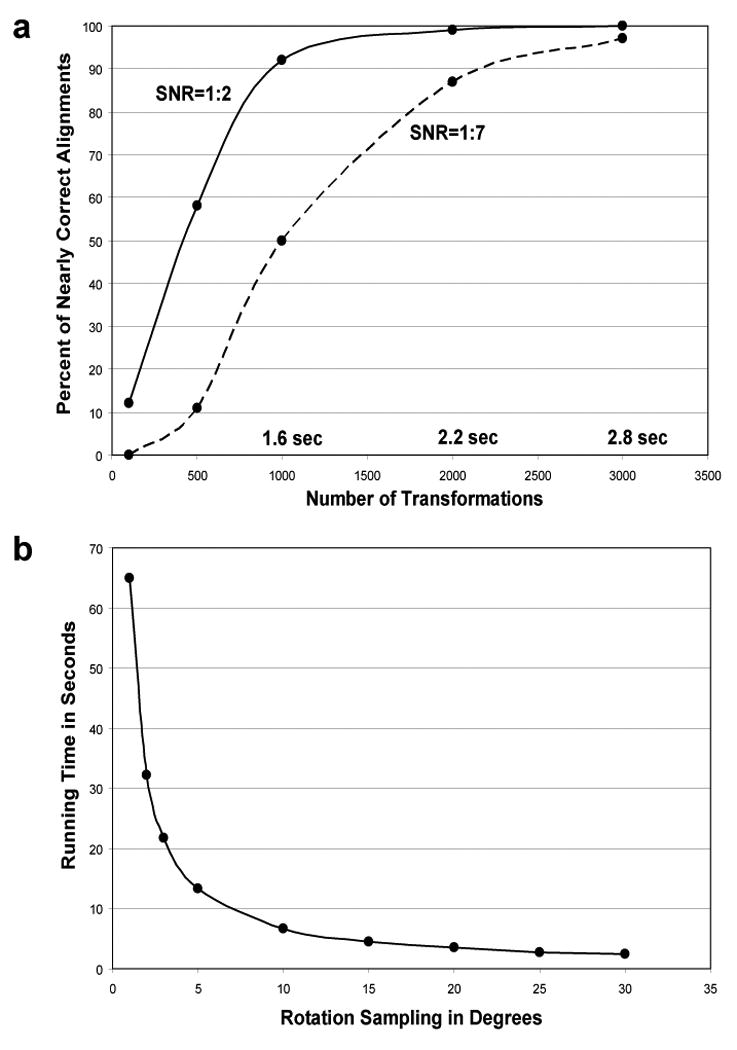
Running time measurements of FE+MI method and exhaustive transformation search implementation with MI as a scoring function. In both methods the translations are limited to at most 10 pixels from image center. (a) Transformation sampling accuracy and running time measurements for the FE+MI alignment method. The graph shows the percentage of nearly correct alignments, i.e., transformation sampling accuracy, of 50S ribosome images at SNR 1:2 and 1:7 with noise-free 70S ribosome templates. The accuracy is displayed as a function of the number of transformations employed after the pose-clustering procedure. The running time scales linearly with the number of transformations as each transformation should be evaluated with the scoring function. The running time of 2.2 seconds for 2000 transformations is equal to the time required for exhaustive rotational sampling at an angular step of 35 degrees. (b) Exhaustive search running time is displayed as a function of the size of angular steps used for rotational sampling.

Figure 7 (b) shows the running time of the exhaustive implementation. These measurements are done based on alignment of two ribosome images, which have 128×128 pixels. The exhaustive search generates all possible translations within 10 pixels from the image center and samples rotational parameter as a function of the graph curve. Similarly, in our feature-extraction method the translations were limited up to 10 pixels from the image center, though the translational parameters are not explicitly generated as in the exhaustive procedure. Exhaustive sampling implementation uses exactly the same code as our method, apart from the procedure that computes a list of transformations.

Source of Errors in the Alignment and Projection Matching Procedures

There are three points at which errors can be made in our alignment procedure. First, the feature-based alignment method can miss the correct transformation, such that the correct superposition is never evaluated by the scoring function. Second, the scoring function can fail to properly rank image alignment even when the correct superposition is tested. Given that two images share enough similarity, a perfect scoring function should always give the highest score to the correct superposition of two images. The third point at which errors can be made lies in the projection matching scheme. The alignment method can perfectly align a raw image and its corresponding model projection, but the matching procedure may select an incorrect higher scoring template for this image. One way in which such errors could occur is that a scoring function cannot be properly normalized, as discussed in the methods section. The last two sources for error are closely related.

We have tested the error sources as follows. First, we measure in how many cases our transformation sampling method misses the correct transformation; i.e., the first source of errors. The results appear in the first row of Table 3 (a,b,c). There is a small drop in sampling accuracy with increased noise level. Then, we measure the second source of errors - the limited ability of mutual information to give the highest score to the correct transformation (second row in Table 3 (a.b,c)). In this case the correct superposition is always tested. Therefore, at least one transformation has zero deviation from an ideal alignment. The MI scoring accuracy drops very quickly after SNR 1:3, 1:7 and 1:10 for the heterogeneous and the two homogeneous alignments correspondingly. The combined effect of all three sources of errors is shown in the last two columns of Table 1 and Table 2.

Table 3.

Measurement of frequency with which the correct alignment is included in the feature-based set of possible alignments and the frequency with which the mutual information scoring function identifies the correct alignment as being the top-scoring alignment. (a) Represents the heterogeneous case, while (b,c) represent the homogeneous examples. “Sampling accuracy” measures the frequency with which a nearly correct transformation (max deviation: rotation 5°, translation (1,1) pixels) is included in the set of transformations that are scored. “Scoring accuracy” measures the frequency with which a correct or a nearly correct transformation scores higher than any other transformation. In the “scoring accuracy” case, a correct transformation is always added to the list of transformation computed by the FE method.

(a) 50S vs 70S
SNR	1:1	1:2	1:3	1:5	1:7	1:10
Sampling accuracy	100%	100%	98%	92%	87%	83%
Scoring accuracy	90%	77%	55%	11%	1%	0%
(b) 70S vs 70S
SNR	1:2	1:5	1:7	1:10	1:15	1:20
Sampling accuracy	100%	99%	98%	94%	89%	84%
Scoring accuracy	100%	97%	81%	14%	0%.	0%
(c) SF3b vs SF3b
SNR	1:2	1:5	1:7	1:10	1:15	1:20
Sampling accuracy	100%	100%	100%	99%	99%	97%
Scoring accuracy	100%	100%	97%	87%	13%	0%

We conclude that our transformation sampling method is not the primary reason for the poor performance of our method at decreasing SNR, but rather the MI scoring function is failing. This shows that the transformation-sampling method has the possibility of being used with different scoring functions to give results better then presented here.

Discussion

Currently one of the most challenging problems in single particle cryo-electron microscopy is the 3D reconstruction of particles that exhibit structural heterogeneity. Computational tools have been developed to study conformational heterogeneity in single particle reconstructions (Elad et al., 2008; Fu et al., 2007; Hall et al., 2007; Penczek et al., 2006b; Scheres et al., 2007; White et al., 2004). However, the success of these procedures relies strongly on the accuracy of image alignment. Alignment of heterogeneous images to a common homogeneous model, using NCCF as implemented in packages such as Imagic (van Heel et al., 2001) and Spider (Frank, 2002b), has a detrimental effect on alignment accuracy.

Here we presented an approach that improves image alignment when the images being aligned are not fully represented by the templates to which they are being compared. We first demonstrated an efficient method for sampling transformational space such that an arbitrary scoring function can be used. Then we showed that using mutual information as a scoring function is more suitable than NCCF in cases where the images being aligned are not fully represented by the templates.

Model independence is an important property of an alignment/matching procedure. If an incorrect model is used, the reconstruction should not converge to a structure that resembles the model. A scoring function is sensitive if it allows the correct alignment when the correct template is used, even with high levels of noise. The high sensitivity of the NCCF is a desirable property if the model is close to the experimental structure. However, when the similarity between an image and template is low (the model is far from the experimental structure), cross-correlation will often produce spurious peaks that reflect an optimal alignment to the noise rather than to the signal. We have shown that within the limited set of conducted experiments, the mutual information based alignment is far less biased by the model, but that it is also less sensitive than NCCF. Using mutual information for the alignment of heterogeneous data that shares some structural elements with the template can result in accurate alignment, but if the data shares no structural elements with the template then the alignment will tend to a completely random alignment, which is preferable.

In previous image-alignment approaches each experimental image was matched to the highest scoring template. Some template images tend to have multiple high scoring images, even those that are not represented by the template. This is a result of the difference in score distributions for different template images. We proposed an iterative projection matching procedure to address this problem. This iterative procedure is shown to improve the accuracy in the case of matching noisy 50S ribosome images to the templates of 70S ribosome for both NCCF and MI based alignments.

The main drawback for using MI in scoring alignments for electron microscopy data is its sensitivity to noise. Minimization of Euclidean distance, or alternatively maximization of cross-correlation, in the alignment of two images is known to optimize the maximum-likelihood estimation when the images are affected by additive Gaussian noise (Scheres et al., 2007). Therefore it is unlikely that MI or other scoring function could give better alignment results at lower SNR in the case of the additive Gaussian noise model. However, when images undergo other types of distortions, like molecular flexibility or varied subunit structure, NCCF might not be the best choice; other functions, like MI, could provide a better alignment. One of the reasons why MI fails at low SNR may be due to its sensitivity to the quantization range of the image gray levels. As discussed above, we achieved better results, especially at low SNR, when images are downscaled to 20 gray levels. However, such a mechanism of noise suppression results in not using the whole information, which may explain the inferior result relative to NCCF at high noise levels. Use of MI for scoring is shown to be of greatest use, when compared with NCCF, for heterogeneous data with SNR 1:1 or higher. Such a high SNR is unrealistic for cryo-EM images of single particles, which can have a SNR as low as 1:10. However the SNR of cryo-EM data can be improved by computing class-averages. Recently, class-averages were successfully used in separating heterogeneous data into homogeneous subsets (Elad et al., 2008; Hall et al., 2007). In those cases, a sufficiently large number of computed class-averages represented relatively homogeneous views of distinct molecular conformations. Consequently, class-averages were classified into subsets that represent projections of homogeneous structures. Below, we list one possible scheme for a reconstruction of multiple structures from heterogeneous data, where our approach could contribute to achieve a better result:

1. Compute class-averages from raw data using, for example, a Multivariate Statistical Analysis (MSA) (Borland and van Heel, 1990). Class-averages can be further refined by applying an additional step of MSA or/and a focused-classification. The unsupervised MSA process of computing class-averages does not require a 3D model and thus does not possess drawbacks of the template based cross-correlation alignment.

2. Apply the proposed FE+MI approach to align class-averages to an initial single model, which may only partially represent the structural data within the class-averages.

3. Apply a method such as CCCL (Hall et al., 2007) to sort the class-averages into structurally homogeneous subsets that can be reconstructed into multiple models.

4. Use iterative multi-model refinement to improve the initial models (Elad et al., 2008; Hall et al., 2007). Here, every raw image is realigned and rematched, using the standard NCCF based alignment, into the most similar projection of one of the models. At this stage, a more sophisticated approach based on maximum likelihood-based alignment and matching (Scheres et al., 2007) can be used to improve the multi-model refinement.

Variations on the scheme can be used to tackle the challenging problem of heterogeneous reconstruction in a number of cases (Elad et al., 2008; Hall et al., 2007). Two of our reported experiments, the Klenow fragment and eIF3-IRES, demonstrate that our proposed FE+MI method is able to improve the accuracy of heterogeneous reconstruction if used as a part of the above scheme.