ASSESSING OBSERVER ACCURACY IN CONTINUOUS RECORDING OF RATE AND DURATION: THREE ALGORITHMS COMPARED

Abstract

The three algorithms most frequently selected by behavior-analytic researchers to compute interobserver agreement with continuous recording were used to assess the accuracy of data recorded from video samples on handheld computers by 12 observers. Rate and duration of responding were recorded for three samples each. Data files were compared with criterion records to determine observer accuracy. Block-by-block and exact agreement algorithms were susceptible to inflated agreement and accuracy estimates at lower rates and durations. The exact agreement method appeared to be overly stringent for recording responding at higher rates (23.5 responses per minute) and for higher relative duration (72% of session). Time-window analysis appeared to inflate accuracy assessment at relatively high but not at low response rate and duration (4.8 responses per minute and 8% of session, respectively).

A review of the use of observational recording across 168 research articles (1995–2005) from the Journal of Applied Behavior Analysis found that 55% of research articles that presented data on free-operant human behavior reported using continuous recording (Mudford, Taylor, & Martin, 2009). Observers collected data on portable laptop or handheld computers in the majority (95%) of those applications. Most data were obtained for discrete behaviors, with 95% of articles reporting rate of occurrence of responding, although duration measures were reported in 36% of articles reviewed.

Despite the ubiquity of continuous recording, there has been little research investigating this type of behavioral measurement. Three empirical studies have investigated variables affecting interobserver agreement and observer accuracy with continuous recording. Interobserver agreement concerns the extent to which observers' records agree with one another. By contrast, observer accuracy concerns agreement between observers' records and criterion records and has been typically quantified using interobserver-agreement computational methods (Boykin & Nelson, 1981). Van Acker, Grant, and Getty (1991) found that observers were more accurate when videotaped observational materials included more predictable and more frequent occurrences of responses to be recorded than when responses occurred less often or were less predictable. Kapust and Nelson (1984), to the contrary, found that observers were more accurate at recording low-rate responding than when observing high-rate behavior. Agreement between observers generally exceeded accuracy when compared with criterion records of the behavior. A third study (Fradenburg, Harrison, & Baer, 1995) reported that agreement between observers using continuous recording was affected by whether the observed individual was alone (75.1% mean agreement) or with peers (87.2% agreement).

Mudford et al. (2009) identified three interobserver agreement algorithms used more than 10 times in the 93 articles that reported continuously recorded data: exact agreement (all intervals version; Repp, Dietz, Boles, Deitz, & Repp, 1976), block-by-block agreement (Page & Iwata, 1986; also known as mean count-per-interval agreement in Cooper, Heron, & Heward, 2007), and time-window analysis (MacLean, Tapp, & Johnson, 1985; Tapp & Wehby, 2000). Each has been applied with observational records of discrete behavioral events and for behaviors measured with duration.

Exact agreement has been subject to considerable theoretical and empirical research relevant to its use with discontinuous recording (e.g., interval recording; Bijou, Peterson, & Ault, 1968; Hawkins & Dotson, 1975; Hopkins & Hermann, 1977; Repp et al., 1976). Block-by-block agreement is a derivative of exact agreement (Page & Iwata, 1986). The relative strengths, weaknesses, and biases of these two methods have been identified for discontinuous recording. However, exact agreement and block-by-block agreement have yet to be empirically investigated concerning their suitability for continuous recording. Time-window analysis has no direct analogue in discontinuous recording, because it was developed specifically for continuous recording (MacLean et al., 1985). There have been anecdotal recommendations from users of time-window analysis (MacLean et al.; Repp, Harman, Felce, Van Acker, & Karsh, 1989; Tapp & Wehby, 2000), but there are no empirical studies to guide researchers on interpreting agreement or accuracy indexes produced by time-window analysis.

Because there has been no published research to date comparing interobserver agreement algorithms for assessing the accuracy of continuously recorded behaviors, the purpose of the present study was to provide preliminary illustrative data on the relative performance of the three commonly used computational procedures: exact agreement, block-by-block agreement, and time-window analysis. The algorithms were applied to observers' recordings of behaviors defined as discrete responses and for behaviors recorded as a duration measure.

METHOD

Participants and Setting

Twelve observers participated voluntarily, having replied to an invitation to acquire experience with continuous recording. Their ages ranged from 20 to 45 years, and 1 was male. Nine had completed (and 1 was studying for) masters' degrees in behavior analysis. The other 2 were advanced undergraduate students who received training to assist with data collection during functional analyses conducted in a research project. No participants had any previous experience with computer-assisted continuous recording, although they had experience with discontinuous methods (partial- and whole-interval recording and momentary time sampling). None had previous experience recording the particular behaviors defined for the present study.

The study was conducted in a quiet university seminar room (measuring approximately 6 m by 5 m). Depending on scheduling, 1 to 3 participants at a time recorded observations from six video recordings projected onto a white wall of the room. If more than one observer was present, they were seated approximately 1.5 m apart so they were unable to see another observer's recording responses.

Recording Apparatus and Software

Observers recorded defined behaviors using one of two types of handheld computer, either a Psion Organiser II LZ64 through its alpha-numeric keypad or a Hewlett Packard iPAQ Pocket PC rx1950 with a touch-screen wand. The raw data were downloaded to a PC for analysis by ObsWin 3.2 software (Martin, Oliver, & Hall, 2003), which had been supplemented with the three agreement algorithms studied.

Observational Materials

Six video recordings were of 5-min (300-s) brief functional analysis sessions (as described by Northup et al., 1991). There was a different client–behavior combination in each sample. The first 50 s of each sample was shown to allow the observers to identify the client and therapists in the video, the behavior of interest, and the setting in the particular video sample. Each video sample was continuous (i.e., unedited) except that there was a 3-s countdown and start indicator superimposed to prompt observers to start recording for the remaining 250 s of the sample.

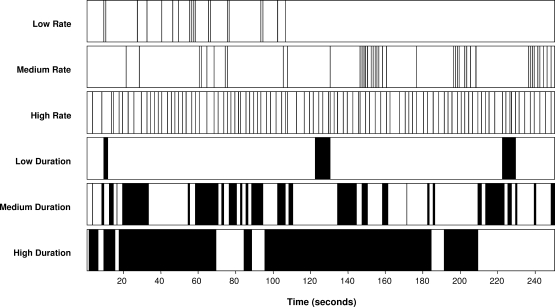
A criterion record had been created for the 250-s samples using a procedure similar to that of Boykin and Nelson (1981). Two graduate research assistants independently examined the video samples to determine the second in which events (i.e., discrete behaviors) occurred or the second in which the onsets and offsets of behaviors with duration occurred. Repeated viewings, slow motion, and frame-by-frame playback were used to measure the samples consistently. Records were compared and differences resolved, except for seven discrepancies concerning occurrence (3% of 233 criterion record events or onsets) that were settled by agreement with a third observer (the first author). The criterion records were used to quantify the relevant dimension of the recorded behaviors in the video samples. We selected the video samples to provide a range of people, behaviors, rates (expressed as responses per minute), and relative durations (expressed as the percentage of each session in which the behavior was observed). Figure 1 shows the six 250-s criterion records, with a vertical line for each target response for event recording or for each second of occurrence of bouts of responding in samples used for duration recording.

Figure 1.

Criterion records for observational samples. Events are shown as a vertical line in each second in which they occurred in the rate samples. Seconds of occurrence of bouts of responding are shown as vertical bars for duration samples.

Definitions of Behaviors and Their Dimensions

Discrete responses recorded were spitting, hand to mouth, and vocalizing. Spitting was defined as an audible “puh” sound. The overall criterion record rate of spitting (Figure 1, first panel) was 4.8 responses per minute. Hand to mouth was defined as the start of new contact between hand or wrist and the triangular area defined by the tip of the nose and imaginary lines drawn from there to the jawline through the corners of the mouth. The criterion rate for this behavior was 11.3 responses per minute (Figure 1, second panel). Vocalizing was the sound of any word (e.g., “car”) or speech-like phrase (e.g., “ga-ga”), and the rate was 23.5 responses per minute (Figure 1, third panel).

Duration behaviors recorded were card holding, therapist attention, and body rocking. Card holding was defined as visible contact between the hand and a greeting card. The criterion record showed that card holding occurred for 8% of the session. Therapist attention was verbal and addressed to the client (e.g., “Come and sit down,” “Do this one,” “later”), and the onset was defined as occurring in the 1st second that the therapist spoke a new sentence after a 1-s break in talking. Offset of attention was defined as the 1st second without any therapist vocalization. Therapist attention occurred for 44.4% of the observation. Body rocking was defined as repetitive rhythmic motion of the torso back and forth, with onset defined as the movement entering its second cycle and offset defined as rhythm disrupted for 1 s, and occurred during 72% of the observation. Panels 4, 5, and 6 in Figure 1 show criterion records for card holding, therapist attention, and body rocking, respectively.

Procedure

Video samples were recorded in the same order by all observers: lowest to highest rates (i.e., spit, hand to mouth, vocalizing), followed by lowest to highest durations (i.e., card holding, therapist attention, rocking). A 5-min break was scheduled between each observational sample, and all observations occurred consecutively in one session (of approximately 60 min in duration).

Written definitions of behaviors to be recorded and a handheld computer were provided to participants. One response topography only was recorded with each video sample, although multiple (nontargeted) behaviors occurred during each sample. Observers were told which behavior was to be recorded before viewing each sample. The instructions were to watch the video sample and, when the start indicator showed on the projection, either to press the code (Z) assigned to record the start of an observation session in the Psion or to touch the wand to “start” on the iPAQ screen. After that, observers were to press the key on the keyboard for the code assigned to the behavior being measured in that sample (Psion) or touch the name of the behavior on screen (iPAQ). If the behavior was defined as a discrete response, they were instructed to press the key or touch the name of the behavior each time they observed a target response. When observers were measuring duration, they were to press the code key (or touch the name) for its onset and again for its offset. The screen on the computers showed whether the behavior was recorded.

At the end of each observation, the projection went blank. At any time after this, observers entered the code for the end of the session (“/” for Psions, “End” for iPAQ). When they did this was not important, because the observational records were restricted to 250 s from the entry of Z or “start.” No further instructions were provided to the observers. Thereafter, the 5-min break occurred, which was followed by the next sample presentation (or the termination of all data collection).

Analyses

Accuracy was computed as agreement between each observer's recorded files and the corresponding criterion records by the exact agreement, block-by-block agreement, and time-window analysis algorithms.

Block-by-block and exact agreement algorithms are similar in that the first step was to impose 10-s intervals on the second-by-second data files to be compared. When computing accuracy, one file was from the observer, and the other file was the criterion record. The level of analysis for discrete data was the number of responses recorded in a given 10-s interval. For duration measures, the number of seconds within a 10-s interval that the response was recorded as occurring was counted for each data file.

The exact agreement algorithm proceeded as follows: First, intervals for which both the observer's and the criterion record agreed on the exact number of responses (or seconds for duration measures), including when both showed nonoccurrence, were counted as agreements. Second, when both data files showed ≥1 s with occurrence in an interval, but there was not exact agreement on how many responses (frequency) or how many seconds (duration), the intervals were counted as disagreements. Third, the typical percentage agreement formula was applied (i.e., agreements divided by agreements plus disagreements multiplied by 100%).

In the block-by-block agreement method, the smaller (S) of the two data files' totals in a specific 10-s interval was divided by the larger (L) data file total within that interval to yield a score between 0 and 1 for every interval. When both data files showed no occurrences during an interval, the intervals were scored as 1 (i.e., agreement on nonoccurrence). After each 10-s interval was scored in the manner described above, the scores from each 10-s interval were summed across all 25 10-s intervals, divided by the number of intervals, and the result was multiplied by 100% to provide a percentage agreement index.

The time-window analysis method involved second-by-second comparisons across the two data files. An agreement was scored when both records contained a recorded response (for discrete behaviors) or 1 s of ongoing occurrence (for behaviors measured with duration). Any second in which only one record contained an event or occurrence of responding was scored as a disagreement. Percentage agreement was calculated by dividing the number of agreements by the total number of agreements plus disagreements and multiplying by 100%. The time-window method has been described as overly stringent for data on discrete responses (MacLean et al., 1985). Consequently, the algorithm allows tolerance for counting agreements by expanding the definition of an agreement to include observations within ±t seconds in the two data files. Thus, rather than requiring that two records must have a response (or second of occurrence) at the exact same point in time, the time-window method permits an agreement to be scored if the records contain a response within a prespecified tolerance interval (t) that is defined by the user. It should be noted that a recorded response (or second of occurrence) in one record can be counted as an agreement with a similar event in the other record once only. The tolerance interval for the present analysis was determined empirically by comparing the effects of varying t from 0 to 5 s on measures of observer accuracy (described below).

RESULTS

Accuracy with Different Recording Devices

Observer accuracy, computed as agreement of observers' records of behavior with criterion records, was examined for observers' recording on the different handheld computers (Psion and iPAQ) separately. The results showed that accuracy varied minimally and not systematically between the devices (graphs that show lack of effects are available from the first author). Thus, data from both types of handheld computer were pooled in all subsequent analyses.

Effects of Varying Tolerance with Time-Window Analysis

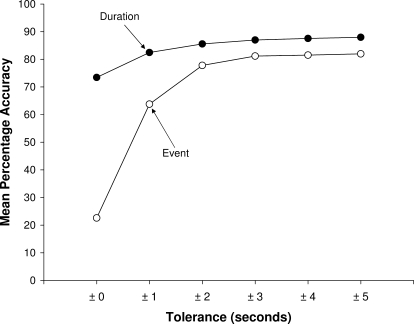
Data on observer accuracy computed using time-window analysis are presented first because there has been no previous empirical research to guide selection of an appropriate tolerance (i.e., time window) for agreement or accuracy. Our review indicated that tolerance interval t has varied from 1 s to 5 s (Mudford et al., 2009); thus, accuracy with tolerance (t) from 0 to ±5 s was computed with the present data sets. Figure 2 shows mean accuracy across tolerances for agreement with a time window ranging from t  =  ±0 s to t  =  ±5 s.

Figure 2.

Mean percentage accuracy computed by the time-window analysis algorithm for behaviors measured as events and behaviors with duration at tolerances for agreement from 0 to ±5 s.

Accuracy with recording of events (i.e., discrete responses recorded without duration) increased markedly from 22.6% at zero tolerance to 77.8% at ±2 s. At tolerances above ±2 s to the maximum time window (±5 s), increase in accuracy increased by only another 4.1%. Accuracy in recording behaviors with duration increased as tolerance was increased; however, gains were less evident than those observed for event recording. Accuracy increased by 12.1% from zero tolerance to 85.6% at t  =  ±2 s.

Based on the accuracy data, a time window of ±2 s can be recommended for two reasons: (a) Increases in accuracy were shown to be relatively small above this level and may only be capitalizing on chance agreement that increases as windows for agreement widen from ±2 s to ±5 s; and (b) results from additional analyses of interobserver agreement with the same data sets showed that levels of accuracy and agreement converged at ±2 s tolerance (results from those analyses are available from the first author). Thus, a ±2 s tolerance interval was used as the basis for observer accuracy with the time-window algorithm in the current analysis.

Accuracy Results across Computational Algorithms

Recordings of response rate

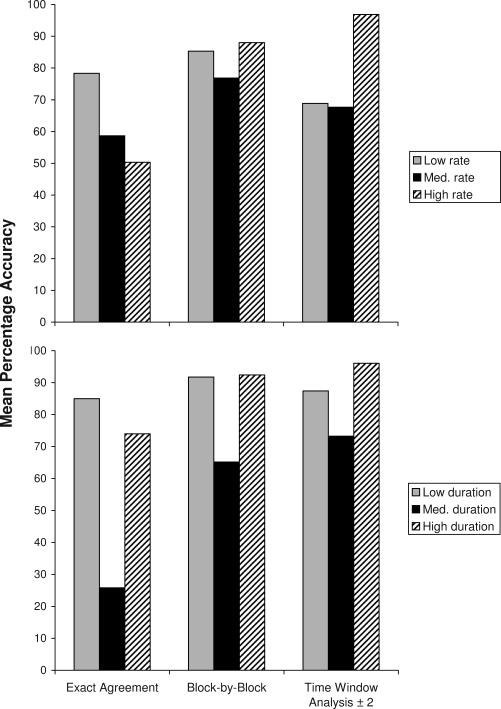
We conducted analyses similar to those of Repp et al. (1976) by examining the relation between variations in response rate and variations in percentage accuracy across computational algorithms. Rates were arbitrarily labeled low (4.8 responses per minute), medium (11.3 responses per minute), and high (23.5 responses per minute). Figure 3 (top) presents percentage accuracy computed with exact agreement, block-by-block, and time-window analysis (t  =  ±2 s) at these different rates. Percentage accuracy measured by exact agreement decreased stepwise from 78.3% to 50.3% as response rate increased from low to high. With block-by-block analysis, low- and high-rate behaviors were recorded with similar levels of accuracy (85.3% and 88%), with the medium-rate behavior being recorded less accurately at 76.8%. Finally, the time-window analysis produced accuracy levels of 68.9%, 67.7%, and 96.8% for the low-, medium-, and high-rate samples, respectively.

Figure 3.

Mean percentage accuracy computed by exact agreement, block-by-block agreement, and time-window analysis with tolerance of ±2 s for low-rate (4.8 responses per minute), medium-rate (11.3 responses per minute), and high-rate (23.5 responses per minute) behaviors (top) and for low-duration (8%), medium-duration (44.4%), and high-duration (72%) behaviors (bottom).

Explanation of the reduction in accuracy with increasing response rate when computed by exact agreement can be advised by consideration of the top three panels in Figure 1. Gaps between vertical lines indicating periods of nonoccurrence are visible. Exact agreement divides the data stream for each sample shown in Figure 1 into 25 10-s intervals, as does the block-by-block agreement algorithm. Further analysis found that the low-, medium-, and high-rate samples contained 16, 12, and 0 intervals with nonoccurrence, respectively. Thus, it was probable that the number of agreements on nonoccurrence decreased with both exact agreement and block-by-block agreement as response rate increased. Conversely, the number of intervals with occurrences, including intervals with multiple occurrences, increased as response rate increased. For example, in the high-rate sample (Figure 1, third panel), every 10-s interval contained two to five events in the criterion record. Consider an interval in which an observer records four events and the criterion record for that interval shows five events. That is scored as an interval of disagreement in exact agreement but as .8 of an agreement with block-by-block agreement. Thus, these data illustrate that it is easier for observers to obtain higher accuracy indexes at lower rates than with higher rates when the exact agreement method is used. Allowance for a partial agreement (e.g., the example of .8 agreement) in the block-by-block agreement algorithm mitigates the effect with high-rate responding.

In time-window analysis, because the algorithm ignores nonoccurrence (unlike exact agreement and block-by-block agreement), low rates of responding in the criterion measure cannot inflate accuracy by increasing agreement on nonoccurrence (Hawkins & Dotson, 1975; Hopkins & Hermann, 1977). However, the question arises as to whether the relatively high level of mean accuracy (96.8%) in the high-rate sample (Figure 3, top) indicates that time-window analysis may exhibit rate-dependent inflationary effects compared to the other two methods. Chance agreement is the proportion of obtained agreement that could result if an observer's recording responses were randomly distributed through an observational session (Hopkins & Hermann). The mean interresponse time in the criterion record for the high-rate sample was 2.55 s. With ±2 s tolerance for locating an agreement event in an observer's or criterion record, a window of up to 5 s is opened, so each window included a mean of 1.96 responses. Therefore, obtained agreement indexes with time-window analysis for relatively high-rate behavior (e.g., 23.5 responses per minute) would likely be influenced by chance agreement.

Recordings of response duration

The low, medium, and high durations of behavior occurred in 8%, 44.4%, and 72% of the session in the criterion records. Figure 3 (bottom) presents percentage accuracy computed with exact agreement, block-by-block agreement, and time-window analysis (t  =  ±2 s) for these different durations. Exact agreement produced lower percentage accuracy than the other algorithms regardless of response duration. Accuracy computed using block-by-block agreement was similar for low and high durations (91.8% and 92.4%) but were lower for medium durations. A similar effect was observed for the time-window analysis (87.4% and 96.1% accuracy for the low- and high-duration samples, respectively). The difference between exact agreement and block-by-block agreement was most noticeable for the medium-duration behavior, with 25.8% accuracy assessed by exact agreement, which was 39.4% less than for block-by-block agreement. The difference was least marked for the low-duration behavior at 85% accuracy measured by exact agreement, compared to 91.8% from block-by-block agreement.

Observers' accuracy at recording the medium-duration behavior was the lowest by all measures of accuracy, and it shows the most pronounced effect of using different algorithms (see solid bars, Figure 3, bottom). As shown in Figure 1 (Panel 5), the criterion record shows 26 onsets of the recorded behavior and many short-duration episodes (e.g., less than 10 s). Therefore, to match precisely the criterion record an observer would have entered 52 key presses at an overall rate of 12.5 responses per minute. This can be compared with the low- and high-duration behaviors recorded, which had only three and six onsets (see Figure 1, Panels 4 and 6, respectively). Thus, the complexity of the observers' task in recording the medium-duration behavior may be the underlying reason for lower accuracy. That is, the relatively high rate of onsets and offsets of the behavior in the medium-duration observational sample might have negatively affected observers' accuracy on their recording of duration across all measures of accuracy.

Explanation for the differences in accuracy across algorithms with the medium-duration sample can be used to demonstrate additional characteristics of the algorithms. To illustrate, the durations of individual occurrences of the behavior (i.e., the width of the bars in Figure 1, Panel 5) were computed. Among the 26 occurrences, 21 were less than 10 s in duration, of which 18 were less than 5 s in duration. Superimposition of 10-s comparison intervals for exact and block-by-block agreement on the criterion record produced four intervals of nonoccurrence and two with 10-s occurrence (i.e., the behavior continued throughout the entire interval). Therefore, 19 of 25 intervals contained between 1 s and 9 s of occurrence. With only four intervals of nonoccurrence, obtaining high agreement using the exact agreement method relies almost exclusively on observers' records agreeing with the criterion record on occurrence exactly, to the second. Considering that the distribution of bout lengths was skewed towards durations of less than 5 s, we view the likelihood of observers obtaining exact agreement accuracy at levels approaching those of block-by-block agreement as low even for trained observers. As with the high-rate sample, the medium-duration sample produced higher accuracy for block-by-block agreement than for exact agreement. The reason for this difference is that during block-by-block agreement, observers can achieve partial agreement on the occurrence of a response within each interval, which may compensate for inexact agreement.

DISCUSSION

In summary, three commonly used methods for computing interobserver agreement for continuously recorded data were applied to data recorded by observers who had no previous experience with continuous computer-based recording. Rate of responding was measured in three video samples, and duration of responding was measured in another three video samples. First, we analyzed accuracy with the time-window analysis algorithm. A tolerance of ±2 s for agreement with criterion records on occurrences of behaviors was allowed in subsequent analyses. Second, the effects of the exact agreement, block-by-block agreement, and time-window analysis on observers' accuracy when recording high, medium, and low rates and durations were investigated. Substantial differences in percentage accuracy were related to the characteristics of the algorithm and observational samples.

The effects of changing tolerance for agreement in the time-window analysis method were originally illustrated with hypothetical data by MacLean et al. (1985), who recommended that a tolerance of ±2 s might be allowed by a “conservative user” (p. 69) when discrete behaviors were recorded. Others have reported that they employed ±2 s tolerance with discrete event recording (e.g., Repp et al., 1989). Results of the current analysis support these previous findings, at least for the observation materials and procedures employed herein.

The developers and users of time-window analysis have not recommended investigating tolerance with duration measures (e.g., MacLean et al., 1985; Repp et al., 1989; Tapp & Wehby, 2000). The current data suggest that the same level of tolerance (±2 s) can be justified when duration is the measure of interest. A standard tolerance (e.g., ±2 s) for reporting accuracy and agreement for recording events or durations may assist in the interpretation of data quality assessed using the time-window analysis algorithm. The unnecessary alternative, with multiple different tolerances for different measures within the same data set, would likely complicate data analysis.

Page and Iwata (1986) discussed the relative merits and disadvantages of exact agreement and block-by-block agreement with simulated interval data, specifically events within intervals. Imposing 10-s intervals on continuous data streams replicates that type of behavioral record. Page and Iwata showed how excessively stringent the exact agreement method can be, with 5% agreement, in comparison with the block-by-block agreement method, which produced 54% agreement with the same manufactured data. In the present study using video samples from analogue functional analyses, the difference in level of agreement was apparent (Figure 3). At the extreme, exact agreement produced accuracy measures close to 40% (37.7% and 39.4%) below those of block-by-block agreement for the high-rate behavior and the medium-duration behavior.

It should be noted that, logically, there can be no possible pair of observers' records for which agreement measured by exact agreement exceeds that measured by block-by-block agreement. Unless observers agree 100% on numbers of occurrences (or number of seconds of occurrence) within all intervals, the exact agreement algorithm will always result in lower apparent agreement than block-by-block agreement, showing that exact agreement is a more stringent measure.

An additional question concerns the extent to which the different methods assess accuracy (or agreement) on particular instances of behavior. Block-by-block and exact agreement present difficulties that result from slicing the data stream into fixed (usually 10-s) intervals. Among other possibilities, two observers' responses within an imposed interval could be up to 9 s apart and count as an agreement or, at the other extreme, could be 1 s apart and count as two disagreements (one in each interval on either side of a cut). These possibilities can occur regardless of the size of the intervals (e.g., if the second-by-second data streams are divided into 5-s or 20-s intervals instead of the typical 10-s intervals). In time-window analysis the continuous record is not divided into intervals before analysis. Windows of opportunity for agreement are opened around an event or ongoing occurrence in observers' or criterion records, with the size of the window being twice the tolerance plus 1 s (e.g., a 5-s window for a 2-s tolerance). Therefore, time-window analysis, with its moving interval for agreement, may be superior in addressing agreement on particular instances of recorded behaviors.

Bijou et al. (1968) pointed out a potential problem with an interval-by-interval agreement method when the large majority of intervals of observation contain either occurrences or nonoccurrences of behavior. Specifically, under such circumstances estimates of percentage agreement are inflated. Hopkins and Hermann (1977) graphically illustrated the relation between rate of behavior and interval-by-interval agreement. For instance, if both observers recorded nonoccurrence in 90% of intervals, the minimum possible level of agreement by the interval-by-interval method is 80%, even if they never agreed on a single interval containing an occurrence of the behavior. Agreement reaches the conventional criterion of 80% required to indicate that recording was sufficiently reliable (e.g., Cooper et al., 2007) but, clearly, users of such data cannot rely on them (see Hawkins & Dotson, 1975). These are examples of the problem of chance agreement and may occur with time-window analysis when behavior is of a sufficiently high rate or duration. Exact agreement and block-by-block agreement also are both susceptible to increasing agreement artifactually when behavior occurs in proportionally few intervals.

Overall, the time-window analysis method with ±2 s tolerance was found to be more lenient than the exact agreement method. However, observers' recording of high-rate (23.5 responses per minute) and high-duration (72% of session) behavioral streams produced accuracy indexes from time-window analysis that, at greater than 96%, were higher than those from exact agreement and block-by-block agreement (Figure 3). Such high percentage accuracy suggests that time-window analysis may provide inflated estimates at high relative durations just as it can for high-rate responding. Hopkins and Hermann (1977) presented formulas for calculating chance agreement with discontinuous records. These formulas require the number of observed intervals to be entered into the denominator. The absence of imposed and fixed intervals for computing agreement by time-window analysis with moving intervals with tolerance (±t s) prohibits counting of intervals in the conventional sense. Thus, chance agreement cannot be computed by conventional methods. Nevertheless, researchers should take caution from the data presented to be aware of artifactually inflated indexes of accuracy from time-window analysis when mean interresponse times are short compared to the duration of the window for agreement defined by tolerance.

Further research on time-window analysis is required. Although the method is resistant to inflated levels of agreement or accuracy at low rates and durations due to chance agreement, it is possible that it might underestimate agreement at those levels of behavior. For accuracy, the time-window method allows decreasing room for errors as response rates decline. For instance, if the criterion record shows one response in 250 s but the observer does not record it, accuracy is zero with time-window analysis (cf. 96% with exact agreement and block-by-block agreement). Another difficulty with time-window analysis is that zero rates in observers' and criterion records produce an incalculable result (zero divided by zero). The same problem has been overcome by users of block-by-block agreement by defining a 10-s interval with 10 s of agreement on nonoccurrence as being complete agreement and scoring as 1.0 in their computations, despite the smaller to larger fraction being zero to zero. Applying the same rule in the time-window analysis algorithm would award 100% agreement for an observational session with no responding recorded by observers or in a criterion record, the same as with exact agreement and block-by-block agreement algorithms (Mudford et al., 2009).

The present research employed video samples with uncontrolled, naturally occurring distributions of responses. Samples were selected for their overall rates and durations and to provide a variety of real clients and response definitions to broaden the pedagogical experience for participating observers. Interactions among response rates, distributions, and durations of behaviors that complicated interpretation of some of the current findings may well be a feature of naturally occurring behaviors. Considering the distributions of responding in Figure 1, every panel (with the possible exception of the third panel) exhibits features that suggest that describing these samples merely by their overall rate or duration is oversimplification. In the top panel, responding was restricted to the first part of the sample. Other panels show some bursts (or bouts) of responding interspersed with relatively long interresponse times. Failure to control the content of samples or to randomize order of presentation may be viewed as limitations of the study. However, the aim was not to compare accuracy across behavioral topographies, clients, rate or duration measures, or observers as they acquired experience. The purpose was to illustrate differences in percentage accuracy depending on the algorithms employed to compute it.

Considerations for researchers selecting methods to compute the accuracy of continuous recording can be derived from the cited studies with discontinuous recording and from the current results. The three methods investigated in the current study all present imperfections if applied across a wide range of rates and durations as may be experienced in studies that demonstrate reduction of behaviors from high to low (or zero) rates and durations (or vice versa when increasing behaviors). Exact agreement and time-window analysis may be considered unsuitable at high rates and durations for opposite reasons, with the former being excessively conservative and the latter being too liberal. Exact agreement and block-by-block agreement may produce inflated indexes of accuracy at low rates and durations.

The generality of these findings regarding measurements of discrete events (i.e., rates in responses per minute) may be restricted by the rates observed (4.8 to 23.5 responses per minute). The range of investigated rates has been lower in previous studies of interobserver agreement (e.g., 1.4 to 6.6 responses per minute, Repp et al., 1976; 1.1 to 3.0 responses per minute, Kapust & Nelson, 1984; 0.3 to 1.2 responses per minute, Van Acker et al., 1991). If the lower ranges are more typical of data reported in behavioral research, further studies should investigate the effects on agreement and accuracy depending on algorithms used at these lower rates.

The current study may stimulate further efforts to determine appropriate measures of accuracy and agreement for continuous data. Manipulation of observational materials may be required to elucidate the effects of different algorithms more systematically than was possible with the video recordings of free-operant behaviors used in our study. The limitations of the three algorithms suggest that other methods, not in common use, should be investigated as well. Further research with real behavioral streams, theoretical analysis (e.g., Hopkins & Hermann, 1977), scripted behavioral interactions (e.g., Van Acker et al., 1991), and studies with manufactured behaviors (e.g., Powell, Martindale, Kulp, Martindale, & Bauman, 1977) are likely to further influence behavior analysts' choice of appropriate agreement and accuracy algorithms.