GENERALITY OF THE MATCHING LAW AS A DESCRIPTOR OF SHOT SELECTION IN BASKETBALL

Abstract

Based on a small sample of highly successful teams, past studies suggested that shot selection (two- vs. three-point field goals) in basketball corresponds to predictions of the generalized matching law. We examined the generality of this finding by evaluating shot selection of college (Study 1) and professional (Study 3) players. The matching law accounted for the majority of variance in shot selection, with undermatching and a bias for taking three-point shots. Shot-selection matching varied systematically for players who (a) were members of successful versus unsuccessful teams, (b) competed at different levels of collegiate play, and (c) served as regulars versus substitutes (Study 2). These findings suggest that the matching law is a robust descriptor of basketball shot selection, although the mechanism that produces matching is unknown.

Behavior theory assumes that the allocation of time and effort among behavior options is a function of the relative reinforcement they generate, an assumption that has been borne out in a variety of investigations of behavior in both the laboratory (Baum, 1979; Herrnstein, 1961) and the natural environment (Billington & DiTomasso, 2003; Borrero et al., 2007; Conger & Killeen, 1974; Martens, Halperin, Rummel, & Kilpatrick, 1990; Reed, Critchfield, & Martens, 2006). For example, Vollmer and Bourret (2000) studied shot selection by members of the men's and women's basketball teams at the University of Florida during the 1998–1999 season. Behavior allocation (measured as the proportion of shots taken that were two-point and three-point field goals) was positively correlated with relative reinforcement frequency (quantified as the proportion of shots made of each type).

Vollmer and Bourret (2000) evaluated basketball shot selection using a variant of the matching law (Baum, 1974; Herrnstein, 1961), which typically is expressed as the generalized matching law (GML):

1

in which B_x and B_y are frequencies of occurrence of the two behaviors, and r_x and r_y are frequencies of reinforcement generated by the two behaviors. When these ratios are logarithmically transformed, a linear function describes the data and usually accounts for most of the variance in behavior allocation in laboratory experiments (Baum, 1979). In this function, the slope (a) equals 1 when behavior allocation is perfectly sensitive to reinforcement differentials and deviates from 1 when changes in behavior allocation are disproportional to relative reinforcement frequency. The y intercept of the function (log b) is a measure of bias or preference for one alternative irrespective of reinforcement frequency.

In Vollmer and Bourret's (2000) application of Equation 1 to shot selection, the number of two- and three-point field goals attempted served as the behavior (B) terms, and the number of field goals made served as the reinforcement (r) terms. Their results are best considered in conjunction with those of two recent extensions that examined data from 11 college men's teams that competed in the Big Ten Conference during a recent season (Hitt, Alferink, Critchfield, & Wagman, 2007) and from 57 professional players who participated in the National Basketball Association (NBA) from 1991 to 2000 (Romanowich, Bourret, & Vollmer, 2007). Collectively, the available studies suggested three noteworthy patterns that were consistent with laboratory findings (e.g., Baum, 1979). First, the GML accounted for most of the variance in behavior allocation, meaning that the ratio of shots taken varied systematically with the ratio of shots made. Second, sensitivity (the a parameter) usually was slightly less than 1 (undermatching), meaning that in covariation between behavior ratio (shots taken) and reinforcement ratio (shots made), the former changed proportionally less than the latter. Third, there was a bias for taking three-point shots, meaning that, across all shot-making ratios, more three-point shots were taken than the shot-making ratio predicts.

To the extent that shots made may be considered to be a measure of reinforcement for shot taking, the available data suggest a parallel between shot selection and reinforcement-based choice. The present investigation addressed the generality of effects that suggest this parallel.

STUDY 1

Study 1 was designed to determine the extent to which findings like those of Vollmer and Bourret (2000) and Hitt et al. (2007) apply to men's teams participating in Division I competition sponsored by the National Collegiate Athletic Association (NCAA). To date, fewer than 2% of these teams have been analyzed for any given season, and the extent to which they are representative of other teams remains to be established.

Method

We sought data from all teams that participated in NCAA men's Division I play during the 2005–2006 season. Regular-season shooting statistics for players on these teams were obtained from a variety of archival electronic sources, primarily Web sites hosted by sponsoring universities. Data were located for 320 of the 332 participating teams, representing all 32 Division I conferences (data from the Big Ten Conference described previously by Hitt et al., 2007, are incorporated into this analysis) plus seven teams that were not aligned with any conference.

Via least squares linear regression, the GML was fitted to the data for each team with individual players serving as one observation. Two- and three-point field goals attempted were used as B_x and B_y, respectively, and two- and three-point shots made were used as r_x and r_y, respectively. A player was included in the analysis if he attempted more than 14 two-point field goals and more than 14 three-point field goals over the course of the season and made at least one two-point and one three-point shot. This eligibility criterion resulted in different numbers of eligible players for different teams. One team with only 2 eligible players was dropped from the analysis because fitting a line to two data points is conceptually meaningless. The remaining teams had 4 to 10 eligible players. A Pearson product-moment analysis revealed no significant relation between number of players and the percentage of variance accounted for by the GML in a team's shot selection (r  =  0.07, p  =  .582).

Results and Discussion

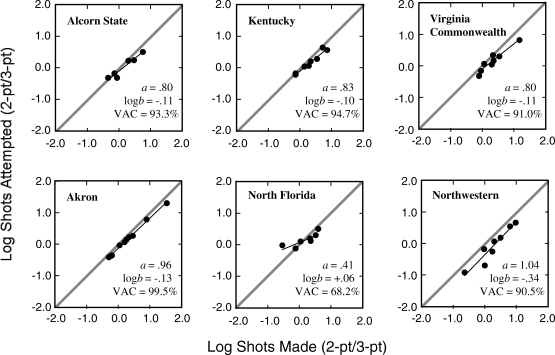
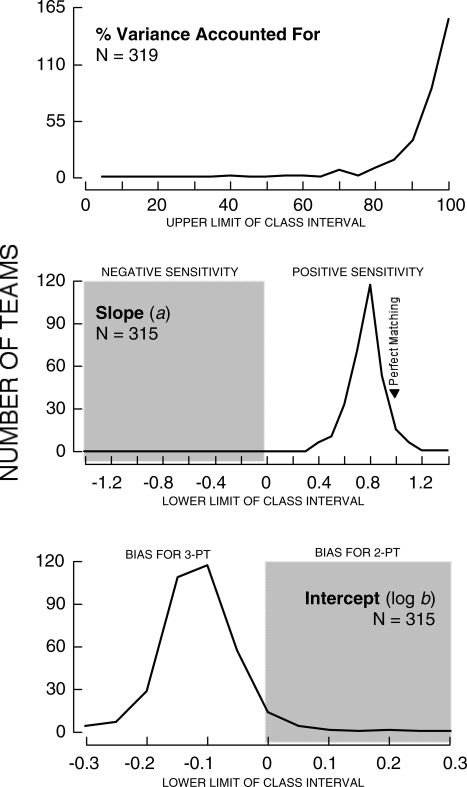
Figure 1 summarizes the relation between shot-taking and shot-making ratios for six illustrative teams; Figure 2 summarizes the results for all 320 teams (results for individual teams may be obtained from the authors). In most cases, the GML accounted for most of the variance in shot selection. Figure 1 (top) shows three teams that approximated the mean variance accounted for of 92% (SD  =  9.8). Better (Akron) and worse (North Florida) fits are illustrated in the bottom row. Overall, Figure 2 (top) shows that the GML accounted for at least 80% of shot-selection variance for 295 of 320 teams and more than half of the variance for all but four teams. These four teams were omitted from analyses that focused on fitted parameters because parameter estimates are unreliable when a model accounts for little variance.

Figure 1.

Relation between shot-selection and shots-made ratios for six illustrative Division I college teams (2005–2006 season). Each data point represents one player's season-aggregate statistics. See text for details.

Figure 2.

Results of fitting the generalized matching law to the shot-selection data of NCAA Division I teams from the 2005–2006 season. Top: variance accounted for by the matching law for 319 teams. Middle: sensitivity estimates (a parameter, or slope) for 315 teams. Bottom: bias estimates (log b parameter or y intercept) for 315 teams.

Figure 2 (middle) shows that 292 of 315 teams exhibited undermatching (a < 1). In Figure 1, optimal sensitivity (a  =  1) is illustrated by a diagonal in each panel. The top row shows three teams that approximated the mean a of .82 (SD  =  .14). The bottom row shows higher (Akron and Northwestern) and lower (North Florida) a values.

Figure 2 (bottom) shows that 298 of 315 teams exhibited a bias for taking three-point shots (as calculated here, positive log b values show a bias for taking two-point shots; negative values show a bias for taking three-point shots). This means that although shot selection varied predictably with shots made, more three-point shots were taken than expected based strictly on the slope of the matching function for the typical team. In each panel of Figure 1, the hypothetical diagonal illustrates the absence of bias (log b  =  0). The top row shows three teams that approximated the mean obtained log b of −0.09 (SD  =  0.06). The bottom row shows a more extreme three-point bias (Northwestern) and a rare case of two-point bias (positive log b; North Florida).

Summary and Conclusions

For most teams that were studied, the GML accounted for most of the variance in shot selection. Sensitivity of shot taking to shot making tended to be suboptimal (undermatching), and shot selection typically was biased toward choosing three-point shots. In this regard, results from 13 Division I college teams that were described in two previous investigations (Hitt et al., 2007; Vollmer & Bourret, 2000) are broadly representative of many Division I college basketball teams.

Because the GML was developed in the context of laboratory choice research (Baum, 1974), it is reasonable to ask how the present findings compare to those of laboratory choice experiments. The most obvious difference is that the GML tends to account for more variance in the laboratory (typically >95%; Baum, 1979), at least in studies of choice by nonhumans. The present findings compare more favorably with those of some laboratory experiments involving human subjects (e.g., Takahashi & Shimakura, 1998). Overall, however, the present findings agree with those of laboratory investigations in suggesting a positive linear relation between behavior allocation and the relative frequency of events that may function as operant consequences.

The present results also agree with laboratory findings in showing bias under conditions of unequal outcomes (two- vs. three-point field goals) and undermatching in behavior allocation. The former is anticipated by laboratory research showing that reinforcer amount or quality is a major predictor of bias (Baum, 1979; Miller, 1976): At any given reinforcement frequency, individuals typically prefer the behavior alternative that produces the larger reinforcer. Applications of the GML to basketball shot selection add to those of laboratory investigations in affirming this tenet of matching theory.

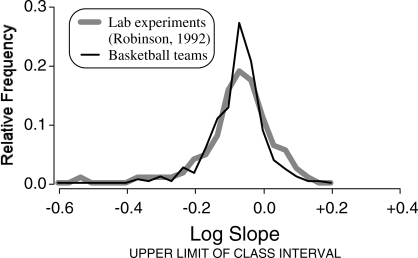
Regarding sensitivity, undermatching is common in laboratory choice experiments (Baum, 1979; Robinson, 1992), and has been replicated in choice making under natural conditions outside of basketball (e.g., Borrero et al., 2007; Conger & Killeen, 1974; Reed et al., 2006). To highlight the parallel between undermatching in shot selection and in laboratory studies, Figure 3 compares the distribution of sensitivity estimates of 315 basketball teams to those of 127 individuals working in laboratory choice experiments, as reported in the review by Robinson (data estimated from Figure 1). Sensitivity estimates were logarithmically transformed in an attempt to normalize the distributions. The resulting two distributions are strikingly similar in terms of both range and modal class interval, with a median slope of just over 0.80 in both cases. These results demonstrate that sensitivity in basketball shot selection, when evaluated at the team-aggregate level, shows variability similar to that of operant choice in the laboratory, when evaluated at the individual level.

Figure 3.

Distribution of sensitivity estimates (a parameter) derived from fitting the generalized matching law to the behavior-allocation data of individuals in laboratory choice experiments (estimated from Figure 1 of Robinson, 1992) and to the shot-selection data of 315 NCAA Division I teams. Sensitivity estimates were logarithmically transformed to normalize the distributions.

STUDY 2

As an extension of previous studies (Hitt et al., 2007; Vollmer & Bourret, 2000), Study 1 addressed generality by showing that the shot selection of many different basketball teams can be successfully described by the GML. A different type of generality concerns the capacity of a theoretical model to account for situation-specific effects within a given domain of application like basketball. Stilling and Critchfield (in press) have labeled this form of generality explanatory flexibility. Explanatory flexibility is demonstrated when a model like the GML produces systematically different results when applied to conditions that differ in face-valid ways. Recently, Romanowich et al. (2007) provided an example of explanatory flexibility in a GML-based analysis of shot selection by professional basketball players before and after important rule changes. They found that shot-selection bias changed in ways that were consistent with the assumption that rule changes altered the reinforcement schedule for attempting three-point field goals.

Study 2 examined the explanatory flexibility of the GML, as applied to basketball shot selection, in three ways. The first question addressed whether the GML reveals systematic differences in shot selection between players on successful and unsuccessful teams that participate at the same level of competition. Based on a preliminary report by Hitt et al. (2007), we predicted that the GML would account for more variance in shot selection by successful teams, and that successful teams would show higher sensitivity.

The second question addressed whether the GML reveals systematic differences in shot selection between players on teams that participate at different levels of competition. NCAA member schools choose to play basketball in one of three divisions that represent a most-to-least continuum involving three important athletic resources: number of games played in a season, number of athletic scholarships granted, and amount of money spent on athletic department business, such as recruiting players and hiring coaches (see http://www.ncaa.org). In the present study, players on the best Division I teams were compared with the best teams in other divisions to determine whether the GML describes shot selection equally well for all levels of play. Based on the widely held assumption that NCAA divisions define a hierarchy of performance quality (Harari & Ominsky, 1994), we predicted that the GML would account for more variance in shot selection by Division I players, and that Division I players would show higher sensitivity than players in other divisions.

The third question addressed whether the GML reveals systematic differences in shot selection by better and worse players. Most previous analyses have focused on the team as the unit of analysis, and each team includes players of varying ability, as suggested by the fact that coaches grant more competition time to some players than to others. Thus, one way to segregate players is according to whether they are regulars (who accumulate considerable playing time) or substitutes (who play less often). We predicted that the GML would account for more variance in shot selection by regulars, and that regulars would show higher sensitivity than substitutes. This prediction assumes that, on average, regulars have better abilities than substitutes, and that, in playing more, they also acquire more contact with the contingencies of shot selection.

Method

For all analyses, a player was included if he attempted at least 14 two-point field goals and at least 14 three-point field goals over the course of the season and made at least one of each type of shot. Via least squares linear regression, the GML was fitted to the data, with two-point and three-point field goals attempted serving as B_x and B_y and two-point and three-point shots made serving as r_x and r_y. Consistent with the approach of Romanowich et al. (2007), in each analysis the GML was applied to the data of all eligible players combined, with each player serving as one observation.

Players on best versus worst Division I teams

In the present analysis, successful and unsuccessful teams were operationally defined according to rating percentage index (RPI) rankings, which take into account win–loss records along with other factors such as quality of opponents faced (see http://www.rpiratings.com/WhatisRPI.html). Season shooting statistics were sought for players on the 30 Division I men's basketball teams with the highest and lowest RPI rankings among the 330 teams competing during the 2004–2005 season. To provide a test of generality, we also compared players on the highest and lowest ranked teams among those from the 2005–2006 season that were examined in Study 1. Data could not be located for several targeted teams, in which case the next available team in the RPI rankings was substituted. For economy of expression, the high-ranked teams will be referred to as top 30 teams, and the low-ranked teams will be referred to as bottom 30 teams. From the resulting 120 teams (list available from the authors), 272 (2004–2005) and 278 (2005–2006) eligible players were identified.

Players in different divisions

Season shooting statistics were sought for players on the most highly rated teams in Divisions I, II, and III during the 2004–2005 season. RPI rankings are not determined for teams in Divisions II and III; therefore, for all divisions, coaches' polls were used to identify the best teams. Because relevant polls rank only 25 teams per division, the present analysis focused on 25 teams per level of play. Top Division I teams were identified from the ESPN/USA Today coaches' poll (http://sports.espn.go.com/ncb/rankings). Data could not be located for two ranked teams, requiring substitution of teams that received considerable voting support in the coaches' poll but were not ranked in the Top 25. Top Division II and III teams were identified from coaches' polls presented by the NCAA (http://www.ncaasports.com/basketball/mens/polls).

Regulars versus substitutes

Players from the top 25 teams in Divisions I, II, and III (2004–2005 season) were considered for this analysis if they participated in at least 20 games during the season. From among 601 eligible players, regulars (n  =  74) were defined as those who played an average of three fourths of each game in which they participated (≥32 min per 40-min game). Substitutes (n  =  73) were defined as those who played an average of one third or less of each game in which they participated. The two types of players took about the same number of shots per minute played (for regulars, M  =  0.47, SD  =  0.11; for substitutes, M  =  0.43, SD  =  0.12).

Results and Discussion

Table 1 summarizes the results of all comparisons in terms of the percentage of variance for which the GML accounted and estimates of sensitivity (a) and bias (log b). For present purposes, sensitivity (a) and bias (log b) estimates are considered to be different for different aggregate data sets if the 95% confidence intervals derived from least squares linear regression do not overlap.

Table 1.

Study 2: Results of GML Analyses

Comparison	Year	N	% of variance	Sensitivity estimate	95% confidence interval	Bias estimate	95% confidence interval
Top 30 teams	2005	182	94.1	.833	.816 to .850	−.099	−.090 to −.108
Bottom 30 teams		190	91.1	.794	.776 to .812	−.073	−.064 to −.082
Top 30 teams	2006	166	94.6	.839	.823 to .855	−.094	−.086 to −.102
Bottom 30 teams		192	83.6	.753	.729 to .777	−.091	−.078 to −.104
Division I	2005	149	94.0	.892	.855 to .928	−.096	−.087 to −.105
Division II		160	93.5	.833	.816 to .850	−.089	−.080 to −.098
Division III		158	81.2	.787	.757 to .817	−.081	−.066 to −.096
Regulars	2005	74	95.5	.867	.845 to .889	−.056	−.044 to −.068
Substitutes		71	72.6	.726	.687 to .765	−.125	−.111 to −.139

Players on best versus worst Division I teams

The GML accounted for most of the variance (≥84%) of shot selection by players on both top 30 and bottom 30 teams, and in both cases revealed both undermatching and a bias for taking three-point shots. These findings are consistent with patterns seen in the majority of team-level analyses (Study 1; Hitt et al., 2007; Vollmer & Bourret, 2000) and in pooled data from several dozen NBA players from different teams (Romanowich et al., 2007).

The GML accounted for more variance in shot selection by players from successful teams, a finding that is consistent with the assumption that better teams have players whose performances are more orderly. Hitt et al. (2007) suggested that sensitivity to shot-making contingencies, as measured via the a parameter of the GML, might contribute to offensive success. In both 2004–2005 and 2005–2006, sensitivity was higher for players on top 30 teams than for players on bottom 30 teams, a finding that is consistent with the assumption that better teams are comprised of players whose shot selection is more finely attuned to shot-making contingencies. Finally, results for bias were consistent with those based on team-level analyses. In 2004–2005, the bias for taking three-point shots was more pronounced for players on top 30 teams than for players on bottom 30 teams, but this finding was not replicated for 2005–2006, when players on successful and unsuccessful teams showed similar magnitudes of three-point shooting bias.

Players in different divisions

For all three divisions, the GML accounted for most of the variance in shot selection (≥81%) and in all cases revealed undermatching and a bias for taking three-point shots. In these general terms, a matching-law analysis provided a similar picture of shot selection for all three NCAA divisions, one that is consistent with the results of previous studies. There were, however, differences across divisions. The GML accounted for somewhat more variance in shot selection for players in Divisions I and II than for players in Division III. In addition, sensitivity for Division I players fell outside the 95% confidence intervals for the other two divisions, which were not different according to this criterion. To the extent that the NCAA divisions represent a competitive hierarchy, these findings are consistent with the assumption that shot-selection matching correlates with competitive success. The strength of bias for taking three-point shots also varied across divisions, with the log b parameter for Division III falling outside the 95% confidence intervals for the other two divisions. This indicates that across a range of shots-made ratios, Division III players were less inclined to attempt three-point shots.

Regulars versus substitutes

The GML accounted for most of the variance in shot selection for both regulars and substitutes and in both cases revealed undermatching and a bias for taking three-point shots. The GML accounted for more variance in shot selection, and there was greater sensitivity for regulars than for substitutes, with the sensitivity difference exceeding 95% confidence intervals. Both findings are consistent with the assumption that regulars are more skilled and often benefit from greater contact with shot-taking contingencies. Substitutes showed a more pronounced bias for taking three-point shots than did regulars, with the difference exceeding 95% confidence intervals.

Past applications of the matching law have not considered the role served by individual players, and in most cases probably intermingled regulars and substitutes in the same analysis. The present study established that a GML analysis can account for performances of both kinds of players and can detect differences in their shot-taking tendencies. Our analysis included no objective measure of athletic skills, but to the extent that regulars are more capable than substitutes, the present analysis agrees with the preceding one in suggesting that orderly shot-selection matching and high sensitivity are associated with good basketball outcomes. A related speculation is that matching outcomes reflect contingency exposure: By virtue of accumulating more playing time than substitutes, regulars contact the contingencies of shot selection more frequently. This speculation is broadly consistent with laboratory studies showing that matching outcomes change systematically as contingency exposure accumulates (Todorov, Olivera Castro, Hanna, de Sa, & Barreto, 1983).

Summary

Study 2 extended the generality of the GML as an account of basketball shot selection in two ways. First, it demonstrated the reliability of effects with additional groups of players beyond those that were examined in Study 1 and in previous reports. In all cases, major findings (good linear fits, undermatching, and three-point shooting bias) were consistent will those of previous reports. Second, this study showed the GML to have considerable explanatory flexibility in that it accounted for shot selection by several different types of players and revealed differences among them. Several of the relevant findings correspond well to lay impressions of basketball. For instance, shot-selection sensitivity was relatively high for players on highly ranked teams who participate at the highest collegiate level and who play extensively, all of whom would be considered to be among the sport's elite athletes. In this way, the present study lends face validity to a GML analysis by suggesting parallels with outcomes that matter to spot observers.

STUDY 3

This study addressed a third kind of generality related to levels of analysis. The matching law was developed explicitly as an account of individual choice (e.g., Herrnstein, 1961); in laboratory studies, it describes individual performance functions in which each of several relative reinforcement conditions serves as an observation (Mazur, 1991). By contrast, to date, all applications of the GML to basketball have pooled the data from multiple players, treating each individual as an observation. These applications, therefore, do not show variations in individual choice. They demonstrate only that between-individuals differences in shot selection are predicted by between-individuals differences in shot-making success. The present study was a first attempt to address the question of whether individual basketball players obey the matching law in the sense that their shot selection varies predictably across situations that vary in terms of shot-making success.

Method

Our analysis was consistent with previous ones in treating the season-aggregate shooting statistics of individual players as one observation (Hitt et al., 2007; Romanowich et al., 2007; Vollmer & Bourret, 2000). It differed from previous studies in evaluating matching functions based on the career data from individual players in the NBA who were selected for study because they often play for many seasons. The analysis treated each season of a player's career as an experimental condition, based on the assumption that the factors that influence player ability and shot selection (e.g., age, experience, coach behavior, personnel on opposing teams, league rules) are relatively constant within a season but may differ across seasons.

The individuals selected for analysis were among the 50 greatest players in NBA history (http://www.nba.com/history/50greatest.html). A player was included in the analysis if his career fell entirely within the period of 1979 (when the NBA first introduced the three-point shot) to 2007 and encompassed at least 10 seasons during which the player (a) accrued at least 720 min of playing time (professional games last 48 min, so this is equivalent to 15 games of the 82 in an NBA team's season), (b) attempted an average of at least one three-point shot per 240 min of playing time (equivalent to five games), and (c) made a least one three-point shot per season. Table 2 lists the nine qualifying players and shows that, in terms of shooting accuracy, these players differed from one another and also varied substantially across seasons. We obtained the number of two-point and three-point shots made and attempted for each season of a qualifying player's career from archival electronic sources (primarily that listed above and http://www.nba.com). Least squares linear regression was used to fit Equation 1 to each player's data.

Table 2.

Career Shooting Statistics for Nine of the 50 Greatest NBA Players

Player	Seasons (eligible, played)	Percentage made
		Two-point shots		Three-point shots
		Career	Range (worst–best eligible seasons)	Career	Range (worst–best eligible seasons)
Charles Barkley	14, 16	58.1	49.5–64.3	26.6	16.0–33.8
Larry Bird	12, 14	50.9	47.0–54.7	37.6	21.2–42.7
Clyde Drexler	14, 15	49.8	45.4–51.5	31.8	20.0–36.0
Magic Johnson	12, 13	54.1	48.7–57.9	30.3	17.6–38.4
Michael Jordan	13, 15	51.0	42.6–55.3	32.7	13.2–42.7
Karl Malone	10, 20	51.9	46.4–56.7	27.4	17.6–40.0
Scottie Pippin	16, 17	50.7	45.5–53.4	32.6	17.4–37.4
John Stockton	19, 19	54.1	48.1–59.4	38.4	13.3–46.2
Isiah Thomas	13, 13	46.8	43.2–50.1	29.0	19.4–33.8

Note. See text for details of how players were identified and for criteria for selecting seasons to include in the analysis.

Results and Discussion

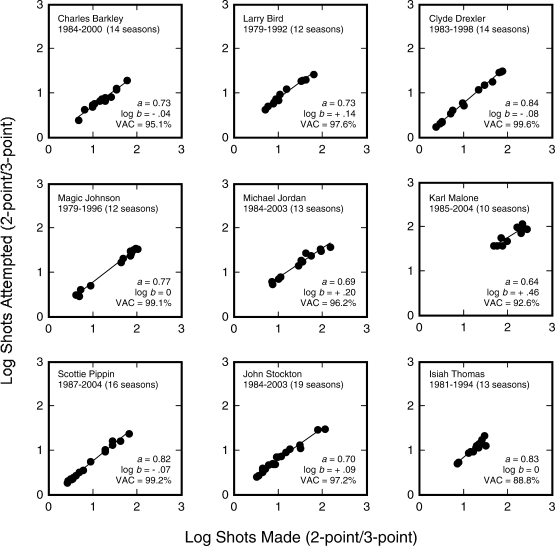
Figure 4 shows matching functions for the individual players listed in Table 2. Two findings are in accord with previous analyses based on pooled data from multiple players: The GML accounted for most of the variance in individual-player shot selection (≥89%), and undermatching was prevalent.

Figure 4.

Relation between shot-selection and shots-made ratios for nine iconic professional basketball players. Each data point represents one season. In each panel, dates show the span of a player's career, with the number of seasons that were included in the analysis shown in parentheses. See text and Table 2 for details.

Figure 4 also reveals two interesting differences between individual-player functions and those reported previously for aggregate data from multiple players. One difference is that sensitivity estimates (range, 0.64 to 0.83) were lower than most that have been obtained from group-aggregate data. A second novel finding was a wide variety of bias estimates. Some players (e.g., Charles Barkley, Clyde Drexler) exhibited a bias for taking three-point shots that has been seen in nearly every previous aggregate-level analysis, although others showed no bias (Magic Johnson, Isiah Thomas) or a pronounced bias for taking two-point shots (Michael Jordan, Karl Malone).

Although the present findings for the first time extend a GML analysis to shot selection by individual basketball players, they leave many questions unanswered, three of which bear mention here. First, how well does the present small sample of players represent shot-selection patterns of NBA players generally? By definition, the best players in history are atypical in some ways; whether shot-selection matching is one of them remains to be determined. Second, as suggested above, how well do team-level analyses represent shot-selection matching by individuals? The present data suggest that individual functions may not always mirror those seen in teams. Third, are there differences in professional and college basketball that affect the matching relation? Further study of shot selection as an individual phenomenon clearly is required.

As future studies of individual-player shot selection are contemplated, we readily acknowledge that a guiding assumption of the present one can be debated. Every casual observer of basketball knows that many of the factors that dictate basketball offensive success (e.g., player health and fatigue, opponent strategy and ability) can vary across games and even across portions of a single game. For our strategy of treating each season as an experimental condition to be tenable, season-by-season variance in such factors would need to exceed more local variance. No data of which we are aware speak objectively to this issue, so it is possible that the season is a poor unit of analysis. Future investigations should explore alternative approaches to evaluating individual shot-selection matching. Despite its limitations, however, the present study is valuable as a first attempt to determine whether individual basketball players obey the matching law. The preliminary evidence suggests that they do.

GENERAL DISCUSSION

The present investigation examined the relevance of the GML to basketball shot selection at a scope of analysis that far exceeds that of previous reports. Previous analyses focused primarily on shot selection by players on approximately a dozen college teams (Hitt et al., 2007; Vollmer & Bourret, 2000); the present Studies 1 and 2 examined data from players representing hundreds of teams. Whereas all past analyses pooled data from multiple players, Study 3 examined shot-selection matching in individual professional players. Across many analyses, the GML accounted for most of the variance in shot selection, thereby demonstrating its reliability in describing basketball shot selection.

Two general effects were replicated that are reminiscent of laboratory findings regarding operant choice. First, three-point shots tended to be taken more often than would be expected based strictly on frequency of shot making. Such bias is not anticipated based on reinforcement frequency (r terms in Equation 1), but is fully expected based on laboratory research showing that reinforcer amount or quality is a major predictor of bias (Baum, 1979; Miller, 1976). Specifically, at any given reinforcement frequency, the behavior alternative that produces the larger reinforcer (in this case three points vs. two points) should be overrepresented. Second, shot taking varied proportionally less than shot making would predict. Such undermatching is common in laboratory choice experiments (Baum, 1979; Robinson, 1992) as well as in choice making under more natural (outside basketball) circumstances (e.g., Borrero et al., 2007; Conger & Killeen, 1974; Martens et al., 1990; Reed et al., 2006).

Previously, Romanowich et al. (2007) showed that the GML could account for changes in shooting tendencies that resulted when basketball rules that govern three-point shot attempts were modified. The present investigation demonstrated additional explanatory flexibility by showing that outcomes of a GML analysis varied systematically as a function of whether the players (a) were members of successful or unsuccessful teams; (b) participated in different NCAA divisions; and (c) served as a regular or a substitute. Such findings lend a measure of face validity to behavior theory. To suggest that behavioral choice principles are expressed in basketball (Hitt et al., 2007; Vollmer & Bourret, 2000) highlights the potential generality of the theory and gratifies the theorist, but may not impress a basketball fan who might wonder instead how behavioral choice theory can improve his or her practical understanding of basketball. In sport, for instance, anything that sheds light on success is compelling. Hitt et al. suggested that shot-selection matching might be correlated with success in a conference championship tournament, although their findings were based on very few games and must be considered to be provisional. Reed et al. (2006) found that play calling by offensive coordinators in the National Football League, as portrayed by the GML, was correlated with team win–loss records. A relation between shot-selection matching and team success, if replicated in other studies, could help to demonstrate why behavior theory merits attention outside its traditional areas of application.

The preceding discussion prompts three notes of caution. First, the present analyses focused only on basketball offense, which is only a part of the game, and shot selection is only a part of offense. Not surprisingly, then, there may be considerable overlap in shot-selection matching between successful and unsuccessful teams, and it remains to be seen how robustly the GML predicts success. Second, to say that matching predicts team success implies a monotonic relation that may not correspond to the conceptual underpinnings of the GML. Note that, in Study 1, team sensitivity values (a) for high-ranked teams ranged as high as 1.43, although in mathematical terms shot taking is most closely tied to shot making when a  =  1 (Davison & McCarthy, 1988). This suggests, perhaps, a curvilinear relation between sensitivity and team success such that slopes distinctly higher or lower than 1 should predict poor team outcomes. Because only a handful of teams had slopes substantially higher than 1, however, the present data set does not allow a test of this prediction. Finally, as Study 3 emphasized, matching is normally conceived as an individual behavioral phenomenon, and existing data show associations between group-aggregate data and various measures of quality of play. A challenge for future studies is to explore the relation between individual success and shot-selection matching.

In evaluating the generality of the matching law as a descriptor of basketball shot selection, the present investigation, like all of its predecessors, does not speak directly to the question of why matching occurs in shot selection. Any attempt to link shot-selection matching to operant choice principles invokes the assumption that behavior allocation (shot selection) adapts to changing reinforcement conditions (shot making). We acknowledge that other interpretations of the present data are possible and that, as every student of behavior knows, descriptive methods like those employed here are ill suited to answering cause–effect questions. The plausibility of an operant interpretation of shot selection probably depends on future studies that employ different methods (e.g., experiments).

The following illustrates the kind of problem that exists within naturalistic basketball data that can be overcome in experiments. In basketball, measures of shots taken and shots made are not independent because a shot can only be made if one is taken. Such interdependence also exists on concurrent interval schedules in the laboratory, but typically subjects make many more responses than the contingencies require for each reinforcer, rendering the lack of independence relatively unimportant. In basketball, however, good players may make half or more of their two-point shots and more than 40% of their three-point shots. A large percentage of shots taken are reinforced; moreover, as players increase in accuracy, this interdependence grows. This provides one possible explanation for our finding that the matching law accounts for more variance in shot selection among successful teams (who presumably have highly accurate shooters) than among unsuccessful teams (who presumably have less accurate shooters). Is the number of shots taken a function of the number made (reinforced), as per an operant interpretation? Or is this an artifact of other variables? Without experimental analysis, it is difficult to distinguish between these interpretations.

Only future studies, then, can clarify whether operant processes really influence basketball shot selection. Our results make clear that previously reported effects (undermatching and a three-point bias) are manifest across several circumstances and levels of analysis. We also identified several conditional patterns that correspond reasonably well to lay expectations about basketball. These include that shot-selection variance and sensitivity vary as a function of team competitiveness and between regulars and substitutes. In this regard, our data clarify the task for future investigations, whatever methods they may employ: to illuminate the mechanisms that underlie these effects.