The report of Nilsson and coworkers in this issue of PNAS (1) is an important step toward understanding the mysterious properties of water.
Water is certainly the most essential of all molecules in nature. Understanding its role in many aspects of life represents the most challenging problem in science. Despite its importance and ubiquity on the earth and despite many centuries of research, water is certainly the most complex liquid, being characterized by counterintuitive properties (“the 64 anomalies of water”). Unlike most liquids, water becomes most dense not when it is coldest but at 4 °C.
Other water anomalies include thermodynamic properties such as isothermal compressibility KT, isobaric heat capacity CP, and thermal expansion coefficient αP (2–4). In particular, these functions, extrapolated from their values in water's metastable supercooled phase (located between its homogeneous nucleation temperature, TH = 231 K, and the melting temperature, TM = 273 K), all appear to diverge at a singular temperature (TS ≃ 228 K). Water can also exist in the liquid form at extremely low temperatures as a glass (3) below the glass transition temperature Tg ∼ 130 K. Just above Tg, glassy water transforms into a highly viscous fluid and finally crystallizes at TX = 150 K (2). The region between TX and TH is a region where bulk liquid water cannot be studied, the so-called no-man's land (4).
Among the many theoretical approaches (5–7) developed to explain water properties, the liquid–liquid critical point (LLCP) hypothesis (7) has received the most substantial support from various experimental (8, 9) and theoretical studies (10, 11). The explanation stems from the role played by the hydrogen bond (HB) interaction among water molecules. More precisely, the HB governs the overall structure and the dynamics of water, giving rise, on decreasing T, to a clustering process for which an open tetrahedrally coordinated HB network gradually develops. The LLCP hypothesis is based on an argument advocating the continuation of the local structure of the liquid water into its amorphous solid phases. Amorphous water is known to display polymorphism: it has a low-density amorphous (LDA) and also a high-density amorphous (HDA) solid phase (12, 13) that can be made below Tg and can be transformed from one to the other by tuning pressure.
It is therefore possible that the liquid state is a mixture of the two corresponding liquid local structures, one corresponding to a low-density liquid (LDL) and the other to a high-density liquid (HDL) (7). The difference between the two liquids lies in their local structures: in the HDL, the local tetrahedrally coordinated HB structure is not fully developed, whereas in the LDL, a more open, locally “ice-like” HB network is realized. In this view, water anomalies are a reflection of the “competition” between these two local liquid forms. An important feature of the LLCP scenario is the presence of a Widom line TW(P), in the T–P phase diagram. The Widom line is the locus of the correlation length maxima in the one phase region beyond the LLCP, where thermodynamic response functions take their maximum values (14, 15). It separates water with more HDL-like local structures at high temperatures from water with more LDL-like local structures at low tempertures. The presence of the Widom line influences quantities such as density, viscosity, relaxation times, and the self-diffusion coefficient, and it offers an explanation of the anomalies in quantities such as specific heat or isothermal compressibility.
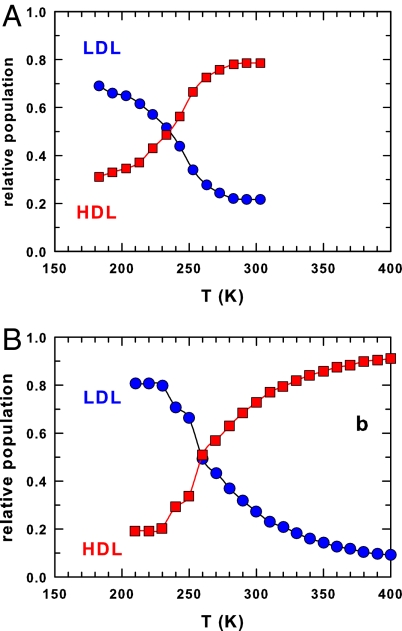
To clarify these aspects one would like to observe two water liquid phases inside the no-man's land. By confining water in nanoporous structures so narrow that the liquid cannot freeze, experiments recently have been made by using neutron and Raman scattering and NMR spectroscopy (9, 16–20). (See Fig. 1.) In particular, in one of these studies (9) the Widom line was identified in the T–P phase diagram, whereas in another one (18) clear signs of the two types, LDL and HDL, of water inside the supercooled region are reported. These findings, however, are open to the criticisms that the behavior of the water may have been altered by the silica pore surfaces or that water confined in very narrow nanopores has a structure different from that of bulk water.
Fig. 1.
The populations of the two liquid local water structures. (A) The populations of the low-density liquid (LDL) and the high-density liquid (HDL) water phases measured in confined geometry by means of light spectroscopy (18). (B) The same populations obtained in bulk water by means of a molecular dynamics simulation for the TIP5P water potential (21).
Very recently (21), by using the electron spin resonance technique, water confined within ice itself has been studied. The mobility of water molecules within tiny pockets of liquid trapped between ice crystallites has been measured down to 90 K. However, the experiment does not measure water dynamics directly, but rather the motion of an organic molecule (TEMPOL, 4-hydroxy-2,2,6,6-tetramethylpiperidine-1-oxyl) is used as a sort of probe diffusing in water, thus sensitive to the water viscosity. Inside the interval 130 < T < 273 K, two motions of the probe reflecting the presence of two distinct types of water are observed: the more viscous LDL form and the more fluid HDL.
The report of Nilsson and coworkers (1) offers key experimental evidence on the long-standing issue of the existence of the two liquid phases in bulk water. These authors demonstrate that the density difference contrast measured in small-angle X-ray scattering (SAXS) is due to large length scale fluctuations between tetrahedral and hydrogen-bond distorted structures related to the low- and high-density water, respectively. Directly from SAXS and spectroscopic information it is inferred that the water structure is due to a temperature-dependent fluctuating equilibrium between the two types of local structure driven by enthalpy minimization (HB tetrahedral-like network) and maximizing entropy (disorder and distorted HB). In addition, differences in these HB structures, typical of the deeply supercooled regime, remain in bulk water even at ambient condition.
The importance of the physical scenario presented by Nilsson and coworkers (1) is twofold. It confirms the existance of water polymorphism and, being defined on density fluctuations concepts, also confirms and highlights the role of the physical quantities related with the concept of the Widom line, demonstrating that the corresponding temperature TW(P) marks, on decreasing T at constant pressure, the crossover from a predominance of an “HDL-like” local structure to a predominance of an “LDL-like” local structure.
It must be stressed that the entire picture present in ref. 1 is consistant with the findings on the dynamical properties of water obtained in previous experiments on confined water (9, 16–20) and in molecular dynamics simulation studies in bulk (14, 15) and also supports the suggestion that the explanation of some water anomalies can be obtained by considering that TW(P) is the locus of the maxima in the thermodynamic response functions. In particular, these properties, just on crossing of the Widom line, TW(P) ≃ 225 K, are as follows:
the observation of the predominance of LDL on the HDL local structure (18, 21),
local maxima in the configurational specific heat (23) and in the absolute value of the thermal expansion coefficient (19, 20).
Scattering methods show the existence of a density minimum in both D2O and H2O, at about 200 K (19, 20). The recent molecular dynamics study on the appearance of the fractional Stokes–Einstein relation in water shows that this phenomenon arises from a specific change in the local water structure and confirms that, as clearly stated in the study by Nilsson et al. (1), the LDL-like local structure persists also at ambient conditions (21).
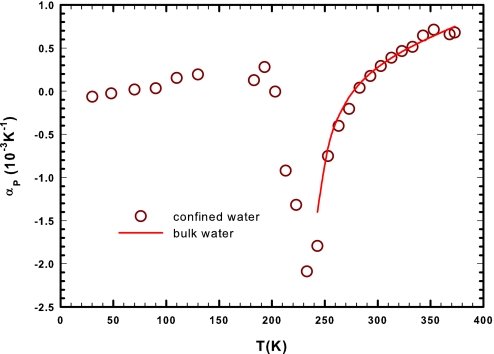
In the context of the water anomalies, the dynamical scenario dominated by large-scale fluctuations in the water correlation functions, as proposed by Nilsson and coworkers (1), can be the clue of their explanation. NMR experiments show a maximum in the water configurational heat capacity just at TW, whereas the density (characterized by the well-known maximum at 277 K and a minimum at about 200 K) has at this temperature (225 K) its flex point reflecting the change in population between the two liquid water phases. Furthermore, from the measured densities, we find that a quantity related to the cross-correlation between the entropy and volume fluctuations, αρ = −(∂ln ρ/∂T)P = 〈δSδV〉/kBTV shows a well-defined minimum at TW (Fig. 2). Thus, the thermal behavior of the two quantities, CP and |αρ|, explains water anomalies, showing that the thermodynamic response functions are characterized by large-scale fluctuations rather than diverging behaviors.
Fig. 2.
The thermal expansion coefficient αρ measured in confined water. The red line is the same quantity obtained from the bulk water density.
Footnotes
The author declares no conflict of interest.
See companion article on page 15214.
References
- 1.Huang C, et al. The inhomogeneous structure of water at ambient conditions. Proc Natl Acad Sci USA. 2009;106:15214–15218. doi: 10.1073/pnas.0904743106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Angell CA. Supercooled water. In: Franks F, editor. Water: A Comprehensive Treatise. Vol 7. New York: Plenum; 2008. pp. 1–81. [Google Scholar]
- 3.Mishima O, Stanley HE. The relationship between liquid, supercooled and glassy water. Nature. 1998;396:329–334. [Google Scholar]
- 4.Debenedetti PG, Stanley HE. Supercooled and glassy water. Phys Today. 2003;56(6):40–46. [Google Scholar]
- 5.Speedy RJ. Stability-limit conjecture. An interpretation of the properties of water. J Phys Chem. 1982;86:982–991. [Google Scholar]
- 6.Stanley HE, Teixeira J. Interpretation of the unusual behavior of H2O and D2O at low temperatures: Tests of a percolation model. J Chem Phys. 1980;73:3404–3422. [Google Scholar]
- 7.Poole PH, Sciortino F, Essmann U, Stanley HE. Phase behaviour of metastable water. Nature. 1992;360:324–328. [Google Scholar]
- 8.Soper AK, Ricci MA. Structures of high-density and low-density water. Phys Rev Lett. 2000;84:2881–2884. doi: 10.1103/PhysRevLett.84.2881. [DOI] [PubMed] [Google Scholar]
- 9.Liu L, et al. Pressure dependence of fragile-to-strong transition and a possible second critical point in supercooled confined water. Phys Rev Lett. 2005;95:117802. doi: 10.1103/PhysRevLett.95.117802. [DOI] [PubMed] [Google Scholar]
- 10.Poole PH, Sciortino F, Grande T, Stanley HE, Angell CA. Effect of hydrogen bonds on the thermodynamic behavior of liquid water. Phys Rev Lett. 1994;73:1632–1635. doi: 10.1103/PhysRevLett.73.1632. [DOI] [PubMed] [Google Scholar]
- 11.Borick SS, Debenedetti PG, Sastry S. A lattice model of network-forming fluids with orientation-dependent bonding: Equilibrium, stability, and implications for the phase behavior of supercooled water. J Phys Chem. 1995;99:3781–3793. [Google Scholar]
- 12.Mishima O, Calvert LD, Whalley E. ‘Melting ice’ I at 77 K and 10 kbar: A new method of making amorphous solids. Nature. 1984;310:393–395. [Google Scholar]
- 13.Mishima O, Calvert LD, Whalley E. An apparently first-order transition between two amorphous phases of ice induced by pressure. Nature. 1985;314:76–78. [Google Scholar]
- 14.Xu LM, et al. Relation between the Widom line and the dynamic crossover in systems with a liquid–liquid phase transition. Proc Natl Acad Sci USA. 2005;102:16558–16562. doi: 10.1073/pnas.0507870102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kumar P, et al. Relation between the Widom line and the breakdown of the Stokes–Einstein relation in supercooled water. Proc Natl Acad Sci USA. 2007;104:9575–9579. doi: 10.1073/pnas.0605880103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mallamace F, et al. The fragile-to-strong dynamic crossover transition in confined water: Nuclear magnetic resonance results. J Chem Phys. 2006;124:161102. doi: 10.1063/1.2193159. [DOI] [PubMed] [Google Scholar]
- 17.Chen S-H, et al. The violation of the Stokes–Einstein relation in supercooled water. Proc Natl Acad Sci USA. 2006;103:12974–12978. doi: 10.1073/pnas.0603253103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mallamace F, et al. Evidence of the existence of the low-density liquid phase in supercooled, confined water. Proc Natl Acad Sci USA. 2007;104:424–428. doi: 10.1073/pnas.0607138104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dazhi L, et al. Observation of the density minimum in deeply supercooled confined water. Proc Natl Acad Sci USA. 2007;104:9570–9574. [Google Scholar]
- 20.Mallamace F, et al. The anomalous behavior of the density of water in the range 30 K < T < 373 K. Proc Natl Acad Sci USA. 2007;104:18387–18391. doi: 10.1073/pnas.0706504104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Banerjee D, Bhat SN, Bhat SV, Leporini D. ESR evidence for 2 coexisting liquid phases in deeply supercooled bulk water. Proc Natl Acad Sci USA. 2009;106:11448–11453. doi: 10.1073/pnas.0900734106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Xu L, et al. Appearance of a fractional Stokes–Einstein relation in water and a structural interpretation of its onset. Nat Phys. 2009;5:565–569. [Google Scholar]
- 23.Mallamace F, et al. NMR evidence of a sharp change in a measure of local order in deeply supercooled confined water. Proc Natl Acad Sci USA. 2008;105:12725–12729. doi: 10.1073/pnas.0805032105. [DOI] [PMC free article] [PubMed] [Google Scholar]