The inhomogeneous structure of water at ambient conditions

Abstract

Small-angle X-ray scattering (SAXS) is used to demonstrate the presence of density fluctuations in ambient water on a physical length-scale of ≈1 nm; this is retained with decreasing temperature while the magnitude is enhanced. In contrast, the magnitude of fluctuations in a normal liquid, such as CCl₄, exhibits no enhancement with decreasing temperature, as is also the case for water from molecular dynamics simulations under ambient conditions. Based on X-ray emission spectroscopy and X-ray Raman scattering data we propose that the density difference contrast in SAXS is due to fluctuations between tetrahedral-like and hydrogen-bond distorted structures related to, respectively, low and high density water. We combine our experimental observations to propose a model of water as a temperature-dependent, fluctuating equilibrium between the two types of local structures driven by incommensurate requirements for minimizing enthalpy (strong near-tetrahedral hydrogen-bonds) and maximizing entropy (nondirectional H-bonds and disorder). The present results provide experimental evidence that the extreme differences anticipated in the hydrogen-bonding environment in the deeply supercooled regime surprisingly remain in bulk water even at conditions ranging from ambient up to close to the boiling point.

Liquid water shows many anomalies in its thermodynamic properties such as compressibility, density variation and heat capacity (1–4). In the low-temperature regime, below the freezing point, these properties deviate strongly from normal and theories, related to a liquid–liquid phase transition between high and low density water, have been proposed to account for these anomalies (5). Although the anomalies are extreme in the supercooled region they are also present at ambient conditions where most of waters' physical, chemical and biological processes of importance occur. In contrast, water at ambient conditions has traditionally been considered as a homogeneous distribution of near-tetrahedral hydrogen-bonded (H-bonded) structures with thermal fluctuations increasing with temperature. This picture has been challenged by recent studies based on X-ray Raman (XRS) and conventional X-ray absorption spectroscopy (XAS) (6), and X-ray emission spectroscopy (XES) (7), suggesting two distinct local structures with tetrahedral as a minority and a highly hydrogen-bond (H-bond) distorted asymmetrical as the majority. In particular the proposed predominant asymmetrical structure has caused intense debate in the last years (see refs. 7 and 8 for detailed discussion).

SAXS and small-angle neutron scattering (SANS) provide the most direct probes of density variations or fluctuations on large length scales in a liquid. Through an enhancement of the structure factor at low momentum transfer, Q, small deviations from the average electron density at different length scales can be reliably identified (9). Previous SAXS studies of water have mostly focused on the supercooled region and given contradictory results where both positive (10–12) and zero enhancement (13, 14) at low Q have been reported. With the development of third-generation synchrotron light sources the ability to perform SAXS has been greatly advanced and measurements can now be performed in a large Q-range with high accuracy and reproducibility (15).

Results

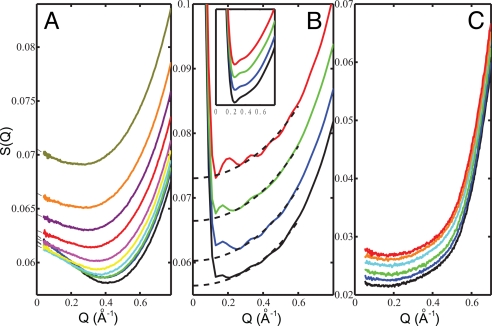
Fig. 1A shows the normalized structure factor, S(Q), derived from the SAXS intensity in ambient water (H₂O) as function of Q for temperatures from 7 to 74 °C in the full Q-range of interest, 0.04–0.78 Å⁻¹ (see SI Methods). All scattering curves show an enhancement approaching Q = 0 after experiencing a minimum ≈0.4–0.5 Å⁻¹, which to first approximation directly indicates the presence of density heterogeneities. In particular, the enhancement becomes smaller with increasing temperature in strong contrast to expectation from simple thermal density fluctuations.

Fig. 1.

SAXS results for ambient and CCl₄ liquid compared with SPC/E MD simulations. (A) Experimental structure factor, S(Q), derived from small angle water scattering intensity as function of scattering momentum transfer Q. The curves, from bottom to top, correspond to increasing temperatures 7, 11, 16, 20, 25, 29, 38, 47, 56, and 74 °C. The extrapolations of scattering intensity to zero-scattering angle using a second order polynomial fit at low Q are represented by dashed lines. (B) The oxygen–oxygen partial structure factor S(Q) for 5, 25, 47, and 67 °C water derived from the SPC/E model using a simulation box containing 40,000 molecules and run for 300–440 ps to reduce artificial oscillations. The mathematical properties of the FT from r to Q space prohibit observation of the behavior below Q = 0.13 Å⁻¹ when using a box size of 106 Å. (Inset) Simulated S(Q) for ambient water from a simulation containing 5,000 water molecules run for 2 ns demonstrating the disappearance of oscillations with extended averaging; the lowest Q accessible is here 0.25 Å⁻¹. The dashed lines indicate smooth curves where the anticipated effects of the box size and limited simulation time are removed. Note the scale of S(Q) in B is larger than that in A due to steeper monotonically decaying curves for the SPC/E water compared with the experimental data. (C) Experimental S(Q) of CCl₄ liquid as function of Q. The curves, from bottom to top, correspond to increasing temperatures 6, 11, 16, 21, 25, and 30 °C.

To address whether the enhancement at low Q can be related to and reproduced by thermal fluctuations in common water models, we have performed molecular dynamics (MD) simulations using the extended simple point charge (SPC/E) potential (see SI Methods). The SAXS signal at low Q is given by the Fourier transform (FT) of the longer intermolecular correlations in real space from the simulation. To model SAXS data it is thus essential to use large simulation boxes (here 40,000 molecules) and also to average over long simulation runs (here longer than 0.3 ns) to reduce artificial oscillations in Q space. Fig. 1B shows the SPC/E oxygen–oxygen partial structure factor, S(Q) (see SI Methods). The finite size of the simulation box causes a sharp artificial increase at Q < 0.13 Å⁻¹ in the FT. The Inset shows the results for smaller simulation boxes with 5,000 molecules, where it was possible to average over significantly longer simulation times (2 ns) resulting in smoother curves, but with the FT artificial increase occurring already at Q = 0.25 Å⁻¹ due to the smaller box size. The most important scattering enhancement observed at small Q in the experiment is completely missing from the SPC/E data even down to Q = 0.13 Å⁻¹. For comparison, Fig. 1C shows S(Q) of CCl₄ measured at temperatures from 6 to 30 °C (see SI Methods) and regarded as representing a “normal” liquid. It is clear that SAXS of CCl₄ shows no temperature-dependent variation at low Q, which is observed, in contrast, in the ambient water as shown in Fig. 1A. Furthermore, the Q dependence from the SPC/E simulation is closer to the experimental data for CCl₄ than for water demonstrating that the observed enhancement of the SAXS signal at low Q for water is not due to normal thermal fluctuations as obtained from standard MD simulations.

Extrapolating the structure factor in Fig. 1A to Q = 0 (dashed curves) by means of a second order polynomial fit to the experimental S(Q) in the range Q = 0.04–0.2 Å⁻¹ we can relate to the isothermal compressibility, χ_T, of water at each temperature (16) via the thermodynamical relation

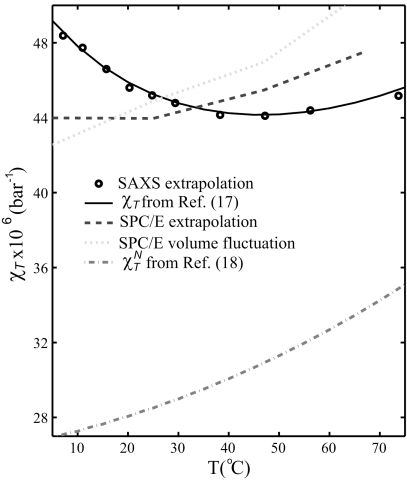
where k_B is the Boltzmann constant, T is the absolute temperature, and n is the molecular number density. We verify our SAXS data and extrapolation by comparing in Fig. 2χ_T derived from the present SAXS data with χ_T from an earlier study (17) measuring the velocity of sound in water; an absolute agreement is observed, confirming the quality of our data and that the density heterogeneities are related to fluctuations in the H-bonded network. If we also extrapolate the 40,000 molecules SPC/E simulations to Q = 0, we determine χ_T as a function of temperature (Fig. 2) and find instead a linear relationship indicative of normal liquid behavior (3, 18, 19), i.e., without the minimum at 46 °C and increase at lower temperatures. Consistent results are obtained using an alternative estimation of χ_T from volume fluctuations in the NPT ensemble in SPC/E simulations run for 12 ns with 7 ns equilibration time, which exhibit a similar trend with temperature as a previous estimation using the NVT ensemble (20). This directly demonstrates that density fluctuations existing in a standard water model such as SPC/E do not reproduce the observed density heterogeneities that the experimental SAXS and isothermal compressibility data clearly indicate. In Fig. 2 we also compare the SPC/E results with the contribution of normal liquid behavior of water to the isothermal compressibility, as estimated from ref. 18, and find a similar temperature dependence albeit shifted in absolute value. It is thus clear that the observed fluctuations in ambient water should be different from random thermal motion and instead similar to what has been discussed in the supercooled regime (10–12).

Fig. 2.

Isothermal compressibility of water, χ_T, derived by extrapolating measured S(Q) at Q = 0.04–0.2 Å⁻¹ to Q = 0 Å⁻¹ (dots) compared with a previous experimental dataset determined from the sound velocity in water (17) (full line). Estimated χ_T from the SPC/E simulations (NVT ensemble) based on an extrapolation of S(Q) to Q = 0 Å⁻¹ for the 40,000 molecule model (dashed line) and direct estimation of χ_T for SPC/E simulations in the NPT ensemble equilibrated 7 ns and sampled over 5 ns (dotted line). The normal contribution of the isothermal compressibility, χ_T^N, extracted from a previous experimental dataset determined by the sound velocity in water–ethanol mixtures (18).

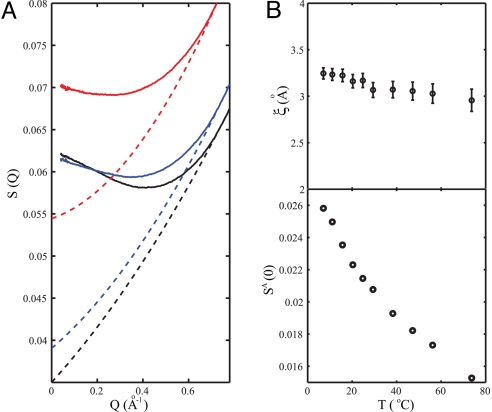
To gain further insight we analyze the SAXS data within the framework of Ornstein-Zernicke (OZ) theory (21) assuming the density fluctuations to result from the presence of either a spinodal (22) or critical point (5). To apply the OZ theory we follow Conde et al. (18) and Kanno and Angell (19) and decompose the total scattering structure factor S(Q) into a part S^N(Q) associated with “normal liquid” behavior and an anomalous part S^A(Q) associated with critical phenomena. We assume that the “normal liquid” part of the scattering factor at Q = 0, S^N(0), is given by Conde's normal contribution to the isothermal compressibility, χ_T^N (see Fig. 2) via Eq. 1. We further assume that the high Q region (>0.7 Å⁻¹) lacks an anomalous contribution because it is dominated by near-neighbor scattering. Based on this we represent S^N(Q) by a second order polynomial fitted to S^N(0) and all data points between Q = 0.74–0.78 Å⁻¹, as shown in Fig. 3A. The anomalous component S^A(Q) is then obtained as the difference between the experimental data and the thus estimated S^N(Q).

Fig. 3.

Ornstein-Zernicke (OZ) analysis of SAXS results of ambient water. (A) The estimation of “normal liquid” contributions, S^N(Q)(dashed lines), to the total scattering factor, S(Q)(solid lines), at 7 (black), 25 (blue) and 74 °C (red) by using the method described in the text, i.e., S^N(Q) is derived by fitting S(Q) between Q = 0.74–0.78 Å⁻¹ and S^N(0) using a second order polynomial function. (B) (Upper) OZ correlation length ξ defined in Eq. 2 as function of temperature. (Lower) The derived S^A(0) as function of temperature.

Within the OZ framework, the anomalous part is described by

where ξ is the correlation length defined in the OZ theory and c depends on temperature but not on Q (21). To derive ξ we fitted S^A(Q) between Q = 0.04–0.19 Å⁻¹ with results plotted in Fig. 3B Upper as function of temperature; the OZ correlation length is ≈3.1 Å, slowly decreasing with increasing temperature. The zero-angle anomalous structure factor, S^A(0) = cξ², is, however, found to decrease more dramatically with temperature as shown in Fig. 3B Lower.

X-ray spectroscopies give further insight into the character of the density heterogeneities indicated by SAXS. In both XES (7) and XRS (6) it has recently been shown that there are temperature-dependent spectral changes that can be connected to the H-bonded environment. XRS corresponds to transitions from a core level to unoccupied states, while XES measures the decay from an occupied valence state to an emptied (excited) core level with the emission of an X-ray photon. Although the valence electrons are delocalized in a condensed phase, the involvement of the core level makes both XRS and XES very local probes of the electronic structure (23). Furthermore, the attosecond time scale of the XRS excitation process and the O 1s life time of ≈4 fs in XES (24) are much shorter than the 1–2 ps typical for H-bond dynamics (25).

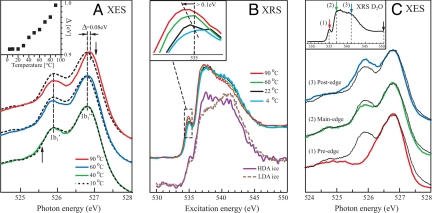
The focus for our discussion will be how the experimental XES and XRS spectra of water vary with temperature and how the energy position of the spectral features relates to similar features in water vapor and ice. Fig. 4A shows the temperature dependence in the lone pair 1b₁ region of the XES spectra for D₂O (see SI Methods); using the heavier isotope minimizes core-hole induced dynamical effects on the spectral line shape (7, 26). All spectra show a split of the lone pair into two peaks, in ref. 7 denoted 1b′₁ and 1b″₁, where the former is close in energy position to the 1b₁ in crystalline ice and the latter to 1b₁ in water vapor. The two peaks can thereby be related to tetrahedral (1b′₁) and H-bond distorted (1b″₁) local structures with further support for this assignment given below. Fig. 4B Upper part shows the temperature-dependent XRS spectra with higher energy resolution (0.5 eV) (see SI Methods) compared with earlier studies (6). The spectral features in XRS and XAS of liquid water and ice have been denoted pre-edge (535 eV), main-edge (537–538 eV) and postedge (540–541 eV) (6). Crystalline ice exhibits a strong postedge whereas gas phase water has nearly all of the intensity in the pre- and main-edge regions (27).

Fig. 4.

XES/XRS spectra of ambient water and amorphous ice. (A) The lone pair 1b₁ region of the O 1s soft X-ray emission spectra of liquid D₂O at 10, 40, 60 and 90 °C using a nonresonant excitation energy of 550 eV. The positions of the corresponding 1b₁ state of crystalline ice (525.6 eV) and gas phase water (527 eV) are indicated with arrows (7). The two lone pair peaks in liquid water are denoted, respectively, 1b′₁, close to the corresponding position in crystalline ice, and 1b″₁, close to gas phase water. The 1b′₁ peak position is independent of temperature whereas the 1b″₁ shifts toward higher energy with increasing temperature. The spectra were normalized to give the same 1b″₁ peak height. (Inset) Energy difference between the 1b″₁ and 1b′₁ peaks as function of temperature. (B) (Upper) X-ray Raman scattering spectra of liquid H₂O at 4, 22, 60 and 90 °C normalized to have the same area. (Inset) Magnification of the pre-edge (535 eV) spectral feature indicating a shift toward lower energy with increasing temperature. (Lower) XRS spectra of LDA and HDA ice from ref. 33. (C) X-ray emission spectra at various excitation energies (full lines) compared with nonresonant excitation (dashed lines) at 550 eV of D₂O water at 25 °C. (Inset) XRS spectrum of D₂O with arrows marking the corresponding excitation energies. Note that the pre-edge excited spectrum has been shifted by 0.45 eV to compensate for the spectator shift of a localized excited intermediate state (7).

We use energy-selective excitation to make a connection between the two X-ray spectroscopies. The XES spectra shown in Fig. 4A were all taken with excitation at 550 eV, well beyond the region with structure-dependent spectral features in the absorption spectrum. Tuning instead the energy to the specific resonant features (pre-, main- and postedge) in the absorption spectrum makes a connection between the two X-ray spectroscopies by selecting the corresponding structural species for XES (7). This is shown in Fig. 4C where resonant XES spectra are compared with nonresonant (550 eV) XES. Normalizing the intensities to the 1b″₁ (distorted) peak, we find that pre-edge excitation essentially eliminates the 1b′₁ (tetrahedral) peak (red), excitation on the main edge gives a slight enhancement of the 1b″₁ (distorted) (green), whereas excitation on the postedge instead enhances the 1b′₁ (tetrahedral) peak compared with the 1b″₁ (blue). Because the absorption postedge feature in ice is much stronger than in the liquid (6), the resonant XES (blue) is consistent with that the 1b′₁ peak is related to tetrahedral-like species. The pre-edge peak in XRS has, however, been assigned to distorted H-bonding configurations (6, 27–31). This assignment is consistent with the observed absence of the 1b′₁ (tetrahedral) and the strong enhancement of the 1b″₁ (distorted) peak when resonantly exciting on the pre-edge feature (red).

The assignment is furthermore fully consistent with the experimentally observed temperature dependence of both XRS and XES: In XRS, the postedge decreases and the pre-edge increases with increasing temperature (see Fig. 4B), similar to the postedge-associated 1b′₁ converting to the preedge-associated 1b″₁ in XES. Hence, both XES and XRS indicate in a consistent manner that water consists of two distinct, interconverting structural species in a ratio that depends on temperature. This is also within the range of possible structures that X-ray and neutron diffraction data allow, as shown in a recent analysis using reverse Monte Carlo modeling (32).

There is another important temperature effect in the XES and XRS spectra indicating changes beyond the interconversion of the two structural species. Both the 1b″₁ (distorted) peak in XES (Fig. 4A) and the related pre-edge feature in XRS (Fig. 4B) shift toward their respective gas phase position with increasing temperature whereas neither the 1b′₁ (tetrahedral) in XES nor the broad postedge feature in XRS shows measurable changes in energy position. This implies that the distorted structural species successively become more distorted with increasing temperature through thermal excitation whereas the tetrahedral-like species do not significantly change their H-bonding. Consequently, a variation in the relative stability of the two structures with temperature is expected.

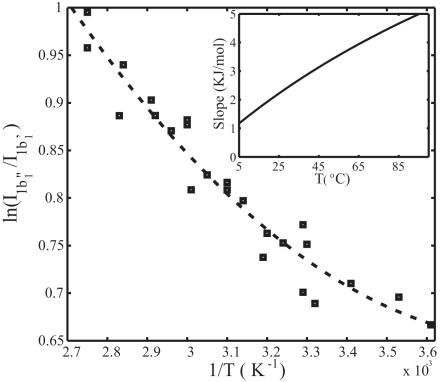
We fitted the XES spectra at each temperature into two spectral components to obtain the intensity ratio I_1b1″/I_1b1′ between distorted and tetrahedral structures; at 25 °C we obtain 2.5 ± 0.5 where the error bar is mainly due to systematic shifts based on different assumptions on the line shapes (see ref. 7 for detailed description). If the energy (ΔΕ) and entropy (ΔS) differences do not depend on temperature, an Arrhenius behavior is expected, i.e., a plot of the ratio, ln(I_1b1″/I_1b1′), between the contributions from the two structural components to the XES spectra versus the inverse temperature (1/T), should give a straight line with the average energy difference (ΔΕ) obtained from the slope:

Fig. 5 plots ln(I_1b1″/I_1b1′) versus the inverse temperature (1/T), where the derivative of the fitted curve is shown in the Inset. We note that the data do deviate from a straight line, indicating that ΔΕ and ΔS vary with temperature between the two local structures. Because the tetrahedral structure in both XES and XRS shows little spectral change with temperature we can assume that the ΔΕ and ΔS variation are mainly attributable to changes of the distorted structure. The conversion of tetrahedral-like to distorted with temperature shows that the tetrahedral-like component is of lower energy. The shifting of 1b″₁ position in XES and the pre-edge in XRS with temperature indicate an increase in entropy of the distorted component as it becomes thermally excited. All of these observations are consistent with that the tetrahedral structure is of lower energy - lower entropy and the distorted structure of higher energy–higher entropy.

Fig. 5.

Plot of the logarithm of the intensity ratio between the fitted XES spectra of 1b″₁ and 1b′₁ versus the inverse temperature, 1/T. The dashed line is a guide to the eye, where the slope is not constant. The slope is shown versus temperature in Inset.

A recent XRS study of ambient water and high density (HDA) and low density amorphous ice (LDA) identified similarities in the liquid water spectrum with that of HDA ice (33) (see Fig. 4B Lower). Based on these spectra it can be hypothesized that the H-bond distorted structure, which dominates liquid water at ambient conditions, corresponds to a thermally excited and volume expanded HDA phase whereas the tetrahedral-like structures are related to LDA. The LDA spectrum can be linked to the tetrahedral structure in water through the strong postedge seen in XRS on LDA ice and through the low energy XES 1b′₁ component in water with energy position close to that of crystalline ice (see Fig. 4A).

Discussion and Conclusions

We analyze further the density fluctuations in the SAXS data in terms of the picture indicated by XES and XRS, namely that, on the time scale of X-ray scattering, the liquid can be viewed as tetrahedral patches surrounded by thermally excited H-bond distorted structures. Although we lack information on the time scale of the fluctuations, the attosecond interaction time of the X-ray scattering process, compared with picoseconds for H-bond dynamics, allows considering the SAXS data as an instantaneous snapshot of the structure. Because we do not detect any major contribution of intermediate structures in neither the XES nor the XRS data we make the simple approximation that the SAXS intensities are mainly connected with a density difference contrast between the two structural species seen as static on the ultrashort time scale of the scattering process. Consequently, we infer a physical picture of the derived OZ correlation length ξ (Fig. 3B Upper) in terms of the radius of gyration, R_G, defined in the Guinier analysis developed for static macroparticle scattering (9). The relationship R_G = $\sqrt{3}$ξ (34) gives R_G decreasing from 5.6 at 7 °C to 5.1 Å at 74 °C. To get a sense of the physical dimensions of the tetrahedral patches we assume a spherical shape giving a diameter, D, of 14.5–13.2 Å by using the relationship D = 2$\sqrt{5/3}$R_G (35). In an earlier light-scattering measurement providing Raman density of states (36), a cross-over frequency between the phonon and fracton regimes has been observed, suggesting the existence of low-density water patches of dimension ≈10–14 Å at 22 °C, similar to the present result.

We can conclude the following experimental observations: On the time scale of the scattering and spectroscopic processes two local structural species coexist with tetrahedral-like patches of dimension of order 1 nm in dynamic equilibrium with H-bond distorted and thermally excited structures. Both the characteristic dimension based on SAXS and the local structure of the tetrahedral-like component based on XES/XRS are relatively insensitive to temperature whereas that of the H-bond distorted component continuously changes as it becomes thermally excited and expands, leading to loss of contrast in SAXS (Fig. 3B Lower). Combining the SAXS and spectroscopy information we infer that the tetrahedral-like patches form as low energy-low entropy structures of lower density than the average of the liquid. The higher density, thermally excited H-bond distorted structure, however, is a high entropy structure where the higher density compensates the loss of enthalpy through a larger number of, but less specific, H-bond interactions.

The picture of ambient water presented here contains many similarities to models describing the anomalies of supercooled water based on a liquid–liquid phase transition between high and low density water (2, 4, 5). The current experimental results indicate that the liquid–liquid transition affects a larger neighborhood in the P-T phase diagram than anticipated, surprisingly extending far into the ambient regime creating an inhomogeneous fluctuating structure. In particular, the domination of the distorted structure in the liquid can be understood because high-density water is on the ambient side of the phase separation, or Widom line (37, 38) (defined as an extension of the coexistence line between low- and high-density liquid in the “one-phase region” for the second critical point scenario (5)), whereas the tetrahedral structure is on the low-temperature side. This is in line with the similar line shape seen in XRS between HDA and water at ambient conditions as shown in Fig. 4B (33) and the observation using infrared spectroscopy of a low density liquid phase in supercooled confined water at temperatures below the Widom line (39). It can furthermore be linked to the previous, much discussed Wernet et al. study (6), because even at room temperature the dominating high-density high-entropy structure can be expected to be highly thermally excited. This would result in much larger H-bond distortions for the distorted than for the tetrahedral component of the liquid, as suggested for the asymmetric species proposed in that study.

The detailed structure of the two types of species reported in the present work and the time scale on which these fluctuations exist, creating temperature-dependent density and structural heterogeneities even in ambient liquid water, are not yet precisely determined, however.

Materials and Methods

The SAXS experiments were performed at beamline 4-2 at the Stanford Synchrotron Radiation Lightsource (SSRL) using a beam energy of 11 keV. A quantum mechanically calculated molecular scattering factor of an isolated water molecule (40) was used to separate S(Q) from the total scattering intensity. The XRS experiments were performed at beamline 6–2 at SSRL, equipped with a Si (311) double crystal monochromator and the Raman scattering was analyzed using 14 Si (440) analyzer crystals selecting 6.46 keV photons with a resolution of ≈0.3 eV and momentum transfers of Q = 2.6 ± 1 Å⁻¹. The O 1s XES measurements (7) were performed with a total energy resolution of 0.35 eV at BL17SU at SPring-8, Japan. Detailed description of the experimental and computational methods is described in the SI Methods.