Summary
With scientific data available at geocoded locations, investigators are increasingly turning to spatial process models for carrying out statistical inference. Over the last decade, hierarchical models implemented through Markov chain Monte Carlo methods have become especially popular for spatial modelling, given their flexibility and power to fit models that would be infeasible with classical methods as well as their avoidance of possibly inappropriate asymptotics. However, fitting hierarchical spatial models often involves expensive matrix decompositions whose computational complexity increases in cubic order with the number of spatial locations, rendering such models infeasible for large spatial data sets. This computational burden is exacerbated in multivariate settings with several spatially dependent response variables. It is also aggravated when data are collected at frequent time points and spatiotemporal process models are used. With regard to this challenge, our contribution is to work with what we call predictive process models for spatial and spatiotemporal data. Every spatial (or spatiotemporal) process induces a predictive process model (in fact, arbitrarily many of them). The latter models project process realizations of the former to a lower dimensional subspace, thereby reducing the computational burden. Hence, we achieve the flexibility to accommodate non-stationary, non-Gaussian, possibly multivariate, possibly spatiotemporal processes in the context of large data sets. We discuss attractive theoretical properties of these predictive processes. We also provide a computational template encompassing these diverse settings. Finally, we illustrate the approach with simulated and real data sets.
Keywords: Co-regionalization, Gaussian processes, Hierarchical modelling, Kriging, Markov chain Monte Carlo methods, Multivariate spatial processes, Space-time processes
1. Introduction
Recent advances in geographical information systems and global positioning systems enable accurate geocoding of locations where scientific data are collected. This has encouraged the formation of large spatiotemporal data sets in many fields and has generated considerable interest in statistical modelling for location-referenced spatial data; see, for example, Cressie (1993), Møller (2003), Banerjee et al. (2004) and Schabenberger and Gotway (2004) for a variety of methods and applications. Here, we focus on the setting where the number of locations yielding observations is too large for fitting desired hierarchical spatial random-effects models. Full inference and accurate assessment of uncertainty often require Markov chain Monte Carlo (MCMC) methods (Banerjee et al., 2004). However, such fitting involves matrix decompositions whose complexity increases as O(n3) in the number of locations, n, at every iteration of the MCMC algorithm: hence the infeasibility or ‘big n’ problem for large data sets. Evidently, the problem is further aggravated when we have a vector of random effects at each location or when we have spatiotemporal random effects.
Approaches to tackle this problem have adopted several different paths. The first seeks approximations for the spatial process by using kernel convolutions, moving averages, low rank splines or basis functions (e.g. Wikle and Cressie (1999), Lin et al. (2000), Higdon (2001), Ver Hoef et al. (2004), Xia and Gelfand (2006), Kammann and Wand (2003) and Paciorek (2007)). Essentially, the process w(s) is replaced by an approximation w̃ (s) that represents the realizations in a lower dimensional subspace. A second approach seeks, instead, to approximate the likelihood either by working in the spectral domain of the spatial process and avoiding the matrix computations (Stein, 1999; Fuentes, 2007; Paciorek, 2007) or by forming a product of appropriate conditional distributions to approximate the likelihood (e.g. Vecchia (1988), Jones and Zhang (1997) and Stein et al. (2004)). A concern is the adequacy of the resultant likelihood approximation. Expertise in tailoring and tuning of a suitable spectral density estimate or a sequence of conditional distributions is required and does not easily adapt to multivariate processes. Also, the spectral density approaches seem best suited to stationary covariance functions. Another approach either replaces the process (random-field) model by a Markov random field (Cressie, 1993) or else approximates the random-field model by a Markov random field (Rue and Tjelmeland, 2002; Rue and Held, 2006). This approach is best suited for points on a regular grid. With irregular locations, realignment to a grid or a torus is required, which is done by an algorithm, possibly introducing unquantifiable errors in precision. Adapting these approaches to more complex hierarchical spatial models involving multivariate processes (e.g. Wackernagel (2003) and Gelfand et al. (2004)), spatiotemporal processes and spatially varying regressions (Gelfand et al., 2003) and non-stationary covariance structures (Paciorek and Schervish, 2006) is potentially problematic.
We propose a class of models that is based on the idea of a spatial predictive process (motivated from kriging ideas). We project the original process onto a subspace that is generated by realizations of the original process at a specified set of locations. The rudiments of our idea appear in Switzer (1989). Our approach is in the same spirit as process model approaches using basis functions and kernel convolutions, i.e. specifications which attempt to facilitate computation. Our version is directly connected to whatever valid covariance structure we seek and is applicable to any class of distributions that can support a spatial stochastic process. We typically use such modelling to describe an underlying process; one that is never actually observed. The modelling provides structured dependence for random effects, e.g. intercepts or coefficients, at a second stage of specification where the first stage need not be Gaussian.
Our objectives differ from Gaussian process regressions for large data sets in machine learning (see, for example, Wahba (1990), Seeger et al. (2003) and Rasmussen and Williams (2006)), where the regression function is viewed as a Gaussian process realization centred on some mean function with a conditionally independent Gaussian model for the data given the regression function. Assuming known process and noise parameters and a large training set, the Gaussian posterior will exhibit the big n problem. Recently, Cornford et al. (2005) turned this machinery to geostatistics. In all of the above, explicit forms for Bayesian prediction (‘kriging’ in the last case) and the associated posterior variance are utilized. However, we are interested in full posterior inference associated with spatiotemporal hierarchical models and parameters therein. Full Bayesian inference would most probably employ MCMC methods (Robert and Casella, 2005), an approach that has been dismissed in the machine learning literature (see, for example, Cornford et al. (2005)). In this sense our current work is more ambitious in its spatial modelling and inferential objectives.
We illustrate with two simulated examples yielding rather complex spatial random fields and with a challenging spatially adaptive regression model fitted to forest biomass data. Section 2 introduces and discusses the predictive process models as well as relevant specification issues. Section 3 considers extensions to multivariate process models. Section 4 describes Bayesian computation issues and Section 5 presents the two examples. Section 6 concludes with a brief discussion including future work.
The programs that were used to analyse the data can be obtained from http://www.blackwellpublishing.com/rss
2. Univariate predictive process modelling
2.1. The customary univariate model
Geostatistical settings typically assume, at locations s ∈ D ⊆ℜ2, a response variable Y(s) along with a p × 1 vector of spatially referenced predictors x(s) which are associated through a spatial regression model such as
| (1) |
i.e. the residual comprises a spatial process w(s), capturing spatial association, and an independent process ε(s), which is often called the nugget. The w(s) are spatial random effects, providing local adjustment (with structured dependence) to the mean, interpreted as capturing the effect of unmeasured or unobserved covariates with spatial pattern.
The customary process specification for w(s) is a mean 0 Gaussian process with covariance function, C(s, s′), which is denoted GP{0, C(s, s′)}. In applications, we often specify C(s, s′) = σ2 ρ(s, s′; θ) where ρ(·; θ) is a correlation function and θ includes decay and smoothness parameters, yielding a constant process variance. In any event, ε(s) ~IIDN(0, τ2) for every location s. With n observations Y = (Y(s1), …, Y(sn))T, the data likelihood is given by Y ~ N(Xβ, ΣY), with ΣY = C(θ) + τ2In, where is a matrix of regressors and . Likelihood-based inference proceeds through maximum likelihood or restricted maximum likelihood methods (e.g. Schabenberger and Gotway (2004)).
With hierarchical models, we assign prior distributions to Ω= (β, θ, τ2) and inference proceeds by sampling from p(Ω|Y), whereas prediction at an arbitrary site s0 samples p{Y(s0)|Y} one for one with posterior draws of Ω by composition (Banerjee et al., 2004). This is especially convenient for Gaussian likelihoods since p{Y(s0)|Ω, Y} is itself Gaussian. Evidently, both estimation and prediction require evaluating the Gaussian likelihood: hence, evaluating the n × n matrix . Although explicit inversion is replaced with faster linear solvers, likelihood evaluation remains expensive for big n.
2.2. The predictive process model
We consider a set of ‘knots’
, which may or may not form a subset of the entire collection of observed locations  . The Gaussian process in model (1) yields
, where
is the corresponding m × m covariance matrix. The spatial interpolant (that leads to kriging) at a site s0 is given by w̃(s0) = E[w(s0)|w*] = cT(s0; θ) C*−1(θ)w*, where
. This single-site interpolator, in fact, defines a spatial process w̃(s) ~ GP{0, w̃(·)} with covariance function
. The Gaussian process in model (1) yields
, where
is the corresponding m × m covariance matrix. The spatial interpolant (that leads to kriging) at a site s0 is given by w̃(s0) = E[w(s0)|w*] = cT(s0; θ) C*−1(θ)w*, where
. This single-site interpolator, in fact, defines a spatial process w̃(s) ~ GP{0, w̃(·)} with covariance function
| (2) |
where
. We refer to w̃(s) as the predictive process derived from the parent process w(s). The realizations of w̃(s) are precisely the kriged predictions conditional on a realization of w(s) over  . The process is completely specified given the covariance function of the parent process and
. The process is completely specified given the covariance function of the parent process and 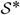 . So, to be precise, we should write w̃
. So, to be precise, we should write w̃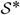 (s), but we suppress this implicit dependence. From equation (2), this process is non-stationary regardless of whether w(s) is. Furthermore, the joint distribution that is associated with the realizations at any set of locations in D is non-singular if and only if the set has at most m locations.
(s), but we suppress this implicit dependence. From equation (2), this process is non-stationary regardless of whether w(s) is. Furthermore, the joint distribution that is associated with the realizations at any set of locations in D is non-singular if and only if the set has at most m locations.
Replacing w(s) in model (1) with w̃(s), we obtain the predictive process model
| (3) |
Since w̃(s) = cT(s)C*−1(θ)w*, w̃(s) is a spatially varying linear transformation of w*. The dimension reduction is seen immediately. In fitting model (3), the n random effects {w(si), i = 1, 2, …, n} are replaced with only the m random effects in w*; we can work with an m-dimensional joint distribution involving only m × m matrices. Evidently, model (3) is different from model (1). Hence, though we introduce the same set of parameters in both models, they will not be identical in both models.
Knot-based linear combinations such as resemble other process approximation approaches. For instance, motivated by an integral representation of (certain) stationary processes as a kernel convolution of Brownian motion on ℜ2, Higdon (2001) proposed a finite approximation to the parent process of the form where uis are independent and identically distributed (IID) N(0, 1) and with k(·; θ) being a Gaussian kernel function. Evidently, Gaussian kernels only capture Gaussian processes with Gaussian covariance functions (see Paciorek and Schervish (2006)). Xia and Gelfand (2006) suggested extensions to capture more general classes of stationary Gaussian processes by aligning kernels with covariance functions. However, the class of stationary Gaussian process models admitting a kernel representation is limited.
The integral representation permits kernel convolution with spatially varying kernels as in Higdon et al. (1999). It can also replace Brownian motion with a stationary Gaussian process on ℜ2. Finite approximations allow replacing the white noise realizations ui with stationary process realizations such as w*. Then, the original realizations are projected onto an m-dimensional sub-space that is generated by the columns of the n × m matrix , where w̃ = Kw*. Alternatively, one could project as w̃ =Zu, where u ~N(0, I), and set to yield the same joint distribution as the predictive process model (3). This approach has been used in ‘low rank kriging’ methods (Kammann and Wand, 2003). We note that we do not want to work with the induced process . It has the induced covariance function cT(s) c(s) but sacrifices properties that we seek below in Section 2.3 (e.g. exact interpolation or Kullback–Leibler (KL) minimization). More general low rank spline models were also discussed in Ruppert et al. (2003), chapter 13, and Lin et al. (2000). Again, we regard the predictive process as a competing model specification with computational advantages, but induced by an underlying full rank process. In fact, these models are, in some sense, optimal projections as we clarify in the next subsection. Also, w̃ (s) does not arise as a discretization of an integral representation of a process and we only require a valid covariance function to induce it.
A somewhat similar reduced rank kriging method has been recently proposed by Cressie and Johannesson (2008). Letting g(s) be a k × 1 vector of specified basis functions on ℜ2, the proposed covariance function is C(s, s′) = g(s)TK g(s′) with K an unknown positive definite k × k matrix that is estimated from the data by using a method-of-moments approach. Such an approach may be challenging for the hierarchical models that we envision here. We shall be providing spatial modelling with random effects at the second stage of the specification. We have no ‘data’ to provide an empirical covariance function.
Lastly, we can draw a connection to recent work in spatial dynamic factor analysis (see, for example, Lopes et al. (2006) and references therein), where K is viewed as an n × m matrix of factor loadings. Neither K nor w* is known but replication over time in the form of a dynamic model is introduced to enable the data to separate them and to infer about them. In our case, the entries in K are ‘known’ given the covariance function C.
2.3. Properties of the predictive process
First, note that w̃(s0) is an orthogonal projection of w(s0) onto a particular linear subspace (e.g. Stein (1999)). Let ℋm+1 be the Hilbert space that is generated by w(s0) and the m random variables in w* (with ℋm denoting the space that is generated by the latter); hence, ℋm+1 comprises all linear combinations of these m + 1 zero-centred, finite variance random variables along with their mean-square limit points. If we seek the element in w̃ (s0) ∈ ℋm that is closest to w(s0) in terms of the inner product norm that is induced by E[w(s) w(s′)], we obtain the linear system , j = 1, …, m, with the unique solution w̃(s0) = cT(s0) C*−1(θ)w*. Being a conditional expectation, it immediately follows that w̃(s0) minimizes E[w(s0) − f(w*)|w*] over all real-valued functions f(w*). In this sense, the predictive process is the best approximation for the parent process.
Also, w̃(s0) deterministically interpolates w(s) over 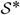 . Indeed, if
we have
. Indeed, if
we have
| (4) |
since
, where ej denotes the vector with 1 in the jth position and 0 elsewhere. So, equation (4) shows that
and
(a property of kriging). At the other extreme, suppose that 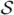 and
and 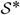 are disjoint. Then w|w* ~ MVN(cT C*−1w*, C − cTC*−1c) where c is the m × n matrix whose columns are the c(si) and C is the n × n covariance matrix of w. We can write w = w̃ + (w − w̃) and the choice of w* determines the (conditional) variability in the second term on the right-hand side, i.e. how close Σw is to Σw̃. It also reveals that there will be less variability in the predictive process than in the parent process as n variables are determined by m < n random variables.
are disjoint. Then w|w* ~ MVN(cT C*−1w*, C − cTC*−1c) where c is the m × n matrix whose columns are the c(si) and C is the n × n covariance matrix of w. We can write w = w̃ + (w − w̃) and the choice of w* determines the (conditional) variability in the second term on the right-hand side, i.e. how close Σw is to Σw̃. It also reveals that there will be less variability in the predictive process than in the parent process as n variables are determined by m < n random variables.
KL-based justification for w̃ (s*) is discussed in Csató (2002) and Seeger et al. (2003). The former offers a general theory for KL projections and proposes sequential algorithms for computations. As a simpler and more direct argument, let us assume that 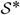 and
and 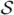 are disjoint and let wa = (w*, w)T be the (m + n) × 1 vector of realizations over
are disjoint and let wa = (w*, w)T be the (m + n) × 1 vector of realizations over  ∪
∪ 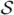 . In model (1), assuming all other model parameters fixed, the posterior distribution for p(wa|Y) is proportional to p(wa) p(Y|w) since p(Y|wa) = p(Y|w). The corresponding posterior in model (3) replaces p(Y|w) with a density q(Y|w*). Letting
. In model (1), assuming all other model parameters fixed, the posterior distribution for p(wa|Y) is proportional to p(wa) p(Y|w) since p(Y|wa) = p(Y|w). The corresponding posterior in model (3) replaces p(Y|w) with a density q(Y|w*). Letting  be the class of all probability densities satisfying q(Y|wa) = q(Y|w*), suppose that we seek the density q ∈
be the class of all probability densities satisfying q(Y|wa) = q(Y|w*), suppose that we seek the density q ∈  that minimizes the reverse KL divergence KL(q, p) = ∫ q log(q/p). In Appendix A we argue that KL{q(wa|Y), p(wa|Y)} is minimized when q(Y|w*) ∝ exp(Ew|w*[log{p(Y|wa)}]). Subsequent calculations from standard multivariate normal theory reveal this to be the Gaussian likelihood corresponding to the predictive process model.
that minimizes the reverse KL divergence KL(q, p) = ∫ q log(q/p). In Appendix A we argue that KL{q(wa|Y), p(wa|Y)} is minimized when q(Y|w*) ∝ exp(Ew|w*[log{p(Y|wa)}]). Subsequent calculations from standard multivariate normal theory reveal this to be the Gaussian likelihood corresponding to the predictive process model.
2.4. Selection of knots
As with any knot-based method, selection of knots is a challenging problem with choice in two dimensions more difficult than in one. Suppose for the moment that m is given. First, in the spline smoothing literature (and in most of the literature on functional data or regression modelling using basis representations), it is customary to place knots at every data point (e.g. Ramsay and Silverman (2005)). This is not an option for us and raises the question of whether to use a subset of the observed spatial locations or a disjoint set of locations. If we use a subset of the sampled locations, should we draw this set at random? If we do not use a subset then we are dealing with a problem that is analogous to a design problem, with the difference being that we already have samples at n locations. There is a rich literature in spatial design which is summarized in, for example, Xia et al. (2006). We need a criterion to decide between a regular grid and placing more knots where we have sampled more. One approach would be a so-called space filling knot selection following the design ideas of Nychka and Saltzman (1998). Such designs are based on geometric criteria, measures of how well a given set of points covers the study region, independent of the assumed covariance function. Stevens and Olsen (2004) showed that spatial balance of design locations is more efficient than simple random sampling. Recently, Diggle and Lophaven (2006) have discussed spatial designs suggesting modification to regular grids. These designs augment the lattice with close pairs or infill. We examine such designs for knot selection in our simulation examples in Section 5.1.1.
To bring in the covariance function, in our setting, since the joint distributions of w and w̃ are both multivariate normal, we might think in terms of using KL distance between these distributions. According to choice, the non-symmetrized distance will involve the covariance matrix of one distribution and the inverse covariance matrix of the other. We cannot obtain the inverse covariance matrix for w and the inverse covariance matrix for w̃ does not exist since the distribution is singular. Moreover, if we try to work with the KL distance for any set of m knots, we have argued above that in this case w and w̃ are the same realization; the KL distance is 0.
In working with kernel convolution approximation, KL distance can be used with any subset of locations because it is not an exact interpolator. In fact, Xia and Gelfand (2005) showed that, working with a regular grid, introduction of a lattice that is larger than the study area is desirable. However, this is justified by the nature of the discrete approximation that is made to an integral representation that is over all of ℜ2. Since the predictive process is not driven by a finite approximation to an integral representation, such expansion does not seem warranted here.
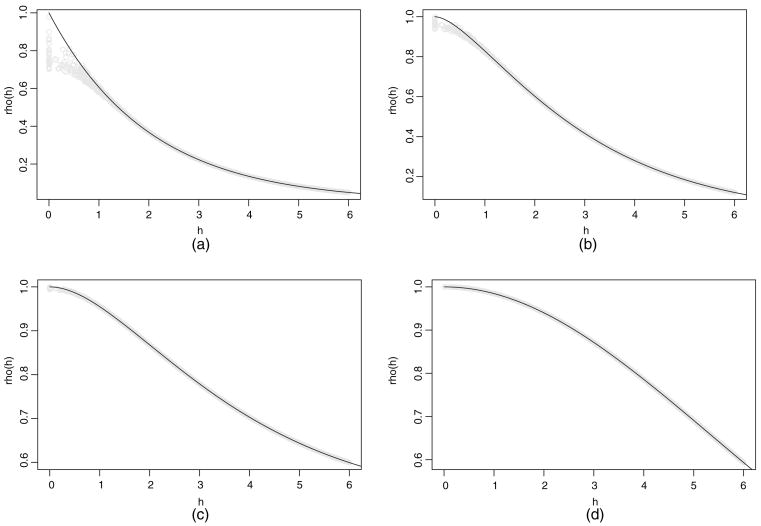
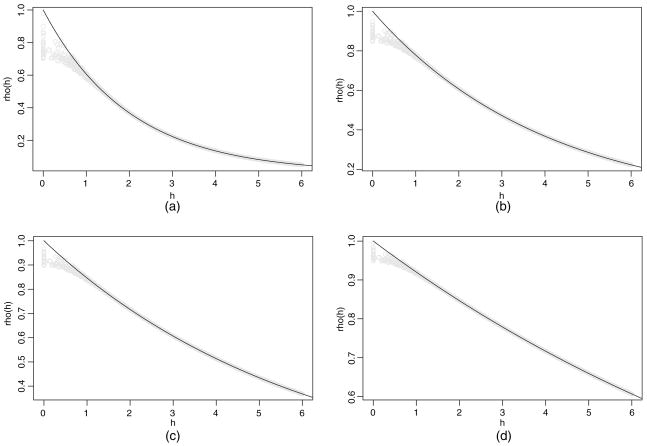
A direct assessment of knot performance is comparison of the covariance function of the parent process with that of the predictive process, given in equation (2) and dependent on 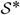 . To illustrate, 200 locations are uniformly generated over a [0, 10] × [0, 10] rectangle. The knots consist of a 10 × 10 equally spaced grid. We employ the Matérn covariance function to make comparisons, setting σ2 = 1 without loss of generality. Fixing the range parameter φ = 2, Fig. 1 overlays the covariances of the parent process and those of the predictive processes for four different values of the smoothness parameter ν. (Covariances for 2000 of the roughly 40 000 distance pairs are plotted for the predictive process.) Alternatively, setting ν = 0.5 (the exponential covariance function), we compare covariances by using four values of the range parameter in Fig. 2.
. To illustrate, 200 locations are uniformly generated over a [0, 10] × [0, 10] rectangle. The knots consist of a 10 × 10 equally spaced grid. We employ the Matérn covariance function to make comparisons, setting σ2 = 1 without loss of generality. Fixing the range parameter φ = 2, Fig. 1 overlays the covariances of the parent process and those of the predictive processes for four different values of the smoothness parameter ν. (Covariances for 2000 of the roughly 40 000 distance pairs are plotted for the predictive process.) Alternatively, setting ν = 0.5 (the exponential covariance function), we compare covariances by using four values of the range parameter in Fig. 2.
Fig. 1.
Covariances of w (s) against distance (——) and covariances of w̃(s) against distance ( ): (a) smoothness parameter 0.5; (b) smoothness parameter 1; (c) smoothness parameter 1.5; (d) smoothness parameter 5
): (a) smoothness parameter 0.5; (b) smoothness parameter 1; (c) smoothness parameter 1.5; (d) smoothness parameter 5
Fig. 2.
Covariances of w (s) against distance (——) and covariances of w̃(s) against distance: (a) range parameter 2; (b) range parameter 4; (c) range parameter 6; (d) range parameter 12
In general, we find that the functions agree better at larger distances and even more so with increasing smoothness and range. There is little additional information in varying m for a given φ and ν. What matters is the size of the range relative to the spacing of the grid for the knots. Indeed, the fact that the comparison is weakest at short distances and is even weaker for shorter ranges merely reflects the fact that observations at the knots will not, in this case, provide much information about dependence for pairs of sites that are very close to each other. With concern about fine scale spatial variation or very short spatial range, a rather dense set of knots may be required (see, for example, Stein (2007)). Then, knot selection incorporating varying density over the domain including a ‘packed’ subset would enable us to inform better about the spatial range and the variance components.
Finally, the choice of m is governed by computational cost and sensitivity to choice. So, in principle, we shall have to implement the analysis over different choices of m. Since we cannot work with the full set of n locations, comparison must be relative and will consider run time (with associated computational stability) along with stability of predictive inference. Indeed, Section 5 below illustrates model performance with various choices of m.
2.5. Non-Gaussian first-stage models
There are two typical non-Gaussian first-stage settings:
binary response at locations modelled by using logit or probit regression and
count data at locations modelled by using Poisson regression.
Diggle et al. (1998) unified the use of generalized linear models in spatial data contexts. See also Lin et al. (2000), Kammann and Wand (2003) and Banerjee et al. (2004). Essentially we replace model (1) with the assumption that E[Y(s)] is linear on a transformed scale, i.e. η (s) ≡ g{E[Y(s)]} = xT(s)β + w(s) where g(·) is a suitable link function. With the Gaussian first stage, we can marginalize over the ws to achieve the covariance matrix τ2 I + cTC*−1c. Though this matrix is n × n, using the Sherman–Woodbury result (Harville (1997); also see Section 4), inversion requires only C*−1. With, say, a binary or Poisson first stage, such marginalization is precluded; we must update the ws in running our Gibbs sampler. Using the predictive process, we must update only the m × 1 vector w*.
A little more clarification may be useful. As described in the previous paragraph, the resulting model would take the form Πi p{Y(si)|β, w*, φ} p(w*|σ2, φ) p(β, φ, σ2). Though w* is only m × 1, updating this vector through its full conditional distribution may be awkward owing to the way that w* enters the likelihood. Computations can be simplified by introducing a small amount of pure error to let η(s) ≡ g{E[Y(s)]} = xT(s)β + w(s) + ε(s) where the ε(s) ~IIDN(0, τ2) with τ2 known and very small. The full model takes the form
The full conditional distribution for w* is now multivariate normal and the η(si) are conditionally independent. General categorical data settings can be treated by using these ideas.
2.6. Spatiotemporal versions
There are various spatiotemporal contexts in which predictive processes can be introduced to render computation feasible. We illustrate three of them here. First, we generalize model (1) to
| (5) |
for s ∈ D and t ∈ [0, T ]. In model (5), the εs are, again, pure error terms, the x(s, t) are local space–time covariate vectors and β is a coefficient vector, which is here assumed constant over space and time but can be spatially and/or temporally varying (see Section 3). We have replaced the spatial random effects w(s) with space–time random effects w(s, t) that come from a Gaussian process with covariance function cov{w(s, t), w(s′, t′)} ≡ C(s, s′; t, t′). There has been recent discussion regarding valid non-separable space–time covariance functions; see, for example, Stein (2005) and discussion therein. Now, we assume data Y(si, ti), i = 1, 2, …, n, where n can be very large because there are many distinct locations, times or both. In any event, the predictive process will be defined analogously to that above: w̃(s, t) = c(s, t)TC*−1w* where now w* is an m × 1 vector associated with m knots over D × [0, T] having covariance matrix C* and c(s, t) is the vector of covariances of w(s, t) with the entries in w*. The spatiotemporal predictive process model w̃(s, t) will enjoy the same properties as w̃(s). Now, the issue of knot selection arises over D × [0, T].
Next, suppose that we discretize time to, say, t = 1, 2, …, T. Now, we would write the response as Yt (s) and the random effects as wt (s). Dynamic evolution of wt (s) is natural, leading to a spatial dynamic model as discussed in, for example, Gelfand et al. (2005). In one scenario the data may arise as a time series of spatial processes, i.e. there is a conceptual time series at each location s ∈ D. Alternatively, it may arise as cross-sectional data, i.e. there is a set of locations that are associated with each time point and these can differ from time point to time point. In the latter case, we can expect an explosion of locations as time goes on. Use of predictive process modelling, defined through a dynamic sequence of sharing the same knots, enables us to handle this.
Finally, predictive processes offer an alternative to the dimension reduction approach to space–time Kalman filtering that was presented by Wikle and Cressie (1999). With time discretized, they envisioned evolution through a discretized integrodifferential equation with spatially structured noise, i.e.
with hs a location interaction function and η a spatially coloured error process. wt (s) is decomposed as where the φk (s)s are deterministic orthonormal basis functions and the as are mean 0 time series. Then, each hs has a basis representation in the φs, i.e. where the bs are unknown. A dynamic model for the k × 1 vector at driven by a linear transformation of the spatial noise process η(s) results. Instead of the above decomposition for wt (s), we would introduce a predictive process model using . We replace the projection onto an arbitrary basis with a projection based on a desired covariance specification.
3. Multivariate predictive process modelling
The multivariate predictive process extends the preceding concepts to multivariate Gaussian processes. A k × 1 multivariate Gaussian process, which is written as w(s) ~ MVGPk {0, Γw(·)} with , is specified by its cross-covariance function Γw(s, s′) which is defined for any pair of locations as the k × k matrix . When s = s′, Γw(s, s) is precisely the dispersion matrix for the elements of w(s). For any integer n and any collection of sites s1, …, sn, we write the multivariate realizations as a kn × 1 vector with w ~ MVN(0, Σw), where . A valid cross-covariance function ensures that Σw is positive definite. In practice, cross-covariances will involve spatial parameters θ and we shall write Γ(s, s′; θ).
Analogous to the univariate setting, we again consider a set of knots 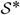 and denote by w* the realizations of w(s) over
and denote by w* the realizations of w(s) over 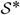 . Then the multivariate predictive process is defined as
. Then the multivariate predictive process is defined as
| (6) |
where
is k × mk and
is the mk × mk dispersion matrix of w*. Equation (6) shows that w̃(s) is a zero-mean multivariate predictive process (k × 1) with cross-covariance matrix given by Γw̃(s, s′) = 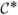 (s; θ)
(s; θ) 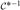 (θ)
(θ) 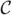 (s′; θ). w̃(s) has properties that are analogous to its univariate counterpart. Its realizations over a finite set with more than m locations have singular joint distributions. A multivariate analogue to equation (4) is immediate, showing that the multivariate predictive process is an interpolator with
for any
. Also, the optimality property in terms of the KL metric carries through.
(s′; θ). w̃(s) has properties that are analogous to its univariate counterpart. Its realizations over a finite set with more than m locations have singular joint distributions. A multivariate analogue to equation (4) is immediate, showing that the multivariate predictive process is an interpolator with
for any
. Also, the optimality property in terms of the KL metric carries through.
Specification of the process requires only Γw(s, s′; θ) along with 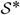 . Here, we adopt a spatially adaptive version of the ‘linear model of co-regionalization’ (Wackernagel, 2006; Gelfand et al., 2004). We model the parent process to be a (possibly) space varying linear transformation w(s) = A(s) v(s), where
and each υi(s) is an independent Gaussian process with unit variance and correlation function ρi(s, s′). Thus, v(s) ~ MVGP{0, Γv (s, s′)} has a diagonal cross-covariance
and yields a valid non-stationary cross-covariance Γw(s, s′) = A(s) Γv (s, s′) AT(s′) for w(s). In general, w(s) is non-stationary even when v(s) is. When A(s) = A is constant, w(s) inherits stationarity from v(s); Γw(s − s′) = AΓv (s − s′)AT. Regardless, as in the one-dimensional case, the induced multivariate predictive process is non-stationary.
. Here, we adopt a spatially adaptive version of the ‘linear model of co-regionalization’ (Wackernagel, 2006; Gelfand et al., 2004). We model the parent process to be a (possibly) space varying linear transformation w(s) = A(s) v(s), where
and each υi(s) is an independent Gaussian process with unit variance and correlation function ρi(s, s′). Thus, v(s) ~ MVGP{0, Γv (s, s′)} has a diagonal cross-covariance
and yields a valid non-stationary cross-covariance Γw(s, s′) = A(s) Γv (s, s′) AT(s′) for w(s). In general, w(s) is non-stationary even when v(s) is. When A(s) = A is constant, w(s) inherits stationarity from v(s); Γw(s − s′) = AΓv (s − s′)AT. Regardless, as in the one-dimensional case, the induced multivariate predictive process is non-stationary.
Since Γw(s, s) = A(s) AT(s), without loss of generality we can assume that is a lower triangular square root; the one-to-one correspondence between the elements of A(s) and Γw(s, s) is well known (see, for example, Harville (1997), page 229). Thus, A(s) determines the association between the elements of w(s) within s. Choices for modelling A(s) include an inverse spatial–Wishart process for A(s) AT(s) (Gelfand et al., 2004) or elementwise modelling with Gaussian and log-Gaussian processes. When stationarity is assumed (so A(s) = A) we could either assign a prior, e.g. inverse Wishart, to AAT or could further parameterize it in terms of eigenvalues and the Givens angles which are themselves assigned hyperpriors (Daniels and Kass, 1999).
We point out that this approach may accrue further benefits in computing 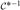 . Letting
and
, we have
. Letting
and
, we have 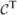 =
= 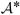 Σv*
Σv* 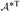 . Since
, this requires m k × k triangular inversions. Turning to Σv*, the diagonal Γv delivers a sparse structure. Permuting the elements of v* to stack the realizations of the υi(s)s over
. Since
, this requires m k × k triangular inversions. Turning to Σv*, the diagonal Γv delivers a sparse structure. Permuting the elements of v* to stack the realizations of the υi(s)s over 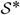 yields
, where
. Since P−1 = PT, the computational complexity resides in the inversion of k m × m symmetric correlation matrices,
, rather than a km × km matrix.
yields
, where
. Since P−1 = PT, the computational complexity resides in the inversion of k m × m symmetric correlation matrices,
, rather than a km × km matrix.
Now, suppose that each location s yields observations on q dependent variables given by a q × 1 vector . For each Yl(s), we also observe a pl × 1 vector of regressors xl(s). Thus, for each location we have q univariate spatial regression equations. They can be combined into a multivariate regression model that is written as
| (7) |
where XT(s) is a q × p matrix ( ) having a block diagonal structure with its lth diagonal being the 1 × pl vector . Note that β = (β1, …, βp)T is a p × 1 vector of regression coefficients with βl being the pl × 1 vector of regression coefficients corresponding to . The spatial effects w(s) form a k × 1 coefficient vector of the q × k design matrix ZT(s), where w(s) ~ MVGP{0, Γw(·, ·)}. The q × 1 vector ε(s) follows an MVN(0, Ψ) distribution modelling the measurement error effect with dispersion matrix Ψ. Model (7) acts as a general framework admitting several spatial models. For instance, letting k = q and ZT(s) = Iq leads to the multivariate analogue of model (1) where w(s) acts as a spatially varying intercept. However, we could envision all coefficients to be spatially varying and set k = p with ZT(s) = XT(s). This yields multivariate spatially varying coefficients, which are multivariate analogues of those discussed in Gelfand et al. (2003). Banerjee et al. (2004), chapter 7, discussed model-based spatial interpolation using model (7) when there are locations where one or several of a multivariate datum are missing. The predictive process versions would simply replace w(s) with w̃ (s) in model (7).
4. Bayesian implementation and computational issues
For fitting the predictive process model corresponding to model (7), we form the data equation
| (8) |
where
is the nq × 1 response vector,
is the nq × p matrix of regressors, β is the p × 1 vector of regression coefficients,
is nq × nk,
is nk × mk and 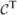 (θ) and w* are as described in Section 3. Given priors, model fitting employs a Gibbs sampler with Metropolis steps using the marginalized likelihood MVN{Xβ, ℤT
(θ) and w* are as described in Section 3. Given priors, model fitting employs a Gibbs sampler with Metropolis steps using the marginalized likelihood MVN{Xβ, ℤT 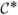 (θ)
(θ) 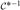 (θ)
(θ) 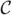 (θ)ℤ+ In ⊗ Ψ}, after integrating out w*.
(θ)ℤ+ In ⊗ Ψ}, after integrating out w*.
To complete hierarchical specifications, customarily we set β ~ MVN(μβ, Σβ), whereas Ψ could be assigned an inverse Wishart prior although, more commonly, independence of pure error for the different responses at each site is adopted, yielding a diagonal
with
. Also, 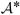 is unknown and needs to be stochastically specified. For A constant,
is unknown and needs to be stochastically specified. For A constant, 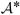 = In ⊗ A and we model AAT with an inverse Wishart prior. Under stationarity,
and we need to assign priors on
. This will again depend on the choice of correlation functions. In general, the spatial decay parameters are weakly identifiable and prior specifications become somewhat delicate. Reasonably informative priors are needed for satisfactory MCMC behaviour. Priors for the decay parameters are set relatively to the size of D, e.g. prior means that imply the spatial ranges to be a chosen fraction of the maximum distance. For the Matérn correlation function, the smoothness parameter ν is typically assigned a prior support of (0, 2) as the data can rarely inform about smoothness of higher orders.
= In ⊗ A and we model AAT with an inverse Wishart prior. Under stationarity,
and we need to assign priors on
. This will again depend on the choice of correlation functions. In general, the spatial decay parameters are weakly identifiable and prior specifications become somewhat delicate. Reasonably informative priors are needed for satisfactory MCMC behaviour. Priors for the decay parameters are set relatively to the size of D, e.g. prior means that imply the spatial ranges to be a chosen fraction of the maximum distance. For the Matérn correlation function, the smoothness parameter ν is typically assigned a prior support of (0, 2) as the data can rarely inform about smoothness of higher orders.
We obtain L samples, say , from p(Ω|data) ∝ p(β) p(A) p(θ) p(Y|β, A, θ, Ψ), where Ω= (β, A, θ, Ψ). Sampling proceeds by first updating βθfrom an MVN(μβ|·, Σβ|·) distribution with
and mean
The remaining parameters are updated by using Metropolis steps, possibly using block updates (e.g. all the parameters in Ψ in one block and those in A in another). Typically, random-walk Metropolis steps with (multivariate) normal proposals are adopted; since all parameters with positive support are converted to their logarithms, some Jacobian computation is needed. For instance, although we assign an inverted Wishart prior to AAT, in the Metropolis update we update A, which requires transforming the prior by the Jacobian .
This scheme requires the determinant and inverse of (ℤT 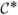 (θ)
(θ) 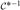 (θ)
(θ) 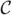 (θ)ℤ + In ⊗ Ψ), which is nq × nq. These tasks are accomplished efficiently in terms of only mk × mk matrices by using Sherman–Woodbury–Morrison-type computations (e.g. Harville (1997)) that evaluate the determinant as |Ψ|n|
(θ)ℤ + In ⊗ Ψ), which is nq × nq. These tasks are accomplished efficiently in terms of only mk × mk matrices by using Sherman–Woodbury–Morrison-type computations (e.g. Harville (1997)) that evaluate the determinant as |Ψ|n|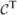 (θ) +
(θ) + 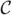 (θ)ℤ(In ⊗ Ψ−1)ℤT
(θ)ℤ(In ⊗ Ψ−1)ℤT 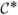 (θ)|/|
(θ)|/|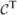 (θ)| and the inverse as
(θ)| and the inverse as
Note that, in updating Ω by using the marginal model, the w*s are not sampled. However, with first-stage Gaussian models the posterior samples of w can be recovered by sampling from
by using composition since we have posterior samples from p(Ω|data) and the first distribution under the integral is a multivariate normal distribution. The sampling is one for one with Ω(l), yielding w*(l) and hence samples w̃(l) = 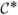 (θ(l))
(θ(l)) 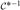 (θ(l))w*(l) as well. For predicting Y(s0) at a new location s0, the w*(l)s produce w̃(l)(s0). Then, Y(l)(s0) is sampled by using model (7) with Ω(l) and w̃(l)(s0).
(θ(l))w*(l) as well. For predicting Y(s0) at a new location s0, the w*(l)s produce w̃(l)(s0). Then, Y(l)(s0) is sampled by using model (7) with Ω(l) and w̃(l)(s0).
The Sherman–Woodbury–Morrison matrix identities have been used in other low rank kriging approaches with marginalized likelihoods, e.g. Cressie and Johannesson (2008). With the likelihood in equation (8) we could avoid marginalizing over the (m × 1)-dimensional vector w* and instead update by using its full conditional distribution (multivariate normal when the first-stage likelihood is Gaussian). Of course, generally, the marginalized sampler achieves faster convergence. However, for models whose first-stage likelihood is non-Gaussian (as we discussed in Section 2.5), marginalization is not feasible, we must update the w*, and the Sherman–Wood-bury–Morrison formula plays no role.
5. Illustrations
Our predictive process implementations were written in C++, leveraging processor-optimized BLAS, sparse BLAS and LAPACK routines (www.netlib.org) for the required matrix computations. The most demanding model (involving 28 500 spatial effects) took approximately 46 h to deliver its entire inferential output involving 15 000 MCMC iterations on a single 3.06-GHz Intel Xeon processor with 4.0 Gbytes of random-access memory running Debian LINUX. Convergence diagnostics and other posterior summarizations were implemented within the R statistical environment (http://cran.r-project.us.org) employing the CODA package.
5.1. Simulation studies
We present two simulation examples. The first example (Section 5.1.1) involves 3000 locations and an anisotropic random field where we estimate the parent model itself to offer comparisons with the predictive process models, whereas the second (Section 5.1.2) is a much larger example with 15 000 locations and a more challenging non-stationary spatial structure that precludes estimation of the parent model with the computational specifications above.
5.1.1. Simulation example 1
Here, we simulated the response Y(s) by using model (1) from 3000 irregularly scattered locations over a 1000 × 1000 domain. In this case we can fit model (1) without resorting to the predictive process; comparison with various choices of m and knot design can be made. The regression component included only an intercept, whereas the spatial process w(s) was generated by using a stationary anisotropic Matérn covariance function given by
where d(s, s′) = (s − s′)TΣ−1(s − s′). We further parameterize Σ= G(ψ) Λ GT(ψ) where G(ψ) is a rotation matrix with angle ψ and Λ is the diagonal matrix with positive diagonal elements λ2. The vector θ= (ν, ψ, Λ) denotes the spatial parameters: ν controls the smoothness, whereas the rate of spatial decay is controlled by the λ2s.
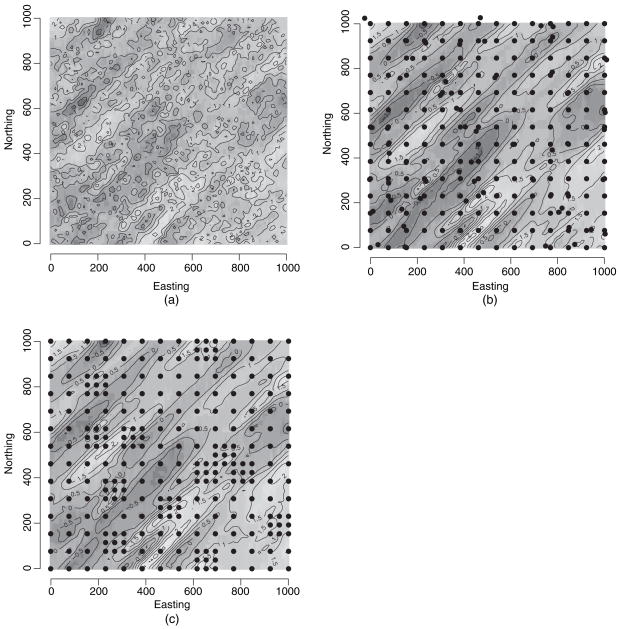
Parameter values generating the simulated process are given in the second column in Table 1. Fig. 3(a) clearly shows the dominant 45.0° orientation of the process. We assign a flat prior to the intercept β, a U(0, π/2) prior for the rotation parameter ψ and a U(10, 400) prior for the λs. This support on the λs corresponds to about 30–1200 distance units for the effective spatial ranges along those axes (i.e. approximately 3λ is the distance at which the correlation drops to 0.05). The remaining process parameters σ2 and τ2 followed IG(2, 1) and IG(2, 0.2) priors respectively. We kept ν = 0.5 as fixed for the analysis in this subsection.
Table 1.
Parameter credible intervals, 50% (2.5% 97.5%), and predictive validation for the predictive process models by using a regular grid of knots†
| Parameter | True value | Results for the following numbers of knots: |
|||
|---|---|---|---|---|---|
| 144 | 256 | 529 | 3000 | ||
| β | 1.0 | 0.94 (0.56, 1.35) | 0.73 (0.34, 1.16) | 0.77 (0.34, 1.21) | 0.72 (0.43, 1.01) |
| ψ | 45.0° | 36.45 (34.66, 38.14) | 42.09 (37.62, 45.80) | 43.83 (40.93, 46.77) | 44.47 (43.18, 45.74) |
| λ1 | 300.0 | 390.4 (330.1, 399.6) | 279.0 (258.6, 311.0) | 323.1 (289.9, 349.0) | 302.6 (275.5, 330.2) |
| λ2 | 50.0 | 62.42 (52.7, 71.99) | 79.41 (59.77, 103.40) | 61.47 (41.50, 84.30) | 47.45 (40.03, 55.13) |
| σ2 | 1.0 | 1.14 (0.87, 1.49) | 1.02 (0.80, 1.54) | 1.31 (0.83, 1.52) | 0.95 (0.87, 1.05) |
| τ2 | 0.2 | 0.56 (0.53, 0.59) | 0.45 (0.42, 0.49) | 0.26 (0.21, 0.29) | 0.16 (0.13, 0.22) |
| Prediction | 95% | 91% | 92% | 93% | 95% |
Entries in italics indicate where the true value is missed. The last column shows results for the parent model.
Fig. 3.
(a) Simulated stationary anisotropic process generated with 3000 sites by using the parameter values given in Table 1, (b) interpolated (posterior mean) surface for the predictive process model overlaid with 256 knots in the lattice plus close pair configuration and (c) interpolated (posterior mean) surface for the predictive process model overlaid with 256 knots in the lattice plus infill configuration
We carried out several simulation experiments with varying knot sizes and configurations. In addition to regular lattices or grids, we also explored two different knot configurations which were described by Diggle and Lophaven (2006) in spatial design contexts. The first, which is called the lattice plus close pairs configuration, considers a regular k × k lattice of knots but then intensifies this grid by randomly choosing m′ of these lattice points and then placing an additional knot close to each of them—say within a circle having the lattice point as centre and a radius that is some fraction of the spacing on the lattice. The second configuration, which is called the lattice plus infill design, also starts with knots on a regular k × k lattice but now intensifies the grid by placing a more finely spaced lattice within m′ randomly chosen cells of the original lattice.
Here we present illustrations with the above designs with knot sizes of 144, 256 and 529. For the uniform grid these were arranged on a square lattice with knots spaced at 91.0, 66.8 and 45.5 units respectively. For the close pair and infill designs we held the number of knots at 144, 256 and 529 (for a fair comparison with the uniform lattice) and adjusted the lattice accordingly. For instance, Fig. 3(b) shows the close pair design with 256 knots by randomly selecting 60 knots from a 14 × 14 lattice and then adding a knot to each of them to form close pairs. Similarly, Fig. 3(c) shows the infill design with 256 knots formed by randomly selecting 12 cells of the original 14 × 14 lattice and adding a finely spaced sublattice in each of these cells. This results in five additional knots in each of those cells, making the total number of knots 142 + 12 × 5 = 256.
For each knot configuration, three parallel MCMC chains were run for 5000 iterations each. Convergence diagnostics revealed 1000 iterations to be sufficient for initial burn-in so the remaining 12 000 (4000 × 3) samples from each chain were used for posterior inference. Table 1 provides parameter estimates for the three knot intensities on a uniform grid along with those from the parent model, i.e. with each of the 3000 locations as a knot, whereas Tables 2 and 3 provide those from the close pair and infill designs respectively. Central processor unit times with the machine specifications that were described earlier were approximately 0.75 h, 1.5 h and 4.25 h for the144, 256 and 529 knot models respectively, whereas for the parent model it was approximately 18 h.
Table 2.
Parameter credible intervals, 50% (2.5% 97.5%), for the predictive process models with 3000 locations by using the lattice plus close pair design with different knot intensities†
| Parameter | True value | Results for the following numbers of knots: |
||
|---|---|---|---|---|
| 144 | 256 | 529 | ||
| β | 1.0 | 1.07 (0.77, 1.40) | 0.63 (0.26, 1.01) | 0.72 (0.35, 1.10) |
| ψ | 45.0′ | 40.58 (38.65, 42.59) | 44.77 (42.68, 46.74) | 43.76 (42.35, 45.98) |
| λ1 | 300.0 | 386.62 (344.01, 399.69) | 291.29 (267.57, 386.78) | 330.00 (295.33, 358.85) |
| λ2 | 50.0 | 49.24 (43.86, 54.58) | 53.40 (46.20, 60.72) | 51.08 (43.98, 60.07) |
| σ2 | 1.0 | 1.34 (1.0, 1.70) | 1.42 (0.89, 1.65) | 1.39 (0.91, 1.66) |
| τ2 | 0.2 | 0.55 (0.52, 0.58) | 0.45 (0.43, 0.48) | 0.24 (0.22, 0.29) |
| Prediction | 95% | 91% | 92% | 92% |
Entries in italics indicate where the true value is missed. The last row provides the empirical coverage of 95% prediction intervals for a set of 100 hold-out locations.
Table 3.
Parameter credible intervals, 50% (2.5% 97.5%), for the predictive process models with 3000 locations by using the lattice plus infill design†
| Parameter | True value | Results for the following numbers of knots: |
||
|---|---|---|---|---|
| 144 | 256 | 529 | ||
| β | 1.0 | 1.18 (0.76, 1.66) | 0.77 (0.39, 1.17) | 0.71 (0.39, 1.02) |
| ψ | 45.0° | 42.12 (40.70, 43.21) | 45.55 (44.46, 46.75) | 43.45 (41.89, 45.13) |
| λ1 | 300.0 | 392.34 (343.23, 399.74) | 316.73 (270.11, 368.57) | 345.85 (286.32, 369.79) |
| λ2 | 50.0 | 58.26 (45.79, 66.46) | 56.05 (47.97, 64.27) | 47.31 (39.64, 55.38) |
| σ2 | 1.0 | 1.72 (0.98, 2.66) | 1.35 (0.92, 1.76) | 1.14 (0.94, 1.37) |
| τ2 | 0.2 | 0.57 (0.54, 0.60) | 0.48 (0.45, 0.50) | 0.25 (0.22, 0.29) |
| Prediction | 95% | 92% | 92% | 93% |
Entries in italics indicate where the true value is missed. The last row provides the empirical coverage of 95% prediction intervals for a set of 100 hold-out locations.
All the tables reveal the improvements in estimation with increasing number of knots, irrespectively of the design. In all three tables we find substantial overlaps in the credible intervals of the predictive process models with those from the original model. Although 144 knots are adequate for capturing the regression term β, higher knot densities are required for capturing the anisotropic field parameters and the nugget variance τ2. The nugget variance, in particular, is a difficult parameter to estimate here with much of the variability being dominated by σ2, yet we see a substantial improvement in moving from 256 knots to 529 knots. Tables 1–3 suggest that estimation is more sensitive to the number of knots than to the underlying design, although the close pair designs appear to improve estimation of the shorter ranges as seen for λ2 with 256 knots. Predictions, however, are much more robust as is seen from the last row of Tables 1–3. These show the empirical coverage of 95% prediction intervals based on a hold-out set of 100 locations. The coverage, although expected to be lower given that there is less uncertainty in the predictive process than in the parent process (Section 2.3), is only slightly so.
5.1.2. Simulation example 2
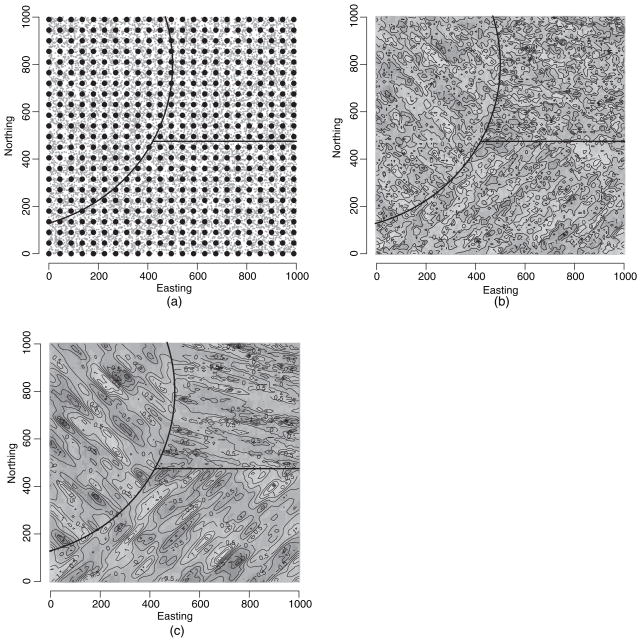
We now present a more complex illustration with 15 000 locations (a fivefold increase from the preceding example) and a more complex non-stationary random field, which renders evaluation of the full model computationally infeasible. We now divide the domain into three subregions and generate Y(s) from these 15 000 locations over a 1000 × 1000 domain by using model (1) and assign a different intercept to each of the three regions. Fig. 4(a) shows the domain and sampling locations along with 529 overlaid knots. We extend the covariance function in the preceding example to a non-stationary version (Paciorek and Schervish, 2006)
Fig. 4.
(a) Three-region domain with 15000 simulated sites (·) beneath the 529 knots (●) that were used to estimate the parent process, (b) interpolated (mean) surface for the ordinary least squares residuals and (c) interpolated (posterior mean) surface for the spatial residuals from the predictive process model with 529 knots
where
with ΣD(s) now varying over space and D(s) indicating the subregion (1, 2 or 3) where s belongs. We again parameterize ΣD(s) = G(ψD(s))Λ GT(ψD(s)) but now acknowledge the rotation angle to depend on the location. The second column in Table 4 presents the parameter values that were used to generate the data. The region-specific parameters are labelled 1–3 clockwise starting with the rounded region in the north-west.
Table 4.
Parameter credible intervals, 50% (2.5% 97.5%), for three knot intensities with 15000 locations†
| Parameter | True value | Results for the following numbers of knots: |
||
|---|---|---|---|---|
| 144 | 256 | 529 | ||
| β1 | 50.0 | 50.00 (49.91, 50.07) | 49.99 (49.86, 50.12) | 49.96 (49.82, 50.10) |
| θ1 | 45.0° | 35.90 (31.93, 39.46) | 31.52 (28.02, 44.81) | 50.80 (41.73, 59.23) |
| λ1,1 | 16.69 | 16.87 (16.51, 17.03) | 16.91 (16.62, 17.66) | 16.86 (16.67, 17.02) |
| λ1,2 | 66.7 | 66.70 (66.56, 66.92) | 66.65 (66.48, 66.79) | 66.63 (66.45, 66.83) |
| β2 | 10.0 | 10.05 (10.00, 10.08) | 10.0 (9.95, 10.04) | 10.05 (9.99, 10.11) |
| θ2 | 75.0° | 70.97 (67.95, 73.15) | 77.59 (75.62, 79.03) | 72.07 (70.11, 75.84) |
| λ2,1 | 5.0 | 5.87 (5.19, 5.94) | 5.53 (4.96, 6.02) | 5.10 (4.86, 5.55) |
| λ2,2 | 50.0 | 49.83 (49.65, 50.40) | 49.82 (49.51, 50.29) | 50.17 (49.88, 50.54) |
| β3 | 25.0 | 24.88 (24.80, 24.96) | 24.84 (24.73, 24.95) | 25.04 (24.90, 25.18) |
| θ3 | 45.0° | 57.12 (54.71, 59.55) | 36.70 (33.51, 42.59) | 38.41 (33.63, 56.98) |
| λ3,1 | 66.7 | 66.63 (66.43, 67.23) | 66.69 (66.47, 66.85) | 66.73 (66.63, 66.97) |
| λ3,2 | 16.69 | 16.674 (16.53, 16.83) | 16.80 (16.65, 17.40) | 16.77 (16.55, 17.36) |
| ν | 0.5 | 0.26 (0.25, 0.37) | 0.43 (0.26, 0.59) | 0.56 (0.45, 0.67) |
| σ2 | 1.0 | 2.46 (1.98, 3.13) | 1.99 (1.00, 3.27) | 1.66 (0.97, 2.09) |
| τ2 | 0.2 | 1.03 (1.01, 1.06) | 0.94 (0.88, 0.96) | 0.53 (0.24, 0.86) |
| Predictive validation | 95% | 90% | 90% | 92% |
Entries in italics indicate where the interval misses the true value. The last row provides the empirical coverage of 95% prediction intervals for a set of 100 hold-out locations.
We assign flat priors to the three intercepts, a U(0, π/2) prior for each of the three region-specific rotation parameters and U(1.7, 300) prior for the λs (corresponding to about 5–900 distance units as spatial range). The remaining process parameters ν, σ2 and τ2 followed U(0, 2), IG(2, 1) and IG(2, 0.2) priors respectively. We again employed uniform grids as well as the close pair and lattice-plus-infill grids with 144, 256 and 529 knots; central processor unit times here were approximately 6 h, 15 h and 33 h respectively. The inference did not vary significantly for these designs, so we present the results for the uniform grid only. For each model, we ran three initially overdispersed chains for 3000 iterations. Convergence diagnostics revealed that 1000 iterations were sufficient for initial burn-in so the remaining 2000 samples from each chain were used for posterior inference.
Table 4 presents the parameter estimates. The overall picture is quite similar to that in Section 5.1.1 with increasing knot density leading to improved estimation, especially for the spatial and nugget variances. Although 144 knots, with their larger separation between knots, provided an inadequate approximation to the underlying non-stationary structure, the models with 256 and 529 knots performed much better, especially the latter. The last row of Table 4 shows the empirical coverage of 95% prediction intervals based on a hold-out set of 100 locations. The coverage, although expected to be lower given that there is less uncertainty in the predictive process than in the parent process (Section 2.3), is only slightly lower. Fig. 4(b) is an image plot of ordinary least squares residuals, and Fig. 4(c) is the spatial residual surface from the predictive process model with 529 knots. These images were constructed by using the same interpolation and contouring algorithm (the MBA package in R). They reveal the smoothing in Fig. 4(c) that is brought about by the predictive process; Fig. 4(c) also makes the region-specific anisotropy more apparent. Indeed, note that regions 1 and 3 have the same rotation angle (θ1 = θ2 = 45°) but reciprocal range parameters (i.e. λ1,1 = λ3,2 = 16.69 and λ1,2 = λ3,1 = 66.7), causing the opposite orientations of the contours, whereas in region 2 the shorter spatial range (λ2,1) yields more concentrated contours along the 75° axis.
5.2. Spatially varying regression example
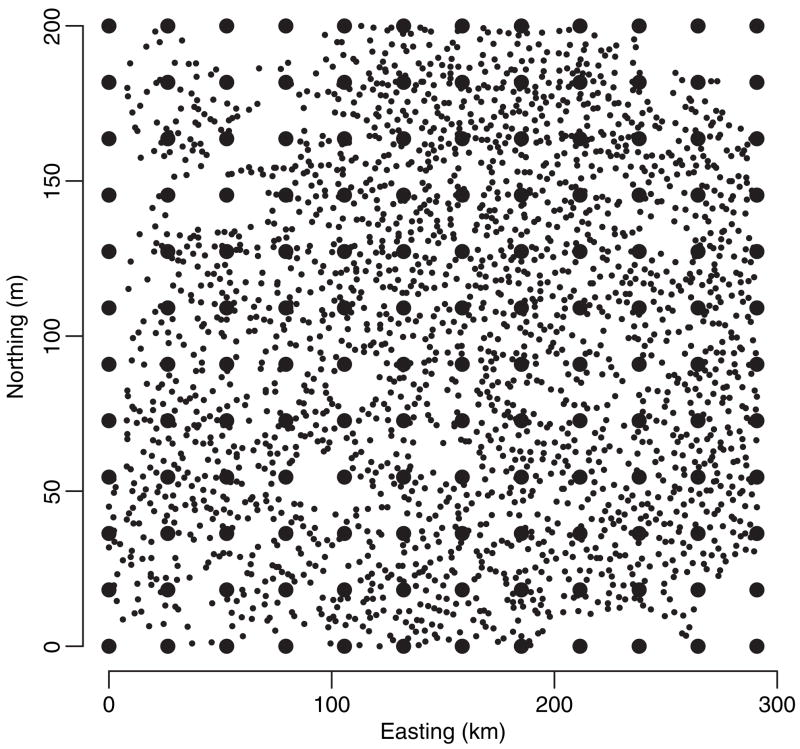
Spatial modelling of forest biomass and other variables that are related to measurements of current carbon stocks and flux have recently attracted much attention for quantifying the current and future ecological and economic viability of forest landscapes. Interest often lies in detecting how biomass changes across the landscape (as a continuous surface) and how homogeneous it is across the region. We consider point-referenced biomass (log-transformed) data observed at 9500 locations that were obtained from the US Department of Agriculture Forest Service ‘Forest inventory and analysis’ programme. Each location yields measurements on biomass from trees in that location and two regressors: the cross-sectional area of all stems above 1.37 m from the ground (basal area) and the number of tree stems (stem density) at that location. Often spatial interpolation of biomass is sought at locations by using either typical values of basal area and stem density measurements or, where available, values from historic data sources. Fig. 5 shows the domain and sampling locations with 144 knots overlaid.
Fig. 5.
Spatial distribution of forest inventory sites: the 9500 georeferenced forest inventory sites (•) overlain with 144 knots (●)
Spatial regression models with only a spatially varying intercept are often found inadequate in explaining biomass. Instead, we opt for spatially varying regression coefficients for the intercept as well as the two regressors (Gelfand et al., 2003). More specifically, we use model (7) with q = 1, k = p = 3 and ZT(s) = XT(s), resulting in Y(s) = xT(s) β̃ (s) + ε(s), where β̃ (s) = β + w(s) are spatially varying regression coefficients. Though we have a univariate response for the model, the modelling for the dependent coefficient surfaces introduces a multivariate spatial Gaussian process w(s). The power of hierarchical modelling is revealed here; we can learn about this multivariate process without ever seeing any observations from it. We cast this into equation (8) as described in Section 4 with n = 9 and n = 500, q = 1, k = p = 3 (yielding 28 500 spatial effects) and . The advantages of such models have been detailed in, for example, Gelfand et al. (2003), who recognized the computational infeasibility of these models with large spatial data sets and resorted to separable covariance structures that restrict the same spatial decay to all the coefficients. Predictive process models enable us to move beyond separability and to employ the more general co-regionalization structures that were discussed in Section 3.
The parameters that we estimate are Ω= (β, A, θ, Ψ), where β is 3 × 1, Ψ is In ⊗ τ2 and A is a 3 × 3 lower triangular matrix. The parameters in the β-vector comprise the model intercept β0, the basal area β1 and tree stem density β2. We assume the Matérn correlation function which adds three φs and three νs. A flat prior was assigned to β. We used the nugget value from an empirical semivariogram calculated by using ordinary least squares residuals to centre the IG(2,0.03) prior that was assigned to the pure error term, τ2. Γ(0) = AAT was assigned an IW{4, diag(0.04)} prior, where, again, semivariograms of the response, scaled by the regressors, were used to guide the magnitude of the scale hyperparameters. Following the discussion in Section 4, we assume that ν ~ U(0, 2) and φ ~ U(3 × 10−4, 0.003), which, if ν = 0.5, describes an effective spatial range interval of 1–100 km.
Predictive process models with 64, 144 and 256 knots were each run with three parallel chains for 5000 iterations (central processor unit times 10 h, 18 h and 46 h respectively). They revealed fairly rapid convergence, benefiting from marginalized likelihoods, with a burn-in of 1000 iterations. The remaining 12 000 samples (4000 × 3) were retained for posterior analysis. (With only 36 knots the distance between adjacent knots (40 km) seemed to exceed the effective spatial ranges that were supported by the data and led to unreliable convergence of process parameters.) Table 5 provides the posterior inference for model parameters corresponding to the various knot densities. The regression in the data is seen to be quite strong with basal area having a significant negative effect and stem density having a significant positive effect on the response. We see a hint of negative association between two of the pairs of coefficient processes and positive association in the other. A pronounced nugget effect (τ2) is seen. The spatial decay parameters for the various slope parameters are quite similar, indicating, perhaps, that a separable covariance model would be adequate. Some shrinkage is seen in the smoothness parameter. These estimates are generally robust across the different knot densities; further increasing the number of knots delivers little gain in estimation.
Table 5.
Inference summary, 50% (2.5%, 97.5%), for spatially varying coefficient models based on three knot densities
| Parameter | Results for the following numbers of knots: |
||
|---|---|---|---|
| 64 | 144 | 256 | |
| β0 | −0.117 (−0.168, 0.034) | −0.115 (−0.163, 0.022) | −0.113 (−0.163, 0.027) |
| β1 | −0.200 (−0.242, −0.029) | −0.200 (−0.243, −0.049) | −0.200 (−0.246, −0.040) |
| β2 | 1.266 (1.213, 1.428) | 1.260 (1.211, 1.412) | 1.262 (1.204, 1.438) |
| Γ00 | 0.006 (0.005, 0.010) | 0.005 (0.004, 0.007) | 0.005 (0.004, 0.007) |
| Γ11 | 0.004 (0.002, 0.019) | 0.005 (0.002, 0.017) | 0.004 (0.002, 0.016) |
| Γ22 | 0.006 (0.004, 0.018) | 0.008 (0.006, 0.021) | 0.005 (0.004, 0.016) |
| Γ1,0/√ (Γ0,0Γ1,1) | −0.449 (−0.740, 0.847) | −0.576 (−0.768, 0.880) | −0.732 (−0.783, 0.817) |
| Γ2,0/√ (Γ0,0Γ2,2) | 0.132 (−0.729, 0.964) | 0.345 (−0.591, 0.971) | 0.673 (−0.014, 0.971) |
| Γ2,1/√(Γ1,1Γ2,2) | −0.843 (−0.944, 0.980) | −0.842 (−0.939, 0.972) | −0.849 (−0.946, 0.973) |
| τ2 | 0.041 (0.041, 0.044) | 0.040 (0.040, 0.043) | 0.041 (0.040, 0.043) |
| φβ0 | 8× 10−5 (7× 10−5, 0.00009) | 7× 10−5 (7× 10−5, 0.00008) | 7× 10−5 (6× 10−5, 0.00010) |
| φβ1 | 7× 10−5 (6× 10−5, 0.00011) | 7× 10−5 (7× 10−5, 0.00012) | 7× 10−5 (6× 10−5, 0.00011) |
| φβ2 | 9× 10−5 (7× 10−5, 0.00011) | 1× 10−4 (8× 10−5, 0.00013) | 9× 10−5 (7× 10−5, 0.00012) |
| νβ0 | 0.426 (0.387, 0.489) | 0.471 (0.366, 0.596) | 0.391 (0.287, 0.569) |
| νβ1 | 0.437 (0.407, 0.534) | 0.408 (0.391, 0.487) | 0.383 (0.330, 0.511) |
| νβ2 | 0.471 (0.422, 0.547) | 0.443 (0.372, 0.548) | 0.432 (0.397, 0.502) |
| Rangeβ0 (km) | 36.405 (30.817, 46.381) | 38.373 (31.946, 46.661) | 35.238 (28.695, 45.151) |
| Rangeβ1 (km) | 42.139 (25.965, 58.568) | 37.811 (22.765, 46.444) | 37.931 (26.622, 48.112) |
| Rangeβ2 (km) | 32.825 (26.040, 57.579) | 29.241 (19.920, 43.809) | 31.311 (22.697, 60.225) |
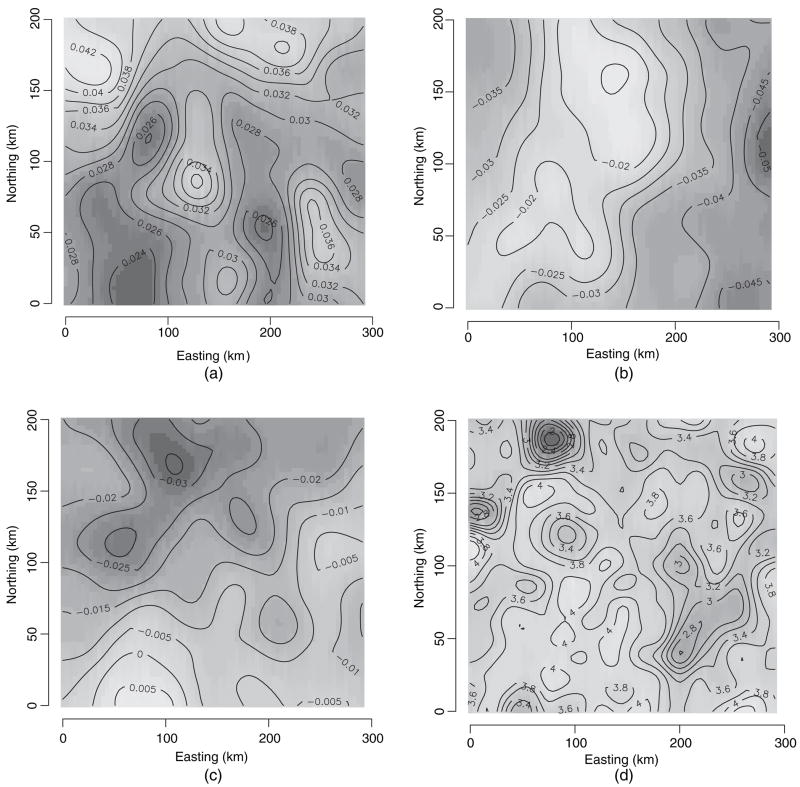
Fig. 6 shows the image contour plots of the residual coefficient processes (i.e. the w̃ (s)s corresponding to each coefficient) as well as that for biomass (using typical values for basal area and stem density). The intercept process seems to be absorbing much of the spatial variation; the two covariate processes are smoother. The predicted biomass surface offers a spatially smoothed version, adjusted for covariates, compared with what is obtained by interpolating the raw response data (which are not shown) and helps to articulate better the zones of higher biomass.
Fig. 6.
Posterior (mean) estimates of spatial surfaces from the spatially varying coefficients model: (a) interpolated surface for the space varying intercept parameter; (b) interpolated surface for the space varying basal area parameter; (c) interpolated surface for the space varying stem density parameter; (d) interpolated surface for predicted (log-)biomass
6. Summarizing remarks and future work
We have addressed the problem of fitting desired hierarchical spatial modelling specifications to large data sets. To do so, we propose simply to replace the parent spatial process specification by its induced predictive process specification. One need not digress from the modelling objectives to think about choices of basis functions, or kernels or alignment algorithms for the locations. The resulting class of models essentially falls under the generalized linear mixed model framework (as in equation (8)).
As in existing low rank kriging approaches, knot selection is required and as we demonstrated in Section 5.1 some sensitivity to the number of knots is expected. Although for most applications a reasonable grid of knots should lead to robust inference, with fewer knots the separation between them increases and estimating random fields with fine scale spatial dependence becomes difficult. Indeed, learning about fine scale spatial dependence is always a challenge (see, for example, Cressie (1993), page 114).
Our examples in Section 5.1 showed that even with fairly complex underlying spatial structures the predictive process model could effectively capture most of the spatial parameters with 529 knots (irrespectively of whether the total number of locations was 3000 or 15 000). A further challenge which was noted in our simulated examples was the situation where the variance components ratio (σ2/τ2 = 5.0) is large so that estimation of τ2 becomes difficult. One possible remedy is reparameterizing (σ2, τ2) in terms of their ratio and the larger variance component (see, for example, Diggle and Ribeiro (2007)). Another option to explore is to modify the predictive process as ẇ (s) = w̃(s) + ε̃(s), where ε̃(s) is an independent Gaussian process with variance C(s, s) − cT(s; θ) C*−1(θ) c(s; θ).
Finally, the goal has been dimension reduction to facilitate likelihood evaluation, to facilitate simulation-based model fitting. Although we have employed MCMC methods to fit these models, faster alternatives that avoid MCMC sampling can also be employed (see, for example, Rue et al. (2007)). In fact, the predictive process approach within a full MCMC implementation is perhaps limited to the order of 104 observations on modest single-processor machines (see Section 5); strategies that are empirical Bayesian in flavour, combining deterministic and simulation aspects, are likely to be the future for fitting very large space–time data sets. Indeed, it is quite common to find that spatial data sets, especially in scientific studies of large-scale global phenomena, contain far more locations than the illustrations here. For instance, Cressie and Johannesson (2008) worked with data of the order of hundreds of thousands. It is also quite common to find space–time data sets with a very large number of distinct time points, possibly with different time points observed at different locations (e.g. real estate transactions). With multiple processors, substantial gains in computing efficiency can be realized through parallel processing of matrix operations (see, for example, Heroux et al. (2006)). We intend to investigate extensively the potential of predictive process models in such settings. More immediately, we intend to migrate our lower level C++ code to the existing spBayes (http://cran.r-project.org) package in the R environment to facilitate accessibility to predictive process models.
Acknowledgments
The work of the first author was supported in part by National Science Foundation grant DMS-0706870, that of the first and second authors was supported in part by National Institutes of Health grant 1-R01-CA95995, that of the third author was partly supported by National Institutes of Health grant 2-R01-ES07750 and that of the last author was supported in part by National Science Foundation grant DEB05-16198.
Appendix A
Consider the set-up in Section 2.3. Letting  be the class of all probability densities satisfying the conditional independence relation q(Y|wa) = q(Y|w*), we want to find the q ∈
be the class of all probability densities satisfying the conditional independence relation q(Y|wa) = q(Y|w*), we want to find the q ∈  that minimizes the relative entropy or KL divergence. The above conditional independence restriction for q implies that
that minimizes the relative entropy or KL divergence. The above conditional independence restriction for q implies that
Using this, we can simplify the KL metric as follows:
Since log{p(Y)} is a constant, minimizing the KL divergence is equivalent to minimizing the first term in this expression. But that expectation must itself be non-negative (in fact it can again be looked on as a KL divergence up to a proportionality constant) so the numerator and denominator must be proportional. The minimizing q(·) density must satisfy q(w*|Y) ∝ p(w*) exp(Ew|w*~p[log{p(Y|wa)}]), which implies that q(Y|w*) ∝ exp(Ew|w*~p[log{p(Y|wa)}]). The remainder follows from standard multivariate normal theory by noting that p(Y|wa) is an MVN(Xβ + w, τ2In) distribution and p(w*, w) is MVN(0, Σwa) whence exp(Ew|w*[log{p(Y|wa)}]) identifies itself as the desired normal density up to a normalizing constant.
Contributor Information
Sudipto Banerjee, University of Minnesota, Minneapolis, USA.
Alan E. Gelfand, Duke University, Durham, USA
Andrew O. Finley, Michigan State University, East Lansing, USA
Huiyan Sang, Duke University, Durham, USA.
References
- Banerjee S, Carlin BP, Gelfand AE. Hierarchical Modeling and Analysis for Spatial Data. Boca Raton: Chapman and Hall–CRC; 2004. [Google Scholar]
- Cornford D, Csato L, Opper M. Sequential, Bayesian geostatistics: a principled method for large datasets. Geogr Anal. 2005;37:183–199. [Google Scholar]
- Cressie NAC. Statistics for Spatial Data. 2. New York: Wiley; 1993. [Google Scholar]
- Cressie N, Johannesson G. Fixed rank kriging for very large data sets. J R Statist Soc B. 2008;70:209–226. [Google Scholar]
- Csato L. PhD Thesis. Aston University; Birmingham: 2002. Gaussian processes—iterative sparse approximation. [Google Scholar]
- Daniels MJ, Kass RE. Nonconjugate Bayesian estimation of covariance matrices and its use in hierarchical models. J Am Statist Ass. 1999;94:1254–1263. [Google Scholar]
- Diggle P, Lophaven S. Bayesian geostatistical design. Scand J Statist. 2006;33:53–64. [Google Scholar]
- Diggle PJ, Ribeiro PJ. Model-based Geostatistics. New York: Springer; 2007. [Google Scholar]
- Diggle PJ, Tawn JA, Moyeed RA. Model-based geostatistics (with discussion) Appl Statist. 1998;47:299–350. [Google Scholar]
- Fuentes M. Approximate likelihood for large irregularly spaced spatial data. J Am Statist Ass. 2007;102:321–331. doi: 10.1198/016214506000000852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelfand AE, Banerjee S, Gamerman D. Spatial process modelling for univariate and multivariate dynamic spatial data. Environmetrics. 2005;16:465–479. [Google Scholar]
- Gelfand AE, Kim H, Sirmans CF, Banerjee S. Spatial modelling with spatially varying coefficient processes. J Am Statist Ass. 2003;98:387–396. doi: 10.1198/016214503000170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelfand AE, Schmidt A, Banerjee S, Sirmans CF. Nonstationary multivariate process modelling through spatially varying coregionalization (with discussion) Test. 2004;13:1–50. [Google Scholar]
- Harville DA. Matrix Algebra from a Statistician’s Perspective. New York: Springer; 1997. [Google Scholar]
- Heroux MA, Padma R, Simon HD, editors. Parallel Processing for Scientific Computing. Philadelphia: Society for Industrial and Applied Mathematics; 2006. [Google Scholar]
- Higdon D. Technical Report. Institute of Statistics and Decision Sciences, Duke University; Durham: 2001. Space and space time modeling using process convolutions. [Google Scholar]
- Higdon D, Swall J, Kern J. Non-Stationary spatial modeling. In: Bernardo JM, Berger JO, Dawid AP, Smith AFM, editors. Bayesian Statistics. 6. Oxford: Oxford University Press; 1999. pp. 761–768. [Google Scholar]
- Jones RH, Zhang Y. Models for continuous stationary space-time processes. In: Diggle PJ, Warren WG, Wolfinger RD, editors. Modelling Longitudinal and Spatially Correlated Data: Methods, Applications and Future Directions. New York: Springer; 1997. [Google Scholar]
- Kammann EE, Wand MP. Geoadditive models. Appl Statist. 2003;52:1–18. [Google Scholar]
- Lin X, Wahba G, Xiang D, Gao F, Klein R, Klein B. Smoothing spline ANOVA models for large data sets with Bernoulli observations and the randomized GACV. Ann Statist. 2000;28:1570–1600. [Google Scholar]
- Lopes HF, Salazar E, Gamerman D. Technical Report. Universidade Federal do Rio de Janeiro; Rio de Janeiro: 2006. Spatial dynamic factor analysis. [Google Scholar]
- Møller J, editor. Spatial Statistics and Computational Methods. New York: Springer; 2003. [Google Scholar]
- Nychka D, Saltzman N. Design of air-quality monitoring networks. Lect Notes Statist. 1998;132:51–76. [Google Scholar]
- Paciorek CJ. Computational techniques for spatial logistic regression with large datasets. Computnl Statist Data Anal. 2007;51:3631–3653. doi: 10.1016/j.csda.2006.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paciorek CJ, Schervish MJ. Spatial modelling using a new class of nonstationary covariance functions. Environmetrics. 2006;17:483–506. doi: 10.1002/env.785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsay JO, Silverman BW. Functional Data Analysis. New York: Springer; 2005. [Google Scholar]
- Rasmussen CE, Williams CKI. Gaussian Processes for Machine Learning. Cambridge: MIT Press; 2006. [Google Scholar]
- Robert CP, Casella G. Monte Carlo Statistical Methods. 2. New York: Springer; 2005. [Google Scholar]
- Rue H, Held L. Gaussian Markov Random Fields: Theory and Applications. Boca Raton: Chapman and Hall–CRC; 2006. [Google Scholar]
- Rue H, Martino S, Chopin N. Technical Report. Norwegian University of Science and Technology; Trondheim: 2007. Approximate Bayesian inference for latent Gaussian models using integrated nested Laplace approximations. [Google Scholar]
- Rue H, Tjelmeland H. Fitting Gaussian Markov Random fields to Gaussian fields. Scand J Statist. 2002;29:31–49. [Google Scholar]
- Ruppert D, Wand MP, Carroll RJ. Semiparametric Regression. Cambridge: Cambridge University Press; 2003. [Google Scholar]
- Schabenberger O, Gotway CA. Statistical Methods for Spatial Data Analysis. Boca Raton: Chapman and Hall–CRC; 2004. [Google Scholar]
- Seeger M, Williams CKI, Lawrence N. Fast forward selection to speed up sparse Gaussian process regression. In: Bishop CM, Frey BJ, editors. Proc. 9th Int. Wrkshp Artificial Intelligence and Statistics; KeyWest: Society for Artificial Intelligence and Statistics; 2003. [Google Scholar]
- Stein ML. Interpolation of Spatial Data: Some Theory of Kriging. New York: Springer; 1999. [Google Scholar]
- Stein ML. Space-time covariance functions. J Am Statist Ass. 2005;100:310–321. [Google Scholar]
- Stein ML. Spatial variation of total column ozone on a global scale. Ann Appl Statist. 2007;1:191–210. [Google Scholar]
- Stein ML, Chi Z, Welty LJ. Approximating likelihoods for large spatial data sets. J R Statist Soc B. 2004;66:275–296. [Google Scholar]
- Stevens DL, Jr, Olsen AR. Spatially balanced sampling of natural resources. J Am Statist Ass. 2004;99:262–278. [Google Scholar]
- Switzer P. Non-stationary spatial covariances estimated from monitoring data. In: Armstrong M, editor. Geostatistics. Vol. 1. Dordrecht; Kluwer: 1989. pp. 127–138. [Google Scholar]
- Vecchia AV. Estimation and model identification for continuous spatial processes. J R Statist Soc B. 1988;50:297–312. [Google Scholar]
- Ver Hoef JM, Cressie NAC, Barry RP. Flexible spatial models based on the fast Fourier transform (FFT) for cokriging. J Computnl Graph Statist. 2004;13:265–282. [Google Scholar]
- Wackernagel H. Multivariate Geostatistics: an Introduction with Applications. 3. New York: Springer; 2006. [Google Scholar]
- Wahba G. Spline Models for Observational Data. Philadelphia: Society for Industrial and Applied Mathematics; 1990. [Google Scholar]
- Wikle C, Cressie N. A dimension-reduced approach to space-time Kalman filtering. Biometrika. 1999;86:815–829. [Google Scholar]
- Xia G, Gelfand AE. Technical Report. Institute of Statistics and Decision Sciences, Duke University; Durham: 2006. Stationary process approximation for the analysis of large spatial datasets. [Google Scholar]
- Xia G, Miranda ML, Gelfand AE. Approximately optimal spatial design approaches for environmental health data. Environmetrics. 2006;17:363–385. [Google Scholar]