Frequency Spectrum of Transepithelial Potential Difference Reveals Transport-Related Oscillations

Abstract

How epithelia transport fluid is a fundamental issue that is unresolved. Explanations offered include molecular engines, local transcellular osmosis, local paracellular osmosis, and paracellular fluid transport. On the basis of experimental and theoretical work done on corneal endothelium, a fluid transporting epithelium, we suggest electroosmotic coupling at the level of the intercellular junctions driven by the transendothelial electrical potential difference as an explanation of paracellular fluid transport. We collect frequency spectra of that potential difference in real-time. For what we believe is the first time for any epithelium, we report that, unexpectedly, the potential difference displays oscillations at many characteristic frequencies. We also show that on both stimulating cell activity and inhibiting ion transport mechanisms, there are corresponding changes in the oscillations amplitudes that mirror changes known previously in rates of fluid transport. We believe these findings provide a novel tool to study the kinetics of electrogenic elements such as channels and transporters, which from this evidence would give rise to current oscillations with characteristic periods going from 150 ms to 8 s.

Introduction

The enigma of how some epithelia transport fluid is central to physiology remains unsolved to this day. Explanations offered include molecular engines (1), local transcellular osmosis (2,3), local paracellular osmosis (4), and paracellular fluid transport (5). Working with a fluid-transporting epithelium, the corneal endothelium, we have recently suggested a variant of paracellular fluid transport in which the trans-tissue electrical potential difference would generate a standing current that would drive fluid transport by electroosmotic coupling at the intercellular junctions (6,7; see also Fig. S1 in the Supporting Material). We have advanced experimental (6,8) and theoretical (9,10) support for the idea of electroosmosis.

It is unclear how the osmolarity of an epithelial paracellular secretion could be regulated. In this regard, the possibility that fluid transport may involve cyclical cell activity has been raised (7,11). During the last decade, evidence for oscillatory processes in cells of fluid-transporting epithelia has appeared occasionally. As examples, there are oscillations induced by cholinergic agonists in cytosolic calcium and volume of acinar cells of rat salivary gland (11), and oscillations in membrane potential (f = 0.09 Hz, or period (τ) = 11 s) of hyperpolarized bovine ciliary pigmented epithelial cells (12). More recently, it has been shown that the induced Cl⁻ secretion linked to salivary secretion of fluid is oscillatory (13), with frequencies of ∼0.3 Hz (τ = 3.3 s), and oscillations of transepithelial electrical potential difference have been described (14) for Malpighian tubule, an insect fluid-transporting epithelium (τ = 30 s).

For completeness, there is a report on ouabain-inhibitable 0.25 Hz fluctuations in short-circuit current across frog skin (15) and another one on fluctuations attributed to the flicker of Na⁺ channels shown by noise analysis of records of transepithelial electrical currents (16), but no frequency spectra in real-time have been determined for any epithelium in the past.

There is some evidence that fluids transported by rat salivary gland (17) and corneal endothelium (6,7) can be hypotonic, whereas the fluid transport overall is isotonic (6,18). Because it seems conceivable that the fluid transported might be subject to periodic adjustments of its osmolarity, we looked for cyclic phenomena connected to fluid transport across rabbit corneal endothelium.

In the average, the electrical potential difference across corneal endothelium (transendothelial electrical potential difference (TEPD)) correlates linearly with the rate of fluid transport (8). Yet, temporal records of the TEPD are curiously noisy, as Fig. 2 exemplifies. Therefore, we decided to investigate the frequency spectrum of the TEPD, for which we incorporated into our experimental setup a fast Fourier transform (FFT) spectrometer. We report that the TEPD is the result of overlapping cyclic phenomena. The oscillatory processes that underlie the TEPD line up in a characteristic spectrum of frequencies between 0 and 15 Hz. We also find that, crucially, during experimental manipulations, the amplitudes of the TEPD oscillations correspond to rates of endothelial fluid transport known previously.

Figure 2.

Transendothelial electrical potential difference as a function of time. The upper curve (TEPD) shows a 10-min segment of a representative experiment (n = 43). The lower curve (CTRL) depicts a record of the potential difference obtained with the solution-filled chamber (R ∼ 15 KΩ; n = 8).

Methods

Experiments were done using in vitro rabbit corneal endothelial preparations and techniques for the recording of electrical potential difference that have been described previously (19,20). Corneas were obtained from New Zealand albino rabbits (∼2 kg) using institutional procedures. Rabbits were euthanized by injecting a sodium pentobarbital solution into the marginal ear vein. The eyes were enucleated immediately. Fig. 1 shows a scheme of the experimental setup. With reference to it, the cornea was deepithelialized and dissected using the method of Dikstein and Maurice (21), and was mounted in a jacketed Ussing chamber (T = 37°C). The endothelial and stromal surfaces were bathed with an air-bubbled HEPES-HCO₃⁻ solution containing (in mmol/L): 104.4 NaCl, 26.2 NaHCO₃, 3.8 KCl, 1 NaH₂PO₄, 0.78 MgSO₄, 1.7 CaCl₂, 6.9 glucose, and 20 HEPES Na. The cornea was supported by a hemispherical stainless steel net, and a hydrostatic pressure difference of 3 cm H₂O applied to the aqueous side helped maintain corneal curvature. Interruption of the bubbling for short periods did not affect the frequency spectra mentioned below.

Figure 1.

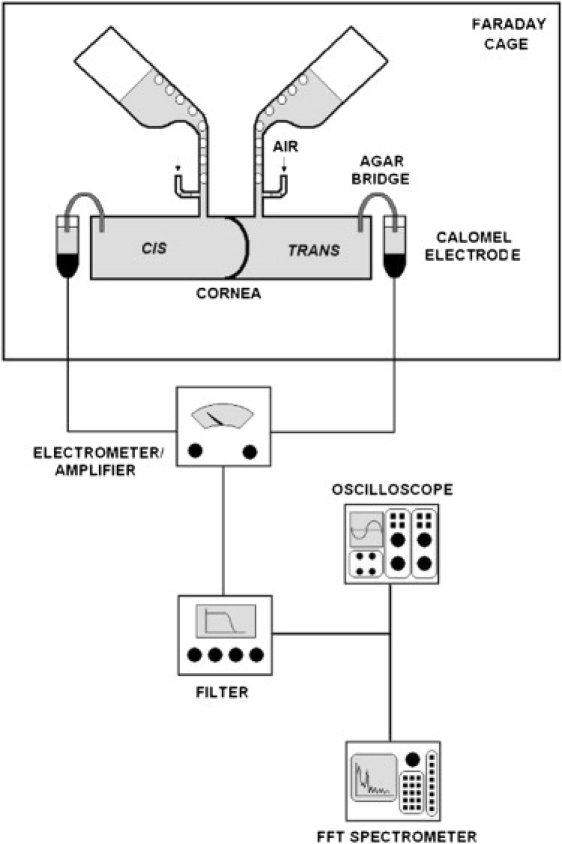
Schematic diagram of the Ussing chamber and instruments used. Cis, endothelial side; trans, stromal side. Temperature-control jackets are not shown. They surround the bottom chambers (Lucite) and the aeration funnels (glass). A stainless-steel hemispherical wire net (not shown) on the trans hemichamber supports the corneal stroma.

Fig. 1 also shows the recording setup schematically. The TEPD was determined with a differential electrometer amplifier (Model 604; Keithley Institutes, Cleveland, OH) connected to calomel electrodes and salt bridges. The TEPD (typically 0.5–1.5 mV) was amplified by the electrometer by 10³ and sent through a filter (HI/LO 1020F; Rockland Labs, Tappan, NY; low pass cutoff = 10 KHz). This processed signal was displayed on an oscilloscope, and sent to the spectrum analyzer (FFT SR 760; Stanford Research Systems, Sunnyvale, CA) and to a recorder.

All chemicals were from Sigma-Aldrich (St. Louis, MO). Inhibitors were dissolved in DMSO to obtain stock solutions, which were then diluted into the bathing solution to a final concentration of 0.1% DMSO. At this concentration, DMSO does not affect the preparation (8). ATP was dissolved in distilled water. All agent additions were made on the endothelial side (cis side, Fig. 1). All plots were done using Origin (Version 7; OriginLab, Northampton, MA); deviations are mean ± SE. Each experiment was done in a different corneal preparation.

Results

Control experiments and spectrum analysis

As mentioned above, temporal records of the TEPD appear noisy. We investigated whether such noise could simply arise from unspecified electrical fields in the surroundings. We obtained temporal records of the electrical potential difference between the two experimental hemichambers (Fig. 1) filled with saline with and without corneal preparations mounted in them. As Fig. 2 exemplifies, the noisy behavior was observed only with preparations present. By comparison, controls with only solution in the chambers were remarkably flat.

Subsequently, we investigated the frequency spectrum of the potential difference. As Fig. 3 shows (in its main plot), the control spectrum generated by the solution-filled chamber is a flat baseline with negligible noise, which rules out possible artifacts from electrodes, electrometer, filter or spectrometer. In contrast, the TEPD showed an unexpectedly rich spectrum of oscillations at several characteristic frequency regions.

Figure 3.

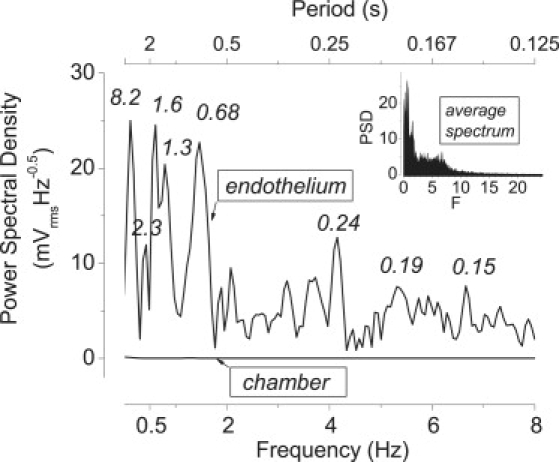
Frequency spectrum of the TEPD. For the curve shown in the insert, the frequency spectra of 10 experiments were averaged (average multiple curves routine; Origin). In the main plot, only the frequency domain of most interest is shown. The upper curve (endothelium) shows an individual frequency spectrum of the TEPD. Numbers near the peaks denote their periods τ in s. The lower line (chamber) shows a control spectrum of the potential difference obtained with the solution-filled chamber (n = 87).

Exploratory experiments showed that there were no detectable oscillations >20 Hz. Hence, given the fixed spectrometer settings, all subsequent recordings were made for the frequency domain 0–24.4 Hz, for which each spectrum acquisition time is 16.4 s. From this, the slowest detectable frequency is 1/16.4 s, or 0.061 Hz; smaller frequencies are considered dc (0 Hz). For a general picture, we focus on the average spectrum of the TEPD. This came from pooling all spectra obtained under initial conditions in the total of 43 experiments carried out; it is shown in Fig. 3, inset. Starting at zero frequency, there are high-amplitude peaks for frequencies <2 Hz, followed by a plateau up to ∼7 Hz. The spectrum amplitude goes subsequently down to the baseline (no detectable cell electric activity) for frequencies >15–20 Hz. In the time domain, the larger amplitude peaks correspond to periods of half to several seconds, and the plateau to ∼140 ms to half a second.

To reduce the noise, typically 10 consecutive spectra within an experiment were averaged. We term this an “individual” spectrum. Fig. 3 (main plot) shows an example of this under control (initial) conditions. The graph shows several peaks of high amplitude (nominal periods of 8.2, 2.3, 1.6, 1.3, and 0.68 s). A total of 46 experiments were done including all manipulations.

For each given preparation, its spectrum was practically unchanged over several hours. On the other hand, although the pattern of amplitudes was always recognizable and presented the largest peaks between 0 and 2 Hz, the frequencies of the main peaks could vary somewhat among different experiments. Hence, the amplitude of the peaks is somewhat broadened by averaging among experiments. To quantify the amplitude at given frequencies, it is plausible to analyze them in individual spectra. Still, the interpretation of individual peak frequencies has to be done in the context of the spectrometer settings. The FFT methodology used is exceedingly useful and possibly crucial in that it is fast and allows one to follow the progression of frequency spectra in real-time during an experiment. However, the price one pays for that convenience is that the frequencies thus determined have a spread. Each amplitude value we report in individual spectra actually corresponds to the average amplitude of a bin of frequencies to the left (less than) the spectrum value. In our case, the width of the frequency bins is 0.061 Hz (24.4 Hz/400 data points). To give an example, a typical low-frequency peak we detect falls at 0.122 Hz, which nominally corresponds to a period of 8.2 s (Fig. 3). However, frequencies in that bin would actually go from 0.061–0.122 Hz, with corresponding periods of 16.4–8.2 s. Similarly, amplitudes at all other frequency points in the spectra recorded correspond to the nominal frequencies minus the bin width range. Averaging among different experiments was done binwise, conserving the same boundaries among frequency bins, which is how the spectrometer presented its data. Such averaging was done for Figs. 4–7; it may give a more accurate picture of the global experimental behavior, but it does not remove the spread noted above. This needs to be considered to put the inherent physics in perspective.

Figure 4.

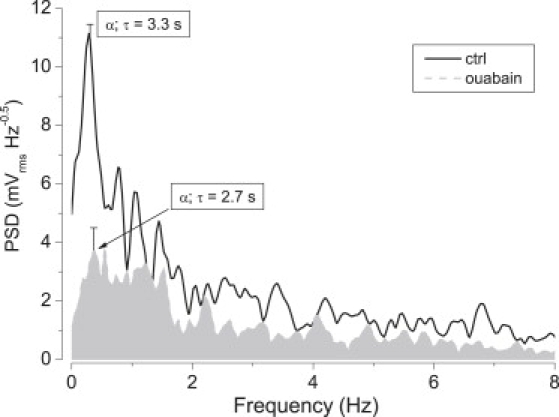
Effects of inhibition with ouabain. Curves are frequency spectra of TEPD before (solid line, control) and ∼10 min after the addition of 100 μM ouabain (dashed line, shaded area). Spectra are averaged (n = 6). Periods are shown for the corresponding highest low-frequency peaks (peak α); deviations are also shown for those peaks.

Figure 5.

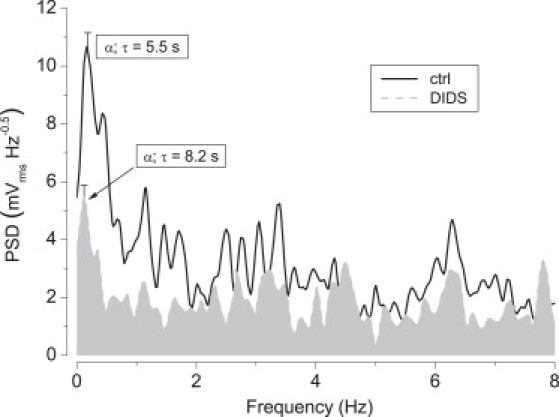
Effects of inhibition with DIDS. Frequency spectra of TEPD before (solid line, control) and ∼10 min after the addition of 100 μM DIDS (dashed line, shaded area). Curves represent the averages of eight experiments. Periods and deviations are shown for the α-peaks.

Figure 6.

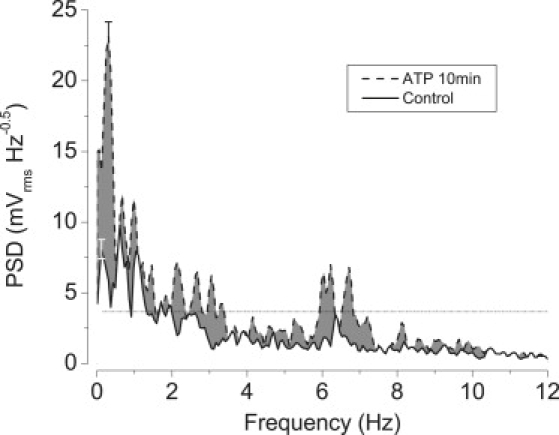
Effect of stimulation with ATP; averages of six experiments. Curves represent spectra under control conditions and 10 min after the addition of 100 μM ATP. Deviations are shown for the α-peaks. The area between the two curves (representing the stimulation by ATP) is shaded. An auxiliary horizontal line (dashed) is drawn at y = 3.6.

Figure 7.

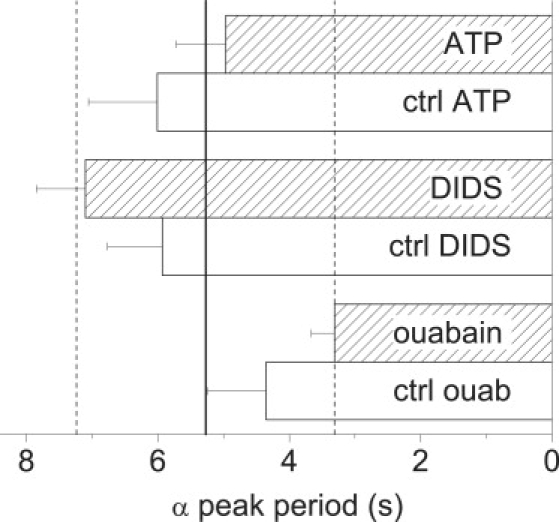
Bars denote averages of the periods for the α-peaks in the different groups of experiments. The vertical lines correspond to the average ± SE for all groups combined (5.3 ± 2.0 s).

Inhibitors that affect membrane transport fittingly decrease the amplitude of the oscillations

There are inhibitory agents known for years to decrease both TEPD and the rate of transendothelial fluid transport. Ouabain and the stilbenes (DIDS and SITS) are possibly the two best characterized. Ouabain, a blocker of the sodium pump, inhibits TEPD (19,22,23) and fluid transport (8,19,23,24). We used ouabain at 100 μM, a concentration that suffices for maximal effects on fluid transport (25). Stilbenes inhibit mainly sodium-bicarbonate cotransporters and chloride-bicarbonate exchangers; SITS inhibits TEPD by 64% (26), and DIDS inhibits transendothelial fluid transport (27,28) by some 52% (8) at the 100 μM concentration.

The effect of ouabain on the amplitude of TEPD oscillations is shown in Fig. 4. In the average of six successful experiments, ouabain caused a drastic decrease of between ∼50 and 70% in the amplitude of oscillations at most frequencies examined. In the remaining experiment (not considered), ouabain failed to inhibit the oscillations. The spectra were taken ∼8–10 min after ouabain challenge, at which times there remains some residual electrogenic activity by the cells, in particular in the area between 0 and 1.5 Hz. There is also a peak at 2.2 Hz that appears spared. For convenience, we label “peak α” the largest low-frequency peak. The highest inhibition due to ouabain was ∼70% for that α-peak, which had periods in the range of ∼3 s (Fig. 4).

The effect of DIDS on the amplitude of TEPD oscillations is shown in Fig. 5. In the average (n = 7), the α-peak occurred at 5.5 s in the control preparations, and at 8.2 s after challenge. As Fig. 5 exemplifies, DIDS produced a ∼50% decrease in the amplitude of that α-peak. At the other frequencies, although the general trend is toward some mild inhibition, there is remarkably well conserved activity as evidenced by peaks at 2.7, 3.2, 4.5, 6.3, and 7.8 Hz (with τ of ∼350, 300, 220, 160, and 130 ms, respectively).

The time course of the inhibitions can be appreciated in the Supporting Material (Fig. S3).

Stimulation increases the amplitude of the oscillations

P2Y2 receptors are present in corneal endothelium (29), and ATP mediates paracrine signaling in this tissue (30). Fittingly, we have reported recently that 100 μM ATP stimulates transendothelial fluid transport significantly (31). We find that addition of 100 μM ATP transiently increases TEPD by ∼25% (data not shown). Correspondingly, we also find that, as depicted in Fig. 6, the amplitude of the TEPD oscillations increases after ATP addition. The threefold increase in the amplitude of peak α is especially noteworthy, but large increases take place practically all across the spectrum.

This allows one to appreciate more clearly the three main groups of oscillations (Fig. 6). An auxiliary horizontal line marks an arbitrary threshold level. At the low frequency end, there is a group between 0 and ∼1 Hz, which exhibits the broad peak α at 0.3 Hz (τ = 3.3 s), by far the highest, and two other peaks at 0.67 and 0.98 Hz (τ of 1.5 and 1 s). This group extends further into lower frequencies, as there is a peak at 0.061 Hz (τ = 16.4 s). The middle group (“mid-frequencies”) is located between ∼2 and 3.5 Hz (τ of ∼280–500 ms), including five peaks (at 1.8, 2.1, 2.7, 3.1, and 3.4 Hz). Finally, the “high-frequency” group falls at ∼6–7.5 Hz (τ of ∼130–170 ms), including three peaks (at 6.0, 6.2, and 6.7 Hz).

The α-peak was invariably the largest one in all spectra, so the value of its period merits special attention. To this end, Fig. 7 gives averages and deviations for its periods in the different experimental groups. As can be seen, that value can vary rather widely; the average is 5.3 s, and the range (±1 SE) goes from 3.3 to 7.3 s. Empirically, in most of the experiments that peak was observed either at 3.3 s or at 8.2 s, but never at both simultaneously. Further considerations about the underlying cell processes are given in the Discussion.

Discussion

Characteristics of the TEPD oscillations observed

Transepithelial electrical potential differences have been treated in the literature largely as stable parameters. Instead, we find that the TEPD is the result of spontaneous oscillations with a reproducible spectrum of frequencies. In fact, as befits the Fourier theorem, the TEPD can be reconstructed by adding a number of sinusoids with the frequencies and amplitudes (Fig. S2).

As mentioned above, we find that the largest peak amplitudes (peak α) most often correspond to oscillations with periods that average 5.3 s (Fig. 7) and can range from 3.3 to 8.2 s. Such relatively wide range may correspond to the same electrogenic player(s) or process functioning at different frequencies. There are also significant oscillations with periods at or near 0.7 and 1.1 s, and these could appear together as in Figs. 3, 4, and 6. We discuss possible adjudication for these and the rest of the peaks below. To be noted, there may be additional endothelial electrical phenomena with periodicities slower than the 0.061 Hz lower limit we consider here.

The actual amplitudes (A) of the oscillations in voltage units are comparatively large. They can be computed from the power spectrum density (PSD) units given here:

$$A=\frac{{({\text{PSD}}^2\times \text{Bw})}^{0.5}}{\text{gain}},$$

where Bw (bandwidth) = 24.4 Hz, gain = 10³. For instance, the 25 mV_rms Hz^−0.5 peaks in Fig. 3 correspond to an amplitude of 123 μV_rms, or 18% of a typical TEPD of 700 μV. This is, of course, quite consistent with and actually accounts for the noisy character of the temporal TEPD recordings exemplified in Fig. 2. It seems important to stress this finding so that future similar readings will not be mistakenly dismissed as equipment-related artifacts.

TEPD oscillations and fluid transport

There is evidence consistent with transendothelial fluid transport being driven by electroosmotic coupling at the intercellular junctions (6,8). Our results are consistent with prior literature (7,9,32), as the amplitudes of the oscillations we see in TEPD at characteristic frequencies increase (with ATP at all frequencies; Fig. 6) and decrease (with ouabain at practically all frequencies; Fig. 4; with DIDS, preferentially at low frequencies; Fig. 5). The TEPD is the driving force for putative fluid flow. Hence, if inhibitors and stimulators affect fluid transport, the amplitude of the TEPD oscillations should be correspondingly affected. This is precisely what happens, which is suggestive and is entirely consistent with the prior literature concerning ionic movements and the dependency of fluid transport on them (7,9,32,33).

Putative osmolarity adjustments

From these results, the TEPD can present wide temporal oscillations (Fig. 2). Given that aquaporin 1 is expressed in corneal endothelium (34) plasma membranes (35), these cell membranes have comparatively high osmotic permeability (36,37). In addition, there is evidence (6) that indicates that the primary electroosmotic secretion could be hypotonic. Hence, adjustments of the osmolarity of the fluid in the cell vicinity are conceivable via local osmosis, and in light of these results they might occur, especially during the intervals at lower TEPD and concomitantly slower secretion.

Possible correlations between electrogenic elements and oscillation peaks

To analyze this point, we will refer to a scheme of endothelial electrogenic elements and their locations that was already used by us to model the endothelium (9), and is condensed here in Fig. 8. By doing pharmacological dissection, we have recently communicated (8) that 52%, 30%, and 18% of the fluid transport rate across rabbit corneal endothelium is respectively inhibited when bicarbonate-, sodium-, and chloride-carried currents across the apical membranes are eliminated. For this discussion, we obtained a separate estimate of the role of each electrogenic process by blocking each one of them in our endothelial model (9). Inhibited processes and corresponding percent theoretical TEPD inhibitions were (1): sodium-bicarbonate cotransporters, 51; sodium channels, 18; sodium pump, 18; potassium channels, 7; and chloride channels, 6. Hence, the simulation is consistent with the results of the pharmacological dissection below. Both point to sodium-bicarbonate cotransport as the main electrogenic player in this preparation.

Figure 8.

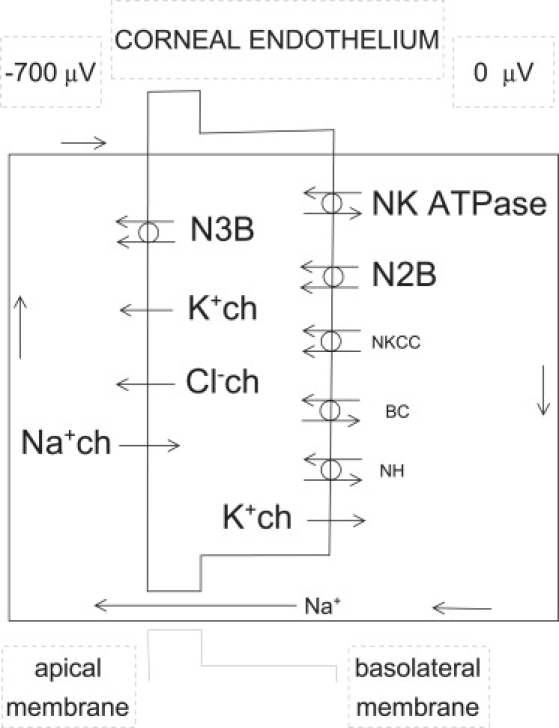
Corneal endothelial plasma membrane transporters and channels. Locations have been previously discussed (9). This simplified scheme shows only elements relevant to transcellular ionic flows. Abbreviations: ch, channel; N3B, 3:1 HCO₃⁻-Na⁺ cotransporter; N2B, 2:1 HCO₃⁻-Na⁺ cotransporter; N, Na⁺; K, K⁺; B, HCO₃⁻; C, Cl⁻; H, H⁺. Electrogenic elements are in large lettering. The local (open circuit) recirculating current is also shown, with its direction marked by arrows. Na⁺ ions preferentially carry the current through the junctions.

Sodium-bicarbonate cotransporters (NBCs)

In this connection, we note that both ouabain (Fig. 4) and DIDS (Fig. 5) inhibited the major low-frequency peaks (or α-peaks), which is consistent with them arising from sodium-bicarbonate cotransport activity. This point is further supported by the simulations shown in Fig. 9, in which both sodium-bicarbonate cotransporters were inhibited by ouabain and DIDS, as expected.

Figure 9.

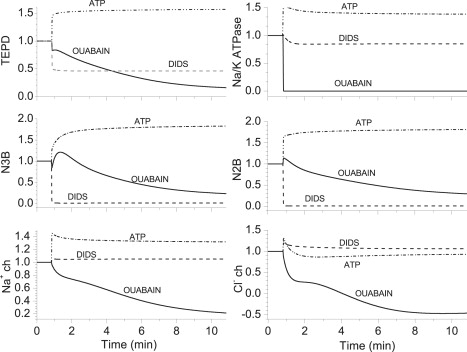
Simulation of the effects of ouabain and DIDS on parameters of the corneal endothelium using our computer program described previously that models the endothelium (9). The runs were set so that after a 50-s control interval, the relative permeabilities of the target elements changed as follows: for the ouabain case, the Na⁺/K⁺ ATPase from 1 to 0.0001; for the DIDS case, (a) the apical Na⁺-HCO₃⁻ cotransporter (N3B), (b) the basolateral Na⁺-HCO₃⁻ cotransporter (N2B), and (c) the basolateral Cl⁻/HCO₃⁻ exchanger, all from 1 to 0.01. For the ATP case, the relative permeabilities were increased by 50% for: (a) the Na⁺/K⁺ ATPase; (b) the N3B; (c) the N2B; (d) the Na⁺ channel, and (e) the Cl⁻ channel. The panels show the temporal changes in the relative turnover rates of (or fluxes through) several electrogenic elements of relevance. Na⁺ ch, Cl⁻ ch: Na⁺ and Cl⁻ channels. The simulations were run for 10 min after inhibition to approximate the times at which spectra were collected after exposure to the agents in actual experiments.

Other elements

We examine the oscillations >1 Hz. Exposure to DIDS (Fig. 5) left the two groups of peaks we termed mid-frequency (2–3.5 Hz) and high frequency (6–7.5 Hz) relatively spared. In terms of the accompanying model (Fig. 8), these might correspond to additional elements such as Na⁺ and Cl⁻ channel activities. This is supported by the literature (see below), and by the simulations of Fig. 9, which show those elements to be largely unaffected by DIDS. Curiously, both ouabain and DIDS left unaffected peaks around τ ∼ 1.3 s (Figs. 4 and 5), which might mean that there are ouabain-insensitive electrogenic elements still unaccounted for. The stimulation by ATP contributed to better delineate the peaks and reinforce the notion of three groups of peaks already observable in Figs. 3 and 5.

The possibility that mid- and high-frequency peaks might correspond to ionic channels has support in literature. Thus, in amygdala neurons, oscillations of 2–10 Hz sensitive to extracellular [Na⁺] and inhibited by tetrodotoxin have been described for the membrane potential (38). Similarly, the frequency spectrum of the membrane potential of the stellate neurons from entorhinal cortex shows a region of characteristic peaks between 3 and 12 Hz that was attributed to Na⁺ channel noise (39). As another example, in olivary neurons, subthreshold oscillations (4–6 Hz) in membrane potential and a resonance peak at 4 Hz were eliminated by Ca²⁺ conductance blockers or removal of external Ca²⁺ (40). In epithelial Na⁺ channels, gating frequencies of 5–10 Hz can be observed (41). For CFTR Cl⁻ channels, there are transition rates of ∼5–15 Hz (42), and gating frequencies >1 Hz (43). For this case, precise identification of the origins of mid- and high-frequency peaks will require further work.

The explanations we have considered this far attribute the observed TEPD oscillations to dynamic characteristics of transporters and channels. There is an alternative that merits discussion, namely, that the oscillations could be due to external signaling processes or biochemical oscillators. In this connection, there are mechanically induced [Ca²⁺]_i transients in corneal endothelium (44), but they occur in times scales of tens of seconds, which are too slow compared to those here. In other preparations, oscillations in [Ca²⁺]_i have periods that go from ∼1 s in the cardiac sinoatrial nodal cells (45) to 1–5 min (46,47). Similarly, in a recent review on biochemical oscillators (48), the fastest oscillations listed are of [Ca²⁺]_i, with periods >1 s. In distinction, the oscillations we describe here have periods between 150 ms and 8 s, so the lower end of our range is one order of magnitude faster. Hence, these TEPD oscillations might be connected with features of transporters/channels operations such as rate of supply of substrate, outward diffusion, and intrinsic transporter/channel kinetics, including possible agonist-mediated gating events (43) that might modify their transition rates.

In conclusion, for what we believe is the first time for any epithelium, we show that its electrical potential difference results from a superposition of oscillations with a recognizable frequency spectrum. The results indicate how the osmolarity of the secretion could be adjusted. The results also point to a fact of interest for other fields: electrogenic transporter/channel assemblies appear to operate at characteristic given frequencies, almost as biochemical oscillators. The current findings may open a window to observe the kinetics of electrogenic membrane transporter assemblies.